Bab 6 Rancangan Petak Terpisah (Split Plot Design)

Dalam percobaan dua faktor, kombinasi perlakuan belum tentu diacak secara sempurna terhadap unit percobaan. Pengacakan sempurna berarti semua kombinasi perlakuan dibuat dan diacak pada semua unit percobaan (atau pada suatu blok di Split Plot RAKL). Dalam suatu rancangan split plot, pengacakan dilakukan bertahap. Petak utama diacak terlebih dahulu, lalu faktor yang ditempatkan sebagai anak petak diacak di tiap petak utama. Rancangan ini dipilih karena beberapa alasan:

  1. Tingkatan kepentingan dari faktor yang dilibatkan. Di Tabel ANOVA, akan terlihat bahwa derajat bebas galat petak utama lebih kecil dari anak petak. Ini berarti faktor pembagi jumlah kuadrat galat akan lebih kecil di petak utama, sehingga kuadrat tengah galat bisa saja lebih besar. Berarti, keragaman (atau kesalahan yang muncul dari faktor acak) lebih besar di petak utama sehingga ketepatan uji di petak utama lebih rendah. Ini dapat terjadi jika peneliti lebih tertarik pada suatu efek (misal, dengan efek varietas daripada lokasi). Oleh karena itu, efek varietas yang harus diduga dengan lebih tepat menjadi anak petak.
  2. Nisbah pengaruh faktor. Jika satu faktor memiliki pengaruh besar, tidak perlu ketepatan tinggi untuk menangkap pengaruh tersebut. Misal diketahui bahan berpengaruh besar pada kualitas suatu pedang (misal, pedang baja lebih kuat dari pedang besi), dan pengaruh waktu tempa lebih kecil. Bahan dapat menjadi petak utama.
  3. Pengembangan dari percobaan yang sudah berjalan. Misal ada percobaan yang mengacak dosen-dosen ke kelas tertentu, lalu di dalam kelas tersebut peneliti tertarik melihat pengaruh bimbingan belajar. Oleh karena itu, kelas yang mengandung dosen menjadi petak utama, lalu bimbingan belajar diacak ke siswa yang menjadi anak petak.
  4. Kendala pengacakan di lapangan. Misal, salah satu faktor tidak bisa atau tidak efisien jika diacak secara karena taraf faktor membutuhkan unit yang besar. Misal, pengolahan lahan membutuhkan traktor, sehingga harus menjadi petak utama dan varietas menjadi anak petak.
  5. Lokasi menjadi petak utama dan perlakuan menjadi anak petak. Misal dicobakan varietas tanaman di kampus IPB Dramaga dan di kampus IPB Baranangsiang.
  6. Waktu (musim, tahun) menjadi petak utama, dan perlakuan menjadi anak petak. Semisal di diacak beberapa kegiatan besar untuk tiap semester, lalu di tiap semester berkegiatan besar tersebut diacak anggota panitianya.
  7. Repeated measurements. Perlakuan menjadi petak utama, lalu waktu-waktu tertentu pengamatan menjadi anak petak

6.1 Split Plot RAL

6.1.1 Pengacakan

Pengacakan pada rancangan petak terpisah di R dapat langsung dilakukan menggunakan fungsi design.split dari library agricolae. Akan digunakan studi kasus berikut:

Dalam usaha menjaga kesehatan lingkungan dilakukan percobaan dengan menggunakan berbagai jenis tanaman untuk menyerap debu di udara. Jenis tanaman yang digunakan antara lain tanaman berdaun kecil licin (J1 dan J2), berdaun kecil kasar (J3, J4), berdaun lebar licin (J5, J6), berdaun lebar kasar (J7, J8), dan berdaun jarum (J9, J10). Percobaan ini dicobakan pada dua lokasi (Cipedak dan Gatot Subroto). Setiap perlakuan diulang 3 kali dan unit-unit percobaan yang digunakan diasumsikan homogen. Dari percobaan ini ingin diketahui jenis tanaman yang mampu menyerap debu paling efektif dan di lokasi mana? Peubah respons yang dicatat dari percobaan ini adalah konsentrasi debu (ppm) yang melekat pada daun tanaman.

Untuk melakukan pengacakan, bangkitkan taraf kedua faktor terlebih dahulu:

Lokasi<-c("Cipedak","Gatot S.")
Jenis<-paste("J",seq(10),sep="")

Pengacakan secara cepat dapat dilakukan dengan menggunakan design.split dari library agricolae. Pastikan design berupa CRD (completely randomized design) jika menggunakan split plot RAL. Argumen fungsi diurutkan sebagai berikut karena lokasi merupakan petak utama, jenis anak petak, dan ada tiga ulangan.

library(agricolae)

bagan<-design.split(Lokasi , Jenis,r=3, design="crd",serie = 0,
             seed = 0, kinds = "Super-Duper", first=TRUE,randomization=TRUE)$book #(utama, anak, ulangan)
knitr::kable(head(bagan),n=10)
plots splots r Lokasi Jenis
1 1 1 Gatot S. J9
1 2 1 Gatot S. J5
1 3 1 Gatot S. J4
1 4 1 Gatot S. J8
1 5 1 Gatot S. J2
1 6 1 Gatot S. J3 
nrow(bagan)
## [1] 60

Bagan memiliki 60 baris, yang masuk akal karena \(A\times B\times r=2\times 10\times 3=60\), di mana faktor A adalah lokasi, B adalah jenis, dan r ulangan. Jika ingin lebih detail, dapat diperhatikan bahwa pengacakan split plot dapat dilakukan sebagai berikut:

  1. Pengacakan RAL untuk plot utama, dengan unit percobaan berjumlah \(A\times r\).
  2. RAKL dengan \(A\times r\) blok, dengan \(B\) unit percobaan di blok tersebut.

Implementasi di agricolae sebagai berikut:

bagan1<-design.crd(Lokasi,r=3,serie=0)
knitr::kable(bagan1$book)
plots r Lokasi
1 1 Gatot S.
2 2 Gatot S.
3 1 Cipedak
4 2 Cipedak
5 3 Cipedak
6 3 Gatot S.

Lalu, fase kedua dari pengacakan. Ada \(2\times 3=6\) blok:

bagan2<-design.rcbd(Jenis,r=6)
knitr::kable(head(bagan2$book),n=10)
plots block Jenis
101 1 J9
102 1 J8
103 1 J6
104 1 J3
105 1 J5
106 1 J7 
nrow(bagan2$book)
## [1] 60

Lakukan merge. Note bahwa tiap plot di pengacakan pertama akan menjadi blok, sehingga merge di x menggunakan plot dan di y menggunakan blok:

baganfin<-merge(bagan1$book,bagan2$book,by.x="plots",by.y="block")
knitr::kable(head(baganfin),n=10)
plots r Lokasi plots.y Jenis
1 1 Gatot S. 101 J9
1 1 Gatot S. 102 J8
1 1 Gatot S. 103 J6
1 1 Gatot S. 104 J3
1 1 Gatot S. 105 J5
1 1 Gatot S. 106 J7 
nrow(baganfin)
## [1] 60

Sehingga terbuat bagan final. Bagan tersebut dapat dilihat dengan beberapa format lain, seperti:

bag2<-bagan[,-c(1,2)]
knitr::kables(list(
  knitr::kable(reshape2::dcast(bag2,Lokasi~Jenis)), #lokasi vs jenis (berapa jenis tertentu di lokasi tertentu)
  knitr::kable(reshape2::dcast(bag2,Lokasi+r~Jenis)) #lokasi, ulangan vs jenis (bagan, tapi tabulasi format wide)
 ),
 caption="Dua cara menunjukkan bagan percobaan"
)
Table 6.1: Dua cara menunjukkan bagan percobaan
Lokasi J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Cipedak 3 3 3 3 3 3 3 3 3 3
Gatot S. 3 3 3 3 3 3 3 3 3 3
Lokasi r J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Cipedak 1 J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Cipedak 2 J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Cipedak 3 J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Gatot S. 1 J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Gatot S. 2 J1 J10 J2 J3 J4 J5 J6 J7 J8 J9
Gatot S. 3 J1 J10 J2 J3 J4 J5 J6 J7 J8 J9

Hal tersebut dapat juga dilakukan dengan alternatif pengacakan dua fase:

knitr::kable(cbind(bagan1$book,bagan2$sketch))
plots r Lokasi 1 2 3 4 5 6 7 8 9 10
1 1 Gatot S. J9 J8 J6 J3 J5 J7 J1 J4 J10 J2
2 2 Gatot S. J10 J4 J9 J2 J1 J7 J3 J6 J5 J8
3 1 Cipedak J9 J2 J10 J8 J1 J6 J3 J5 J7 J4
4 2 Cipedak J2 J3 J7 J5 J4 J9 J1 J6 J10 J8
5 3 Cipedak J5 J7 J10 J3 J4 J6 J9 J2 J8 J1
6 3 Gatot S. J4 J9 J5 J6 J2 J7 J10 J8 J1 J3

6.1.1.1 Pengacakan edibble

Untuk split plot RAL, dapat dibuat dua unit di set_units(). Pertama adalah petak utama, dan anak petak berupa unit yang nested_in() petak utama. Taraf lokasi diacak ke petak utama (lokasi~mainplot), dan jenis ke anak petak (jenis~unit):

library(edibble)

desSPRAL<-design(name="Lokasi dan Jenis vs. Penyerapan Debu") %>%
  set_units(mainplot=2,
            unit=nested_in(mainplot, 10)) %>%
  set_trts(lokasi=Lokasi,
           jenis=Jenis) %>%
  allot_trts(lokasi~mainplot,
             jenis~unit) %>%
  assign_trts("random", seed=420) %>% serve_table

knitr::kable(head(desSPRAL,n=10))
mainplot unit lokasi jenis
mainplot1 unit1 Gatot S. J6
mainplot1 unit2 Gatot S. J8
mainplot1 unit3 Gatot S. J1
mainplot1 unit4 Gatot S. J10
mainplot1 unit5 Gatot S. J3
mainplot1 unit6 Gatot S. J7
mainplot1 unit7 Gatot S. J9
mainplot1 unit8 Gatot S. J2
mainplot1 unit9 Gatot S. J4
mainplot1 unit10 Gatot S. J5

Plot dari rancangan tersebut dapat dilihat:

deggust::autoplot(desSPRAL)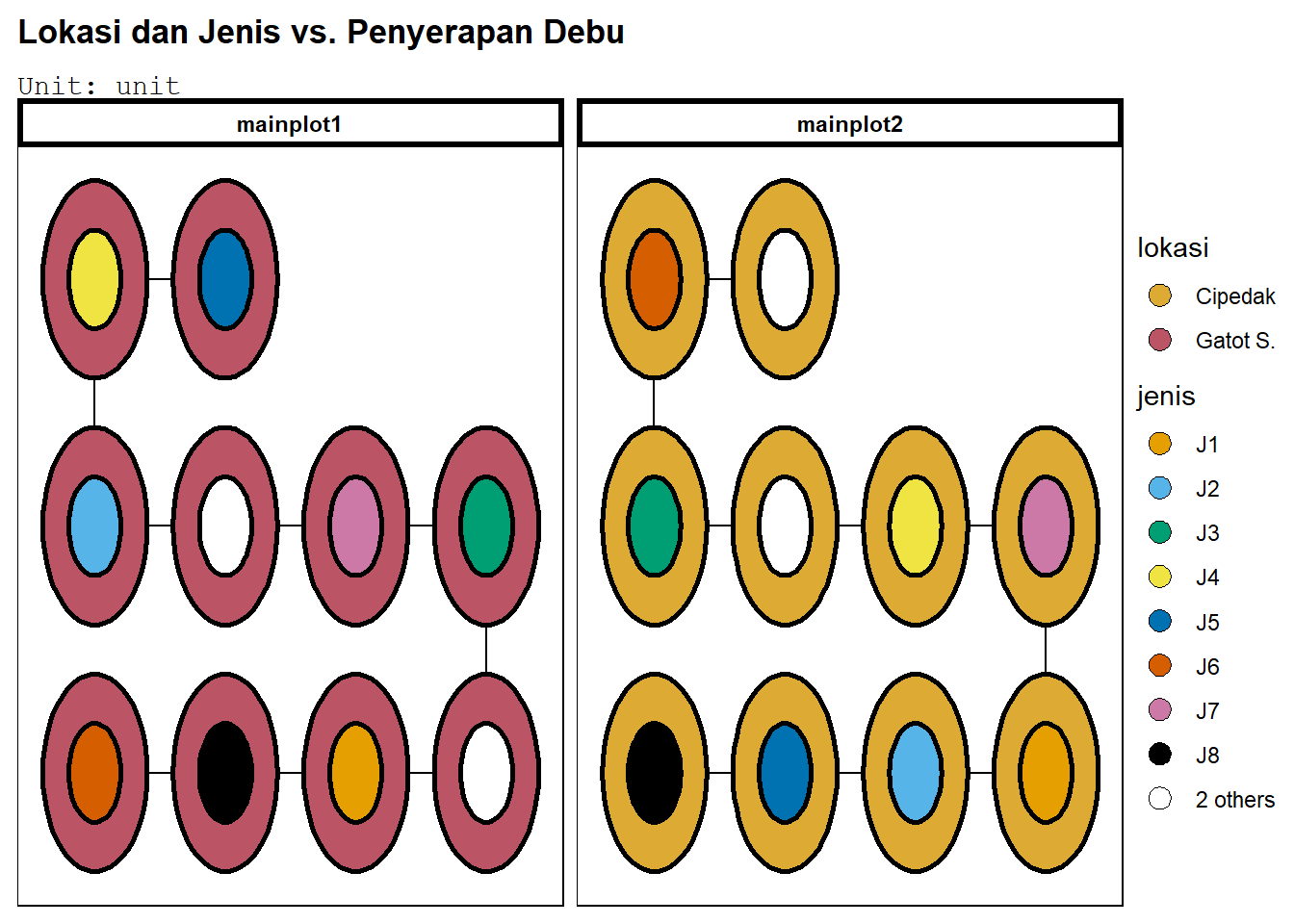

Edibble juga dapat membuat rancangan split plot secara default:

spd<-takeout(menu_split(t1 = 2, t2 = 10, r = 1, seed=420))
examine_recipe(spd)
## design("Split-Plot Design | Split-Unit Design") %>%
##   set_units(mainplot = 2,
##              subplot = nested_in(mainplot, 10)) %>%
##   set_trts(trt1 = 2,
##            trt2 = 10) %>%
##   allot_trts(trt1 ~ mainplot,
##              trt2 ~ subplot) %>%
##   assign_trts("random", seed = 420) %>%
##   serve_table()

Dapat dilihat bahwa cara pembuatan rancangan sama dengan yang dibuat sebelumnya. Plot juga sama:

deggust::autoplot(spd)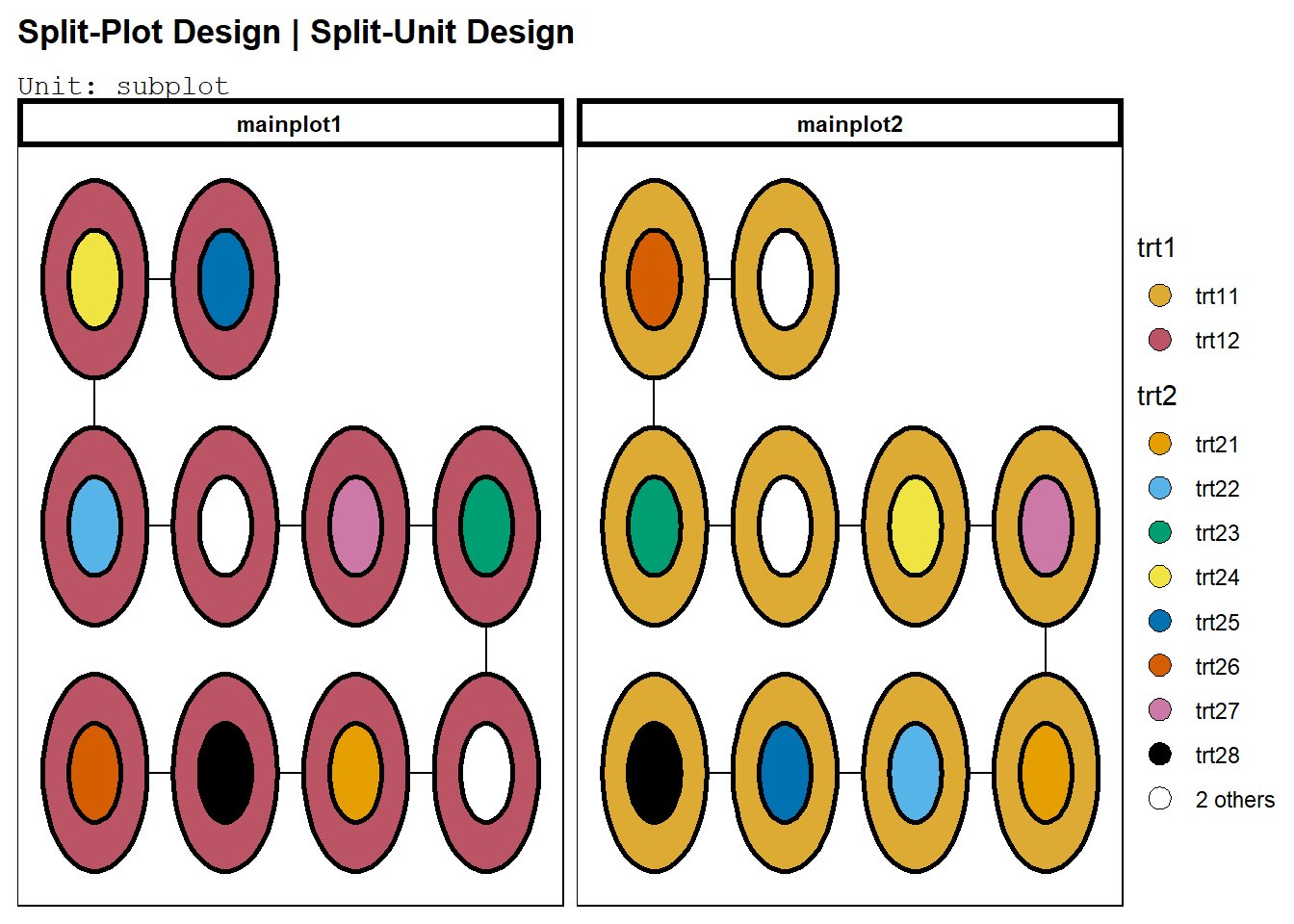

6.1.2 ANOVA

Model linear aditif bagi split plot RAL adalah: \[ y_{ijk} = \mu + \alpha_i + \delta_{k(i)} + \beta_j + (\alpha\beta)_{ij} + \epsilon_{ijk} \]

Dengan:

  1. \(y_{ijk}\) adalah nilai pengamatan pada faktor A taraf ke-i dan faktor B taraf ke-j pada ulangan ke-k.
  2. \(\mu\) komponen aditif dari rataan umum.
  3. \(\alpha_i\) pengaruh utama faktor A. Diasumsikan \(\sum_{i=1}^a \alpha_i=0\) bagi model tetap dan \(\alpha\sim N(0,\sigma_a^2)\) bagi model acak.
  4. \(\beta_{j}\) pengaruh utama faktor B. Diasumsikan \(\sum_{j=1}^b \beta_j=0\) bagi model tetap dan \(\beta\sim N(0,\sigma_b^2)\) bagi model acak.
  5. \((\alpha\beta)_{ij}\) komponen interaksi faktor A dan faktor B. Diasumsikan \(\sum_{i=1}^p\sum_{i=1}^t (\alpha\beta)_{ij}=0\) bagi model tetap dan \((\alpha\beta)_{ij}\sim N(0,\sigma_{ab}^2)\) bagi model acak.
  6. \(\delta_{k(i)}\sim N(0,\sigma_{\delta}^2)\) komponen acak dari petak utama.
  7. \(\epsilon_{ijk}\sim N(0,\sigma^2)\) komponen acak anak petak.

Dan hipotesis pengaruh petak utama, anak petak, dan interaksi. \[ \begin{aligned} \text{Pengaruh petak utama (Faktor A)}&:\\ H_{0}&:\alpha_{1}=\ldots=\alpha_{a}=0 \text{ faktor A tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu i di mana }\alpha_{i}\neq 0\\ \\ \text{Pengaruh anak petak (Faktor B)}&:\\ H_{0}&:\beta_{1}=\ldots=\beta_{b}=0 \text{ faktor B tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu j di mana }\beta_{j}\neq 0\\ \\ \text{Pengaruh interaksi }&:\\ H_{0}&:(\alpha\beta)_{11}=(\alpha\beta)_{12}=\ldots=(\alpha\beta)_{ab}=0 \text{ interaksi tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada sepasang ij di mana }(\alpha\beta)_{ij}\neq 0\\ \end{aligned} \]

Dan tabel ANOVA:

Sumber Keragaman db JK KT F-hit F(dbP,dbG)
A a-1 JKA JKA/dbA KTA/KTGA
Galat (a) a(r-1) JKGA JKGA/dbGA
B (b-1) JKB JKB/dbB KTB/KTGB
AB (a-1)(b-1) JKAB JKAB/dbAB KTAB/KTGB
Galat (b) a(b-1)(r-1) JKGB JKGB/dbGB
Total abr-1 JKT

Jumlah kuadrat tersebut dihitung dengan: \[ \begin{aligned} FK&=\frac{y^2_{...}}{abr}\\ JKT&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(y_{ijk}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r y_{ijk}^2-FK\\ JKST&=\sum_{i=1}^a\sum_{k=1}^r\left(\bar{y}_{i.K}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{k=1}^r \frac{y_{i.k}^2}{b}-FK\\ JKA&=\sum_{i=1}^a\left(\bar{y}_{i..}-\bar{y}_{...}\right)^2=\sum_{i=1}^a \frac{y_{i..}^2}{br}-FK\\ JKG_{a}&=JKST-JKA\\ JKB&=\sum_{j=1}^b\left(\bar{y}_{.j.}-\bar{y}_{...}\right)^2=\sum_{j=1}^b \frac{y_{.j.}^2}{ar}-FK\\ JKP&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b \frac{y_{ij.}^2}{r}-FK\\ JKAB&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{i..}-\bar{y}_{.j.}+\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2-JKA-JKB\\ &=JKP-JKB-JKA\\ JKG_{b}&=JKT-JKP-JKG_{a} \end{aligned} \]

6.1.3 Analisis menggunakan R

Akses data:

library(googlesheets4)
SPlot<-read_sheet("https://docs.google.com/spreadsheets/d/1CL0DZ8Ub_sTvDcj-jy_UR3P3KKY1vptEz1SapQ_yMpY/edit?usp=sharing")
## √ Reading from "SplitPlots".
## √ Range 'Sheet1'.
knitr::kable(head(SPlot),n=10)
No Lokasi Jenis Ulangan Konsentrasi debu
1 Cipedak J1 1 0.0312
2 Cipedak J1 2 0.0317
3 Cipedak J1 3 0.0321
4 Cipedak J2 1 0.0270
5 Cipedak J2 2 0.0272
6 Cipedak J2 3 0.0277

Akan dilakukan dua hal untuk membersihkan data. Pertama, satuan respon akan dikalikan 1000 karena satuan awalnya relatif kecil. Jika dikalikan 1000 jumlah kuadrat dan kuadrat tengah akan terlihat lebih jelas:

SPlot$`Konsentrasi debu`<-SPlot$`Konsentrasi debu`*1000

Lalu, pastikan semua faktor telah menjadi… faktor:

SPlot$Ulangan<-as.factor(SPlot$Ulangan)
SPlot$Jenis<-as.factor(SPlot$Jenis)
SPlot$Lokasi<-as.factor(SPlot$Lokasi)

Lakukan ANOVA. Seperti di percobaan faktorial, sintaks \(a*b\) akan menghasilkan pengaruh faktor dan interaksi secara bersamaan. Oleh karena itu, tulis saja sintaks tersebut tanpa harus menspesifikasi pengaruh tiap faktor. Terdapat sintaks yang berbeda, yaitu di Error(Ulangan:Lokasi). Pada dasarnya sintaks ini memerintahkan R untuk menghitung ANOVA bagi plot utama. Dihitung \(JKG_{Lokasi}\) dan pengaruh lokasi diuji menggunakan kuantitas tersebut. Tabel ANOVA akan terbagi dua menjadi Error: Ulangan:Lokasi - di plot utama, dan Error: Within - di dalam plot utama, dalam kata lain di anak petak. Pastikan ulangan sudah merupakan faktor (jika belum, derajat bebas akan beda).

aovSPlot1<-aov(`Konsentrasi debu`~Lokasi*Jenis+Error(Ulangan:Lokasi),data=SPlot)
## Warning in aov(`Konsentrasi debu` ~ Lokasi * Jenis + Error(Ulangan:Lokasi), : Error() model is
## singular
summary(aovSPlot1)
## 
## Error: Ulangan:Lokasi
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## Lokasi     1 105404  105404   45587 2.89e-09 ***
## Residuals  4      9       2                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##              Df Sum Sq Mean Sq F value Pr(>F)    
## Jenis         9 160762   17862  343631 <2e-16 ***
## Lokasi:Jenis  9  20732    2304   44314 <2e-16 ***
## Residuals    36      2       0                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Terbentuk tabel ANOVA yang mirip dengan Excel, dengan kesimpulan sama yaitu tolak \(H_{0}\) bagi tiap pengaruh. Ini berarti lokasi, jenis, dan interaksi lokasi dengan jenis berpengaruh pada respon. ANOVA Split Plot RAL dapat juga dianalisis melalui package lme4:

library(lme4)
## Loading required package: Matrix
aovSPlot2<-lmer(`Konsentrasi debu`~Lokasi*Jenis+(1|Ulangan:Lokasi),data=SPlot)
knitr::kable(anova(aovSPlot2))
npar Sum Sq Mean Sq F value
Lokasi 1 2369.655 2369.655 45586.53
Jenis 9 160762.103 17862.456 343631.14
Lokasi:Jenis 9 20731.646 2303.516 44314.17

Nilai F dari ANOVA tersebut sama dengan sebelumnya. Karena setidaknya salah satu pengaruh jenis dan lokasi beda dari nol, dapat dibuat kontras sebagai uji lanjut:

contrasts(SPlot$Jenis)<-cbind(c(1, -4, 1, 1, 1, 1, 1, 1, 1,-4), c(0, 1, 0, 0, 0, 0, 0, 0, 0, -1),
                              c(1, 0, 1, 1, 1, -1, -1, -1, -1, 0), c(1, 0, 1, -1, -1, 0, 0, 0, 0, 0),
                              c(1, 0, -1, 0, 0, 0, 0, 0, 0, 0), c(0, 0, 0, 1, -1, 0, 0, 0, 0, 0),
                              c(0, 0, 0, 0, 0, 1, 1, -1, -1, 0), c(0, 0, 0, 0, 0, 1, -1, 0, 0, 0),
                              c(0, 0, 0, 0, 0, 0, 0, 1, -1, 0))
summary(aovSPlot1,split=list(Jenis=list("Jarum vs Lainnya"=1, "J9 vs J10"=2, "Kecil vs Lebar"=3, "Licin vs Kasar (kecil)"=4,
           "J1 vs J2 (kecil licin)"=5, "J3 vs J4 (kecil kasar)"=6, "licin vs kasar (lebar)"=7,
           "J5 vs J6 (lebar licin)"=8, "J7 vs J8 (lebar kasar)"=9)))
## 
## Error: Ulangan:Lokasi
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## Lokasi     1 105404  105404   45587 2.89e-09 ***
## Residuals  4      9       2                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##                                        Df Sum Sq Mean Sq F value Pr(>F)    
## Jenis                                   9 160762   17862  343631 <2e-16 ***
##   Jenis: Jarum vs Lainnya               1  24359   24359  468603 <2e-16 ***
##   Jenis: J9 vs J10                      1  29839   29839  574023 <2e-16 ***
##   Jenis: Kecil vs Lebar                 1   1048    1048   20168 <2e-16 ***
##   Jenis: Licin vs Kasar (kecil)         1   8740    8740  168142 <2e-16 ***
##   Jenis: J1 vs J2 (kecil licin)         1  25855   25855  497393 <2e-16 ***
##   Jenis: J3 vs J4 (kecil kasar)         1  11248   11248  216388 <2e-16 ***
##   Jenis: licin vs kasar (lebar)         1   9842    9842  189338 <2e-16 ***
##   Jenis: J5 vs J6 (lebar licin)         1  11025   11025  212095 <2e-16 ***
##   Jenis: J7 vs J8 (lebar kasar)         1  38806   38806  746532 <2e-16 ***
## Lokasi:Jenis                            9  20732    2304   44314 <2e-16 ***
##   Lokasi:Jenis: Jarum vs Lainnya        1   3456    3456   66495 <2e-16 ***
##   Lokasi:Jenis: J9 vs J10               1   3680    3680   70799 <2e-16 ***
##   Lokasi:Jenis: Kecil vs Lebar          1     84      84    1618 <2e-16 ***
##   Lokasi:Jenis: Licin vs Kasar (kecil)  1   1301    1301   25021 <2e-16 ***
##   Lokasi:Jenis: J1 vs J2 (kecil licin)  1   3374    3374   64907 <2e-16 ***
##   Lokasi:Jenis: J3 vs J4 (kecil kasar)  1   1325    1325   25496 <2e-16 ***
##   Lokasi:Jenis: licin vs kasar (lebar)  1   1606    1606   30887 <2e-16 ***
##   Lokasi:Jenis: J5 vs J6 (lebar licin)  1   1960    1960   37697 <2e-16 ***
##   Lokasi:Jenis: J7 vs J8 (lebar kasar)  1   3946    3946   75908 <2e-16 ***
## Residuals                              36      2       0                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Semua kontras menolak \(H_{0}\). Ini berarti jenis berbeda yang hendak dibandingkan benar-benar beda dalam hal konsentrasi debu. Lalu, dapat dibuat plot interaksi:

library(ggplot2)
ggplot2::ggplot(aes(x = Jenis, y = `Konsentrasi debu`, group = Lokasi, colour = Lokasi), data = SPlot) + geom_line()+ theme_bw()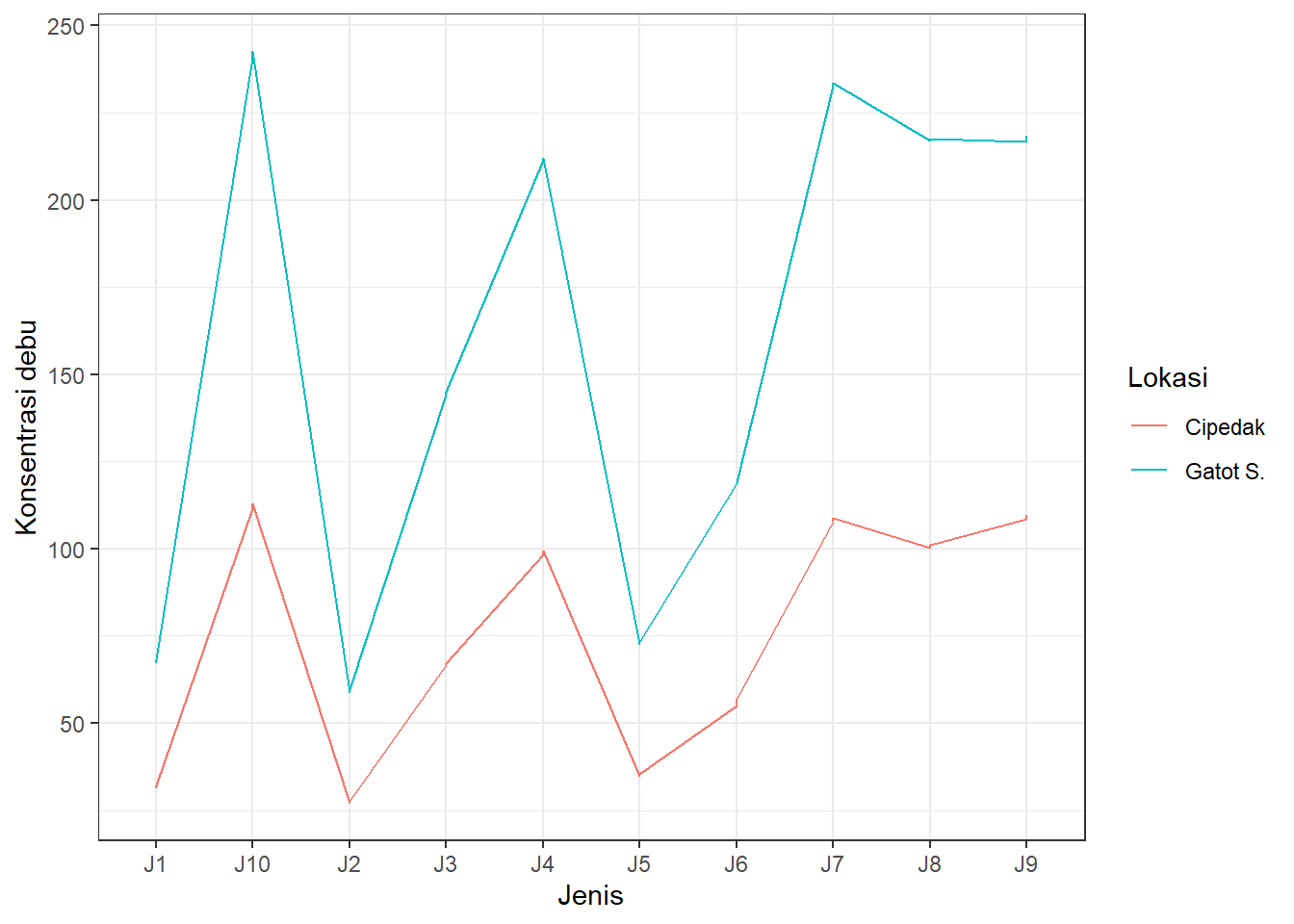

Dapat dilihat bahwa garis tak sepenuhnya sejajar walaupun tak pernah berpotongan. Misal, ada kenaikan konsentrasi debu yang lebih besar di Gatot Subroto daripada Cipedak antara jenis tanaman yang sama (misal J5 vs. J6). Untuk memastikan bahwa RAL tepat, dapat dibuat facet per ulangan yang memisahkan plot menjadi per ulangan:

ggplot2::ggplot(aes(x = Jenis, y = `Konsentrasi debu`, group = Lokasi, colour = Lokasi), data = SPlot) + geom_line() + 
  facet_wrap(~ Ulangan) + theme_bw()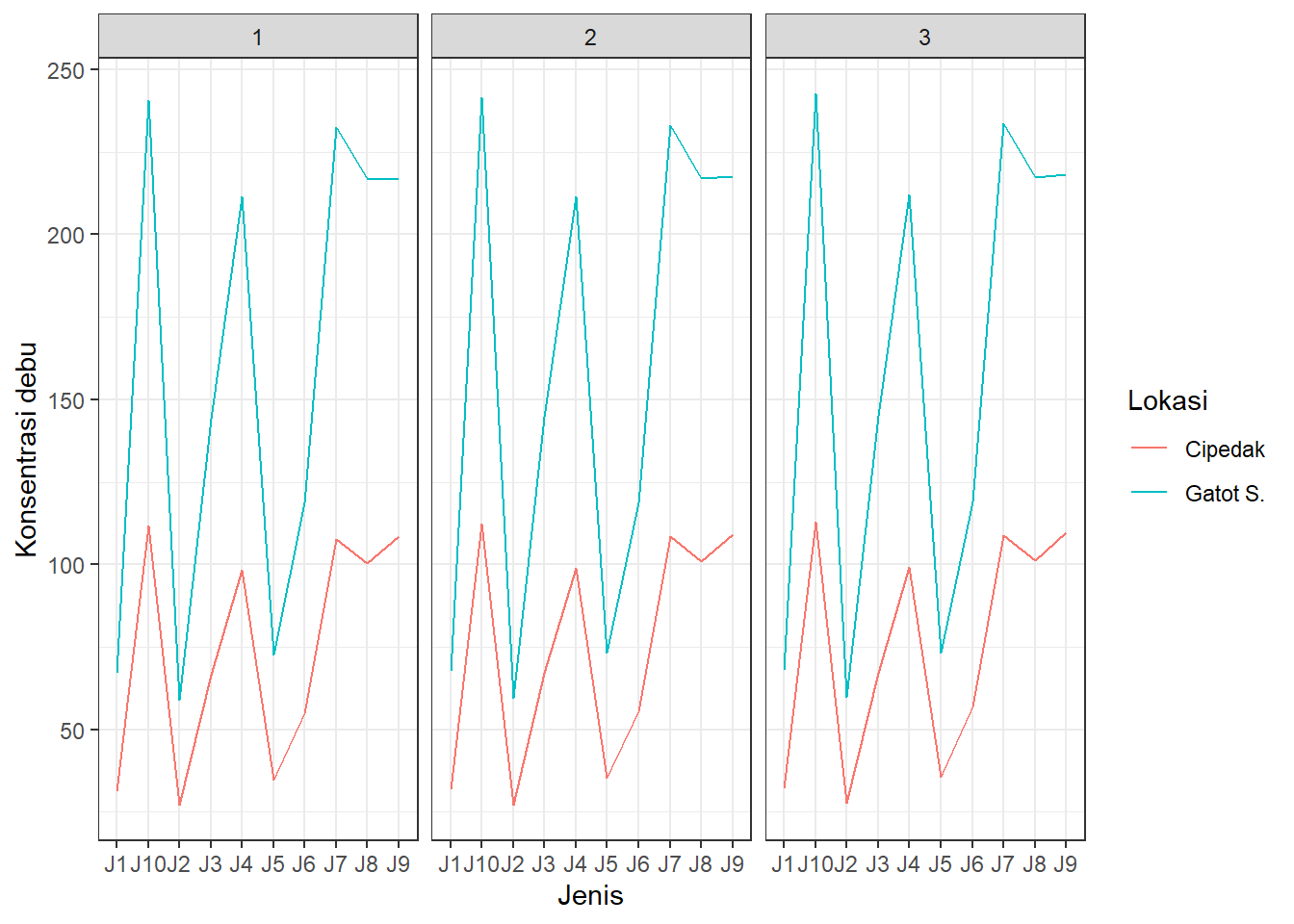

Terlihat bahwa pola interaksi relatif sama antara ulangan, sehingga dapat dianggap bahwa unit percobaan benar-benar homogen.

6.2 Split Plot RAK

Kondisi unit percobaan split plot belum tentu homogen. Oleh karena itu, dapat digunakan Split Plot RAK untuk mengatasi pengaruh keragaman yang muncul dari satu arah. Pengelompokan menjadi blok dilakukan di petak utama, dengan pengacakan anak petak relatif sama. Dalam pembahasan Split Plot RAK, akan digunakan kasus oats:

Produksi oat dari sebuah percobaan split-plot menggunakan tiga varietas dan empat taraf penggunaaan nitrogen. Percobaan dilaksanakan di enam blok yang berisi tiga petak utama yang dibagi menjadi empat anak petak. Varietas diaplikasikan di petak utama dan pemumupukan nitrogen diaplikasikan ke anak petak.

Peubah-peubah dalam dataset oats adalah:

  1. B: Blok, dengan taraf I, II, III, IV, V dan VI.
  2. V: Varietas, 3 taraf.
  3. N: Perlakuan pupuk nitrogen. Taraf \(0.0cwt\), \(0.2cwt\), \(0.4cwt\), dan \(0.6cwt\).
  4. Y: Produksi di \(1/4\) pound per sub-plot. Tiap sub-plot sebesar \(1/80\) acre.

Data tersebut ada dalam package MASS:

data(oats, package = "MASS")
str(oats)
## 'data.frame':    72 obs. of  4 variables:
##  $ B: Factor w/ 6 levels "I","II","III",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ V: Factor w/ 3 levels "Golden.rain",..: 3 3 3 3 1 1 1 1 2 2 ...
##  $ N: Factor w/ 4 levels "0.0cwt","0.2cwt",..: 1 2 3 4 1 2 3 4 1 2 ...
##  $ Y: int  111 130 157 174 117 114 161 141 105 140 ...

6.2.1 Pengacakan

Pertama, ambil taraf-taraf dari varietas dan konsentrasi pupuk nitrogen:

V<-levels(oats$V)
N<-levels(oats$N)

Pengacakan secara cepat dapat dilakukan dengan menggunakan design.split dari library agricolae. Dalam kasus ini, design berupa RCBD (randomized complete block design) jika menggunakan split plot RAK. Argumen fungsi diurutkan sebagai berikut karena varietas merupakan petak utama, nitrogen anak petak, dan ada tiga blok.

library(agricolae)

bagan2<-design.split(V, N,r=6, design="rcbd",serie = 0,
                     seed = 0, kinds = "Super-Duper",
                     first=TRUE,randomization=TRUE) 
        #(utama, anak, ulangan)
knitr::kable(head(bagan2$book),n=10)
plots splots block V N
1 1 1 Golden.rain 0.2cwt
1 2 1 Golden.rain 0.0cwt
1 3 1 Golden.rain 0.4cwt
1 4 1 Golden.rain 0.6cwt
2 1 1 Marvellous 0.4cwt
2 2 1 Marvellous 0.2cwt 
nrow(bagan2$book)
## [1] 72
nrow(oats)
## [1] 72

Jumlah baris di bagan sama dengan jumlah baris di data oats, yaitu \(3\times 4\times 6=72\). Mirip dengan Split Plot RAL, pengacakan dapat dilakukan dengan algoritma:

  1. Pengacakan RAKL untuk plot utama.
  2. RAKL dengan \(A\times r\) blok, dengan \(B\) unit percobaan di blok tersebut.

\(A\) adalah jumlah taraf faktor di plot utama dan \(B\) adalah jumlah taraf faktor di anak petak.

6.2.1.1 Pengacakan edibble

Untuk split plot RAKL, dapat dibuat tiga unit di set_units(). Pertama adalah blok, lalu petak utama yang nested_in(blok), dan anak petak yang nested_in() petak utama. Taraf varietas diacak ke petak utama (V~mainplot), dan nitrogen ke anak petak (jenis~subplot):

library(edibble)

desSPRAKL<-design(name="Oats") %>%
  set_units(blok=6,
            mainplot=nested_in(blok,3),
            subplot=nested_in(mainplot, 4)) %>%
  set_trts(nitrogen=N,
           varietas=V) %>%
  allot_trts(varietas~mainplot,
             nitrogen~subplot) %>%
  assign_trts("random", seed=420) %>% serve_table

knitr::kable(head(desSPRAKL,n=10))
blok mainplot subplot nitrogen varietas
blok1 mainplot1 subplot1 0.0cwt Golden.rain
blok1 mainplot1 subplot2 0.6cwt Golden.rain
blok1 mainplot1 subplot3 0.2cwt Golden.rain
blok1 mainplot1 subplot4 0.4cwt Golden.rain
blok1 mainplot2 subplot5 0.2cwt Marvellous
blok1 mainplot2 subplot6 0.6cwt Marvellous
blok1 mainplot2 subplot7 0.0cwt Marvellous
blok1 mainplot2 subplot8 0.4cwt Marvellous
blok1 mainplot3 subplot9 0.4cwt Victory
blok1 mainplot3 subplot10 0.2cwt Victory

Plot dari rancangan tersebut dapat dilihat:

deggust::autoplot(desSPRAKL)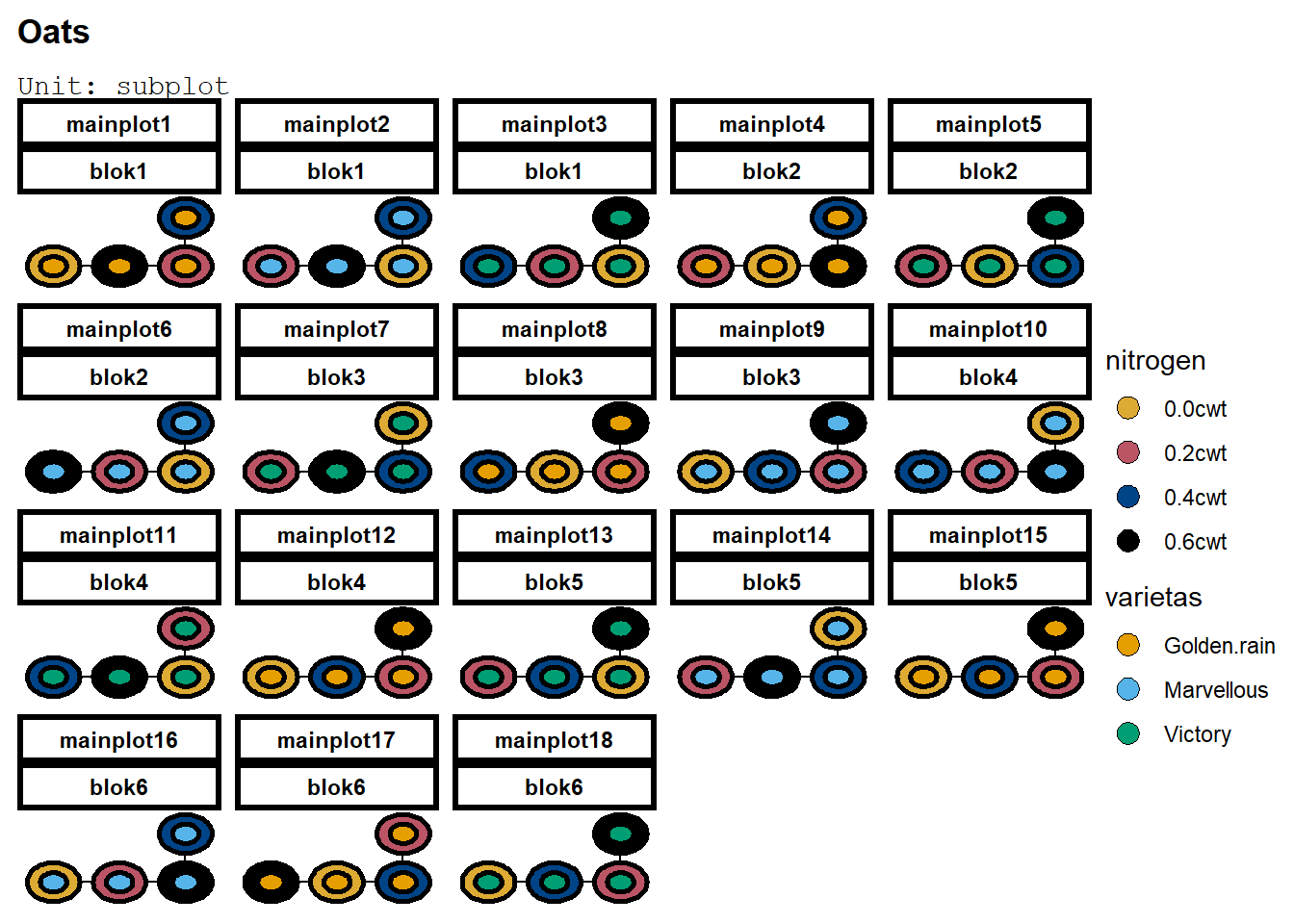

Agar plot tersebut terlihat lebih rapih, dapat digunakan facet_wrap() untuk memisahkan plot tersebut per blok atau per plot utama:

deggust::autoplot(desSPRAKL)+facet_wrap(~blok)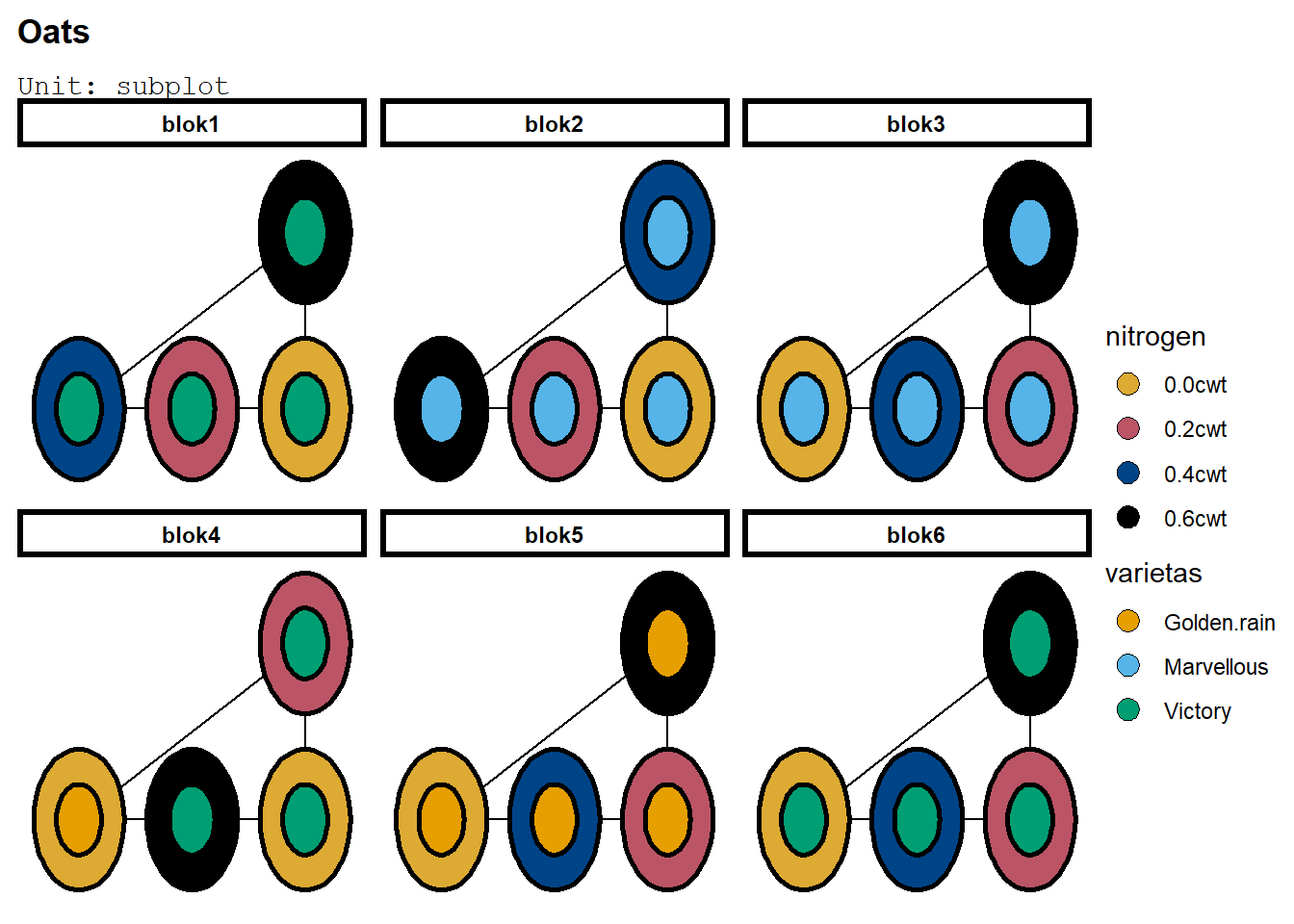

deggust::autoplot(desSPRAKL)+facet_wrap(~mainplot)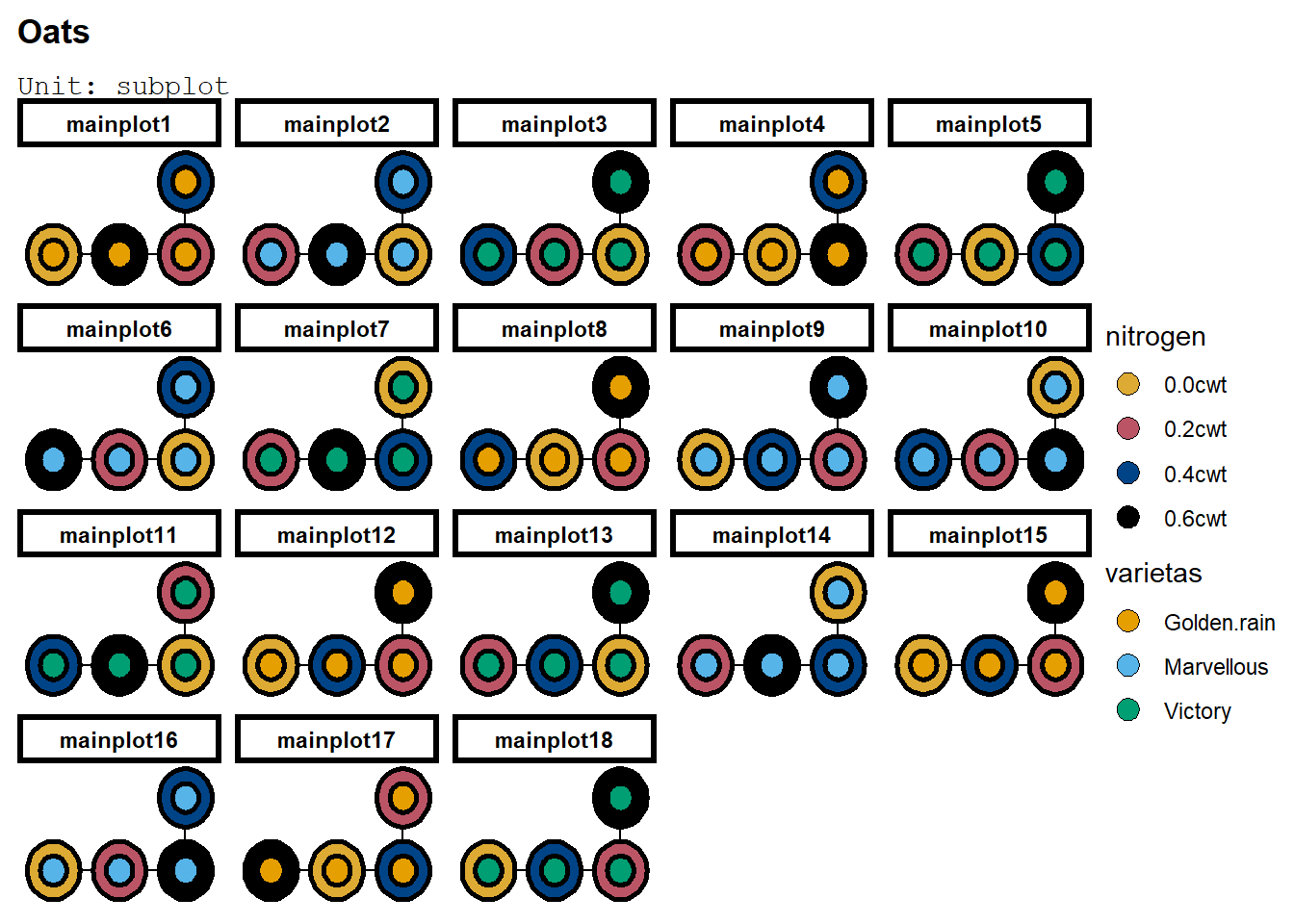

6.2.2 ANOVA

Model linear aditif bagi split plot RAL adalah: \[ y_{ijk} = \mu + \alpha_i + K_{k}+ \delta_{k(i)} + \beta_j + (\alpha\beta)_{ij} + \epsilon_{ijk} \]

Dengan:

  1. \(y_{ijk}\) adalah nilai pengamatan pada faktor A taraf ke-i dan faktor B taraf ke-j pada blok ke-k.
  2. \(\mu\) komponen aditif dari rataan umum.
  3. \(\alpha_i\) pengaruh utama faktor A. Diasumsikan \(\sum_{i=1}^a \alpha_i=0\) bagi model tetap dan \(\alpha\sim N(0,\sigma_a^2)\) bagi model acak.
  4. \(\beta_{j}\) pengaruh utama faktor B. Diasumsikan \(\sum_{j=1}^b \beta_j=0\) bagi model tetap dan \(\beta\sim N(0,\sigma_b^2)\) bagi model acak.
  5. \(K_{k}\) pengaruh utama kelompok.
  6. \((\alpha\beta)_{ij}\) komponen interaksi faktor A dan faktor B. Diasumsikan \(\sum_{i=1}^p\sum_{i=1}^t (\alpha\beta)_{ij}=0\) bagi model tetap dan \((\alpha\beta)_{ij}\sim N(0,\sigma_{ab}^2)\) bagi model acak.
  7. \(\delta_{k(i)}\sim N(0,\sigma_{\delta}^2)\) komponen acak dari petak utama.
  8. \(\epsilon_{ijk}\sim N(0,\sigma^2)\) komponen acak anak petak.
Dan hipotesis pengaruh petak utama, anak petak, dan interaksi. $$ \[\begin{aligned} \text{Pengaruh petak utama (Faktor A)}&:\\ H_{0}&:\alpha_{1}=\ldots=\alpha_{a}=0 \text{ faktor A tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu i di mana }\alpha_{i}\neq 0\\ \\ \text{Pengaruh anak petak (Faktor B)}&:\\ H_{0}&:\beta_{1}=\ldots=\beta_{b}=0 \text{ faktor B tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu j di mana }\beta_{j}\neq 0\\ \\ \text{Pengaruh interaksi }&:\\ H_{0}&:(\alpha\beta)_{11}=(\alpha\beta)_{12}=\ldots=(\alpha\beta)_{ab}=0 \text{ interaksi tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada sepasang ij di mana }(\alpha\beta)_{ij}\neq 0\\ \\ \text{Pengaruh kelompok}&:\\ H_{0}&:K_{1}=\ldots=K_{k}=0 \text{ Kelompok tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu k di mana }K_{k}\neq 0\\ \end{aligned}\]

$$

Dan tabel ANOVA:

Sumber Keragaman db JK KT F-hit F(dbP,dbG)
Blok r-1 JKK JKK/dbA KTK/KTGA
A a-1 JKA JKA/dbA KTA/KTGA
Galat (a) (a-1)(r-1) JKGA JKGA/dbGA
B (b-1) JKB JKB/dbB KTB/KTGB
AB (a-1)(b-1) JKAB JKAB/dbAB KTAB/KTGB
Galat (b) (a-1)(b-1)(r-1) JKGB JKGB/dbGB
Total abr-1 JKT

Jumlah kuadrat tersebut dihitung dengan: \[ \begin{aligned} FK&=\frac{y^2_{...}}{abr}\\ JKT&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(y_{ijk}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r y_{ijk}^2-FK\\ JKST&=\sum_{i=1}^a\sum_{k=1}^r\left(\bar{y}_{i.k}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{k=1}^r \frac{y_{i.k}^2}{b}-FK\\ JKA&=\sum_{i=1}^a\left(\bar{y}_{i..}-\bar{y}_{...}\right)^2=\sum_{i=1}^a \frac{y_{i..}^2}{br}-FK\\ JKK&=\sum_{k=1}^r \left(\bar{y}_{..k}-\bar{y}_{...}\right)^2=\sum_{k=1}^r \frac{y_{..k}^2}{ab}-FK\\ JKG_{a}&=JKST-JKA-JKK\\ JKB&=\sum_{j=1}^b\left(\bar{y}_{.j.}-\bar{y}_{...}\right)^2=\sum_{j=1}^b \frac{y_{.j.}^2}{ar}-FK\\ JKP&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b \frac{y_{ij.}^2}{r}-FK\\ JKAB&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{i..}-\bar{y}_{.j.}+\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2-JKA-JKB\\ &=JKP-JKB-JKA\\ JKG_{b}&=JKT-JKP-JKG_{a} \end{aligned} \]

6.2.3 Analisis menggunakan R

Sama seperti Split Plot RAL, perlu ditambah sintaks Error(Blok:Utama) di aov:

aovSPlotRAK1<-aov(Y~V*N+B+Error(B:V),data=oats)
## Warning in aov(Y ~ V * N + B + Error(B:V), data = oats): Error() model is singular
summary(aovSPlotRAK1)
## 
## Error: B:V
##           Df Sum Sq Mean Sq F value Pr(>F)  
## V          2   1786     893   1.485 0.2724  
## B          5  15875    3175   5.280 0.0124 *
## Residuals 10   6013     601                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## N          3  20020    6673  37.686 2.46e-12 ***
## V:N        6    322      54   0.303    0.932    
## Residuals 45   7969     177                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dapat juga digunakan lme4:

library(lme4)
fit.oats <- lmer(Y ~ B + V * N + (1 | B:V), data = oats)
knitr::kable(anova(fit.oats))
npar Sum Sq Mean Sq F value
B 5 4675.0427 935.0085 5.2800486
V 2 526.0578 263.0289 1.4853399
N 3 20020.5000 6673.5000 37.6856497
V:N 6 321.7500 53.6250 0.3028236

Nilai F dan derajat bebas dari kedua tabel ANOVA sama, tetapi jumlah kuadrat berbeda. Fungsi sp.plot dari library agricolae juga dapat digunakan untuk menghitung tabel ANOVA tersebut. Sintaks metode tersebut adalah with(data, sp.plot(blok, petak utama, anak petak, Y)).

with(oats,sp.plot(block=B, pplot=V, splot=N, Y=Y))
## 
## ANALYSIS SPLIT PLOT:  Y 
## Class level information
## 
## V    :  Victory Golden.rain Marvellous 
## N    :  0.0cwt 0.2cwt 0.4cwt 0.6cwt 
## B    :  I II III IV V VI 
## 
## Number of observations:  72 
## 
## Analysis of Variance Table
## 
## Response: Y
##     Df  Sum Sq Mean Sq F value    Pr(>F)    
## B    5 15875.3  3175.1     NaN       NaN    
## V    2  1786.4   893.2  1.4853    0.2724    
## Ea  10  6013.3   601.3     NaN       NaN    
## N    3 20020.5  6673.5 37.6856 2.458e-12 ***
## V:N  6   321.8    53.6  0.3028    0.9322    
## Eb  45  7968.7   177.1     NaN       NaN    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## cv(a) = 23.6 %, cv(b) = 12.8 %, Mean = 103.9722

Jumlah kuadrat dan kuadrat tengah galat sama, tetapi metode tersebut tidak dapat menguji pengaruh blok.

Karena setidaknya salah satu pengaruh konsentrasi pupuk nitrogen beda dari nol dan taraf faktor tersebut kuantitatif dengan jarak sama, dapat digunakan polinomial orthogonal sebagai uji lanjut. Polinomial orthogonal dapat dimasukkan dengan manual atau dengan contr.poly:

#contr.poly:
contrasts(oats$N)<-contr.poly(levels(oats$N))
aovSPlotRAK1<-aov(Y~V*N+B+Error(B:V),data=oats)
## Warning in aov(Y ~ V * N + B + Error(B:V), data = oats): Error() model is singular
summary(aovSPlotRAK1,split=list(N=list("Linear"=1, "Kuadratik"=2,
                                    "Kubik"=3)))
## 
## Error: B:V
##           Df Sum Sq Mean Sq F value Pr(>F)  
## V          2   1786     893   1.485 0.2724  
## B          5  15875    3175   5.280 0.0124 *
## Residuals 10   6013     601                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##                  Df Sum Sq Mean Sq F value   Pr(>F)    
## N                 3  20020    6674  37.686 2.46e-12 ***
##   N: Linear       1  19536   19536 110.323 1.09e-13 ***
##   N: Kuadratik    1    480     480   2.713    0.106    
##   N: Kubik        1      4       4   0.020    0.887    
## V:N               6    322      54   0.303    0.932    
##   V:N: Linear     2    168      84   0.475    0.625    
##   V:N: Kuadratik  2     11       6   0.031    0.969    
##   V:N: Kubik      2    142      71   0.402    0.671    
## Residuals        45   7969     177                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Terlihat bahwa pengaruh konsentrasi pupuk nitrogen linear setelah diuji melalui polinomial orthogonal.

6.3 Latihan Soal

  1. Petani John. Sumber: ANOVA and Mixed Models: A Short Intro Using R (Lukas Meier, 2018)

Petani John memiliki delapan petal tanah yang berbeda. Dia mengacak dan menerapkan dua “skema” pemupukan (“kontrol” dan “baru”) dengan cara yang seimbang ke delapan plot. Selain itu, setiap plot dibagi menjadi empat subplot. Di setiap plot, empat varietas stroberi yang berbeda diacak ke subplot. John tertarik pada efek skema pemupukan dan varietas stroberi pada massa buah. Per subplot, ia mencatat massa buah setelah jangka waktu tertentu. Buat bagan percobaan dan analisis datanya!

Data dapat diakses dengan sintaks R berikut:

book.url <- "http://stat.ethz.ch/~meier/teaching/book-anova"
john <- readRDS(url(file.path(book.url, "data/john.rds")))
summary(john)
##       plot     fertilizer variety      mass      
##  1      :4   control:16   A:8     Min.   : 7.70  
##  2      :4   new    :16   B:8     1st Qu.:11.57  
##  3      :4                C:8     Median :14.30  
##  4      :4                D:8     Mean   :13.94  
##  5      :4                        3rd Qu.:16.75  
##  6      :4                        Max.   :20.60  
##  (Other):8
  1. Benih

Dalam suatu percobaan tanaman, seorang petani menggunakan percobaan 2 faktor untuk melihat bagaimana kedua faktor tersebut mempunyai pengaruh terhadap pertumbuhan serta hasil tanaman, Untuk faktor pertama petani menggunakan (Takaran pupuk kandang: K1, K2, K3) diletakkan sebagai petak utama, sedangkan untuk faktor kedua (Jumlah benih per lubang: J1, J2, J3) dianggap sebagai anak petak. Setiap perlakuan diulang sebanyak 3 kali, dan unit-unit percobaan diasumsikan homogen.

Buat bagan dan analisis datanya!

  1. Buat plot interaksi untuk data oats! Pisahkan plot tersebut menjadi facet untuk tiap blok.