Lecture 3 Linear Regression

3.1 Overview

In this lecture we will introduce linear regression. We will start with the simple linear regression in Section 3.2 and focus on the history, model assumptions, and properties of the least squares estimator. Finally, we will extend this model by adding more covariates to obtain a multiple linear regression in Section 3.3 and in Section 3.4 finally show that with likelihood estimation we obtain the same result as with OLS.

3.2 Simple Linear Regression

3.2.1 History on Linear Models

Linear models have a rich history, tracing back to early statistical work in the 19th century. One foundational study about the concept of “regression” was conducted by Sir Francis Galton, who explored the relationship between the heights of parents and their children: 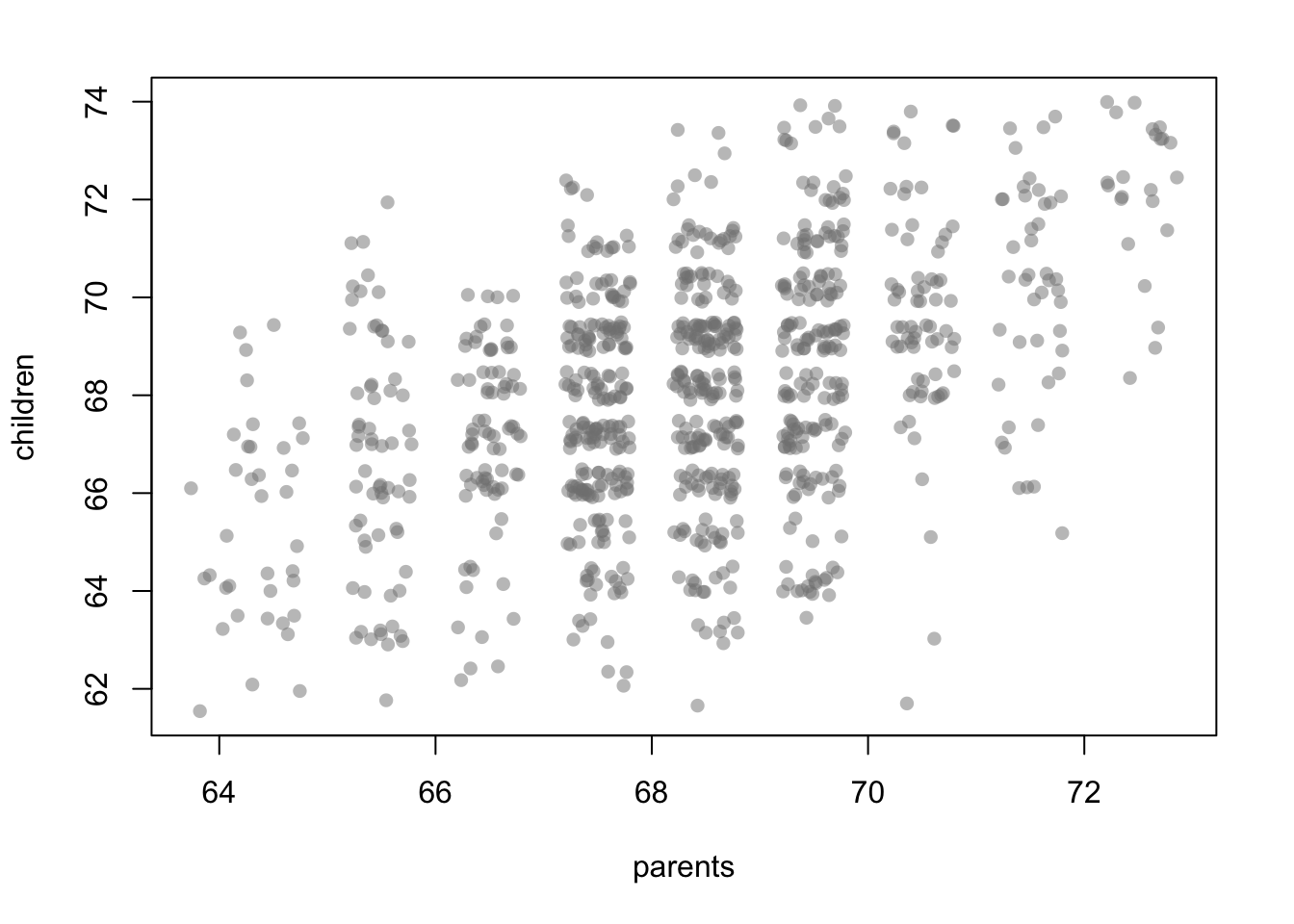In the plot it can be observed that an extreme value in the heights of the parents does not automatically lead to an extreme value for the child. Instead, there is a tendency to “regress to” the (conditional) mean.

3.2.2 Regression Equation

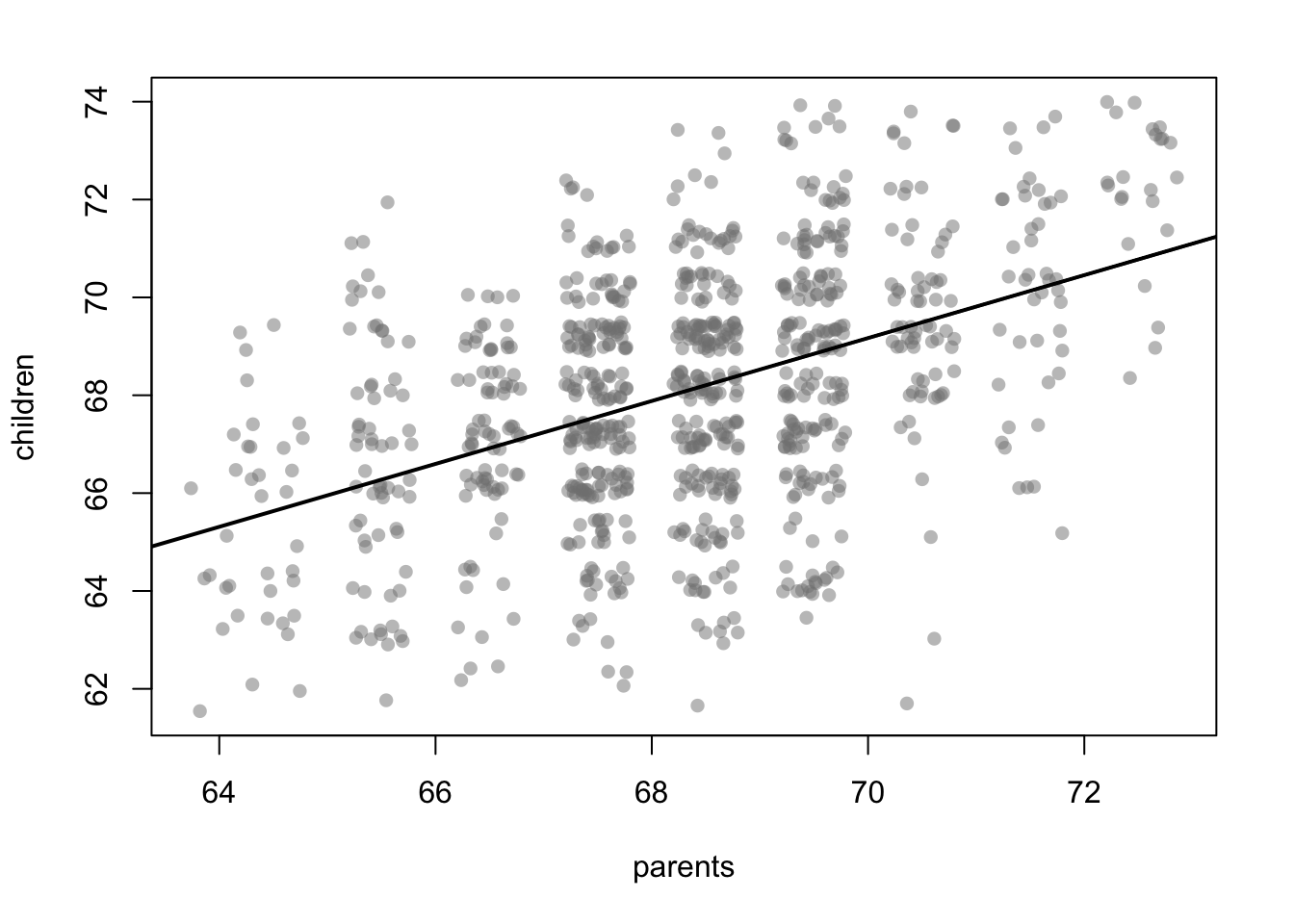
To capture this relationship between two variables, a simple linear line that represents this conditional mean of the data, can be used.

We explain a so-called response variable $Y_i$ by using the function $f(x_i)$, which models the average relationship between the covariates and the response. Moreover, we add $\varepsilon_i$ as a residual (error term) to capture the unexplainable random noise.

$$\begin{array}{lllll} Y_i & = & f(x_i) & + & \varepsilon_i \\ \mbox{response} & = & \mbox{average} & + & \mbox{error} \\ \mbox{variable} & & \mbox{relationship} & & \mbox{term} \\ \end{array}$$

There are many different options to model equation $f(x_i)$. In our case with only one covariate, a simple linear line can be used to represent the conditional mean of the data: $$Y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$$ i.e. $$f(x_i) = \beta_0 + \beta_1 x_i$$ where $\beta_0$ is the intercept, $\beta_1$ the slope coefficient, and $x_i$ a single covariate. The challenge now is determining how to find the best estimates for $\beta_0$ and $\beta_1$ that accurately fit the data.

3.2.3 Concept: Least Squares Estimation

Carl Friedrich Gauss’ development of the method of least squares provided an elegant solution to this problem. The core idea is to minimize the sum of squared differences between the regression line and the observed data:

$$\left(\hat{\beta_0}, \hat{\beta_1} \right)^\top = \underset{\beta_0, \beta_1}{\operatorname{argmin}} \sum_{i=1}^n \left(Y_i - (\beta_0 + \beta_1 x_i) \right)^2 \\ \text{where} \quad Y_i - (\beta_0 + \beta_1 x_i) = \varepsilon_i$$

Squaring the differences ensures that larger deviations are given more weight and eliminates the issue of residuals canceling each other out due to differing signs.

In the case of Sir Francis Galton’s height example the resulting regression line looks as follows:

3.2.4 Application: Least Squares Estimation

For a better understanding we provide an interactive shiny application. The example used in the app focuses on the influence of speed in mph on the braking distance in feet. We mark the data points in blue and the regression line in red. Further, the plot shows three green squares, which represent the squared residuals of three random observations. Summing up these squares over all data points yields the residual sum of squares $SSR$ which is shown in the top left corner. You can move the sliders and observe how the red regression line adapts. Since minimizing the $SSR$ is the goal in OLS estimation, aim to reduce it in order to find the best fit.

Click here for the full version of the ‘Linear Regression’ shiny app.

3.2.5 Model Assumptions

• The error terms are independently and identically distributed (iid) with $E(\varepsilon_i) = 0$ and $\mathop{\mathrm{Var}}(\varepsilon_i) = \sigma^2$ (homoscedastic variance).

• For determining Test- and Confidence Intervals we additionally assume the error terms $\varepsilon_i$ to be normally distributed, i.e. $\varepsilon_i \sim N(0,\sigma^2)$.

Thus, the resulting distribution of $Y_i$ is

• $E(Y_i) = E(\beta_0 + \beta_1 x_i + \varepsilon_i) = \beta_0 + \beta_1 x_i + E(\varepsilon_i) = \beta_0 + \beta_1 x_i,$
• $\mathop{\mathrm{Var}}(Y_i) = \mathop{\mathrm{Var}}(\beta_0 + \beta_1 x_i + \varepsilon_i) = \mathop{\mathrm{Var}}(\varepsilon_i) = \sigma^2,$ $$\Rightarrow Y_i \overset{iid}{\sim} N(\beta_0 + \beta_1 x_i,\sigma^2).$$

3.2.6 Result: Least Squares Estimator

The least squares estimators for the intercept and the slope are:

• $\hat{\beta_1} = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}$
• $\hat{\beta_0} = \bar{y} - \beta_1 \bar{x}$

We provide a full derivation of both results in the following dropdown:

Derivation

We start with the sum of squared residuals (SSR) for a simple linear regression model:

$$SSR = \sum_{i=1}^n \left( y_i - (\beta_0 + \beta_1 x_i) \right)^2$$

The goal is to minimize $SSR$ with respect to $\beta_0$ and $\beta_1$. To do so, we take partial derivatives with respect to $\beta_0$ and $\beta_1$, and set them to zero:

1. Partial Derivative with Respect to $\beta_0$: $$\frac{\partial SSR}{\partial \beta_0} = -2 \sum_{i=1}^n \left( y_i - (\beta_0 + \beta_1 x_i) \right) = 0$$

   Simplify: $$\sum_{i=1}^n y_i = n\beta_0 + \beta_1 \sum_{i=1}^n x_i$$

   Rearrange to express the first equation: $$\beta_0 n + \beta_1 \sum_{i=1}^n x_i = \sum_{i=1}^n y_i \tag{1}$$

2. Partial Derivative with Respect to $\beta_1$: $$\frac{\partial SSR}{\partial \beta_1} = -2 \sum_{i=1}^n x_i \left( y_i - (\beta_0 + \beta_1 x_i) \right) = 0$$

   Simplify: $$\sum_{i=1}^n x_i y_i = \beta_0 \sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2$$

   Rearrange to express the second equation: $$\beta_0 \sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2 = \sum_{i=1}^n x_i y_i \tag{2}$$

---

From equations (1) and (2), we now solve for $\beta_0$ and $\beta_1$:

1. Rewrite equation (1) for $\beta_0$: $$\beta_0 = \frac{1}{n} \left( \sum_{i=1}^n y_i - \beta_1 \sum_{i=1}^n x_i \right)$$

2. Substitute this expression for $\beta_0$ into equation (2): $$\frac{1}{n} \left( \sum_{i=1}^n y_i - \beta_1 \sum_{i=1}^n x_i \right) \sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2 = \sum_{i=1}^n x_i y_i$$

3. Simplify to isolate $\hat{\beta_1}$: $$\beta_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

   Where $\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i$ and $\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$.

4. Use the value of $\beta_1$ to compute $\hat{\beta_0}$: $$\beta_0 = \bar{y} - \beta_1 \bar{x}$$

3.2.7 Properties of the Least Squares Estimator

There are two important properties of the LS-estimator: unbiasedness and consistency.

• Unbiased: The LS-estimator is unbiased, i.e. $$E(\hat{\beta}_0) = \beta_0, \qquad E(\hat{\beta}_1) = \beta_1.$$

• Variance: $$\begin{aligned} \mathop{\mathrm{Var}}(\hat{\beta}_0) & = & \sigma^2 \displaystyle \frac{\sum\limits_{i=1}^{n} x_i^2}{n \sum\limits_{i=1}^{n} (x_i-\bar{x})^2}, \\ \mathop{\mathrm{Var}}(\hat{\beta}_1) & = & \displaystyle \frac{\sigma^2}{\sum\limits_{i=1}^{n} (x_i-\bar{x})^2}.\end{aligned}$$

• If $n \rightarrow \infty$ $$\sum\limits_{i=1}^{n} (x_i - \bar{x})^2 \rightarrow \infty$$ holds, $\hat{\beta}_0$ and $\hat{\beta}_1$ are consistent as well since the variances decrease towards zero.

In the following we provide proofs for both conditions:

Proof: Unbiasedness

1. Estimator for $\hat{\beta}_1$

The formula for the slope estimator $\hat{\beta}_1$ is:

$$\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

Substitute $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$ and break into terms:

$$\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x}) \left(\beta_0 + \beta_1 x_i + \varepsilon_i - \bar{y}\right)}{\sum_{i=1}^n (x_i - \bar{x})^2} \\= \frac{\sum_{i=1}^n (x_i - \bar{x}) \left(\beta_0 - \bar{y}\right) + \sum_{i=1}^n (x_i - \bar{x}) \beta_1 x_i + \sum_{i=1}^n (x_i - \bar{x}) \varepsilon_i}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

The first term simplifies because:

$$\sum_{i=1}^n (x_i - \bar{x}) = 0 \quad (\text{since } \bar{x} \text{ is the mean of } x_i)$$

For the second term:

$$\sum_{i=1}^n (x_i - \bar{x}) x_i = \sum_{i=1}^n (x_i - \bar{x}) (\bar{x} + (x_i - \bar{x})) = \sum_{i=1}^n (x_i - \bar{x})^2$$

So this term simplifies to:

$$\beta_1 \sum_{i=1}^n (x_i - \bar{x})^2$$

For the third term:

$$\sum_{i=1}^n (x_i - \bar{x}) \varepsilon_i$$

Since $\varepsilon_i$ is iid random with $\mathbb{E}[\varepsilon_i] = 0$, its expectation is:

$$\mathbb{E}\left[\sum_{i=1}^n (x_i - \bar{x}) \varepsilon_i\right] = 0$$

Thus, the expectation of $\hat{\beta}1$ is:

$$\mathbb{E}\left[\hat{\beta}_1\right] = \frac{\beta_1 \sum_{i=1}^n (x_i - \bar{x})^2}{\sum_{i=1}^n (x_i - \bar{x})^2} = \beta_1.$$

---

2. Estimator for $\hat{\beta}_0$

The formula for the intercept estimator $\hat{\beta}_0$ is:

$$\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}$$

Substitute $\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$ and $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$:

$$\bar{y} = \frac{1}{n} \sum_{i=1}^n (\beta_0 + \beta_1 x_i + \varepsilon_i) = \beta_0 + \beta_1 \bar{x} + \bar{\varepsilon}$$

Here, $\bar{\varepsilon} = \frac{1}{n} \sum_{i=1}^n \varepsilon_i$, and since $\mathbb{E}[\varepsilon_i] = 0$, we have $\mathbb{E}[\bar{\varepsilon}] = 0$

Now substitute into $\hat{\beta}_0$:

$$\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x} = (\beta_0 + \beta_1 \bar{x} + \bar{\varepsilon}) - \hat{\beta}_1 \bar{x}$$

Taking the expectation: $$\mathbb{E}\left[\hat{\beta}_0\right] = \beta_0 + \beta_1 \bar{x} - \mathbb{E}\left[\hat{\beta}_1\right] \bar{x}$$

From the previous result, $\mathbb{E}\left[\hat{\beta}_1\right] = \beta_1$. Substituting:

$$\mathbb{E}\left[\hat{\beta}_0\right] = \beta_0 + \beta_1 \bar{x} - \beta_1 \bar{x} = \beta_0$$

Proof: Variance and Consistency

1. Variance of $\hat{\beta}_1$:

Using the definition of $\hat{\beta}_1$:

$$\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i-\bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

We can rewrite the numerator: $$\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(\beta_0 + \beta_1x_i+\varepsilon_i-\bar{\beta_0} - \bar{\beta_1}\bar{x} - \bar{\varepsilon})}{\sum_{i=1}^n (x_i - \bar{x})^2}$$ Since the coefficients are constants, we can rewrite $\bar{\beta_0} = \beta_0$ and $\bar{\beta_1} = \beta_1$. Furthermore, by definition $\bar{\varepsilon} = 0$. Hence, the numerator can be summarized as: $$\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(\beta_1(x_i-\bar{x})+\varepsilon_i)}{\sum_{i=1}^n (x_i - \bar{x})^2} \\ = \beta_1 + \frac{\sum_{i=1}^n (x_i - \bar{x})\varepsilon_i}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

We take the variance: $$\text{Var}(\hat{\beta_1}) = \text{Var}\left( \beta_1 + \frac{\sum_{i=1}^n (x_i - \bar{x})\varepsilon_i}{\sum_{i=1}^n (x_i - \bar{x})^2}\right)$$ Since the coefficient $\beta_1$ is assumed as fix, its (co-)variance is equal to zero:

$$\text{Var}(\hat{\beta}_1) = \text{Var}\left(\frac{\sum_{i=1}^n (x_i - \bar{x}) \varepsilon_i}{\sum_{i=1}^n (x_i - \bar{x})^2}\right)$$

The denominator $\sum_{i=1}^n (x_i - \bar{x})^2$ is a constant, so we can pull it out by squaring:

$$\text{Var}(\hat{\beta}_1) = \frac{\text{Var}\left(\sum_{i=1}^n (x_i - \bar{x}) \varepsilon_i\right)}{\left(\sum_{i=1}^n (x_i - \bar{x})^2\right)^2}$$ Now the only random part are the $\varepsilon_i$, which are independent and identically distributed with $\text{Var}(\varepsilon_i) = \sigma^2$. The variance of this weighted sum of independent variables is:

$$\text{Var}\left(\sum_{i=1}^n (x_i - \bar{x}) \varepsilon_i\right) = \sum_{i=1}^n (x_i - \bar{x})^2 \text{Var}(\varepsilon_i) \\ = \sigma^2 \sum_{i=1}^n (x_i - \bar{x})^2$$

Thus:

$$\text{Var}(\hat{\beta}_1) = \frac{\sigma^2 \sum_{i=1}^n (x_i - \bar{x})^2}{\left(\sum_{i=1}^n (x_i - \bar{x})^2\right)^2}$$

Simplify: $$\text{Var}(\hat{\beta}_1) = \frac{\sigma^2}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

---

2. Variance of $\hat{\beta}_0$:

Using $\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}$, the variance is:

$$\text{Var}(\hat{\beta}_0) = \text{Var}(\bar{y}) + \bar{x}^2 \text{Var}(\hat{\beta}_1) - 2\bar{x} \, \text{Cov}(\bar{y}, \hat{\beta}_1)$$

Variance of $\bar{y}$: Since $\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$ and $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$, the variance of $\bar{y}$ is:

$$\text{Var}(\bar{y}) = \frac{\sigma^2}{n}$$

Covariance of $\bar{y}$ and $\hat{\beta}_1$: We add this term since both $\bar{y}$ and $\hat{\beta}_1$ consist of the random variable $\varepsilon_i$. However, the covariance $\text{Cov}(\bar{y}, \hat{\beta}_1)$ is 0 because $\bar{y}$ depends on the average of $\varepsilon_i$, which is zero by definition. Further, $\hat{\beta}_1$ depends on the deviations from $\bar{x}$ (see above), which are orthogonal to $\bar{y}$.

Combine terms: Substitute into the formula:

$$\text{Var}(\hat{\beta}_0) = \frac{\sigma^2}{n} + \bar{x}^2 \frac{\sigma^2}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

Factor out $\frac{\sigma^2}{\sum_{i=1}^n (x_i - \bar{x})^2}$:

$$\text{Var}(\hat{\beta}_0) = \frac{\sigma^2 \sum_{i=1}^n x_i^2}{n \sum_{i=1}^n (x_i - \bar{x})^2}$$

3. Consistency

Both terms tend towards zero when $n \to \infty$:

For $\text{Var}(\hat{\beta_1})$: $$\lim_{n \to \infty} \frac{\sigma^2}{\sum_{i=1}^n (x_i - \bar{x})^2} = 0$$

For $\text{Var}(\hat{\beta_0})$: $$\lim_{n \to \infty} \frac{\sigma^2 \sum_{i=1}^n x_i^2}{n \sum_{i=1}^n (x_i - \bar{x})^2} = 0$$

Unless the $x_i$’s are constant (which they’re not in most cases), the sums in both denominators keeps increasing as you add more data points.

Hence, the estimators are asymptotically efficient.

3.3 Multiple Linear Regression

Until now we only considered models with one covariate $X$. From now on consider $p$ covariates $X_1,\dots,X_p$ with observations $x_{1},\dots,x_{n}$ for each covariate. Extending the example from above, we could probably also be interested in the parents’ income or the diet of the children as influence factors of the height.

General model assumption: $$\begin{array}{lllll} Y_i & = & f(x_i) & + & \varepsilon_i \\ \mbox{response} & = & \mbox{average} & + & \mbox{error} \\ \mbox{variable} & & \mbox{relationship} & & \mbox{term} \\ \end{array}$$

From now we call this model just linear model.

3.3.1 Model Formulation

The formula of the linear regression model is as follows:

$$Y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} + \varepsilon_i,$$ i.e., $$f(x_{i1},\dots,x_{ip}) = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}$$

In matrix notation this can be rewritten as: $$\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon},$$

where:

• $\mathbf{y}$ is an $n \times 1$ vector of observed responses,
• $\mathbf{X}$ is an $n \times (p+1)$ design matrix (with rows corresponding to observations and columns to predictors, including a column of $1$s for the intercept),
• $\boldsymbol{\beta}$ is a $(p+1) \times 1$ vector of coefficients to be estimated,
• $\boldsymbol{\varepsilon}$ is an $n \times 1$ vector of residuals (assumed to be i.i.d. with $\varepsilon \sim N(0, \sigma^2 \mathbf{I})$).

3.3.2 Least Squares Estimation

Estimate the unknown regression coefficients by minimizing the squared differences between $Y_i$ and $\beta_0+\beta_1 x_{i1} + \ldots + \beta_p x_{ip}$:

$$\hat{\boldsymbol{\beta}} = \left(\hat{\beta_0}, \dots, \hat{\beta_p} \right)^\top = \underset{\beta_0, \dots, \beta_p}{\operatorname{argmin}} LS(\beta_0,\beta_1,\dots,\beta_p)$$

with $LS$ being the least squares criterion: $$LS(\beta_0,\beta_1,\dots,\beta_p) := \sum_{i=1}^{n} ({ Y_i} - \beta_0 - \beta_1 x_{i1} - \ldots - \beta_p x_{ip})^2$$

The derivation of the coefficient vector is provided in the dropdown:

Derivation

Goal: Minimize the Residual Sum of Squares ($SSR$)

The least squares criterion equals the residual sum of squares ($SSR$). In matrix notation it is formulated as: $$\text{SSR}(\boldsymbol{\beta}) = \|\mathbf{y} - \mathbf{X}\boldsymbol{\beta}\|^2 = (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^\top (\mathbf{y} - \mathbf{X}\boldsymbol{\beta}).$$

Expanding the quadratic form: $$\text{SSR}(\boldsymbol{\beta}) = \mathbf{y}^\top \mathbf{y} - 2\boldsymbol{\beta}^\top \mathbf{X}^\top \mathbf{y} + \boldsymbol{\beta}^\top \mathbf{X}^\top \mathbf{X} \boldsymbol{\beta}.$$

Expanding the quadratic form: $$\text{SSR}(\boldsymbol{\beta}) = \mathbf{y}^\top \mathbf{y} - 2\boldsymbol{\beta}^\top \mathbf{X}^\top \mathbf{y} + \boldsymbol{\beta}^\top \mathbf{X}^\top \mathbf{X} \boldsymbol{\beta}.$$

Step 1: First-order condition:

To minimize $\text{SSR}(\boldsymbol{\beta})$, take the derivative with respect to $\boldsymbol{\beta}$ and set it equal to zero:

$$\frac{\partial \text{SSR}(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = -2 \mathbf{X}^\top \mathbf{y} + 2 \mathbf{X}^\top \mathbf{X} \boldsymbol{\beta} = 0.$$

Simplify: $$\mathbf{X}^\top \mathbf{X} \boldsymbol{\beta} = \mathbf{X}^\top \mathbf{y}.$$

Step 2: Solve for $\boldsymbol{\beta}$:

If $\mathbf{X}^\top \mathbf{X}$ is invertible (i.e., $\mathbf{X}$ has full column rank), we can solve for $\boldsymbol{\beta}$ as: $$\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}.$$ Thus, this is the OLS estimator for $\boldsymbol{\beta}$.

3.3.3 Interpretation

For $\beta_{0}:$ The average $Y_i$ if all $x_{i1},\dots,x_{ip}$ are zero.

For $\beta_{j}$ with $j>0$:

• $\beta_{j} > 0$: If the covariate $X_j$ increases by one unit, the response variable $Y$ increases (ceteris paribus) by $\beta_j$ on average.
• $\beta_{j} < 0$: If the covariate $X_j$ increases by one unit, the response variable $Y$ decreases (ceteris paribus) by $\beta_j$ on average.

3.4 Likelihood Estimation

With the Gaussian error we can also use likelihood inference:

$$Y_i \overset{iid}{\sim} N(\beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} ,\sigma^2)$$

This yields the same result as LS-estimation:

Proof

1. Likelihood Function

Given the normality of the residuals $\varepsilon_i$, the likelihood of observing the data $y = (y_1, \dots, y_n)^\top$ given the parameters $\boldsymbol{\beta}$ and $\sigma^2$ is:

$$L(\boldsymbol{\beta}, \sigma^2 | y) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - \mathbf{x}_i^\top \boldsymbol{\beta})^2}{2\sigma^2}\right),$$

where $\mathbf{x}_i = (1, x_{i1}, x_{i2}, \dots, x_{ip})^\top$ is the vector of predictors for the $i$-th observation.

The log-likelihood function is: $$\ell(\boldsymbol{\beta}, \sigma^2 | y) = -\frac{n}{2} \log(2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (y_i - \mathbf{x}_i^\top \boldsymbol{\beta})^2.$$

2. Maximizing the Log-Likelihood

To estimate $\boldsymbol{\beta}$, we maximize the log-likelihood $\ell(\boldsymbol{\beta}, \sigma^2 | y)$ w.r.t. to it.

Since $-\frac{n}{2} \log(2\pi\sigma^2)$ does not depend on $\boldsymbol{\beta}$, we focus on the second term:

$$Q(\boldsymbol{\beta}) = -\frac{1}{2\sigma^2} \sum_{i=1}^n (y_i - \mathbf{x}_i^\top \boldsymbol{\beta})^2.$$

Maximizing $Q(\boldsymbol{\beta})$ with respect to $\boldsymbol{\beta}$ is equivalent to minimizing:

$$SSR(\boldsymbol{\beta}) = \sum_{i=1}^n (y_i - \mathbf{x}_i^\top \boldsymbol{\beta})^2 = \|\mathbf{y} - \mathbf{X}\boldsymbol{\beta}\|^2,$$ which is equivalent to the LS criterion (Residual Sum of Squares: $SSR$). Consequently, the resulting estimators are equivalent, too.

Likelihood estimation has an advantage over OLS because it utilizes the full probability distribution of the data and thus more information. While OLS minimizes residuals and focuses on the relationship between predictors and the response, likelihood estimation incorporates information about the variance structure and shape of the residual distribution, enabling more efficient parameter estimates and richer inference. It allows for estimating additional parameters (e.g., error variance) and allows for hypothesis testing, model comparison, and application to more complex models like GLMs.