5 Series temporales
Fecha última actualización: 2025-11-24
Instalación/carga librerías/datos utilizados
if (!require(zoo)) install.packages('zoo')
library(zoo)
if (!require(urca)) install.packages('urca')
library(urca)
if (!require(GGally)) install.packages('GGally')
library(GGally)
if (!require(pxR)) install.packages('pxR')
library(pxR)
if (!require(fpp3)) install.packages('fpp3')
library(fpp3)
if (!require(tidyverse)) install.packages('tidyverse')
library(tidyverse)
source("utilidades.R")Las series temporales son datos que van cambiando a la largo del tiempo, como por ejemplo la población mundial a lo largo de los años o los datos de facturación diaria de una empresa o el consumo energético por horas en una ciudad. Dada su gran importancia dedicaremos este capítulo a estudiarlas como un caso especial de análisis exploratorio de datos. Aquí veremos una breve introducción al tema. Para un análisis más detallado ver, por ejemplo, [HyAt21].
5.1 Los objetos tsibble
Para almacenar y gestionar las series temporales utilizaremos un tipo de objeto especial que se llama tsibble de la librería fpp3 especializado en la gestión de series temporales. Esencialmente un tsibble es un tibble en el que unos de los campos es una variable temporal que se gestiona de forma especial. Vamos a introducir las características de un objeto tsibble a través de un ejemplo: vamos a leer una tabla con los datos de la evolución anual de la población por países y regiones donde seleccionaremos la población mundial y la de tres continentes.
owid_population <- read_csv("https://ctim.es/AEDV/data/owid_population.csv") %>%
as_tibble() %>%
filter(
Entity == "World" |
Entity == "Europe" |
Entity == "Asia" |
Entity == "Africa"
)
owid_population## # A tibble: 888 × 4
## Entity Code Year `Population (historical estimates)`
## <chr> <chr> <dbl> <dbl>
## 1 Africa <NA> 1800 81273172
## 2 Africa <NA> 1801 81313551
## 3 Africa <NA> 1802 81418900
## 4 Africa <NA> 1803 81525621
## 5 Africa <NA> 1804 81633731
## 6 Africa <NA> 1805 81743247
## 7 Africa <NA> 1806 81854174
## 8 Africa <NA> 1807 81966528
## 9 Africa <NA> 1808 82080332
## 10 Africa <NA> 1809 82195596
## # ℹ 878 more rowsA continuación construimos un tsibble a partir de esta tabla
tsibble(
date = owid_population$Year,
population = owid_population$`Population (historical estimates)`,
location = owid_population$Entity,
index = date,
key = location
)Uno de los campos del tsibble siempre es un dato temporal, en este ejemplo, el año. Al construir el tsibble hay que identificar ese campo usando el nombre index. Además, cuando como en este caso, hay varias series temporales, hay que identificar con el nombre key el campo (o campos) que identifican estas series temporales de tal forma que para cada combinación de los campos indexy key hay, como máximo, una sola fila (registro) en la tabla.
La porción de código anterior para crear un tsibble es equivalente a la siguiente donde construimos el tsibble añadiendo a un tibble la información sobre que campos corresponden a index y key:
owid_population <- owid_population %>%
select(
date=Year,
population=`Population (historical estimates)`,
location=Entity
)%>%
as_tsibble(index = date,key=location)
owid_population## # A tsibble: 888 x 3 [1Y]
## # Key: location [4]
## date population location
## <dbl> <dbl> <chr>
## 1 1800 81273172 Africa
## 2 1801 81313551 Africa
## 3 1802 81418900 Africa
## 4 1803 81525621 Africa
## 5 1804 81633731 Africa
## 6 1805 81743247 Africa
## 7 1806 81854174 Africa
## 8 1807 81966528 Africa
## 9 1808 82080332 Africa
## 10 1809 82195596 Africa
## # ℹ 878 more rowsEs muy importante que el tipo de la variable temporal usada en la serie temporal coincida con la frecuencia a la que se toman los datos. Por ejemplo, en el tibble anterior los datos son anuales, y podemos observar que el tssible lo reconoce correctamente porque al imprimirlo, en la primera línea aparece [1Y]. Si los datos son mensuales, debe aparecer [1M]. Por tanto, si no se reconoce automáticamente la frecuencia temporal, hay que hacer un mutate para convertir la variable temporal a la frecuencia adecuada usando las funciones yearquarter, yearmonth, yearweek. Si la variable es tipo Date estándar, se entiende la frecuencia es diaria (es decir, un dato por día).
5.2 Visualización
Vamos a visualizar estas series temporales usando la función autoplot:
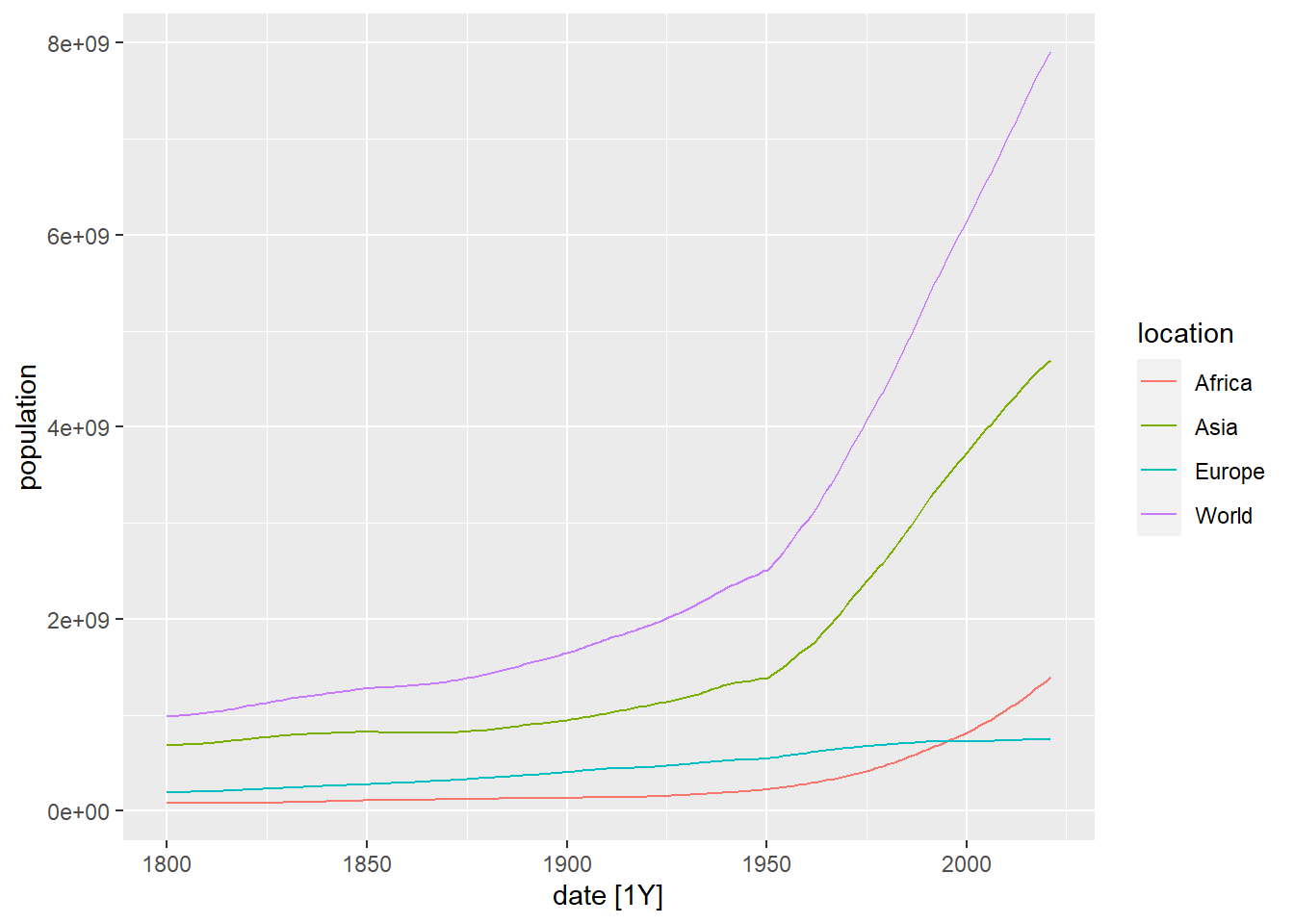
Figure 5.1: Dibujo de la evolución de la población en el mundo, Africa, Asia y Europa usando autoplot
A continuación dibujamos las mismas series separando cada una en una gráfica:
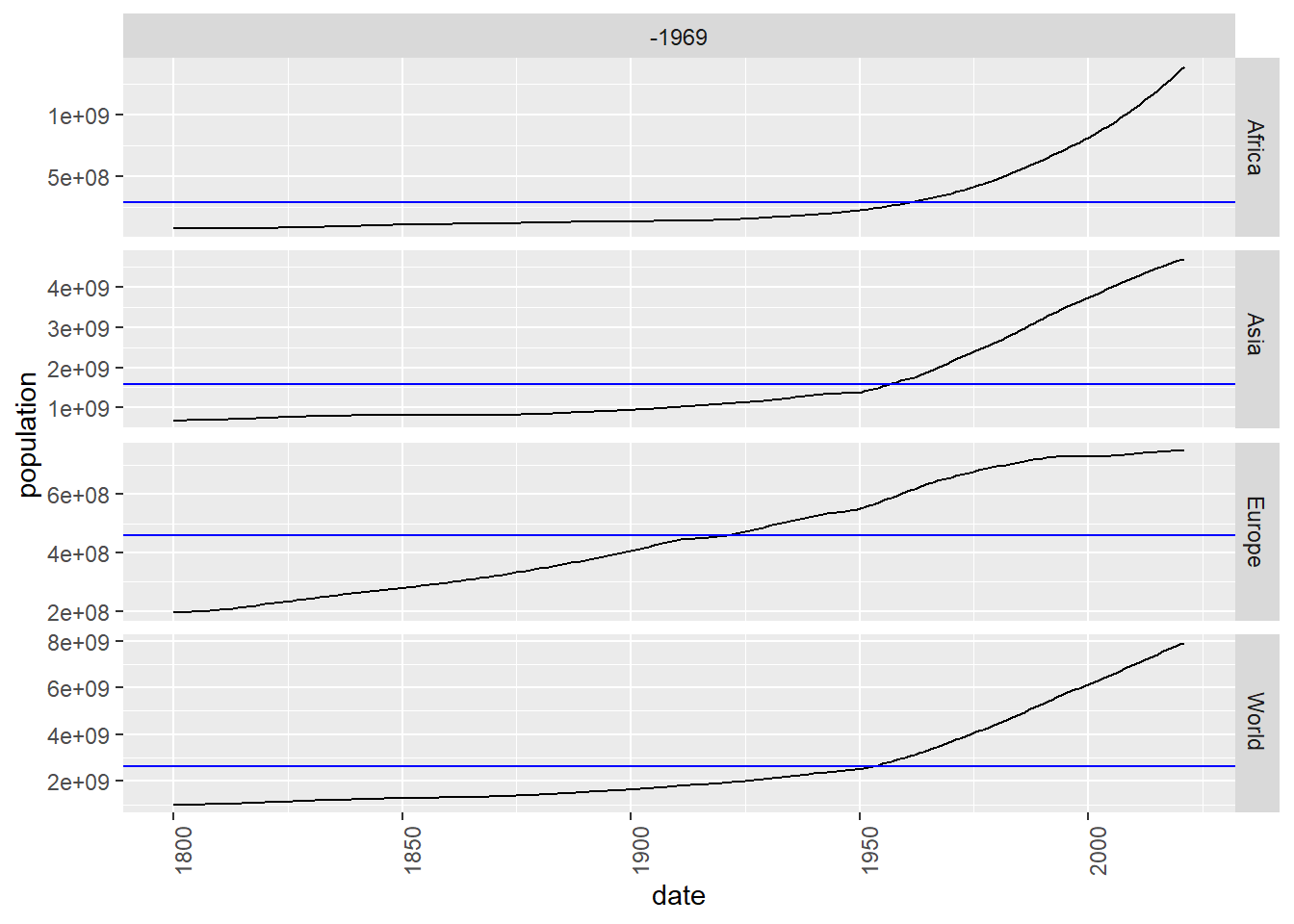
Figure 5.2: Dibujo por separado de la evolución de la población en el mundo, Africa, Asia y Europa usando gg_subseries
Ahora hacemos los mismo pero poniendo las gráficas en forma de cuadrícula. Como podemos observar, es posible utilizar la función ggplot para dibujar tsibbles:
owid_population %>%
ggplot(aes(x=date,y=population)) +
geom_line() +
facet_wrap(~location,scales = "free") 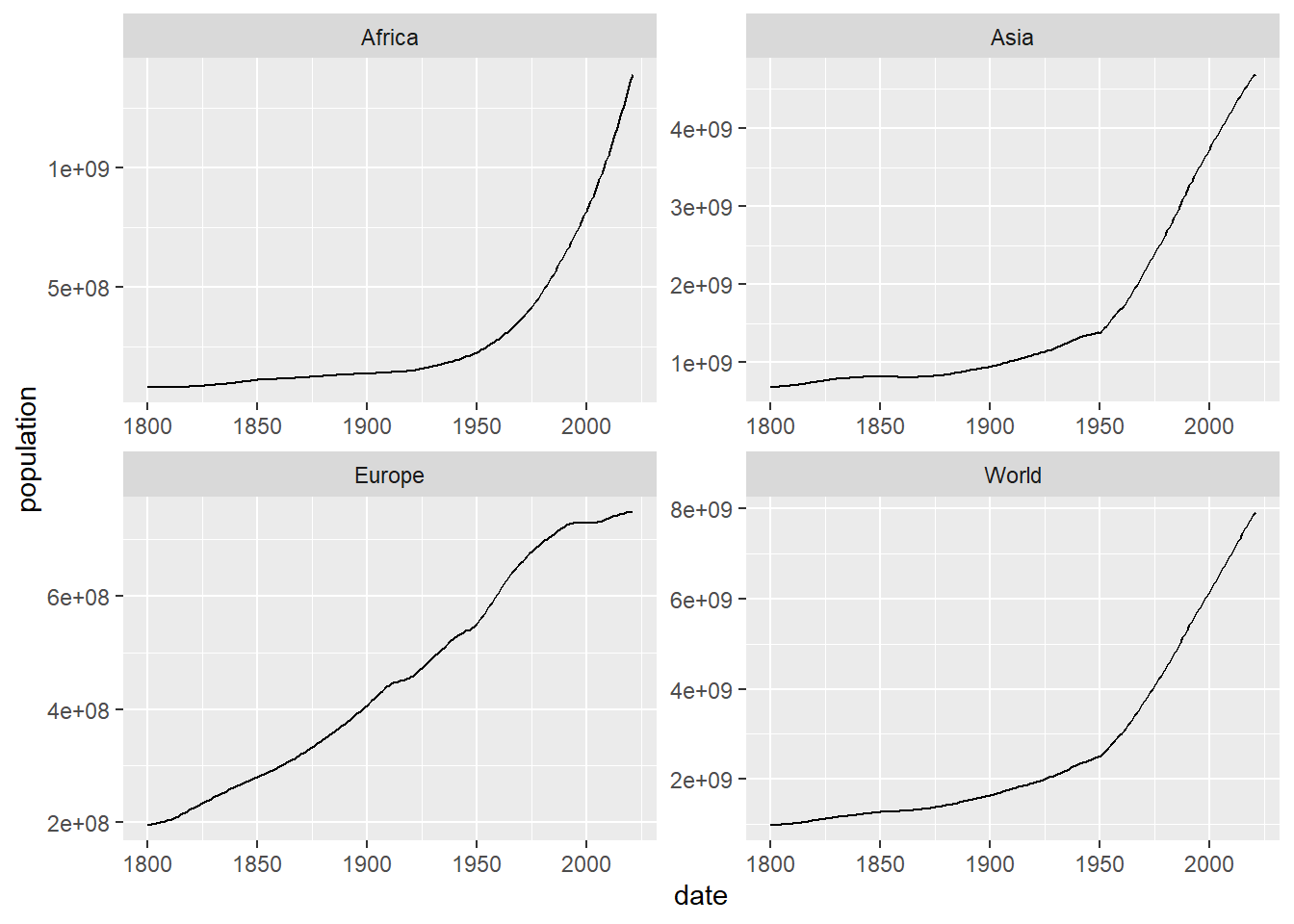
Figure 5.3: Dibujo por separado, en una cuadrícula, de la evolución de la población en el mundo, Africa, Asia y Europa usando facet_wrap
Podemos también comparar las series temporales entre sí. En la siguiente tabla con gráficos, construida usando la función pivot_wider y ggpairs de la librería GGally se muestra, en la diagonal, la función de densidad de la distribución de valores, en la parte inferior los gráficos de puntos que ponen en correspondencia los valores de una serie con otra y en la parte superior el valor de la correlación entre cada par de series de datos, cuanto más cerca de 1 está ese valor, mejor se ajusta a la recta de regresión los valores combinados de cada par de series temporales. Podemos observar que la evolución de la población en Europa tiene un comportamiento diferente que en las otras regiones lo que produce un menor valor de la correlación al comparar Europa con la otras regiones.
owid_population %>%
pivot_wider(values_from=population, names_from=location) |>
GGally::ggpairs(columns = 2:5)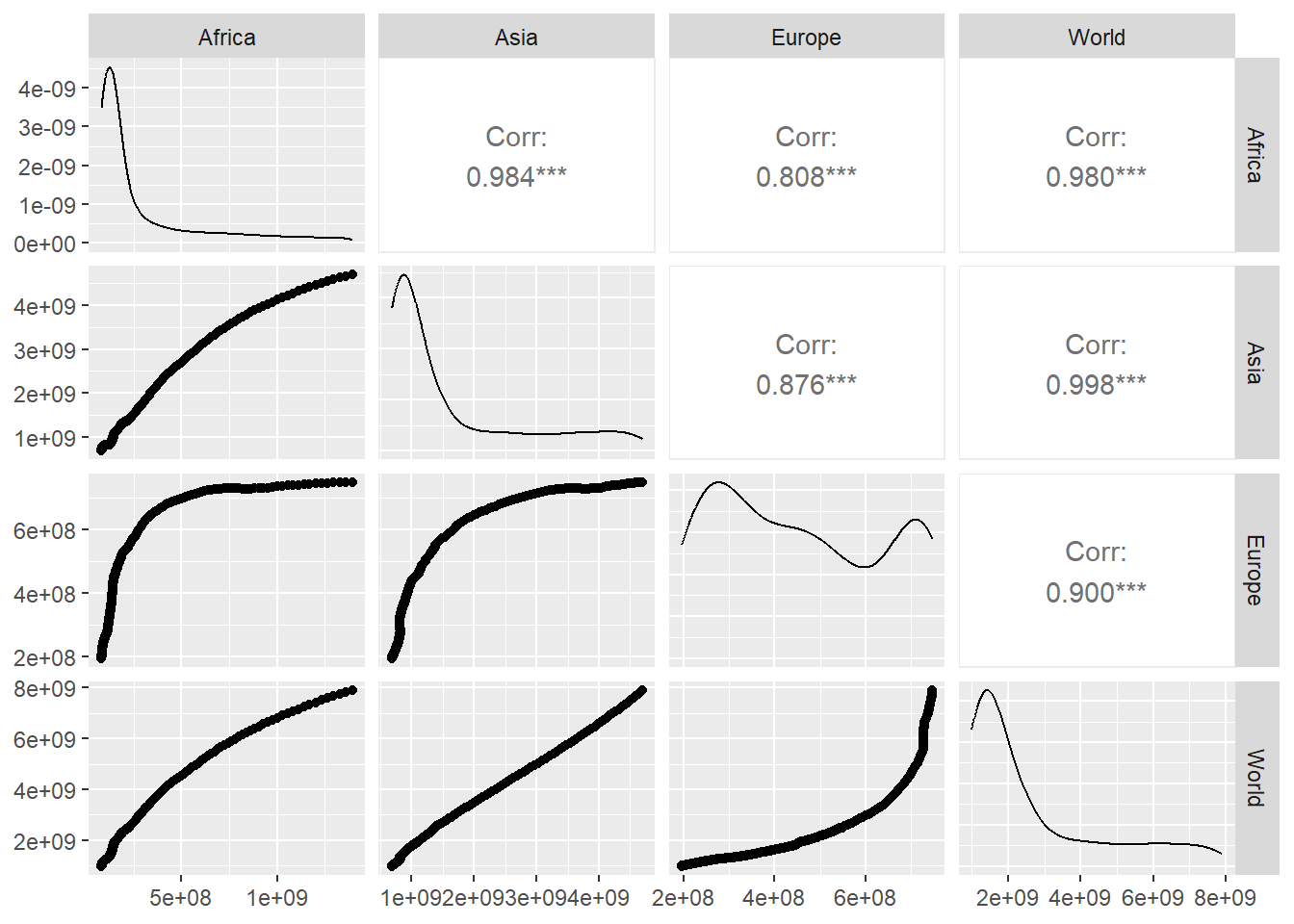
Figure 5.4: Ilustración de la relación entre la evolución de la población en el mundo, Africa, Asia y Europa usando la función ggpairs
5.3 Estacionalidad
Muchas series temporales presentan estacionalidad. Por ejemplo, en un lugar turístico como Canarias, los movimientos mensuales de pasajeros en los aeropuertos dependen del mes de año, de acuerdo con los flujos estacionales de turistas. En este caso, nuestra serie temporal tiene una estacionalidad de 12. Por ejemplo, observamos que, cada año, en agosto es cuando más pasajeros hay y que en enero/febrero es cuando suele haber menos. Vamos a estudiar las llegadas mensuales de pasajeros a Canarias utilizando una consulta realizada al ISTAC y almacenada en nuestra carpeta local data.
istac_aeropuertos <- read.px("https://ctim.es/AEDV/data/istac_aeropuertos.px") %>%
as_tibble()
istac_aeropuertos## # A tibble: 355 × 5
## Periodos Aeropuertos.de.origen Aeropuertos.de.destino Clases.de.tráfico
## <fct> <fct> <fct> <fct>
## 1 2020 Abril (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 2 2020 Marzo (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 3 2020 Febrero … TOTAL AEROPUERTOS DE… CANARIAS Regular
## 4 2020 Enero (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 5 2019 TOTAL (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 6 2019 Diciembr… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 7 2019 Noviembr… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 8 2019 Octubre … TOTAL AEROPUERTOS DE… CANARIAS Regular
## 9 2019 Septiemb… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 10 2019 Agosto (… TOTAL AEROPUERTOS DE… CANARIAS Regular
## # ℹ 345 more rows
## # ℹ 1 more variable: value <dbl>Observamos que además de datos mensuales, en la tabla aparece el TOTAL de datos anuales. Vamos a quitar esos registros, así como los registros que no tengan un valor disponible de la llegada de pasajeros y los valores del año 2020 cuyos datos se encuentran muy afectados por la epidemia de la COVID-19
istac_aeropuertos <- istac_aeropuertos %>%
filter(word(Periodos,2)!="TOTAL" & is.na(value)==FALSE & word(Periodos,1)!="2020")
istac_aeropuertos## # A tibble: 252 × 5
## Periodos Aeropuertos.de.origen Aeropuertos.de.destino Clases.de.tráfico
## <fct> <fct> <fct> <fct>
## 1 2019 Diciembr… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 2 2019 Noviembr… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 3 2019 Octubre … TOTAL AEROPUERTOS DE… CANARIAS Regular
## 4 2019 Septiemb… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 5 2019 Agosto (… TOTAL AEROPUERTOS DE… CANARIAS Regular
## 6 2019 Julio (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 7 2019 Junio (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 8 2019 Mayo (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 9 2019 Abril (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## 10 2019 Marzo (p) TOTAL AEROPUERTOS DE… CANARIAS Regular
## # ℹ 242 more rows
## # ℹ 1 more variable: value <dbl>La función word nos permite extraer la palabra, que ocupa una posición determinada, de un string. A continuación creamos un tsibble con los datos. Para construir la variable temporal tenemos que manipular el formato de fechas que usa en esta tabla el ISTAC para pasarlo a un formato de fecha estándar y después pasarlo a un formato de fecha mensual usando yearmonth
istac_aeropuertos <- tsibble(
date = paste(
word(istac_aeropuertos$Periodos,1),
word(istac_aeropuertos$Periodos,2),"1"
) %>%
as.Date(format="%Y %B %d") %>% yearmonth(),
pasajeros = istac_aeropuertos$value,
index = date
)
istac_aeropuertos## # A tsibble: 252 x 2 [1M]
## date pasajeros
## <mth> <dbl>
## 1 1999 ene. 117785
## 2 1999 feb. 120128
## 3 1999 mar. 130011
## 4 1999 abr. 140767
## 5 1999 may. 137081
## 6 1999 jun. 147560
## 7 1999 jul. 193930
## 8 1999 ago. 230282
## 9 1999 sep. 194375
## 10 1999 oct. 173292
## # ℹ 242 more rowsA continuación dibujamos la serie temporal donde se aprecia una clara estacionalidad.
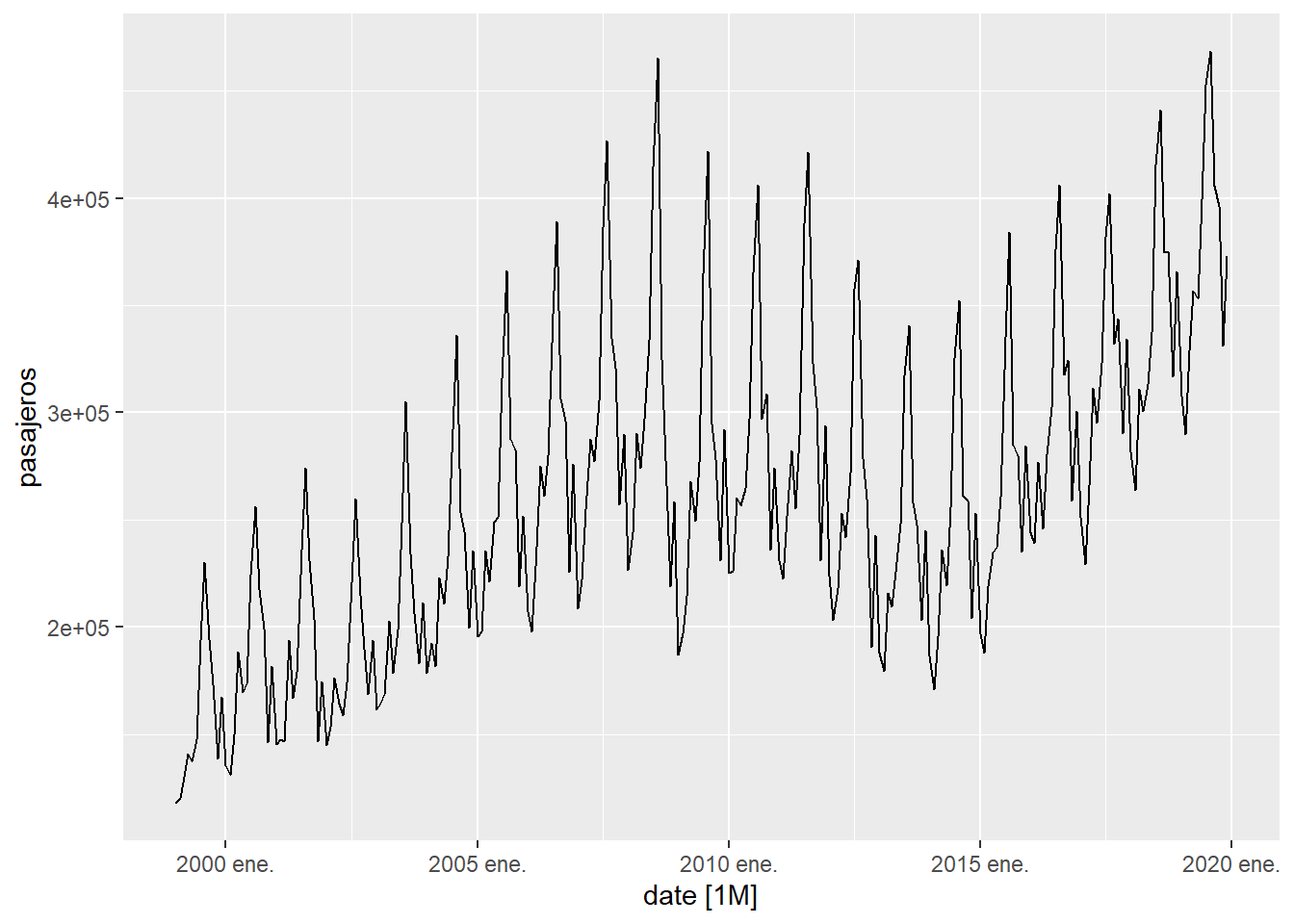
Figure 5.5: Evolución de la llegada de pasajeros a Canarias
Otro gráfico interesante es dibujar la serie temporal separándola en periodos de 12 meses. De esta manera se aprecia claramente que el mes con más movimiento de viajeros es agosto.
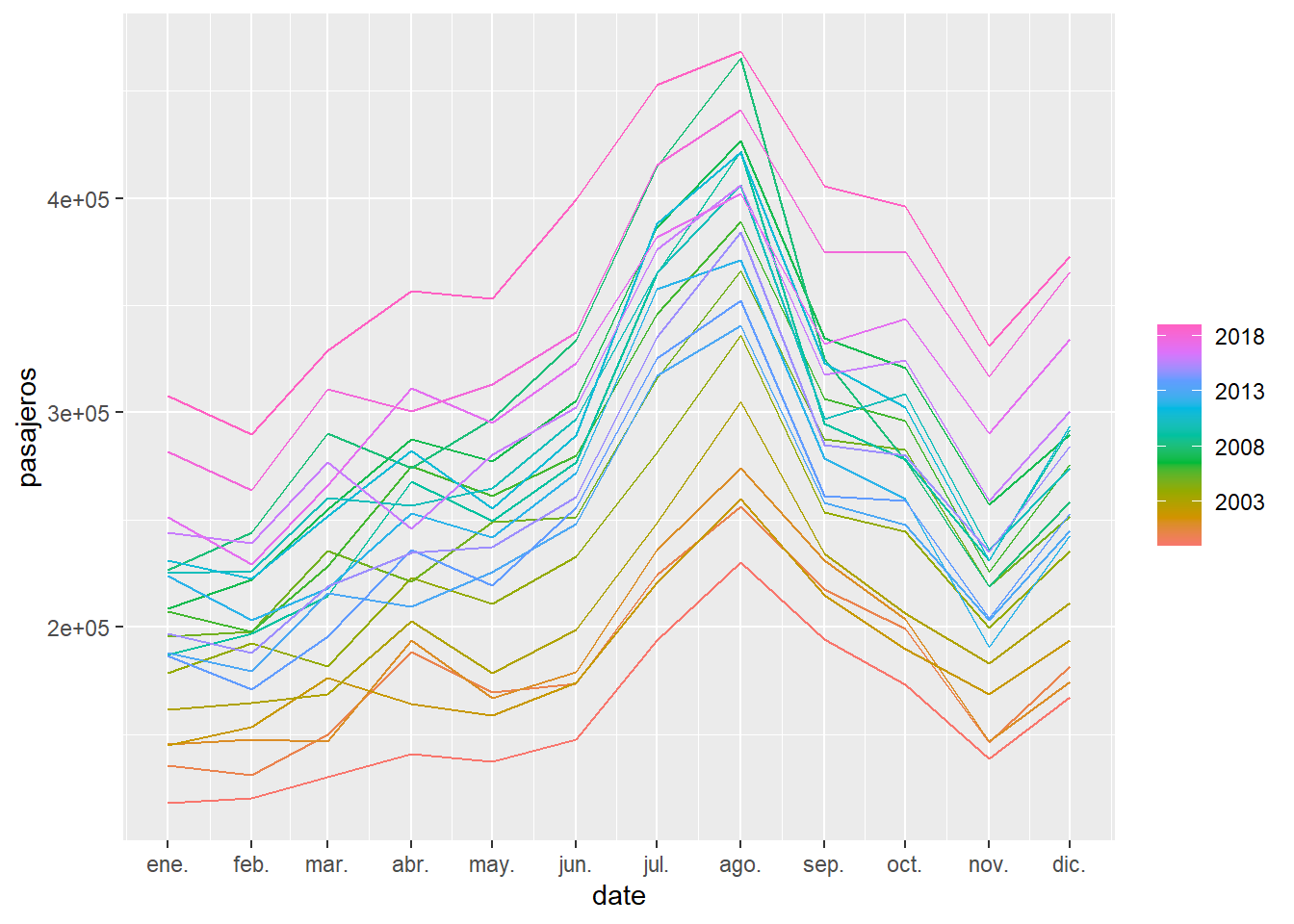
Figure 5.6: Para la serie de llegada de pasajeros a Canarias, se representa cada serie anual como una curva independiente
En la siguiente gráfica se separa por meses y vemos para cada mes como va evolucionando por años.
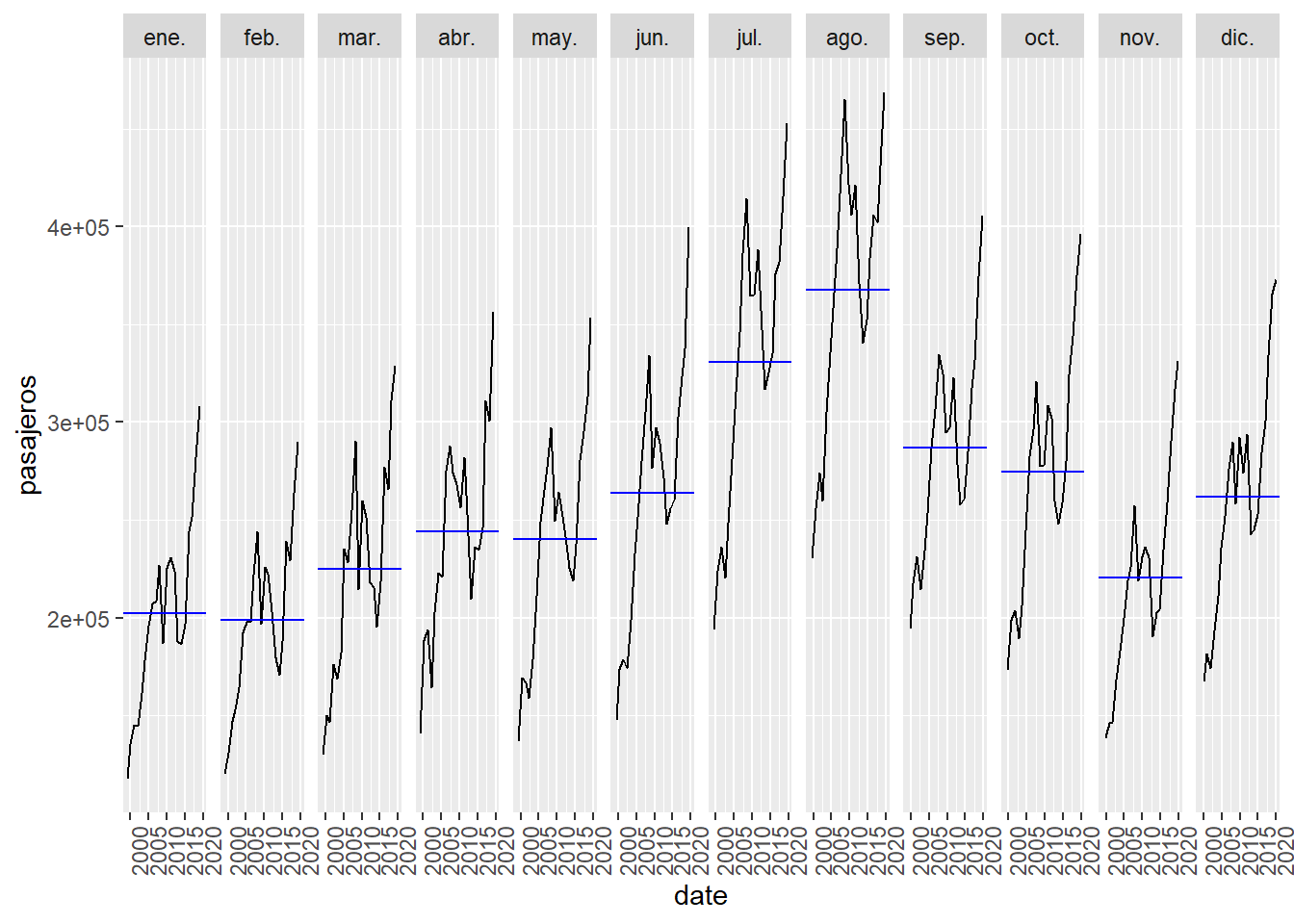
Figure 5.7: Para la serie de llegada de pasajeros a Canarias se representa la evolución por meses
En la siguiente gráfica se representa un diagrama de dispersión con la variable observada, que llamaremos \(y_t\), con respecto al valor de la misma variable \(l\) meses antes \(y_{t-l}\). Es decir para \(l=1\) (lag 1) se dibujan los puntos \((y_{t},y_{t-1})\). Es decir, estaríamos comparando el dato de febrero con el de enero, el de marzo con febrero, etc.. En este caso, como tenemos una estacionalidad de 12 meses, podemos observar que la nube de puntos \((y_{t},y_{t-12})\) (lag 12) es la que más se concentra alrededor de la recta de regresión que aparece dibujada. Es decir cuando comparamos el dato de cada mes, con el dato del mismo mes del año anterior. Una forma de “adivinar” la estacionalidad de una serie temporal sería mirar estas gráficas y ver cuando los puntos se concentran alrededor de la recta de regresión.
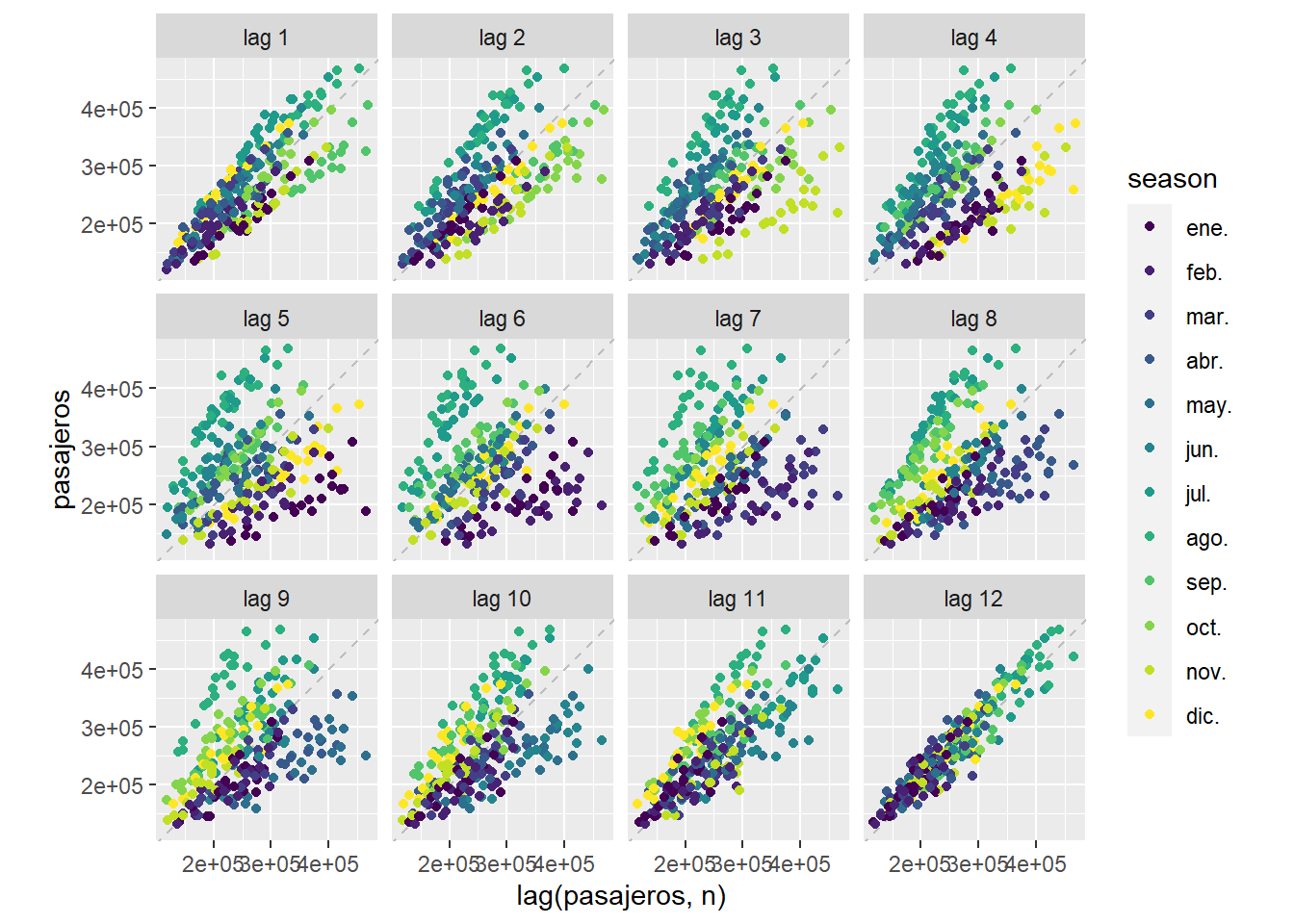
Figure 5.8: Para la serie de llegada de pasajeros a Canarias \(y_t\), se representan los puntos \((y_{t},y_{t-l})\)
En algunos casos puede existir una doble estacionalidad. Por ejemplo, si estudiamos los datos de ventas diarias en el comercio, por un lado tienen una estacionalidad semanal, puesto que las ventas dependen del día de la semana y por otro lado tiene una estacionalidad anual, porque el día concreto del año puede tener un fuerte efecto en las ventas, es decir, por ejemplo, durante los días de las fiestas navideñas se vende más que en los días de finales de enero. Por otro lado, al final de cada mes las empresas suelen acumular los datos de facturación atrasados lo que produce un pico artificial de ventas registradas el último día de mes.
5.4 Descomposición STL
Una forma habitual de gestionar la estacionalidad de una serie temporal, que denotamos por \(y_t\), es usar algún modelo para extraer la estacionalidad, que denotamos por \(S_t\) y descomponer la serie como
\[ y_t = S_t + L_t + \mathcal{E}_t \] donde \(L_t\) representa una curva de tendencia de \(y_t\) liberada de su componente estacional y \(\mathcal{E}_t\) representa el error en la descomposición cometido por el modelo. Un modelo muy utilizado para obtener esta descomposición es el denominado STL (“Seasonal and Trend decomposition using Loess”), que permite, también, gestionar una doble estacionalidad. Vamos a aplicar, en primer lugar, el método STL para descomponer la serie temporal de llegadas de viajeros a Canarias:
istac_aeropuertos |>
model(
STL(pasajeros ~ season(period = 12),
robust = TRUE)
) |>
components() |>
autoplot()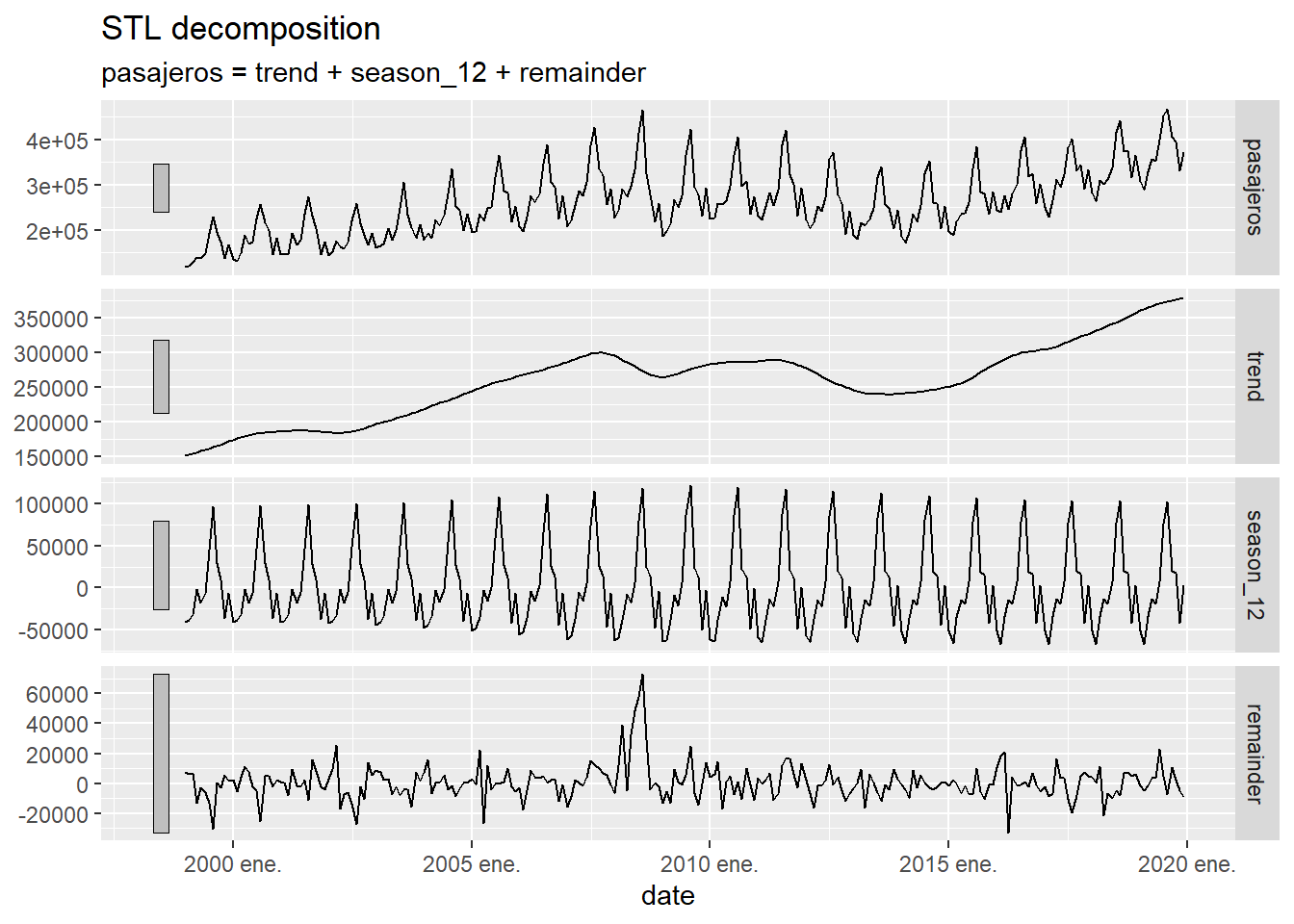
Figure 5.9: Descomposición de una serie temporal usando el método STL
La primera gráfica que se presenta es la serie temporal original \(y_t\), la segunda es su versión suavizada \(L_t\), la tercera es la estacionalidad \(S_t\) y la cuarta el error del modelo \(\mathcal{E}_t\). Por cuestiones de espacio y tiempo, no se explicará en este curso el fundamento matemático del método STL que se puede encontrar en CCMT90.
Para presentar un ejemplo con doble estacionalidad vamos a utilizar los datos de venta diaria al por menor de grandes empresas en España publicados por el INE. Concretamente, el dato original utilizado es el porcentaje de las ventas acumuladas hasta ese día del mes, respecto al total vendido el mes anterior. Por ejemplo el dato del 15/03/2023 es 49.9, lo que representa que hasta ese día del mes se vendió el 49.9% de lo que se vendió en todo mes anterior. Para apreciar mejor la estacionalidad, en lugar de trabajar con el dato acumulado del mes vamos a trabajar con el dato diario, es decir el porcentaje de venta cada día, respecto al total de ventas del mes anterior. Para obtener ese dato basta hacer la diferencia, cada día, del valor acumulado ese día con el acumulado del día anterior.
# lectura de la tabla del INE y gestión de las fechas
ine_comercio_diario_acumulado <- read.xlsx("https://ctim.es/AEDV/data/ine_comercio_diario_acumulado.xlsx") %>%
as_tibble() %>%
mutate(date= as.Date(date,format = "%d/%m/%Y"))
# creación de un tsibble con los datos acumulados cada mes
ine_comercio_diario_acumulado <- tsibble(
date = ine_comercio_diario_acumulado$date,
value = ine_comercio_diario_acumulado$value,
index = date
)
# creación de un tsibble con la diferencia de los datos acumulados cada mes
ine_comercio_diario <- ine_comercio_diario_acumulado
for(i in 2:(length(ine_comercio_diario$date)) ){
if(format(ine_comercio_diario$date[i],"%m") == format(ine_comercio_diario$date[i-1],"%m")){
ine_comercio_diario$value[i]=ine_comercio_diario_acumulado$value[i]-ine_comercio_diario_acumulado$value[i-1]
}
}Para ilustrar la doble estacionalidad vamos a dibujar la serie temporal ine_comercio_diario en un periodo de 3 meses. Donde se puede apreciar la estacionalidad semanal (las mayores ventas corresponden a viernes y sábados y las menores a domingos) y la estacionalidad anual (cada año en los últimos días de diciembre se vende más, después las ventas bajan a partir de la segunda semana de enero y empiezan a subir en marzo). Además, a final de cada mes se produce un fuerte repunte de las ventas registradas debido a que, por el sistema de contabilidad que usan muchas empresas, el día último de cada mes se contabilizan más ventas.
ine_comercio_diario %>%
filter(date>= as.Date("2022-12-15") & date<= as.Date("2023-03-15")) %>%
autoplot(value)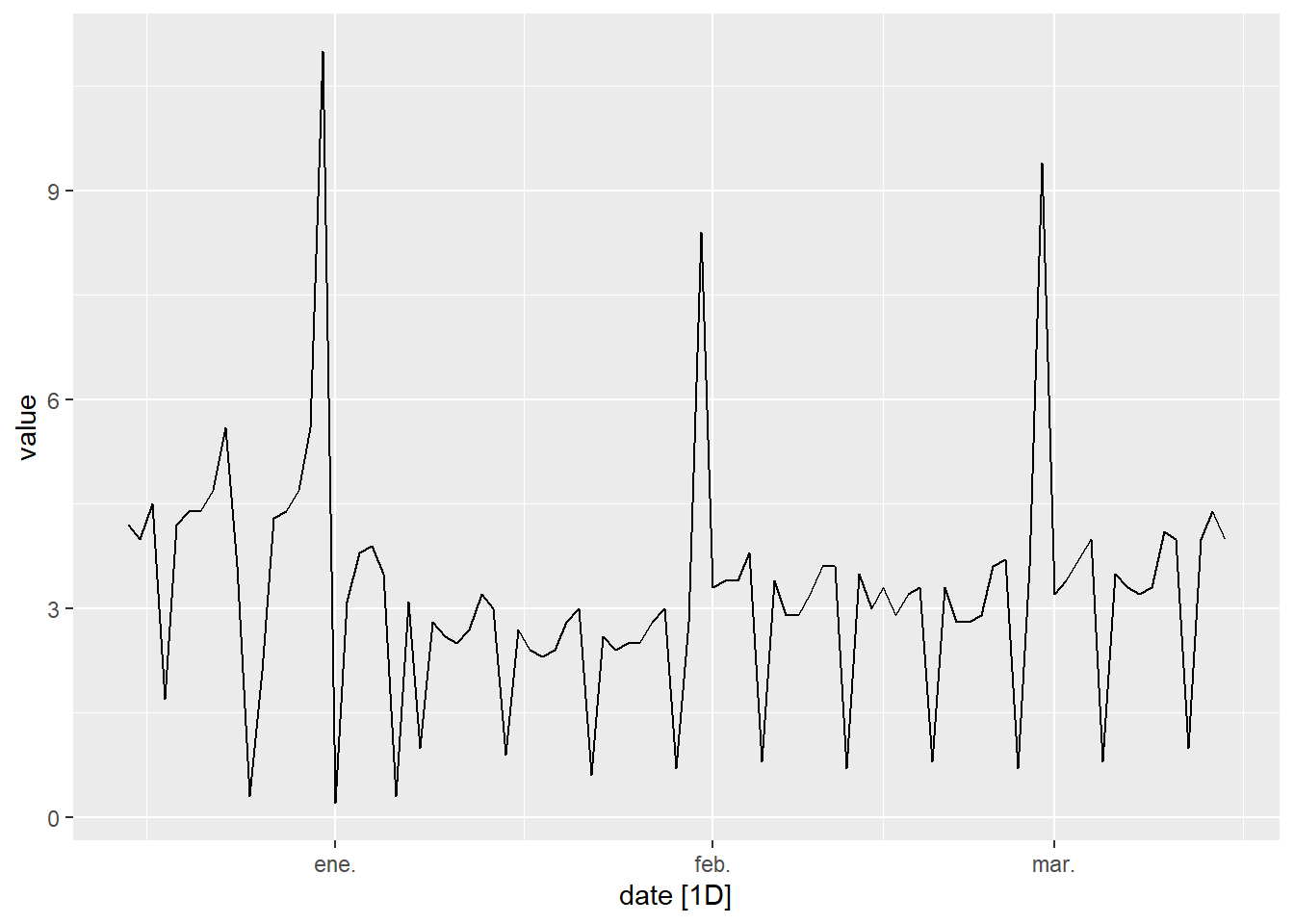
Figure 5.10: Datos de ventas de comercio en España en un periodo de 3 meses
A continuación vamos a aplicar el método STL para descomponer la serie temporal ine_comercio_diario. Observamos que aparece una estacionalidad semanal y otra anual. A la vista de la evolución de la curva de tendencia (trend) se observa como las ventas han ido bajando a partir del 2020 (un comportamiento que no es visible al observar los datos originales).
ine_comercio_diario %>% model(
STL(value ~ season(period = 7) +
season(period = 365.25),
robust = TRUE)
) %>%
components() |>
autoplot() 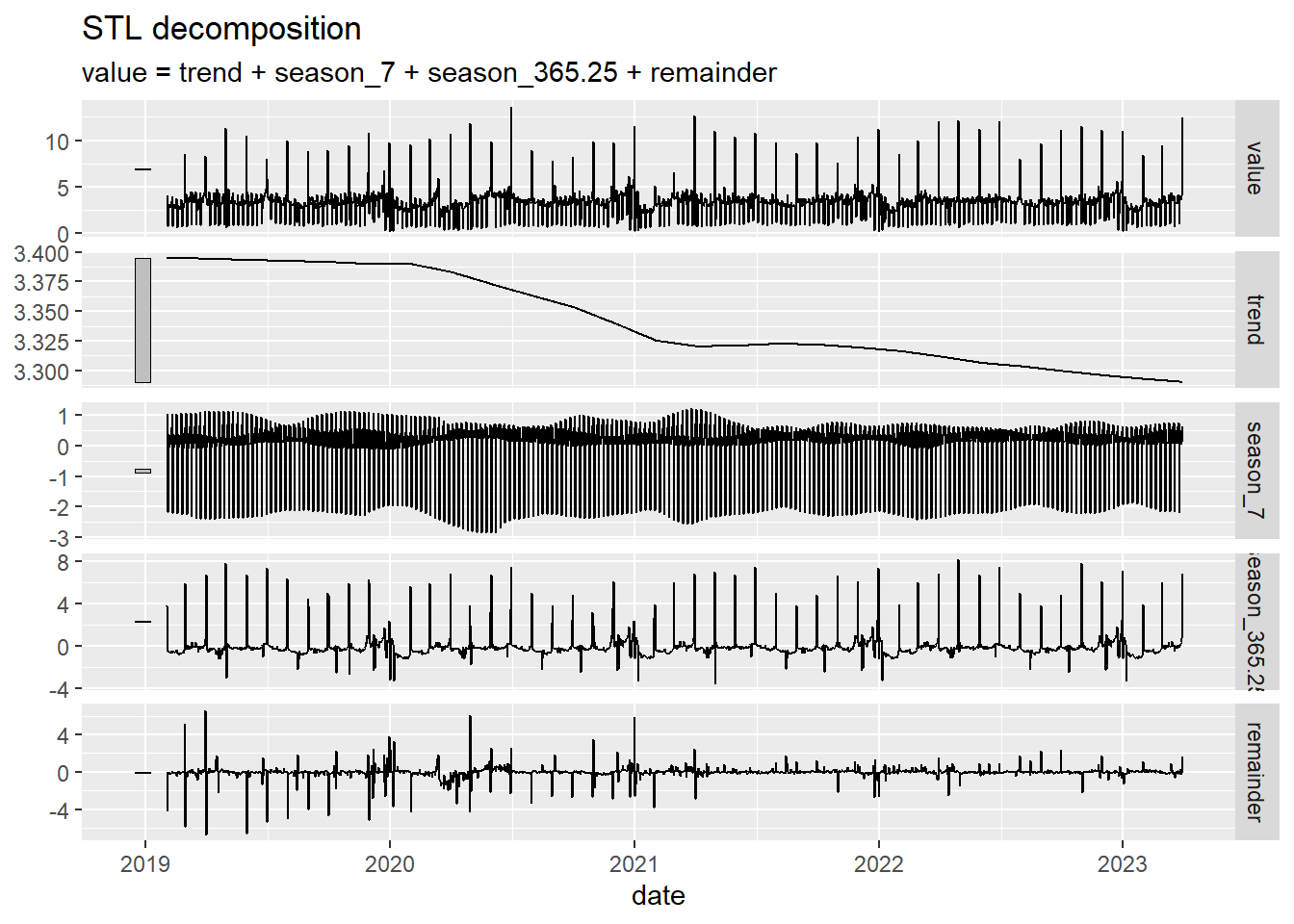
Figure 5.11: Cálculo de la descomposición STL con doble estacionalidad
5.5 Predicción
Un aspecto fundamental en el análisis de series temporales es hacer predicciones del futuro valor de la serie temporal a partir de los valores que conocemos. Para ello es necesario utilizar modelos matemáticos de predicción. Nosotros aquí vamos a introducir, brevemente, dos de los modelos más utilizados, como son el suavizado exponencial y los modelos ARIMA. En general, denotaremos por \(y_t\) el valor observado de la serie temporal en el instante \(t\) y por \(\hat y_{t+h|t}\) el valor que predice el modelo para el instante \(t+h\) usando los datos observados hasta el instante \(t\). Además, estudiaremos como se pueden aplicar estos modelos al caso de doble estacionalidad.
5.6 Suavizado exponencial
Vamos a introducir este modelo predictivo progresivamente, empezando por su versión más sencilla y posteriormente ir añadiendo nuevas características al modelo.
Promediado
La versión más sencilla de este modelo viene dada por
\[\hat y_{t+1|t} = \alpha y_t + (1-\alpha) \hat y_{t|t-1},\] es un modelo iterativo de predicción donde el valor de predicción es un promedio pesado por la variable \(\alpha\) entre el valor observado el día anterior y la predicción del modelo para el día anterior. Arrancando las iteraciones desde el principio tendríamos :
\[ \hat y_{2|1} = \alpha y_1 + (1-\alpha) l_0\\ \hat y_{3|2} = \alpha y_2 + (1-\alpha) \hat y_{2|1}=\alpha y_2+(1-\alpha)\alpha y_1 + (1-\alpha)^2 l_0\\ \hat y_{4|3} = \alpha y_3 + (1-\alpha) \hat y_{3|2}= \alpha y_3+\alpha(1-\alpha) y_2+(1-\alpha)^2\alpha y_1 + (1-\alpha)^3 l_0\\ ........\]
Dado que el valor \(y_{1|0}\) no existe, se sustituye por \(l_0\) que es un parámetro del modelo junto al valor de \(\alpha\). En la práctica, para calcular los parámetros de un modelo se minimiza un error de predicción entre los valores estimados y los valores observados. Como puede observarse de las ecuaciones anteriores, el valor de \(\hat y_{t+1|t}\) se puede expresar como un promediado pesado de todos los valores anteriores de \(y_t\) donde el peso de cada término va decayendo según vamos hacia el pasado. Este comportamiento es lo que da nombre a este método de predicción (suavizado exponencial).
Suavizado y tendencia
La siguiente versión de este modelo introduce la variable \(b_t\) (la pendiente o tendencia), y \(l_t\) que determina el valor suavizado de la serie temporal:
\[ l_t = \alpha y_t +(1-\alpha)(l_{t-1}+b_{t-1})\\ b_t = \beta^*(l_t -l_{t-1})+(1-\beta^*)b_{t-1}\\ \hat y_{t+h|t}=l_t+hb_t, \] este modelo se proyecta hacia el futuro usando una recta, por tanto, se ajustará bien a series temporales que varíen linealmente. Este modelo tendrá como parámetros \(\alpha\), \(l_0\), \(\beta^*\) y \(b_0\).
Modelo amortiguado
Para que el modelo se pueda ajustar mejor a series temporales no lineales se puede introducir un parámetro adicional \(\phi\) que permite “amortiguar” la predicción usando la siguiente modificación del modelo:
\[ l_t = \alpha y_t +(1-\alpha)(l_{t-1}+\phi b_{t-1})\\ b_t = \beta^*(l_t -l_{t-1})+(1-\beta^*)\phi b_{t-1}\\ \hat y_{t+h|t}=l_t+(\phi+\phi^2+\cdots+\phi^h)b_t, \]
Estacionalidad
Para tener en cuenta la estacionalidad se introduce una nueva serie \(s_t\). La estacionalidad se puede introducir de forma multiplicativa o de forma aditiva de la siguiente forma :
\[ \text{estacionalidad multiplicativa : } \hat y_{t+h|t}=(l_t+(\phi+\phi\cdots+\phi^h)b_t)*s_{t-m+h\%m} \\ \text{estacionalidad aditiva : } \hat y_{t+h|t}=l_t+(\phi+\cdots+\phi^h)b_t +s_{t-m+h\%m} \] donde \(m\) es el periodo de la estacionalidad (por ejemplo \(m=12\) para una estacionalidad mensual) y \(h\%m\) es el resto de la división entre \(h\) y \(m\). De esta forma la estacionalidad se extiende hacia el futuro de forma periódica, con periodo \(m\). La estacionalidad también afecta a las otras ecuaciones del modelo, veamos como quedaría el modelo para una estacionalidad aditiva:
\[ l_t = \alpha (y_t -s_{t-m})+(1-\alpha)(l_{t-1}+b_{t-1})\\ b_t = \beta^*(l_t -l_{t-1})+(1-\beta^*)b_{t-1}\\ s_t=\gamma(y_t-l_{t-1}-b_{t-1})+(1-\gamma)s_{t-m}\\ \hat y_{t+h|t}=l_t+hb_t+s_{t-m+h\%m}, \] En el caso de una estacionalidad multiplicativa el modelo quedaría
\[ l_t = \alpha \frac{y_t}{s_{t-m}}+(1-\alpha)(l_{t-1}+b_{t-1})\\ b_t = \beta^*(l_t -l_{t-1})+(1-\beta^*)b_{t-1}\\ s_t=\gamma\frac{y_t}{l_{t-1}+b_{t-1})}+(1-\gamma)s_{t-m}\\ \hat y_{t+h|t}=(l_t+hb_t)s_{t-m+h\%m}, \]
Para analizar el error, \(\varepsilon_t\), que se comete entre el valor que predice el modelo y el valor observado se pueden usar también modelos aditivos o multiplicativos del error. Es decir, dado un valor observado, \(y_t\), y su aproximación por el modelo \(\hat y_{t|t-1}\) se puede definir el error \(\varepsilon_t\) de las siguientes formas :
\[ \text{error aditivo : } y_t=\hat y_{t|t-1}+\varepsilon_t\\ \text{error multiplicativo : } y_t=\hat y_{t|t-1}(1+\varepsilon_t) \]
Estimación óptima
Como puede observarse, este modelo presenta una variedad de opciones. Para aglutinar esta información se utiliza la notación ETS(Opción Error, Opción tendencia, Opción estacionalidad). Respecto al error (la E en el string ETS), el modelo puede ser aditivo (A) o multiplicativo (M), respecto a la tendencia (la T en el string ETS), puede no tener tendencia (N), con tendencia simple (A) o con tendencia con amortiguamiento (A\(_d\)), con respecto a la estacionalidad (la S en el string ETS) puede ser sin estacionalidad (N) con estacionalidad aditiva (A) o con estacionalidad multiplicativa (M). Por ejemplo un modelo ETS(M,A,N) sería un modelo con error multiplicativo, tendencia simple y sin estacionalidad. Afortunadamente, nosotros no necesitamos decidir que modelo elegir y calcular los valores óptimos de sus parámetros, podemos usar la función model de la librería fpp3 que calcula automáticamente el mejor modelo y parámetros que se ajustan a nuestra serie temporal. Por ejemplo, vamos a calcular el mejor modelo que se ajusta a la serie de datos de la población mundial:
## Series: population
## Model: ETS(M,A,N)
## Smoothing parameters:
## alpha = 0.8635692
## beta = 0.708906
##
## Initial states:
## l[0] b[0]
## 980810630 4967560
##
## sigma^2: 0
##
## AIC AICc BIC
## 7864.834 7865.112 7881.847Observamos que para esta serie temporal el mejor modelo es ETS(M,A,N), es decir
error multiplicativo, tendencia simple y sin estacionalidad. Además vemos como la
función ha calculado los parámetros óptimos del modelo. Los valores de AIC, AICc
y BIC son indicadores de la calidad del ajuste del modelo a la serie temporal,
cuanto más pequeños sean estos valores, mejor será dicho ajuste. Estos indicadores de calidad del ajuste también tienen en cuenta el número de parámetros optimizados en el modelo. Cuanto mayor es el número de parámetros peor se considera el modelo pues se puede producir el fenómeno denominado “overfitting” que consiste en que si hay muchos parámetros, el modelo se puede ajustar muy bien a los datos de la muestra, pues manejamos muchos grados de libertad, pero puede fallar mucho en nuevos datos que no se han contemplado en el ajuste (como es el caso de la predicción en el futuro).
Una vez calculado el modelo de ajuste vamos a utilizarlo para hacer una predicción
de la población mundial a 20 años vista usando la función forecast
## # A fable: 20 x 5 [1Y]
## # Key: location, .model [1]
## location .model date
## <chr> <chr> <dbl>
## 1 World ETS(population) 2022
## 2 World ETS(population) 2023
## 3 World ETS(population) 2024
## 4 World ETS(population) 2025
## 5 World ETS(population) 2026
## 6 World ETS(population) 2027
## 7 World ETS(population) 2028
## 8 World ETS(population) 2029
## 9 World ETS(population) 2030
## 10 World ETS(population) 2031
## 11 World ETS(population) 2032
## 12 World ETS(population) 2033
## 13 World ETS(population) 2034
## 14 World ETS(population) 2035
## 15 World ETS(population) 2036
## 16 World ETS(population) 2037
## 17 World ETS(population) 2038
## 18 World ETS(population) 2039
## 19 World ETS(population) 2040
## 20 World ETS(population) 2041
## # ℹ 2 more variables: population <dist>, .mean <dbl>El campo .mean nos indica el valor de la predicción y el campo population nos
indica la distribución de probabilidad del valor esperado. Esta distribución nos
permite calcular intervalos de confianza, de gran importancia para estudiar el
rango esperado de valores en el que se mueve nuestra predicción. Por ejemplo, en el caso anterior, para el año 2022, el modelo predice que la población mundial sigue una distribución normal de media \(\mu=8 \cdot 10^9\) y varianza \(\sigma^2=1.5 \cdot 10^{14}\). Teniendo en cuenta que se trata de una distribución normal, los intervalos de confianza tienen la forma \([\mu-c \cdot \sigma,\mu+c\cdot \sigma]\) donde \(c\) depende del porcentaje deseado. Por ejemplo para el intervalo de confianza al \(80\%\), tenemos que \(c=1.28\), y para el intervalo de confianza al \(95\%\), \(c=1.96\). En particular, en nuestro ejemplo de la población mundial para el año 2022, el intervalo de confianza al \(95\%\) es
\[ [8 \cdot 10^9-1.96\sqrt{1.5 \cdot 10^{14}},8 \cdot 10^9+1.96\sqrt{1.5 \cdot 10^{14}}] \] Es importante observar que el cálculo de estos intervalos de confianza asume que los residuos (errores) del modelo de predicción siguen una distribución normal no correlada (que podemos interpretar como que el error en un instante temporal de la serie no depende del error en otros instantes temporales) y de varianza constante que se mantiene en el futuro. En particular, si en el futuro cambian mucho las condiciones que determinan la evolución de la serie temporal, el valor real de la serie temporal puede estar muy alejado del intervalo de confianza calculado. Por ejemplo, un evento como el confinamiento durante la epidemia de la COVID-19, convierte en completamente inútiles las predicciones para ese periodo realizadas en el pasado para muchas series temporales como, por ejemplo, el número esperado de pasajeros que se desplazan en avión.
En la siguiente gráfica se muestra la predicción y a su alrededor los intervalos de confianza del 80% y 95%. Es decir, en el 80% de los casos el valor real de la población se encontrará dentro de la franja de color azul oscuro. A la izquierda de la predicción se dibuja el valor observado de la población posterior al año 2000. Puede apreciarse que, como es esperable, cuanto más nos adentramos en el futuro, mayor es el tamaño del intervalo de confianza debido a que el grado de incertidumbre es mayor.
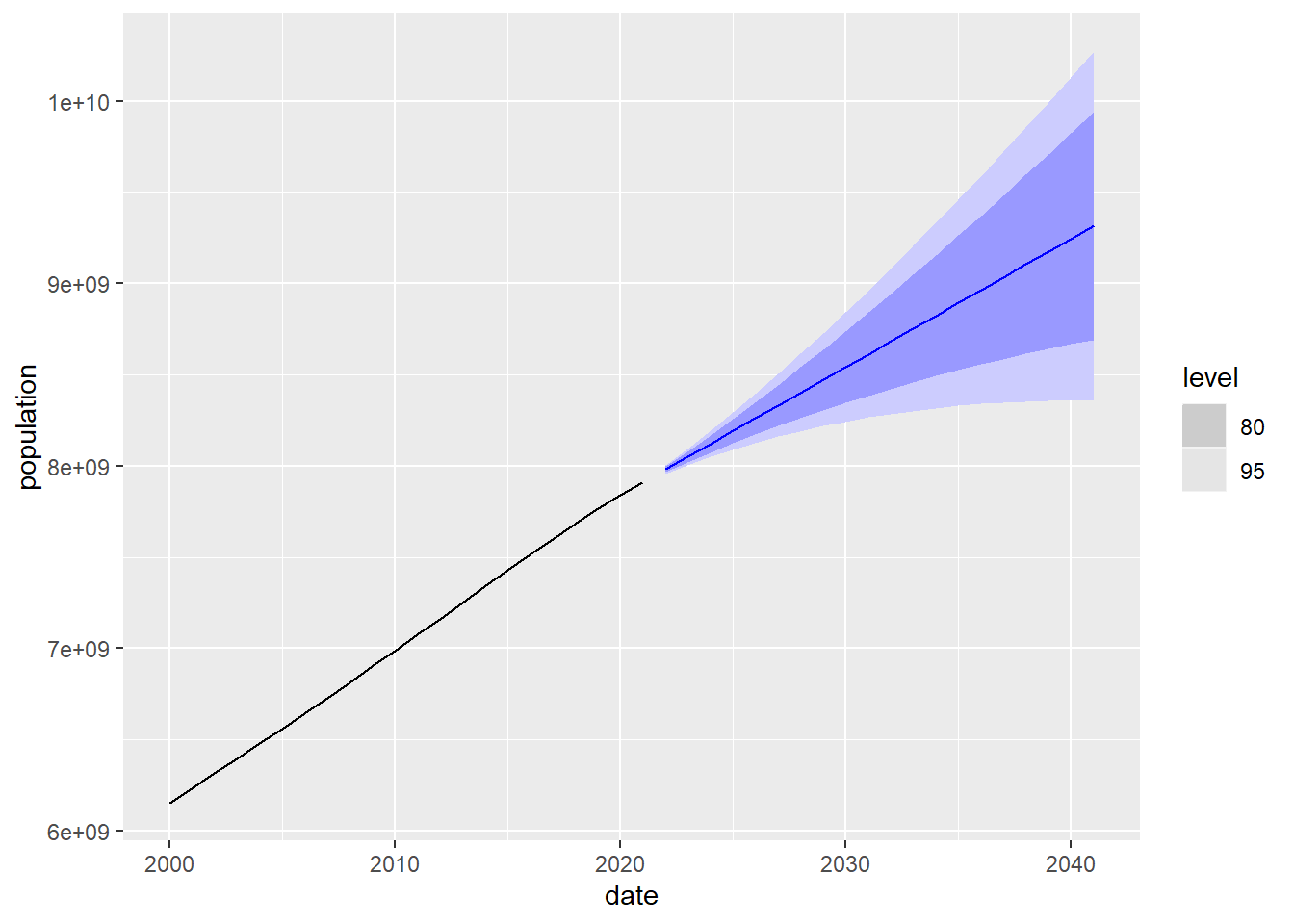
Figure 5.12: Predicción a 20 años de la población mundial usando el modelo de suavizado exponencial
Ahora repetiremos el proceso con la serie temporal de llegadas de viajeros a Canarias, que es una serie temporal con estacionalidad. Observamos que en este caso el mejor modelo es del tipo ETS(M,A,M), que corresponde con una serie con estacionalidad multiplicativa. Además, en este caso la predicción falla totalmente debido al enorme impacto que tuvo la epidemia de la COVID en el movimiento de pasajeros. Esto nos dice que los modelos predictivos, como los que se estudian aquí, se basan en que los factores que condicionan la evolución la serie temporal serán los mismos en el futuro que en el pasado. Cuando se producen eventos que modifican estos factores de evolución, la fiabilidad de la predicción se puede deteriorar mucho.
## Series: pasajeros
## Model: ETS(M,A,M)
## Smoothing parameters:
## alpha = 0.541925
## beta = 0.002598776
## gamma = 0.09755761
##
## Initial states:
## l[0] b[0] s[0] s[-1] s[-2] s[-3] s[-4] s[-5]
## 145152 1894.426 0.9742414 0.8335583 1.053734 1.134229 1.412889 1.244848
## s[-6] s[-7] s[-8] s[-9] s[-10] s[-11]
## 0.9980586 0.9339813 0.9840955 0.8667885 0.7843986 0.7791779
##
## sigma^2: 0.0032
##
## AIC AICc BIC
## 6227.709 6230.325 6287.710Nótese que en el modelo ETS, cuando hay estacionalidad de periodo \(m\), el número de parámetros puede aumentar mucho pues se requiere, además del parámetro \(\gamma\), \(m-1\) parámetros para controlar los valores iniciales de \(s_t\).
## # A fable: 24 x 4 [1M]
## # Key: .model [1]
## .model date
## <chr> <mth>
## 1 ETS(pasajeros) 2020 ene.
## 2 ETS(pasajeros) 2020 feb.
## 3 ETS(pasajeros) 2020 mar.
## 4 ETS(pasajeros) 2020 abr.
## 5 ETS(pasajeros) 2020 may.
## 6 ETS(pasajeros) 2020 jun.
## 7 ETS(pasajeros) 2020 jul.
## 8 ETS(pasajeros) 2020 ago.
## 9 ETS(pasajeros) 2020 sep.
## 10 ETS(pasajeros) 2020 oct.
## # ℹ 14 more rows
## # ℹ 2 more variables: pasajeros <dist>, .mean <dbl>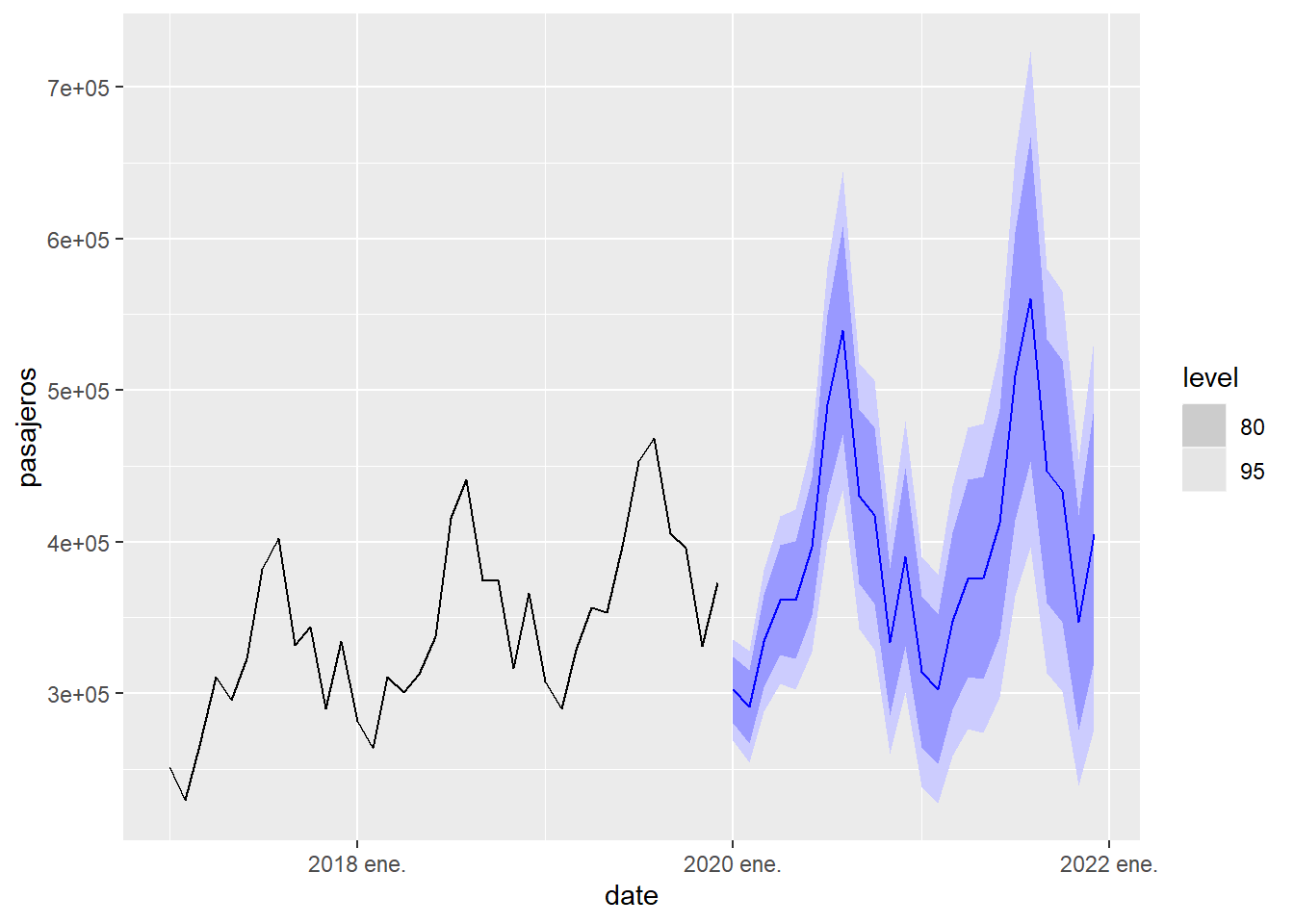
Figure 5.13: Predicción a 2 años de la llegada de pasajeros a Canarias usando el modelo de suavizado exponencial
Este modelo de suavizado exponencial descompone la serie temporal usando \(l_t\) (una versión suavizada de la serie temporal), \(b_t\) (la tendencia o “slope”), \(s_t\) ( la estacionalidad o “season”) y el error (remainder), que al ser multiplicativo se expresa como \(1+\varepsilon_t\) . En la siguiente gráfica se ilustra esta descomposición:
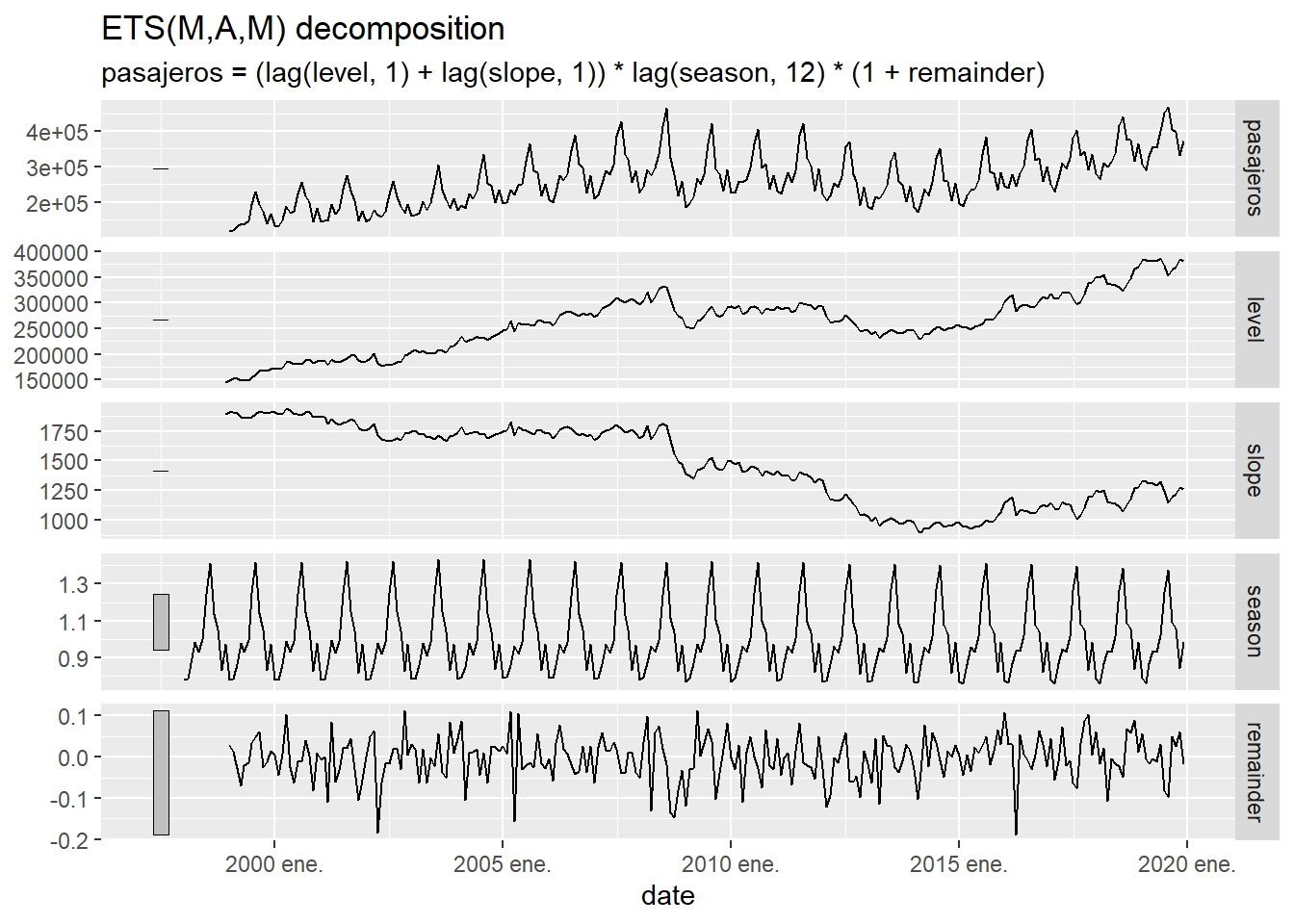
Figure 5.14: Descomposición de la serie temporal de llegadas a las aeropuertos canarios usando el modelo de suavizado exponencial.
Gestión de la doble estacionalidad
Este modelo no está diseñado para gestionar directamente una doble estacionalidad. Una manera alternativa de proceder para gestionar la estacionalidad es utilizar la descomposición STL de la serie temporal, aplicar el modelo de suavizado exponencial sin estacionalidad para predecir el valor de la curva de tendencia \(L_t\) obtenido en la descomposición STL y predecir el valor de \(y_t\) a partir de esa predicción usando además una extensión periódica de la estacionalidad \(S_t\) calculada por la descomposición STL. Esto nos permite combinar estacionalidades con diferentes periodos. A continuación vamos a aplicar este procedimiento a la serie temporal ine_comercio_diario:
# Aplicación descomposición STL combinada con ETS sin estacionalidad
fit <- decomposition_model(
STL(value ~ season(period = 7) + # añadimos estacionalidad semanal
season(period = 365.25), # añadimos estacionalidad anual
robust = TRUE),
ETS(season_adjust ~ season("N")) # Cálculo modelo ETS sin estacionalidad
)
# Cálculo y dibujo predicción a un año vista
ine_comercio_diario %>%
model(fit) %>%
forecast(h =365) %>%
autoplot( ine_comercio_diario%>%
filter(date>= as.Date("2022-01-01"))
)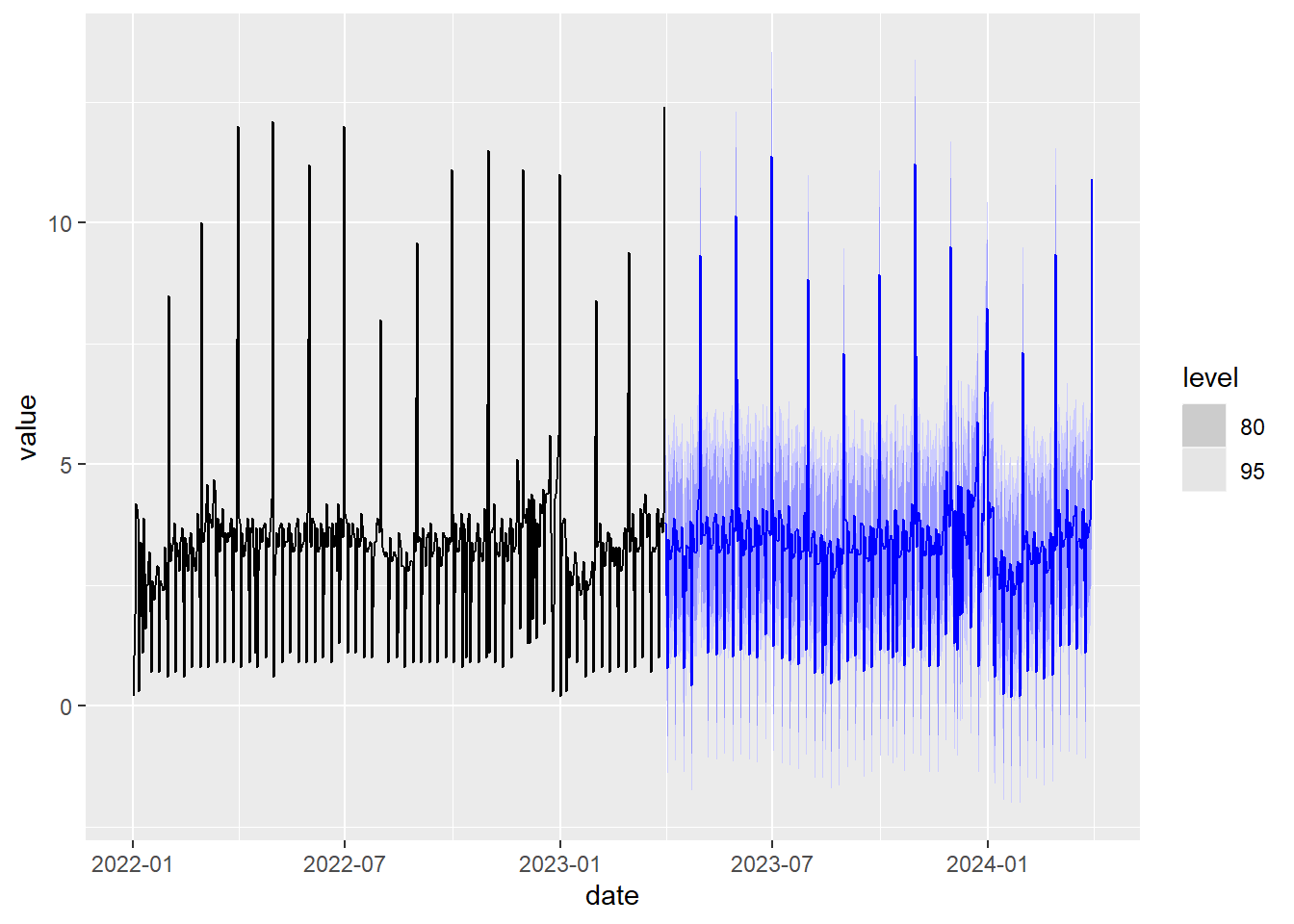
Figure 5.15: Predicción usando la descomposición STL y el suavizado exponencial.
5.7 El modelo ARIMA
Modelo autoregresivo (AR)
La versión más sencilla del modelo de predicción ARIMA es el denominado modelo autoregresivo (AR) donde cada valor observado \(y_t\) se aproxima como una combinación lineal de valores observados anteriormente, es decir :
\[ y_t = c + \phi_1 y_{t-1}+\phi_2 y_{t-2}+ \cdots +\phi_p y_{t-p}+ \varepsilon_t \] donde \(p\) representa el número de valores en el pasado que se toman para aproximar el valor de \(y_t\), y \(\varepsilon_t\) es el error de aproximación. \(c\) y \(\phi_1,...,\phi_p\) son los parámetros del modelo. Vamos a expresar esta ecuación introduciendo el operador, \(B\), de desplazamiento temporal :
\[ By_t = y_{t-1} \] usando el operador \(B\) podemos escribir la ecuación del modelo AR como:
\[ (1-\phi_1B-\phi_2B^2-\cdots\phi_pB^p)y_t = c + \varepsilon_t \]
Derivadas
Para que el modelo AR funcione bien la serie temporal no debe tener una tendencia definida de crecimiento o decrecimiento. La manera habitual de intentar eliminar la tendencia de una serie temporal es utilizar en el modelo alguna derivada de la serie temporal en lugar de la propia serie temporal. La derivada primera se define como :
\[ (1-B)y_t=y_t-y_{t-1}. \] La derivada segunda sería la derivada de la derivada, es decir:
\[ (1-B)^2y_t=(1-B)(y_t-y_{t-1})=y_t-y_{t-1} -(y_{t-1}-y_{t-2})=y_t-2y_{t-1}+y_{t-2}. \] Por tanto, con esta notación, la derivada de orden \(d\) sería \((1-B)^dy_t\). Al calcular las derivadas de una serie temporal, ésta va perdiendo su tendencia. Para ilustrar esto, en las siguientes gráficas mostramos la serie temporal de la población mundial y sus primeras 3 derivadas. Como se puede observar, en la derivada tercera ya la serie temporal no tiene un patrón de crecimiento definido.
p1 <- owid_population %>%
filter(location=="World") %>%
autoplot(population)
data <- owid_population %>%
filter(location=="World")
data$derivada_1 <- derivada(data$population)
p2 <- data %>% autoplot(derivada_1)
data$derivada_2 <- derivada(data$derivada_1)
p3 <- data %>% autoplot(derivada_2)
data$derivada_3 <- derivada(data$derivada_2)
p4 <- data %>% autoplot(derivada_3)
wrap_plots(p1, p2, p3, p4, ncol = 2, nrow = 2)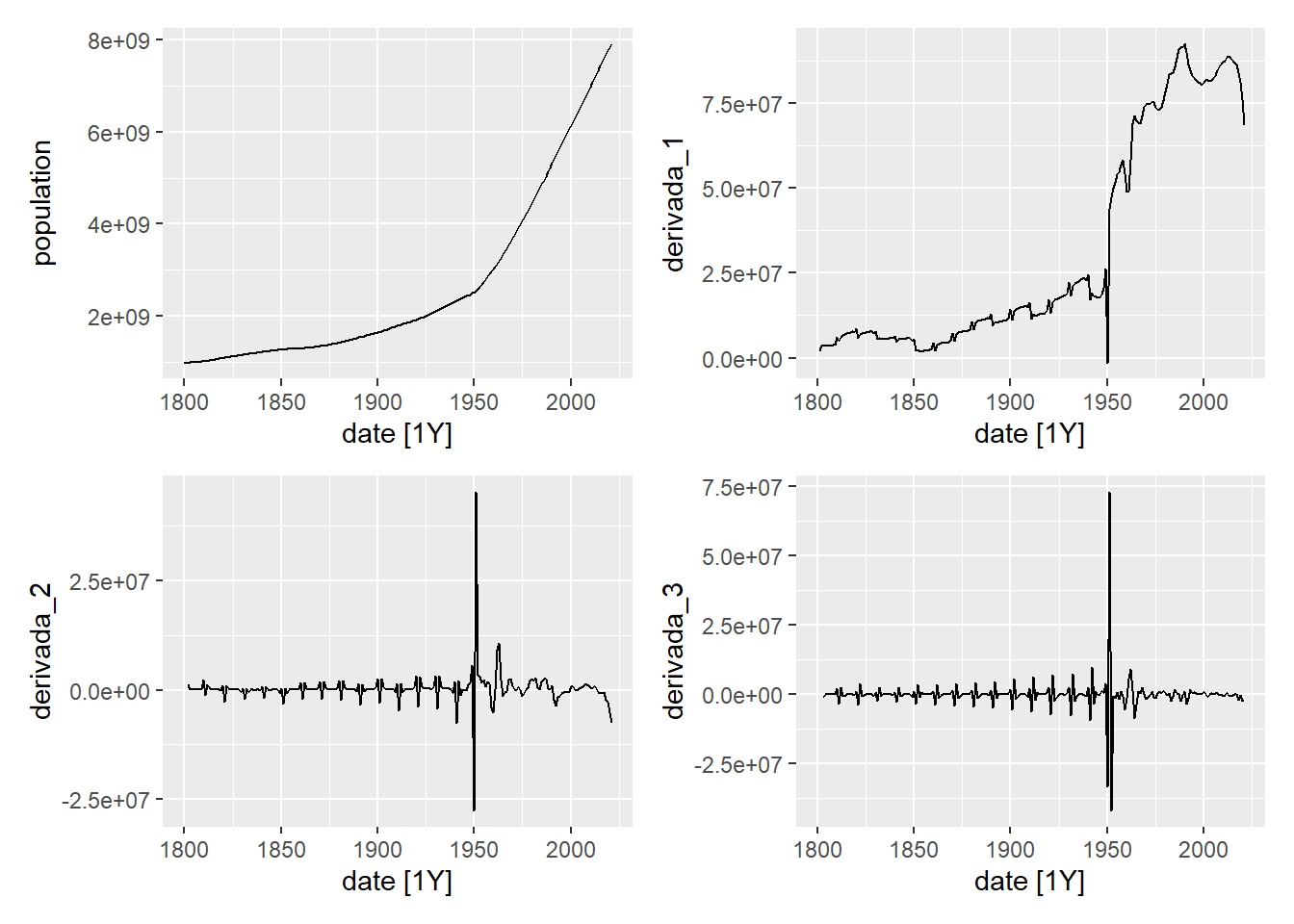
Figure 5.16: Serie temporal de la población mundial y sus derivadas
Al reemplazar en el modelo (AR) la serie original por su derivada de orden d obtenemos el modelo
\[ (1-\phi_1B-\phi_2B^2-\cdots-\phi_pB^p)(1-B)^dy_t = c + \varepsilon_t \] donde aparece como parámetro adicional el orden, \(d\), de la derivada utilizada.
ARIMA(p,d,q)
A continuación, para mejorar el modelo se añade a la predicción una combinación lineal de los errores pasados (esta parte del modelo se denomina (MA) ), llegando al modelo ARIMA no estacional dado por:
\[ (1-\phi_1B-\cdots\phi_pB^p)(1-B)^dy_t = c + \varepsilon_t + \theta_1\varepsilon_{t-1}+\cdots \theta_q\varepsilon_{t-q} \] que se puede expresar también como :
\[ (1-\phi_1B-\cdots-\phi_pB^p)(1-B)^dy_t = c + (1 + \theta_1B+\cdots \theta_qB^q)\varepsilon_{t} \] A este modelo se le denomina ARIMA(p,d,q). Definiendo las funciones
\[ \phi(B)=1-\phi_1B-\cdots-\phi_pB^p \\ \theta(B)=1 + \theta_1B+\cdots \theta_qB^q \] el modelo ARIMA(p,d,q) se puede definir de forma más compacta como
\[ \phi(B)(1-B)^dy_t=c+\theta(B)\varepsilon_{t} \]
ARIMA(p,d,q)(P,D,Q)\(_m\)
Para introducir una estacionalidad de periodo \(m\) en el modelo ARIMA se utilizan diferencias entre el valor de una variable y su estado \(m\) instantes anteriores. Esto se consigue haciendo \((1-B^m)y_t\). Consideremos las nuevas funciones:
\[ \Phi(B^m)=1-\Phi_1B^m-\cdots-\Phi_PB^{mP} \\ \Theta(B^m)=1 + \Theta_1B^m+\cdots \Theta_QB^{mQ} \]
El modelo general ARIMA con estacionalidad se denota como ARIMA(p,d,q)(P,D,Q)\(_m\) y se define como
\[ \phi(B)\Phi(B^m)(1-B)^d(1-B^m)^Dy_t=c+\theta(B)\Theta(B^m)\varepsilon_{t} \]
Predicción con ARIMA
Para hacer predicciones en el futuro usando el modelo ARIMA despejamos de la ecuación del modelo \(y_t\) y nos queda
\[ y_t=c+\left(1-\phi(B)\Phi(B^m)(1-B)^d(1-B^m)^D\right)y_t+\theta(B)\Theta(B^m)\varepsilon_{t} \] Tal y como se construye el modelo, la segunda parte de la igualdad es una combinación lineal de valores anteriores a \(y_t\), es decir \(y_{t-1},y_{t-2},...,\), pero no de \(y_t\) y una combinación lineal de valores de \(\varepsilon_t\). Si \(y_T\) es el último valor conocido de \(y_t\), entonces el último valor que podemos calcular del error observado es \(\varepsilon_T\). En la fórmula de predicción, siempre consideraremos que \(\varepsilon_t=0\) para \(t>T\). Podemos entonces definir la predicción \(\hat y_{T+1|T}\) como
\[ \hat y_{T+1|T}=c+\left(1-\phi(B)\Phi(B^m)(1-B)^d(1-B^m)^D\right)y_{T+1}+\theta(B)\Theta(B^m)\varepsilon_{T+1} \]
La parte derecha de la ecuación se puede evaluar con los datos conocidos porque, por lo dicho anteriormente, solo intervienen valores de \(y_t\) con \(t\leq T\) y asignamos \(\varepsilon_{T+1}=0\). Ahora iterativamente vamos aplicando la fórmula para obtener la predicción en tiempos posteriores tomando como valores de \(y_t\) anteriores los observados (para \(t \leq T\)) y los que predice el modelo para (\(t>T\)). De la misma forma \(\varepsilon_t\) será el valor observado para \(t \leq T\) y 0 para \(t>T\). Por ejemplo para calcular \(\hat y_{T+2|T}\) se utiliza \(y_{t+1}=\hat y_{T+1|T}\) a la derecha de la ecuación y \(\varepsilon_{T+2}=0\).
Estimación óptima
Al igual que en el caso de los modelos de suavizado exponencial, para calcular automáticamente el modelo
ARIMA óptimo para una serie temporal utilizaremos la función modelque suministra
la librería. Esta función puede tomar algún tiempo en ejecutarse
fit <- owid_population %>%
filter(location=="World") %>%
model(ARIMA(population,stepwise = FALSE, approx = FALSE))
report(fit)## Series: population
## Model: ARIMA(2,2,4)
##
## Coefficients:
## ar1 ar2 ma1 ma2 ma3 ma4
## 1.0186 -0.8519 -1.366 1.3471 -0.3992 0.1736
## s.e. 0.0742 0.0686 0.098 0.1454 0.1330 0.0855
##
## sigma^2 estimated as 1.444e+13: log likelihood=-3642.69
## AIC=7299.37 AICc=7299.9 BIC=7323.13Observamos que el modelo resultante es un ARIMA(2,2,4) sin estacionalidad. Si en la llamada a la función ARIMA quitamos los parámetros stepwise = FALSE, approx = FALSE, la función tardará menos en calcular el resultado, pero el ajuste del modelo será menos preciso. Mirando
los coeficientes obtenidos, el modelo resultante sería
\[ (1-1.0186B+0.8519B^2)(1-B)^2y_t=\varepsilon_{t} -1.366\varepsilon_{t-1} + 1.3471\varepsilon_{t-2} - 0.3992\varepsilon_{t-3} + 0.1736\varepsilon_{t-4} \] los valores de AIC, AICc y BIC son ligeramente inferiores a los obtenidos usando el modelo de suavizado exponencial y por ello, para esta serie temporal el modelo que mejor se ajusta es el ARIMA.
A continuación vamos a realizar una predicción de la población mundial a 20 años vista. Observamos que el modelo de suavizado exponencial aplicado anteriormente a esta serie predice una población de 9.317 millones para 2041 y el modelo de ARIMA predice 9.260 millones.
## # A fable: 20 x 5 [1Y]
## # Key: location, .model [1]
## location .model date
## <chr> <chr> <dbl>
## 1 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2022
## 2 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2023
## 3 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2024
## 4 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2025
## 5 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2026
## 6 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2027
## 7 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2028
## 8 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2029
## 9 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2030
## 10 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2031
## 11 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2032
## 12 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2033
## 13 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2034
## 14 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2035
## 15 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2036
## 16 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2037
## 17 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2038
## 18 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2039
## 19 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2040
## 20 World ARIMA(population, stepwise = FALSE, approx = FALSE) 2041
## # ℹ 2 more variables: population <dist>, .mean <dbl>Vamos ahora a dibujar la predicción usando el modelo ARIMA con con los intervalos de confianza junto a la serie observada desde el año 2000. Visualmente observamos que los intervalos de confianza son más pequeños que los de la gráfica para el modelo ETS, lo que también nos indica un mejor ajuste del modelo ARIMA.
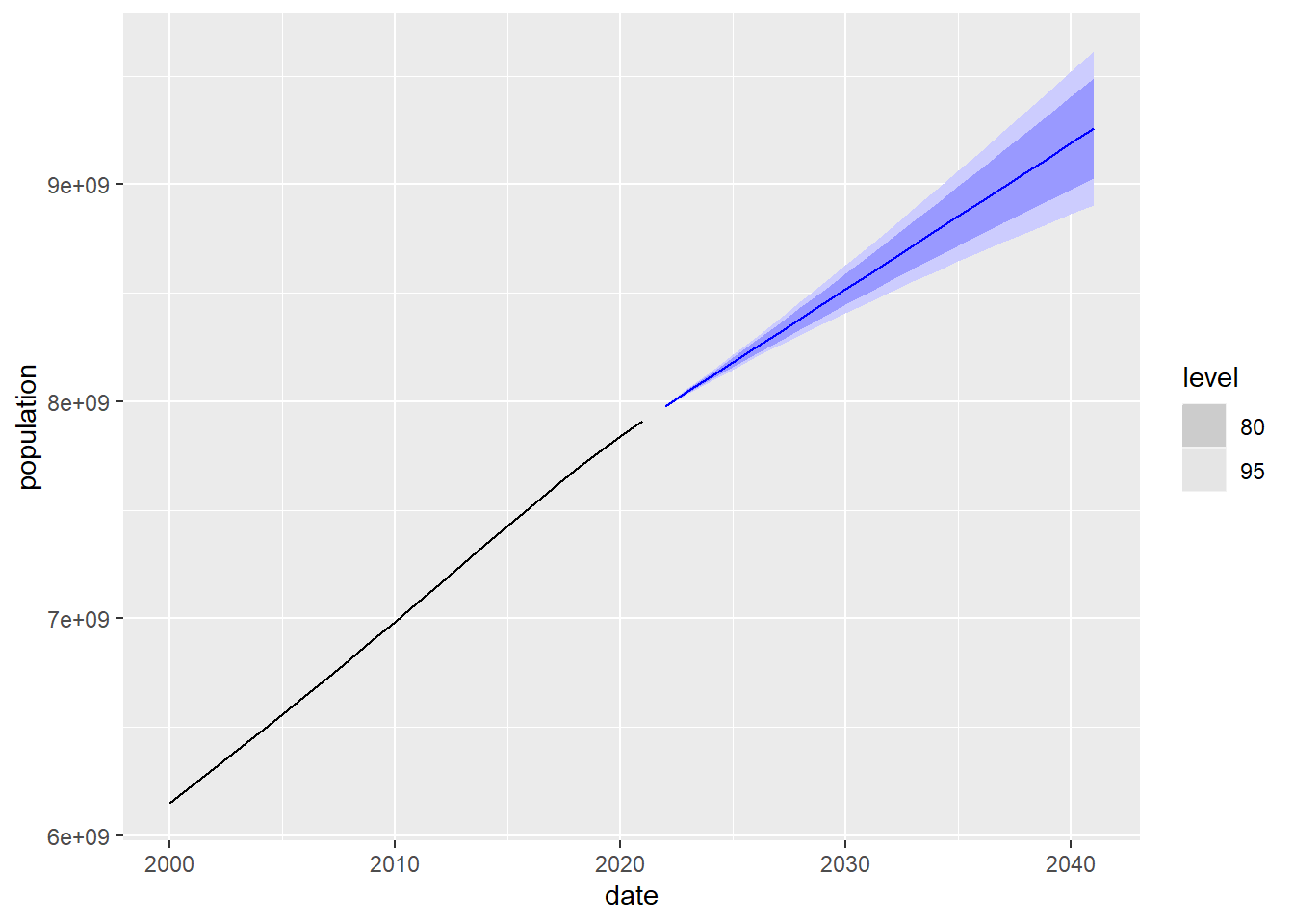
Figure 5.17: Predicción a 20 años de la población mundial usando el modelo ARIMA
A continuación aplicamos el modelo ARIMA al estudio de la serie temporal de la llegada de viajeros a las Islas Canarias.
## Series: pasajeros
## Model: ARIMA(1,0,1)(2,1,1)[12] w/ drift
##
## Coefficients:
## ar1 ma1 sar1 sar2 sma1 constant
## 0.9456 -0.3465 -1.0375 -0.5581 0.4769 1506.8730
## s.e. 0.0233 0.0741 0.0912 0.0602 0.0992 831.2593
##
## sigma^2 estimated as 198330585: log likelihood=-2634.69
## AIC=5283.38 AICc=5283.86 BIC=5307.74Observamos que en este caso se obtiene un modelo ARIMA(1,0,1)(2,1,1)\(_{12}\). A partir de los parámetros estimados se obtiene que el modelo viene dado por
\[ (1-0.95B)(1+1.038B^{12}+0.56B^{24})(1-B^{12})y_t=1506.87+(1-0.35B)(1+0.48B^{12})\varepsilon_{t} \] En esta serie temporal también observamos que el modelo ARIMA se ajusta mejor a la serie temporal que el suavizado exponencial al tener los valores de AIC, AICc y BIC más pequeños. Nótese que cuando hay estacionalidad con periodo alto, el modelo ARIMA gestiona, en general, con menos parámetros la estacionalidad comparado con el modelo ETS. Si el periodo de la estacionalidad es \(m\), ETS siempre requiere \(m\) parámetros numéricos para gestionar la estacionalidad, sin embargo el modelo ARIMA requiere \(P+Q+1\) parámetros numéricos. En particular, para el ejemplo anterior, ETS requiere 12 parámetros numéricos para gestionar la estacionalidad y ARIMA requiere 4 parámetros numéricos.
A continuación calculamos una predicción a 2 años usando este modelo y una gráfica con la predicción, los intervalos de confianza y los datos observados desde 2017
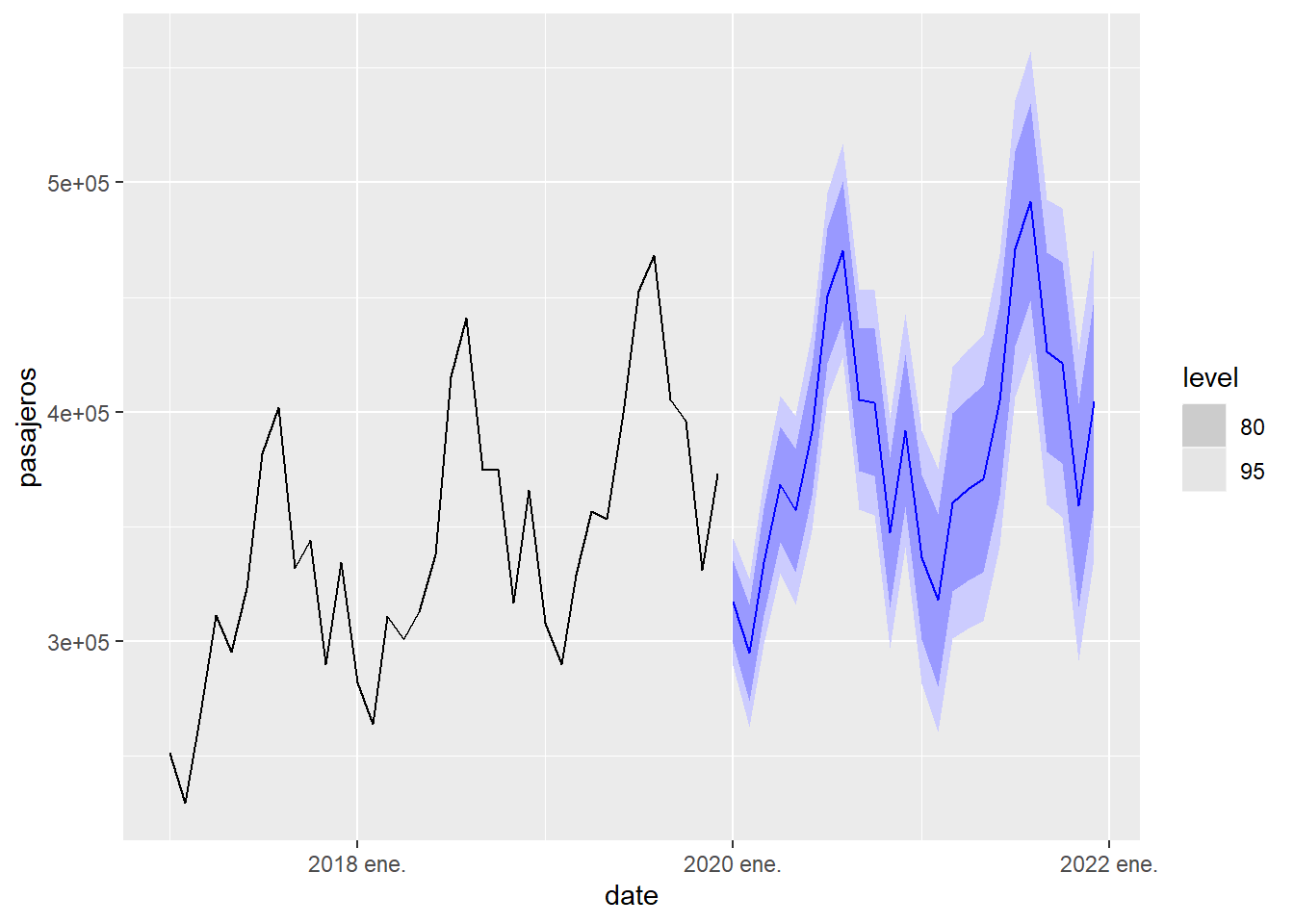
Figure 5.18: Predicción a 2 años de la llegada de pasajeros a Canarias usando el modelo ARIMA
Gestión de la doble estacionalidad
Al igual que el modelo de suavizado exponencial, este modelo tampoco está diseñado para gestionar directamente una doble estacionalidad. Para ilustrar un método distinto a la descomposición STL para gestionar la doble estacionalidad vamos a presentar el método de regresión armónica dinámica (Dynamic Harmonic Regression) que usa una combinación de series de Fourier para aproximar la estacionalidad de una serie temporal. Una serie de Fourier de periodo \(m\) y orden \(K\), que denotaremos por \(f_{m,K}(t)\), viene dada por la siguiente combinación de senos y cosenos
\[
f_{m,K}(t)=\sum_{k=0}^K\alpha_k \ cos(\frac{2\pi kt}{m})+\sum_{k=1}^K\beta_k \ sin(\frac{2\pi kt}{m})
\]
Las series de Fourier son una forma clásica en Análisis Matemático de aproximar funciones periódicas. Los coeficientes \(\alpha_k\) y \(\beta_k\) se adaptan para ajustarse a la función periódica que queramos y \(K\) representa la complejidad de la aproximación, cuanto mayor sea \(K\), mejor aproximada estará la función periódica, pero con un costo computacional superior, siendo \(m/2\) el valor máximo de \(K\). Para eliminar la estacionalidad del modelo ARIMA con este método, lo que se hace es aplicar el modelo ARIMA sin estacionalidad a la serie temporal \(\tilde{y}_t=y_t-f_{m,K}(t)-f_{m',K'}(t)\), donde \(m\) y \(m'\) son los periodos de las estacionalidades involucradas. La serie \(\tilde{y}_t\) corresponde a la serie \(y_t\) libre de su estacionalidad. Los valores de \(K\) y \(K'\) determinan la calidad de la aproximación de \(y_t\) por la serie de Fourier, el problema es que si \(K\) o \(K'\) son valores altos, el costo computacional para calcular todos los parámetros puede ser también alto y tardar mucho tiempo su ejecución. Además, si la serie temporal original presenta picos pronunciados, como es el caso de la serie ine_comercio_diario, entonces la serie de Fourier tiene que incorporar muchos términos (valor de \(K\) o \(K'\) alto) para aproximar dichos picos. A continuación se presenta una aplicación de esta técnica a la serie ine_comercio_diario:
fit <- ine_comercio_diario %>%
model(
dhr=ARIMA(value ~ PDQ(0, 0, 0) + pdq(d = 0) + # usamos ARIMA sin estacionalidad y sin derivar
fourier(period = 7, K = 3) + # añadimos serie de Fourier de periodo m=7 con K=3
fourier(period = 365.25, K = 50) # añadimos serie de Fourier de periodo m=365.25 con K=50
)
)
fit %>% #dibujamos la predicción a un año vista.
forecast(h = 365) %>%
autoplot( ine_comercio_diario%>%
filter(date>= as.Date("2022-01-01"))
)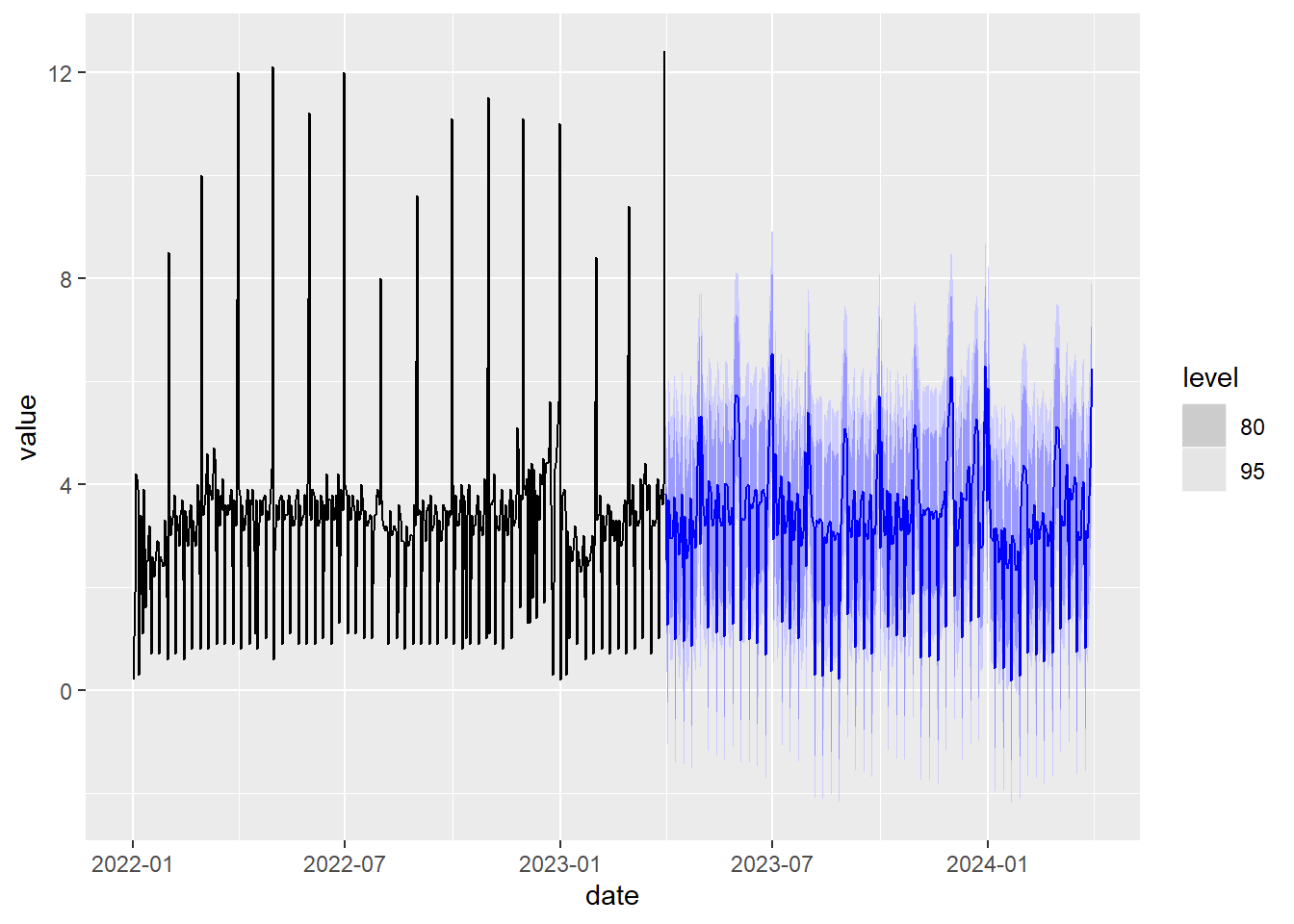
Figure 5.19: Predicción con doble estacionalidad usando series de Fourier y el modelo ARIMA
Si ejecutamos este código, observamos que tarda bastante debido a un valor alto de \(K=50\) y a pesar de ello, los picos de la serie temporal no se predicen bien en el futuro debido a que todavía haría falta un valor mayor de \(K\) para que la serie de Fourier pudiese aproximar mejor dichos picos. Es decir, esta técnica de gestionar la estacionalidad con series de Fourier funciona bien cuando el periodo es pequeño o la serie temporal evoluciona suavemente y no tiene picos aislados pronunciados. El método de descomposición STL para gestionar la doble estacionalidad es mucho más rápido y gestiona bien los picos sin costos computacionales añadidos.
5.8 Resumen modelos de predicción
Es importante tener en cuenta las hipótesis de trabajo y el modo de funcionamiento de los modelos de predicción a la hora de aplicarlos. El modelo ETS asume que, una vez compensada la estacionalidad, la tendencia de la serie temporal es apróximadamente lineal. Esta tendencia lineal se puede amortiguar suavemente usando el parámetro de amortiguamiento. El modelo ETS utiliza todos los valores pasados de la serie para hacer la predicción, pero el peso de cada valor va decayendo según vamos hacia el pasado. El número de parámetros numéricos del modelo crece mucho cuando hay una estacionalidad con periodo \(m\) alto, por tanto no resulta aconsejable gestionar la estacionalidad dentro del modelo para \(m\) muy altos, como por ejemplo \(m=365\) cuando trabajamos con un dato diario con periodicidad anual. El modelo ARIMA, asume, que una vez compensada la estacionalidad, alguna derivada de la serie temporal es una serie “sin tendencia”, es decir oscila alrededor de un valor constante. El modelo ARIMA utiliza solo una cola de valores hacia el pasado para calcular la predicción, pero posee mucho más libertad que el modelo ETS para fijar los elementos del pasado que participan en la predicción y su peso en la predicción. Además el número de parámetros numéricos que necesita para gestionar la estacionalidad no depende del periodo \(m\).
Como hemos visto, la estacionalidad simple se puede compensar dentro del propio modelo de predicción. También se puede compensar fuera del modelo usando la descomposición STL o las series de Fourier. Estas últimas técnicas permiten gestionar estacionalidad doble, algo que no se puede gestionar dentro de los modelos de predicción estudiados. El uso de las series de Fourier no es aconsejable para series temporales que presenten fuertes variaciones y una estacionalidad con periodo \(m\) alto.
En este curso, para aplicar los modelos de predicción a una serie temporal usamos las librerías especializadas de
Ry por tanto, nosotros no calcularemos “a mano” la configuración y parámetros de los modelos. Sin embargo es importante saber interpretar el resultado obtenido para entender que estamos haciendo. Por ejemplo el modelo ETS(E,T,S) tiene 3 tipos de opciones que hacen referencia a :- E: Si el modelo de error es aditivo o multiplicativo.
- T: Si el modelo tiene tendencia y si se usa amortiguamiento. En la práctica, lo habitual es que la serie tenga alguna tendencia, bien a crecer, o bien a decrecer.
- S: Si el modelo incluye estacionalidad que puede ser aditiva o multiplicativa.
La interpretación de los parámetros del modelo ARIMA(p,d,q)(P,D,Q)\(_m\) es :
- \(m\) : la periodicidad de la estacionalidad, es decir, esperamos que cada \(m\) días (o unidades temporales de la serie) tienda a repetirse la serie. Si \(m>1\), este valor, de forma natural, introduce la serie \(m\) espaciada dada por \(y_t,y_{t-m},y_{t-2m},y_{t-3m},...\) y lo mismo para la serie de errores anteriores \(\varepsilon_t,\varepsilon_{t-m},\varepsilon_{t-2m},\varepsilon_{t-3m},...\)
- p : tamaño de la cola de valores de la serie temporal involucrada en el diseño de la predicción.
- P : tamaño de la cola de valores de la serie temporal \(m\) espaciada involucrada en el diseño de la predicción.
- q : tamaño de la cola de valores de la serie de errores involucrada en el diseño de la predicción.
- Q : tamaño de la cola de valores de la serie de errores \(m\) espaciada involucrada en el diseño de la predicción.
- d : orden de la derivada de la serie temporal involucrada en el diseño de la predicción.
- D : orden de la derivada de la serie temporal \(m\) espaciada involucrada en el diseño de la predicción.
Las librerías que usamos para ajustar los modelos de predicción suministran estimadores, como el AIC, AICc y BIC, de la calidad del ajuste del modelo a la serie temporal para los datos conocidos. Aunque no entraremos aquí en el estudio de estos estimadores de calidad, si decir que cuanto más pequeño sea su valor, mejor es la calidad del ajuste, lo cual nos permite comparar la calidad del ajuste de los modelos estudiados. Estos estimadores de calidad también tienen en cuenta el número de parámetros numéricos que se optimizan. Utilizar muchos parámetros numéricos se considera algo negativo en la calidad del ajuste debido al mencionado problema de “overfitting”.
Los modelos utilizan la serie completa para ajustar los parámetros. Si, en el pasado, el comportamiento de la serie era muy diferente, quizás pueda ser una buena idea recortar la serie antes de hacer la predicción. Hay que tener en cuenta que si hay estacionalidad, los métodos suelen requerir, al menos 2 periodos completos de datos, es decir si tenemos datos diarios con una estacionalidad anual (\(m=365\)), necesitamos que la serie tenga más de 730 datos para gestionar la estacionalidad.
Una predicción sin intervalos de confianza asociados es de muy escasa utilidad porque sin saber el rango esperado de fluctuación del valor no es posible interpretar la calidad esperada del resultado. Para ilustrar esto, imaginemos la predicción de un número de lotería entre 0 y 99999 en base a los números de lotería que han salido en el pasado. El valor esperado de la predicción, que normalmente no estará lejos de 50000, es un valor completamente inútil para predecir el número que saldrá hoy, pero sin intervalos de confianza no podríamos valorar el interés y pertinencia de esta predicción. Incluso si los intervalos de confianza que suministran los modelos son razonablemnte pequeños para una predicción a corto plazo, hay que ser prudentes a la hora de interpretarlos porque asumen que el error en la estimación es una distribución normal de varianza constante y decorrelada (lo que podemos interpretar como que el error en un día es independiente del error el resto de días). Además de que, en la práctica, esto solo se verifica de manera aproximada y con bastante margen de error, se asume, que, en el futuro, la distribución del error diario es la misma, conservando su varianza. Esto, es una hipótesis razonable, al menos a corto plazo, en series que se mueven con una inercia estable, como, por ejemplo, una población. Sin embargo, esta hipótesis no se cumple en series donde eventos externos pueden, en muy corto plazo, cambiar totalmente la tendencia de la serie temporal como en el caso, por ejemplo, de la cotización de valores en bolsa, o el precio de la energía (nótese el efecto de un evento como la guerra en Ucrania). Incluso en series relativamente estables en el pasado, como los movimientos de pasajeros en los aeropuertos, un evento como la epidemia de la COVID-19, hace inútil cualquier predicción realizada en el pasado. Dicho esto, con todas sus limitaciones asociadas, hacer predicciones es un elemento fundamental e indispensable en la cadena de decisiones en cualquier empresa, organización o país.
5.9 Rellenar huecos en una serie temporal y sustituir datos anómalos.
En ocasiones, hay huecos en las series temporales, es decir faltan datos en fechas intermedias o bien hay datos anómalos como es el caso de la llegada mensual de viajeros a los aeropuertos canarios durante el periodo de la pandemia provocada por la COVID-19. Para estudiar este asunto vamos a usar datos obtenidos a partir de una consulta al ISTAC:
istac_aeropuertos2 <- read_csv("https://ctim.es/AEDV/data/istac_aeropuertos2.csv")%>%
as_tibble()%>%
mutate(mes = yearmonth(as.Date(paste0("01/",mes),format="%d/%m/%Y"))) %>%
as_tsibble(index = mes,key=aeropuerto)
istac_aeropuertos2 %>%
autoplot()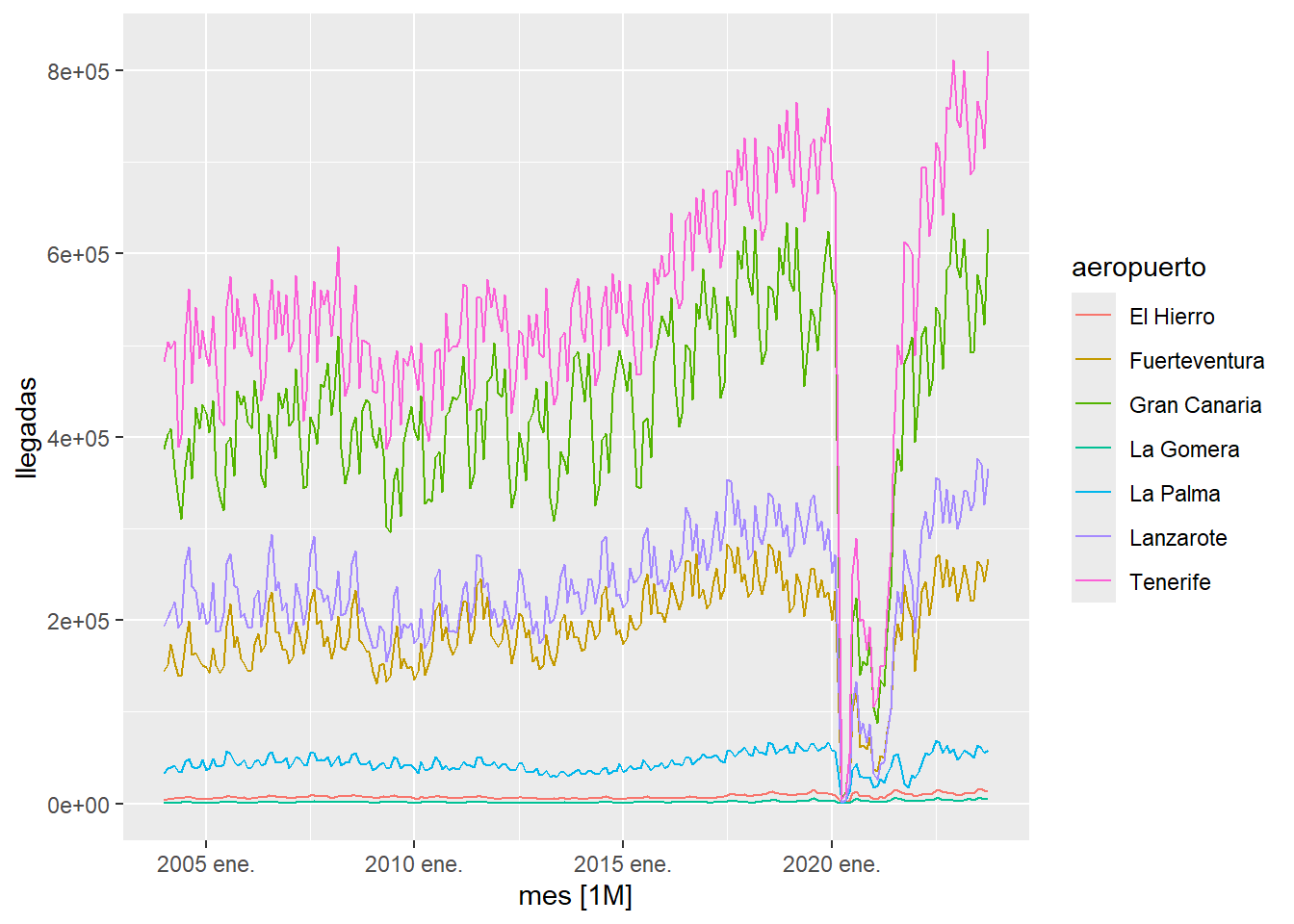
observamos que hay un periodo de tiempo muy afectado por la pandemia, para estudiar como hubiesen sido las series temporales si no hubiese existido la pandemia vamos a proceder en primer lugar a eliminar de las series los datos afectados y posteriormente cubrir, con la función fill_gaps, los huecos creados con valores NA:
istac_aeropuertos2 <- istac_aeropuertos2 %>%
filter(mes>=as.Date("2022-06-01") | mes<as.Date("2020-02-01") ) %>%
fill_gaps()
istac_aeropuertos2 %>%
autoplot()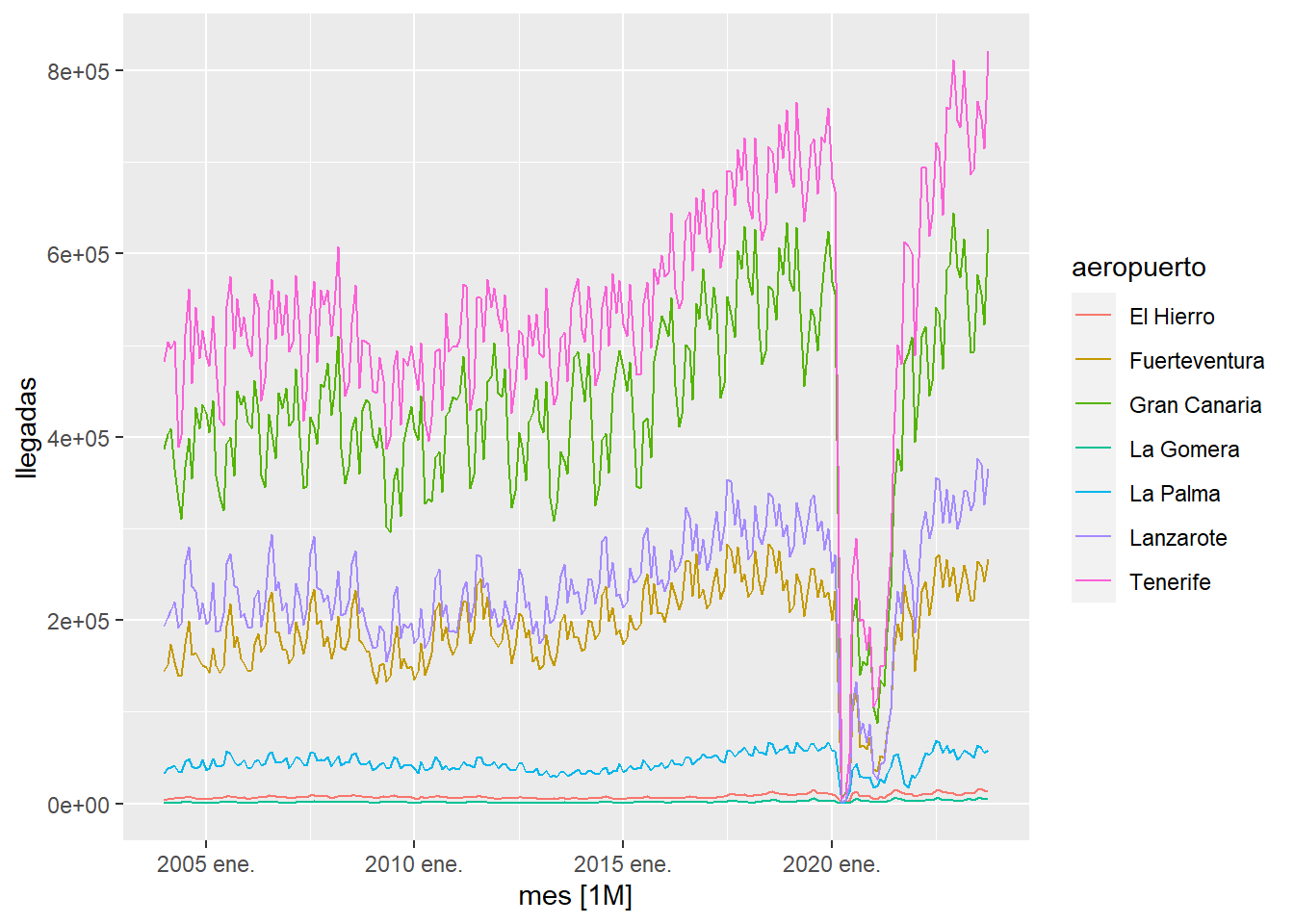
como se aprecia en la gráfica anterior, ya no aparecen los datos anómalos en las series temporales. Ahora lo que haremos es rellenar los huecos creados construyendo un modelo ARIMA con los datos existentes e interpolando los valores ausentes con el modelo ARIMA :
istac_aeropuertos2 %>%
model(ARIMA(llegadas))%>%
interpolate(istac_aeropuertos2)%>%
autoplot() +
labs(title="Rellenado de huecos usando un modelo ARIMA")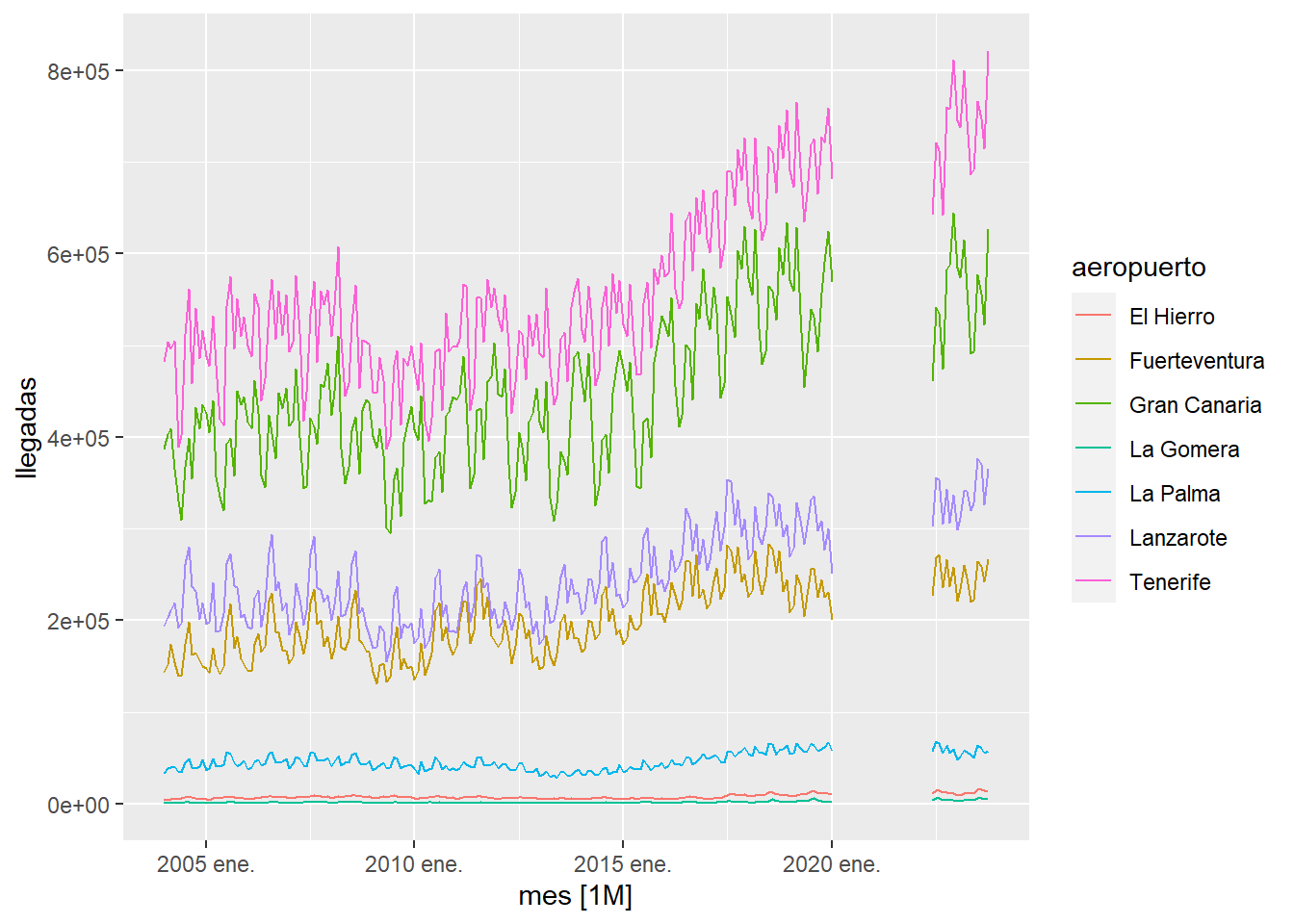
Una manera más sencilla de rellenar los huecos es utilizar la función na.approx que utiliza interpolación lineal para rellenar los huecos dentro de la serie. Este método básico funciona bien cuando los huecos son pequeños y no hay estacionalidad. Si lo aplicamos a la serie anterior observamos que el resultado es mucho peor que rellenar usando un modelo ARIMA.
istac_aeropuertos2 %>%
group_by(aeropuerto)%>%
mutate(llegadas=na.approx(llegadas,na.rm=FALSE)) %>%
ungroup() %>%
autoplot() +
labs(title="Rellenado de huecos con interpolación lineal")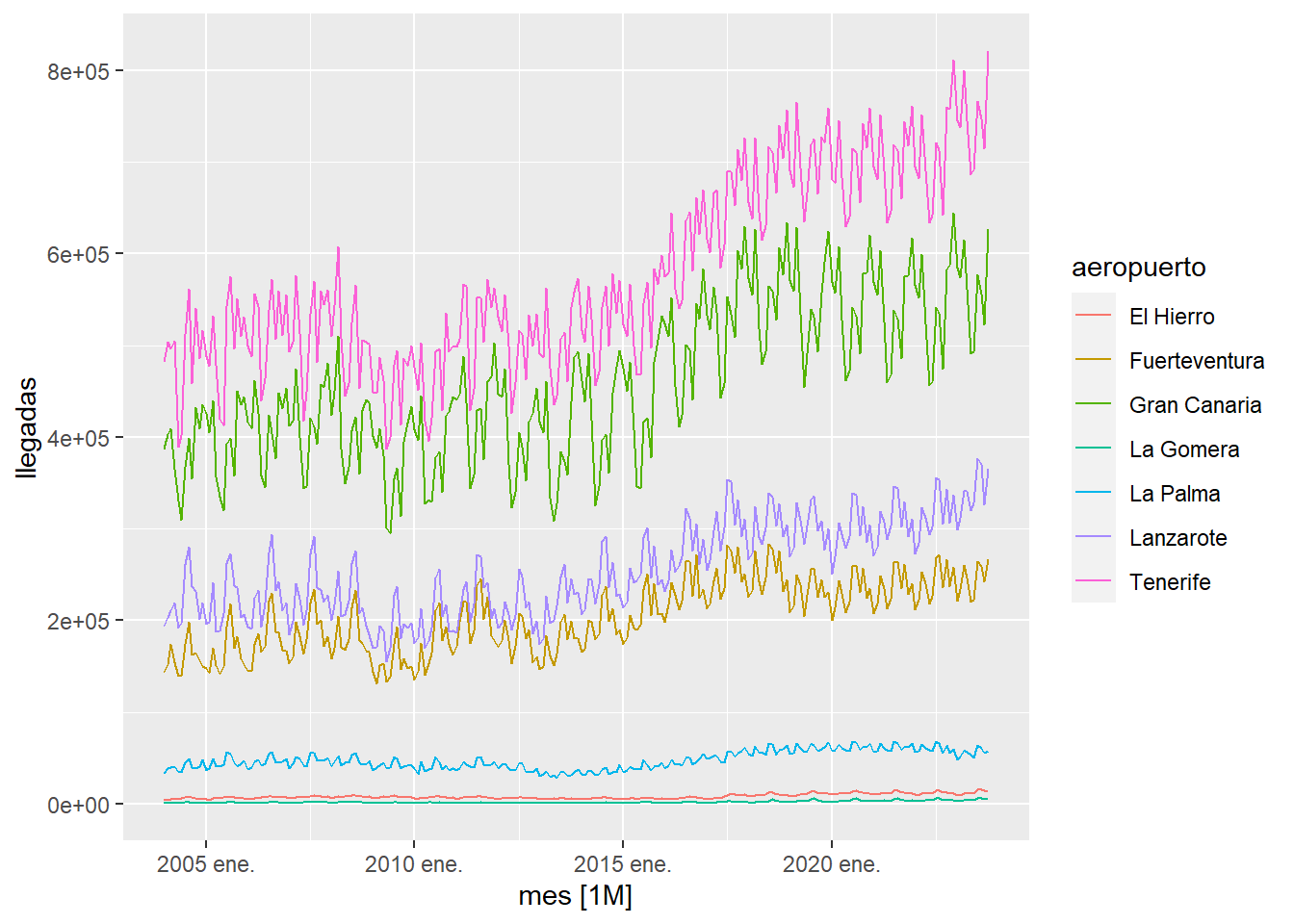
Para algunos procedimientos, como la descomposición STL, es necesario rellenar los huecos de las series temporales. A continuación se pone, para el total de llegadas a Canarias, el resultado de dicha descomposición STL usando ARIMA o interpolación lineal para rellenar los huecos. Observamos que en el caso de ARIMA la interpolación es tan perfecta que resulta irreal, lo cual detectamos porque los residuos son muy pequeños en la zona que hemos interpolado. Por el contrario al usar la interpolación lineal los residuos salen muy grandes debido a la mala calidad de la interpolación.
ts <- istac_aeropuertos2 %>%
as_tibble() %>%
group_by(mes) %>%
summarise(llegadas=sum(llegadas)) %>%
ungroup() %>%
as_tsibble(index=mes)
ts %>% model(ARIMA(llegadas))%>%
interpolate(ts) %>%
model(STL(llegadas,robust = TRUE)) %>%
components() %>%
autoplot() +
labs(title="STL con ARIMA para rellenar huecos")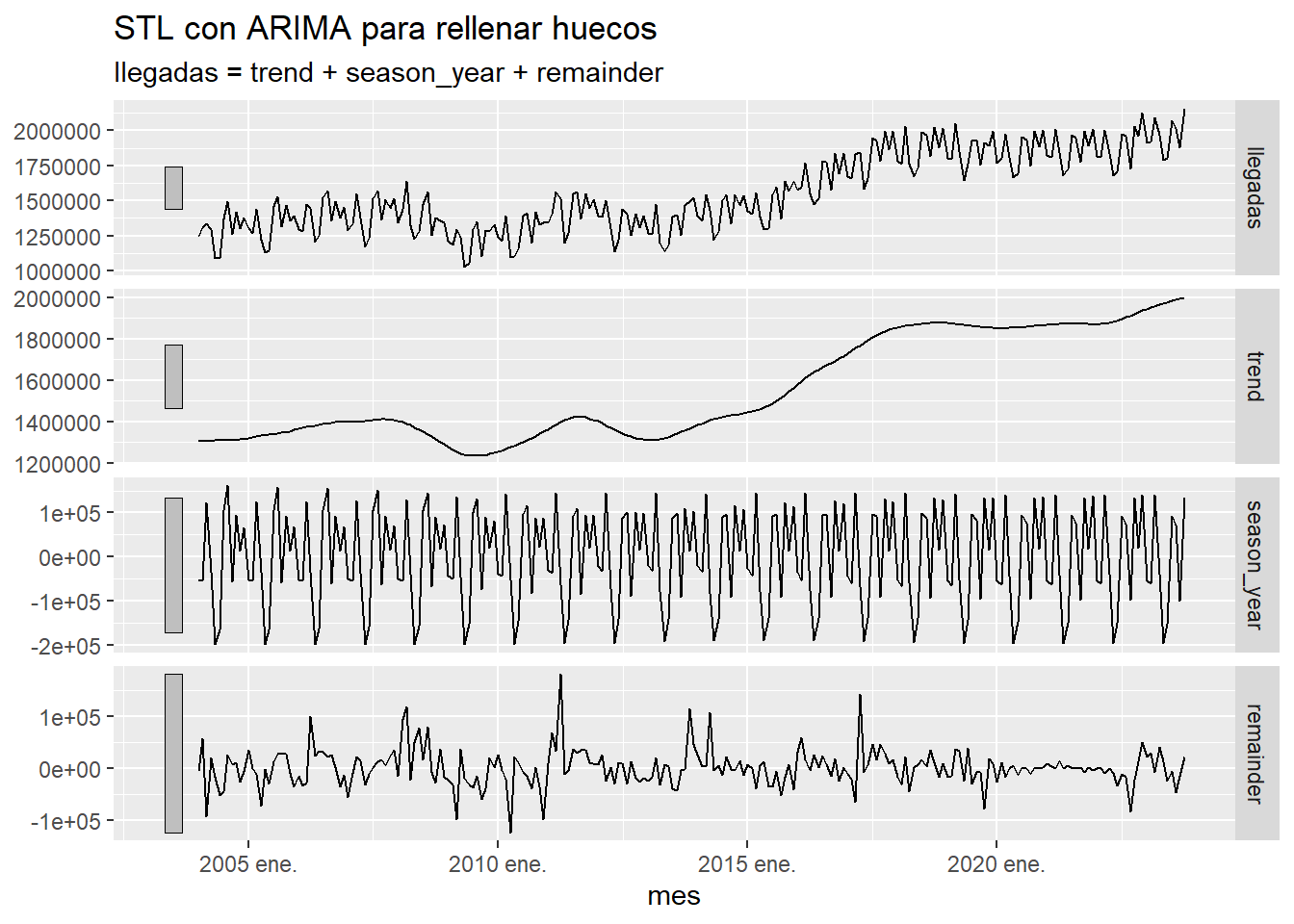
ts %>%
mutate(llegadas=na.approx(llegadas,na.rm=FALSE)) %>%
model(STL(llegadas,robust = TRUE)) %>%
components() %>%
autoplot() +
labs(title="STL con interpolación lineal para rellenar huecos")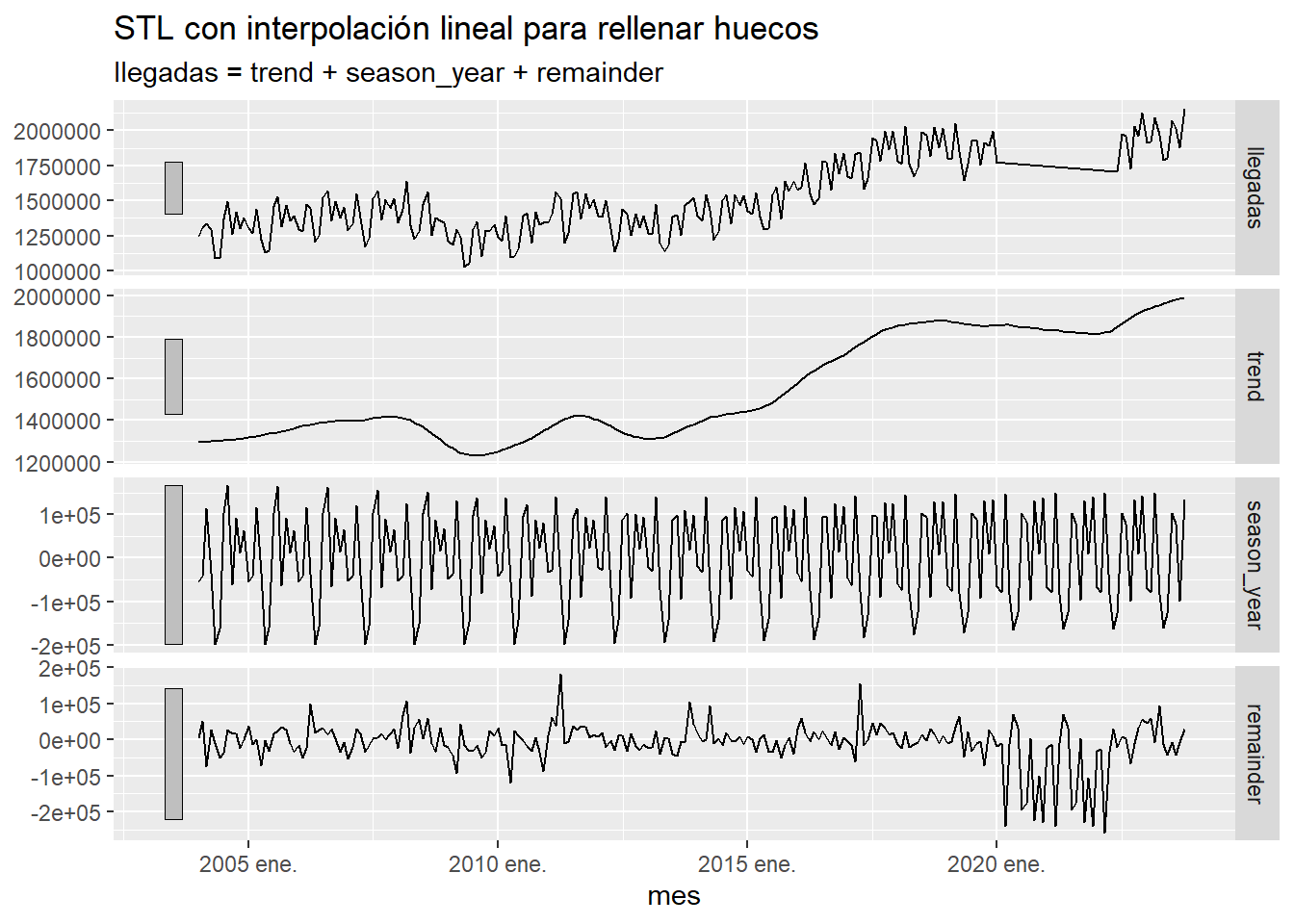
Referencias
[HyAt21] Rob J Hyndman and George Athanasopoulos. Forecasting: Principles and Practice (3rd Ed), OTexts, 2023.
[CCMT90] R. B.,Cleveland, W. S., Cleveland, J. E., McRae, and I. J. Terpenning. STL: A seasonal-trend decomposition procedure based on loess. Journal of Official Statistics, 6(1), 3–33, 1990