8 Análisis de atributos
Fecha última actualización: 2025-11-21
Instalación/carga librerías/datos utilizados
if (!require(highcharter)) install.packages('highcharter')
library(highcharter)
if (!require(openxlsx)) install.packages('openxlsx')
library(openxlsx)
if (!require(plotly)) install.packages('plotly')
library(plotly)
if (!require(ggplot2)) install.packages('ggplot2')
library(ggplot2)
if (!require(tidyverse)) install.packages('tidyverse')
library(tidyverse)
source("utilidades.R")8.1 Introducción
De manera general, podemos considerar que el análisis de atributos consiste en estudiar, comparar y manipular las variable numéricas (atributos) de nuestro dataset. En primer lugar estudiaremos la relación que puede existir entre dos variables numéricas cualesquiera para lo cual utilizaremos la regresión lineal combinada con transformaciones no-lineales como la transformación de Yeo-Johnson. A continuación veremos la matriz de correlación que nos suministra una visión global de la relación entre todos los atributos numéricos de nuestro dataset. Por último presentaremos el análisis de componentes principales denominado ACP (o PCA en inglés) que tiene como objetivo reemplazar la variables numéricas originales por nuevas variables obtenidas como combinación lineal de dichas variables originales con objeto de conseguir una nueva colección de variables que representen mejor, y de manera más compacta, la información contenida globalmente en la colección de variables inicial, de tal manera que podamos reducir el número de variables finales (bajar la dimensión) pero manteniendo la información fundamental contenida en las variables originales.
8.2 Relación entre dos variables
Correlación
Una manera habitual de estudiar la relación entre dos variables numéricas es usar la correlación. Dados dos variables \(x_k\) e \(y_k\) la correlación viene dada por la fórmula:
\[ r=\frac{\sum_{k=1}^m(x_{k}-\bar x)(y_{k}-\bar y)} {\sqrt{\sum_{k=1}^m(x_{k}-\bar x)^2\sum_{k=1}^m(y_{k}-\bar y)^2}} \]
Donde, \(\bar x\) y \(\bar y\) representan la media de las respectivas variables, y \(m\) es el número de observaciones (tamaño de la muestra). El valor de la correlación \(r\) se mueve en el rango entre -1 y 1 y se puede interpretar de la siguiente manera:
- Si \(r=1\) la variable \(y_k\) se puede obtener de forma exacta y lineal a partir de \(x_{k}\), si el valor de una variable aumenta también aumenta la otra, y si dibujamos la gráfica de dispersión de ambas variables, todos los puntos caen de forma exacta sobre la recta de regresión.
- Si \(r=0\) no existe relación entre ambas variables y la gráfica de dispersión, normalmente, nos dará una nube de puntos dispersa.
- Si \(r=-1\), el caso es idéntico a \(r=1\) con la única diferencia de que, en este caso, cuando una variable aumenta, la otra disminuye.
Una propiedad importante de la correlación es que es independiente de la unidad de medida de las variables (siempre que la transformación entre las medidas sea lineal), es decir, da igual medir una población en millones o en miles, o una temperatura en grados Celsius o Fahrenheit, la correlación de estas variables con otras variables da el mismo valor independientemente de la unidad de medida utilizada.
Veamos un ejemplo comparando el total de delitos cometidos y el total de consumo de pan y cereales obtenidos, por comunidades autónomas, a través de consultas al INE. Para calcular la correlación usamos la función cor.
INE.CONSUMO.PAN.DELITOS <- read_csv("https://ctim.es/AEDV/data/INE.CONSUMO.PAN.DELITOS.csv") %>%
as_tibble()
INE.CONSUMO.PAN.DELITOS## # A tibble: 19 × 3
## `Comunidades y Ciudades Autónomas` total.consumo.pan.cereales total.delitos
## <chr> <dbl> <dbl>
## 1 01 Andalucía 6957. 68853.
## 2 02 Aragón 1117. 8458.
## 3 03 Asturias, Principado de 927. 7825.
## 4 04 Balears, Illes 944. 10590.
## 5 05 Canarias 1805. 19146.
## 6 06 Cantabria 500. 4392.
## 7 07 Castilla y León 2130. 14720.
## 8 08 Castilla - La Mancha 1718. 11670.
## 9 09 Cataluña 6140. 58416.
## 10 10 Comunitat Valenciana 4167. 44809.
## 11 11 Extremadura 926. 7206.
## 12 12 Galicia 2389. 17904.
## 13 13 Madrid, Comunidad de 5289. 45146.
## 14 14 Murcia, Región de 1198. 12126.
## 15 15 Navarra, Comunidad Foral de 528. 4244.
## 16 16 País Vasco 1834. 15788.
## 17 17 Rioja, La 263 2372.
## 18 18 Ceuta 65.6 1759.
## 19 19 Melilla 62.8 1458.paste("correlación =",
cor(
INE.CONSUMO.PAN.DELITOS$total.consumo.pan.cereales,
INE.CONSUMO.PAN.DELITOS$total.delitos)
)## [1] "correlación = 0.98987954033385"Observamos una correlación alta entre ambas variables. Vamos a ilustrar la relación entre las variables con un diagrama de dispersión:
p <- INE.CONSUMO.PAN.DELITOS %>%
ggplot(aes(total.consumo.pan.cereales,total.delitos,label=`Comunidades y Ciudades Autónomas`)) +
geom_point() +
geom_smooth(method = lm, se = FALSE)
ggplotly(p)
Observamos que como la correlación es alta, los puntos se encuentran próximos a la recta de regresión. Este ejemplo nos ilustra además que una alta correlación entre variables no implica que exista una causalidad entre la variables observadas, es decir, el consumo de pan y cereales no es un factor que provoque delincuencia. La correlación alta es debida a que ambas variables crecen con la población y la relación entre ellas es indirecta dado que las comunidades con más población consumen más pan y a la vez se producen más delitos. Establecer relaciones de causalidad, exclusivamente a partir de la correlación entre variables, es un error habitual que el buen científico de datos debe evitar. En este caso, la población sería lo que se denomina, una variable latente, es decir, una variable que explica el comportamiento observado pero que no se encuentra entre las variables estudiadas.
Recta de regresión
Al estudiar la posible relación lineal entre 2 variables utilizamos la recta de regresión que podemos expresar como \(y=ax+b\). Los coeficientes \(a\) y \(b\) de la recta de regresión se calculan minimizando el error cuadrático entre la recta y la nube de puntos dado por
\[ Error(a,b)=\sum_{k=1}^m (ax_k+b-y_k)^2 \] Vamos a medir la calidad del ajuste por la recta de regresión de dos formas distintas. En primer lugar usando el \(RMSE\) (root mean square error) dado por
\[ RMSE=\sqrt{\frac{\sum_{k=1}^m (ax_k+b-y_k)^2}{m}} \] Como vemos, el \(RMSE\) se calcula directamente a partir de la fórmula anterior \(Error(a,b)\) y podemos decir que los coeficientes de la recta de regresión son los que minimizan el \(RMSE\). Cuanto más pequeño sea el valor de \(RMSE\) mejor es el ajuste.
Otra forma de medir la calidad del ajuste es usar el coeficiente de determinación \(R2\) dado por
\[ R2=1 - \frac{\sum_{k=1}^m (ax_k+b-y_k)^2}{\sum_{k=1}^m (y_k-\bar y)^2} \]
\(R2\) se mueve entre 0 y 1. Cuanto más cerca de 1, mejor es el ajuste por la recta de regresión, al igual que para la correlación, el valor 1 corresponde a una relación lineal perfecta. Si \(R2\) vale cero no hay relación lineal entre las variables. El valor de \(R2\), al igual que la correlación, es independiente de la unidad de medida de las variables o de si las variables están estandarizadas o no (estandarizar una variable consiste en restar la media y dividir por la desviación típica).
Relación no lineal entre variables
Puede ser que el ajuste lineal entre las variables mejore si le aplicamos previamente a alguna de ellas (o a las dos) una transformación no-lineal (como un logaritmo) antes de calcular la correlación. Esto es lo que hacemos en el cuadro de mandos de ejemplo Dashboard3.Rmd del tema anterior, donde se estudia como transformar los atributos, usando la función sqrt, logaritmo o la transformación de Yeo-Johnson para estudiar la relación entre pares de atributos. La transformación de Yeo-Johnson ([YeJo00]), \(T(y;\lambda)\), que depende de un parámetro \(\lambda\) se define como:
\[ T(y;\lambda)=\left\{ \begin{array} [c]{ccc}% \frac{(y+1)^{\lambda}-1}{\lambda} & si & y\geq0,\quad\lambda\neq0\\ \log(y+1) & si & y\geq0,\quad\lambda=0\\ -\frac{(-y+1)^{2-\lambda}-1}{2-\lambda} & si & y\leq0,\quad\lambda\neq2\\ -\log(-y+1) & si & y\leq0,\quad\lambda\neq2 \end{array} \right. \]
A continuación presentamos la gráfica de esta transformada para diferentes valores del parámetro \(\lambda\)
Figure 8.1: Gráfica de la transformada de Yeo-Johnson para diferentes valores del parámetro lambda
En el cuadro de mandos, cuando se selecciona la opción YeoJohnson, se calcula automáticamente el valor de \(\lambda\) que suministra un mejor ajuste lineal entre las variables y se imprime su valor en la primera columna. Para valorar la calidad del ajuste obtenido, en la primera columna del cuadro de mando se imprimen los siguientes valores :
correlation: el valor de la correlación estudiado anteriormente.
sd(residuos): la desviación típica de los residuos. Como la media de los residuos de la regresión lineal es cero, se cumple que \(RMSE=\)sd(residuos).
R2: el coeficiente de determinación. El criterio utilizado para calcular \(\lambda\) en la transformada de Yeo-Johnson es maximar este valor.
Al estudiar en este cuadro de mandos la relación entre los atributos life_expectancy y gdp_per_capit observamos en la siguiente imagen que no existe una buena relación lineal entre ellos:
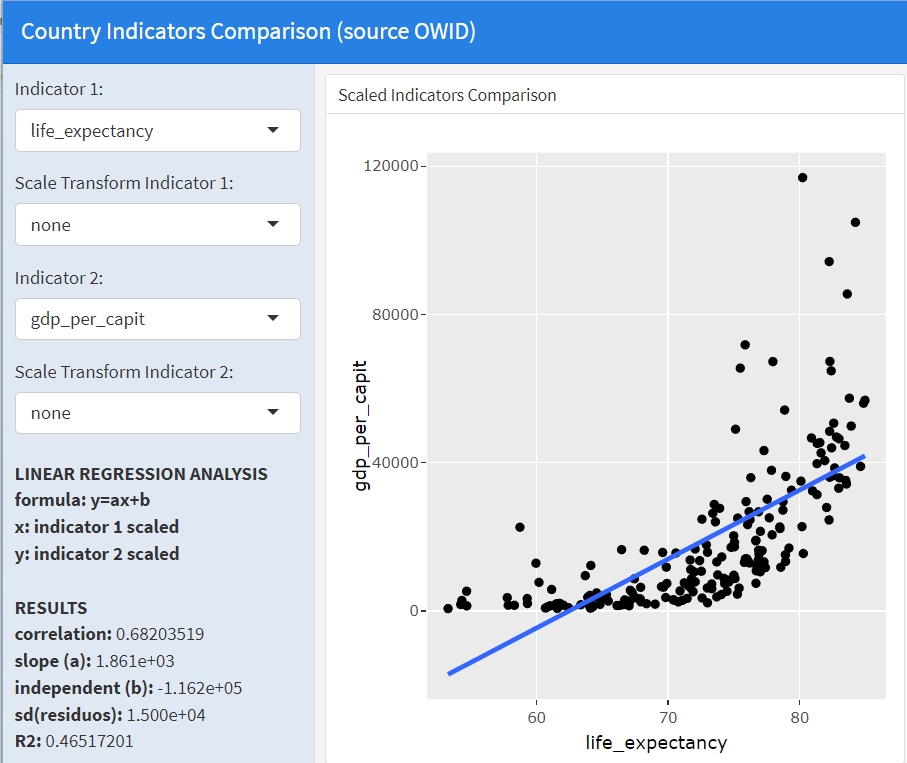
Sin embargo, al activar la opción “YeoJohnson” en el cuadro de mandos, se aplica la transformada Yeo-Johnson a la segunda variable y, como podemos observar en la siguiente imagen, obtenemos un ajuste lineal mucho mejor con un valor de \(\lambda=5.1e-3\). Ello nos indica que existe una relación no-lineal entre ambas variables que ha sido capturada usando la transformación de Yeo-Johnson.
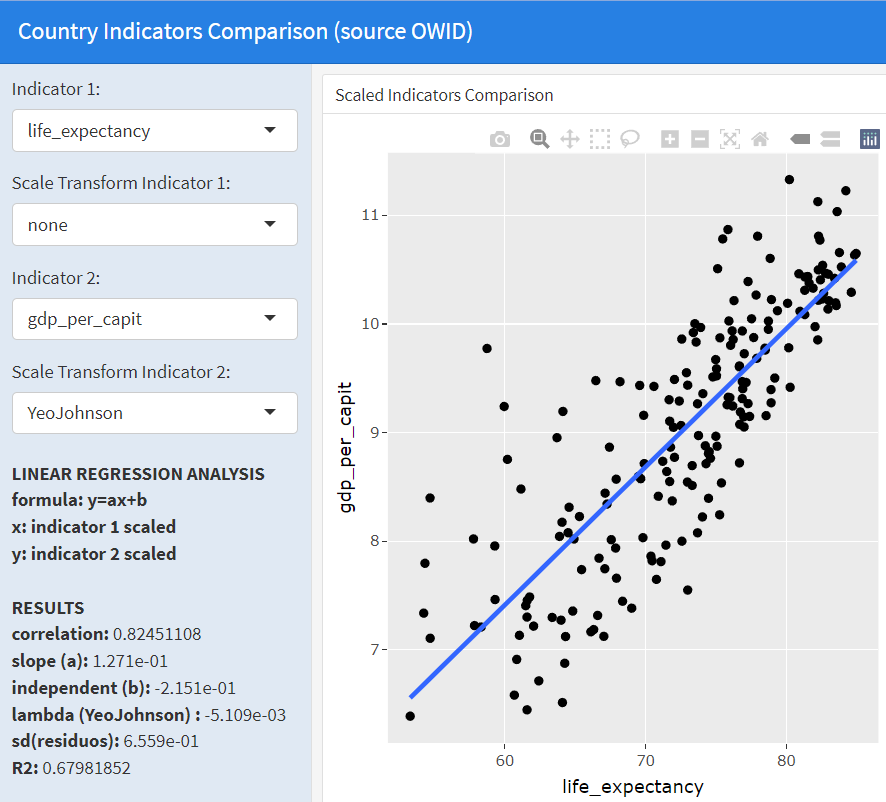
8.3 La matriz de correlación
La matriz de correlación se obtiene calculando la correlación para todos los pares de atributos y poniendo el resultado en forma de matriz. Resulta muy útil para tener una visión global de las relaciones entre todos lo atributos. Por ejemplo, en la siguiente gráfica interactiva visualizamos la matriz de correlación de la tabla owid_country. Previamente hay que quitar las variables no numéricas, puesto que la correlación solo se calcula para variables numéricas y además hay que eliminar los valores NA antes de hacer el cálculo.
owid_country %>%
select(-location,-continent,-iso_code) %>% # eliminamos de la tabla las variables no-numéricas
cor(use='complete.obs') %>% # cálculo matriz correlación eliminando NA previamente
hchart() # dibujo interactivo matriz de correlación
Figure 8.2: Matriz de correlación usando hchart
De la exploración de los valores de correlación, observamos, que aged_65_older y aged_70_older están muy relacionadas, que population y cardiovasc_death_rat están muy poco relacionadas con el resto de variables y que extreme_poverty, tiene, en general, correlación negativa con el resto de variables, es decir que cuando esta variable crece, las otras decrecen.
La manera anterior de dibujar la matriz de correlación puede fallar en los cuadros de mandos. Por ello hemos diseñado una función alternativa en plotly:
# FUNCIÓN PARA DIBUJAR LA MATRIZ DE CORRELACIÓN
plot_correlation <- function(
M, # matriz de correlación
show_values = TRUE, # flat para controlar si se imprimen los valores en las celdas
title = "matriz de correlación" # título del gráfico
) {
# Texto dentro de la celda (2 decimales)
cell_text <- round(M, 2)
# Escala personalizada: rojo -> blanco -> azul
custom_colors <- list(
c(0, "red"), # mínimo (-1) → azul
c(0.5, "white"),# 0 → blanco
c(1, "steelblue") # máximo (+1) → rojo
)
# Crear heatmap interactivo
plot_ly(
x = colnames(M),
y = rownames(M),
z = M,
type = "heatmap",
colorscale = custom_colors,
zmin = -1,
zmax = 1,
text = if (show_values) cell_text else NULL,
texttemplate = if (show_values) "%{text}" else NULL,
textfont = list(color = "black"),
hovertemplate = "X: %{x}<br>Y: %{y}<br>Correlación: %{z:.4f}<extra></extra>"
) %>%
layout(
title = title,
xaxis = list(title = "", tickangle = 45),
yaxis = list(title = "", autorange = "reversed")
)
}owid_country %>%
select(-location,-continent,-iso_code) %>% # eliminamos de la tabla las variables no-numéricas
cor(use='complete.obs') %>%
plot_correlation (show_values = TRUE)
Figure 8.3: Matriz de correlación usando plotly
8.4 Análisis de componentes principales (ACP)
En lo que sigue, para desarrollar los conceptos de esta sección, denotaremos por el vector \(x_j=(x_{1j},x_{2j},..,x_{mj})\) a cada atributo (o variable), donde \(m\) representa el número de observaciones (número de países en nuestro ejemplo). Es decir, que si el primer atributo (\(j=1\)) es la población, entonces, \(x_{i1}\) representaría la población del país \(i\).
Diremos que una variable \(x_j\) no aporta información nueva a nuestro análisis de datos si se puede obtener a partir de las otras variables. Es decir si
\[ x_{ij}=F(\{x_{ik}\}_{k\neq j}) \quad \forall i \]
para una cierta función \(F\). Por tanto, podemos quitar \(x_j\) de nuestro análisis de datos sin perder información. En particular, si la correlación entre dos variables está cerca de 1 o -1, podemos quitar una de ellas porque una se puede obtener a partir de la otra. Por ejemplo, en la tabla owid_country se guardan como indicadores el porcentaje de personas mayores de 65 años y el de personas mayores de 70 años. Estos dos indicadores están muy relacionados entre sí. Si usamos el tablero de mando Dashboard3.Rmd, observamos que el factor de correlación es de \(0.99\), y por tanto, se puede calcular con precisión una en función de la otra a partir de la recta de regresión, que en este caso viene dada por
\[ \text{aged_70_older} = 0.68\cdot \text{aged_65_older} -0.39 \] Por tanto, podríamos eliminar el indicador de porcentaje de mayores de 70 años de nuestro análisis de datos sin perder información relevante. Otro ejemplo de variable que podríamos desechar son las variables que poseen un valor constante (en este caso la función \(F\) sería una constante). Este tipo de variables se consideran desechables porque no aportan nada a la hora de discriminar entre unos países y otros.
En esta sección vamos a estudiar como combinar las variables y reducir su número sin perder información relevante. A este problema se le denomina reducción de la dimensionalidad.
Una limitación de las técnicas que vamos a analizar es que solo usaremos combinaciones lineales de las variables, es decir sumas de variables multiplicadas por unos coeficientes, eso deja fuera dependencias más complejas como las que vienen dadas por la función logaritmo o la transformación de Yeo-Johnson utilizadas en el cuadro de mandos Dashboard3.Rmd. Una forma de añadir transformadas no-lineales sería, antes de empezar con nuestro análisis lineal, añadir/sustituir en la tabla, variables que sean el resultado de aplicar transformaciones no-lineales a las variables iniciales. Por ejemplo, a la vista de los resultados del cuadro de mandos Dashboard3.Rmd, podríamos sustituir la variable gdp_per_capit por log(gdp_per_capit) que posee una mejor relación lineal con las otras que la variable inicial.
El análisis de componentes principales, ACP, (PCA en inglés) transforma las variables \(x_j\) en otras nuevas, \(y_j\), haciendo combinaciones lineales de las iniciales. El objetivo del ACP es buscar las combinaciones lineales de \(x_j\) que maximizan la varianza de \(y_j\) en orden descendente, es decir, \(y_1\) es la combinación lineal con mayor varianza posible e \(y_n\), es la combinación lineal con menor varianza posible. Cuando la varianza de \(y_j\) es muy pequeña consideramos que no aporta información relevante y la desechamos, de esta forma reducimos la dimensionalidad quedándonos solo con las variables \(y_j\) con varianza significativa, que son las que denominamos componentes principales.
Fundamento teórico
Conceptos algebraícos necesarios
Definición: El producto escalar de dos vectores \(u\) y \(v\) de tamaño n se define como \((u,v)=u_1v_1+\cdots + u_nv_n\). Los vectores siempre los consideraremos en vertical, es decir podemos escribir \((u,v)=u^Tv\), donde \(u^T\) es el vector traspuesto.
Definición: Una matriz cuadrada \(U\) es ortonormal (o unitaria) si se cumple \(U^TU=Id\), es decir que la traspuesta por ella misma es la matriz identidad. Por tanto, para una matriz ortonormal la inversa es la traspuesta.
Teorema: Los vectores columna de una matriz ortonormal \(U=(u_1,\cdots,u_n)\) (con \(u_k=(u_{1k},\dots,u_{nk})\)) cumplen que \((u_k,u_k)=1\) y si \(k\neq k'\) entonces \((u_k,u_{k'})=0\) es decir los vectores son perpendiculares.
Definición: el número real \(\lambda_k\) es un autovalor de la matriz cuadrada \(A\), si existe un vector \(u_k=(u_{1k},\dots,u_{nk})\), no nulo, denominado autovector, tal que \(Au_k=\lambda_k u_k\). Si \(u_k\) es autovector, entonces, al multiplicarlo por cualquier número diferente de cero, sigue siendo autovector. Por ello siempre podemos ajustar el autovector para que cumpla \((u_k,u_k)=1\).
Teorema: Si la matriz cuadrada \(A\) de dimensión n es simétrica, entonces posee n autovalores que podemos ordenar en forma decreciente, \(\lambda_1 \geq \lambda_{2} \geq \cdots \geq \lambda_n\) y además posee una matriz ortonormal de autovectores \(U=(u_1,u_2,..,u_n)\) formada por los autovectores \(u_k\) en columnas.
Teorema: Si \(X\) es una matriz cualquiera de tamaño mxn, entonces \(A=X^TX\) es cuadrada de tamaño nxn, simétrica y todos sus autovalores son mayores o iguales que cero.
Definición: Dados dos variables \(x_j\) y \(x_{j'}\), la covarianza \(Cov(x_{j},x_{j'})\) entre ellas se define como:
\[ Cov(x_{j},x_{j'})=\frac{\sum_{i=1}^m(x_{ij}-\bar x_j)(x_{i{j'}}-\bar x_{j'})} {m-1} \] donde \(m\) es el número de observaciones.
Definición: Si \(X=(x_1,x_2,...,x_n)\) es una matriz que representa \(n\) variables \(x_1,x_2,...,x_n\), la matriz de covarianza de \(X\) viene dada por la matriz \(\Sigma\) de dimensión \(n\times n\) cuyos elementos son \(\Sigma_{jj'}=Cov(x_{j},x_{j'})\)
Definición: Tipificar una variable, \(x_j\), consiste en restarle su media y dividirla por su desviación típica. Las variables tipificadas tienen media cero y varianza y desviación típica igual a 1.
Teorema: Si \(X=(x_1,x_2,...,x_n)\) es una matriz que representa \(n\) variables \(x_1,x_2,...,x_n\) tipificadas, entonces la matriz de covarianza \(\Sigma\) cumple:
\[ \Sigma=\frac{X^TX}{m-1} \] además
\[ \lambda_1+\lambda_2+..+\lambda_n=n \] donde \(\lambda_j\) son los autovalores de la matriz de covarianza \(\Sigma\). Además, como la matriz de covarianza \(\Sigma\) es proporcional a \(X^TX\), sus autovectores son los mismos y los autovalores de \(X^TX\) son los de \(\Sigma\) multiplicados por \(m-1\).
Fundamento matemático del ACP
Consideremos n variables \(x_j\) (los vectores columna de nuestra tabla), y las observaciones en forma de matriz \(X=x_{ij}\) de tamaño mxn. Vamos a sustituir \(X\) por una nueva colección de variables \(Y=XU\) donde \(U\) es una matriz ortonormal de tamaño n. Es decir, las nuevas variables \(y_j=Xu_j\) son combinaciones lineales de las anteriores obtenidas a partir de una matriz ortonormal que se pueden expresar como :
\[ y_1=u_{11}x_1+u_{21}x_2+\cdots+u_{n1}x_n\\ y_2=u_{12}x_1+u_{22}x_2+\cdots+u_{n2}x_n\\ \cdots \\ y_n=u_{1n}x_1+u_{2n}x_2+\cdots+u_{nn}x_n\\ \]
El análisis por componentes principales es una técnica para elegir la matriz ortonormal \(U\) de tal manera que las variables \(y_j=Xu_j\) (las componentes principales) estén ordenadas de forma descendente en función de su varianza, es decir, la primera componente principal \(y_1=Xu_1\) corresponde a la combinación lineal de las variables originales que tiene la mayor varianza posible, \(y_2=Xu_2\) sería la combinación ortogonal a la anterior (\((u_1,u_2)=0\)) con la mayor varianza posible, \(y_3=Xu_3\) sería la combinación ortogonal a las anteriores (\((u_1,u_3)=0\) y \((u_2,u_3)=0\)) con la mayor varianza posible, y así sucesivamente. Cuanto mayor es la varianza de \(y_j\) más información contiene la variable en términos, por ejemplo, de distinguir entre las diferentes observaciones. Nótese que una variable con valor constante (es decir varianza cero) no aporta ninguna información para discernir entre unas observaciones y otras. Dado que las variables \(x_j\) pueden tener magnitudes y varianzas muy distintas, para equilibrar la aportación de cada variable, primero se tipifican, es decir se le resta su media y se divide por la desviación típica. Es decir, consideraremos que las variables \(x_j\) tienen media cero y desviación típica 1. Si la media de cada variable \(x_j\) es cero, la media de \(y_j=Xu_j\) que es una combinación lineal de \(x_j\) también tendrá media cero y por tanto su varianza será
\[\text{Var}(y_j)=\frac{\sum_{i=1}^m y_{ij}^2}{m-1}=\frac{y_j^Ty_j}{m-1}=\frac{u_j^TX^TXu_j}{m-1}\] la clave para maximizar la varianza son los autovectores de la matriz \(A=X^TX\). Si \(\lambda_j\) son los autovalores ordenados de \(A\) en forma descendente, es decir \(\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_n\) y \(u_j\) sus correspondientes autovectores, entonces
\[\text{Var}(y_j)=\frac{u_j^TX^TXu_j}{m-1}=\frac{u_j^T\lambda_j u_j}{m-1}=\frac{\lambda_ju_j^T u_j}{m-1}=\frac{\lambda_j}{m-1}\] por tanto, el procedimiento para calcular las componentes principales de \(X\) se puede dividir en los siguientes pasos:
Tipificar la variables originales \(x_j\) para que tenga media cero y varianza 1.
Calcular los autovalores \(\lambda_j\) (ordenados de forma descendente) y autovectores \(u_j\) de la matriz \(X^TX\)
Las componentes principales son \(y_j=Xu_j\) y su varianza es \(\frac{\lambda_j}{m-1}\)
Ejemplo de ACP
Para ilustrar el proceso del cálculo de las componentes principales vamos a tomar un caso sencillo extraído de la tabla owid_country donde usaremos 3 variables (\(x_1\)=human_development_index, \(x_2\)=aged_65_older y \(x_3\)=aged_70_older ) y las observaciones de 5 países (China, Canada, Nigeria, Brazil y Germany). Para calcular el ACP la tabla solo puede tener variables numéricas. Para conservar el nombre de los países se usa la función column_to_rownames que asigna los países como nombres de cada fila, de esta manera se gestionan como un elemento externo a la tabla y no interfieren con el cálculo del ACP.
data <- owid_country %>%
filter( # filtramos los 5 países que se usarán
location == "China" |
location == "Canada" |
location == "Nigeria" |
location == "Brazil" |
location == "Germany"
) %>%
column_to_rownames(var="location") %>%
select(human_development_index,aged_65_older,aged_70_older)
data## human_development_index aged_65_older aged_70_older
## Brazil 0.765 8.552 5.060
## Canada 0.929 16.984 10.797
## China 0.761 10.641 5.929
## Germany 0.947 21.453 15.957
## Nigeria 0.539 2.751 1.447A continuación imprimimos las variables tipificadas usando la función scale y su matriz de correlación que muestra una alta correlación entre las variables .
## human_development_index aged_65_older aged_70_older
## Brazil -0.1409164 -0.4824390 -0.4932478
## Canada 0.8552170 0.6718445 0.5253853
## China -0.1652124 -0.1964691 -0.3389525
## Germany 0.9645488 1.2836202 1.4415691
## Nigeria -1.5136370 -1.2765565 -1.1347540
## attr(,"scaled:center")
## human_development_index aged_65_older aged_70_older
## 0.7882 12.0762 7.8380
## attr(,"scaled:scale")
## human_development_index aged_65_older aged_70_older
## 0.1646366 7.3049644 5.6320575Por tanto la matriz \(X\) está definida por:
\[ \begin{array} [c]{cccc} & x_{1} & x_{2} & x_{3}\\ \text{Brazil} & -0.14 & -0.48 & -0.49\\ \text{Canada} & 0.86 & 0.67 & 0.53\\ \text{China} & -0.17 & -0.20 & -0.34\\ \text{Germany} & 0.96 & 1.28 & 1.44\\ \text{Nigeria} & -1.51 & -1.28 & -1.13 \end{array} \] Las nuevas variables \(y_j\) que vamos a construir como combinación lineal de \(x_1,x_2\) y \(x_3\) tienen la forma:
\[y_{j}=u_{1j}\left( \begin{array}{c} -0.14 \\ 0.86 \\ -0.17 \\ 0.96 \\ -1.51% \end{array}% \right) +u_{2j}\left( \begin{array}{c} -0.48 \\ 0.67 \\ -0.20 \\ 1.28 \\ -1.28% \end{array}% \right) +u_{3j}\left( \begin{array}{c} -0.49 \\ 0.53 \\ -0.34 \\ 1.44 \\ -1.13% \end{array}% \right) =Xu_{j}\]
Como \(y_j\) tiene siempre media cero, su varianza es \(\frac{y_j^Ty_j}{4}=\frac{u_j^TX^TXu_j}{4}\). Si \(u_j\) es un autovector normalizado de \(X^TX\) para el autovalor \(\lambda_j\), tendremos que la varianza de \(y_j\) es \(\frac{u_j^TX^TXu_j}{4}=\frac{\lambda_ju_j^Tu_j}{4}=\frac{\lambda_j}{4}\)
Calculamos ahora la matriz \(X^{T}X\): \[ X^{T}X=\left( \begin{array} [c]{ccc}% 4.00 & 3.85 & 3.68\\ 3.85 & 4.00 & 3.96\\ 3.68 & 3.96 & 4.00 \end{array} \right) \] A continuación, a mano, o usando cualquier software de cálculo matemático, calculamos la matriz ortonormal \(U\) con los autovectores de \(X^TX\)
\[U=\left( \begin{array} [c]{ccc}% 0.57 & 0.78 & 0.26\\ 0.58 & -0.16 & -0.79\\ 0.58 & -0.61 & 0.55 \end{array} \right) \]
Simultáneamente se calculan los autovalores de \(X^{T}X\) que son: \(\lambda_{1}=11.66\),\(\lambda_{2}=0.33\), y \(\lambda_{3}=0.02\) (observamos que la suma de los autovalores es aproximadamente \(12=n\cdot(m-1)=3\cdot4\)) y por tanto las desviaciones típicas de \(y_j\) son \(\sigma_j=\sqrt{\lambda_j/4}\), es decir: \(\sigma_1=1.71\), \(\sigma_2=0.29\), \(\sigma_3=0.07\). Las componentes principales quedan entonces como:
\[ \begin{array} [c]{c}% y_{1}=0.57 \cdot x_{1}+0.58 \cdot x_{2}+0.58 \cdot x_{3}\\ y_{2}=0.78 \cdot x_{1}-0.16 \cdot x_{2}-0.60 \cdot x_{3}\\ y_{3}=0.26 \cdot x_{1}-0.79 \cdot x_{2}+0.55 \cdot x_{3}% \end{array} \]
y, por tanto, la nueva tabla de valores, \(Y=XU\), da como resultado:
\[ \begin{array} [c]{cccc} & y_{1} & y_{2} & y_{3}\\ \text{Brazil} & -0.65 & 0.27 & 0.08\\ \text{Canada} & 1.18 & 0.24 & -0.02\\ \text{China} & -0.40 & 0.11 & -0.073\\ \text{Germany} & 2.13 & -0.33 & 0.02\\ \text{Nigeria} & -2.27 & -0.28 & -0.00 \end{array} \]
Cálculo ACP con prcomp
La función prcomp realiza de forma automática todo el proceso para el cálculo de las componentes principales. Vamos a utilizarla para el ejemplo anterior:
La función prcomp devuelve una estructura (en este ejemplo la hemos llamado pca1) que almacena, en el campo sdev, la desviación típica de las componentes principales \(y_j\), en el campo rotation la matriz de autovectores \(U\) y en el campo x las componentes principales \(Y=XU\). A continuación se imprimen estos resultados. Se puede observar que los resultados son los mismos que hemos calculado para este ejemplo en la sección anterior.
## [1] 1.70716366 0.28734312 0.05501071## PC1 PC2 PC3
## human_development_index 0.5708408 0.7790411 0.2592986
## aged_65_older 0.5845568 -0.1638432 -0.7946375
## aged_70_older 0.5765709 -0.6051863 0.5489222## PC1 PC2 PC3
## Brazil -0.6468462 0.2677714 0.0760700585
## Canada 1.1838460 0.2382161 -0.0237206224
## China -0.4045875 0.1086123 -0.0727761422
## Germany 2.1321196 -0.3313071 0.0214026069
## Nigeria -2.2645318 -0.2832927 -0.0009759008Visualización ACP
El objetivo principal del ACP es reducir la dimensionalidad quedándonos con las primeras componentes principales que acumulan mayor varianza y desechando el resto. El criterio para decidir con cuantas componentes principales nos quedamos se basa justamente en el análisis de su varianza. Normalmente se analiza la varianza de las componentes principales \(y_j\) en términos relativos, es decir el porcentaje que representa la varianza de \(y_j\) respecto a la varianza global dada por la suma de todas las varianzas (\(\sum_jVar(y_j)\)). Para visualizar esto, utilizamos un gráfico de barras interactivo, creado con plotly, con el porcentaje de varianza explicada por cada componente principal.
p <- tibble(
label=paste("PC",1:length(pca1$sdev)), # creación etiquetas para el eje horizontal
varPercent = pca1$sdev^2/sum(pca1$sdev^2) * 100 # cálculo porcentaje de varianza explicada
) %>%
ggplot(aes(x=label,y=varPercent)) + # creación gráfico de barras interactivo
geom_bar(stat = "identity") +
labs(x= "Componentes Principales",
y= "Porcentaje varianza explicada")+
geom_text(aes(label=paste0(round(varPercent,digits = 1),"%")),
size=3,
colour = "blue",
nudge_y = 1.
)
ggplotly(p)
Figure 8.4: Porcentaje varianza explicada por cada componente principal usando ggplotly
Para decidir con cuantas componentes principales nos quedamos podemos, por ejemplo, quedarnos con las componentes principales que acumulen más de un 90% de la varianza explicada. Otro criterio, sería, por ejemplo, eliminar las componentes principales con la varianza explicada inferior al 2%. Para este ejemplo, con el primer criterio, solo nos quedaríamos con la primera componente principal, y con el segundo criterio con las dos primeras.
Un gráfico habitual para visualizar los resultados del ACP es hacer un gráfico de dispersión donde se pone el resultado de los valores de las dos primeras componentes principales para cada observación, es decir se representan los puntos \((y_{i1},y_{i2})\) para \(i=1,\cdots,m\), de esta manera se aprecia como están distribuidos los valores de las dos primeras componentes. Además, para visualizar la contribución de cada variable \(x_j\) a las dos primeras componentes, se dibuja, para cada \(j\) un segmento que va desde el \((0,0)\) hasta el \((u_{j1},u_{j2})\) para \(j=1,\cdots,n\). \(u_{j1}\) es el coeficiente de \(x_j\) en la combinación lineal de la primera componente \(y_1\) y
\(u_{j2}\) es el coeficiente de \(x_j\) en la combinación lineal de la segunda componente \(y_2\). Si este segmento se alinea con el eje x, significa que \(x_j\) aporta poco a la segunda componente, y si además es el segmento de mayor magnitud magnitud, significa que \(x_j\) aporta a la primera componente más que el resto de variables. Para realizar este gráfico utilizaremos la función hchart:
Figure 8.5: Gráfica ilustrativa de las dos primeras componentes principales usando hchart
A continuación vamos a reproducir el experimento, pero tomando todos los indicadores y para todos los países. Primero preparamos los datos y calculamos el ACP. Como el cálculo del ACP solo permite variables numéricas, tenemos que eliminar las variables no numéricas de la tabla. Para conservar los nombres de los países, en lugar de gestionarlo como variable, lo gestionamos como nombre de cada registro, de esta manera no interfiere en el cálculo del ACP
data <- owid_country %>%
na.omit() %>% # quitamos los registros con algún NA
column_to_rownames(var="location") %>% # asignamos el campo location como nombre de las filas
select(-continent,-iso_code) # eliminamos las variables no-numéricas
pca2 <- prcomp(data,scale = TRUE) # calculamos el ACP Ahora realizamos la gráfica de barras con el porcentaje de varianza explicada por cada componente principal. Por defecto, la gráfica de barras ordena por orden alfabético las etiquetas del eje x, para que use el orden usado al crear las etiquetas usamos la función fct_inorder que impide que se cambie el orden en el vector de etiquetas.
p <- tibble(
label=fct_inorder(paste("PC",1:length(pca2$sdev))),
varPercent = pca2$sdev^2/sum(pca2$sdev^2) * 100
) %>%
ggplot(aes(x=label,y=varPercent)) +
geom_col() +
labs(x= "Componentes Principales",y= "Porcentaje varianza explicada")+
geom_text(aes(label=paste0(round(varPercent,digits = 1),"%")), size=3, colour = "blue",nudge_y = 1.)
ggplotly(p)
Figure 8.6: Porcentaje varianza explicada por cada componente principal usando ggplotly
Por último presentamos la gráfica que ilustra el resultado para las dos primeras componentes (con el parámetro choices seleccionamos las dos componentes que se van a representar).
Figure 8.7: Gráfica ilustrativa de las dos primeras componentes principales usando hchart
Referencias
[Ke23] Zoumana Keita. Principal Component Analysis in R Tutorial, 2023.
[Ku22] Joshua Kunst. Hchart Function, 2022.
[UGA] Data Analysis in the Geosciences (Principal Components Analysis), University of Georgia.