Chapter 2 Data Acquisition
In the Chapter 1.3.2 discussion of the 5A Method, we described observation and experimentation as two ways to gather data. Observation comprises the passive collection of data during a process or event without any attempt to intervene. Experimentation involves the active planning and control over a data-generating process before and during collection. In fact, the design of experiments is an entire sub-discipline of statistics focused on the proper assemblage of experimental data. Regardless of the collection methodology, this text focuses on the acquisition of existing data. Manually gathering observations and designing experiments are beyond our scope. The one exception to this rule is the simulation of experimental data, given it can be conducted virtually.
Based on our decomposition of the problem-solving process, data acquisition includes more than importing collected data. Existing data is seldom in a form sufficient for analysis. More often, data tables must be aggregated from multiple disparate sources and organized for a particular purpose. Furthermore, combined tables often require cleaning to avoid errors and summary to affirm the quality and quantity. Collectively, these tasks are referred to as data wrangling. A significant portion of a data scientist’s work revolves around wrangling prior to any data analysis. Thus, we combine this concept with import under the umbrella of data acquisition. Before we examine the various ways we import and wrangle data, we must first establish a consistent lexicon for referencing data and its structure.
2.1 Data Structures
Generally speaking, data structures refer to the ways we organize, manage, store, and access data. It is helpful to learn and use the proper terminology of data structures to avoid miscommunication and to ensure the application of appropriate problem solving methods and tools. This chapter is devoted to developing a deeper understanding of the data we seek to acquire.
The word data is the plural form of the Latin word datum which loosely means “a given fact”. The online publication Towards Data Science provides an interesting article on the etymology and modern usage of the word at this link. Although datum is technically the singular form and data is the plural form, it is common to hear “data” used for both. Data can be broadly split into two categories: structured and unstructured. Structured data is comprised of clearly-defined facts that can be organized into a consistent format such as a table of rows and columns. An example of structured data is a roster of student names, majors, class years, and emails for a given course. Unstructured data is more diverse and typically cannot be consistently organized into a single schema. Examples of unstructured data include collections of text files, images, videos, or audio files. The vast majority of this text focuses on solving problems that leverage structured data.
Structured data is typically organized into rectangular tables of observations (rows) and variables (columns). Observations, sometimes referred to as cases, represent the individual units about which data is collected. An observation is a person, place, or thing. It is critically important to understand the observational unit of the data to avoid misinterpreting analytic results. Variables, sometimes called features, are descriptors of each observation. For example, if an observation is a dog, then potential variables could be breed, color, weight, and age. Observations and variables are organized into data tables that offer a consistent format for searching and analyzing data.
A particular form of structured data is known as tidy data. The concept of tidy data was popularized by Hadley Wickham and is described extensively in his book R for Data Science (Wickham et al. 2023). There are three rules for a rectangular data table to be tidy:
- Every row represents a unique observation
- Every column represents a unique variable
- Every cell contains a single value
Any other configuration is referred to as untidy or messy data. Placing data in tidy form is not merely a matter of aesthetics. Tidy data is much easier to store, access, and analyze. It is also particularly well-suited for vectorized programming languages (e.g., R). In fact, we will make extensive use of a suite of R libraries known as the tidyverse throughout this text. Prior to exploring the tidyverse or explaining what it means for a language to be vectorized, we must distinguish between variable types and data types.
2.1.1 Variable Types
Structured data can include variables of many different types. In order to maintain consistency throughout the problem solving process, we organize variable types into the hierarchical structure of terminology shown in Figure 2.1.
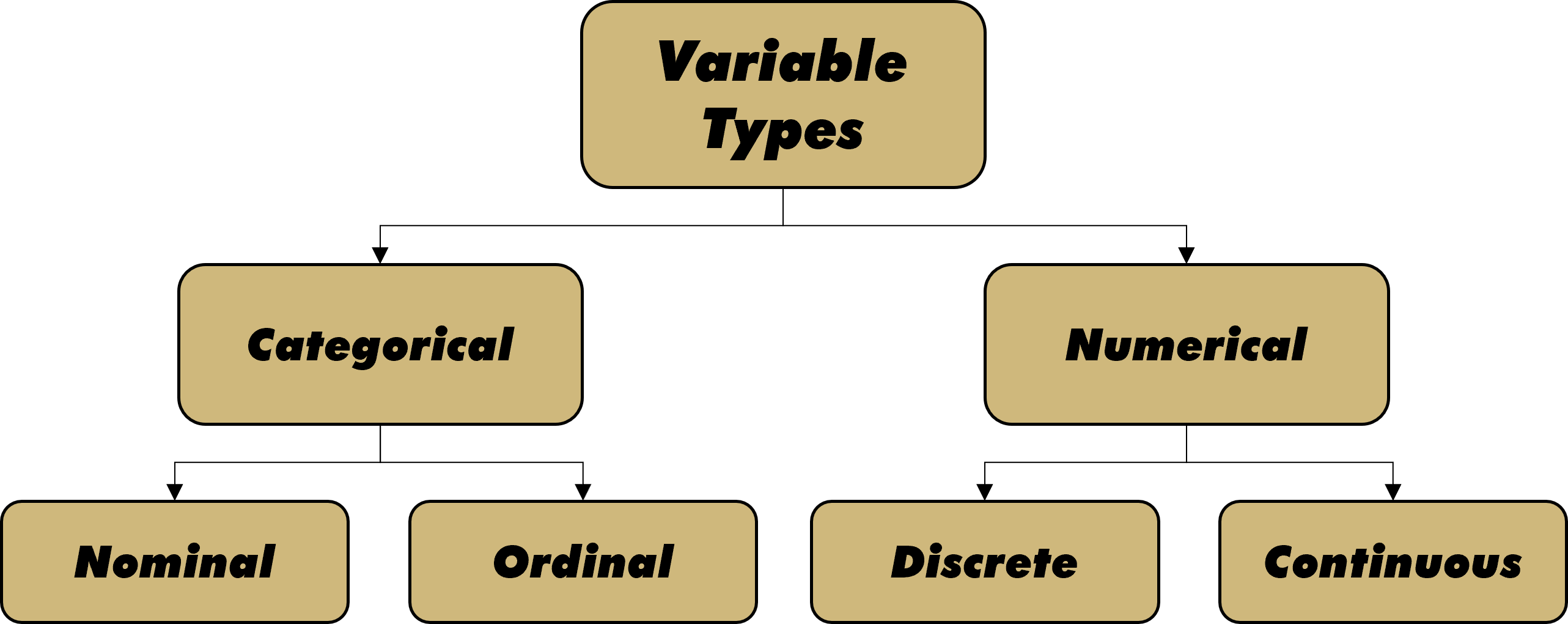
Figure 2.1: Types of Variables
Initially we split variables into either categorical or numerical. Sometimes this split is referred to as qualitative and quantitative. Regardless, the difference is typically identified by words versus numbers. Though the distinction between certain variable types can depend on context and interpretation, we attempt to provide relatively stable definitions below.
Categorical variables can be nominal or ordinal. Nominal (named) variables consist of unordered symbols, words, or text. A nominal variable might assign colors to an object, such as “red”, “yellow”, or “blue”. Alternatively, it might provide the description of an object, such as “This one is heavy”, “That one is square”, or “The other one smells rotten”. Whether individual words or multi-word text, nominal variables have no natural precedence. By contrast, ordinal (ordered) variables exhibit an innate ordering. An ordinal variable might assign grades to an object, such “below average”, “average”, or “above average”. Equivalently, it could apply the standard academic lettering structure of “A” through “F”. Regardless, ordinal variables assign values according to a commonly-known or well-defined arrangement.
Numerical variables can be discrete or continuous. Discrete (countable) variables comprise numerical values that only occur at defined intervals. Often such variables are applied to counting physical objects such as people, places, or things. However, even decimal values can be interpreted as discrete in certain contexts. For example, $3.03 is equivalent to 303 pennies. It would not make sense to request $3.035 because we cannot physically provide half of a penny (without a saw!). Continuous (measurable) variables have no set intervals between values. For any two values we choose, there are infinitely more between them. Here we must acknowledge the difference between theory and practice. In practice, all numerical values are treated as discrete as soon as we round them. For example, a person’s height is a continuous variable in theory, but often treated as discrete (nearest inch) in practice.
To clarify variable types even further, we reference the tidy data set in Table 2.1. On six separate occasions, a coffee lover visited a local shop and purchased a drink. Each row (observation) represents a single visit, while each column (variable) describes the visit and drink. We explore each variable in greater detail below.
| date | shop | drink | size | ounces | stars | notes |
|---|---|---|---|---|---|---|
| 2023-02-12 | Downtown | Drip | Small | 12 | 1 | Cold and gross |
| 2023-02-13 | Downtown | Mocha | Medium | 16 | 3 | Just okay |
| 2023-02-15 | Park | Mocha | Medium | 16 | 4 | Delicious and fast |
| 2023-02-17 | Library | Drip | Large | 20 | 5 | Wow, amazing! |
| 2023-02-19 | Park | Latte | Medium | 16 | 3 | Good service |
| 2023-02-20 | Downtown | Latte | Small | 12 | 2 | So slow! |
The date of the visit is a numerical, continuous variable. One might ask why it is not discrete, given the date is listed at daily intervals. But this is solely an issue of rounding! Time is a theoretically continuous concept. In practice we might choose to round time to the year, month, day, hour, minute, or second. But that rounding does not change the inherent continuity of time.
The shop location is a categorical, nominal variable. The values are location names, with no clear ordering. That said, the concept of location can take on many different forms. Rather than a vague name, we might choose to provide the precise latitude and longitude of the coffee shop. Much like time, space is an inherently continuous concept. So the change to geographic location would dramatically change the variable type.
The drink type in also nominal, but size is an ordinal variable. There is a clear ascending order to the words small, medium, and large. Such a universal order does not exist for words like drip, mocha, and latte. We may each have our own order of preference for the different drink types based on opinion, but that does not make the variable inherently ordinal. Large is bigger than small regardless of our opinion.
The cup ounces is clearly numerical, but the distinction between discrete and continuous is somewhat challenging. On the one hand, the measurement of volume (space) is a continuous concept. On the other hand, cups only come in discrete size options. This is not an issue of rounding. A coffee shop has a countable number of cup size options that correspond with the ordered size names (small, medium, and large). Ultimately, the cup ounces could safely be treated as discrete or continuous depending on the application.
By contrast, the star rating is undoubtedly a discrete variable. The assigned rating is effectively counting stars. Even if we allow for “half stars” the rating is still discrete because there are set intervals. Once again, the distinction between discrete and continuous comes down to counting versus measuring. We count physical objects, while we measure time and space.
The notes variable is our first example of multi-word text, which identifies it as categorical and nominal. But the notes variable is a different type of nominal than shop or drink. The one-word, repeated shop and drink names can be grouped if we choose. For a much larger data table, we might be interested in summarizing characteristics of only the downtown shop or only mocha drinks. Later in the text, we will learn to “group by” such distinct names. For free text variables like the visit notes, groupings likely make no sense because there is no guarantee that any value will be repeated.
The preceding discussion focuses primarily on the conceptual characteristics of an observation described by a variable. However, when conducting data science on a technical platform, a computer must assign specific data types to the values permitted for each variable. In the next section, we delineate these data types and link them to the appropriate variable types.
2.1.2 Data Types
There is an important difference between how a data scientist defines a variable type and how a computer interprets the values of a variable as a data type. The hierarchical structure in Figure 2.2 depicts how many coding languages, including R, interpret data types.
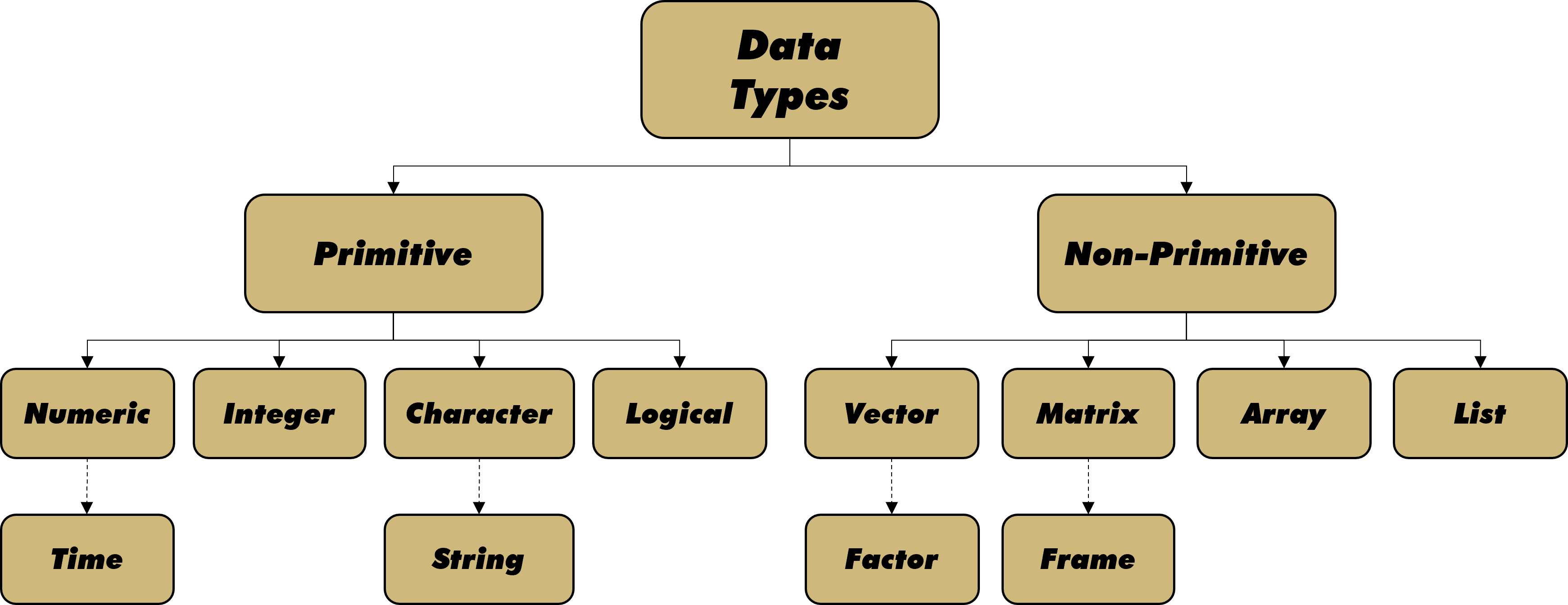
Figure 2.2: Types of Data
Primitive data types refer to individual values, while non-primitive types comprise collections of many data values. At the primitive level, data can be numeric, integer, character, or logical. Numeric data is generally associated with continuous variables. Thus, measurements of time and space typically fall into this category. Many computer languages offer control over the precision of numerical data (e.g., single versus double precision). Though generally considered numeric, dates and times require some special care with regard to horizon and format. Integer data is often related to discrete variables, based on the requirement for set intervals. Of course, this is not a perfect association given our previous discussion of discrete rounding to non-integer values (e.g., half stars).
Primitive character data includes individual symbols and letters, as well as collections (strings) of the same. One could rightfully argue that strings are non-primitive, given they comprise multiple primitive characters. We include strings as primitive here because R makes little distinction between a variable value with one character or many characters. Whether nominal or ordinal, character data is generally applied to categorical variables.
Sometimes called boolean, logical data refers to binary values such as TRUE and FALSE. Data of this type can be considered either numerical or categorical, depending on the context. In analysis, we often treat logical variables as the numerical values 1 (TRUE) and 0 (FALSE). For other applications, we might prefer to use categories with the literal words TRUE and FALSE. Regardless, logical data is associated with a variable that takes on one of only two possible values.
Non-Primitive data combines multiple values across one or more dimensions. Vectors are one-dimensional collections of primitive data values of the same type. Thus, we can have vectors of numerical, integer, character, or logical values. A special type of character vector that comprises categorical variable values is a factor. A factor is an appropriate data type for nominal or ordinal variables that can be grouped. We reserve a deeper discussion of factors for a section on categorical variables in Chapter 3.
Across two dimensions, we aggregate data into matrices of rows and columns. A useful way to think about a data matrix is a collection of column vectors. A data frame is a special type of matrix. In this text, we use the term matrix when the columns (vectors) are all of the same data type. By contrast, we use the term frame when the columns are permitted to be of different data types. Most of the data acquired and analyzed in this text is in the form of a data frame.
An array allows for three or more dimensions, while a list is a collection of non-primitive data of different dimensions. For example, a list could consist of two vectors, three matrices, one data frame, and five arrays. Lists are a useful format for storing or transmitting a large data set consisting of dissimilar data types.
Let’s examine the structure of a built-in table from the tidyverse library (aka package) and identify the data types. The code and output shown in the grey boxes below is generated from RStudio. Code blocks such as this appear throughout the text and include comments preceded by a single hash tag symbol (#). The first time we use a new package, we must install it using install.packages("name") in the console. We only have to install a package once. But we do need to load the package with the library() function for each new RStudio session. Readers are encouraged to duplicate the same results in their own R script as practice.
## tibble [234 × 11] (S3: tbl_df/tbl/data.frame)
## $ manufacturer: chr [1:234] "audi" "audi" "audi" "audi" ...
## $ model : chr [1:234] "a4" "a4" "a4" "a4" ...
## $ displ : num [1:234] 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...
## $ year : int [1:234] 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...
## $ cyl : int [1:234] 4 4 4 4 6 6 6 4 4 4 ...
## $ trans : chr [1:234] "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...
## $ drv : chr [1:234] "f" "f" "f" "f" ...
## $ cty : int [1:234] 18 21 20 21 16 18 18 18 16 20 ...
## $ hwy : int [1:234] 29 29 31 30 26 26 27 26 25 28 ...
## $ fl : chr [1:234] "p" "p" "p" "p" ...
## $ class : chr [1:234] "compact" "compact" "compact" "compact" ...The table called mpg contains fuel efficiency data collected by the Environmental Protection Agency (EPA) for popular car models between 1999 and 2008. The str() function lists the structure of the data table. First we see that the entire table is a special type of data frame called a tibble. For our purposes the differences between a tibble and data frame are unimportant, so we do not dwell on them here. The mpg data frame has 234 rows (observations) and 11 columns (variables). Each observation is a unique car and each variable describes that car. The variables include manufacturer, model, displacement, and so on. We can obtain further information about the meaning of each variable by typing ?mpg in the console and reviewing the help tab.
After each variable name, R lists the primitive data type associated with the variable’s values. For example, the manufacturer is defined as character (chr) data. This makes perfect sense, because the listed example values (e.g., “audi”) are the names of car companies. Manufacturer is a nominal, categorical variable, so its values are assigned the character type. As another example, the engine displacement variable has the numerical (num) data type. Since displacement measures the volume of an engine, the variable is continuous. Consequently, its values are numeric. As a final example, the cylinders variable is identified as integer (int) because it counts the discrete number of cylinders in the car’s engine. Though we don’t see an example in this data frame, logical data types are identified with logi.
When we refer to R as a vectorized (or vector-based) programming language, we mean that R is specifically-designed to perform operations on vector data. Let’s look at a simple example using two of the columns from the mpg data frame. We access the columns of a data frame by placing a dollar sign between the frame name and column name.
## int [1:234] 18 21 20 21 16 18 18 18 16 20 ...## int [1:234] 29 29 31 30 26 26 27 26 25 28 ...We see that each column is a vector of integer values. The str() output provides the first few values of the vectors as examples. Now, what if we want to know the difference between highway and city fuel efficiency for each car? Due to the vectorized nature of R, we treat each column as an individual object and simply subtract them.
## int [1:234] 11 8 11 9 10 8 9 8 9 8 ...The difference between the vectors is simply a vector of differences! With non-vectorized languages, differences like this require a loop that applies the difference function to each element one at a time. Now suppose we want to know if cars have a highway efficiency greater than 30 miles per gallon?
## logi [1:234] FALSE FALSE TRUE FALSE FALSE FALSE ...As with the differences, there is no need for a loop that checks the magnitude of each element relative to 30 mpg. Instead, we automatically obtain a vector of logical values. It gets better! What if we want to know the total number of cars with an efficiency greater than 30 mpg?
## [1] 22R is designed to check the inequality for each element and return a 1 (TRUE) or 0 (FALSE). The sum() function then adds up the binary values across all elements. The result is that 22 out of the 234 cars have a fuel efficiency greater than 30 mpg. The more we leverage the vector-based nature of R throughout the text, the more we will grow to appreciate its power. For now, the point of this example is simply to demonstrate the meaning of a language being vectorized.
When solving data-driven problems using a vector-based programming language like R we prefer our data in tidy frames with well-defined variable and data types. But where do we obtain such data and how do we access it within RStudio? In the next section, we answer this question by presenting the various locations from which data is imported.
2.2 Importing
A vast and diverse array of collected data already exists in the wider world. For educational purposes, the built-in data sets (e.g., mpg) provide great exemplars. However, in practice we also want to acquire and analyze data from other sources. We might have local files on our own computer or we might find data online. In the ideal case, we have access to a well-designed and expertly-managed relational database. Regardless, data scientists must have the capacity to locate and import data from a variety of sources. When real-world data is not available, we often simulate our own data using known characteristics of the associated system.
In the sections that follow we introduce the libraries and functions required to import collected data into RStudio from common sources. Local data is obtained directly from R libraries or provided as separate files by the authors. Online data is accessed via listed web links and databases are remotely queried. Finally, simulated data is produced within RStudio. Let’s import some data!
2.2.1 Local Data
Once a data table has been loaded onto a personal device, we refer to it as local. In some cases, data sets are automatically included when we download analytic software or coding environments. Other times, we obtain data files from outside sources and save them on our own machine. We investigate examples of both cases below.
Built-in Data
There are many freely-available data sets in the basic R installation and even more from specific libraries. Let’s load the tidyverse library and then review all of the available data sets.
After executing the empty data() function, we receive a new tab in our RStudio work space called “R data sets”. Within that tab we see all of the available data organized by package (library). For example, under the dplyr library we see a data set called starwars. If we want to view that data in a table, we first call the data() function with the table name as the input. This imports the data and we display it as a table using the view() function.
We now have a tab in our work space that shows the data in a user-friendly table. From the table, we determine there are 87 observations (rows) and 14 variables (columns). Each observations is a specific Star Wars character and each variable describes that character. For example, the first row is associated with Luke Skywalker, who is 172 cm tall, weighs 77 kg, has blonde hair, and so on. Further information is available in the help menu by executing ?starwars in the console.
It turns out, this data set isn’t quite tidy! The films, vehicles, and starships columns all include cells that have more than one value. That breaks Rule #3 for tidy data from Chapter 1.3. Each of these columns is actually a list of vectors rather than a single vector. We can isolate individual elements of a list using double-brackets[[]] after the name. For example, we obtain Luke Skywalker’s films in the following manner.
## [1] "The Empire Strikes Back" "Revenge of the Sith"
## [3] "Return of the Jedi" "A New Hope"
## [5] "The Force Awakens"Don’t get upset Star Wars fans! It doesn’t appear the films were updated after The Force Awakens. Regardless, it is clear why the data is stored in this list format. To have an individual film in each cell, we would need to repeat the Luke Skywalker row five times. But then we would have duplicated rows and violate Rule #1. This is a case where we choose to treat the vector of films as a “single value” and label the data frame “tidy” for all intents and purposes.
Most packages in R come with at least a few data sets. We can always review the available data sets using the empty data() function. But what if we have a non-R data file on our computer that we want to import into RStudio? We answer this question in the next section.
Data Files
There exists a wide variety of file types for storing and sharing data. One of the most common file types is the comma-separated values (CSV) format. When viewed in its raw form, a CSV is simply a long list of values separated by commas (hence the name!). However, we can easily transform a CSV into a tidy data frame using functions from the readr library. This package is already included in the tidyverse suite, so there is no need to load it separately.
Suppose we have the dietary facts for Starbucks drinks in the form of a CSV on our hard drive (or cloud server). We import the file into RStudio using the read_csv() function and name it coffee. The left arrow (<-) assigns the name on the left to the object on the right.
The CSV file happens to already be in the current working directory. But we can list the entire file path between the quotes (e.g., “C:/Users/me/Documents/…/starbucks.csv”), if necessary. Notice, the slashes are in the opposite direction of what most file systems use. Now we can view the Starbucks data in table form.
The data includes 242 observations (rows) and 20 variables (columns). Each observation represents a specific drink and each variable describes that drink. One important task accomplished behind the scenes by the read_csv() function is the assignment of data types. What data types did the function choose for each variable? Let’s check the structure to find out. Rather than the basic str() function, let’s use a similar function from the dplyr library called glimpse(). Like readr, the dplyr package is already included in the tidyverse.
## Rows: 242
## Columns: 20
## $ id <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 1…
## $ Beverage_category <chr> "Coffee", "Coffee", "Coffee", "Coffee", "Cla…
## $ Beverage <chr> "Brewed Coffee", "Brewed Coffee", "Brewed Co…
## $ Size <chr> "Short", "Tall", "Grande", "Venti", "Short",…
## $ Beverage_prep <chr> "Solo", "Solo", "Solo", "Solo", "Nonfat Milk…
## $ Calories <dbl> 3, 4, 5, 5, 70, 100, 70, 100, 150, 110, 130,…
## $ `Total Fat (g)` <chr> "0.1", "0.1", "0.1", "0.1", "0.1", "3.5", "2…
## $ `Trans Fat (g)` <dbl> 0.0, 0.0, 0.0, 0.0, 0.1, 2.0, 0.4, 0.2, 3.0,…
## $ `Saturated Fat (g)` <dbl> 0.0, 0.0, 0.0, 0.0, 0.0, 0.1, 0.0, 0.0, 0.2,…
## $ `Sodium (mg)` <dbl> 0, 0, 0, 0, 5, 15, 0, 5, 25, 0, 5, 30, 0, 10…
## $ `Total Carbohydrates (g)` <dbl> 5, 10, 10, 10, 75, 85, 65, 120, 135, 105, 15…
## $ `Cholesterol (mg)` <dbl> 0, 0, 0, 0, 10, 10, 6, 15, 15, 10, 19, 19, 1…
## $ `Dietary Fibre (g)` <dbl> 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0,…
## $ `Sugars (g)` <dbl> 0, 0, 0, 0, 9, 9, 4, 14, 14, 6, 18, 17, 8, 2…
## $ `Protein (g)` <dbl> 0.3, 0.5, 1.0, 1.0, 6.0, 6.0, 5.0, 10.0, 10.…
## $ `Vitamin A (% DV)` <dbl> 0.00, 0.00, 0.00, 0.00, 0.10, 0.10, 0.06, 0.…
## $ `Vitamin C (% DV)` <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.…
## $ `Calcium (% DV)` <dbl> 0.00, 0.00, 0.00, 0.02, 0.20, 0.20, 0.20, 0.…
## $ `Iron (% DV)` <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.08, 0.…
## $ `Caffeine (mg)` <chr> "175", "260", "330", "410", "75", "75", "75"…We obtain similar information as the str() function, just in a slightly different format. For example, the abbreviation for data type uses <dbl> for double-precision numeric instead of num. The read_csv() function generally does a good job of guessing the appropriate data type for each variable. However, it isn’t always perfect and we sometimes need to manually change the data type. This can be accomplished within the function using the col_types parameter (see ?read_csv()) or after the data is imported.
Currently the id variable is listed as numeric, but its values are integer identifiers for each unique drink. We can change the data type for this variable after import using one of the as.xxx() functions.
#change data type for id variable
coffee$id <- as.integer(coffee$id)
#display structure of id variable
glimpse(coffee$id)## int [1:242] 1 2 3 4 5 6 7 8 9 10 ...The values in the id column are now of the integer type rather than numeric. Any of the primitive data types can be assigned in this manner by replacing integer with numeric, character, or logical in the as.xxx() function. A few other variables in this data frame warrant type changes. But we reserve further discussion for a later section on data cleaning.
Not only can we import local CSV files into RStudio, we can export data frames to CSV files as well. Often we want to share data with others after importing, aggregating, and cleaning. The benefit of a format like CSV is its portability and readability on various platforms. As a simple demonstration, let’s convert a built-in data set to a local CSV.
Recall, the mpg data set includes the fuel efficiency and other characteristics of various cars as measured by the EPA. If we want to save this data frame to our hard drive as a CSV file, then we apply the write_csv() function.
In this case, we choose to name the file epa_cars.csv and save it in the working directory. As with importing, we can export a file to any directory we like as long as we list the full path. After navigating to the appropriate directory, we find the new CSV file. Now we can open or share it using whatever software we choose (e.g., Microsoft Excel).
Portable file types like CSV are great once we have them on our own computer (or cloud server). But how do we get these files in the first place? Perhaps a fellow data scientist emails the CSV. Alternatively, we might download it from a website. The latter case alludes to accessing data online and we explore this further in the next section.
2.2.2 Online Data
For some web-based data, it may be as simple as downloading a pre-made CSV file. There are a plethora of data-focused sites, such as Kaggle, that provide free access to CSV files from a variety of domains. In other cases, websites include data in the form of tables embedded in hypertext markup language (HTML) or in an application programming interface (API). Further still, data might be remotely accessed from a secure database using structured query language (SQL). We introduce all three sources below.
HTML Data
Extracting data from an HTML page is often referred to as web scraping. As an example, let’s review the Wikipedia page for the most-followed Tik Tok accounts in our web browser at this link. Scrolling down the webpage, we notice a few different data tables. Suppose we want to import the first table, titled “Most-followed accounts”, into RStudio. For this task, we use functions from a package called rvest designed to “harvest” data. Remember, the first time we encounter a new package we must install it from the console. In this case, we use install.packages("rvest"). After the one-time installation, we need only load the package with the library() function.
There are functions in the rvest package that permit extracting all kinds of data (including text) from a website. For this introduction to web scraping we only focus on extracting data that is already in the form of a table. We need the read_html() and html_nodes() functions.
#import full html webpage
tiktok <- read_html("https://en.wikipedia.org/wiki/List_of_most-followed_TikTok_accounts")
#extract tables from html webpage
tiktok_tabs <- html_nodes(tiktok,"table")The read_html() function imports all the necessary information from the webpage we specify. Then, the html_nodes() function extracts the parts of the webpage we want. The parts (nodes) of the webpage are known as “tags” in HTML language and we can specify what parts we want with a great level of detail. The result, which we name tiktok_tabs, is a list of all the tables found on the webpage. We specify the first table on the list using double-brackets and automatically turn it into a data frame using the html_table() function.
#extract first table from list
tiktok_top50 <- html_table(tiktok_tabs[[1]])
#view Top 50 most followed
view(tiktok_top50)After executing the view() function, we are able to see the Tik Tok data in an RStudio table. Beware, the web scraping process is not always perfect. Often HTML tables are not tidy and require wrangling prior to any analysis. We describe such tasks in Chapter 2.2. For now, we explore another source of online data.
API Data
Another very common method for obtaining data online is via an API. An API is a structure for organizations to provide users access to particular data without full read and write access to their database. However, the structure and parameters of APIs are not all the same. It is generally necessary to review an organization’s documentation for their API to know how to properly request and receive the data. We demonstrate the broad strokes of accessing an API in an example below.
Two packages assist with accessing an API in RStudio: httr and jsonlite. The httr library provides functions for requesting and receiving data via hypertext transfer protocol (HTTP). Yes, that’s the same “http” that appears at the beginning of web addresses! Many web developers provide data in JavaScript object notation (JSON) format. Hence, the jsonlite package provides functions to transform data sets from the JSON format to tidy data frames.
In order to get data from an API we need to make a GET request. There are other request types, like POST and PUT, but we are currently just interested in getting the data. The httr package includes functions for requests, but we need the web address for the API we want to get the data from. In this context, web addresses are often referred to as “endpoints”. We obtain the endpoint by first searching the web, in a browser, for the API we desire.
Imagine we are interested in investigating car crashes in the city of Chicago. Lucky for us, the Chicago Police Department makes this data publicly available at the following link. There is a lot of great information about the database on this page, but we are particularly interested in two things. First, there is metadata about all the rows (observations) and columns (variables) listed further down on the page. This information is helpful for understanding the data we intend to import. Second, we notice in the upper-right corner of the page that there is a drop-down for “Actions” that includes the API. After clicking on that button, we are provided an API endpoint to copy and paste into our GET request.
Now that we have the endpoint, we can request data from the server. There are three steps to acquire data from an API. First, we request the data from the server. Then, we parse the response to isolate the content we need. Finally, we transform the parsed content into a data frame. We list these steps in the code below and explain them in detail afterward.
#request data from API
crash <- GET("https://data.cityofchicago.org/resource/85ca-t3if.json")
#parse response from API
crash2 <- content(crash,"text")
#transform json to data frame
crash3 <- fromJSON(crash2)The GET() function from the httr library manages the request to the server and we save the response as the object crash. For various reasons, the request may not always be successful. We check the status of the request using the http_status() function.
## $category
## [1] "Success"
##
## $reason
## [1] "OK"
##
## $message
## [1] "Success: (200) OK"Our request was successful! If some sort of error (e.g., 404 not found) occurs with a request, we can identify it here and attempt to resolve it. Successful requests return a response with headers and a body. We next need to parse the body of the response into a useful object. Often it is helpful to know the format of the response prior to parsing. We obtain the response type using http_type().
## [1] "application/json"The response is in JSON format. Perhaps that is not surprising given the endpoint includes “.json”, but this will not always be the case. To extract the contents of the response, we use the content() function. By doing this, we convert the response data from raw bytes to human-readable text saved as the object crash2. However, that data is still stored in the hierarchical structure of JSON format. We transform it to a rectangular data frame using the fromJSON() function and finally obtain a viewable table called crash3.
The data consists of 1000 observations (rows) and 47 variables (columns). Each observation is an individual car crash incident and the variables describe that incident. The city of Chicago website states the data includes hundreds of thousands of crashes, so why did we only receive 1000? It is common practice for web developers to limit the response size of API requests to help manage web traffic. So, we might have to make multiple requests to obtain the full data set we seek.
In this section, we barely scratched the surface of web scraping and API requests. Due to the complexity and diversity of web-based applications, it is difficult to provide a “one size fits all” set of procedures for data import. Additionally, some websites purposely prevent scraping to discourage the use of proprietary data. Similarly, some APIs require paid subscriptions to gain access to the endpoint. Data is an extremely valuable resource! In the next section, we introduce data management systems (aka databases) as an acquisition source.
Databases
Importing data from an API is convenient when we do not have access to an organization’s entire database. However, if we were employed by said organization, we likely would have access to the database. In that case, it would be important to know how to remotely access and query the database for the information we need. Most production-level databases employ SQL to read from and write to the associated data tables. Learning the SQL programming language is beyond the scope of this text, but there are packages for R (e.g., RPostgres) that bridge the gap between R code and SQL code. We recommend resources for further study of SQL at the end of the chapter.
2.2.3 Simulated Data
All of the data sets discussed in the previous sections were collected by outside entities prior to our import. Collecting our own data from real-world systems can be costly in terms of time, money, and effort. An alternative method of data collection is via computer simulation. Well-designed simulations accurately model an authentic system and permit testing of various scenarios without the risks associated with doing the same in reality. For example, airline pilots spend dozens of hours in flight simulators prior to ever taking responsibility for a real aircraft with passengers. Simulated data provides an assessment of the pilot’s performance in a low-risk environment. Similarly, data scientists often simulate and assess real-world processes using known parameters and distributions for the system.
With simulation, we create our own variable values rather than acquiring them elsewhere. Such variables are referred to as random variables because their values involve some amount of uncertainty. Several types of random variables have well-defined distributions of values. In this section, we demonstrate the simulation of data from three common distributions: Binomial, Uniform, and Normal. These distributions appear so frequently in real-world systems that they’ve been afforded their own names. Though we remain focused on introductory examples here, these distributions are fundamental to more advanced study in probability and statistics.
Binomial Distribution
We begin with the simple example of flipping a coin. Imagine we are interested in generating a data set consisting of the results (heads or tails) from flipping a coin 500 times. Do we really want to do this by hand in reality? We could, but it would be tedious and unnecessary. We can instead complete this experiment virtually. There exist a variety of functions for generating random variable values in R. Flipping a coin is a special case of a Binomial distribution, which models the number of “successes” out of a set number of trials. In order to generate random outcomes from a Binomial distribution, we apply the rbinom() function from the purrr library. As with many libraries we employ in the book, purrr is already included in the tidyverse package.
## [1] 0Prior to simulating the coin flip we set a randomization seed using the set.seed() function. We employ randomization seeds to make our work reproducible. Without setting the seed, there is no guarantee that different computers will produce the same results. After all, it’s random! However, in the academic and research environments we often want to ensure that others can replicate our results. In this text we always set randomization seeds to help students reproduce the content. But, in general, it is not strictly necessary for simulation. When setting a seed, the user can pick any number (e.g., 303) they like.
After setting the randomization seed, we simulate a coin flip with the rbinom() function. Suppose we define a coin flip as a trial, turning up heads as success (1), and turning up tails as failure (0). With the given parameter settings, we modeled one flip (n=1) of one coin (size=1) that has equal chance (prob=0.5) of heads or tails. The result of 0 indicates the coin turned up tails. As long as readers set the same seed of 303, their coin flip will turn up tails as well. While one coin flip is interesting, our goal is 500 coin flips.
#simulate flipping one coin 500 times
set.seed(303)
coin <- data.frame(flip=rbinom(n=500,size=1,prob=0.5))
#display structure of coin flips
glimpse(coin)## Rows: 500
## Columns: 1
## $ flip <int> 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1,…The previous code creates a data frame named coin that consists of n=500 observations (rows) and 1 variable (column). Each observation is a flip and the variable lists the result. Glimpsing the resulting data frame, we observe a sequence of tails (0), heads (1), heads (1), heads (1), etc. Imagine how long this experiment would require if completed manually. Instead, the simulation completes it almost instantly.
What if we want to flip three coins at once and count the number of heads? In the verbiage of the Binomial distribution, this random variable is equivalent to counting the number of successes (heads) out of three trials (flips). We repeat the three-coin experiment 500 times and view the results below.
#simulate flipping three coins 500 times
set.seed(303)
three_coins <- data.frame(flips=rbinom(n=500,size=3,prob=0.5))
#display structure of coin flips
glimpse(three_coins)## Rows: 500
## Columns: 1
## $ flips <int> 1, 2, 2, 2, 2, 3, 2, 1, 1, 1, 3, 2, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2…In the three_coins data frame, the variable value indicates the number of heads for each observation. The first flip of three coins resulted in 1 head. The second flip of three coins produced 2 heads, and so on. Using techniques presented later in the chapter, we can summarize the results of this simulation in Table 2.2.
| heads | count |
|---|---|
| 0 | 57 |
| 1 | 197 |
| 2 | 198 |
| 3 | 48 |
Based on these results, it appears our three flips most frequently result in one or two heads. Zero or three heads occur much less frequently. This makes intuitive sense if we think of flipping three coins in reality. It would be relatively rare to get all heads (3) or all tails (0). Some mix of heads and tails is more likely.
Though we demonstrate one of the simplest applications here, the Binomial distribution is appropriate for simulating any random process with two possible outcomes (success or failure) where each trial is independent of previous trials and the probability of success is constant. Let’s try another common experiment with a known distribution.
Uniform Distribution
Imagine we are interested in generating a data set consisting of the numbers (face values) that result from rolling two dice 500 times. Rolling a single, six-sided die exemplifies a discrete Uniform distribution. It is discrete because there are only six specific outcomes. It is uniform because every one of the outcomes has an equal likelihood of happening, given a fair die. In order to generate values for a discrete Uniformly-distributed random variable, we apply the rdunif() function.
## [1] 3For this simple example, we simulate rolling the die once (n=1). We provide the lower bound (a=1) and upper bound (b=6) for the possible integer outcomes. The result of 3 simulates the face value after rolling a single six-sided die. Again, we set the seed prior to simulating the die roll to ensure anyone reproducing this example also “rolls a 3”. Next, we want to roll two dice 500 times.
#simulate rolling two dice, 500 times
set.seed(303)
dice <- data.frame(die1=rdunif(n=500,a=1,b=6),
die2=rdunif(n=500,a=1,b=6))
#dislay structure of die rolls
glimpse(dice)## Rows: 500
## Columns: 2
## $ die1 <dbl> 3, 5, 2, 1, 1, 5, 5, 3, 4, 4, 1, 1, 1, 6, 2, 1, 6, 6, 5, 3, 6, 3,…
## $ die2 <dbl> 3, 1, 2, 3, 6, 2, 2, 5, 6, 5, 5, 3, 1, 6, 4, 3, 6, 5, 3, 2, 1, 5,…Our code creates a data frame named dice that consists of 500 observations (rows) and 2 variables (columns). Each observation is a roll and the variables list the face value of each die. The first roll is a 3 and a 3. The second roll is a 5 and a 1, and so. Suppose we want to add the face values of the two dice on each roll and summarize the frequency of possible sums. In this case, we obtain Table 2.3.
| sum | count |
|---|---|
| 2 | 19 |
| 3 | 18 |
| 4 | 38 |
| 5 | 42 |
| 6 | 81 |
| 7 | 88 |
| 8 | 64 |
| 9 | 47 |
| 10 | 49 |
| 11 | 34 |
| 12 | 20 |
From the table we see that a sum of seven occurs most frequently, while sums of two and twelve occur much less frequently. There are far more ways for two dice to add up to seven than there are ways to add up to two or twelve. This fact is the premise for the design of a popular table game called craps. Again, imagine how long this data set would require to obtain manually by physically rolling dice. Compare that to the milliseconds required to obtain it with the simple code above. Simulation is a powerful tool for data scientists!
Dice rolls represent a discrete random variable because values in between 3 and 4, for example, are not possible. But the Uniform distribution can also be modeled as continuous. Suppose we simply need to generate 100 random numbers. One option is to draw 100 values between 0 and 1 from the continuous Uniform distribution using the runif() function.
#simulate 100 random numbers
set.seed(303)
rando <- data.frame(num=runif(n=100,min=0,max=1))
#dislay structure of random numbers
glimpse(rando)## Rows: 100
## Columns: 1
## $ num <dbl> 0.30961600, 0.83457367, 0.60981555, 0.73997696, 0.64968413, 0.9805…We refer to this type of Uniform distribution as continuous because any value between 0 and 1 is permitted. Of course, we must round at some point in order to view the number, but the variable remains continuous in theory. Because it is continuous, we cannot create a table of frequencies for individual values. Instead, we count occurrences within a range of values as in Table 2.4.
| value | count |
|---|---|
| 0-0.25 | 23 |
| 0.25-0.50 | 26 |
| 0.50-0.75 | 26 |
| 0.75-1 | 25 |
As expected with a Uniform distribution, we witness a roughly equal count within each equally-sized range of values. We will learn how to generate these summary tables in future sections. For now, we examine arguably the most well-known continuous distribution in existence.
Normal Distribution
Continuous random variables often involve measures of space or time. A variety of natural phenomena produce measurements that follow what is known as the Normal distribution. Sometimes it is referred to as the Gaussian distribution after famed mathematician Carl Friedrich Gauss. The Normal distribution is a symmetric, bell-shaped curve defined by two parameters: mean and standard deviation. The mean determines the center of the bell curve, while the standard deviation determines its spread (width). We explore means and standard deviations much more in Chapter 3. For now, we simply employ them as parameters to simulate data.
As an example, significant research has shown that the height of adult humans follows the Normal distribution. One such research effort is available at this link. The mean height of adults depends largely on biological sex, but other factors such as genetics and environment can have an impact. The standard deviation measures the amount of variability in height from one person to the next. For biological females in countries across the world, studies have found their height to be Normally distributed with an average of 5 foot, 4.8 inches and a standard deviation of 2.8 inches. This information provides us the parameters we need to simulate the heights of biological females. Rather than having to locate and measure dozens or hundreds of people, we leverage past research and simulate the heights on a computer. For this, we use the rnorm() function.
#simulate 1,000 female heights
set.seed(303)
females <- data.frame(height=rnorm(n=1000,mean=64.8,sd=2.8))
#display structure of heights
glimpse(females)## Rows: 1,000
## Columns: 1
## $ height <dbl> 63.40857, 65.58075, 65.87651, 64.99203, 63.18101, 68.47890, 61.…We now have a data frame of heights for 1,000 biological females. The first is 5 foot, 3.4 inches tall, the second is 5 foot, 5.6 inches tall, and so on. As before, imagine how long this would take to collect in reality compared to the completion time of the simulation. We will not always know the exact distribution of results from a given process. For such complex systems, simulation may be more challenging. That said, when the system is simple or well-defined enough to model, simulation is an efficient option. Let’s summarize the number of heights within one, two, and three standard deviations of the mean height in Table 2.5.
| heights | count |
|---|---|
| -3 stdev | 12 |
| -2 stdev | 136 |
| -1 stdev | 336 |
| +1 stdev | 354 |
| +2 stdev | 134 |
| +3 stdev | 28 |
Here the label “-1” refers to values between the mean and one standard deviation below the mean. The label “-2” refers to values between one and two standard deviations below the mean. Finally, the label “-3” refers to values between two and three standard deviations below the mean. Categories with a plus sign are similar but refer to values above the mean. The majority of the heights are within one standard deviation above and below the mean. Heights occur less and less frequently as we get further from the mean. This turns out to be a well-known characteristic of the bell-shaped Normal distribution. An empirical rule states that roughly 68% of values under a Normal distribution are within one standard deviation of the mean. Meanwhile, approximately 95% and 99.7% are within two and three standard deviations, respectively.
In the previous sections we introduced the various ways data scientists import data. Whether local, online, or simulated, data is obtained in many forms from diverse sources. As a result, the data is not always aggregated, organized, and/or summarized in the manner required to answer the research question. Worse yet, it may contain unintentional errors or inconsistencies that must be cleaned up prior to analysis. These tasks are referred to as data wrangling, which is the focus of the next chapter.
2.3 Wrangling
Once we import data, from whatever source, we generally want to aggregate, organize, summarize, and/or clean it in preparation for analysis. Collectively, these tasks are referred to as data wrangling or data munging. The dplyr library from the tidyverse includes a collection of functions specifically designed for efficient data wrangling. We demonstrate many of these functions in the sections that follow.
2.3.1 Organizing Data
Data wrangling is best demonstrated with an example. The nycflights13 package includes data regarding all commercial flights that departed New York City (NYC) airports in the year 2013. We’ll use data frames from this package to demonstrate numerous wrangling functions.
#load nycflights13 library
library(nycflights13)
#import and view flights table
data(flights)
view(flights)We begin with the flights table, which includes over 300 thousand flights (rows) described by 19 characteristics (columns). One way to categorize wrangling activities is to split them between row functions and column functions. Row functions organize and summarize observations, while column functions do the same for variables. Let’s begin with rows.
Organizing Rows
One of the first activities we might like to apply to observations is filtering. Filtering limits which rows remain in the table based on some criteria. The simplest form of filtering retains only the first few or last few rows. We achieve this with basic head() or tail() functions.
## # A tibble: 5 × 19
## year month day dep_time sched_dep_time dep_delay arr_time sched_arr_time
## <int> <int> <int> <int> <int> <dbl> <int> <int>
## 1 2013 1 1 517 515 2 830 819
## 2 2013 1 1 533 529 4 850 830
## 3 2013 1 1 542 540 2 923 850
## 4 2013 1 1 544 545 -1 1004 1022
## 5 2013 1 1 554 600 -6 812 837
## # ℹ 11 more variables: arr_delay <dbl>, carrier <chr>, flight <int>,
## # tailnum <chr>, origin <chr>, dest <chr>, air_time <dbl>, distance <dbl>,
## # hour <dbl>, minute <dbl>, time_hour <dttm>Often we use these simple functions to view a few exemplar rows of larger data frames, rather than attempting to consume them all at once. Notice our use of the head() function above is purely for viewing. We did not delete any rows out of the flights table or create any new tables. We can perform more complex filtering and save the results as a new table to avoid overwriting the original. For example, imagine we are only interested in United Airlines (UA) flights that departed from John F. Kennedy (JFK) or Fiorello LaGuardia (LGA) airports and traveled more than 1,000 miles in any month other than January. We achieve this with the following filter() function.
#filter flights table
flights_filter <- flights %>%
filter(carrier=="UA",
origin %in% c("JFK","LGA"),
distance>1000,
month!=1)A powerful tool in the dplyr wrangling library is the pipe operator (%>%). We think of the pipe operator as a composition of functions. But rather than executing “inside out” like most mathematical compositions, the pipe operator permits execution from “top to bottom”. Thus, each time we apply the pipe operator it acts on the cumulative result of all functions above it. When using multiple pipe operators and functions, we refer to the result as a wrangling pipeline.
In plain language, the pipeline above starts with the flights table and filters it according to our specifications. We then save the filtered data frame as flights_filter to avoid overwriting the original. The double-equals sign (==) is a logical check that only keeps the rows that return TRUE. The “in” operator (%in%) performs the same logical check when we are interested in multiple possibilities. The inequality sign (>) functions as expected and can be paired with the equals sign (>=) when appropriate. Finally, the not-equal-to sign (!=) uses an exclamation point to negate equality. The commas between all logical checks are interpreted like the word “and”. Thus, we keep rows where all of the logical checks return TRUE. The resulting data frame is reduced from over 300 thousand rows to only 8,336 rows.
## [1] 8336Many of these rows are missing values for one or more variables. In R, missing values are indicated with NA for “not applicable”. We discuss missing values much more in the section on data cleaning. But suppose we simply want to eliminate any rows with missing values. We do this with the na.omit() function.
#eliminate rows with missing values
flights_omit <- flights_filter %>%
na.omit()
#count rows in omit table
nrow(flights_omit)## [1] 8199After eliminating any rows with missing values, the data frame retains 8,199 rows. In other words, there were 137 rows with at least one missing value. Eliminating all such rows is not always the best approach, depending on the question at hand. However, this option is available when we only want complete observations.
Another common row-wrangling activity is sorting. We might like to have the observations arranged into a particular order. Suppose we want flight time sorted descending within each of the two airports in our filtered data frame. We sort using the arrange() function.
Upon viewing the sorted table, we find all the JFK flights first due to alphabetical order. Within the JFK flights, the longest air time of 421 minutes comes first and the times descend as requested. The default method of sorting is ascending (or alphabetical), but we override this by wrapping the associated variable in the desc() function. Notice we piped the filtered and omitted flights table into the sorting function. Instead, we can accomplish the filtering, omission, and sorting in a single pipeline.
#filter, omit, and sort flights table
flights_all <- flights %>%
filter(carrier=="UA",
origin %in% c("JFK","LGA"),
distance>1000,
month!=1) %>%
na.omit() %>%
arrange(origin,
desc(air_time))The result is exactly the same as if we split the filtering, omission, and sorting into three separate pipelines. However, the single pipeline is far more efficient. We can make wrangling pipelines as complex as we like by stacking dplyr functions one after the other, separated by pipe operators. Now let’s see how to organize the variables in our data.
Organizing Columns
The analog to filtering and sorting rows in a data frame is selecting columns. Just as we might only be interested in particular observations, we might also limit our analysis to specific variables. Perhaps we only want to investigate the flight origin, carrier, number, and time. We reduce the previously-filtered and sorted data frame to the appropriate columns using select().
The resulting data frame consists only of the four selected columns, in the requested order. The default logic for the select() function is to keep the listed variables. If we prefer to remove listed variables, then we simply precede the variable name with a minus sign (-). Sometimes we wish to keep a variable, but change its name. Renaming is achieved with the rename() function. We might prefer the flight number to be named flight_num and its time to be named flight_time.
#rename time variable
flights_rename <- flights_select %>%
rename(flight_num=flight,
flight_time=air_time)When renaming, the new name always comes before the old name. After viewing the flights_rename data frame we see the new variable names. As with the row-wrangling functions, we can stack the column-wrangling variables into a single pipeline. In fact, we can mix all the wrangling functions (row or column) into a single, sequential pipeline. We demonstrate them separately here for educational purposes, but in practice it is more efficient to combine them.
Yet another column-wrangling activity is creating new variables. New variables are generally computations, logical checks, or categorizations involving existing variables. We demonstrate one of each using the mutate() function.
#create three new variables
flights_mutate <- flights_rename %>%
mutate(flight_hrs = flight_time/60,
flight_lng = flight_hrs>=6,
flight_cat = ifelse(flight_hrs<3,"short",
ifelse(flight_hrs<6,"medium",
"long")))First we create a numeric variable that converts the flight time from minutes to hours and name it flight_hrs. In R there is a critical difference between a single-equals sign (=) and a double-equals sign (==). A single-equals assigns values to a variable, while a double-equals checks the values of a variable. A single-equals represents a statement whereas a double-equals represents a question.
The second new variable is of the logical type. The flight_lng variable is equal to TRUE if the flight is long and FALSE otherwise. We define “long” as being at least six hours and perform the logical check using flight_hrs>=6. Note, we use the new flight hours variable in the creation of the long flight variable. This works since the flight hours variable is created before the long flight variable.
The final new variable creates flight length categories with character-type values. Rather than a simple TRUE or FALSE, we name the flight lengths short, medium, and long based on time thresholds of three and six hours. We apply nested if-then-else logic to create the categories using the ifelse() function. If the flight is less than three hours, then it is short. If it is between three and six hours, then it is medium. Finally, if it is greater than or equal to six hours, then it is long. The ordering for the ifelse() function is always logical check, then TRUE condition, then FALSE condition.
The dplyr suite includes a very powerful function that accomplishes filtering, ordering, renaming, and creating columns all at once. Let’s reconstruct the most recent table using the transmute() function. In fact, we will start all the way back at the original flights table and create the full pipeline here.
#complete all organizing tasks
flights_transmute <- flights %>%
filter(carrier=="UA",
origin %in% c("JFK","LGA"),
distance>1000,
month!=1) %>%
na.omit() %>%
arrange(origin,
desc(air_time)) %>%
transmute(origin,
carrier,
flight_num=flight,
flight_time=air_time,
flight_hrs = flight_time/60,
flight_lng = flight_hrs>=6,
flight_cat = ifelse(flight_hrs<3,"short",
ifelse(flight_hrs<6,"medium",
"long")))The flights_transmute data frame is exactly the same as flights_mutate. However, we wrangled the original flights data frame into the final result with a single pipeline. When it comes to wrangling, there is a difference between organizing and summarizing. So far, we’ve performed organizing tasks like filtering and sorting. Next we explore common ways to summarize characteristics of variables in a data frame.
2.3.2 Summarizing Data
Common methods for summarizing the values of a variable include counts, totals, and averages. Such values are referred to as statistics. Any number computed from the values of a variable in a data set is considered a statistic. We explore many more statistics in Chapter 3.1. For now, we introduce the summarize() function with a few common statistics.
#summarize flight hours variable
flights_transmute %>%
summarize(count=n(),
total=sum(flight_hrs),
average=mean(flight_hrs))## # A tibble: 1 × 3
## count total average
## <int> <dbl> <dbl>
## 1 8199 37211. 4.54Across all of the 8,199 flights, the total hours are more than 37,211. The average time for an individual flight is around 4.5 hours. Counts, totals, and averages are computed with the n(), sum(), and mean() functions, respectively. Rather than summarize across all rows, we often prefer to group rows according to a categorical variable. Below we compute the same statistics after grouping by the flight time category using the group_by() function.
#summarize flight hours by category
flights_transmute %>%
group_by(flight_cat) %>%
summarize(count=n(),
total=sum(flight_hrs),
average=mean(flight_hrs)) %>%
ungroup()## # A tibble: 3 × 4
## flight_cat count total average
## <chr> <int> <dbl> <dbl>
## 1 long 468 2880. 6.15
## 2 medium 7474 33582. 4.49
## 3 short 257 750. 2.92Now the count statistic offers a little more value. We see that most flight are in the medium length category, with relatively few in the long and short categories. Not surprisingly then, the majority of the total flight hours exist in the medium category as well. Given the thresholds for the categories, the average flight times should not be surprising. A medium flight is between 3 and 6 hours, so an average of 4.5 hours is sensible. Meanwhile, the average long flight is more than 6 hours and the average short flight is less than 3 hours.
It is good practice to ungroup() the data frame after summarizing. Otherwise, we risk unintentional grouped calculations in later analyses. Also, in more complex pipelines, we might compute multiple summaries according to different groupings. In such cases, we must ungroup and regroup between summaries. We can also group by multiple categories. Returning to the original flights table, imagine we want the count, total time, and average time of flights by origin and destination airport.
#summarize flight hours by origin and destination
flights_dest <- flights %>%
select(origin,dest,air_time) %>%
na.omit() %>%
group_by(origin,dest) %>%
summarize(count=n(),
total=sum(air_time),
average=mean(air_time)) %>%
ungroup() %>%
arrange(origin,desc(count))This summary is large enough to warrant saving as its own data frame. Notice, we first eliminated any rows missing the origin, destination, or flight time. Then we grouped by both origin and destination before computing our statistics. Finally, after ungrouping, we sorted the summary to list the most frequent destination first for each origin airport.
Upon viewing the new data frame, we see a summary of 223 combinations of origin and destination airports. The origin airports are listed alphabetically with Newark International (EWR) first. For each origin, the destinations are listed in descending order of flight frequency. For example, we see that the most common destination for flights out of Newark is O’Hare International (ORD) in Chicago. This pipeline demonstrates the complex combinations of row and column functions we can craft to obtain interesting insights from a single data frame. In the next section, we describe methods for combining multiple data frames.
2.3.3 Aggregating Data
Often the data we need does not reside in a single table. It may not even be obtained from the same source. As a result, we need tools for joining tables together in order to aggregate the required data into a single location. Continuing with the NYC airport data, we import two tables from the nycflights13 library.
The airports data frame lists the name and location of each airport based on the Federal Aviation Administration (FAA) abbreviation. Note, these details do not exist in the flights data frame. Unless we’ve flown into a particular airport before, we may not know the correct abbreviation. However, we can combine all of this information into a single table using join functions. In the subsections that follow, we explore four types of joins: left, inner, semi, and anti.
Left Join
For simplicity, let’s first reduce the focus of the flights data frame. Suppose we are only interested in flights out of Newark in the month of January.
#wrangle flights data
flights_ewr <- flights %>%
filter(month==1,
origin=="EWR") %>%
select(time_hour,carrier,flight,dest,tailnum) %>%
na.omit()The flights_ewr table includes all of the flights from Newark in January of 2013 along with the destination and aircraft. But what are all of the destination airport abbreviations? We could manually look them up, but that would get tedious. Instead, we join the airports table to the flights_ewr table using the left_join() function. There is also a right_join() function, but it is seldom applied because we can simply reverse the order of the tables and use a left_join().
The left_join() function maintains every row and column in the left (first) table and adds matching information from the right (second) table. In this case, the flights_ewr table is left (first) and we add matches from the airports table. But we must indicate which characteristic to match on. This is referred to as the key. The key for this particular join is the FAA abbreviation, because that is the unique identifier contained in both tables. Since the column containing the FAA abbreviation has a different header in each table, we specify the connection with by=c("dest"="faa"). Had the columns in both tables been named faa, we could simply use by="faa".
The flights_ewr2 data frame now includes the destination airport name and location in addition to the original flight information. In essence, we added the columns from the airports table to the flights_ewr table and correctly matched the rows by airport code. There is no need to research what airport uses the code IAH, because the table now lists George Bush Intercontinental airport as the name. After careful inspection of the flights_ewr2 table, we notice some of the airport names are missing. Let’s isolate these cases using the is.na() function.
#isolate missing airport names
flights_missing <- flights_ewr2 %>%
filter(is.na(name)) %>%
arrange(dest)The is.na() function returns TRUE if the value in the specified column is NA. When combined with the filter() function, we maintain the rows with missing airport names. After viewing the new data frame, there appear to be three airports (BQN, SJU, and STT) that have no name. These abbreviations (codes) do not exist in the airports data frame, so there is no information to join. An online search reveals these airports are in Puerto Rico and the U.S. Virgin Islands. So, they do exist! For some reason, their FAA code is simply not in the airports table. We could also isolate the airports that do have a name by negating the is.na() function with an exclamation point.
#isolate non-missing airport names
flights_notmissing <- flights_ewr2 %>%
filter(!is.na(name)) %>%
arrange(dest)Notice the flights_missing data frame has 141 rows and the flights_notmissing data frame has 9,718 rows. Added together, these two tables comprise the 9,859 rows in the original flights_ewr2 data frame. We simply split the original table into airports that do and do not have a listed name.
Inner Join
The left_join() function maintains every row in the first table, regardless of whether a matching key exists in the second table. When there is no matching key, the associated row is assigned NA values just as we saw in the previous section. To eliminate rows with missing airport names, we combine the !is.na() and filter() functions. However, a more direct method exists. The inner_join() function only keeps rows from the first table that have a matching key in the second table. In other words, we only keep airports from the first table that have a matching code (and thus name) in the second table. Let’s find non-missing airports using an inner join.
#inner join airports table
flights_notmissing2 <- flights_ewr %>%
inner_join(airports,by=c("dest"="faa"))Now there are no airport names missing from the associated column. The Puerto Rico and U.S. Virgin Islands airports are automatically removed because they had no matching key. This new table includes the exact same number of rows and columns as the flights_notmissing table, but we obtain them in a more efficient manner.
Both left and inner joins can be thought of as similar to the mutate() function. We add new columns to the first table, just as with mutate(). However, those new columns happen to come from a second table rather than being created manually. In order to make sure the rows of the new column properly align with the rows of the original table, we use keys. Another class of joins behave like the filter() function. We demonstrate these types of joins in the next two sections.
Semi Join
The semi_join() function is very similar to the inner_join(). But there is a subtle difference. A semi join only acts as a filter on the first table. It does not add any columns from the second table. Instead, the semi_join() function only includes columns from the first table and eliminates rows that do not have a matching key in the second table. We demonstrate this below.
#semi join airports table
flights_notmissing3 <- flights_ewr %>%
semi_join(airports,by=c("dest"="faa"))The flights_notmissing3 table has the same number of rows (9,718) as the previous two iterations. However, there are only 5 columns because the first table (flights_ewr) only has 5 columns. A semi join removes rows from the first table that have no match in the second table, without adding any columns from the second table. In this way, it behaves more like a filter than a mutation of new columns. Not surprisingly, there is also a filtering join for non-matching keys.
Anti Join
The anti_join() function performs the opposite filter as the semi_join(). Specifically, an anti join keeps the rows from the first table that do not have a matching key in the second table. We apply anti_join() to find airport codes that exist in the first table but not the second table.
#anti join airports table
flights_missing2 <- flights_ewr %>%
anti_join(airports,by=c("dest"="faa")) %>%
arrange(dest)Our anti joined table has the same 141 rows as the left joined and filtered table (flights_missing) but only 5 columns rather than 12. Again, semi and anti joins do not add columns from the second table. Ultimately, the data scientist must decide the appropriate type of join for the task at hand. If the goal is to create a new data frame that combines columns from multiple tables, then a left or inner join is likely appropriate. On the other hand, if the objective is to check whether observations in one table have matches (or not) in another table, then semi or anti joins are the better option.
In addition to organizing, summarizing, and aggregating, a critical wrangling activity is data cleaning. Seldom is a data set free from errors that could impact the validity of subsequent analysis. In the next section, we examine methods for identifying and resolving the most common errors in data.
2.3.4 Cleaning Data
Previously, we discussed tidiness as a preferred characteristic of data frames. Tidiness refers primarily to the structure of the data in terms of the rows, columns, and elements. However, even tidy data can contain errors or inconsistencies that negatively impact analyses and conclusions. The resolution of such issues is known as data cleaning. Clean data is consistent and error free. Ultimately, we want our data to be tidy and clean.
In this section, we discuss common errors and inconsistencies that data scientists encounter. These issues include poorly-named or incorrectly-typed variables, as well as duplicated observations or levels. We demonstrate cleaning methods in the context of example data from the National Football League (NFL). Each year the NFL invites college athletes to attend the Scouting Combine and demonstrate their physical prowess in a variety of events. Their performance at the Combine can have a significant impact on if and when they get drafted into the NFL.
Player performance data from the Combine is widely available online. A companion file named nfl_combine.csv includes data gathered online from the years 2000 through 2020. However, this data was gathered and aggregated manually over multiple years, so some cleaning is likely in order. Let’s import and review the structure of the data using functions from the tidyverse.
#import NFL combine data
combine <- read_csv("nfl_combine.csv")
#display structure of combine data
glimpse(combine)## Rows: 4,201
## Columns: 12
## $ Year <dbl> 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 202…
## $ Player <chr> "Jabari Zuniga\\ZuniJa00", "Chase Young\\YounCh04", "Davi…
## $ Pos <chr> "DL", "DL", "LB", "DL", "TE", "OL", "S", "LB", "OL", "DL"…
## $ School <chr> "Florida", "Ohio St.", "Utah St.", "South Carolina", "Geo…
## $ Height <dbl> 6.25, 6.42, 6.17, 6.42, 6.42, 6.42, 5.75, 6.17, 6.50, 6.3…
## $ Wt <dbl> 264, 264, 230, 258, 244, 320, 203, 241, 350, 308, 264, 31…
## $ `40YD` <dbl> 4.64, NA, 4.79, 4.73, 4.78, 4.85, 4.45, 4.63, 5.32, 5.04,…
## $ Vertical <dbl> 33.0, NA, 33.5, 34.5, 34.5, 36.5, 36.0, 32.0, 29.0, 25.5,…
## $ BenchReps <dbl> 29, NA, 16, 20, 21, 24, NA, 21, 26, 17, 32, NA, 23, NA, N…
## $ `Broad Jump` <dbl> 127, NA, 114, 123, 120, 121, 124, 121, 110, 101, 119, 113…
## $ `3Cone` <dbl> NA, NA, 7.34, 7.25, 7.18, 7.65, NA, 7.07, 8.26, 7.72, 7.3…
## $ Shuttle <dbl> NA, NA, 4.37, 4.44, 4.46, 4.68, NA, 4.27, 5.07, 4.78, NA,…Our data consists of 4,201 observations (rows) which represent individual players who performed at the Combine during the 20-year time period. The data frame also includes 12 variables (columns) that describe demographic and performance characteristics for each player. Details on the rules and expectations for each event are available at this link. We begin the cleaning process by focusing on the names and types for each variable.
Variable Names and Types
When naming variables in a data frame, there are both rules and best practices. Rules specific to R prevent variable names that begin with a number or have spaces. This explains the tick marks around the variables 40YD, Broad Jump, and 3Cone in the structure output above. Variable names with numbers and spaces invariably cause confusion when used in computations. Thus, R identifies the current names as problematic. In fact, some import functions in R will automatically rename such variables by placing an “X” before numbers or a period “.” in place of a space.
Best practices focus more on consistency. For example, it is good practice to consistently begin variable names with upper-case or lower-case letters. Mixing both can lead to confusion, particularly in data sets with dozens or even hundreds of variables. It is also good practice to avoid mixing abbreviations with full names. Choose one or the other and be consistent. Let’s remedy the naming issues by renaming some of the variables.
#rename variables
combine2 <- combine %>%
rename(Position=Pos,
Weight=Wt,
Forty=`40YD`,
Bench=BenchReps,
Broad=`Broad Jump`,
Cone=`3Cone`)For naming, we choose one-word, spelled-out, capitalized names with no numbers. This consistent convention may seem picky, but it will prevent confusion and ease understanding throughout the analysis and presentation of results. Next, we must address the variable types.
Currently, the 12 variables consist of 9 double-precision numbers and 3 character strings. These variable types represent the “best guess” by the read_csv() function when we imported the data. That does not mean they are correct! In fact, some of the variable types should be changed. For example, the Year variable is more appropriately represented by an integer than a double-precision number. If we had higher-fidelity data, such as the day and time of the event, then the date-time variable type would be appropriate for Year. As another example, the Position variable is better treated as a factor than a character string. This is because there are a finite number of positions a player can be assigned, which affords natural grouping. The same is true for School but not Player. Let’s change these variable types using as.xxx() functions.
#retype variables
combine3 <- combine2 %>%
mutate(Year=as.integer(Year),
Position=as.factor(Position),
School=as.factor(School),
Bench=as.integer(Bench))
#display structure
glimpse(combine3)## Rows: 4,201
## Columns: 12
## $ Year <int> 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2…
## $ Player <chr> "Jabari Zuniga\\ZuniJa00", "Chase Young\\YounCh04", "David Wo…
## $ Position <fct> DL, DL, LB, DL, TE, OL, S, LB, OL, DL, DL, OL, OL, TE, WR, LB…
## $ School <fct> Florida, Ohio St., Utah St., South Carolina, Georgia, Iowa, M…
## $ Height <dbl> 6.25, 6.42, 6.17, 6.42, 6.42, 6.42, 5.75, 6.17, 6.50, 6.33, 6…
## $ Weight <dbl> 264, 264, 230, 258, 244, 320, 203, 241, 350, 308, 264, 312, 3…
## $ Forty <dbl> 4.64, NA, 4.79, 4.73, 4.78, 4.85, 4.45, 4.63, 5.32, 5.04, 4.8…
## $ Vertical <dbl> 33.0, NA, 33.5, 34.5, 34.5, 36.5, 36.0, 32.0, 29.0, 25.5, 32.…
## $ Bench <int> 29, NA, 16, 20, 21, 24, NA, 21, 26, 17, 32, NA, 23, NA, NA, 1…
## $ Broad <dbl> 127, NA, 114, 123, 120, 121, 124, 121, 110, 101, 119, 113, 10…
## $ Cone <dbl> NA, NA, 7.34, 7.25, 7.18, 7.65, NA, 7.07, 8.26, 7.72, 7.39, N…
## $ Shuttle <dbl> NA, NA, 4.37, 4.44, 4.46, 4.68, NA, 4.27, 5.07, 4.78, NA, 4.8…We now have clearly and consistently named and typed variables. The majority of the events measure time or space, so double-precision numbers are appropriate. The one exception is bench press repetitions, because only full repetitions count. Player names are legitimate character strings that should not be repeated or grouped. On the other hand, player position and school are repeated and should permit grouping. Consequently, we label these two variables as factors with various levels (categories). But what if there are errors, such as misspellings or duplicates, in the level names? We investigate this issue in the next subsection.
Factor Level Names
Identifying errors in factor levels can require a great deal of effort and/or subject matter expertise. However, a good way to start is to review the unique levels of each factor using the levels() function. As an example, let’s look at the first 10 unique schools.
## [1] "Abilene Christian" "Air Force" "Akron"
## [4] "Ala-Birmingham" "Alabama" "Alabama A&M"
## [7] "Alcorn State" "Appalachian St." "Appalachian State"
## [10] "Arizona"We see a great example of what is likely an error. Do we think “Appalachian St.” and “Appalachian State” are actually different schools? It might take a bit of research to be sure, but this is almost certainly the same school. This error will cause problems when we try to group and summarize anything according to school.
#count players per school
combine3 %>%
group_by(School) %>%
summarize(count=n()) %>%
ungroup() %>%
head(n=10)## # A tibble: 10 × 2
## School count
## <fct> <int>
## 1 Abilene Christian 4
## 2 Air Force 1
## 3 Akron 4
## 4 Ala-Birmingham 5
## 5 Alabama 100
## 6 Alabama A&M 1
## 7 Alcorn State 1
## 8 Appalachian St. 3
## 9 Appalachian State 8
## 10 Arizona 28There are a total of 11 players from Appalachian State, but the group label error caused them to be split into two different schools. Maybe this was a one-time error? To be sure, we need to find any school in the data that has “State” or “St.” in the name. We can accomplish this using functions from yet another package within the tidyverse suite. The stringr library includes pattern-matching functions for character strings. Even though the School variable is a factor, the level names are treated as character strings. We can find “State” or “St.” in the level names using the str_detect() function.
#find State schools
combine3 %>%
filter(str_detect(School," State") | str_detect(School," St\\.")) %>%
group_by(School) %>%
summarize(count=n()) %>%
ungroup() %>%
head(n=10)## # A tibble: 10 × 2
## School count
## <fct> <int>
## 1 Alcorn State 1
## 2 Appalachian St. 3
## 3 Appalachian State 8
## 4 Arizona St. 6
## 5 Arizona State 41
## 6 Arkansas State 5
## 7 Ball St. 1
## 8 Ball State 4
## 9 Boise St. 10
## 10 Boise State 25The str_detect() function is a logical check that returns TRUE when the string in quotes is found within the specified column (variable). The vertical line | is read as the word “or”. The double-slashes \\ ensure the period after “St” is treated as part of the string rather than a special character. So, if the School name includes the string “State” or “St.”, then the filter keeps it. We then count all such school names. Unfortunately, we now see that the “State” versus “St.” issue is pervasive. Most State schools have a mix of both cases. Luckily, there is another stringr function that easily remedies this issue. We can replace every occurrence of the abbreviation “St.” with the full word “State” using the str_replace() function.
#replace St. with State
combine4 <- combine3 %>%
mutate(School=as.factor(str_replace(School, " St\\.", " State")))
#count players per school
combine4 %>%
group_by(School) %>%
summarize(count=n()) %>%
ungroup() %>%
head(n=10)## # A tibble: 10 × 2
## School count
## <fct> <int>
## 1 Abilene Christian 4
## 2 Air Force 1
## 3 Akron 4
## 4 Ala-Birmingham 5
## 5 Alabama 100
## 6 Alabama A&M 1
## 7 Alcorn State 1
## 8 Appalachian State 11
## 9 Arizona 28
## 10 Arizona State 47Now all of the State schools are properly grouped. All 11 players from Appalachian State are together, as are the 47 Arizona State players, and so on. There could be more insidious errors within the levels names, such as random misspellings. However, these issues are much more difficult to detect in a systematic manner. A manual review of all level names is likely required to be certain that no misspellings exist. In addition to accidental repetition of level names, entire observations might be duplicated.
Duplicate Observations
During data collection, human errors naturally occur. One such error is the accidental duplication of the same observation. In the context of our example, this would represent the same player being entered twice in the data table. We check to see if there are any complete duplicates using the duplicated() function.
## [1] 1The duplicated() function is a logical check that returns TRUE for an observation if it has a duplicate in the data frame. By summing the TRUE (1) and FALSE (0) values, we obtain the total number of duplicates. There is one duplicate, but what player is it? We can extract the duplicated row by filtering on it.
## # A tibble: 1 × 12
## Year Player Position School Height Weight Forty Vertical Bench Broad Cone
## <int> <chr> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
## 1 2008 "Aqib Ta… CB Kansas 6.08 202 4.44 38 10 131 6.82
## # ℹ 1 more variable: Shuttle <dbl>A player named Aqib Talib has two identical rows entered in the table. As complete duplicates, these rows represent the same year, player, position, etc. We should not have such duplicates in the data, because a player can only perform in the Combine once. We can eliminate all complete duplicates using the distinct() function.
#remove complete duplicates
combine5 <- combine4 %>%
distinct()
#total all duplicates
sum(duplicated(combine5))## [1] 0## [1] 4200The distinct() function retains only unique rows in the data frame. When we re-check for duplicates afterward, there are none. The data frame is reduced from 4,201 rows to 4,200 given the removal of the one duplicate. Complete duplicates such as this are relatively easy to detect. With a unique identifier, like the code included in the player name, we can be confident that a duplicate is an error. However, we sometimes encounter partial duplicates that are not so obvious. When most, but not all, values are duplicated for two observations it can be difficult to determine whether it is an error.
So, how do we find partial duplicates? There is no “one-size fits all” answer to this question. We must dig into the data and familiarize ourselves with it enough that we notice when a partial duplicate reveals itself. A good place to start is to apply the duplicated() function to an individual column that should not have duplicates. In our case, the Player column should not be duplicated.
## [1] 2Sadly, it appears there are two duplicated player names in the data! Keep in mind, these players cannot be complete duplicates because we already removed all complete duplicates. All we know is that their name is duplicated. Let’s filter out these two players.
## # A tibble: 2 × 12
## Year Player Position School Height Weight Forty Vertical Bench Broad Cone
## <int> <chr> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
## 1 2019 "David L… CB Michi… 5.92 196 4.45 39.5 15 120 6.45
## 2 2007 "Buster … WR Flori… 6.08 207 4.41 NA NA NA NA
## # ℹ 1 more variable: Shuttle <dbl>Two players named David Long and Buster Davis have their names duplicated. Let’s isolate any row with David Long’s name and try to determine what is causing this error.
## # A tibble: 2 × 12
## Year Player Position School Height Weight Forty Vertical Bench Broad Cone
## <int> <chr> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
## 1 2019 "David L… LB Michi… 5.92 227 4.45 39.5 15 120 NA
## 2 2019 "David L… CB Michi… 5.92 196 4.45 39.5 15 120 6.45
## # ℹ 1 more variable: Shuttle <dbl>There are two David Longs from the University of Michigan who competed in the 2019 Combine. But one of them is a 227 pound linebacker and the other is a 196 pound corner back. Did David Long perform in the Combine as a linebacker and then magically lose 31 pounds and perform nearly the same as a cornerback?! Probably not. Let’s perform the same check for Buster Davis.
## # A tibble: 2 × 12
## Year Player Position School Height Weight Forty Vertical Bench Broad Cone
## <int> <chr> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
## 1 2007 "Buster … ILB Flori… 5.75 239 4.64 31 24 104 7.28
## 2 2007 "Buster … WR Flori… 6.08 207 4.41 NA NA NA NA
## # ℹ 1 more variable: Shuttle <dbl>Similar weirdness exists for Buster Davis. The two rows represent the same year, player, and school but different positions and performances. Without access to the original data collectors, it’s hard to know how or why these duplicates happened and which ones, if any, are correct. Consequently, we choose to remove both rows from the data for both players. This is a matter of the data scientist’s judgment and is not always the right answer for every situation.
#remove Long and Davis
combine6 <- combine5 %>%
filter(!Player %in% c("David Long\\LongDa01",
"Buster Davis\\DaviBu99"))
#count rows in data frame
nrow(combine6)## [1] 4196After removing all the rows associated with David Long and Buster Davis, the data frame is down to 4,196 rows. So far, we’ve focused on cleaning existing values in the columns (variables) and rows (observations) of a data frame. But what if values are missing from the data? In the final section of the chapter, we investigate the resolution of missing values and conclude the discussion of data acquisition.
2.3.5 Imputing Data
At the intersection of each row and column of a data frame we encounter the variable value for an individual observation. However, these values are sometimes missing. Data could be missing because it does not (or cannot) exist. Alternatively, the data could exist but not be recorded. Whether intentional or otherwise, missing data can present issues with certain analysis techniques. So how should we proceed? There are three primary options for dealing with missing data.
- Keep missing values
- Remove missing values
- Replace missing values
Depending on the analytic technique we plan to employ, we may be able to keep all observations and work around the missing data. If the associated row has values for most of the other variables, then we may not want to sacrifice the entire observation. This is particularly true when the missing variable value cannot exist. Imagine a set of survey data that asks adults the number of pregnancies they have experienced. There is an important difference between a biological female who records a value of zero and a biological male who leaves the value blank. In this case, the blank value is impossible rather than missing.
When the data consists of many observations (e.g., hundreds or thousands) with recorded values, we may be willing to remove a few rows with missing values. By removing the entire row, we avoid potential analytic issues related to missing data. On the other hand, there are situations where we cannot afford to lose any of our observations and cannot have missing values in the analysis. In this case, we may choose to replace the missing values with an appropriate estimate. The construction of artificial variable values is known as imputing.
There are a variety of techniques for imputing variable values. The simplest approach is to assign the average or most-common value among the non-missing cases. More sophisticated approaches assign values based on some subgroup to which the missing observation belongs. For example, if the missing value is the height of an adult then we would prefer to assign an average based on the biological sex of the missing observation. Further still, some methods for imputing attempt to predict the value of the missing variable based on the values of the non-missing variables. We present such methods in Chapter 5. For now, we examine missing values within the NFL Combine data.
In the data that remains in combine6, there are many missing (NA) values for the performance measurements. This could be caused by a player declining to perform in certain events, which is allowed. Alternatively, the player may have competed in the event and the associated score did not get recorded. Without access to the original data source, it is difficult to know which is the case. If we choose to eliminate any rows that contain an NA, we simply apply the na.omit() function we’ve encountered before. But before deleting these rows, we might want to determine if any patterns exist in the missing values. This could help improve the data collection process and reveal important insights. The visdat library offers a variety of functions to visualize an entire data set in a single graphic. One such function displays missing values.
#load visdat library
library(visdat)
#visualize missing data
combine6 %>%
arrange(Position) %>%
vis_miss(sort_miss=TRUE)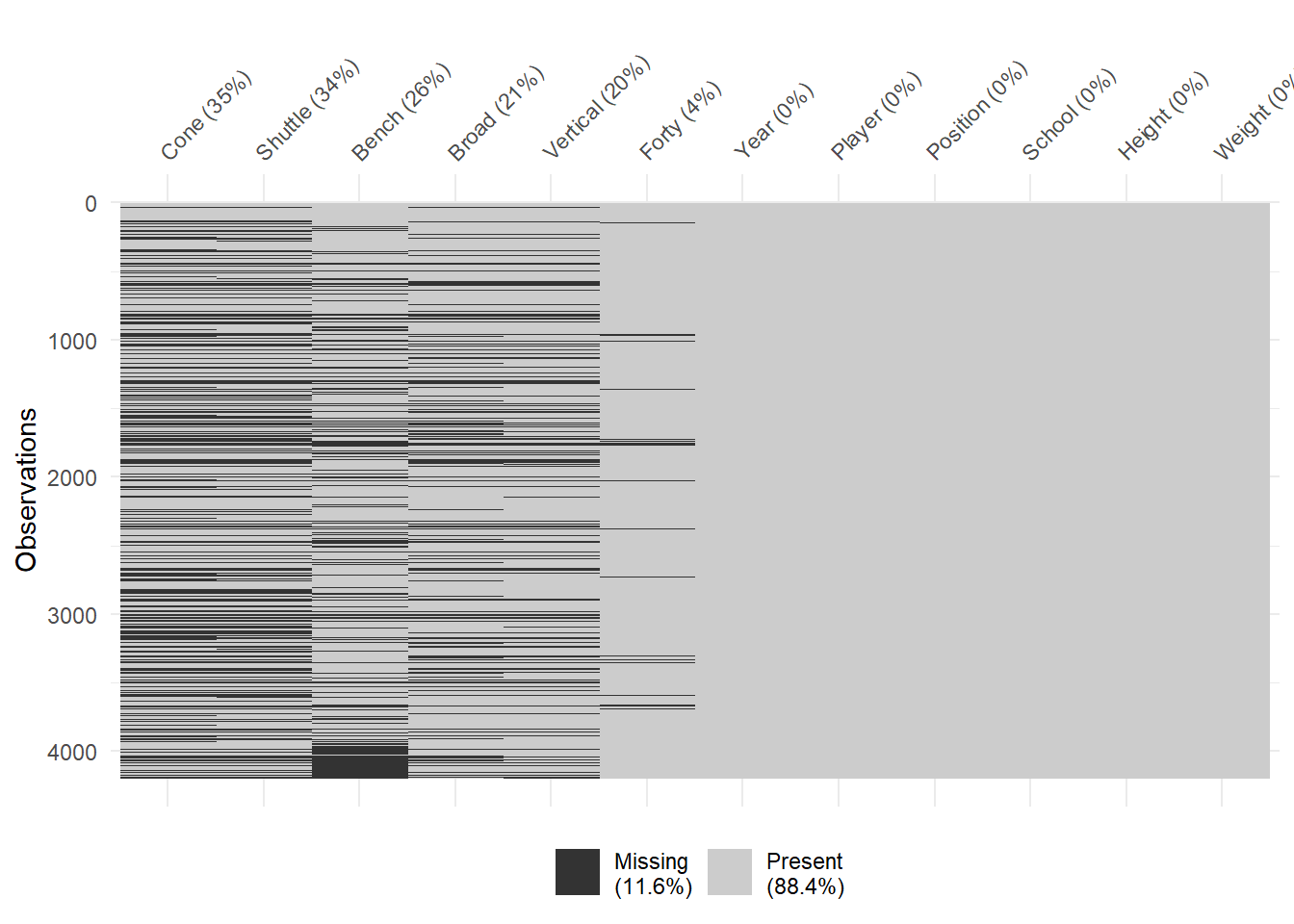
Figure 2.3: Missing Variable Values for each Observation
The vismiss() function distinguishes missing from non-missing values. With the sort_miss option set to TRUE the variables are sorted from most to least missing. Based on Figure 2.3, it appears the cone and shuttle drills have the most players with missing values. Perhaps many players choose not to compete in these events. By contrast, almost no one misses the forty-yard dash. An interesting pattern that jumps out is the large clump of missing values at the bottom of the bench press column. Prior to calling the vis_miss() function, we sorted the rows alphabetically by position. In alphabetical order, the wide receiver position appears last. Thus, a disproportionately large number of wide receivers miss the bench press. This could be because the position values speed over strength. Rather than record a poor performance, many wide receivers simply decline the event.
If we feel confident that the missing data is simply due to players declining to compete, then we might choose to keep all of the rows with missing values. In this case, we must work around the missing values for certain computations. For instance, we might want to know the average cone drill time for players that competed in that event. If we attempt to apply the mean() function to the cone drill column, we get an empty result.
## [1] NAWith its default settings, the mean() function does not know how to handle all of the missing values. However, we can remove the NA values from the calculation using the na.rm=TRUE option. This does not delete the missing values from the data. It simply ignores them when computing the average.
## [1] 7.277486With the missing values out of the way, we find the average cone drill time (for those who competed) is a little over 7 seconds. The option to remove missing values is available for most functions that calculate a statistic for a variable. The final method for dealing with missing values is to try and “fill in the blanks” with actual (or imputed) values. For actual values we need access to the original data source. In certain contexts, it might be possible to conduct some forensic research and discover the real value for an observation. For example, we might find a video online of a player performing in the Combine event for which data is missing. In other situations, there is no way to determine the actual value or if it existed in the first place. In these cases we might choose to impute reasonable values using the available data.
For all players missing a cone drill time, we could impute a value of 7.28 seconds (i.e., the mean time). However, there is compelling evidence that the performance in each event is related to the player’s position. As a result, it may be more accurate to impute mean values by position. Let’s summarize the mean cone drill time grouped by position. For simplicity, we only display the first five positions.
#compute grouped mean cone time
combine6 %>%
group_by(Position) %>%
summarize(avg_cone=mean(Cone, na.rm=TRUE)) %>%
ungroup() %>%
head(n=5)## # A tibble: 5 × 2
## Position avg_cone
## <fct> <dbl>
## 1 C 7.69
## 2 CB 6.93
## 3 DE 7.32
## 4 DL 7.55
## 5 DT 7.70Here we see the value of imputing grouped means. While defensive ends (DE) perform close to the overall mean of 7.28 seconds, the other positions perform quite differently. Corner backs (CB) are much faster and defensive tackles (DT) are much slower. Thus, we would not want to impute the overall average to either of these positions. Regardless, whenever values are imputed it is incredibly important that the stakeholder or a domain expert is solicited for input. For the purposes of this case study, we choose to leave the missing values in place and assume it is a result of players declining to compete. In addition to missing values, we might also like to check for implausible values. A good initial check for plausibility is to summarize the data and review the maximum, minimum, and/or most common values.
## Year Player Position School
## Min. :2000 Length:4196 WR : 633 Ohio State : 109
## 1st Qu.:2005 Class :character CB : 483 Alabama : 100
## Median :2010 Mode :character RB : 394 USC : 100
## Mean :2010 DT : 342 Miami (FL) : 99
## 3rd Qu.:2015 OT : 341 Florida : 98
## Max. :2020 DE : 340 Florida State: 96
## (Other):1663 (Other) :3594
## Height Weight Forty Vertical Bench
## Min. :5.42 Min. :155.0 Min. :4.220 Min. :19.00 Min. : 2.00
## 1st Qu.:6.08 1st Qu.:205.0 1st Qu.:4.520 1st Qu.:30.50 1st Qu.:17.00
## Median :6.17 Median :239.0 Median :4.660 Median :33.50 Median :21.00
## Mean :6.16 Mean :246.2 Mean :4.761 Mean :33.18 Mean :21.07
## 3rd Qu.:6.33 3rd Qu.:295.0 3rd Qu.:4.980 3rd Qu.:36.00 3rd Qu.:25.00
## Max. :6.83 Max. :375.0 Max. :5.990 Max. :46.00 Max. :49.00
## NA's :151 NA's :843 NA's :1082
## Broad Cone Shuttle
## Min. : 83 Min. :6.420 Min. :3.730
## 1st Qu.:109 1st Qu.:6.960 1st Qu.:4.190
## Median :116 Median :7.190 Median :4.350
## Mean :115 Mean :7.277 Mean :4.388
## 3rd Qu.:122 3rd Qu.:7.550 3rd Qu.:4.560
## Max. :147 Max. :9.000 Max. :5.380
## NA's :889 NA's :1483 NA's :1412Generally this requires some subject matter expertise, but we are looking for values that seem implausible. For example, if the maximum of the Height variable was 8.5 feet, then we could be fairly certain the value is an error. Similarly, if the minimum of the Weight column was 50 pounds, we could be confident a mistake was made upon data entry. If the most common School at the Combine was listed as an online-only college, then something went wrong. Beyond common knowledge, it can be difficult to identify extreme or unlikely values. In light of this, we commit an entire section to the discussion of outliers in Chapter 3. After a variety of wrangling tasks, we are left with a data frame that appears consistent and error free. Only now should we proceed with analyzing the data via exploration, inference, or prediction. We dive deep into all of these approaches in the next three chapters using case studies of real-world data sets to motivate the methods and tools.
2.4 Resources: Data Acquisition
Below are the learning objectives associated with this chapter, as well as exercises to evaluate student understanding. Afterward, we provide recommendations for further study on the topic of data acquisition.
2.4.1 Learning Objectives
After completing this chapter, students should be able to:
- Define the common terminology of data structures and apply it to real-world data.
- Diagnose messy data structures and implement the required steps to make it tidy.
- Identify appropriate variable types and sub-types for the columns of a data set.
- Assign suitable primitive data types to variable values in a coding environment.
- Determine appropriate non-primitive data types for groups of variable values.
- Locate and import data into a coding environment from local and online sources.
- Simulate data from the Binomial, Uniform, and Normal probability distributions.
- Organize data by filtering, sorting, creating, and deleting rows and columns.
- Summarize data via counts, proportions, sums, and averages of variable values.
- Group data by factors and compute common summaries within the associated levels.
- Join data frames by selecting the correct type of aggregation and primary key.
- Compare and contrast observations between two data frames using join functions.
- Find and resolve inconsistencies in naming variables and the levels of a factor.
- Identify and resolve duplicated or missing observations and variable values.
2.4.3 Further Study
In this chapter, we provide an introduction to how data is structured, imported, and wrangled in RStudio. But there is much more to learn on these topics. Below we offer some additional resources related to data acquisition.
Though we focus on collected data, the design of experiments is foundational to the disciplines of statistics and data science. A highly-regarded textbook on this topic is Douglas C. Montgomery’s Design and Analysis of Experiments (Montgomery 2017). In its eighth edition, this book includes applications in a wide variety of domains and leverages multiple software platforms including Design-Expert and SAS.
Data acquisition is so fundamental to data science, that additional resources abound. Bradley C. Boehmke’s Data Wrangling with R provides a comprehensive presentation of data structures, import, and wrangling in one text (Boehmke 2016). The data import portion of the book includes chapters on importing and exporting to Microsoft Excel as well as on web scraping.
A solid option for learning SQL is SQL for Data Scientists: A Beginner’s Guide for Building Datasets for Analysis by Renee M.P. Teate (Teate 2021). Not only does the author provide a great introduction to coding SQL queries, but it is presented in the context of common data science problems. With a wide variety of examples, readers get the dual benefit of learning how to query relational databases and how to analyze the associated data.
A valuable guide for data workflow in general is Principles of Data Wrangling by Joseph M. Hellerstein and others (Hellerstein et al. 2016). The book acknowledges that professional data scientists spend more than half of there time performing wrangling tasks. Consequently, organized and repeatable workflows are critical. Though not specific to R, the underlying principles are nevertheless applicable.
For a deeper dive into data cleaning, a valuable resource is Statistical Data Cleaning with Applications in R by Mark van der Loo and Edwin de Jonge (Loo and Jonge 2018). With a specific focus in R, this book is a nice supplement to the skills developed here. Cleaning methods address numerical, categorical, and text data types. There is even an entire chapter on imputing missing values.