Chapter 4 Inferential Analyses
The second type of analysis conducted by data scientists leverages inferential statistics. The related methods and tools differ from exploratory analysis in their intended use. The results of an exploratory analysis are intended to describe the distributions of and associations between variables within the acquired data set. With inferential analysis we seek to extend the results beyond the acquired data. Specifically, we employ estimates from sample data to make claims about the distributions and associations for variables in the larger population from which the data is acquired.
As an example, imagine we are asked to determine the proportion of American adults who are obese based on body mass index (BMI). It would be nearly impossible to acquire BMI values for every adult in the population. Instead, we gather a representative sample of the population and compute the obesity proportion within the sample. Suppose we acquire BMI values for one thousand of the 260 million adults in the United States. Within the sample, we find that 420 (42%) of the adults are obese. The true obesity proportion is called the population parameter and its value is unknown. But we estimate the true proportion with the sample statistic of 42%. Thus, inference consists of estimating population parameters using sample statistics.
Even though we cannot know the true obesity proportion in the population of 260 million adults, we can obtain a defensible estimate using a representative sample of one thousand adults. This highlights a key characteristic of samples: they should be representative of the population. Ideally, when we calculate a statistic from a sample we get a number that is close to what we would get for the parameter in the population. If the sample of one thousand Americans represents the population well, then the obesity proportion in the entire population should be close to 42%. When a sample does not represent the population well, we say it is biased.
After obtaining a representative sample, the two most common analytic tools in inferential analyses are confidence intervals and hypothesis tests. Confidence intervals provide a margin of error around our estimates. For example, we might determine that the obesity proportion for American adults is 42% plus or minus 2 percentage-points. By providing a range of plausible values we acknowledge the variability associated with estimating a population parameter from a sample statistic. Rather than computing a range of likely values for a parameter, hypothesis tests assess the plausibility of a particular value. If, for example, someone claims that 45% of Americans are obese, then we evaluate the claim using a hypothesis test. Depending on the variability of obesity, it is possible a population with a rate of 45% could produce a sample with a rate of 42%. The majority of this chapter is devoted to computing confidence intervals and conducting hypothesis tests for various types of parameters. But we begin with a discussion of random sampling techniques and the statistics we typically compute from unbiased samples.
4.1 Data Sampling
In order to infer a plausible value, or range of values, for a population parameter the associated statistic should be calculated from a representative sample. There are a variety of methods to obtain a representative sample, but the gold standard is random sampling. A sample is considered random if every possible combination of observations of a certain size has the same chance of being selected from the population. Often we refer to the individual observations in a random sample as being independent and identically distributed (iid). Independence exists when the variable values of each observation have no influence on the values of the other observations. Random variable values are identically distributed when there is no change to the data-generating process during sampling. We present the most common forms of random sampling in the first subsection.
The risk imposed by not sampling randomly is the potential introduction of bias. A biased sample is likely to produce biased statistics. A statistic is biased when its value consistently differs from the value of its associated parameter. Since the true parameter value is unknown in most applications, bias can be difficult to detect. The best approach is to avoid bias by employing random sampling techniques that have been shown to produce representative samples. In the next subsection, we introduce common sources of bias that are minimized by random sampling.
Prior to discussing sampling methods and bias, it is worth noting the importance of sample size. While the method of gathering the sample impacts its bias, the size of the sample affects its variance. When the number of observations in a sample is too small, statistical estimates can vary wildly from one sample to the next. For example, if we only sampled five adults from the entire population and recorded their weights, then we might witness a 100% obesity rate simply by chance. Another sample of five adults might return a 0% obesity rate, again purely by chance. Very large samples make it much less likely we will witness such extreme fluctuations in statistics. Two separate samples of one thousand adults might produce obesity rates of 40% and 44%, but this represents much less variability. While there is no one “magic” number for the minimum sample size across all analytic techniques, more is generally better.
4.1.1 Sampling Methods
After defining the population of interest, researchers obtain a sample via the random selection of observations. Random sampling is conducted in a variety of forms. The preferred approach is often driven by the researcher’s access to the population and/or the parameter of interest. Regardless of approach, the goal is to acquire a subset of data that represents the population well. Below we briefly introduce four common random sampling methods.
Simple random sampling is the most straight-forward method for collecting an unbiased sample. In a simple random sample, every individual observation in the population has an equal chance of being selected for inclusion. Imagine writing the names of all 260 million American adults on individual pieces of paper, mixing them up in a bag, and then blindly drawing one thousand names out of the bag. In theory, this would provide each adult in the population an equal chance of being included in the sample. In practice we use a random number generator, rather than pieces of paper, but the concept of simple random sampling is the same.
Systematic sampling involves selecting observations at fixed intervals. In a systematic sample, researchers generate a random starting point and then select the observations that occur at the appropriate increments after the starting point. Imagine we plan to gather a sample of adults entering a department store. We might randomly generate a starting time each day and then survey every 5th adult that comes in the store until closing. Alternatively, we could choose to survey one adult every 5 minutes after the starting time. In either case, if the starting point and arrivals are random then the sample is considered random.
Stratified sampling involves splitting the population into sub-groups prior to sampling. Stratified sampling is often employed when researchers want to ensure that certain sub-groups appear in the sample in the same proportion as in the population. Typical sub-groups in human research include sex, race, socioeconomic status, etc. Once the population is split into these sub-groups (strata), observations are randomly sampled within each group. In the obesity example, researchers might want to ensure a proportionate number of biological males and females in the sample. If the ratio in the population is 51% female and 49% male, then the researchers might choose to randomly sample 510 females and then randomly sample 490 males. Without the strata, there is no guarantee that the sample includes males and females in the correct proportion.
Cluster sampling is similar to stratified sampling but there are key differences. In cluster sampling, the population is also split into sub-groups. However, each sub-group should itself be representative of the entire population. Then a set number of sub-groups (clusters) are randomly sampled and every observation in the selected clusters is included in the sample. Suppose we identify zip codes in America as the clusters. Then we randomly sample a certain number of zip codes. Finally, every person who lives in the selected zip codes gets included in the sample. If each cluster truly represents the population, then the collection of clusters should as well. For the obesity example, zip code may not be the best clustering rule since certain regions of the country have obesity rates well above or below the national average.
Given that stratified and cluster sampling both involve sub-grouping the population, they can be easily confused. Figure 4.1 depicts the critical difference in how the sub-groups are created.
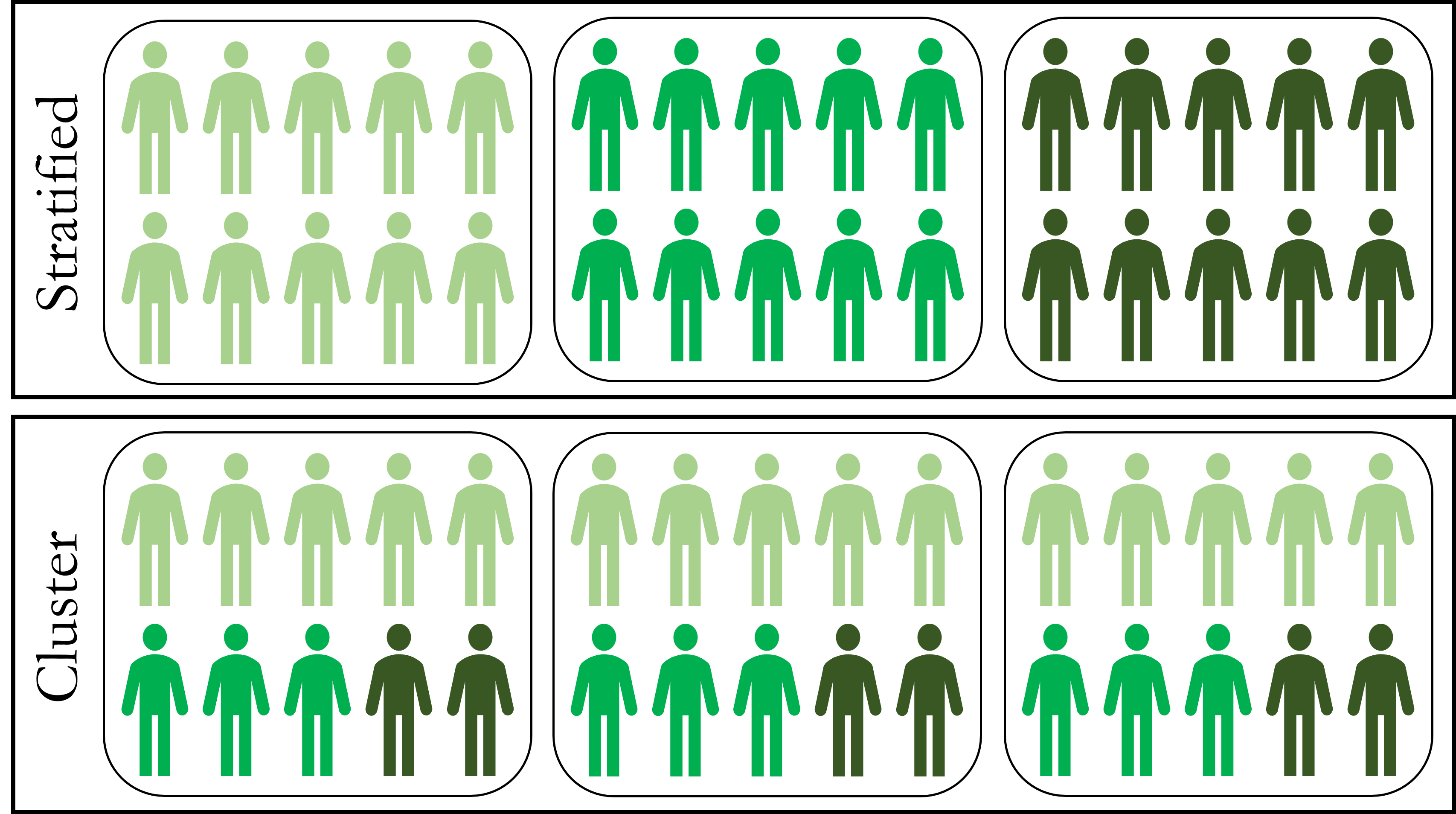
Figure 4.1: Stratified versus Cluster Sampling
Suppose researchers want to ensure that low, medium, and high income adults are represented in the sample in the same proportions as in the population. Stratified sampling splits the population into the three income strata first. Then researchers randomly sample the desired number of observations (based on proportion in the population) from each strata. By contrast, cluster sampling splits the population into clusters that already include the proper proportions of income status. Then researchers randomly select entire clusters for inclusion in the sample. If executed properly, either method can ensure an unbiased sample.
If a sample is not collected randomly, then it may suffer from bias. A biased sample does not represent the population and subsequent statistics poorly estimate the associated parameter. Below we list common sources of bias that emerge in samples that are not collected randomly.
Self-selection bias occurs when the observational units have control over whether to be included in the sample or not. One example is when data is collected using a voluntary survey. If a certain subset of people are more likely to choose to respond, then their answers may not be reflective of the entire population. If American adults are asked to participate in a survey regarding obesity, members may not be equally likely to volunteer due to social pressures regarding body image. Consequently, the study may underestimate the proportion of obese adults in the population.
Undercoverage bias happens when observations in the sample are not collected in proportion to the population. Often this happens when researchers only gather easily-accessible data (convenience sampling). Imagine if researchers only gathered BMI information from randomly selected patients at a local clinic. Given the demonstrated connections between obesity and other health issues, a sample of clinic patients may overestimate the obesity proportion in the population. On the other hand, a sample gathered from members of a local gym might underestimate the obesity proportion. Both examples suffer from undercoverage of the population.
Survivorship bias occurs when a sample only includes data from a subset of the population that meets a certain criteria. As an example, consider a health survey sent out to active members of a local gym. The survey does not consider the health of members who quit going to the gym, so the results will likely be overly optimistic. Survivorship could also be an issue of mobility. If a study consists of body measurements collected in person, then the sample may underestimate the obesity proportion due to an inability or unwillingness to physically report.
Even when the observations in a sample are gathered randomly, it is possible for bias to emerge due to how the data is collected. Issues such as faulty equipment, administrative errors, and lack of cooperation by participants can all bias the data. Below we list sources of bias due to data collection methods.
Non-response bias happens when observational units refuse to contribute to part of the sample data. Unlike self-selection, the sample may include participants in the correct proportions. But certain observations may be missing variable values due to non-response. One example might be a survey that requests sensitive information like political affiliation, religious beliefs, or sexual preference. In the obesity example, some respondents may refuse to provide body weight as part of the survey. In that case, the analysis could misrepresent the true proportion of obese adults even if the correct proportion participates in the survey.
Observer bias occurs when the researcher’s personal opinions influence the data collection process. This type of bias can occur intentionally or unintentionally. An obvious case of this type of bias would occur if a researcher were asked to determine a person’s obesity status based on sight, rather than measured values. Another case might be a researcher who is not familiar with the measurement equipment and uses it incorrectly. Though some observer biases are quite obvious, there are other more subtle ways that researchers allow their personal viewpoints or expectations to be reflected in the data collection.
Recall bias occurs when the researcher or subject is more or less likely to remember the correct data value. This can happen when there is a time lag between when the data occurred and when it was collected. For example, a subject may not accurately remember their own body weight if they have not recently measured it. Similarly, the researcher may forget the correct measured weight if they do not record it immediately. Recall bias can also occur when the context of the research is unique to the study subject. Someone who has struggled with weight loss may be much more likely to have recently weighed themselves and remember the value. These examples highlight why data should be collected in an objective, repeatable manner whenever possible.
4.1.2 Inferential Statistics
In Chapter 3.1.1 we discuss descriptive statistics as a method of data summary. In the context of exploratory analysis, a statistic is descriptive because we only aim to summarize variable values within the acquired data. We are describing what we observe. On the other hand, inferential statistics are intended to summarize variable values beyond the acquired data. Specifically, we want to estimate a population parameter using a sample statistic. Our goal when computing sample statistics remains to characterize the frequency, centrality, dispersion, and correlation of variable values. We also use similar metrics such as the proportion, mean, standard deviation, and correlation coefficient. The difference lies in the application of each statistic. In an inferential analysis, we infer the unknown value of a parameter in the entire population based on the known value of a statistic computed from a representative sample.
In order to distinguish between an unknown parameter and a known statistic, it is useful to introduce a bit of notation. Often, but not always, we represent population parameters using Greek letters. For example, the population mean is typically denoted as \(\mu\). The associated sample statistic adds a “hat” to the symbol to indicate an estimate of the unknown value. Hence, the sample mean would appear as \(\hat{\mu}\). Unfortunately, this is not entirely consistent across textbooks and other resources. The sample mean, for example, is frequently labeled with the symbol \(\bar{x}\) in a variety of contexts. As a result, it is critical to clearly define and consistently apply notation. In this text, we employ the “hat” methodology throughout.
Random sampling and objective data collection help avoid bias. With an unbiased sample, data scientists can compute inferential statistics that accurately estimate population parameters. These sample statistics are referred to as point estimates because they offer a one-number approximation of the associated parameter. But the precision of such estimates cannot be determined from a single value. Instead, we prefer a range of values that plausibly capture the population parameter. Such ranges of values are referred to as confidence intervals.
4.2 Confidence Intervals
Inferential statistics are often sensitive to the data that happens to be randomly selected for the sample. Different samples produce different estimates for the population parameter of interest. Hence, a single point estimate provides no information about the variability across samples. We remedy this concern by constructing an interval of estimates within which we are confident the population parameter lies. We call this range of values a confidence interval. In order to construct confidence intervals, we must first carefully describe the distribution of a statistic.
4.2.1 Sampling Distributions
The observed value of a statistic depends on which members of the population are selected for the sample. Since population members are selected randomly, different samples are likely to produce different statistics. A sampling distribution captures the range and frequency of values we can expect to observe for a statistic. Rather than basing the estimation of a parameter on a single point, a sampling distribution describes the entire range of possible values. We demonstrate this concept with an example.
True Distribution
Suppose our population of interest is every song that appeared on the Billboard Top 100 music chart in the year 2000. Furthermore, imagine the parameter we want to estimate is the median ranking of a song in its first week on the charts. The tidyverse package happens to include the entire population in the data set called billboard. In the following code chunk, we import and wrangle the data to isolate the first week.
#import billboard data
data(billboard)
#wrangle data to only include week 1
billboard_pop <- billboard %>%
select(artist,track,wk1)
#review data structure
glimpse(billboard_pop)## Rows: 317
## Columns: 3
## $ artist <chr> "2 Pac", "2Ge+her", "3 Doors Down", "3 Doors Down", "504 Boyz",…
## $ track <chr> "Baby Don't Cry (Keep...", "The Hardest Part Of ...", "Kryptoni…
## $ wk1 <dbl> 87, 91, 81, 76, 57, 51, 97, 84, 59, 76, 84, 57, 50, 71, 79, 80,…The population consists of 317 songs, along with their first week ranking. Typically, we do not have access to the entire population of interest. If we did, there would be no reason to estimate a parameter. We could simply compute it directly! In this case, the median first-week ranking for a song in the year 2000 is 81 (see below).
## [1] 81Thus, half of all songs in the population have a first-week ranking greater than 81 out of 100. However, as previously stated, we typically will not know this value because we will not have access to the entire population. Instead, we draw a random sample from the population and compute the sample median as a point estimate. Let’s extract a random sample of 50 songs and compute the sample median ranking.
#set randomization seed
set.seed(1)
#select 50 random song rankings
billboard_samp1 <- sample(x=billboard_pop$wk1,size=50,replace=FALSE)The sample() function randomly selects size=50 rows from the population of all song rankings. We do so without replacement (replace=FALSE) because we do not want the same song to appear more than once. The result is a sample of 50 randomly selected song rankings in billboard_samp1. From the sample, we compute the point estimate for median first-week ranking.
## [1] 81.5Based on the sample of 50 songs, our best estimate for the true median first-week ranking is 81.5 out of 100. Here we use “true” median interchangeably with “population” median. Remember, in practice we will not know that the true median is 81. We will only know the sample median of 81.5. As result, we will not know whether 81.5 is an accurate estimate or not. Even more concerning, we will not know what estimate would result from a different sample. For this academic exercise, let’s see what happens with a different randomization seed.
#set randomization seed
set.seed(1000)
#select 50 random song rankings and compute the mean
median(sample(x=billboard_pop$wk1,size=50,replace=FALSE))## [1] 80Changing the randomization seed simulates drawing a different 50 songs from the population. For simplicity, we skip the step of defining the sample vector and directly compute the median. Had we sampled these 50 songs, our point estimate for median first-week ranking would be 80 out of 100. Both point estimates are relatively close to the true parameter value, but we have no way of knowing that in practice because we will not have access to the whole population.
Next, we take this exercise of repeated sampling a step further. Imagine we had the capability to randomly sample 50 songs from the population 1,000 times. Each time we compute the sample median ranking of the 50 songs as in the previous two cases. In order to expedite the sampling process, we employ a for() loop.
#initiate empty data frame
results <- data.frame(med=rep(NA,1000))
#repeat sampling process 1000 times and save median
for(i in 1:1000){
set.seed(i)
results$med[i] <- median(sample(x=billboard_pop$wk1,size=50,replace=FALSE))
}Prior to initiating the loop, we define an empty data frame called results to hold all 1,000 sample medians. We then fill the empty data frame one sample median at a time within the loop. The result is a vector of 1,000 median first-week rankings. Rather than attempt to view these values directly, we depict them in a density plot.
#plot sampling distribution
ggplot(data=results,aes(x=med)) +
geom_density(color="black",fill="#CFB87C",adjust=3) +
geom_vline(xintercept=true_median,color="red",linewidth=1) +
labs(title="Billboard Top 100 for the Year 2000",
x="Sample Median Week 1 Ranking",
y="Density") +
scale_x_continuous(limits=c(72,90),breaks=seq(72,90,2)) +
theme_bw()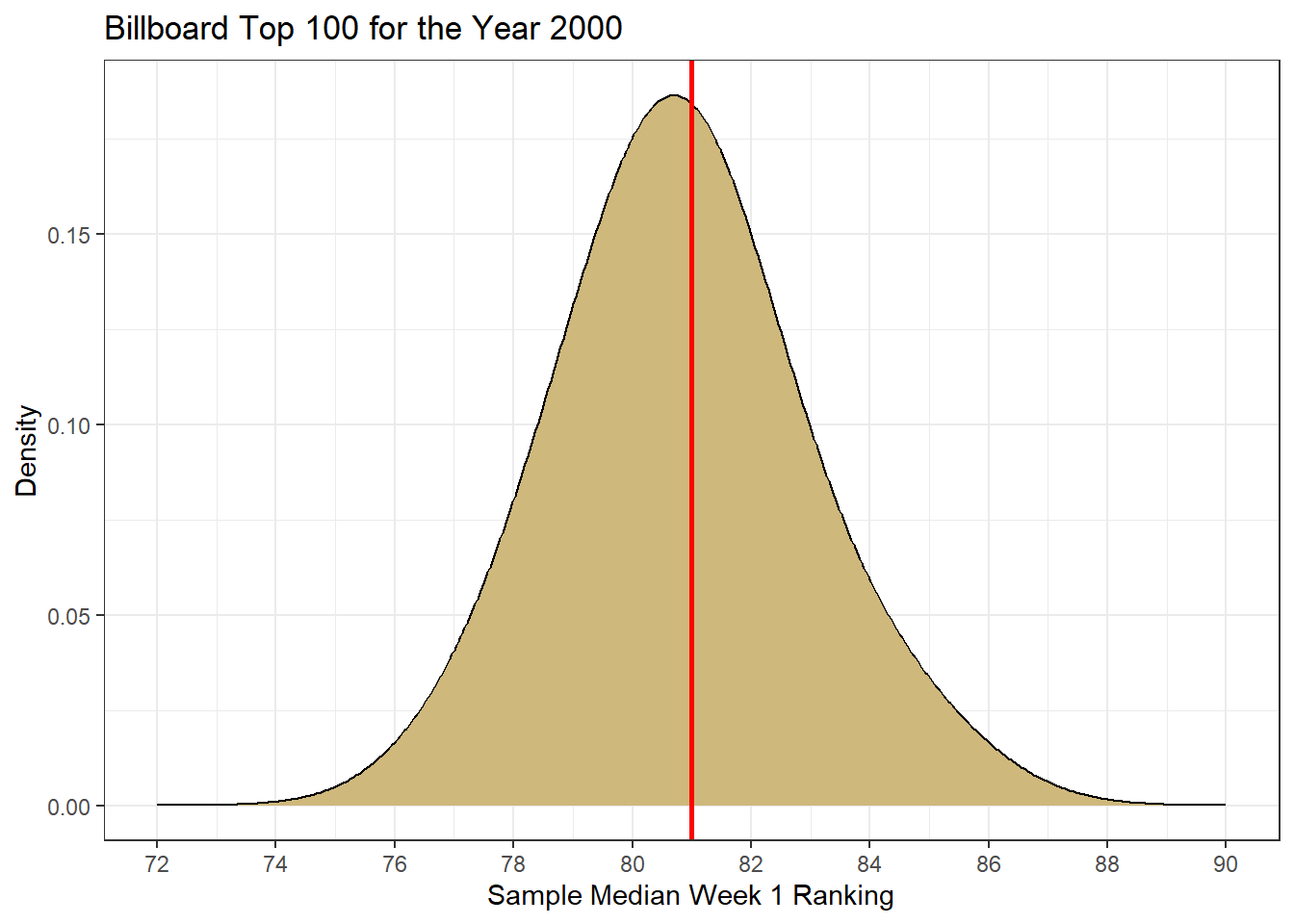
Figure 4.2: Sampling Distribution for Median Week 1 Ranking
The density plot depicted in Figure 4.2 represents the true sampling distribution for median first-week ranking. It provides us an indication of the range and frequency of values we can expect to observe for the median. In this case, we see that the median first-week ranking for a song on the Billboard Top 100 ranges between about 72 and 90 out of 100. However, those extreme values are very unlikely. Instead, we expect to see median rankings close to 81 where the density is much greater. This also happens to be near the true median ranking (red line).
What we learn from this exercise is that sample medians tend to be very close to the population median. In general, the larger our sample size the more likely the sample median will be close to the population median. With a sample size of 50 songs, the sample median rarely differs more than six ranks from the true median. The vast majority of the samples produce a median within two ranks of the population median.
This simulated example of repeatedly sampling from a population provides the intuition regarding the variability of a statistic. However, this is not how inferential statistics is conducted in practice. Due to limitations of time, money, and resources we seldom have the luxury of more than one sample from the population. So, how can we construct a sampling distribution if we only have a single sample and thus a single point estimate?
Bootstrapped Distribution
Initially it may seem impossible to create a distribution of many statistics out of a single sample. In fact, this seeming impossibility is the origin of the name for the method we use: bootstrapping. At some point around the late-1800s the phrase “pull yourself up by your bootstraps” originated. The literal interpretation suggests someone lift themselves off the ground by pulling on the loops attached to their own boots. But the figurative use encourages someone to be self-sufficient in the face of a difficult, if not impossible, task.
Bootstrapping, also known as bootstrap resampling, is a method for constructing a distribution of multiple statistics from a single sample. In essence, we treat the single sample as though it were the entire population. Then we sample from that “population” repeatedly just as we demonstrated in the previous subsection. Two important differences are that we perform the resampling with replacement and our sample size is the same as the “population” size.
Resampling with replacement permits observations to appear in each sample more than once. At first this may seem counter-intuitive. Won’t including the same values in the sample multiple times compromise the accuracy of our statistic? The answer is no and the reason is due to the randomness of the resampling. Values that appear in greater frequency in the original sample (“population”) will generally appear in greater frequency in the resample (“sample”). This is exactly how we want the resampling to behave. Furthermore, since the resample size is the same as the original sample size the only way to obtain different values for the statistic is to allow replacement.
To demonstrate the resampling process, we return to the Billboard Top 100 example. The first sample we drew from the entire population is named billboard_samp1. We now assume these 50 songs are the only sample we have access to. The 50-song sample is treated as the “population” from which we resample. Once again we leverage a for() loop, but now we set the parameter replace=TRUE.
#initiate empty data frame
results_boot <- data.frame(med=rep(NA,1000))
#repeat sampling process 1000 times and save sample medians
for(i in 1:1000){
set.seed(i)
results_boot$med[i] <- median(sample(x=billboard_samp1,size=50,replace=TRUE))
}The bootstrap resampling results in 1,000 sample medians. Each one estimates the true median first-week ranking for songs in the Billboard 100. From the resampled statistics, we produce a histogram of sample medians. Here we choose a histogram, rather than a density plot, to emphasize that the bootstrap sampling distribution is intended to estimate the true sampling distribution.
#plot resampling distribution
ggplot(data=results_boot,aes(x=med)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$med,0.05),
color="red",linetype="dashed",linewidth=1) +
geom_vline(xintercept=quantile(results_boot$med,0.95),
color="red",linetype="dashed",linewidth=1) +
labs(title="Billboard Top 100 for the Year 2000",
subtitle="Sampling Distribution",
x="Sample Median Week 1 Ranking",
y="Count") +
scale_x_continuous(limits=c(72,90),breaks=seq(72,90,2)) +
theme_bw()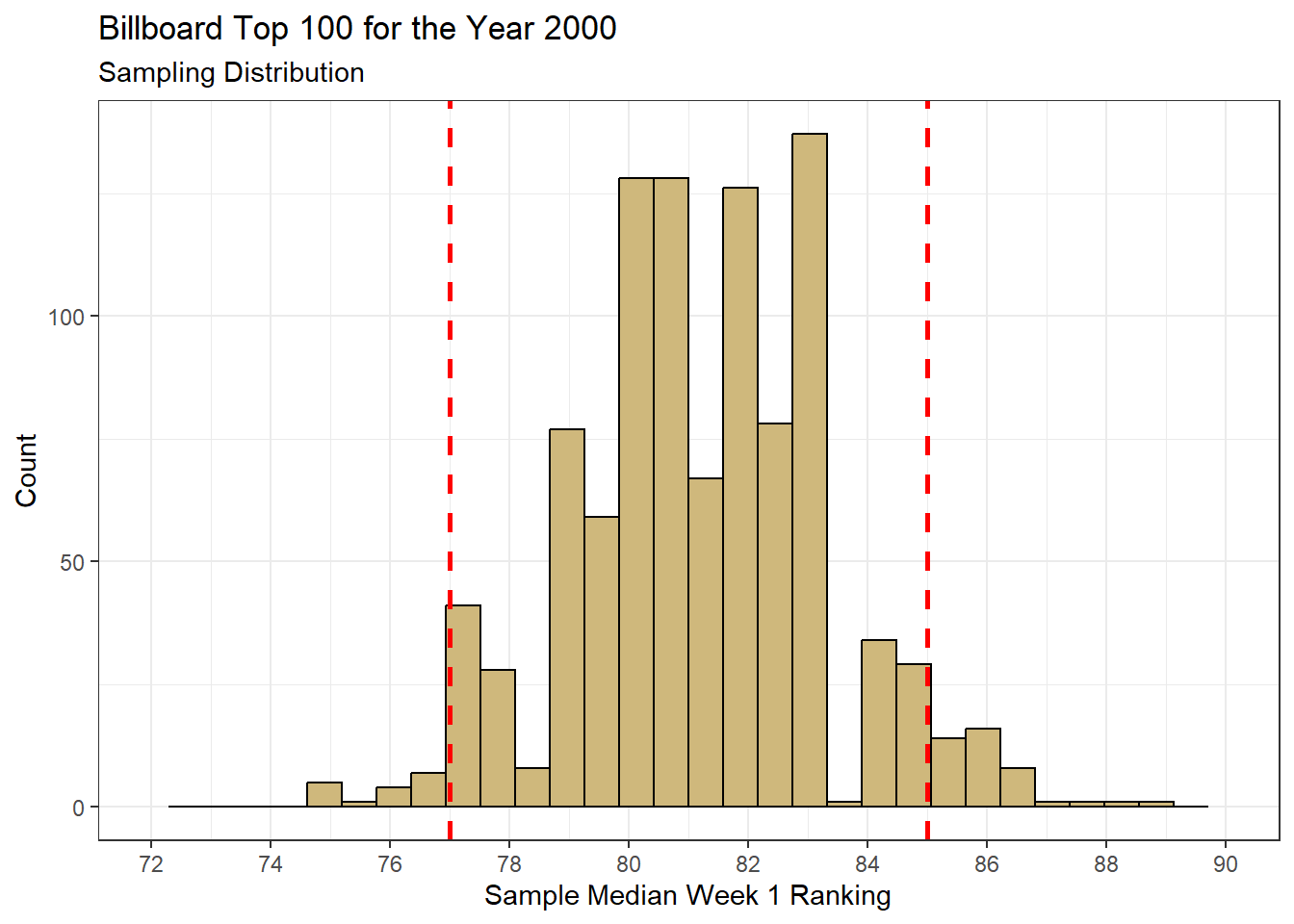
Figure 4.3: Bootstrap Resampling Distribution for Median Week 1 Ranking
The shape and range of the bootstrap sampling distribution in Figure 4.3 is similar to the true sampling distribution in Figure 4.2. However, we notice its center is shifted slightly to the right. This is because the resampled statistics are computed from an original sample with a median of 81.5. Remember, we have no idea in this case that the true median is 81. We simply know that the bootstrap distribution represents a plausible range of values for the true median.
The concept of “plausible range” of values finally brings us to the construction of a confidence interval. Based on the bootstrap distribution, we might expect the true median song ranking to be anywhere from 77 to 85. But the benefit of a confidence interval is in the assignment of a confidence level. How sure are we that a given range of estimated values captures the true value? Perhaps we want to be 90% confident that we capture the true median. We determine the bounds associated with 90% confidence using the quantiles of the bootstrap distribution. The dashed red lines in Figure 4.3 are set at the 0.05 and 0.95 quantiles. These values are equivalent to the 5th and 95th percentiles. They are computed using the quantile() function.
## 5%
## 77## 95%
## 85We see that 5% of the observed sample medians are less than 77 and 5% are greater than 85. The sample median rankings in between these quantiles represent the middle 90%. Consequently, we can say that we are 90% confident that the true median first-week ranking of songs is between 77 and 85 out of 100. This statement represents a confidence interval. As it turns out, the true median of 81 is in the interval but we will never know this with certainty. What we do know is that 90% of our resamples resulted in median rankings between the bounds of the confidence interval. Thus, it is likely we captured the true median ranking.
In practice, common confidence levels range between 90% and 99%. Higher confidence levels result in wider intervals for the same data. If we want to be more confident we captured the true parameter value, we have to provide a wider interval. Think of this relationship using the analogy of fishing. If we want to be more confident that we’ll catch a fish, then we have to cast a wider net. Regardless of the interval width or confidence level, the combination is superior to a single point estimate. After all, it is much easier to catch a fish with a net than with a spear!
We continue to demonstrate the use of confidence intervals for real-world problems in future sections. In all cases, we seek a plausible range of values for an unknown population parameter using sample statistics. For this introductory text in data science, we focus on computational approaches (i.e., bootstrap resampling) for constructing confidence intervals. More advanced or mathematically-focused texts traditionally construct confidence intervals using theoretical sampling distributions. However, the application of theory typically requires more restrictive technical conditions than those imposed by the computational methods presented here.
4.2.2 Population Proportion
Provided a sufficiently large random sample, we can construct confidence intervals for any population parameter. By far the most commonly investigated parameters are the proportion, mean, and slope. In this section, we conduct inference on a population proportion. Afterward, we pursue similar analyses for the mean of a population and slope of a regression line.
Proportions are frequently computed from the levels of a factor (i.e., grouped categorical variable). Imagine we gather a random sample of 100 dogs from kennels across our local area, along with their rabies vaccination status. In this case our factor has two levels: vaccinated and not vaccinated. We might be interested in the true proportion of dogs that have been vaccinated for rabies in our local area. We estimate the population proportion (\(p\)) based on the sample proportion (\(\hat{p}\)) among our 100 dogs. This is the essence of inferential analyses. We want to apply the proportion of vaccinated dogs in the sample to the entire population of dogs in the local area. Different samples of 100 dogs would likely result in different sample proportions. Consequently, we prefer to determine a range of plausible proportions within the population in the form of a confidence interval.
In this section, we return to the 5A Method for solving data-driven problems. We begin with a problem requiring a confidence interval for a single proportion. As usual, we leverage the tidyverse throughout the problem-solving process.
Ask a Question
The New York City (NYC) Department of Health and Mental Hygiene (DOHMH) maintains an open data site at the following link. The available data includes health inspections at restaurants throughout the city and indicators for any violations. When a restaurant suffers a “critical” violation it means inspectors discovered issues that are likely to result in food-borne illness among customers. Imagine you are considering a vacation in NYC and want to answer the following question: What proportion of restaurants in Manhattan are likely to make me sick?
A wide variety of people are likely concerned with the answer to this question. Locals and tourists alike should be informed of the risks associated with eating at Manhattan’s restaurants. In this case, we are specifically focused on the risk of food-borne illness. To be fair, someone could fall ill after eating at a restaurant due to a contagious customer or something else unrelated to health code violations. Our focus is solely on risks associated with critical health code violations. Thanks to the DOHMH’s transparency with their data, we have the capacity to answer this question.
Acquire the Data
The DOHMH website offers an API to access the results of all planned and completed health inspections. The site includes a wide variety of metadata explaining the meaning, structure, and limitations of the data tables. For example, only restaurants in an active status are included. Any permanently-closed restaurants are removed. Newly-registered restaurants that have not yet been inspected are indicated with an inspection date in the year 1900. Inspected restaurants include the inspection date and whether or not there was a violation. Multiple violations during the same inspection result in multiple rows in the table.
Let’s access the API and import inspection results specifically for the borough of Manhattan. We can filter the results of an API call using the query=list() option. We find the variable names (e.g., boro) to filter on using the site’s metadata. As described in Chapter 2.2.2, the httr and jsonlite packages ease the import of data from APIs.
#load libraries
library(httr)
library(jsonlite)
#request data from API
violations <- GET("https://data.cityofnewyork.us/resource/43nn-pn8j.json",
query=list(boro="Manhattan"))
#parse response from API
violations2 <- content(violations,"text")
#transform json to data frame
violations3 <- fromJSON(violations2)The final result of our query in violations3 is the 1,000 most recent records in the DOHMH database. It is common for APIs to limit the amount of returned data in order to prevent overloading servers. Although we could obtain additional data by conducting multiple queries, we have more than enough for our purposes. Next, we perform a variety of data wrangling tasks.
First we remove records for restaurants that have not yet been inspected. These restaurants have an inspection date of January 1, 1900 according to the DOHMH website. Since our statistic of interest is based on inspection results, we cannot include restaurants that have not been inspected. Another task is to limit the data to only the most recent inspection for each restaurant. Inspections from years past are not relevant to the current status of a restaurant, since conditions may have changed. After sorting and grouping, we extract the most recent inspection using the slice_head() function. Finally, we simplify the inspection results to a binary indicator of whether the inspectors found a critical violation.
#identify most recent restaurant inspections
inspections <- violations3 %>%
filter(inspection_date!="1900-01-01T00:00:00.000") %>%
select(camis,inspection_date,critical_flag) %>%
distinct() %>%
na.omit() %>%
arrange(camis,desc(inspection_date),critical_flag) %>%
group_by(camis) %>%
slice_head(n=1) %>%
ungroup() %>%
transmute(restaurant=camis,
date=as_date(inspection_date),
critical=ifelse(critical_flag=="Critical",1,0))
#review data structure
glimpse(inspections)## Rows: 564
## Columns: 3
## $ restaurant <chr> "40365166", "40365726", "40365942", "40368752", "40372971",…
## $ date <date> 2022-03-31, 2022-10-26, 2023-08-24, 2025-01-08, 2024-09-12…
## $ critical <dbl> 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0,…After wrangling, we are left with a sample of unique restaurants, the most recent inspection date, and whether inspectors found a critical violation. This cleaned and organized sample is ready for analysis.
Analyze the Data
The ultimate goal of our analysis is a confidence interval for the true proportion of Manhattan restaurants with a critical health violation. But we begin with a point estimate. Given that the critical violation variable is binary, we can compute the sample proportion using the mean() function.
## [1] 0.5342067Our sample statistic is \(\hat{p}=0.53\). This means 53% of the inspected restaurants in the sample have critical health code violations. That is disconcerting! However, this point estimate is based on a single sample. Depending on sampling variability, we might obtain higher or lower proportions in a different sample. This is why we prefer to provide a range of likely values along with a confidence level. Let’s generate multiple sample proportions using bootstrap resampling, as presented earlier in the chapter.
#initiate empty data frame
results_boot <- data.frame(prop=rep(NA,1000))
#resample 1000 times and save sample proportions
for(i in 1:1000){
set.seed(i)
results_boot$prop[i] <- mean(sample(x=inspections$critical,
size=nrow(inspections),
replace=TRUE))
}The previous code simulates 1,000 samples from the population of restaurants using resampling with replacement. The result is a vector of sample proportions we depict in a histogram.
#plot resampling distribution
ggplot(data=results_boot,aes(x=prop)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$prop,0.05),
color="red",linetype="dashed",linewidth=1) +
geom_vline(xintercept=quantile(results_boot$prop,0.95),
color="red",linetype="dashed",linewidth=1) +
labs(title="NYC Manhattan Restaurant Inspections",
subtitle="Sampling Distribution",
x="Proportion of Restaurants with Critical Violations",
y="Count",
caption="Source: NYC DOHMH") +
theme_bw()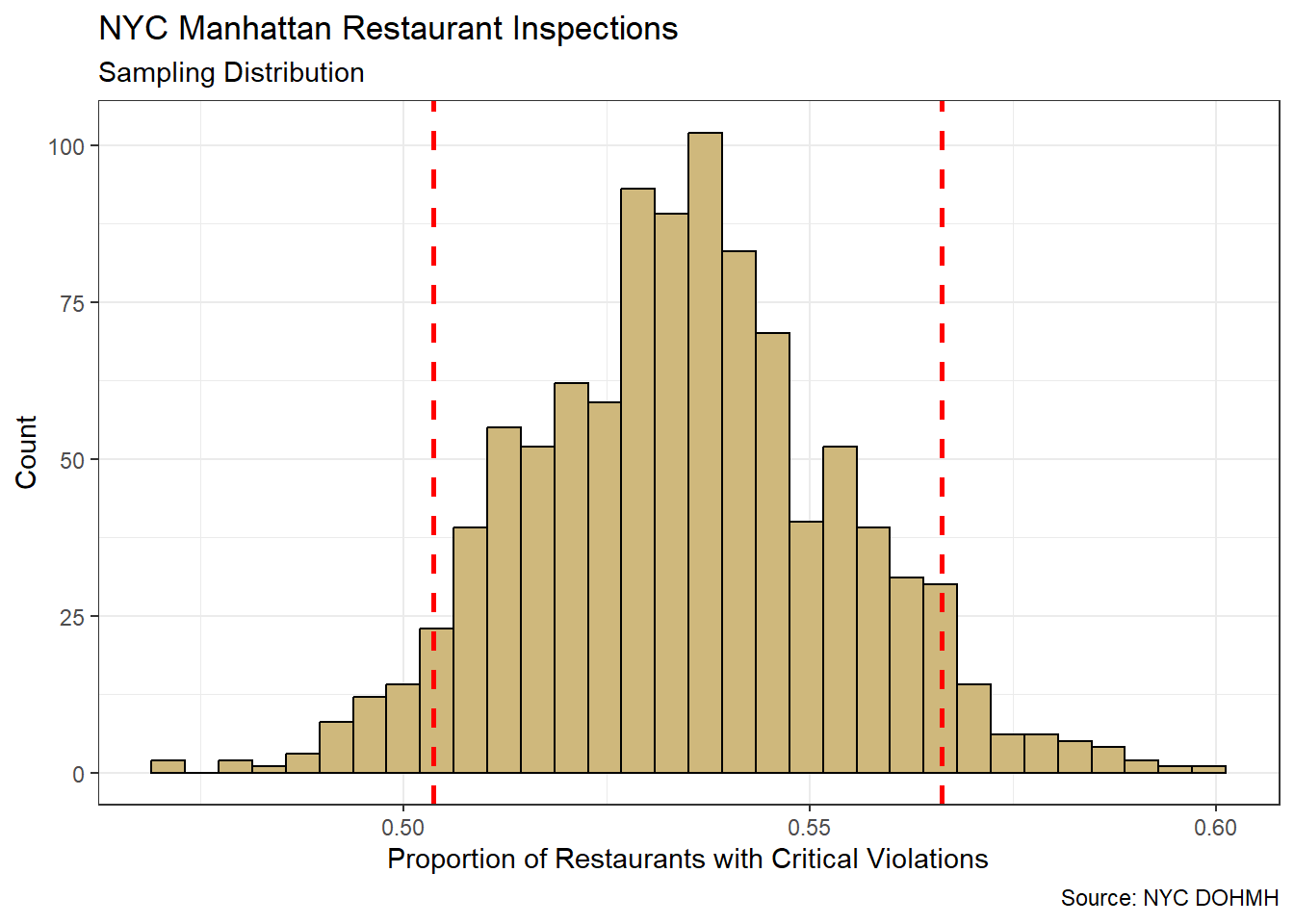
Figure 4.4: Bootstrap Resampling Distribution for Sample Proportion
The bootstrap resampling distribution in Figure 4.4 displays the range of sample proportions we might expect to observe with repeated sampling from the population. The symmetric, bell-shaped appearance of the distribution is not a coincidence. Mathematical theory tells us that the sampling distribution for a proportion follows the Normal distribution. However, our computational approach to confidence intervals does not require this assumption of a named distribution. Instead, we simply rely on the quantiles of the unnamed bootstrap distribution.
The quantile boundaries (dashed red lines) in Figure 4.4 depict the middle 90% of sample proportions. We compute these boundaries directly with the quantile() function.
## 5% 95%
## 0.503639 0.566230Based on this analysis, we are 90% confident that the true proportion of Manhattan restaurants with critical health code violations is between 0.504 and 0.566. In terms of notation, we write this as \(p \in (0.504,0.566)\). In other words, we are confident the population proportion is in this interval. If we require a greater level of confidence in our results, then we must accept a wider interval. Let’s construct a 95% confidence interval.
## 2.5% 97.5%
## 0.4978166 0.5720888As expected, this interval is wider. Specifically, we are 95% confident that the true proportion of Manhattan restaurants with critical health code violations is between 0.498 and 0.572. Often the appropriate confidence level is determined in collaboration with domain experts. With that in mind, we move to the advising step of the 5A Method.
Advise on Results
When presenting confidence intervals to domain experts, it is common to express them in terms of margin of error. Rather than listing the bounds of the interval, this presentation method provides the center and spread. For example, we might say we are 95% confident that the true proportion of Manhattan restaurants with critical health code violations is 0.535 plus or minus 0.037. The value of 0.037 acts as the margin of error for the point estimate. Splitting the interval in half like this is only appropriate when the sampling distribution is symmetric around its center. However, due to mathematical theory, the sampling distribution for the proportion will always be symmetric when the sample size is large.
A common mistake when interpreting the results of an inferential analysis is to describe the confidence level as a probability. It is not accurate, for example, to say there is a 95% probability the true proportion is between 0.498 and 0.572. This interpretation implies that the population proportion is a random value. That is not the case! Though unknown, the true proportion of violating restaurants is a fixed constant. There is no randomness involved. The randomness lies in our estimate of the confidence interval bounds, not in the true value. This is why we always use the word “confidence” rather than “probability” when presenting intervals.
In addition to proper interpretation, we should also be careful to describe the limitations of the results. Our entire analysis assumes that the most-recently-inspected restaurants are representative of the entire population of restaurants in Manhattan. In collaboration with domain experts, we might discover biases that challenge this assumption. Perhaps restaurants that have previous violations get inspected more frequently or with a higher priority. If this is the case, then our sample might be biased toward restaurants more likely to have a critical violation. On the other hand, we also know that the data excludes restaurants that have permanently closed. If a large number of these restaurants closed due to health code violations, then the remaining restaurants may be biased in the opposite direction. In practice, it can be difficult to obtain a perfectly unbiased sample. Regardless, it is important to identify and resolve issues of bias in our data.
The quality control of the data collection can also compromise our analysis. The DOHMH site states:
“Because this dataset is compiled from several large administrative data systems, it contains some illogical values that could be a result of data entry or transfer errors. Data may also be missing.”
Missing data and errors may or may not invalidate our conclusions. The impact largely depends on the magnitude of the issues and their prevalence with violating versus non-violating restaurants. We removed missing values during our data wrangling process, but it is difficult to identify errors without direct access to those who collected the data. Regardless, all such limitations should be revealed to stakeholders along with the results. Once all of the data issues are resolved we can answer the research question.
Answer the Question
Based on a large sample of recently-inspected restaurants in Manhattan it appears more likely than not that a customer is at risk of food-borne illness. We can say with 95% confidence that the proportion of restaurants with critical health code violations is between 0.498 and 0.572. Said another way, 53.5% of restaurants are likely to make you sick (margin of error 3.7%). Consequently, patrons may want to conduct more careful research on current health code status before selecting a restaurant.
Regarding the reproducibility of these results, the connection to the API ensures the most current data. When repeating the data acquisition and analysis presented here, there is no guarantee of obtaining exactly the same results. A different sample of inspections could result in different proportions and intervals. However, if the inspections included in our sample are representative of those we might expect in the future, then our results remain relevant.
4.2.3 Population Mean
In the previous section, we present confidence intervals for a population proportion. This approach lends itself well to conducting inference on categorical variables. Specifically, it facilitates the estimation of frequency within the levels of a factor. However, we also require methods for estimating numerical variables. Rather than frequency, we are often interested in the central tendancy of numerical variables. By far the most common measure of centrality is the arithmetic mean (i.e., the average). Hence we now demonstrate the estimation of a population mean (\(\mu\)) based on the sample mean (\(\hat{\mu}\)) and its margin of error.
In this section, we construct confidence intervals for a single population mean. However, we introduce a different type of interval compared to the previous section. Rather than two-sided confidence intervals, we present one-sided confidence bounds. The vast majority of the process for constructing intervals remains the same. But the formulation and interpretation of the analysis differs. We highlight these important differences throughout the section. We begin by loading the tidyverse and offering an exemplar research question.
Ask a Question
The Women’s National Basketball Association (WNBA) was founded in 1996 and currently consists of 12 professional teams. Each team plays a total of 40 games in a season and each game consists of four 10-minute quarters. As with any basketball league, the team that has the most points when times expires wins the game. Since a team’s points are comprised of individual players’ points, the scoring efficiency of each player on the court is critically important. By efficiency, we mean the number of points scored given the number of minutes on the court. On this note, imagine we are asked the following question: What is a lower bound for the average scoring efficiency of players in the WNBA?
While the Men’s NBA has historically received more attention, the WNBA recently witnessed its most-watched season in 21 years according to ESPN. As a result, the interest in answering our research question is likely on the rise. However, our question could benefit from greater specificity. Does “players” refer to anyone who has ever played in the WNBA or current players? What makes a lower bound “reasonable” in this context? For our purposes, we assume the interest is in current players and therefore recent seasons. In terms of the bound, we choose to focus on players who are afforded a reasonable opportunity to score, in terms of time on the court. Here we impose a minimum of 10 minutes per game, but this is easily adjusted. Without any such limit, an obvious and uninteresting lower bound is zero. Next we seek a source for our player data.
Acquire the Data
In almost all cases, we prefer to obtain our data directly from the primary source. The WNBA offers an API for player statistics, but rather than accessing it directly we leverage functions from the wehoop package. The library of available functions provides a more intuitive and efficient method for obtaining the desired data by scraping the Entertainment and Sports Programming Network (ESPN) website. After installing the package for the first time, we load the library and import the two most-recent seasons using the load_wnba_player_box() function.
#load wehoop library
library(wehoop)
#import 2022-2023 seasons
wnba <- load_wnba_player_box(seasons=c(2022,2023))The resulting data frame includes over 5,300 player-game combinations described by 57 variables. Most of the variables are not of interest for our current research question or those in subsequent sections. So, we wrangle the data to isolate the desired information.
#wrangle data
wnba2 <- wnba %>%
transmute(season,date=game_date,team=as.factor(team_name),
location=as.factor(home_away),player=athlete_display_name,
position=as.factor(athlete_position_name),
minutes,points,assists,rebounds,turnovers,fouls) %>%
na.omit() %>%
filter(minutes>=10)
#review data structure
glimpse(wnba2)## Rows: 3,828
## Columns: 12
## $ season <int> 2022, 2022, 2022, 2022, 2022, 2022, 2022, 2022, 2022, 2022, …
## $ date <date> 2022-09-18, 2022-09-18, 2022-09-18, 2022-09-18, 2022-09-18,…
## $ team <fct> Aces, Aces, Aces, Aces, Aces, Aces, Sun, Sun, Sun, Sun, Sun,…
## $ location <fct> away, away, away, away, away, away, home, home, home, home, …
## $ player <chr> "A'ja Wilson", "Kiah Stokes", "Chelsea Gray", "Kelsey Plum",…
## $ position <fct> Forward, Center, Guard, Guard, Guard, Guard, Forward, Forwar…
## $ minutes <dbl> 40, 27, 37, 33, 37, 22, 36, 40, 29, 36, 29, 18, 36, 24, 33, …
## $ points <int> 11, 2, 20, 15, 13, 17, 12, 11, 13, 17, 6, 11, 19, 2, 11, 17,…
## $ assists <int> 1, 0, 6, 3, 8, 0, 2, 11, 0, 1, 3, 1, 3, 0, 7, 6, 2, 1, 0, 5,…
## $ rebounds <int> 14, 5, 5, 1, 5, 2, 8, 10, 8, 6, 1, 0, 4, 7, 2, 6, 2, 0, 0, 6…
## $ turnovers <int> 1, 1, 2, 5, 1, 1, 2, 4, 1, 2, 0, 3, 0, 0, 4, 3, 2, 1, 1, 2, …
## $ fouls <int> 2, 3, 3, 2, 2, 2, 5, 1, 4, 3, 1, 3, 1, 3, 0, 1, 3, 1, 1, 1, …After reducing and renaming the variables of interest, eliminating observations with missing data, and filtering to isolate cases for which a player had at least 10 minutes on the court, we are left with a clean and sufficient data set. But does this data represent a random sample? After all, we extracted every player-game combo for two seasons and artificially imposed a 10-minute requirement for minutes played. Perhaps a more relevant question is whether this data is representative of the population of interest. Since we are interested in the scoring efficiency of current players who are afforded sufficient opportunity, in terms of minutes played, this sample is likely representative. With that said, we proceed to our analysis.
Analyze the Data
Our population parameter of interest is the true mean scoring efficiency of WNBA players. Scoring efficiency is computed by dividing points and minutes to obtain points-per-minute. Since we limit our observations to cases with at least 10 minutes of court time, we have no concern for division by zero. After adding this new variable, we depict the distribution of points-per-minute in a histogram.
#compute points-per-minute
wnba3 <- wnba2 %>%
mutate(ppm=points/minutes)
#display distribution of points-per-minute
ggplot(data=wnba3,aes(x=ppm)) +
geom_histogram(color="black",fill="#CFB87C",
boundary=0,closed="left",binwidth=0.05) +
geom_vline(xintercept=mean(wnba3$ppm),color="red",
linewidth=0.75) +
labs(title="WNBA Players (2022-2023 seasons)",
x="Points-per-Minute",
y="Count",
caption="Source: ESPN") +
scale_x_continuous(limits=c(0,1.5),breaks=seq(0,1.5,0.1)) +
theme_bw()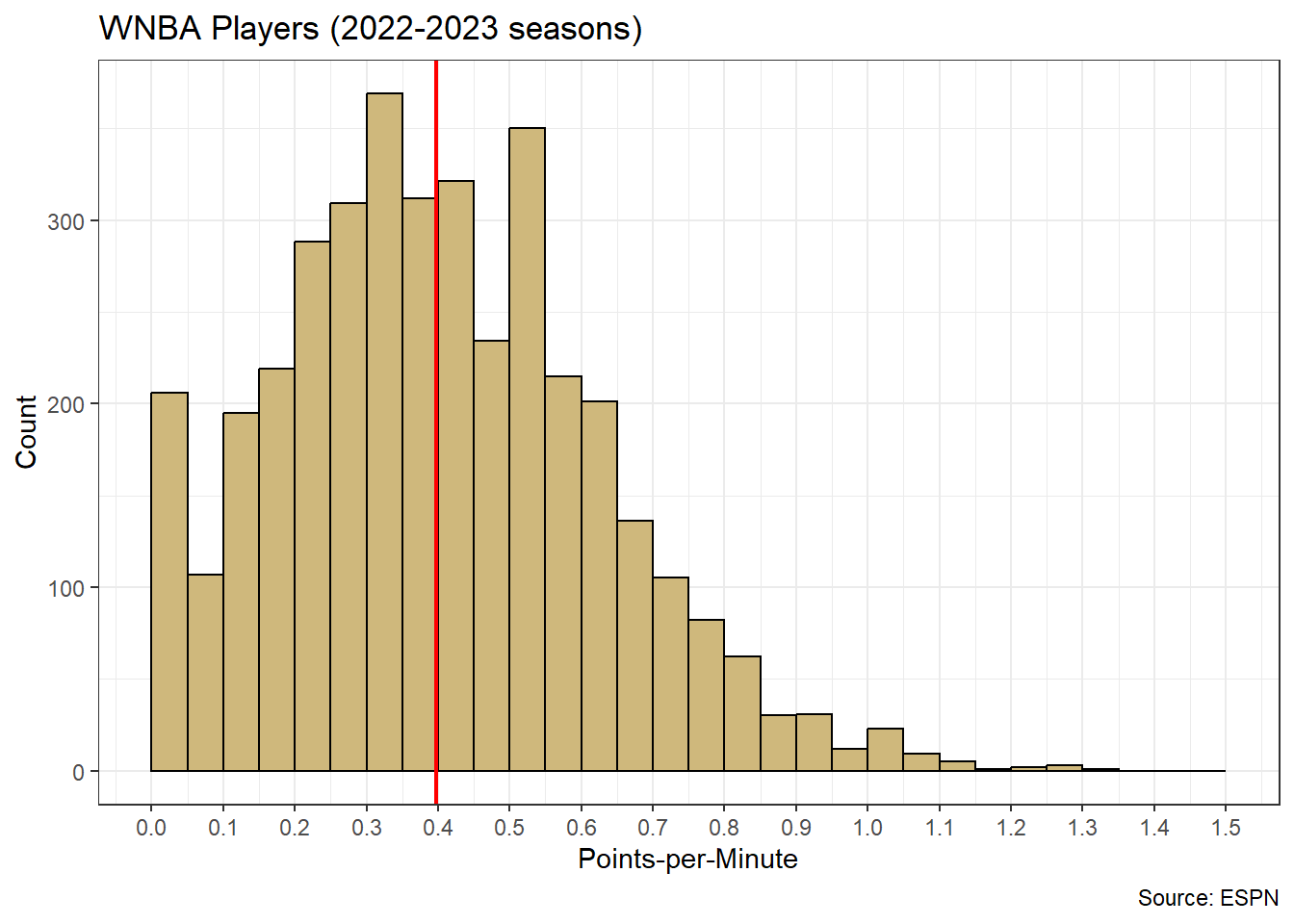
Figure 4.5: Distribution for Individual Player Points-per-Minute
Figure 4.5 displays the distribution of points-per-minute for individual players. We observe an obvious right skew, with most players around the sample mean (red line) of \(\hat{\mu}=0.4\) points-per-minute and a few players with efficiencies as high as 1.3 points-per-minute. Right-skewed distributions are not uncommon for variables with a natural minimum. In this case, it is impossible for a player to have a scoring efficiency below zero. Note, this is not a sampling distribution for average points-per-minute. To obtain that distribution we first conduct bootstrap resampling.
#initiate empty data frame
results_boot <- data.frame(avg=rep(NA,1000))
#resample 1000 times and save sample means
for(i in 1:1000){
set.seed(i)
results_boot$avg[i] <- mean(sample(x=wnba3$ppm,
size=nrow(wnba3),
replace=TRUE))
}
#view summary of sample means
summary(results_boot$avg)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.3854 0.3947 0.3972 0.3973 0.3999 0.4097The bootstrapped sample means vary between efficiencies of 0.385 and 0.410. So, while individual scoring efficiency may vary between 0 and 1.3, the average efficiency varies across a much smaller range. This reduction in variability is a very common phenomenon caused by averaging. Let’s view the resampled means in a histogram.
#plot resampling distribution
ggplot(data=results_boot,aes(x=avg)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$avg,0.05),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="WNBA Players (2022-2023 seasons)",
subtitle="Sampling Distribution",
x="Average Points-per-Minute",
y="Count",
caption="Source: ESPN") +
scale_x_continuous(limits=c(0.385,0.41),breaks=seq(0.385,0.41,0.005)) +
theme_bw()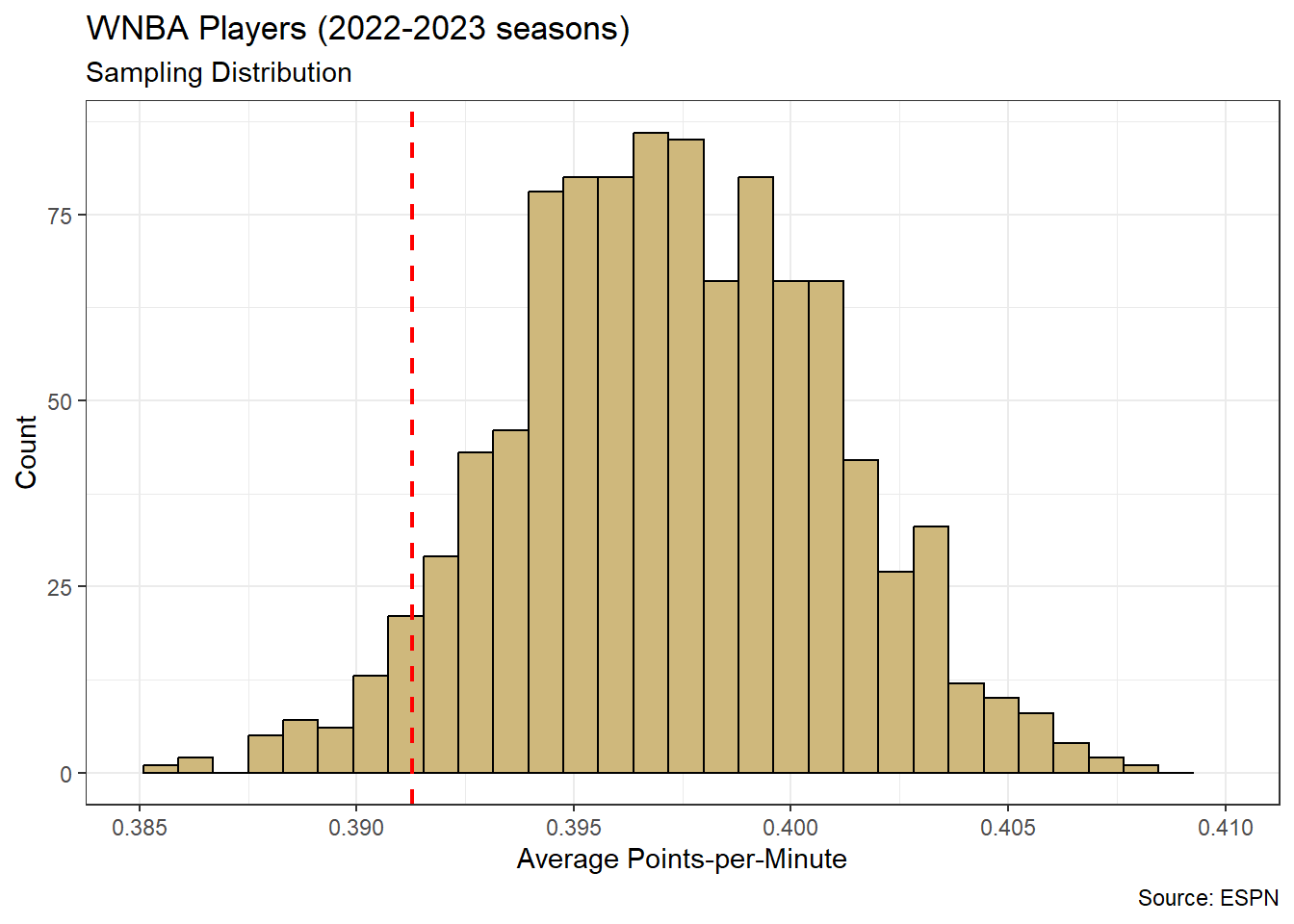
Figure 4.6: Distribution for Average Player Points-per-Minute
The sampling distribution for average points-per-minute appears relatively symmetric. Mathematical theory tells us that the sample mean follows the t-distribution, which is similar to the Normal distribution. However, we do not need to name the sampling distribution in order to compute a lower bound for the mean. The red dashed line in Figure 4.6 represents a 95% lower confidence bound. Of the 1,000 resampled means, 95% are greater than this threshold. We compute the bound directly using the quantile() function.
## 5%
## 0.3912825Thus, we are 95% confident that the true mean scoring efficiency for a WNBA player is at least 0.391 points-per-minute. In mathematical notation we would write \(\mu \in (0.391,\infty)\), because we are confident the population mean is in this interval. If we require greater confidence, then we must move the lower bound to the left. A smaller lower bound captures a larger range of values and permits greater confidence.
Advise on Results
When interpreting our confidence bound, it is important to distinguish between the performance of individual players and the average player. In Figure 4.5, we notice that it is possible for individual players to achieve scoring efficiencies as low as 0 points-per-minute. However, such values are nearly impossible for the average player in Figure 4.6. Not a single one of our hypothetical average players had an efficiency below 0.38, let alone 0. This helps speak to the use of the word “reasonable” in our research question. Although 0 is a valid lower bound for scoring efficiency, it is not informative regarding the average player. Some individual players will certainly have games with no points, even with at least 10 minutes on the court. But the average player will seldom perform worse than 0.391 points-per-minute.
In reference to the 10 minute time restriction, this assumption presents a great opportunity for collaboration with domain experts. Perhaps 10 minutes is too restrictive in the eyes of those who have a more nuanced understanding of the game of basketball. Coaches or managers may consider 5 minutes, for example, a “reasonable” opportunity to score. Data scientists should facilitate discussions regarding the costs and benefits of adjusting this restriction. If the time on the court is too low, then the data may be biased toward a scoring efficiency of zero. Does this truly reflect a player’s ability to score or their lack of opportunity? On the other hand, if the time limit is increased too high, then there may not be sufficient data in the sample. For example, only a little over 25% of the players in the sample were on the court for more than 30 minutes. Are we willing to ignore 75% of the data in order to impose this higher restriction? By collaborating effectively to answer these questions, data scientists and domain experts can identify the appropriate threshold. Assuming the current value of 10 minutes is acceptable, we are prepared to answer our research question.
Answer the Question
Based on a recent sample of over 3,800 player-game combinations, a reasonable lower bound for average scoring efficiency in the WNBA is 0.391 points-per-minute (95% confidence). This estimate is valid for players who are afforded the equivalent of one quarter (10 minutes) on the court. While it is possible for a given player to score zero points in a game, regardless of time on the court, the average player will seldom perform worse than our lower bound of 0.391 point-per-minute.
By providing all of the code for acquiring and analyzing the data, we have rendered our work reproducible for others. If stakeholders determine that more seasons should be considered, then they can easily be added in the API call. If domain experts determine that the time on the court restriction should be lowered to 5 minutes, then this can be quickly adjusted and the analysis re-run. The same is true for the confidence level, if there is a desire to change it. The value of reproducible analysis also lies in the capacity of others to check our work and expand on it. While some research in industry must understandably protect proprietary data and/or techniques, we should always strive for transparency whenever possible.
4.2.4 Population Slope
So far, we have discussed statistical inference for population proportions and means. These two parameter types are by far the most common summaries of categorical and numerical variables. However, we can pursue inference for any population parameter of interest using the computational approaches demonstrated here. Often we are interested in estimating the values of parameters within a statistical model. For example, in Chapter 3.3.2 we introduced the linear regression model in Equation (4.1).
\[\begin{equation} y = \beta_0+\beta_1 x \tag{4.1} \end{equation}\]
If a variable \(y\) is linearly associated with another variable \(x\), then the slope parameter \(\beta_1\) describes the direction and size of the effect. From the standpoint of inferential statistics, \(\beta_1\) is a population parameter. It represents the true association between the variables \(y\) and \(x\) in the population. Just as with any parameter, we estimate the true value of \(\beta_1\) based on a statistic computed from a random sample. In order to fit a linear regression model to sample data, we employ the least squares method and produce a point estimate denoted \(\hat{\beta}_1\). This sample statistic represents the average change in \(y\) we expect to observe when there is a one unit increase in \(x\). But, as always, we prefer a plausible range of values for our parameter rather than a single point estimate. Thus, in this section we present methods for constructing confidence intervals for slope parameters in the context of an example.
Ask a Question
In Chapter 3.3.2, we explore linear association between numerical variables using sample data from the Palmer Station Long Term Ecological Research (LTER) Program. Recall, the program studies various penguin species on the Palmer Archipelago in Antarctica. Based on visual evidence, we identify a linear association between a penguin’s body mass and its flipper length. Given the exploratory focus, we limit our insights to the observed data. If we wish to extend those insights to the entire population of Palmer penguins, then we require more formal inferential techniques. Hence, we ask the following question: What is the association between body mass and flipper length for all penguins on the Palmer Archipelago?
In part, we already have an answer to this question. We computed a point estimate for the association between body mass and flipper length in the previous chapter. However, we have no idea of the precision around that estimate. There could be a great deal of variability in the association from one penguin to the next. Thus, the range of plausible slope values remains unanswered.
Acquire the Data
We have access to a sample of body measurements for Palmer penguins in the palmerpenguins package. We import and wrangle the sample data below.
#load palmerpenguins library
library(palmerpenguins)
#import penguin data
data(penguins)
#wrangle penguin data
penguins2 <- penguins %>%
select(flipper_length_mm,body_mass_g) %>%
na.omit()
#review data structure
glimpse(penguins2)## Rows: 342
## Columns: 2
## $ flipper_length_mm <int> 181, 186, 195, 193, 190, 181, 195, 193, 190, 186, 18…
## $ body_mass_g <int> 3750, 3800, 3250, 3450, 3650, 3625, 4675, 3475, 4250…Our sample consists of the flipper length (in millimeters) and body mass (in grams) for 342 different penguins. From previous exploration, we know the sample consists of three different penguin species. However, our research question does not indicate an interest in distinguishing species. Thus, we pursue our analysis independent of this factor.
Analyze the Data
Prior to computing a point estimate or constructing a confidence interval for our slope parameter, we display the linear association between our numerical variables in a scatter plot.
#create scatter plot
ggplot(data=penguins2,aes(x=flipper_length_mm,y=body_mass_g)) +
geom_point() +
geom_smooth(method="lm",formula=y~x,se=FALSE) +
labs(title="Palmer Penguin Measurements",
x="Flipper Length (mm)",
y="Body Mass (g)",
caption="Source: Palmer Station LTER Program") +
theme_bw()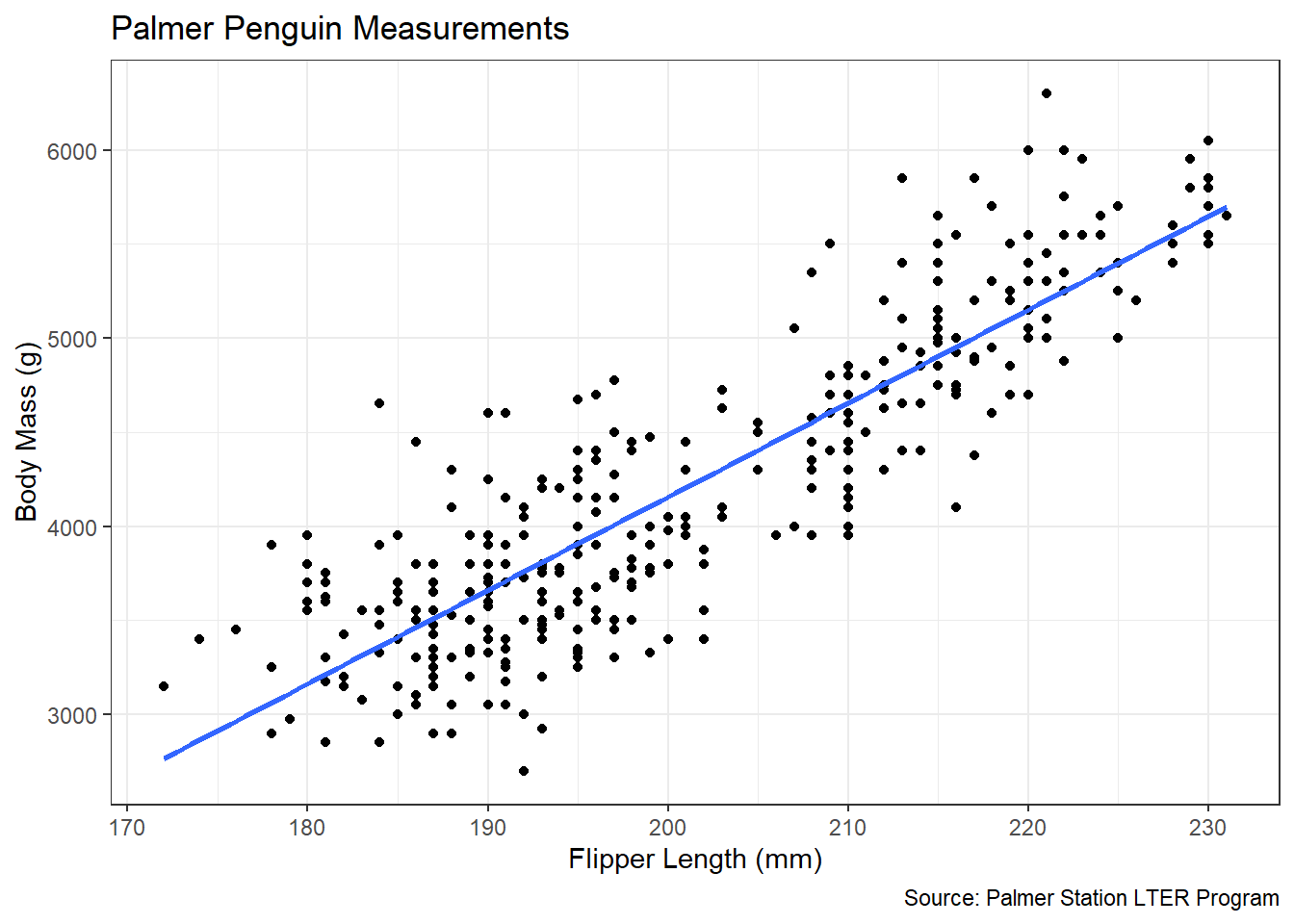
Figure 4.7: Linear Association between Flipper Length and Body Mass
Figure 4.7 suggests a strong, positive, linear association between a penguin’s flipper length and its body mass. This relationship makes intuitive sense, because we would expect a penguin with longer flippers to be larger in general and thus weigh more. The blue line in the scatter plot represents the best-fit line resulting from the least squares method. The focus of our analysis is the true slope (\(\beta_1\)) of this line. Keep in mind, the observed slope in the scatter plot represents a point estimate (\(\hat{\beta}_1\)) based on the sample data. Our interest is in using this estimate to make inferences about the slope for the entire population of penguins. To begin, we need the numerical value for the estimated slope.
#fit simple linear regression
model <- lm(body_mass_g~flipper_length_mm,data=penguins2)
#extract estimated coefficients
coefficients(summary(model))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5780.83136 305.814504 -18.90306 5.587301e-55
## flipper_length_mm 49.68557 1.518404 32.72223 4.370681e-107In the previous code, we fit a simple linear regression model using the lm() function. We then extract the estimated coefficients \(\hat{\beta}_0\) and \(\hat{\beta}_1\) from the summary output. The majority of the summary output is beyond the scope of this text, so we limit our focus to the Estimate column. The values in this column indicate an estimated intercept of \(\hat{\beta}_0=-5780.83\) and an estimated slope of \(\hat{\beta}_1=49.69\). Since our current interest is the slope, we isolate this value in the second row and first column of the table.
## [1] 49.68557For every one millimeter increase in flipper length, we expect a 49.69 gram increase in average body mass. But, as with proportions and means, this represents a point estimate of the slope based on a single sample. Were we to obtain a new sample of penguin measurements, the estimated slope would likely be different. Thus, we need a sampling distribution for the estimated slope to determine the range of plausible values. We once again accomplish this with bootstrap resampling. However, we must be careful to resample both flipper length and body mass for a given penguin. Otherwise, we cannot fit a simple linear regression model and extract the estimated slope. We use the sample_n() function to ensure both columns of our data frame are included in the resamples.
#initiate empty data frame
results_boot <- data.frame(beta=rep(NA,1000))
#resample 1000 times and save sample slopes
for(i in 1:1000){
set.seed(i)
penguins_i <- sample_n(penguins2,size=nrow(penguins2),replace=TRUE)
model_i <- lm(body_mass_g~flipper_length_mm,data=penguins_i)
results_boot$beta[i] <- coefficients(summary(model_i))[2,1]
}The thousand bootstrapped resamples result in a variety of estimated slopes that associate body mass with flipper length. Let’s view the resampled slopes in a histogram.
#plot resampling distribution
ggplot(data=results_boot,aes(x=beta)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$beta,0.025),
color="red",linetype="dashed",linewidth=0.75) +
geom_vline(xintercept=quantile(results_boot$beta,0.975),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="Palmer Penguin Measurements",
subtitle="Sampling Distribution",
x="Estimated Slope",
y="Count",
caption="Source: Palmer Station LTER Program") +
theme_bw()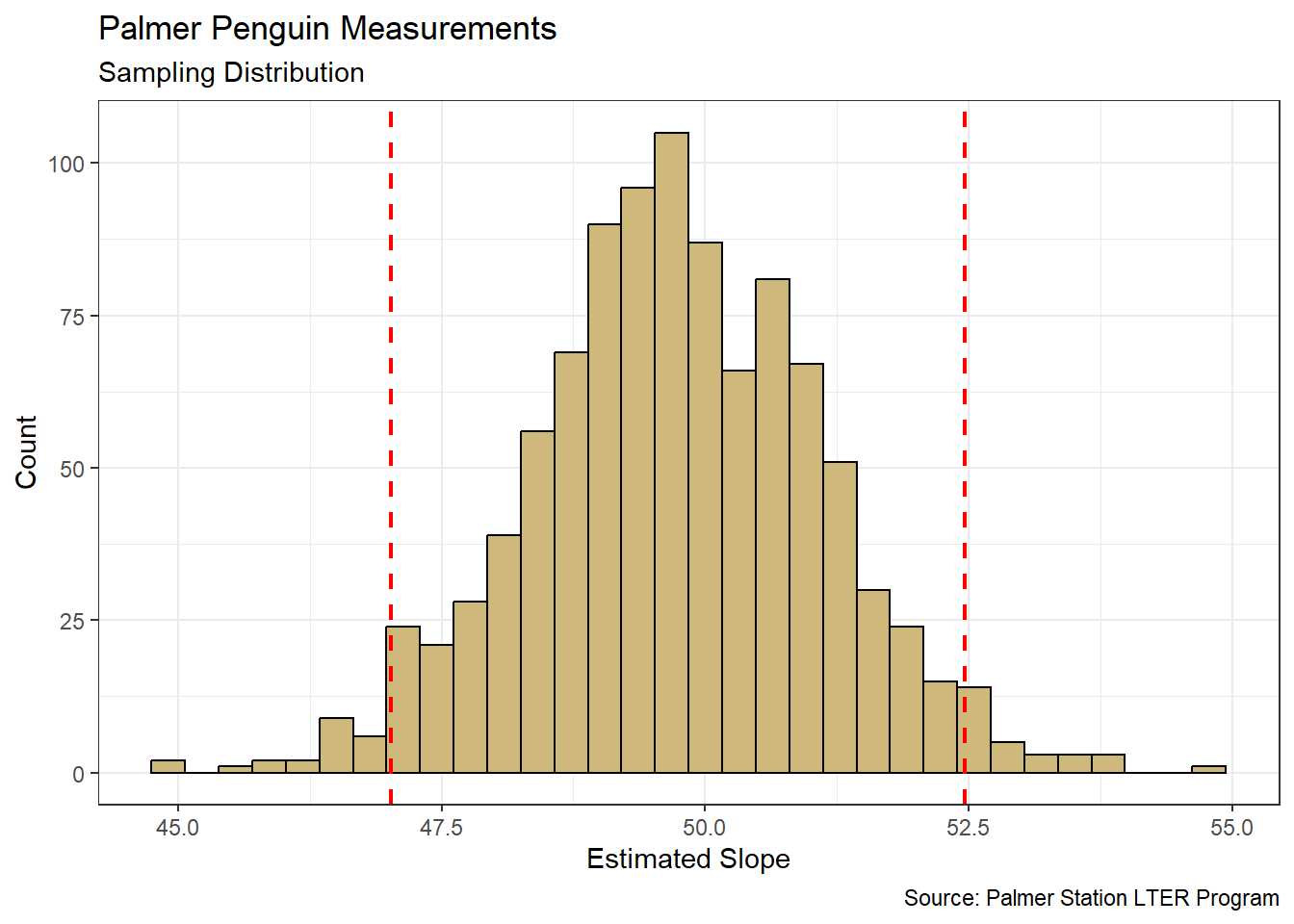
Figure 4.8: Distribution for average increase in Body Mass per unit increase in Flipper Length
Based on the sampling distribution in Figure 4.8, it appears we might observe slopes anywhere between 45 and 55 grams per millimeter. Similar to the sample mean, theory indicates that the sample slope follows the symmetric t-distribution. But that assumption is not required here. A plausible range of values is represented by the bounds (dashed red lines) of a 95% confidence interval. We compute these bounds directly using the quantile() function.
## 2.5% 97.5%
## 47.01807 52.46620We are 95% confident that the true slope parameter that associates body mass with flipper length is between 47.02 and 52.47 g/mm (i.e., \(\beta_1 \in (47.02,52.47)\)). Said another way, for every one millimeter increase in flipper length we are 95% confident that the average body mass increases by between 47.02 and 52.47 grams.
Advise on Results
When interpreting these results for stakeholders, we must be careful to identify the population to which we refer. The sample data only includes three species of penguin on the Palmer Archipelago.
## Adelie Chinstrap Gentoo
## 152 68 124We can confidently state that our estimated association between body mass and flipper length applies to Adelie, Chinstrap, and Gentoo penguins. But if other species of penguin exist on the Palmer Archipelago, we would not want to extrapolate our results to those species. It’s possible that the association between body mass and flipper length varies dramatically for other species, so we should not assume that our estimate applies universally.
An important value that is not included in our confidence interval is zero. If zero was in our interval, then it would be plausible that there is no association between body mass and flipper length. In other words, body mass and flipper length would be independent. Such results can be challenging to convey to a broad audience when a point estimate suggests a non-zero slope. Imagine for a moment that our original point estimate for the slope was 3 g/mm, but the confidence interval was -1 to 7 g/mm. The point estimate indicates a positive association between body mass and flipper length, but the confidence interval suggests there could be no association at all. In such cases, we must explain that the positive association in the original sample is simply due to the randomness of sampling. The evidence of an association in the sample is not strong enough to believe that it exists in the entire population.
Answer the Question
Based on a sample of 342 penguins from the Palmer Archipelago, there appears to be a strong, positive, linear association between body mass and flipper length. Specifically, we can say with 95% confidence that the average increase in body mass for a one millimeter increase in flipper length is between 47.02 and 52.47 grams. While these results should only be applied to Adelie, Chinstrap, and Gentoo penguins, it makes intuitive sense that penguins with longer flippers are larger in general and thus weigh more.
The preceding sections presented methods for computing a plausible range of values for a single population parameter. However, we are sometimes interested in the difference between two population parameters. Given sample data for two independent populations, we can construct confidence intervals for the difference in parameters using the same bootstrapping approach. We demonstrate such confidence intervals in the next section.
4.2.5 Two Populations
Another common method of inference regards the difference between two population parameters. Returning to the kennel example, imagine we are interested in how the proportion of vaccinated dogs in our local area compares to that of a neighboring city. In this case there are two distinct populations of dogs: our local area and the neighboring area. Consequently, there are two parameters of interest: the true proportion of vaccinated dogs in our area (\(p_1\)) and the true proportion in the neighboring area (\(p_2\)). We can estimate the difference between these two parameters (\(p_1-p_2\)) by building a confidence interval via bootstrap resampling.
Given we are interested in two different populations, we require two independent samples. We then resample (with replacement) from each sample, compute separate statistics, and finally calculate a difference in statistics (\(\hat{p}_1-\hat{p}_2\)). By repeating this bootstrapping process, we obtain a sampling distribution for the difference. Differences in proportions or means are the most common, but we can compare any statistic we choose. In this section, we demonstrate a difference in proportions using the New York City health inspection data.
Ask a Question
The New York City (NYC) Department of Health and Mental Hygiene (DOHMH) website offers data on all five boroughs in the city. In this context, we might consider all active restaurants within a borough as a population. Thus, our problem includes five populations from which we obtain a sample of restaurant inspections. Using these samples, we compare the proportion of restaurants with critical health code violations for two different boroughs. Suppose we ask the following question: What is the difference in the proportion of restaurants likely to make me sick in the Bronx versus Manhattan?
Given the focus on the physical health of patrons, we should pause to consider the potential ethical implications of answering this question. On the one hand, answering this question could potentially prevent patrons from suffering food-borne illness at NYC restaurants. On the other hand, if there is a significant difference, then there could be financial impacts for owners of non-violating restaurants in the “worse” borough. Patrons might choose to avoid all restaurants in a certain borough if our analysis suggests a higher proportion. Is this fair to those business owners? Do the health benefits outweigh the financial costs? These are challenging questions that should be considered prior to acquiring the data.
Acquire the Data
We acquire the data for both boroughs using the same methodology as in Chapter 4.2.2. The only difference is that we execute two separate API calls, one for each borough. Then, we combine the two data frames into one and perform the same wrangling tasks to obtain only the most recent inspections for each restaurant. For convenience, we have completed all of these steps ahead of time and saved the results in a file called restaurants.csv. This file actually includes data for all five boroughs, but we filter on the two boroughs of interest.
#import and filter inspection data
inspections <- read_csv("restaurants.csv") %>%
filter(borough %in% c("Manhattan","Bronx"))
#review data structure
glimpse(inspections)## Rows: 1,414
## Columns: 4
## $ restaurant <dbl> 30075445, 40364296, 40364443, 40364956, 40365726, 40365942,…
## $ borough <chr> "Bronx", "Bronx", "Manhattan", "Bronx", "Manhattan", "Manha…
## $ date <date> 2023-08-01, 2022-01-03, 2022-08-08, 2022-05-02, 2022-10-26…
## $ critical <dbl> 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0,…After all of our data wrangling tasks, we are left with inspection records for 1,414 restaurants across the two boroughs. We now have a clean, organized sample of restaurant inspections to support our analysis.
Analyze the Data
The ultimate goal of our inferential analysis is to construct a confidence interval for the difference in proportions. Prior to inference, we often conduct a brief exploratory analysis. Let’s compute the sample proportion of violating restaurants in each borough.
#compute sample statistics
inspections %>%
group_by(borough) %>%
summarize(count=n(),
prop=mean(critical)) %>%
ungroup()## # A tibble: 2 × 3
## borough count prop
## <chr> <int> <dbl>
## 1 Bronx 727 0.583
## 2 Manhattan 687 0.534Based on the sample, 58% of restaurants in the Bronx have critical violations (\(\hat{p}_1=0.58\)). This is true for only 53% of the restaurants in Manhattan (\(\hat{p}_2=0.53\)). So, we might be inclined to believe that there is a 5 percentage-point difference between the two boroughs. But we must resist drawing conclusions based purely on a single point estimate. The benefit of a confidence interval is the consideration for the variability in results across multiple samples and multiple point estimates. In order to obtain a distribution of point estimates (i.e., differences in proportions) we employ bootstrap resampling.
#initiate empty vector
results_boot <- data.frame(diff=rep(NA,1000))
#extract samples for each borough
manhat <- inspections %>%
filter(borough=="Manhattan") %>%
pull(critical)
bronx <- inspections %>%
filter(borough=="Bronx") %>%
pull(critical)
#repeat bootstrapping process 1000 times
for(i in 1:1000){
set.seed(i)
manhat_prop <- mean(sample(x=manhat,
size=length(manhat),
replace=TRUE))
bronx_prop <- mean(sample(x=bronx,
size=length(bronx),
replace=TRUE))
results_boot$diff[i] <- bronx_prop-manhat_prop
}
#review data structure
glimpse(results_boot)## Rows: 1,000
## Columns: 1
## $ diff <dbl> 0.09949164, 0.03954358, 0.01334270, 0.02314551, 0.03567131, 0.014…As usual, we begin the bootstrapping process by defining an empty vector to hold our statistics. However, we include a new step to account for the two different populations. Using the pull() function within a dplyr pipeline, we convert the violation column for each borough into a vector. Then, within the for loop, we resample from each vector with replacement and calculate the proportion of violations. Finally, we compute the difference between boroughs and save the result in our empty vector.
Even in the first few bootstrap results, we see a variety of differences between the boroughs ranging from 1 to 10 percentage-points. We listed the Bronx first in the difference, so positive values indicate a higher proportion in the Bronx. In Figure 4.9, we depict the distribution of all the differences. The dashed red lines represent the bounds of a 95% confidence interval.
#plot sampling distribution and bounds
ggplot(data=results_boot,aes(x=diff)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$diff,0.025),
color="red",linewidth=1,linetype="dashed") +
geom_vline(xintercept=quantile(results_boot$diff,0.975),
color="red",linewidth=1,linetype="dashed") +
labs(title="NYC Restaurant Inspections (Bronx versus Manhattan)",
subtitle="Sampling Distribution",
x="Difference in Proportion of Violating Restaurants",
y="Count",
caption="Source: NYC DOHMH") +
theme_bw()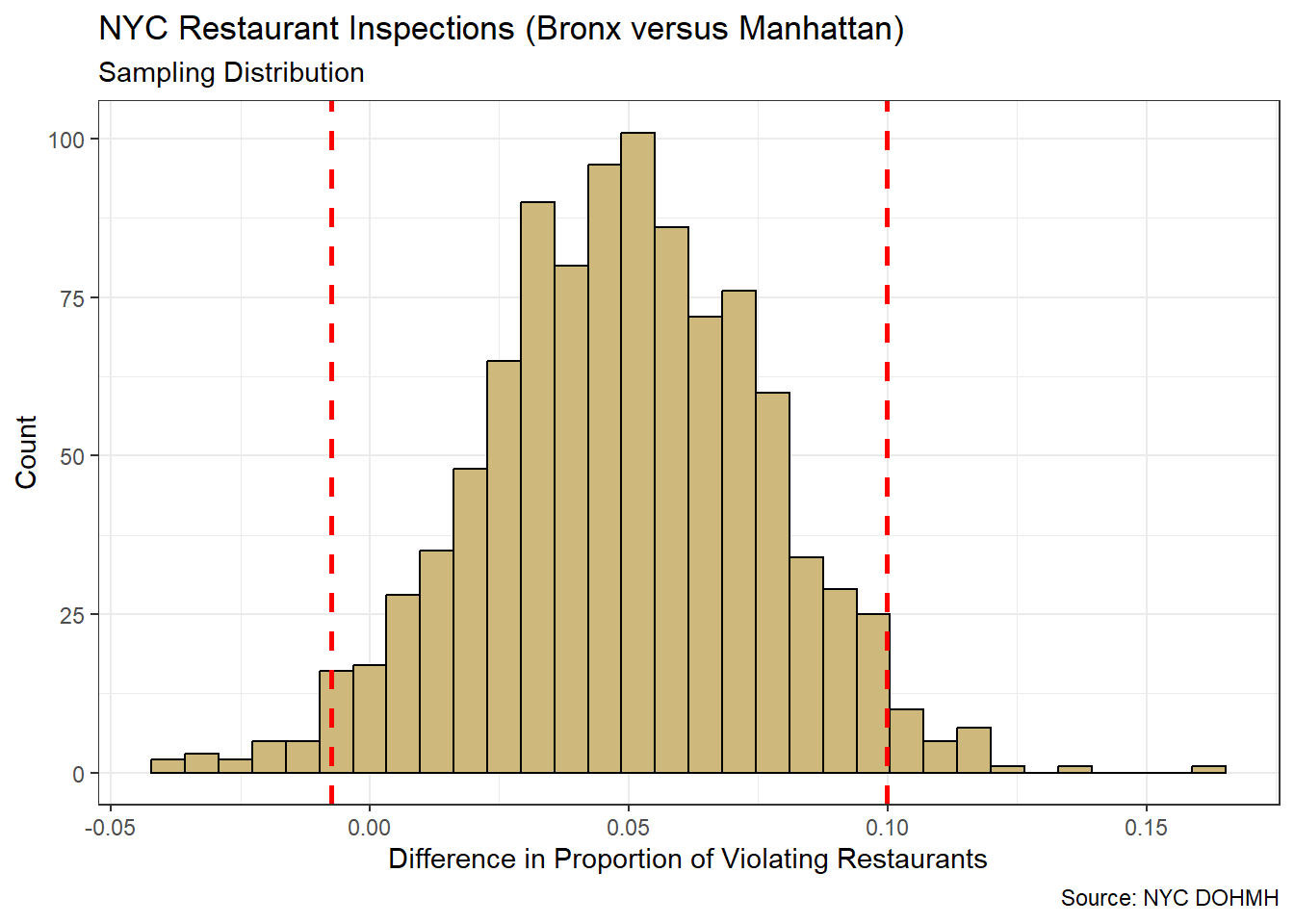
Figure 4.9: Bootstrap Sampling Distribution for Difference in Proportions
The majority of differences depicted in the sampling distribution are positive. A positive difference suggests the Bronx has a higher proportion of violating restaurants than Manhattan. However, there are some negative differences as well. In fact, some of them are within the 95% confidence interval.
## 2.5% 97.5%
## -0.007452212 0.099830013Based on the quantiles of the sampling distribution, we are 95% confident that the difference in true proportions between the Bronx and Manhattan is between -0.007 and +0.100. In other words, we are confident that \(p_1-p_2 \in (-0.007,0.100)\). Of critical importance is the fact that zero is in the interval. A value of zero suggests there is no difference between the two boroughs. So, even though the majority of our resamples suggest the Bronx is “worse” in terms of restaurants, we cannot rule out the possibility that Manhattan is just as bad.
Advise on Results
When conducting inference, it is important to always solicit the desired confidence level from the stakeholders before initiating the analysis. This is a matter of ethics in the scientific process. In certain cases, changing the confidence level can change the answer to the question. For example, if a particular stakeholder was intent on making the Bronx look worse, then they could simply lower the confidence level to 90%.
## 5% 95%
## 0.003296933 0.093925506At the 90% confidence level, zero is no longer in the interval. Now a stakeholder could claim that the proportion of violating restaurants in the Bronx appears to be higher. By contrast, if a different stakeholder was adamant that the boroughs are the same, then they could strengthen their argument by raising the confidence level to 99%.
## 0.5% 99.5%
## -0.02727474 0.11744549At the 99% level, zero is even further from the boundary of the interval. Such gaming of the process to support a preconceived notion is unethical. Stakeholders and data scientists should carefully collaborate prior to the analysis in order to select the appropriate level of confidence in the results. Afterward, the results speak for themselves. They should not be changed to accommodate a desired outcome.
Ethical concerns aside, the fact that our conclusion changes when the confidence level changes is troublesome. We prefer our analytic results to be robust to reasonable changes in confidence level. If a difference of zero were in the interval, regardless of confidence level, then we could feel secure that the boroughs are likely the same. Similarly, if zero was consistently outside (below) the interval, then we could be convinced the Bronx is worse. The variability in results weakens our conclusions. Still, we should prefer an ethical yet weak answer to our research questions over unethical answers of any strength.
Answer the Question
Based on a sample of hundreds of recent health code inspections, we find no strong evidence for a difference in critical violations between Bronx and Manhattan restaurants. Within the observed inspections, the Bronx did witness a higher proportion of violations by 5 percentage-points. However, the margin of error for the difference is large enough to include zero (at the 95% level). Thus, it is entirely plausible that there is truly no difference in the proportion of violators across the two populations of restaurants. That said, both boroughs exhibit a disturbingly-high proportion of restaurants with critical health code violations. In either case, it appears more likely than not that a restaurant will put us at risk of food-borne illness.
Though we avoided the ethical concern of labeling the Bronx as “worse” than Manhattan, there is still the matter of both boroughs receiving a high proportion of violations. Might our results discourage tourists from eating at restaurants in either borough? Could this lead to negative financial repercussions for all restaurants, including those that do not have violations? The answer to these questions could very well be yes. But are these impacts outweighed by protecting patrons from food-borne illness? Again, the answer could be yes. Ideally, the efforts of the NYC DOHMH to make these inspections public would encourage restaurants in all NYC boroughs to improve health code conditions and offer patrons a safer environment.
4.2.6 Many Populations
TBD
Answer the Question
Throughout the sections of Chapter 4.2, we describe methods for constructing an interval of likely values for an unknown population parameter. However, we might also like to evaluate the plausibility of a particular value for a parameter. Perhaps someone claims a specific value and we wish to assess whether the claim is reasonable. Such assessments are known as hypothesis tests.
4.3 Hypothesis Tests
Confidence intervals provide a range of likely values for a population parameter. However, for some problems we already have a claimed value for the parameter. We can directly evaluate the plausibility of such claims using a method known as hypothesis testing. Hypothesis testing provides a repeatable process for evaluating the plausibility of a claim regarding one or more population parameters. Given it is an inferential approach, we employ sample data as our evidence for the assessment of a claim regarding the population. There are six steps to any hypothesis test.
- Formulate the hypotheses
- Choose a significance level
- Calculate a test statistic
- Determine the null distribution
- Compute a p-value
- Choose the best hypothesis
We demonstrate each of these steps for multiple parameters throughout the section using case studies and the 5A Method. However, we first establish some intuition regarding the terminology of hypothesis testing and the required analytic techniques. Just as confidence intervals largely rely on estimating a sampling distribution, hypothesis tests leverage what is known as a null distribution.
4.3.1 Null Distributions
The term “null” is used repeatedly throughout the hypothesis testing process. In general, null implies no value or lack of existence. But a more useful synonym in the context of hypothesis testing is to think of null as the “default” state. In other words, the null is what we assume to be true before we conduct the test. Thus, the null value for a population parameter is the assumed value prior to the test. Similarly, the null distribution represents the range of values we might expect to observe for a sample statistic if the population parameter is equal to the null value. We first describe the concept of the null in a non-technical context, and then introduce the technical tools for statistical inference.
Legal Hypothesis Test
In the United States, a trial by jury is a form of hypothesis test. Suppose there is a massive string of bank robberies and a shady character named Jane Smith is arrested as the mastermind. Jane pleads not guilty and will be tried by a jury of her peers. Let’s explore how Jane’s trial is conducted as a hypothesis test.
Every test consists of two possible hypotheses. First, the null hypothesis for any trial in the US court system is that the defendant is innocent of the crime. That is the default condition, because if there was no trial we would have to assume that Jane is innocent. The purpose of the trial is to look for evidence of Jane’s guilt. Thus, the alternate hypothesis is that Jane is not innocent (guilty). The court will never been able to 100% prove either guilt or innocence. However, if the evidence of guilt is strong enough, then the court will reject the assumption of innocence.
Now the court must decide what strength of evidence is “strong enough” to reject the assumption of innocence. The required strength of evidence depends on the severity of the crime in question. For the highest level of crimes, the court requires evidence that suggests guilt “beyond a shadow of a doubt.” This threshold for the strength of evidence is known as the level of significance for the test. It is critically important that this threshold is selected before conducting the test. Otherwise, we might be accused of manipulating the threshold to achieve a desired outcome.
Next, the prosecution must present all the evidence that speaks to Jane’s guilt. The evidence of the alternate hypothesis is known as the test statistic. Every piece of evidence provided by the prosecution is an observation in the data that will be aggregated by the jury into a single metric that evaluates Jane’s guilt. This single metric must be tailored to the parameters associated with the hypotheses. In other words, the manner in which the jury aggregates the evidence in a robbery trial might be different than if it were a murder trial. Similarly, the calculation of the test statistic depends on the population parameters of interest in the hypotheses.
Then, Jane’s defense team tries to present a convincing story and timeline of events under the assumption of her innocence. The defense’s case acts as the null distribution for the trial. In other words, the defense is trying to show the jury that circumstantial evidence can just coincidentally occur even if Jane is innocent. For example, the defense might explain that Jane is on a security video from one of the banks because she actually has an account there. Or they might explain that Jane just purchased a fancy new car because she inherited money from a family member. The defense wants to show the jury that all of the events and circumstances presented by the prosecution could happen to an innocent person.
Once the prosecution and defense have rested their respective cases, the jury must deliberate. The deliberation is focused on comparing the prosecution’s case to the defense’s case. The baseline for the jury is to consider all of the random circumstances that could happen to an innocent person. The baseline is the null distribution because the null hypothesis is innocence. The defense’s case acts as an anchor for what the jury believes could conceivably happen to an innocent person. Then the jury must overlay the prosecution’s case on the defense’s case. They must ask, “Is the evidence presented by the prosecution likely or unlikely under the assumption of Jane’s innocence?” The measurement of likely or unlikely under the null distribution is known as a p-value. A p-value answers the question, “How likely is the prosecution’s evidence if Jane is innocent?” If the answer is very likely then perhaps the jury decides Jane is not guilty. But, if the answer is very unlikely then the jury might decide Jane is guilty.
Ultimately, the comparison of the defense’s case and the prosecution’s case will result in a decision by the jury. This decision is made by comparing the p-value to the level of significance. The selected threshold for likely versus unlikely is “shadow of a doubt.” When the jury makes their assessment of likelihood (p-value) in the previous step, they must compare it to this required threshold (level of significance). Is the evidence of guilt beyond a shadow of a doubt or is it not beyond? If the likelihood of guilt is beyond a shadow of a doubt, then the jury will reject the null hypothesis. In other words, Jane is found guilty. If the likelihood of guilt is not beyond a shadow of a doubt, then the jury will fail to reject the null hypothesis. In other words, Jane is found not guilty.
Notice we do not claim to have proven innocence. There is no need to prove innocence, because that is the assumption (null) to start with! The entire purpose of the trial is to seek evidence of guilt. So, the conclusion of the trial is focused on whether the evidence was strong enough to believe the alternate hypothesis. In the next subsection, we explain the same six steps of hypothesis testing in the context of statistics.
Statistical Hypothesis Test
In the context of statistics, the steps for hypothesis testing are exactly the same as those presented above for the legal system. However, we formalize many of the steps with mathematical notation and computation. Though this text purposely avoids excessive notation in favor of common language, hypothesis testing benefits from a bit more structure. Consequently, we introduce the prevailing syntax employed for each step.
The null and alternate hypotheses of a statistical hypothesis test reference a specific population parameter. As with confidence intervals, the most common parameters are the proportion (\(p\)), the mean (\(\mu\)), and the slope (\(\beta_1\)). The null hypothesis states the default or assumed value for the parameter, while the alternate lists a claimed range of values. Typically the null hypothesis is denoted with \(H_0\) and the alternate is identified by \(H_A\). All of this notation is combined to state the hypotheses of the test.
As an example, suppose a friend claims that the median middleweight boxer enters the ring weighing more than the limit of 160 pounds. The parameter of interest is the median (\(m\)). The assumed (null) value for the median middleweight boxer is the limit of 160 pounds. The claimed (alternate) value is greater than 160 pounds. Thus, we write the hypotheses as follows.
\[ \begin{aligned} H_0:& \; m = 160 \\ H_A:& \; m > 160 \end{aligned} \]
This notation provides a compact statement of the test hypotheses. The next step is to select the level of significance. Recall, the significance indicates the strength of evidence required to reject the null hypothesis. Another way to think about it is our willingness to incorrectly reject the null hypothesis. If we require stronger and stronger evidence, then we are less and less likely to be wrong. In statistics, we use the symbol \(\alpha\) to represent the significance level and it typically ranges between 0.10 and 0.01. These values indicate the likelihood of incorrectly rejecting the null hypothesis. Imagine we select 0.01 as our significance level. A value of \(\alpha=0.01\) means we are only willing to be wrong about rejecting the null 1% of the time. That level of certainty requires relatively strong evidence in the form of a test statistic.
In this context, the test statistic is a point estimate for the population parameter of interest. If the parameter is the population median, then the statistic is the sample median. As stated in the introduction to this chapter, we typically denote point estimates with a “hat” over the parameter symbol. For our boxing theme, imagine we weighed a random sample of middleweight fighters and obtained a median of \(\hat{m}=165\) pounds. This point estimate of 165 pounds is our evidence in favor of the alternate hypothesis. Although the test statistic is greater than 160 pounds, we cannot automatically reject the null hypothesis. We first need to know the likelihood of obtaining this test statistic value if in fact the null hypothesis is true. We might have obtained a median weight of 165 pounds purely by chance.
The null distribution provides the range and frequency of test statistic values we expect to observe in a sample drawn from a population that abides by the null hypothesis. Even if the median middleweight boxer in the population enters the ring at exactly 160 pounds, we shouldn’t be shocked if a random sample returns a median of 160.5 or even 161 pounds. That could happen just by accident. But what about 165 pounds? Could that happen by accident? We cannot answer this question until we have a null distribution.
There are two methods for obtaining a null distribution: theory and simulation. For certain population parameters and technical conditions, mathematical theory has determined an appropriate null distribution. The most common parameters tend to follow the Normal or t-distribution. But, not all population parameters have a named null distribution supported by mathematical theory. Instead, we simulate a null distribution by leveraging the structure of the problem and computational power. Regardless of the construction method, a null distribution depicts likely values for the test statistic in a world defined by the null hypothesis.
For our boxing example, we need to know the distribution of sample median weights if the population median weight is truly 160 pounds. Suppose we obtain the null distribution in Figure 4.10.
Figure 4.10: Null Distribution for Median Weight of Middleweight Boxers
Not surprisingly, the null distribution is centered on 160 pounds. If the true median in the population is 160, then we would expect most sample medians to be near 160 as well. But we also observe some sample medians as low as 152 and as high as 168 pounds. These values are very rare, but they do occasionally occur. Now that we have a null distribution, we can assess the rarity of the test statistic (red line).
By combining a null distribution and a test statistic, we can compute a p-value. The p-value indicates the likelihood of observing the test statistic (or more extreme) on the null distribution. In other words, how likely is it we would observe a weight of 165 pounds (or more) on the distribution in Figure 4.10? The value 165 is relatively far into the right tail of the distribution and thus has a low frequency. Consequently, median weights of 165 pounds and more are rare. How rare? We can answer this question by determining the proportion of values under the density curve to the right of 165 pounds.
Using methods we explain later in the chapter, suppose we determine that 0.006 of the weights depicted in the null distribution are greater than or equal to 165 pounds. Thus, less than 1% of sample medians are 165 pounds or more. That’s pretty rare! Said another way, if the median weight in the population of middleweight boxers is truly 160 pounds, then there is less than a 1% chance we would observe a median weight of 165 pounds (or more) in a sample. This insight represents strong evidence in favor of the alternate hypothesis.
The final step to reach a conclusion in a statistical hypothesis test is to compare the p-value to the significance level. The significance level dictates how strong the evidence needs to be, while the p-value indicates how strong the evidence actually is. If the p-value is smaller than \(\alpha\), then we reject the null hypothesis. In our case, 0.006 is less than \(\alpha=0.01\), so we reject the null hypothesis (\(m=160\)). We no longer have faith in the default assumption that the median middleweight boxer enters the ring at 160 pounds. Instead, we have strong evidence in support of the alternate hypothesis (\(m>160\)) that the median boxer weighs more than 160 pounds.
As with confidence intervals, we continue to demonstrate the use of hypothesis tests for real-world problems in future sections. We also continue to focus on computational approaches (i.e., simulation) for constructing null distributions and reserve theoretical methods for other texts. For the remainder of the chapter, we return to the 5A Method for problem solving and pursue inferential analyses for proportions, means, and slopes.
4.3.2 Population Proportions
Hypothesis tests of proportions are often intended to verify adherence to process requirements. For example, a manufacturer may dictate that no more than 1% of products off of an assembly line are defective. An election might require that at least 51% of voters choose the winning candidate. Clinical trials may stipulate that a vaccine is effective for 85% of patients. Regardless, each process specifies a target value for the population proportion (\(p\)). We evaluate the proximity to that target using the sample proportion (\(\hat{p}\)) as our test statistic.
The existence of a specific value of interest is the primary distinction between hypothesis tests and confidence intervals. Confidence intervals are more general because they provide a plausible range of values for a parameter. There is no target per se. We are simply interested in estimating the parameter value. By contrast, hypothesis tests are used to compare the parameter to a specific value. In this section, we investigate the population proportion and test its value using functions from the tidyverse.
Ask a Question
In Chapter 3.2.4 we introduced the Vision Zero Chicago initiative and explored the timing of car crashes using a heat map. In addition to day of week and time of day information, the Chicago Data Portal includes ambient lighting conditions during crashes. For purposes of this case study, suppose the Chicago Department of Transportation (CDOT) posts the following statistic: “When it is dark outside, one-in-five car crashes result in injury.” Imagine we are skeptical of this report and believe the true proportion is lower. Consequently, we seek the answer to the following question: Is there significant evidence that the proportion of nighttime car crashes resulting in injury is less than 20%?
Given this question involves human injury, it is clearly concerning. But the references to “dark outside” and “nighttime” are somewhat vague. How little sunlight must there be before we can objectively label it as darkness? We might prefer specific time windows, but of course sunrise and sunset vary by season. Since we have the time of day that crashes occur, we could cross-reference them with historical sunrise and sunset times to produce our own assessment of darkness. However, there is no need for this additional step because the available data has already accounted for it.
Acquire the Data
Similar to previous chapters that investigated the Chicago data, we could query the API and obtain the lighting and injury information. For simplicity, we offer a random sample of crashes spanning January to May of 2023 in the file crashes.csv.
## Rows: 1,500
## Columns: 2
## $ lighting_condition <chr> "DAYLIGHT", "DAYLIGHT", "DAYLIGHT", "DAYLIGHT", "DA…
## $ injuries_total <dbl> 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, …The data includes 1,500 car crashes and delineates the lighting conditions and total number of injuries. We see the label “DAYLIGHT” as one of the lighting conditions, but what are the other levels?
## [1] "DARKNESS" "DAWN" "DAYLIGHT" "DUSK"Clearly we want to include the darkness level in our analysis and not the daylight level. The decision of whether to include dusk or dawn depends on the interpretation of CDOT’s statement regarding crashes when it is “dark” outside. Obviously dusk is darker than daylight, but did CDOT intend for the reader to include dusk? Ideally, we could ask representatives of CDOT about their intent, but that may not be an option. The conservative approach is to only include crashes during darkness in our analysis.
#wrangle crash data
crashes2 <- crashes %>%
filter(lighting_condition=="DARKNESS") %>%
transmute(injury=if_else(injuries_total!=0,1,0))
#review data structure
glimpse(crashes2)## Rows: 433
## Columns: 1
## $ injury <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, …After limiting the sample to only crashes during darkness, we are left with 433 observations. Since our research question does not reference the number of injuries in a crash, we reduce the injury variable to a binary indicator with a value of 1 when there was at least one injury and 0 otherwise. We are now prepared to conduct a hypothesis test.
Analyze the Data
Our null hypothesis for the test comprises the CDOT statement that one-in-five crashes result in injury. Since CDOT is clearly the authority on car crashes in the city of Chicago, their reported value should be assumed true until demonstrated otherwise. The purpose of our test is to seek evidence that the proportion of crashes resulting in injury is less than what CDOT claims. If we let \(p\) represent the true proportion of crashes, then the hypotheses are written as follows.
\[ \begin{aligned} H_0:& \; p = 0.20 \\ H_A:& \; p < 0.20 \end{aligned} \]
Next, we must select a significance level (\(\alpha\)). Recall, the level of significance indicates our willingness to incorrectly reject the null hypothesis. Suppose we select \(\alpha=0.10\). So, if the true proportion of crashes is in fact 0.20, then there is a 10% chance we will find it is less than 0.20. The real-world implication of such a mistake is that we believe nighttime driving is safer than it actually is. Whether this is an acceptable risk ultimately depends on the decision maker.
The next step in the process is to compute a test statistic. Since the parameter of interest is the population proportion, an appropriate statistic is the sample proportion.
## [1] 0.1893764Within our random sample of 433 nighttime crashes, 18.9% (\(\hat{p}=0.189\)) resulted in injury. This is less than the 20% value stated by CDOT. However, it is relatively close. Is our observed value enough less than 20% to stop believing what CDOT claims? In order to answer this question, we require a null distribution. Mathematical theory indicates the sample proportion follows a Normal distribution. However, we can simulate the null distribution without making this assumption.
If CDOT is correct that 20% of all nighttime crashes result in injury, then each individual crash also has a 20% chance of resulting in injury. Think of this as flipping an unfair coin that has a 20% chance of heads (injury) and an 80% chance of tails (no injury). Assuming car crashes are independent of one another, which seems reasonable, we can simulate injuries using the Binomial distribution from Chapter 2.2.3.
#initiate empty vector
results_sim <- data.frame(prop=rep(NA,1000))
#repeat simulation process 1000 times
for(i in 1:1000){
set.seed(i)
results_sim$prop[i] <- mean(rbinom(n=433,size=1,prob=0.2))
}
#review data structure
glimpse(results_sim)## Rows: 1,000
## Columns: 1
## $ prop <dbl> 0.1893764, 0.2147806, 0.2101617, 0.2217090, 0.2193995, 0.2170901,…For each of the 1,000 instances of the loop above, we simulate 433 car crashes. In each independent crash there is a 20% chance of injury. We then compute the proportion resulting in injury across the 433 crashes. By reviewing the results, we see proportions varying above and below 20% simply due to the randomness of simulation. Let’s display those proportions using a histogram in Figure 4.11.
#plot null distribution and test stat
ggplot(data=results_sim,aes(x=prop)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_sim$prop,0.1),
color="red",linewidth=1,linetype="dashed") +
geom_vline(xintercept=test_stat,color="red",linewidth=1) +
labs(title="Chicago Car Crashes in Darkness",
subtitle="Null Distribution",
x="Sample Proportion Resulting in Injury",
y="Count",
caption="Source: CDOT") +
scale_x_continuous(limits=c(0.14,0.26),breaks=seq(0.14,0.26,0.02)) +
theme_bw()
Figure 4.11: Simulated Null Distribution for Proportion of Crashes with Injury
As expected, the null distribution appears symmetric and bell-shaped. Yet, we have no need to label it as a Normal distribution. Instead, we use the 1,000 simulated values to determine the rarity of our test statistic (solid red line). Even when each individual crash has a 0.20 chance of injury, the proportion of injuries across all crashes ranges between 0.15 and 0.25. In light of these results, an observed proportion of 0.189 does not appear so rare. In fact, values less than our equal to this occur about 28% of the time.
## [1] 0.28A p-value of 0.28 indicates there is a 28% chance we would observe a proportion of 0.189 (or lower) even if the null hypothesis is true. That’s not very rare! It is certainly not rare enough to satisfy our significance level of 10%. The dashed red line in Figure 4.11 depicts the rejection threshold associated with a significance of \(\alpha=0.10\). Since our test statistic does not surpass this threshold, we cannot reject the null hypothesis.
The conclusion for the hypothesis test is that we fail to reject the null hypothesis. We do not have sufficient evidence to reject CDOT’s statement that the true proportion of crashes resulting in injury is 0.20. Instead, the observed proportion of 0.189 appears to have occurred purely due to random sampling.
Advise on Results
When advising stakeholders on the results of a hypothesis test, we must be careful with subtle differences in terminology. The appropriate conclusion for our test is that we “fail to reject” the null hypothesis. Notice we did not say that we “accept” the null hypothesis. Think of this in the context of the legal hypothesis test. At the end of a trial the jury foreperson might state, “we the jury find the defendant not guilty.” Importantly the foreperson does not say, “we the jury find the defendant innocent.” The jury does not need to find the defendant innocent because that was already the going-in assumption! The purpose of the trial was to find evidence of guilt (or not). Similarly, we have no reason to “accept” the null hypothesis that the true proportion of crashes is one-in-five. Since CDOT is the authority on such matters, their reported value is the default. The purpose of our test was to seek strong evidence that the proportion is less than one-in-five and we failed to find such evidence.
Another common mistake in interpretation is to apply the word “prove” to the results of a hypothesis test. It would be incorrect to state, “we have proven that one-in-five nighttime crashes results in injury”. In the strict mathematical sense, we have proven nothing! Absolute proof requires the demonstration of a fact in every possible circumstance. Since we base the conclusions of a hypothesis test on a sample, by definition we have not considered every possible circumstance. As a result, we should never use the word “prove” to describe the results of a hypothesis test. Instead, we should refer to what the evidence suggests. Our evidence does not suggest that the proportion of nighttime crashes resulting in injury is less than 0.20. This interpretation leads us to answer the research question.
Answer the Question
Based on a random sample of 433 nighttime crashes in the city of Chicago, we have no reason to question CDOT’s statement regarding injury proportions. Specifically, we have no strong evidence that the proportion of crashes resulting in injury is less than 0.20. While this analysis cannot prove that the true proportion is 20%, we find no reason to question this value’s validity.
There is at least one important limitation to our results. We only included the first five months of the year in our sample. It is possible that the summer and fall seasons witness different injury proportions. Ideally, we would reproduce our analysis using all twelve months over multiple years. A more robust sample would strengthen our conclusions regarding the true proportion. For now, we move on to testing another common population parameter.
4.3.3 Population Means
The sample proportion is a useful statistic for estimating the prevalence of factor levels in a population. When investigating a numerical variable, the most common statistic by far is the sample mean. As a measure of centrality, the mean is employed as an indicator of “typical” variable values. Of course, mean values can be misleading when the distribution of a variable is skewed or multi-modal. Thus, exploratory analyses are always an important first step. Regardless, we use the same six-step process to test claims regarding the mean of a population.
Here we demonstrate a two-tailed test rather than a one-tailed test. In this context, the word “tail” is used to refer to the extreme left and right ends of the null distribution. The number of tails considered in the null distribution is directly related to the form of the alternate hypothesis. If the alternate hypothesis includes an inequality (\(>\) or \(<\)), then the test is one-tailed because we are only investigating the likelihood of values in a single end (tail) of the null distribution. On the other hand, if the alternate hypothesis involves a “not equal to” sign (\(\neq\)), then the test is two-tailed. This is due to the requirement to check the likelihood of values in both ends (tails) of the null distribution. Typically, we pursue a two-tailed test when there is no specific claim about which direction to investigate. We demonstrate this approach with an example using the 5A Method and functions from the tidyverse.
Ask a Question
Similar to other school districts across the United States, most high school juniors (11th grade) in the State of Colorado complete the Scholastic Aptitude Test (SAT). Often, colleges use the exam results as a threshold for admission and/or as a metric for competitive scholarships. Although the SAT has witnessed various changes to its structure over time, the two primary examination categories remain verbal (reading and writing) and math. Each category has a maximum score of 800 points and results tend to follow a symmetric, bell-shaped (i.e., Normal) distribution centered on an overall mean. For our purposes, imagine it is commonly believed among Colorado schools that the mean math score is 460 points. We suspect otherwise and pose the following question: Is there significant evidence that the mean score on the math portion of the SAT is not 460 for Colorado schools?
Note that our research question references schools rather than students. Although the SAT is completed by individual students, the test results are often publicly reported at the school level. In other words, individual student scores are summarized in some way (typically averaged) and a single score is reported for the entire school. As a result, the unit of observation for our study is schools. Luckily, the associated data is easily acquired.
Acquire the Data
The Colorado Department of Education (CDE) offers open access to historical test scores at this link. Available files are in portable document format (pdf) and Microsoft Excel spreadsheets (xls). Extracting data tables from a pdf can be challenging, but functions do exist to ease the process. Spreadsheet tables are easier to import, but are often not in tidy format. Rather than belabor these difficulties, we offer a random sample of math results from the CDE site in the file test_scores.csv.
## Rows: 500
## Columns: 5
## $ Year <dbl> 2021, 2022, 2023, 2022, 2023, 2023, 2021, 2022, 2022, 2021, 2…
## $ District <chr> "Big Sandy 100J", "Plateau Valley 50", "Education reEnvisione…
## $ School <chr> "Simla High School", "Plateau Valley High School", "Ascend Co…
## $ Students <dbl> 16, 22, 43, 78, 393, 400, 91, 341, 17, 43, 23, 23, 128, 117, …
## $ Score <dbl> 509, 479, 543, 454, 524, 440, 467, 514, 509, 482, 540, 423, 5…The data includes 500 school-level math scores randomly selected from the years 2021 to 2023. All Students are high school juniors and the overall school Score is computed as an average of individual scores. For quality-control purposes we produce a summary of the school scores and check for outliers.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 329.0 432.0 467.5 472.4 513.2 654.0We previously investigated outliers in Chapter 3.2.3 and apply similar techniques here. With an interquartile range (IQR) of 81.2, scores must be above 635 or below 310.2 to be considered outliers. There are no low-scoring outliers, but we do find three high-scoring outliers (see below).
## # A tibble: 3 × 5
## Year District School Students Score
## <dbl> <chr> <chr> <dbl> <dbl>
## 1 2022 Jefferson County R-1 D'Evelyn Junior/Senior High School 134 648
## 2 2021 Poudre R-1 Liberty Common Charter School 87 654
## 3 2023 Jefferson County R-1 D'Evelyn Junior/Senior High School 125 653Two of the outlying scores are from the same school (D’Evelyn) in consecutive years. Perhaps that school has a remarkable test-prep program or extraordinary faculty and students? Is the same true for the other school (Liberty) on the list? Some research may be required to answer these questions, if we believe the results are suspect. However, the scores are only slightly beyond the outlier threshold and still well below the maximum of 800. So, we decline further investigation and move on to the analysis.
Analyze the Data
As with any hypothesis test, we begin by stating the null and alternate hypotheses. The assumed value for the mean math score (\(\mu\)) of the entire population of Colorado schools is 460. The purpose for the test is to seek evidence that the mean is not 460. Here we have no preconceived notions about whether the true mean is above or below 460 points. We simply claim that it is not the commonly-accepted value of 460.
\[ \begin{aligned} H_0:& \; \mu = 460 \\ H_A:& \; \mu \neq 460 \end{aligned} \]
Next we choose the level of significance (\(\alpha\)) for the test. The smaller the value for \(\alpha\), the stronger the evidence required to reject the null hypothesis. Suppose we select a significance level of \(\alpha=0.01\). In other words, there is a 1% chance we will find the mean score is not equal to 460 when in fact it is. The evidence we use to draw this conclusion is based on a test statistic.
## [1] 472.372Our test statistic of \(\hat{\mu}=472\) provides the best estimate of the mean math score in the entire population of Colorado schools. Clearly, the sample mean is not equal to 460. But we cannot immediately reject 460 as the population mean. We may have simply observed a sample mean of 472 due to randomness. In order to determine the likelihood of observing this value, we require a null distribution.
The null distribution will tell us the chances of obtaining a sample mean of 472 if the population mean is truly 460. But, we need more than just the mean (center) of the population to produce a distribution. We also need to know the shape (modality and symmetry) and spread. For this, we take advantage of the test being designed to produce Normally distributed results. Figure 4.12 displays the distribution of school scores.
#compute sample standard deviation
std_dev <- sd(scores$Score)
#display score distribution
ggplot(data=scores,aes(x=Score)) +
geom_histogram(color="black",fill="#CFB87C",
binwidth=25,boundary=300,closed="left") +
geom_vline(xintercept=c(test_stat-std_dev,test_stat+std_dev),
color="red",linewidth=1,linetype="dashed") +
geom_vline(xintercept=c(test_stat-2*std_dev,test_stat+2*std_dev),
color="red",linewidth=0.75,linetype="dashed") +
geom_vline(xintercept=c(test_stat-3*std_dev,test_stat+3*std_dev),
color="red",linewidth=0.50,linetype="dashed") +
labs(title="Colorado SAT Math Scores (2021-2023)",
subtitle="School Average",
x="Score (out of 800)",
y="Count",
caption="Source: CDE") +
scale_x_continuous(limits=c(300,700),breaks=seq(300,700,50)) +
scale_y_continuous(limits=c(0,100),breaks=seq(0,100,20)) +
theme_bw()
Figure 4.12: Distribution of SAT Math Scores
The distribution of scores appears unimodal and symmetric. Nearly all of the scores are within three standard deviations (dashed red lines) of the mean, as expected for the Normal distribution. Here again we see the few outlying scores in the right tail of the distribution. This visual evidence, along with the known test design, is likely enough to safely assume that school scores are Normally distributed. It also appears plausible from Figure 4.12 that the mean score is 460, as indicated by our null hypothesis. Yet, we cannot be sure based on a single sample. Instead, we must simulate many samples from the null population and record the means.
In the code below, we assume that school scores are Normally distributed with a mean of 460 and a standard deviation of 53.5. This is the same standard deviation observed in our sample. We then simulate 1,000 distinct samples of 500 schools each and record the mean scores.
#initiate empty vector
results_sim <- data.frame(avg=rep(NA,1000))
#repeat simulation process 1000 times
for(i in 1:1000){
set.seed(i)
results_sim$avg[i] <- mean(rnorm(n=500,mean=460,sd=std_dev))
}
#review data structure
glimpse(results_sim)## Rows: 1,000
## Columns: 1
## $ avg <dbl> 461.2125, 463.3033, 462.8133, 458.4393, 459.7119, 457.5420, 462.40…The simulation produced sample means above and below the assumed population mean of 460. We visualize these values in the null distribution depicted in Figure 4.13.
#plot null distribution and test stat
ggplot(data=results_sim,aes(x=avg)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_sim$avg,0.995),
color="red",linewidth=1,linetype="dashed") +
geom_vline(xintercept=quantile(results_sim$avg,0.005),
color="red",linewidth=1,linetype="dashed") +
geom_vline(xintercept=test_stat,color="red",linewidth=1) +
labs(title="Colorado SAT Math Scores (2021-2023)",
subtitle="Null Distribution",
x="Sample Mean Score",
y="Count",
caption="Source: CDE") +
scale_x_continuous(limits=c(450,475),breaks=seq(450,475,5)) +
scale_y_continuous(limits=c(0,150),breaks=seq(0,150,25)) +
theme_bw()
Figure 4.13: Simulated Null Distribution for Mean SAT Math Score
Our null distribution is unimodal, symmetric, and centered on a mean score of 460. Theory suggests this particular null distribution is Normal, but we do not require that assumption here. Purely due to randomness, we witness sample means below 455 and others above 465. Such scores are plausible when sampling from a population with a mean of 460. However, scores outside the rejection thresholds (dashed red lines) defined by \(\alpha=0.01\) are not reasonable. With a two-tailed test, we split the significance level such that \(\alpha/2=0.005\) resides in each tail. In other words, 0.5% of values are in the left tail and 0.5% are in the right tail. It is extremely unlikely we would observe these values, if the null hypothesis is true.
Notice that our observed mean (solid red line) of 472 is well beyond the upper rejection threshold. When simulating a true mean score of 460 points, not a single sample mean was as high as 472. In effect, we have obtained a p-value of 0. Said another way, if the average school truly achieves a score of 460, then there is almost no chance we would observe a mean score of 472 (or more) in a sample. Consequently, we reject the null hypothesis.
Advise on Results
When presenting the results of a hypothesis test to stakeholders, it is important to clearly identify the unit of observation and the parameter of interest. Our test is directed at the mean school score, not the mean student score. Yet, the school score itself is a mean of individual students! In a sense, we have computed an average of averages. This is an important distinction. If we average student scores within each school and subsequently calculate the average over all schools, then we are not guaranteed to get the same value as if we simply average all students across all schools. Let’s demonstrate this with a simple example.
Suppose we have three schools (A, B, and C). School A only has five students who all score 465 points. School B only has five students who all score 470 points. Finally, School C has 1,000 students who all score 300 points. At the school level, the average score is 412 (\((465+470+300)/3\)). But at the student level the average score is 302 (\((5\cdot465+5\cdot470+1000\cdot300)/1010\))! This phenomenon is similar to Simpson’s Paradox which we discussed in Chapter 3.3.2. Results depend on how we choose to aggregate our data. Either of these statistics could be correct, depending on the question at hand. The mean of 412 is appropriate when referencing the average school, but the mean of 302 is representative of the average student. Our case study addressed the average school, so this critical difference must be clearly communicated to stakeholders.
Answer the Question
Using a random sample of 500 school-level math scores, we find significant evidence that the true mean score is not 460 points. Although it does appear that the mean score is greater than 460, further analysis in the form of a confidence interval is required to present an accurate estimate. In this test, we simply demonstrated that 460 points is not a plausible estimate for the true mean. Herein lies an important distinction between the uses for confidence intervals and hypothesis tests. Confidence intervals suggest what a parameter is, whereas hypothesis tests indicate what a parameter is not.
By providing the code used to execute the test, we have rendered our work reproducible. However, there is no guarantee that future analysts will obtain the same results when new test data is introduced. Our evidence is based on the years 2021 through 2023. If this time window is extended with older or newer data, then the results of the test could vary.
4.3.4 Population Slopes
In Chapter 4.2.4, we construct a confidence interval for the slope parameter \(\beta_1\) of the linear regression model in Equation (4.1). As with the estimation of any population parameter, we can also complete a hypothesis test for the slope. Though we can test claims for any value of the slope, we are most often interested in determining whether the slope differs from zero. If zero is a plausible value for the slope, then there is no evidence of an association between the variables \(x\) and \(y\). In other words, \(x\) and \(y\) are independent of one another. We investigate hypothesis tests on the slope in the context of an example below.
Ask a Question
In a paper by Keith W. Penrose and others, the authors explore the body composition of adult biological males between the ages of 22 and 81 years (Penrose et al. 1985). The goal of the research is to develop a predictive model for lean body weight based on various measurements (e.g., chest, abdomen, and thigh circumference) of the human subjects. Suppose instead we are interested in modeling the linear association between two of the body measurements. Since dimensions of the human body tend to grow in proportion to one another, we might expect to find strong associations between many pairs of measurements. Imagine we are faced with the following question: Is there evidence of an association between an adult male’s height and abdominal circumference?
Any time we plan to analyze data gathered from human subjects, we must carefully consider potential ethical concerns. Can the data be obtained in a manner that does not physically or emotionally harm the subjects? Do we have the capacity to protect the anonymity of our subjects and their data? Will the insights and applications of the subsequent analytic results impose negative consequences for the study subjects or others? If the answer to any of these questions is yes, then we should likely not conduct the study. In our current case study, the data includes measurements that can be obtained without causing harm. The observations are completely anonymous and our purpose is simply to better understand association within the human body. Consequently, there do not appear to be any obvious ethical concerns with the use of the data. That said, we should be careful with the interpretation of any insights from the data in terms of biological sex. The available data only includes biological males, so it would not be appropriate to extrapolate our discoveries to females.
Acquire the Data
Continuing on the theme of ethics, responsible researchers make their work repeatable by offering access to the study data. The Penrose research is no exception, as the body composition data is publicly available. In the file bodycomp.csv all measurements are in centimeters (cm). With the exception of height, every variable represents the circumference of the listed body part. Below we import the data and isolate our variables of interest.
#import body composition data
bodycomp <- read_csv("bodycomp.csv")
#wrangle body composition data
bodycomp2 <- bodycomp %>%
select(Height,Abdomen) %>%
na.omit()
#review data structure
glimpse(bodycomp2)## Rows: 251
## Columns: 2
## $ Height <dbl> 174.6, 162.6, 173.4, 176.5, 186.7, 177.2, 176.5, 193.0, 184.8,…
## $ Abdomen <dbl> 126.2, 122.1, 118.0, 115.9, 115.6, 113.9, 113.8, 113.7, 113.4,…Our wrangled data consists of heights and abdominal circumferences for 251 adult males. In the spirit of quality control, we also summarize the measurements to ensure the range of values for each variable is reasonable.
## Height Abdomen
## Min. :162.6 Min. : 69.40
## 1st Qu.:173.4 1st Qu.: 84.55
## Median :177.8 Median : 90.90
## Mean :178.6 Mean : 92.33
## 3rd Qu.:183.5 3rd Qu.: 99.20
## Max. :197.5 Max. :126.20The heights range from about 163 cm (5 ft, 4 in) to 198 cm (6 ft, 6 in). The abdominal circumferences range from roughly 69 cm (27 in) to 126 cm (50 in). Based on common knowledge of adult heights and pant sizes, these bounds appear reasonable. The remaining question is whether larger abdominal circumferences tend to be associated with greater heights. The answer is found by pursuing a hypothesis test.
Analyze the Data
Prior to completing a hypothesis test for the slope parameter, we display the linear association between our numerical variables in a scatter plot.
#create scatter plot
ggplot(data=bodycomp2,aes(x=Abdomen,y=Height)) +
geom_point() +
geom_smooth(method="lm",formula=y~x,se=FALSE) +
labs(title="Adult Male Body Composition",
x="Abdominal Circumference (cm)",
y="Height (cm)",
caption="Source: Penrose 1985") +
theme_bw()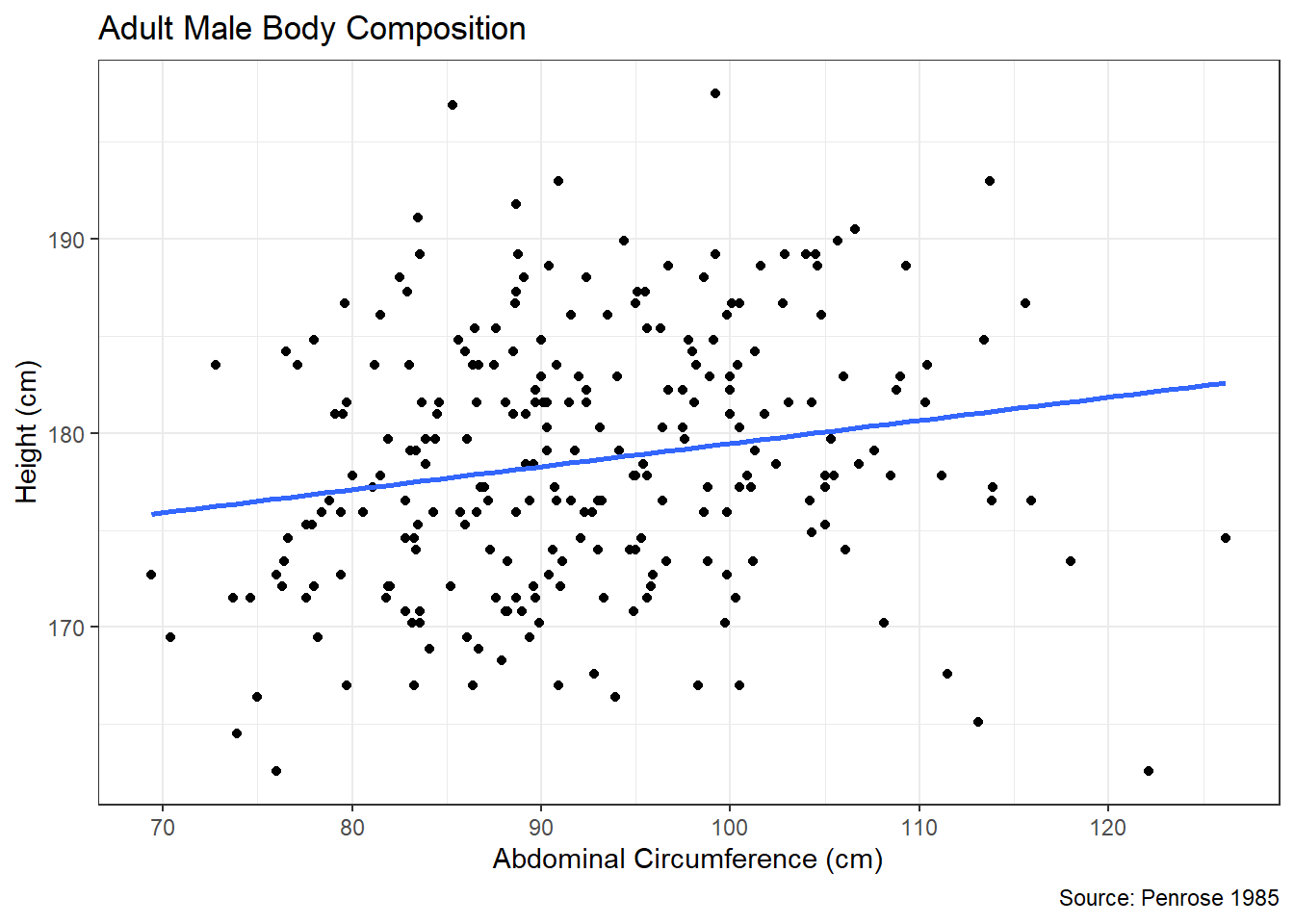
Figure 4.14: Linear Association between Abdomen Circumference and Height
The scatter plot in Figure 4.14 suggests a positive, linear association between abdominal circumference and height. However, the relationship appears weak given the dispersal of the points. We compute a more objective measure of strength in the form of a correlation coefficient.
## [1] 0.1832923With a correlation coefficient below 0.25, we could defensibly state there is no association between the variables. But a more objective method to evaluate the association is with a hypothesis test on the slope of a linear regression model. The estimated slope depicted by the blue line in Figure 4.14 appears to be positive. Yet the wide spread of the points around the line introduces a great deal of variability when attempting to estimate the true association. It may be possible that the true slope is zero (i.e., flat line). We initiate our test by assuming this flat line and seeking evidence that the slope is non-zero.
\[ \begin{aligned} H_0:& \; \beta_1=0 \\ H_A:& \; \beta_1\neq0 \end{aligned} \]
With no particular reason to vehemently avoid a false positive, we choose a significance level of \(\alpha=0.05\). Since this is a two-sided hypothesis test, we know the significance is split into \(\alpha/2=0.025\) in each tail of the null distribution. Before we generate the null distribution we compute the test statistic.
#estimate linear regression model
model <- lm(Height~Abdomen,data=bodycomp2)
#extract slope coefficient
test_stat <- coefficients(summary(model))[2,1]
#view estimated slope
test_stat## [1] 0.1190496The slope of the blue line in Figure 4.14 is \(\hat{\beta_1}=0.12\). This value implies that every one centimeter increase in abdominal circumference is associated with a 0.12 centimeter increase in height, on average. But we do not know how rare this sample slope might be if there is truly no association between height and abdominal circumference. Given the observed variance in the sample, perhaps we detected an association purely by chance? To be sure, we must generate a null distribution.
Rather than assume a particular named distribution (e.g., Binomial or Normal) for the null, we employ a method known as randomization. Sometimes this approach is referred to as “shuffling” because it mimics the random shuffling of cards in a deck. In our case, we aim to shuffle the abdomen circumferences assigned to each subject. By randomly assigning abdomens to heights, we break any association that may exist between them and thus simulate the null hypothesis. We present the necessary code below, followed by an explanation.
#initiate empty vector
results <- data.frame(beta=rep(NA,1000))
#repeat randomization process 1000 times and save results
for(i in 1:1000){
set.seed(i)
bodycomp3 <- bodycomp2 %>%
transmute(Height,
Shuffle=sample(x=Abdomen,size=nrow(bodycomp2),
replace=FALSE))
model2 <- lm(Height~Shuffle,data=bodycomp3)
results$beta[i] <- coefficients(summary(model2))[2,1]
}
#review randomized slopes
glimpse(results)## Rows: 1,000
## Columns: 1
## $ beta <dbl> 0.0617256817, -0.0446289699, -0.0434625121, -0.0006750169, -0.086…In order to simulate no association, we randomly shuffle the abdominal circumferences while holding the heights fixed. This is achieved by sampling without replacement from the entire column of abdomen measurements. We then estimate simple linear regression models with the shuffled data and extract the slopes. The results include positive and negative slopes around zero. Let’s display the slopes in a histogram.
#plot randomized null distribution
ggplot(data=results,aes(x=beta)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=test_stat,
color="red",linewidth=0.75) +
geom_vline(xintercept=quantile(results$beta,0.025),
color="red",linetype="dashed",linewidth=0.75) +
geom_vline(xintercept=quantile(results$beta,0.975),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="Adult Male Body Composition",
subtitle="Null Distribution",
x="Estimated Slope Parameter",
y="Count",
caption="Source: Penrose 1985") +
theme_bw()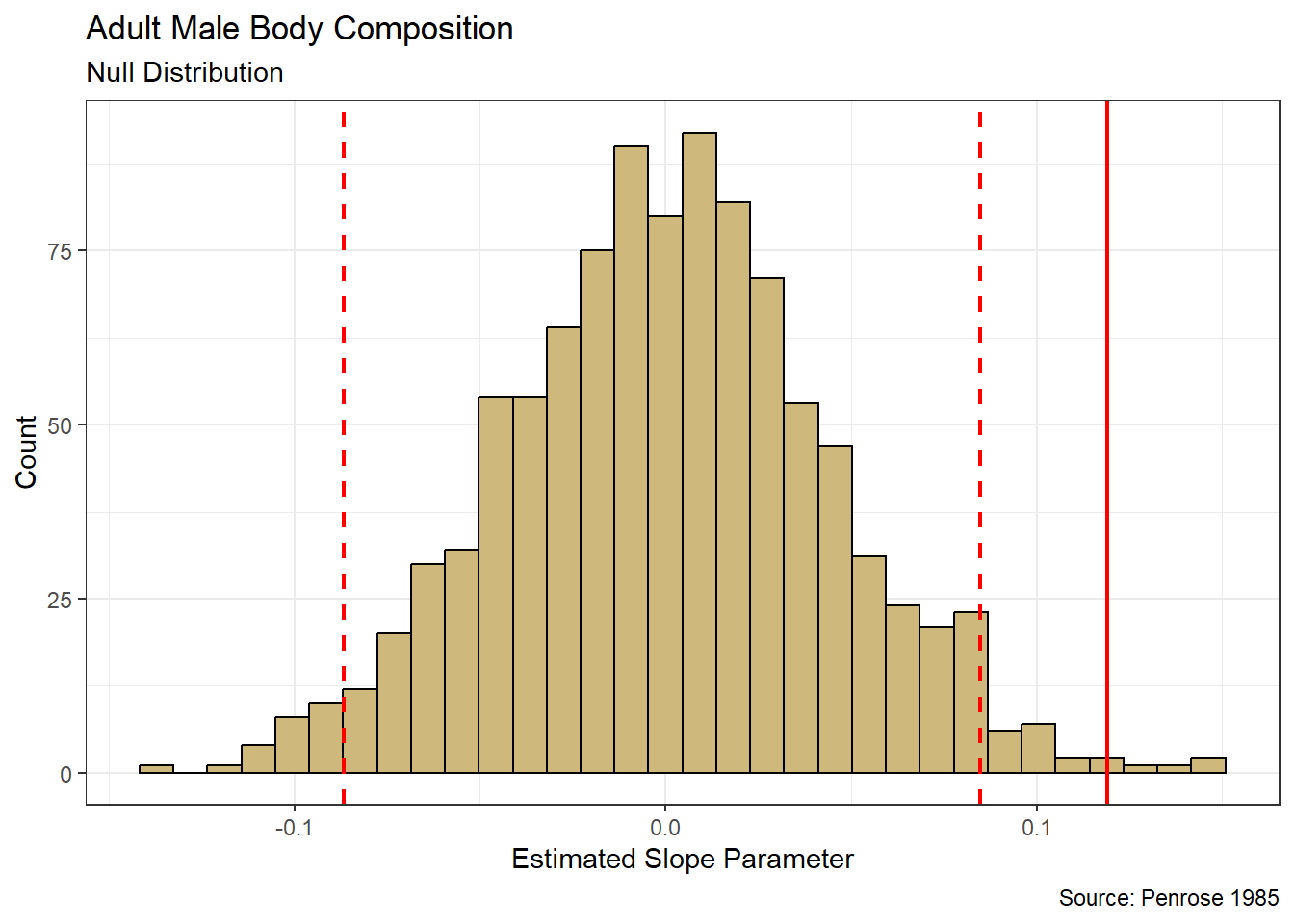
Figure 4.15: Randomized Null Distribution for Slope
Figure 4.15 depicts the distribution of sample slopes we might expect to observe even if there is no relationship between height and abdominal circumference. The significance thresholds (dashed red lines) indicate that sample slopes between about -0.85 and +0.85 are not sufficiently rare under the null hypothesis. However, our test statistic (solid red line) of 0.12 is beyond the upper threshold. We calculate the p-value for the test statistic below.
## [1] 0.005Since the p-value of 0.005 is less than the upper significance level of \(\alpha/2=0.025\), we must reject the null hypothesis. In other words, we have sufficient statistical evidence to suggest the true slope parameter that associates height and abdominal circumference is not zero. There does appear to be some association between the two variables.
Advise on Results
When presenting these results to stakeholders, it may prove difficult to explain the discrepancy between the correlation coefficient and the p-value. The correlation of 0.18 seems to indicate no association, while the p-value suggests there is an association. But we must remember that the threshold of 0.25 for the correlation coefficient is somewhat arbitrary. Technically there is some non-zero correlation, but it is so weak that we might report it as none at all. That same weakness is demonstrated by the proximity of the test statistic to the significance threshold in Figure 4.15. In fact, if we had chosen a much smaller significance level (say \(\alpha=0.008\)), then we would have failed to reject the null hypothesis. So, in a way, the correlation coefficient and p-value both indicate a very weak association between height and abdominal circumference.
There also exists an important difference in purpose between the correlation coefficient and estimated slope. The slope describes the “steepness” of the linear relationship, while the correlation measures the “compactness” of the linear relationship. Two regression lines with the same slope can have different correlation coefficients depending on the dispersal of the points around the lines. Lower variability of the points around a line (compactness) will lead to greater correlation, even if the slope of the line (steepness) remains the same. In the case of our example, the best estimate for the steepness of the regression line is 0.12 but the points are not very compact around the line.
Answer the Question
Based on the body composition of 251 adult males, there does appear to be an association between height and abdominal circumference. A one centimeter increase in abdominal circumference is expected to result in a 0.12 cm increase in body weight, on average. However, this association is very weak and may be considered non-existent depending on the required strength of evidence. Intuitively, the very weak association makes sense. An adult eventually reaches a maximum height and remains near that height for the remainder of their life. By contrast, abdominal circumference can vary greatly throughout an adult’s lifetime based on diet, exercise, and health conditions. Thus, adults with a larger abdomen are not necessarily taller.
4.3.5 Two Populations
Just as with confidence intervals, hypothesis tests can be extended to two or more population parameters. In the case of exactly two populations, we are often interested in whether they differ with regard to a particular parameter. For example, we might formulate the following hypotheses:
\[ \begin{aligned} H_0:& \; m_1 = m_2 \\ H_A:& \; m_1 \neq m_2 \end{aligned} \]
In this case, we assume that the median of the first population (\(m_1\)) is the same as the median of the second population (\(m_2\)). The purpose of the test is to seek evidence that the medians are not the same. Of course, we can replace the “not equal to” sign with inequalities if we have reason to assess whether one population median is greater than the other. For reasons that will be made clear in this section, it is often more intuitive to rewrite the hypotheses as:
\[ \begin{aligned} H_0:& \; m_1 - m_2 = 0 \\ H_A:& \; m_1 - m_2 \neq 0 \end{aligned} \]
Algebraically, there is no difference in the two sets of hypotheses. However, the new formulation specifically addresses the difference between the parameters. We assume the difference is zero (no difference) and seek evidence that the difference is not zero (some difference). Although this may seem subtle, the new formulation eases the interpretation of the null distribution during our analysis. We demonstrate this with another case study.
Ask a Question
An important statistic in the Women’s National Basketball Association (WNBA), as in any basketball league, is rebounds. Offensive rebounds occur when a player gains possession of the ball after their own teammate misses a shot, while defensive rebounds occur after an opponent misses their shot. The sum of offensive and defensive rebounds results in a player’s total rebounds. Often taller player have an advantage in gaining rebounds, given their ability to reach higher than shorter players. In terms of player position, centers tend to be the tallest players on the court. But what about forwards and guards? Is there a difference in their ability to gain rebounds? This uncertainty leads to the following research question: Is there a significant difference in mean rebounding efficiency between guards and forwards in the WNBA?
Savvy basketball fans may challenge the specificity of our research question. There are multiple types of guards and forwards. Point guards are typically charged with coordinating the offense and distributing the ball, while shooting guards are tasked with scoring. Small forwards typically fulfill roles similar to shooting guards, while power forwards tend to more closely resemble centers. Given the differences in roles on the court, there are likely differences in opportunity and expectation regarding rebounds. However, since our goal here is to demonstrate differences between two (versus four) parameters, we maintain the more general labels of guard and forward.
Acquire the Data
We could obtain our data from the WNBA API via the wehoop package just as we did in Chapter 4.2.3. However, to ease the acquisition process, we offer the same wrangled data set from the previous section in the file wnba_stats.csv.
This data includes all three player positions (center, forward, and guard) and a variety of statistics unrelated to our current research question. Additionally, it imposes the 10 minutes of game play restriction, but does not include a variable for rebounding efficiency. As with scoring efficiency, we measure rebounding efficiency in units of rebounds-per-minute. In the following code, we wrangle the WNBA data by limiting it to our variables of interest.
#wrangle WNBA data
wnba2 <- wnba %>%
filter(position %in% c("Forward","Guard")) %>%
transmute(position=as.factor(position),
rpm=rebounds/minutes)
#review data structure
summary(wnba2)## position rpm
## Forward:1400 Min. :0.00000
## Guard :1966 1st Qu.:0.07692
## Median :0.14286
## Mean :0.15915
## 3rd Qu.:0.22222
## Max. :0.72222Our data frame now consists of rebounding efficiencies for 1,400 forwards and 1,966 guards. Though there exists a disparity between the number of observations for each position, there is more than enough for each from a statistical perspective. The efficiency values range from 0 (no rebounds) to 0.72 rebounds-per-minute. In a 40 minute game, the maximum efficiency amounts to nearly 30 rebounds. However, the maximum number of rebounds in the data is 20 (see below).
## [1] 20This apparent disconnect is caused by the fact that most players are not on the court for the entire 40 minutes of a game. Very large efficiency values are associated with players who achieve a large number of rebounds in a short period of time. Having resolved these potential outliers, we proceed to analyzing our data.
Analyze the Data
In order to assess the claim that rebounding efficiency differs between the two positions, we require a two-sided hypothesis test. Prior to that, let’s generate a comparative box plot to build some intuition regarding any observed differences in the efficiency distributions.
#create comparative boxplot for position
ggplot(data=wnba2,aes(x=rpm,y=position)) +
geom_boxplot(color="black",fill="#CFB87C") +
labs(title="WNBA Players (2022-2023 seasons)",
x="Rebounds-per-Minute",
y="Count",
caption="Source: ESPN") +
scale_x_continuous(limits=c(0,0.8),breaks=seq(0,0.8,0.1)) +
theme_bw()
Figure 4.16: Distribution for Individual Player Rebounds-per-Minute
Though there is some overlap in the distributions in Figure 4.16, it appears forwards generally achieve a higher rebounding efficiency compared to guards. The upper 75% of efficiencies for forwards nearly exceeds the lower 75% for guards. This difference could be a result of height disparities or strategic usage. Regardless, the box plot represents strong initial evidence of a difference between the positions. However, we formalize the evaluation of evidence in a hypothesis test.
The null hypothesis for our test is that the true mean rebounding efficiency for forwards (\(\mu_F\)) and guards (\(\mu_G\)) is the same. The alternate hypothesis is that the true means are different (i.e., the difference is not zero). In statistical notation, we display these hypotheses as follows:
\[ \begin{aligned} H_0:& \; \mu_F-\mu_G=0 \\ H_A:& \; \mu_F-\mu_G \neq 0 \end{aligned} \]
Next we establish a level of significance for our test. Suppose we choose \(\alpha=0.10\). Thus, we accept a 10% chance of reporting a difference between positions when in fact they are the same. After determining the appropriate significance level, we compute the observed difference in sample means.
#compute difference in means
test_stat <- as.numeric(wnba2 %>%
group_by(position) %>%
summarize(avg=mean(rpm)) %>%
ungroup() %>%
summarize(avg[1]-avg[2]))
#view difference in means
test_stat## [1] 0.1112764The observed difference in average rebounding efficiency between forwards and guards is \(\hat{\mu}_F-\hat{\mu}_G=0.11\). In other words, every 10 minutes the average forward achieves one more rebound than the average guard. The remaining question is whether this difference in a sample is sufficient to believe a difference exists in the population. To answer that question, we require a null distribution.
Once again we employ the method of randomization to simulate the null distribution. Below, we randomly shuffle the efficiency values assigned to each position. When efficiencies are randomly assigned, there cannot possibly be an association with position.
#initiate empty vector
results_rand <- data.frame(diff=rep(NA,1000))
#repeat randomization process 1000 times
for(i in 1:1000){
set.seed(i)
results_rand$diff[i] <- as.numeric(wnba2 %>%
mutate(shuffle=sample(x=rpm,size=nrow(wnba2),
replace=FALSE)) %>%
group_by(position) %>%
summarize(avg=mean(shuffle)) %>%
ungroup() %>%
summarize(avg[1]-avg[2]))
}The null distribution represents the difference in mean efficiency we might expect to observe in a sample if there is no difference between forwards and guards in the population. Below we depict these differences in a histogram, along with the significance thresholds. Here we refer to thresholds (plural) because the alternate hypothesis did not specify a positive or negative difference. Thus, we split the significance level into \(\alpha/2=0.05\) in each tail of the null distribution in Figure 4.17.
#plot null distribution
ggplot(data=results_rand,aes(x=diff)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_rand$diff,0.05),
color="red",linetype="dashed",linewidth=0.75) +
geom_vline(xintercept=quantile(results_rand$diff,0.95),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="WNBA Players (2022-2023 seasons)",
subtitle="Null Distribution",
x="Difference in Average Rebounds-per-Minute",
y="Count",
caption="Source: ESPN") +
theme_bw()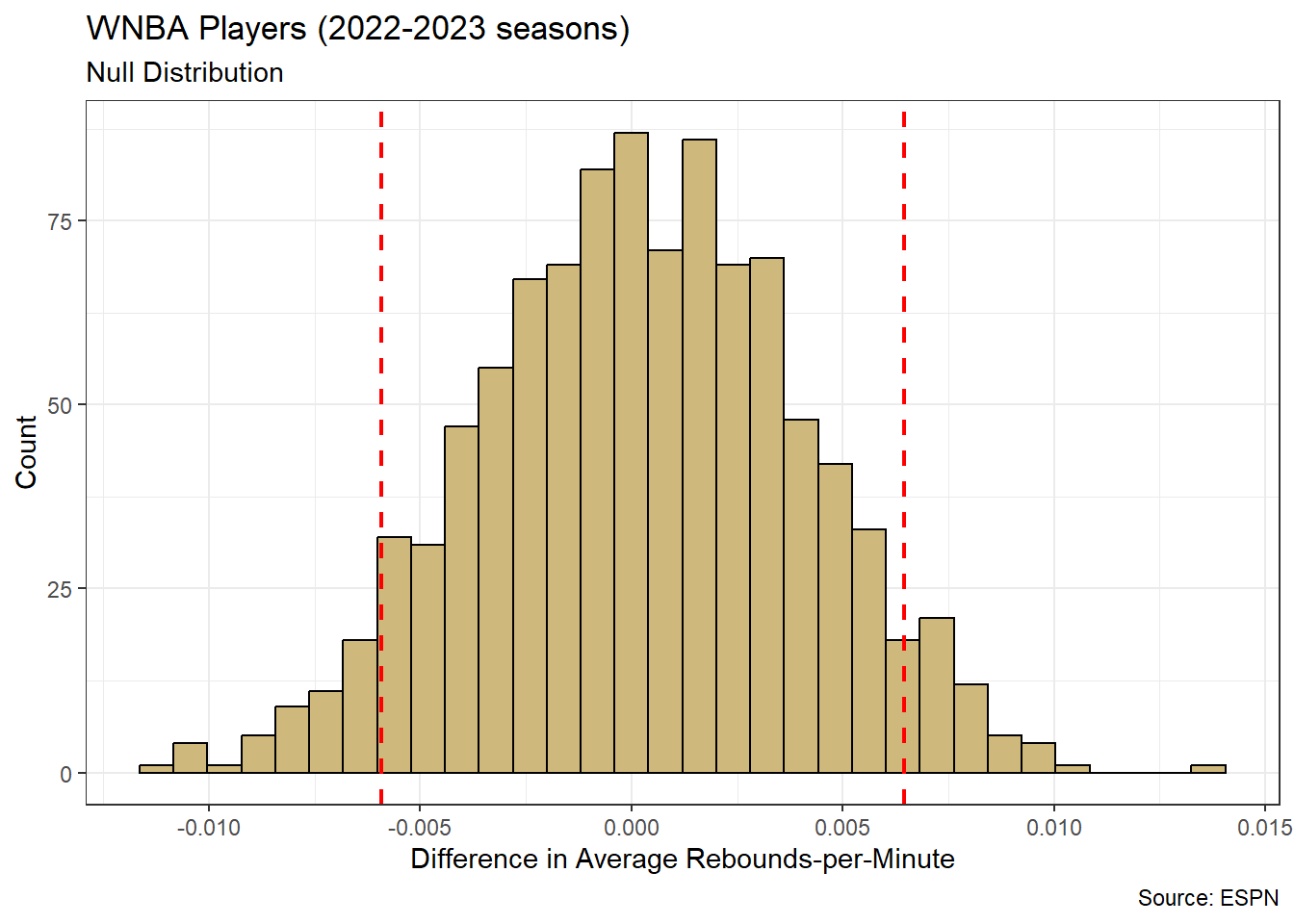
Figure 4.17: Distribution for Difference in Average Rebounds-per-Minute
As indicated by the null hypothesis, the null distribution is centered on a difference of zero. If there is no difference in average rebounding efficiency between forwards and guards, then we might randomly witness sample differences of up to 0.01 in either direction. Based on our level of significance, an observed difference beyond about 0.006 is sufficiently rare to question the validity of the null hypothesis. Our test statistic value of 0.11 is so large that it does not appear on the plot! In fact, not a single value from the randomized null distribution reached a magnitude of 0.11. We check this fact directly by computing the p-value with the following code.
## [1] 0Notice when computing the p-value we must account for both tails of the null distribution. In this case, the p-value indicates the proportion of simulated differences that are greater than 0.11 or less than -0.11. Based on the resulting p-value of 0, it is nearly impossible to observe a difference in mean efficiency of 0.11 if there is truly no difference between the positions. Consequently, we reject the assumption that forwards and guards achieve the same average rebounding efficiency. Instead, we appear to have very strong evidence of a difference between positions.
Advise on Results
Given the results of our hypothesis test, it is tempting to report to stakeholders that we have significant statistical evidence that forwards have a greater rebounding efficiency than guards. After all, the observed test statistic suggests forwards have an efficiency 0.11 higher than guards. But the purpose of a two-tailed test is to detect any difference, not just in one direction. If we want to test the specific claim that the average rebounding efficiency of forwards is greater than that of guards, the we should conduct a one-tailed test. In this particular example, the one-tailed test will still result in rejecting the null hypothesis since the test statistic is so large. However, in general, there is no guarantee that a one-tailed and two-tailed test will result in the same conclusion. For a given null distribution, it is possible for a two-tailed test to fail to reject, while a one-tailed test (at the same significance level) does reject. As always, it is important to collaborate with domain experts to establish the appropriate test and level of significance before computing the test statistic and null distribution. This order of events avoids accusations of unethical practices solely to achieve a particular conclusion.
Another important consideration when interpreting the results of a hypothesis test for stakeholders is the impact of the sample size. All else being equal, larger samples produce null distributions with less variability (i.e. spread). By contrast, smaller samples increase the variability of the null distribution and reduce our capacity to reject the null hypothesis. In order to demonstrate this, let’s randomly select 300 observations from the original 3,366 observations using the sample_n() function.
Using this smaller sample of rebounding efficiencies, we construct a new randomized null distribution.
#initiate empty vector
results_rand2 <- data.frame(diff=rep(NA,1000))
#repeat randomization process 1000 times
for(i in 1:1000){
set.seed(i)
results_rand2$diff[i] <- as.numeric(wnba2_small %>%
mutate(shuffle=sample(x=rpm,size=nrow(wnba2_small),
replace=FALSE)) %>%
group_by(position) %>%
summarize(avg=mean(shuffle)) %>%
ungroup() %>%
summarize(avg[1]-avg[2]))
}
#plot null distribution
ggplot() +
geom_histogram(data=results_rand2,aes(x=diff),
color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_rand2$diff,0.05),
color="red",linetype="dashed",linewidth=0.75) +
geom_vline(xintercept=quantile(results_rand2$diff,0.95),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="WNBA Players (2022-2023 seasons)",
subtitle="Smaller Sample Null Distribution",
x="Difference in Average Rebounds-per-Minute",
y="Count",
caption="Source: ESPN") +
theme_bw()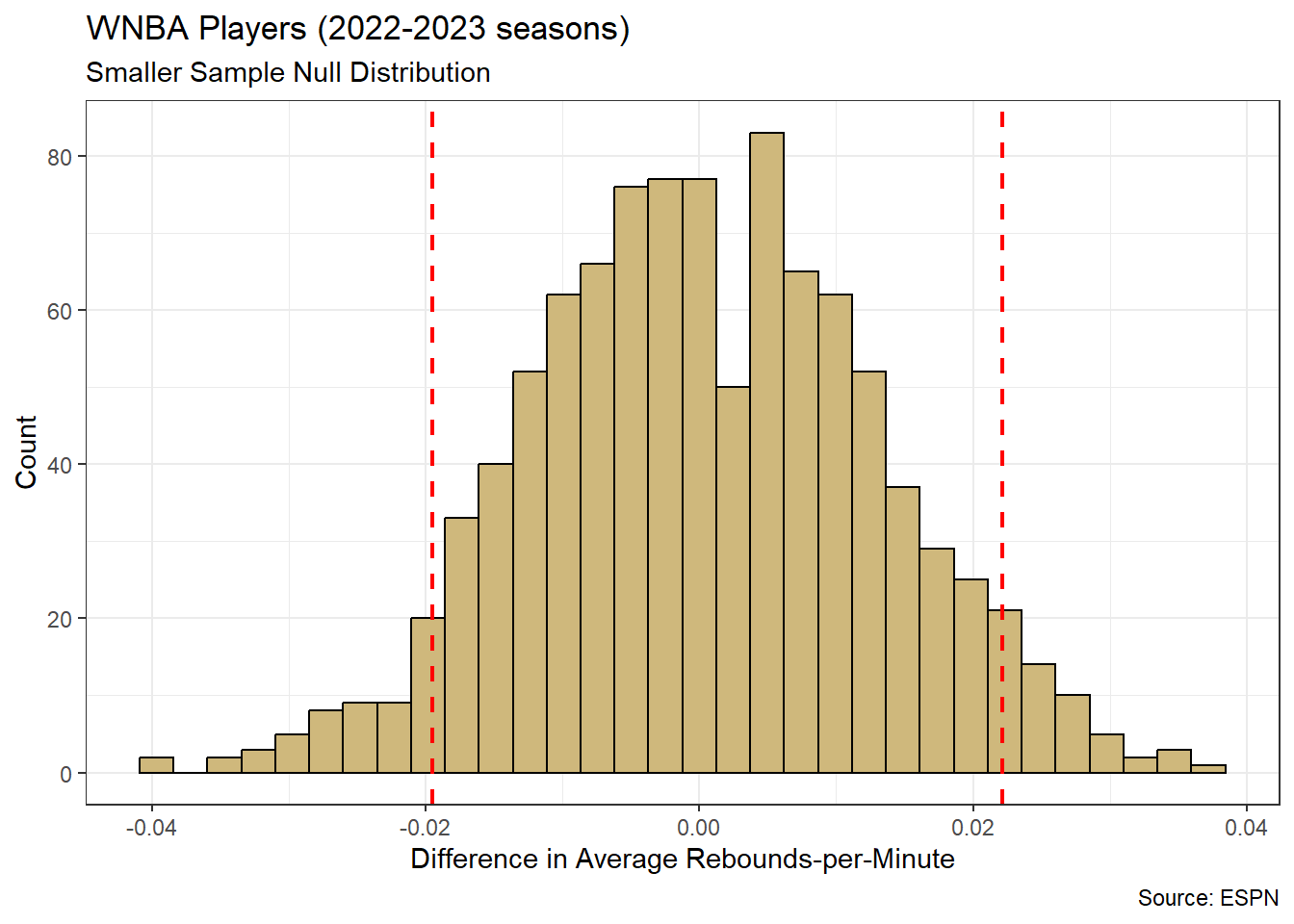
Figure 4.18: Distribution for Difference in Average Rebounds-per-Minute (smaller sample)
Though the shapes are similar, note the \(x\)-axis values in Figure 4.18 compared to Figure 4.17. In the larger sample null distribution, we only need an observed difference of 0.006 to reject the null hypothesis. On the other hand, the smaller sample null distribution requires a difference greater than 0.022. The burden of evidence is much stronger when the sample is smaller. This is because the variability of the mean is greater when the sample size is smaller. To overcome the additional variability, we require stronger evidence.
From a statistical perspective, large sample sizes offer a number of benefits. However, there is a difference between statistical significance and practical significance. In our larger sample null distribution, any difference in rebounding efficiency greater than 0.006 is considered statistically significant. This does not necessarily mean that domain experts find such a difference practically significant. A difference of 0.006 is roughly equivalent to forwards achieving an additional rebound every 4 games compared to guards. Do coaches and managers of a team actually care about this difference? Maybe or maybe not, but the answer is not as straight forward as in the statistical realm. In terms of collaboration, it is just as important for data scientists to learn about practical significance as it is for domain experts to learn about statistical significance.
Answer the Question
Based on a random sample of 1,400 forwards and 1,966 guards in the WNBA, we have strong statistical evidence to suggest a difference in average rebounding efficiency. Said another way, it appears there is a difference in the average rebounds-per-minute between forwards and guards. While the data suggests forwards typically have a larger rebounding efficiency than guards, additional testing is required to formalize this conclusion since we conducted a two-sided (versus one-sided) test.
A logical extension to this analysis is to increase the specificity to the two different types of guards and forwards. However, with four different parameters to compare, we can no longer employ the methods demonstrated in this section. Instead, we must use a special type of test presented in the next section.
4.3.6 Many Populations
The next logical step after comparing two population means is to compare three or more means. The process for comparing means across multiple populations is commonly referred to as the analysis of variance (ANOVA). As with population proportions, difficulties arise when attempting to compare more than two means. We could simply conduct multiple pair-wise tests on the differences in means. But the number of tests grows relatively quickly with the number of means. For example, the comparison of 5 population means requires 10 pair-wise tests. In general, for \(k\) different means we require the following number of tests:
\[ \text{Number of Tests}={k \choose 2}=\frac{k!}{2(k-2)!} \]
The exclamation point refers to the factorial which is computed by multiplying the associated value by every smaller integer down to one. Thus, \(5!=5\cdot4\cdot3\cdot2\cdot1=120\). Not only is the number of tests a computational burden, but the more tests we conduct the more likely we are to suffer a false positive. Recall, that our level of significance (\(\alpha\)) represents the chance of detecting a difference between two populations when none exists. When we perform many individual tests, our chance that at least one of them witnesses a false positive is greater than we might expect. In general, if we perform \(k\) tests each at significance level \(\alpha\), then our probability of at least one false positive is:
\[ \text{False Positive Rate}=1-(1-\alpha)^k \]
So, if we conduct 5 independent tests each at a significance level of 0.10, then the overall chance of at least one false positive is \(1-0.90^5=0.41\). Even though each individual test only has a 10% chance of a false positive, there is a 41% chance that at least one of the five will have a false positive! Consequently, performing multiple difference in means tests is not ideal. ANOVA is designed to overcome this issue. Rather than conducting multiple tests, ANOVA evaluates the difference between populations in a single test. We demonstrate this with an example problem a functions from the tidyverse.
Ask a Question
In Chapter 3.2.3 we explored the average birth weight for babies whose mothers practiced various smoking habits. The sample data was part of the Child Health Development Studies (CHDS) conducted by the Public Health Institute in the early 1960s. Using that same data, suppose we are now interested in formally evaluating differences in average birth weight for populations of mothers who did and did not smoke during their lifetimes or pregnancies. Specifically, we ask the following question: Is there a difference in birth weight for babies whose mothers did and did not smoke before or during pregnancy?
Acquire the Data
The data we require is included as part of the mosaicData package in a file named Gestation. Below we import and wrangle the data.
#load library
library(mosaicData)
#import data
data(Gestation)
#wrangle data
Gestation2 <- Gestation %>%
transmute(smoke=fct_collapse(as.factor(smoke),
Never="never",
Before=c("until current pregnancy",
"once did, not now"),
During="now"),
weight=wt/16) %>%
na.omit()Our goal with the data wrangling is two-fold. First, we limit the smoking habit populations to three categories: never, before, and during. While mothers who never smoked in their lifetime and mothers who actively smoked during pregnancy are straightforward categories, the other two descriptors in the original data are ambiguous. The labels “until current pregnancy” and “once did, not now” both imply some amount of smoking before pregnancy, but none during pregnancy. Thus, we combine these into a single population. Our second goal with wrangling is to convert the birth weight from ounces to pounds, simply to make the values a bit more intuitive. We then inspect our resulting data frame.
## Rows: 1,226
## Columns: 2
## $ smoke <fct> Never, Never, During, Before, During, Before, Never, Never, Nev…
## $ weight <dbl> 7.5000, 7.0625, 8.0000, 7.6875, 6.7500, 8.5000, 8.6250, 8.2500,…The data consists of smoking habits and birth weights (in pounds) for 1,226 mothers. We are now ready to pursue our analysis.
Analyze the Data
Prior to conducting our ANOVA hypothesis test, we generate a comparative box plot to explore initial evidence of a difference between the smoking populations.
#create comparative boxplot
ggplot(data=Gestation2,aes(x=weight,y=smoke)) +
geom_boxplot(fill="#CFB87C") +
geom_vline(xintercept=mean(Gestation2$weight),color="red",
linewidth=1) +
labs(title="Child Health and Development Studies (CHDS)",
x="Birth Weight (pounds)",
y="Mother's Smoking Status",
caption="Source: Public Health Institute") +
scale_x_continuous(limits=c(3,12),breaks=seq(3,12,1)) +
theme_bw()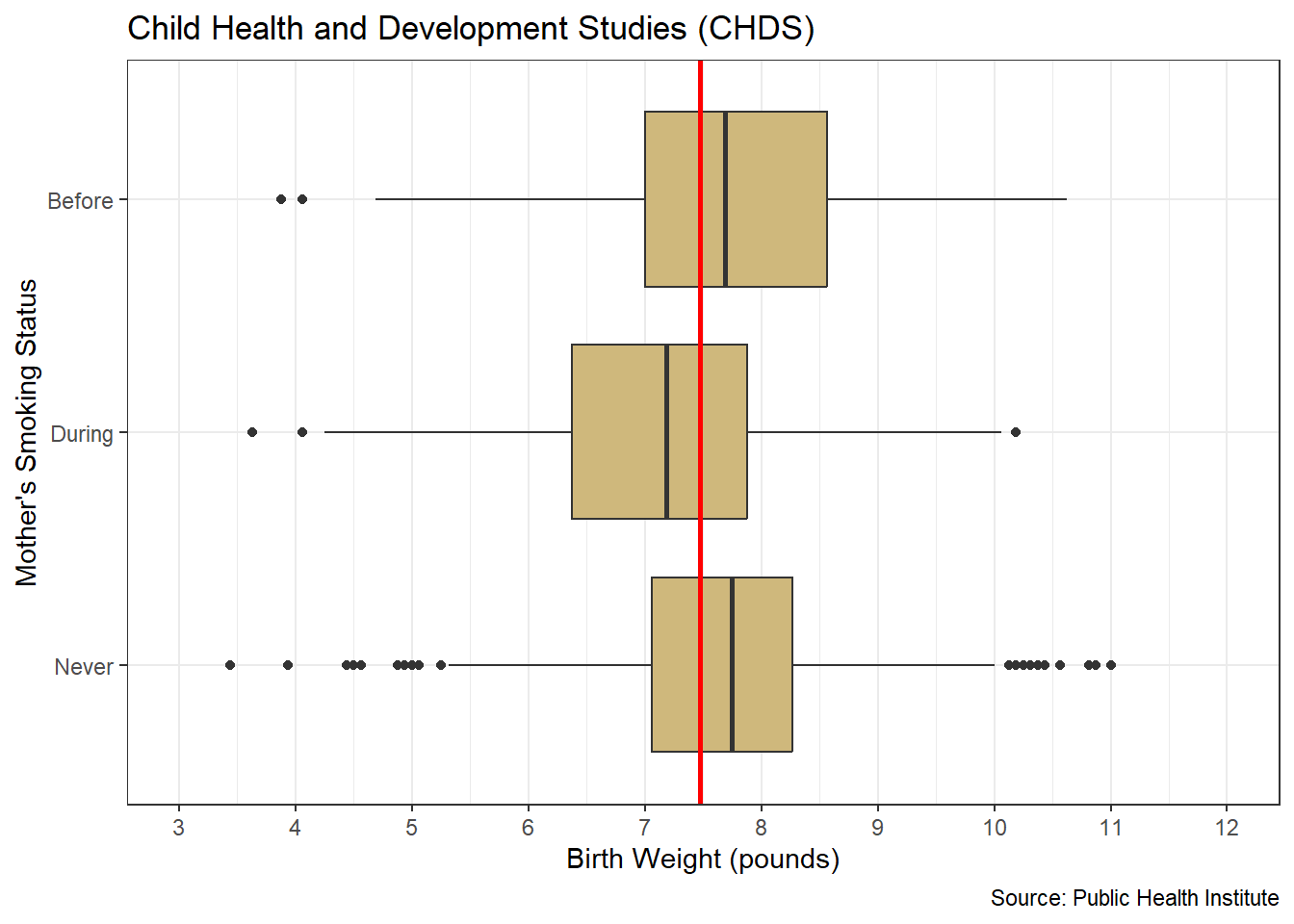
Figure 4.19: Comparative Box Plot of Birth Weight versus Smoking Status
The red line in Figure 4.19 represents the overall average birth weight, regardless of smoking status. Based on the interquartile range (IQR) for each smoking population, it appears that mothers who smoked during pregnancy birthed more babies with below average weights. By contrast, mothers who never smoked or who stopped smoking prior to pregnancy appear to have more above average birth weights. We check this numerically by summarizing the birth weights by smoking status.
#compute stats within populations
Gestation2 %>%
group_by(smoke) %>%
summarize(count=n(),
avg=mean(weight),
stdev=sd(weight)) %>%
ungroup()## # A tibble: 3 × 4
## smoke count avg stdev
## <fct> <int> <dbl> <dbl>
## 1 Never 544 7.67 1.07
## 2 During 484 7.13 1.13
## 3 Before 198 7.74 1.14The sample size for mothers who smoked before pregnancy is smaller than the other two populations. However, there is still more than enough data for our purposes. While each of the populations have similar sample standard deviations (spread), the sample mean (center) for mothers who smoked during pregnancy is lower than the other two. We have reasonable initial evidence for a difference in mean birth weights, but we formally assess this evidence with a hypothesis test.
Let \(\mu_1\), \(\mu_2\), and \(\mu_3\) be the true mean birth weight for babies whose mother never smoked, smoked during pregnancy, and smoked before pregnancy, respectively. Our null hypothesis is that the mean birth weights are the same, regardless of the mother’s smoking habits. The alternate hypothesis is that at least one smoking status experiences a different mean birth weight.
\[ \begin{aligned} H_0:& \; \mu_1=\mu_2=\mu_3 \\ H_A:& \; \text{At least one mean differs} \end{aligned} \]
In the context of this test, the significance level represents the probability of reporting a difference between populations when in fact they are the same. Given the potential consequences of ostracizing a particular population, we choose a very small significance level of \(\alpha=0.005\). Thus, we only risk a half-a-percent chance of a false positive.
Next we must compute a test statistic that measures evidence in favor of the alternate hypothesis. With three distinct means, a “difference in means” does not really make sense. As with goodness-of-fit tests, we instead construct a composite statistic that incorporates all of our populations. In words, our test statistic measures both the variance between populations and the variance within populations. Hence the name analysis of variance!
\[ \text{Test Statistic}=\frac{\text{Variance between Populations}}{\text{Variance within Populations}} \]
The numerator of our ANOVA test statistic measures the variance between the three smoking populations. Think of this value as a measure of the total distance of the blue boxes from the red line in Figure 4.19. The further the individual average weights from the overall average weight, the more distinct the smoking populations. The denominator of the test statistic measures the variance within the three smoking populations. Think of this as the total width of the blue boxes in Figure 4.19. The closer the individual weights to their own average weight, the more predictable the smoking populations. A large test statistic value suggests the three smoking populations are predictably distinct in terms of birth weights. Rather than compute these variances manually, we leverage the aov() function for ANOVA tests.
## Df Sum Sq Mean Sq F value Pr(>F)
## smoke 2 92 45.99 37.66 <2e-16 ***
## Residuals 1223 1494 1.22
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The summary of the ANOVA output includes a number of values beyond the scope of this text. Here we focus on two columns. The variance between smoking populations is the value in the Mean Sq column and the smoke row. The variance within smoking populations is the value in the Mean Sq column and the Residuals row. The column title refers to mean squared deviation, which is our measure of variance. The ratio of the two variances represents the test statistic, which is listed in the F value column. This column title references the fact that our test statistic follows the F distribution. We extract the test statistic element of the output by referencing the appropriate row and column in the list.
## [1] 37.65731It is difficult to interpret the significance of a test statistic value of 37.66 without knowing what values are common under the null hypothesis. If all three populations truly have the same mean, then would it be rare to witness a test statistic of 37.66 in a sample? We simulate equal means by randomizing the birth weights across the smoking populations. Then we repeatedly complete ANOVA calculations and retrieve the associated test statistics.
#initiate empty vector
results <- data.frame(fstat=rep(NA,1000))
#repeat randomization process 1000 times and save results
for(i in 1:1000){
set.seed(i)
Gestation3 <- Gestation2 %>%
transmute(smoke,
shuffle=sample(x=weight,size=nrow(Gestation2),
replace=FALSE))
anova2 <- aov(shuffle~smoke,data=Gestation3)
results$fstat[i] <- summary(anova2)[[1]][1,4]
}The results of our randomization process provide 1,000 test statistics aligned with the null hypothesis of equal means. These values represent the null distribution, which we depict in Figure 4.20.
#plot null distribution
ggplot(data=results,aes(x=fstat)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results$fstat,probs=0.995),color="red",
linewidth=1,linetype="dashed") +
labs(title="Child Health and Development Studies (CHDS)",
subtitle="Null Distribution",
x="Test Statistic",
y="Count",
caption="Source: Public Health Institute") +
theme_bw()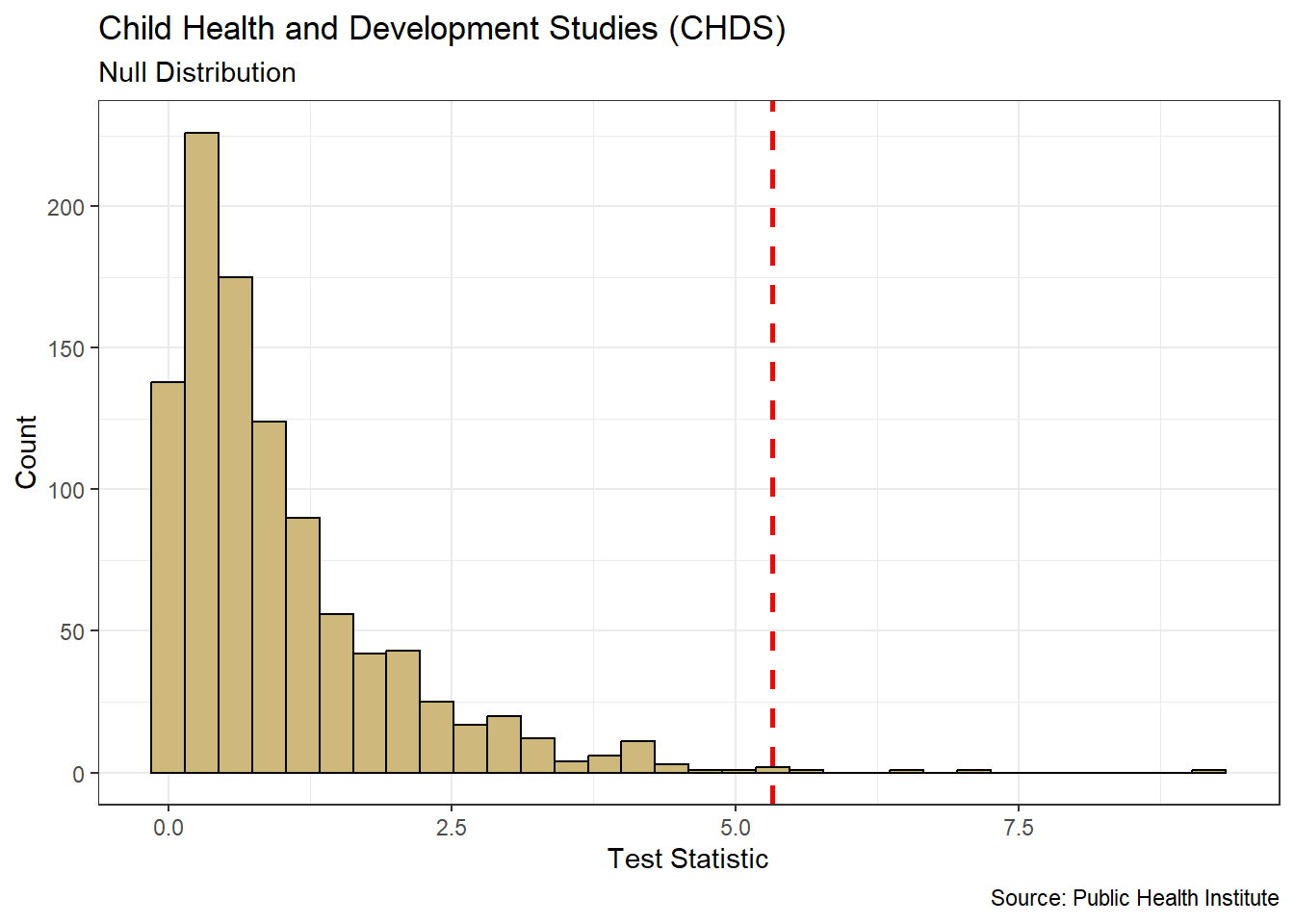
Figure 4.20: Randomized Null Distribution for Test Statistic
As previously mentioned, this right-skewed shape is known as an F distribution. But, given our computational approach, the label is unnecessary for the purposes of comparing a test statistic to the significance threshold. The significance level of \(\alpha=0.005\) places the threshold at the dashed red line in Figure 4.20. In order to reject the null hypothesis, we require a test statistic greater than 5.32. The observed test statistic value of 37.66 is so large that it does not appear on the plot. Consequently, our evidence is well beyond that required to reject the null hypothesis.
Another way to interpret the results of the ANOVA is to compare the p-value to the significance level. Since there are no values in the null distribution as extreme as 37.66, our p-value is effectively 0. Given this is less than the significance level of 0.005, we reject the null hypothesis. The p-value suggests that it is nearly impossible to witness our observed sample data if in fact the population means are all equal. On the contrary, we have strong evidence to suggest that average birth weights differ according to the mother’s smoking habits.
Advise on Results
When presenting the results of an ANOVA to stakeholders, it is important to point out that we have only identified that some difference exists between populations. We have not identified which population differs from the others. Based on the box plots in Figure 4.19, we might suspect that mothers who smoke during pregnancy represent the distinct population. However, the ANOVA does not explicitly evaluate this suspicion. Instead, we need to compute multiple difference in means confidence intervals to identify the distinct population. That brings us right back to our multiple comparisons problem!
With three different populations, we must construct \({3 \choose 2}=3\) confidence intervals. But we know that our chances of at least one interval missing the true difference in means grows with the number of intervals. Consequently, the confidence level of each interval must be larger than we might otherwise choose. For example, in order to achieve an overall confidence level of 99.5% (aligned with \(\alpha=0.005\)), each individual confidence level must be 99.83%. If we are 99.83% confident that each of the three intervals captures the true difference in means, then we are 99.5% (\(0.9983^3=0.995\)) confident that they all capture the true difference. We compute all three intervals below using bootstrapping.
#isolate each population
never <- Gestation2 %>%
filter(smoke=="Never") %>%
select(weight)
during <- Gestation2 %>%
filter(smoke=="During") %>%
select(weight)
before <- Gestation2 %>%
filter(smoke=="Before") %>%
select(weight)
#initiate empty data frame
results_boot <- data.frame(avg1=rep(NA,10000),
avg2=rep(NA,10000),
avg3=rep(NA,10000))
#resample 10,000 times and save sample means
for(i in 1:10000){
set.seed(i)
results_boot$avg1[i] <- mean(sample(x=never$weight,replace=TRUE))
results_boot$avg2[i] <- mean(sample(x=during$weight,replace=TRUE))
results_boot$avg3[i] <- mean(sample(x=before$weight,replace=TRUE))
}
#compute confidence intervals for differences
quantile(results_boot$avg1-results_boot$avg2,probs=c(0.00085,0.99915))## 0.085% 99.915%
## 0.3196815 0.7591244## 0.085% 99.915%
## -0.3424356 0.2251479## 0.085% 99.915%
## -0.8923586 -0.3058853The first interval represents the difference between mean birth weights for mothers who never smoked and those who smoked during pregnancy. We are 99.83% confident that this difference is between 0.32 and 0.76 pounds. Since both bounds of the interval are positive, it appears mothers who never smoke do experience greater birth weights. A similar result is true for the third interval, which compares mothers who smoked during pregnancy to those who stopped smoking prior to pregnancy. Since both bounds are negative, it appears mothers who stop smoking witness greater birth weights. However, the second confidence interval includes zero within the bounds. This suggests it is plausible that mothers who never smoke and mothers who stop smoking experience the same average birth weights (i.e., a difference of zero).
Even with only three populations, we see the challenges associated with performing multiple comparisons. In order to impose such a high level of confidence on each interval, we increase the number of bootstrap resamples to 10,000. Otherwise, we may not obtain sufficient observations in the tails of the sampling distribution. This grows computationally expensive as the number of compared populations increases. However, if we want to objectively isolate the populations that differ from the others with a high level of confidence, then we must accept this cost. Had the ANOVA test failed to reject the null hypothesis, there would be no reason to conduct multiple comparisons. Since the ANOVA did reject the null, our stakeholders will likely want to know which population differs. After conducting multiple comparisons, we can confidently state that the population of mothers who smoke during pregnancy experience lower average birth weights than the other two populations.
Of course we still must distinguish statistical significance from practical significance. As data scientists, we can speak to the statistical significance present in our results. But only domain experts should speak to the practical significance. Compared to mothers who never smoke or who stop smoking, mothers who smoke during pregnancy are likely to birth babies between about 0.3 and 0.8 pounds lighter. Does such a weight difference introduce potential health risks for the baby? Data scientists are unlikely to be qualified to answer this question. Thus, careful collaboration with domain experts is critical.
Answer the Question
Based on a sample of 1,226 live births, it appears there is an association between a mother’s smoking habits and the birth weight of the baby. Specifically, mothers who smoke during pregnancy are likely to give birth to babies between about 0.3 and 0.8 pounds lighter than mothers who never smoke or who stop smoking prior to pregnancy. Further research is likely necessary to determine if this weight difference is associated with health risks for the baby. Additionally, these results do not consider any other impacts beyond birth weight that may be associated with a mother’s smoking habits.
4.4 Resources: Inferential Analyses
Below are the learning objectives associated with this chapter, as well as exercises to evaluate student understanding. Afterward, we provide recommendations for further study on the topic of inferential analysis.
4.4.1 Learning Objectives
After completing this chapter, students should be able to:
- Summarize the common types of random sampling and their appropriate applications.
- Define the common types of sampling bias and how each can be avoided or remedied.
- Distinguish between and compute common population parameters and sample statistics.
- Describe the key components of a confidence interval and their impact on its width.
- Explain and execute bootstrap resampling with replacement based on a random sample.
- Construct bootstrap sampling distributions and visualize confidence intervals or bounds.
- Construct confidence intervals or bounds for a population proportion, mean, or slope.
- Interpret intervals or bounds for a proportion, mean, or slope in real-world context.
- Construct and interpret intervals or bounds for the difference in two or more parameters.
- Describe the key steps of a hypothesis test and their impact on the final conclusion.
- Distinguish between one and two-sided hypotheses, and their impact on significance.
- Construct a simulated null distribution and visualize the p-value and significance.
- Complete hypothesis tests of a claim regarding a population proportion, mean, or slope.
- Interpret hypothesis test results for a proportion, mean, or slope in real-world context.
- Complete and interpret hypothesis tests for the difference in two or more parameters.
4.4.3 Further Study
In this chapter we introduce the most common computational methods for inferential statistics. Though we purposely avoid more traditional methods involving mathematical theory, such approaches are nevertheless valuable knowledge for all data scientists. Below we suggest additional resources regarding both computational and theoretical methods of inferential statistics.
A comprehensive textbook with a modern approach to both probability and statistics is Computational Probability and Statistics by Bradley Warner and others (Warner et al. 2023). The book opens with an introduction to random variables and probability distributions before moving on to inferential statistics and predictive modeling. In all cases, the focus is on computational methods as opposed to more traditional mathematical theory. As such, it is a fantastic resource for an introductory course in probability and statistics.
Another great resource that combines both computational and mathematical approaches to inference is Introduction to Modern Statistics by Mine Cetinkaya-Rundel and Johanna Hardin (Cetinkaya-Rundel and Hardin 2021). The authors present confidence intervals and hypothesis tests for means, proportions, and regression parameters. For those seeking a single resource for an intermediate statistics course, this book would be a great option.
In its seventh edition, Mathematical Statistics with Applications by Dennis Wackerly and others remains one of the go-to texts for a strong foundation in statistical theory (Wackerly et al. 2008). This extensive textbook is designed for a traditional two-semester sequence in calculus-based probability and statistics. After decades of editions, it is an incredibly reliable resource for those who want to dive deep into the mathematical theory.
An approachable algebra-based text is Mario F. Triola’s Elementary Statistics (Triola 2021). After 14 editions, Triola’s book continues to be a user-friendly option covering everything from data exploration to probability distributions to inferential statistics. The delivery is application-based, with real data sets, and leverages mathematical formulas founded in theory.