Chapter 5 Predictive Analyses
The third and final type of analysis conducted by data scientists involves predictive modeling. As we might expect from the title, this approach involves predicting the unknown value of one variable using known values of other variables. In the context of modeling, we refer to the response and the predictors. The response variable represents the output or dependent variable in a model. The predictors represent the inputs or independent variables. Predictive modeling differs from inferential statistics primarily in its use of predictor variables. Inferential techniques, such as confidence intervals and hypothesis tests, provide reasonable estimates of the mean response, but they do not leverage potentially-valuable information provided by associated predictors. By contrast, predictive models are designed to identify and employ associated predictors and produce a better estimate of the response than the mean alone.
There exist a wide variety of methods for modeling data. Consequently, we open this chapter by decomposing various model types and the associated terminology. Specifically, we distinguish supervised from unsupervised models, regression from classification, and finally parametric from nonparametric models. Each combination of model types has its own unique purpose, methods, and tools. While we provide introductory applications for many models, additional course work is required to master the full suite of options. After establishing the foundations of modeling, we focus on the types of variables we hope to predict.
We construct models to predict two types of response variables: numerical and categorical. Models designed to predict numerical variable values are referred to as regression models. Thus, response variables such as height, weight, cost, duration, and distance lend themselves well to regression modeling. On the other hand, we predict categorical variables using classification models. In the context of factors (grouped categorical variables), we can think of this as predicting the appropriate level for the response. Factors such as test results (pass/fail), game outcomes (win/lose), and logical conclusions (true/false) require classification models. While categorical response variables are not limited to binary outcomes (e.g., pass/fail), that is our focus in this text. More advanced multinomial classification is reserved for other offerings.
5.1 Data Modeling
In general, a model is a mathematical representation of a real-world system or process. When that model is constructed based on random sample data from a stochastic process, we refer to it as a statistical model. Further still, we use the label statistical learning model, because the associated algorithms “learn” distributions and associations from the sample data. Let’s investigate the primary types of models data scientists construct.
5.1.1 Model Types
While there are many types of statistical learning models, we normally identify them based on the three criteria described in the subsections that follow.
Supervised versus Unsupervised
The first major division of statistical learning models identifies whether they are supervised or unsupervised. Put simply, supervised models include a response variable and unsupervised models do not. When a response variable is present, its values “supervise” the associated algorithm to produce an accurate model. Since the objective of this chapter is to predict a response, all of the models are supervised. Common supervised statistical learning methods include:
- Linear Regression
- Logistic Regression
- Discriminant Analysis
- Smoothing Splines
- \(K\)-Nearest Neighbors
- Decision Trees
When our analysis does not include an identified response variable, we instead construct unsupervised models. Unsupervised models lend themselves well to exploratory analyses. When we have no response variable to explain or predict, what remains to explore? We seek to understand relationships between the independent variables. For example, there may exist inherent clusters of observations based on combinations of independent variable values. We introduced this unsupervised approach in Chapter 3.3.6. Another common point of interest is whether independent variables are associated with one another. In these cases, we can distill the behavior of many independent variables down into a smaller number of features that exhibit similar behavior. We described this process of dimension reduction in Chapter 3.3.7. Typical unsupervised learning methods include:
- Cluster Analysis
- Principal Components Analysis
If the appropriate modeling approach is supervised (i.e., includes a response variable), then the next division of methods regards the type of response variable.
Regression versus Classification
A response variable can be numerical (quantitative) or categorical (qualitative). Numerical variables can be discrete (counts) or continuous (measures), while categorical variables can be ordinal (ranks) or nominal (names). Numerical response variables require regression modeling, while categorical response variables require classification modeling.
When the response variable is numerical, we choose from among a suite of regression methods. Most regression algorithms assume the numerical response is a continuous variable, even if the observed values are discrete (e.g., integer). Thus, data scientists must be careful in accurately interpreting the explanations or predictions of a discrete response when treating it as continuous. Drawing from the previous list of supervised learning methods, regression approaches include:
- Linear Regression
- Smoothing Splines
- \(K\)-Nearest Neighbors
- Decision Trees
For categorical response variables, we apply classification methods. By far, the most common form is binary classification. Such problems distinguish True from False, Win from Lose, and Success from Failure. However, in all such cases we typically simplify the two categories to 1 and 0. That said, multinomial methods also exist for the classification of more than two categories. Sometimes the distinction between a discrete numerical response and an ordinal categorical response is unclear. For example, the categories January, February, and March might easily be replaced with the numbers 1, 2, and 3 for month. Both are valid, but the choice could impact the modeling approach. Common classification methods include:
- Logistic Regression
- Discriminant Analysis
- \(K\)-Nearest Neighbors
- Decision Trees
This list highlights two interesting points. Firstly, logistic regression is listed as a method for classification. This naming choice is unfortunate given our desire to clearly distinguish between modeling approaches. The second point of interest is that \(K\)-Nearest Neighbors and Decision Trees are on both lists. This is not a mistake. Some supervised learning methods offer the flexibility to conduct either regression or classification. Once we have identified the type of response we wish to predict, we must decide on the structure with which to model the response. In this regard, we have the choice between parametric or nonparametric methods.
Parametric versus Nonparametric
For certain problems we have much more information about the structure of the stochastic process that generates response data. We might know, for example, that a response variable is linearly associated with a certain predictor. At the very least, we might be able to safely assume such an association based on what we observe in a sample. In other cases, the functional form of the association between two variables may not be so clear. Not only might linearity be inappropriate, but we might have no clear idea of any functional form to apply. This knowledge (or lack thereof) regarding the structure of associations is what distinguishes parametric from nonparametric models.
With parametric models, we apply a specific functional form to the association between the predictors and the response. That form could be linear, log-linear, polynomial, or any other function that specifies a particular structure. The problem is thus reduced to estimating the parameters within that structure. For example, if we decide two variables \(x\) and \(y\) are linearly associated, then the model can be represented as \(y=\beta_0+\beta_1 x\). We then apply a statistical learning algorithm to estimate the intercept and slope parameters (\(\beta_0\) and \(\beta_1\)). Popular parametric modeling approaches include:
- Linear Regression
- Logistic Regression
- Discriminant Analysis
In each of the parametric methods listed above, we assume a specific functional form. When using nonparametric methods, there is no need to make such assumptions. Rather than presuming the data is generated from a process with a strict functional form, nonparametric methods estimate behaviors and derive associations directly from the data. The benefit of nonparametric methods is that they avoid potential mis-identification of structure. For instance, what if the association we think is linear is actually not linear? We can avoid this by not assuming linearity (or any other form) in the first place. However, the cost is that nonparametric approaches generally require much more data in order to identify unstructured associations. Common nonparametric methods include:
- Smoothing Splines
- \(K\)-Nearest Neighbors
- Decision Trees
When selecting a statistical modeling approach, we choose between supervised or unsupervised, regression or classification, and parametric or nonparametric based on the research question, the variable types, and the data-generating process. We describe a few common modeling combinations in the sections that follow. But first we must discuss the appropriate methods for validating a model’s performance.
5.1.2 Model Validation
There are two primary stages in the development of a statistical learning model. First, we must construct a functional relationship between the predictors and the response. This might involve estimating the parameters of an equation or tailoring the stages of an algorithm, depending on the type of model. Regardless, we refer to this stage as training the model. During training, the model learns how best to associate the predictors with the response. After constructing the model, we need to evaluate its performance. We would not want to deploy a model in a real-world scenario without knowing how accurately it can predict the response. We refer to this stage as testing the model. In testing, we learn what to expect from the model prior to deployment. But we must be careful which portion of the sample data we use to train the model versus test the model. This concern leads to the need for a validation set.
A validation set is a portion of the sample data we hold out specifically for evaluating the accuracy of the model. In this way, the data we use to train the model is distinct from the data we use to test the model. The validation set approach tends to result in better estimates of a model’s prediction accuracy because the testing data plays the role of “future” data that was not available when designing the model. Think of this like the difference between practice problems and exam problems in a class. If the practice problems are exactly the same as the exam problems, then a student may score well simply because they memorized the answers. However, if the exam problems are slightly different from the practice problems, then a high score is a much more accurate reflection of genuine understanding. In the same way, when a model is tested on the same data with which it was trained, it may appear artificially accurate. We call this phenomenon overfitting.
When a model is overfit it has been tailored too specifically to one data set and will not typically perform as well on other data. By splitting a sample into training and testing sets, we can avoid overfitting. But what proportion of the sample should be included in each set? If the training set is too large, then the assessment of accuracy on a small testing set will be highly variable. On the other hand, if the training set is too small, then the model will be poorly estimated and introduce bias. A common compromise between these two issues is to select between 70 and 80% of the sample for training. This choice affords sufficient data for the model to learn the associations between predictors and the response, while also reserving enough testing data to compute a reliable accuracy estimate.
The methods for computing the accuracy of a model against a testing set depend on whether we are pursuing regression or classification. The remainder of the chapter distinguishes these two model types and provides example applications of the validation set approach.
5.2 Regression Models
In Chapters 3.3.2 and 4.2.4, respectively, we explored associations and computed inferential statistics for linear regression models. Regression was the appropriate method because the variables of interest were numerical. However, in neither chapter did we attempt to predict a response. With exploratory analysis, the goal was simply to describe the association between numerical variables with a linear equation. We then produced an interval estimate for the slope of that equation using inferential techniques. In this chapter, our objective is to predict the response variable (\(y\)) in a linear equation using the predictor variable (\(x\)).
5.2.1 Simple Linear Regression
By far the most common supervised, parametric, regression model for predicting a numerical response value \(y\) is the simple linear regression model. The qualifier simple indicates there is only one predictor variable \(x\). In later sections we address the case of multiple predictor variables. After estimating the intercept (\(\beta_0\)) and slope (\(\beta_1\)) of a simple linear regression model using the least-squares algorithm, we obtain the function shown in Equation (5.1).
\[\begin{equation} \hat{y} = \hat{\beta}_0+\hat{\beta}_1 x \tag{5.1} \end{equation}\]
The “hat” symbols above the intercept and slope acknowledge that the parameters were estimated from sample data. Consequently, when we input a value for \(x\), the predicted response \(\hat{y}\) is also an estimate. We demonstrate this estimation process in an example below.
Ask a Question
The National Oceanic and Atmospheric Administration (NOAA) seeks to better understand and predict changes in the Earth’s climate and weather. This mission includes a variety of scientific research related to tropical storms in the Atlantic Ocean. One of the many devastating characteristics of a tropical storm is the maximum sustained wind speed, particularly when the storm reaches the classification of a hurricane. Based on the physics of hurricanes, there is a strong relationship between the low pressure center (“eye”) of a storm and the wind speeds produced around its perimeter (“wall”). Consequently, we should be able to predict a storm’s wind speed based on its air pressure. Let’s investigate with the following specific question: What maximum sustained wind speed would we predict for a tropical storm with a central air pressure of 950 millibars?
There is nothing unique about the choice of the value 950. We aim to demonstrate the use of a predictive model for a specific input and this air pressure value is as good as any. The techniques we discuss here are appropriate for a much broader range of air pressures. As a result, our research question is likely of concern to anyone interested in the science or destructive capacity of a tropical storm. A better understanding of the associations between various physical characteristics of a storm could improve our ability to predict the danger to the local populace. That said, the correlation between air pressure and wind speed is widely understood by the scientific community, so we likely won’t reveal anything groundbreaking here! Regardless, the process of answering our question is a valuable academic exercise.
Acquire the Data
The NOAA website offers open access to a number of data tools related to climate and weather. But there is also a convenient data set built into the dplyr package called storms. The data is from NOAA and includes attributes for tropical storms in the Atlantic Ocean from 1975 through 2021. Import, wrangle, and review the data using the code below.
#import storm data
data(storms)
#wrangle storm data
storms2 <- storms %>%
select(wind,pressure) %>%
na.omit()
#review data structure
glimpse(storms2)## Rows: 19,066
## Columns: 2
## $ wind <int> 25, 25, 25, 25, 25, 25, 25, 30, 35, 40, 45, 50, 50, 55, 60, 6…
## $ pressure <int> 1013, 1013, 1013, 1013, 1012, 1012, 1011, 1006, 1004, 1002, 1…Each of the over 19 thousand observations refers to the measurement of a storm’s maximum sustained wind speed (in knots) and the air pressure (in millibars) inside the eye at the start of every six-hour time interval. The word “knot” is short-hand for nautical miles per hour, where a nautical mile is equivalent to 1.15 standard miles. As described in Chapter 5.1.2, we must randomly split this sample data into training and testing sets prior to estimating a model. In the code chunk below, we randomly select 75% of the observations for training and reserve the remaining 25% for testing.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(storms2),
size=floor(0.75*nrow(storms2)),
replace=FALSE)
#split sample into training and testing
training <- storms2[rows,]
testing <- storms2[-rows,]The original sample consists of 19,066 rows. We randomly select 75% of these rows to be part of the training set. But 75% of 19,066 is 14,299.5, so we round down to an integer using the floor() function. We could just as easily have rounded in other ways. The goal is to define an integer number of rows as close as possible to the desired percentage. The resulting 14,299 random row numbers are assigned to the training set. The remaining 4,767 row numbers are assigned to the testing set. With our sample data properly prepared for predictive analysis, we can determine the best model.
Analyze the Data
As always, before estimating a linear model we should ensure that the association between our predictor and response is plausibly linear. Figure 5.1 displays the relationship between air pressure and wind speed in the training data.
#create scatter plot
ggplot(data=training,
mapping=aes(x=pressure,y=wind)) +
geom_point(position="jitter",alpha=0.2) +
labs(title="Atlantic Ocean Tropical Storms (1975-2021)",
subtitle="Training Data",
x="Air Pressure at Storm Center (millibars)",
y="Maximum Sustained Wind Speed (knots)",
caption="Source: NOAA") +
scale_x_continuous(limits=c(875,1025),breaks=seq(875,1025,25)) +
scale_y_continuous(limits=c(0,200),breaks=seq(0,200,25)) +
theme_bw()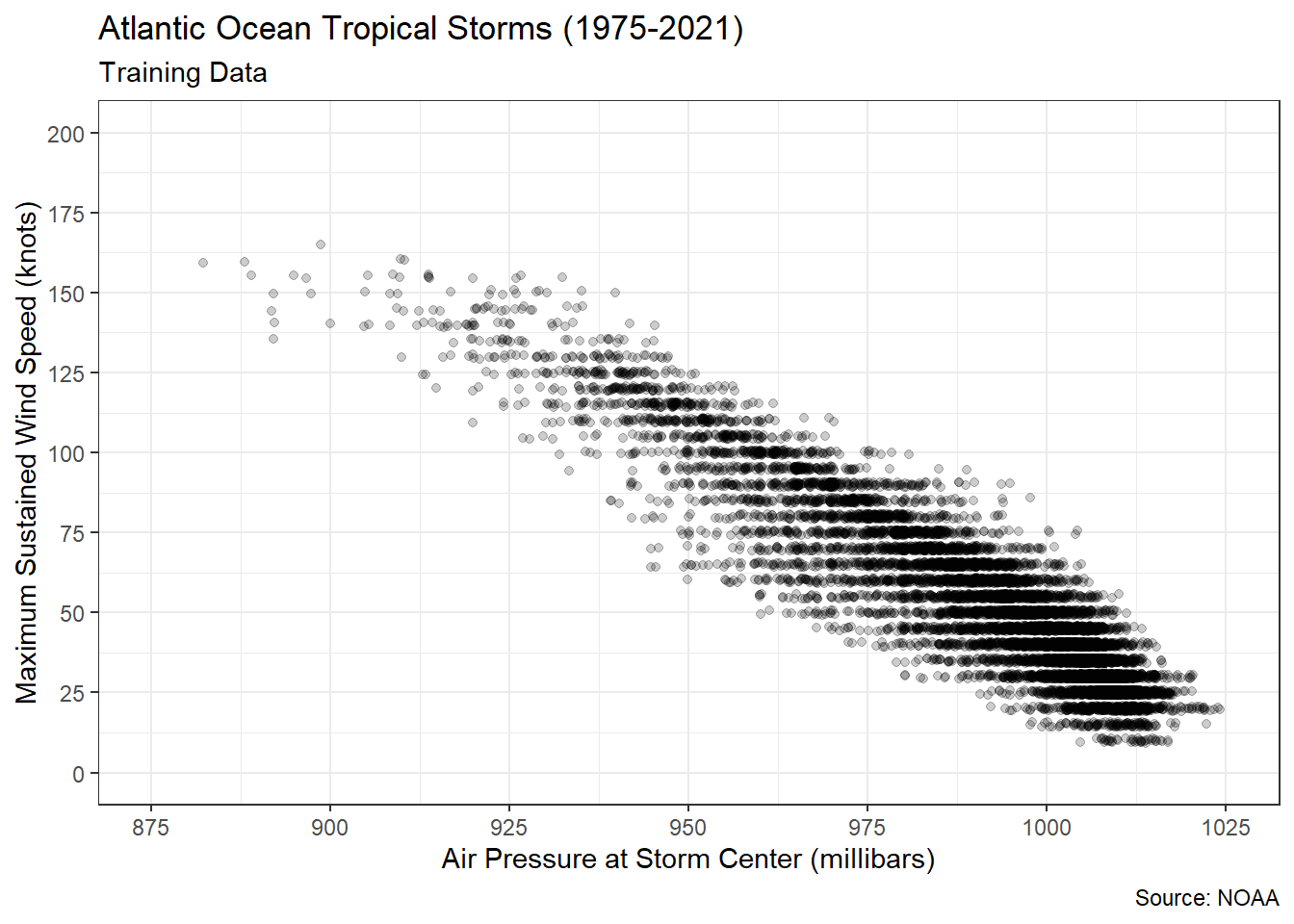
Figure 5.1: Linear Association between Air Pressure and Wind Speed
There appears to be a very strong, decreasing, linear association between the variables. As the air pressure inside the storm center increases, the maximum sustained wind speed appears to decrease. This aligns with what scientists know about pressure gradients. Wind moves from areas of high pressure to areas of low pressure. The larger the difference (gradient) between the two pressures, the faster the wind moves. Thus, very low pressure storm centers draw very high wind speeds. We can confirm our visual evidence by computing a Pearson correlation coefficient.
## [1] -0.9275745A coefficient value of -0.93 confirms a very strong, negative correlation. Based on both visual and numerical evidence, we can feel confident that a linear model is appropriate. Figure 5.2 adds the best-fit line to the scatter plot.
#create scatter plot
ggplot(data=training,
mapping=aes(x=pressure,y=wind)) +
geom_point(position="jitter",alpha=0.2) +
geom_smooth(method="lm",formula=y~x) +
geom_segment(x=950,xend=950,y=-10,yend=105,
linewidth=0.75,linetype="dashed",color="red") +
geom_segment(x=860,xend=950,y=105,yend=105,
linewidth=0.75,linetype="dashed",color="red") +
labs(title="Atlantic Ocean Tropical Storms (1975-2021)",
subtitle="Training Data",
x="Air Pressure at Storm Center (millibars)",
y="Maximum Sustained Wind Speed (knots)",
caption="Source: NOAA") +
scale_x_continuous(limits=c(875,1025),breaks=seq(875,1025,25)) +
scale_y_continuous(limits=c(0,200),breaks=seq(0,200,25)) +
theme_bw()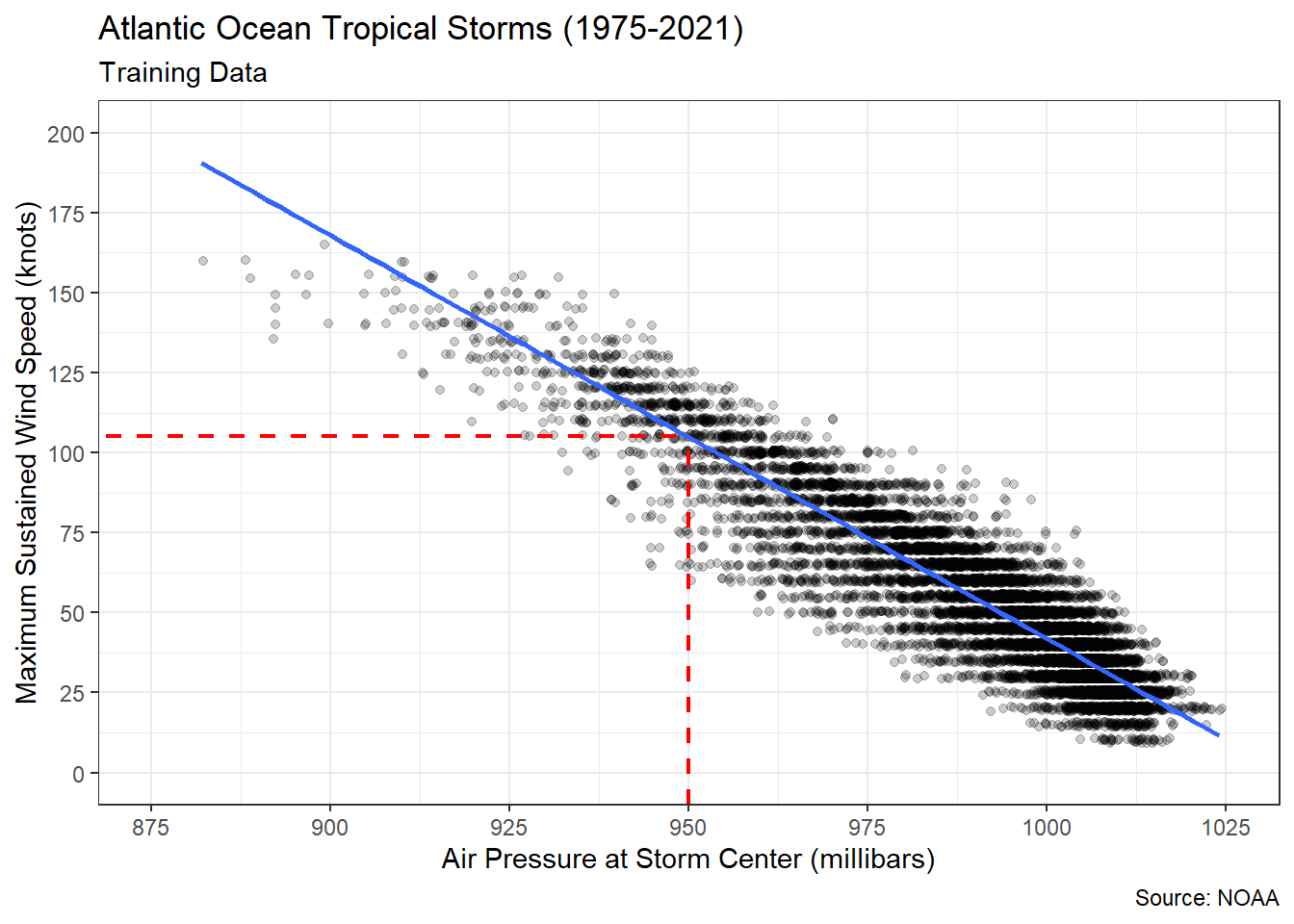
Figure 5.2: Linear Association between Air Pressure and Wind Speed
The best-fit (blue) line offers our first chance to try and answer the research question. Purely based on a visual inspection (dashed red line), it appears a storm with a central air pressure of 950 millibars should produce wind speeds around 105 knots. That said, there are observations in the scatter plot that vary between 60 to 125 knots even when the air pressure is fixed at 950 millibars. We’ll address this variability soon enough. First, let’s determine the equation of the best-fit line.
#estimate simple linear regression model
model <- lm(wind~pressure,data=training)
#review parameter estimates
coefficients(summary(model))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1301.535105 4.216796087 308.6550 0
## pressure -1.259642 0.004243529 -296.8382 0The least-squares algorithm estimated an intercept of \(1301.54\) knots and a slope of \(-1.26\) knots/millibar. In other words, for every one millibar increase in air pressure we expect a reduction in maximum wind speed of 1.26 knots. Returning to the functional form from the introduction to this section, we can write Equation (5.2).
\[\begin{equation} \hat{y}=1301.54 - 1.26 x \tag{5.2} \end{equation}\]
Using this equation, we can obtain a predicted wind speed (\(\hat{y}\)) for any air pressure (\(x\)) of interest. If we input \(x=950\), then we obtain \(\hat{y}=1301.54-1.26 \cdot 950=104.54\). That is very close to our visual estimate of 105 millibars! But there is no reason to perform the arithmetic manually. Instead, we use the predict() function.
## 1
## 104.8755Within the predict() function we reference the name of the linear model and the new data we want to input. The result is a similar prediction that varies only due to rounding. In one sense we could stop here and answer our research question. The answer appears to be 105 millibars. However, we must recall the lessons of Chapter 4. The prediction \(\hat{y}=105\) is merely a point estimate. If we had sampled different storms, then we would likely obtain a different model and a different prediction. We would prefer to have a plausible range of values for the prediction and a measure of confidence. Luckily, we can employ the same bootstrap resampling techniques we already learned.
#initiate empty data frame
results_boot <- data.frame(wind=rep(NA,1000))
#resample 1000 times and save predictions
for(i in 1:1000){
set.seed(i)
storms_i <- sample_n(training,size=nrow(training),replace=TRUE)
model_i <- lm(wind~pressure,data=storms_i)
results_boot$wind[i] <- predict(model_i,newdata=data.frame(pressure=950))
}In the previous code chunk, we repeatedly resample the training set with replacement. This process simulates gathering new storm measurements from the population. After each resample, we fit a simple linear regression model and predict the wind speed for the 950 millibar air pressure. Each time we obtain a slightly different prediction. We can review the distribution of these predictions in Figure 5.3.
#plot resampling distribution
ggplot(data=results_boot,
mapping=aes(x=wind)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$wind,0.05),
color="red",linetype="dashed",linewidth=0.75) +
geom_vline(xintercept=quantile(results_boot$wind,0.95),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="Atlantic Ocean Tropical Storms (1975-2021)",
subtitle="Prediction Distribution for 950 millibars Air Pressure",
x="Maximum Sustained Wind Speed (knots)",
y="Count",
caption="Source: NOAA") +
scale_x_continuous(limits=c(104,106),breaks=seq(104,106,0.25)) +
theme_bw()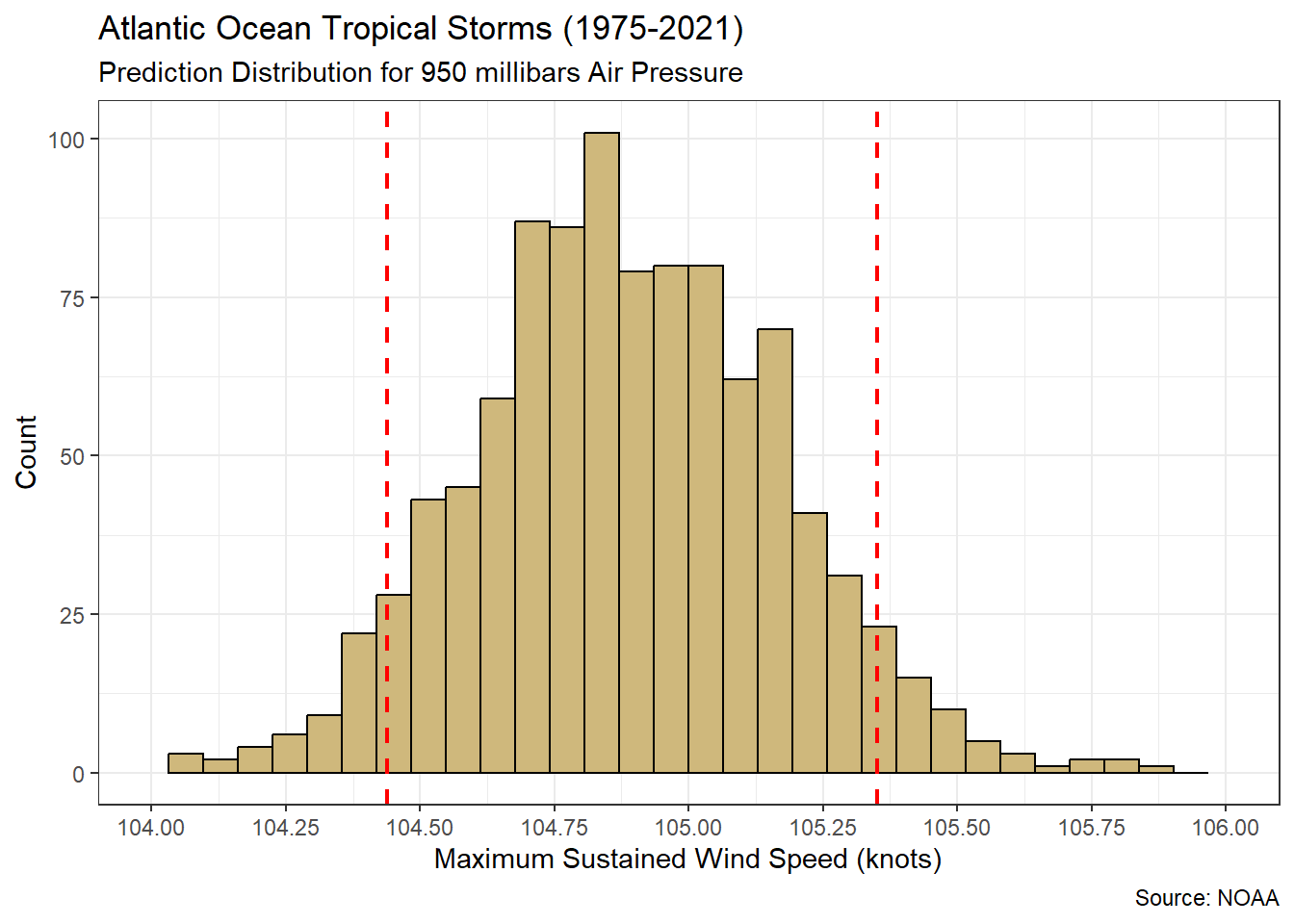
Figure 5.3: Distribution for predicted maximum wind speed (knots) when air pressure is 950 millibars
Over 1,000 simulated training sets, our prediction of the maximum wind speed varies between 104 and 106 knots. A 90% confidence interval (red dashed lines) ranges between 104.44 and 105.35 knots. Hence, when the central air pressure of a storm is 950 millibars we are 90% confident that the maximum sustained wind speed will be between 104.44 and 105.35 knots, on average. As usual, the confidence interval is far superior to a single point estimate.
Advise on Results
A key point when advising stakeholders on the results of a predictive analysis regards the proper interpretation of the predicted response (\(\hat{y}\)). Importantly, \(\hat{y}\) represents the average (mean) response value given a particular predictor value \(x\). It was not an accident that we included the phrase “on average” at the end of our confidence interval interpretation. When we predict a wind speed of 105 knots, we are not suggesting that the next storm with a pressure of 950 millibars will produce winds of exactly 105 knots. We are saying that the next 1,000 storms (for example) with a pressure of 950 millibars will produce an average wind speed of 105 knots.
The same careful interpretation applies to the interval estimates. Our 90% confidence interval refers to the average wind speed of all storms that have a central air pressure of 950 millibars. If we wanted to predict the wind speed of the next storm that has a pressure of 950 millibars, then the 90% confidence interval would be much wider. It is much more difficult to precisely predict the behavior of a single event than the average behavior of many events. This is a relatively foundational concept in statistics. We can observe the difference in the two intervals using the predict() function.
#compute 90% confidence interval
predict(model,newdata=data.frame(pressure=950),
interval="confidence",level=0.9)## fit lwr upr
## 1 104.8755 104.5447 105.2063#compute 90% prediction interval
predict(model,newdata=data.frame(pressure=950),
interval="prediction",level=0.9)## fit lwr upr
## 1 104.8755 89.21584 120.5352By adding two optional terms in the predict() function we transform a point estimate into an interval estimate. In this case, R is relying on mathematical theory to produce the lower and upper interval bounds. We will not belabor the details here. Our current purpose is to provide some intuition regarding the precision of our predictions. When we choose the option interval="confidence" and set the level to 90%, we are mimicking the bootstrap resampling from the previous section. The minor differences in the bounds are due to applying theory rather than computation. We refer to this estimate as a confidence interval for the mean response.
The second estimate is known as a prediction interval. A prediction interval seeks to estimate the next response value rather than the average response value. Notice the bounds are much wider. The next storm with a pressure of 950 millibars could plausibly produce winds anywhere from 89.22 to 120.54 knots. A single storm could vary greatly and we observed that first-hand in the scatter plot in Figure 5.2. But averaging tends to reduce variability. When we average the wind speeds of the next 1,000 storms with a pressure of 950 millibars, we obtain a much more precise range of plausible values.
Both types of intervals are incredibly value, but it is important for data scientists to apply them appropriately. When reporting the 90% confidence interval to a stakeholder, it is critical they understand that the estimate refers to the mean response. Imagine you provide the precise confidence interval of 104.54 to 105.21 knots and the next storm with a pressure of 950 millibars produces winds of 120 knots. A stakeholder might think your analysis is questionable, even though this wind speed is included in the prediction interval. Thus, it is important to clearly communicate this distinction.
Answer the Question
Based on a training set of 14,299 Atlantic storm measurements between 1975 and 2021, we predict an average maximum sustained wind speed between 104.44 and 105.35 knots when the air pressure of the eye is 950 millibars. This prediction is only valid for tropical storms in the Atlantic Ocean and the model should only be applied to central air pressures between 882 and 1,024 millibars. Other air pressure values are outside the range of the training data and require extrapolation. Further research is required to test a broader range of air pressures.
While the prediction of an individual input value is useful, we prefer to predict all the values in the testing set and to determine the overall accuracy of the model. After all, prediction models are only valuable if we can expect them to be consistently close to the actual response for a variety of input values. That said, there are many different measures for the proximity of predictions and observed values. In the next section, we describe one of the most common measure of regression accuracy.
5.2.2 Regression Accuracy
The primary metric for evaluating the quality of a prediction model is accuracy. However, the concept of accuracy has a slightly different meaning depending on whether we are predicting a numerical or categorical (factor) variable. When predicting the levels of a factor, we simply count the number of times the predictions are correct or incorrect. But with a continuous numerical variable, our predictions for the response will seldom (if ever) be exactly correct. As a result, we instead measure accuracy in terms of distance from the correct value. A common metric for the aggregate distance of all predictions from the correct numerical value is root mean squared error (RMSE).
The calculation for RMSE proceeds exactly how the name implies. First we compute the error as the distance between the true value and the predicted value. Because those distances can be positive or negative, depending on whether we over or under-estimate the true value, we square the error. In order to aggregate the squared errors for all predictions made by the model, we compute the mean. However, that mean is in squared units which is not very intuitive in real-world context. Thus, we take the square root to return to the original units of the response variable. In mathematical notation, RMSE is represented as follows:
\[\begin{equation} \text{RMSE}=\sqrt{\frac{\sum (y-\hat{y})^2}{n}} \tag{5.3} \end{equation}\]
In Equation (5.3), \(y\) is the actual response value, \(\hat{y}\) is the predicted response value, and \(n\) is the number of predictions. In a sense, RMSE is the average distance of our predictions from the actual response values. In general, an accurate regression model is one that produces a small RMSE. We can avoid overfitting by splitting our sample data into training and testing sets. Then we estimate the parameters of the model using the training data and evaluate the model’s accuracy using the testing data. We demonstrate this process below using the tidyverse and a familiar example.
Ask a Question
We once again return to the penguins of the Palmer Archipelago in Antarctica. In Chapters 3.3.2 and 4.2.4 we explored the linear association between a penguin’s flipper length and its body mass. As part of an exploratory analysis, we established a strong, positive, linear association between the two variables. Then we applied inferential statistics to demonstrate the significance of that association and an interval estimate for the slope parameter. Now we turn our attention to the development of a predictive model and ask the following question: How accurately can we predict the body mass of a Palmer penguin based on its flipper length?
An accurate predictive model for body mass could be incredibly useful for the scientists at Palmer Station. Perhaps flipper length is much easier than body mass to collect for new specimens. If so, then a predictive model could avoid the need for weighing or help calibrate the required scales. A predictive model could also assist with diagnosing penguins that have a weight dramatically different from what would be expected for their size. At the very least, such a model would provide validation for real-world measurements.
Acquire the Data
As with our previous two encounters, we import the data from the palmerpenguins package and isolate the variables of interest.
#load palmerpenguin library
library(palmerpenguins)
#import penguin data
data(penguins)
#wrangle penguin data
penguins2 <- penguins %>%
select(flipper_length_mm,body_mass_g) %>%
na.omit()For this example, we randomly select 75% of the observations for training. The randomness of selection is critical because we want the training and testing sets to have similar distributions. We implement the split in the code below.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(penguins2),size=floor(0.75*nrow(penguins2)),replace=FALSE)
#split sample into training and testing
training <- penguins2[rows,]
testing <- penguins2[-rows,]The original sample consists of 342 rows (penguins). We randomly select 75% of these rows to be part of the training set. But 75% of 342 is 256.5, so we round down using the floor() function. The resulting 256 row numbers are assigned to the training set. The remaining 86 row numbers are assigned to the testing set. Just as a quality check on the two data sets, let’s compute the mean body mass of the penguins in each set.
## [1] 4200.098## [1] 4206.686The average body mass of penguins in the training and testing sets are within 7 grams of one another. Given the average penguin weighs over 4,000 grams, we feel relatively confident that the random split maintained similar distributions. We are now ready to estimate a regression model using the training data and validate its accuracy using the testing data.
Analyze the Data
For consistency, we re-create the scatter plot and best-fit line from previous chapters. However, in this case we only use the training data. We do not permit the model to consider the testing data until the end of our analysis.
#create scatter plot
ggplot(data=training,aes(x=flipper_length_mm,y=body_mass_g)) +
geom_point() +
geom_smooth(method="lm",formula=y~x,se=FALSE) +
geom_segment(x=215,xend=215,y=2500,yend=4900,
linewidth=0.75,linetype="dashed",color="red") +
geom_segment(x=169,xend=215,y=4900,yend=4900,
linewidth=0.75,linetype="dashed",color="red") +
labs(title="Palmer Penguin Measurements",
subtitle="Training Data",
x="Flipper Length (mm)",
y="Body Mass (g)",
caption="Source: Palmer Station LTER Program") +
theme_bw()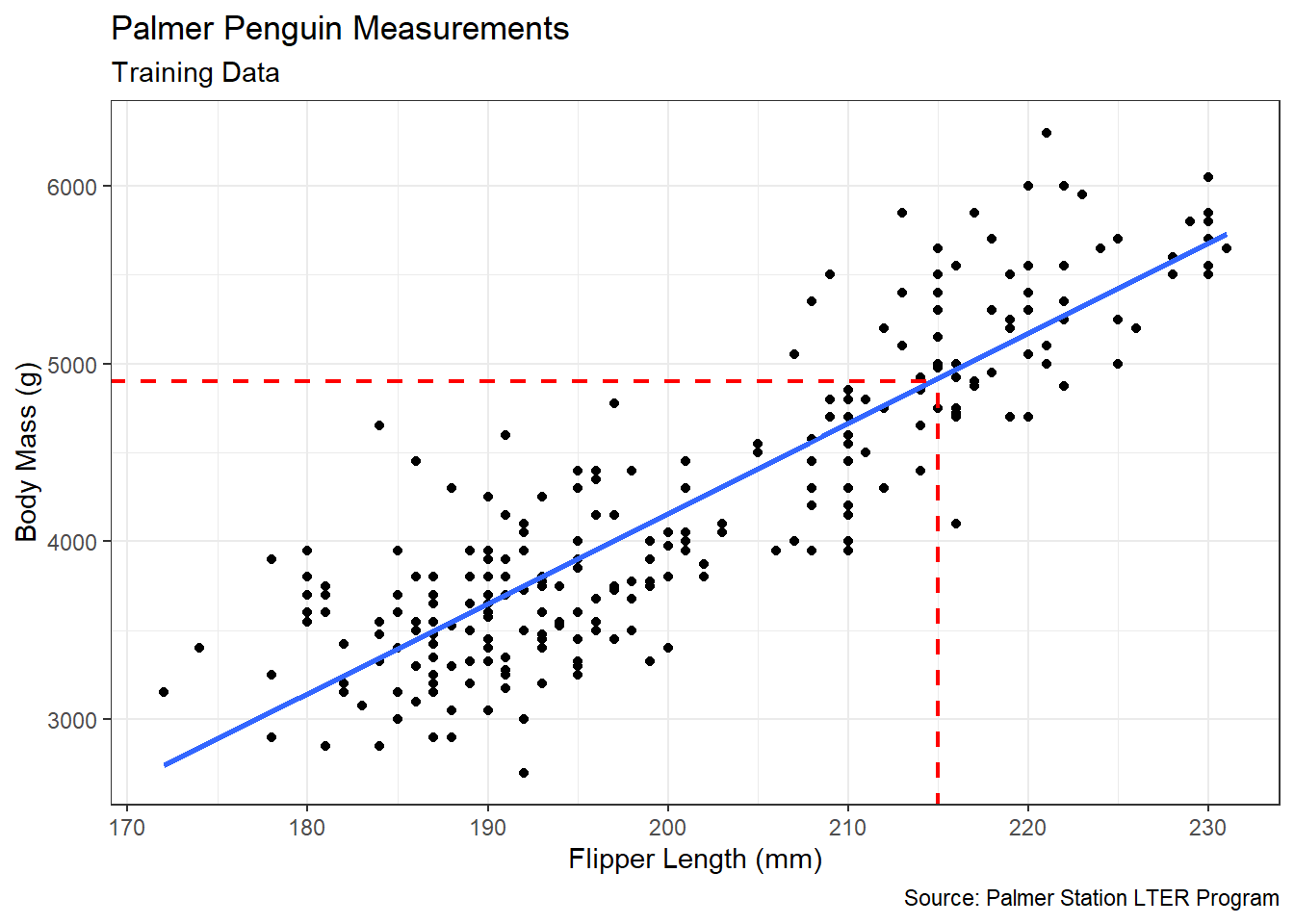
Figure 5.4: Linear Association between Flipper Length and Body Mass
Figure 5.4 displays the same strong, positive, linear association we observe in previous sections. But our intended use for the best-fit line is very different than before. We now hope to use the best-fit line to estimate an unknown body mass based on a known flipper length. If, for example, we are asked to predict the body mass of a penguin with 215 mm flippers, we might consult the dashed red line in the scatter plot. It appears the average penguin with 215 mm flippers has a body mass of about 4,900 grams. Yet, there is no need to estimate this value visually. We instead estimate the parameters of the best-fit line using the training data and compute the prediction directly.
#estimate simple linear regression model
model <- lm(body_mass_g~flipper_length_mm,data=training)
#review parameter estimates
coefficients(summary(model))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5974.51250 354.319942 -16.86191 2.555754e-43
## flipper_length_mm 50.65933 1.759747 28.78784 6.108672e-82We consult the Estimate column for the intercept and slope of the best-fit line. Thus, the blue line in Figure 5.4 has the following equation:
\[\begin{equation} \text{Body Mass}=50.66 \cdot \text{Flipper Length}-5974.51 \tag{5.4} \end{equation}\]
Based on Equation (5.4), the average penguin with 215 mm flippers is predicted to have a body mass of 4,917.39 grams. Our visual estimate was very close! But the algebraic prediction is more precise. We can avoid rounding and obtain an even more precise estimate using the predict() function.
## 1
## 4917.244The predict() function requires two arguments. The first is the model with which to make the prediction. The second is a data frame of input values to predict. In this case, we only use the single value of 215. Of course, we have no idea how accurate this individual prediction might be for a given penguin. Upon review of the scatter plot, penguins with 215 mm flippers have a variety of body masses. To assess the overall prediction accuracy of the model, we now apply the entire testing set.
#estimate body mass for entire testing set
testing_pred <- testing %>%
mutate(pred_body_mass_g=predict(model,newdata=testing))
#review structure of predictions
glimpse(testing_pred)## Rows: 86
## Columns: 3
## $ flipper_length_mm <int> 181, 195, 190, 197, 194, 183, 184, 181, 190, 179, 19…
## $ body_mass_g <int> 3625, 4675, 4250, 4500, 4200, 3550, 3900, 3300, 4600…
## $ pred_body_mass_g <dbl> 3194.827, 3904.057, 3650.761, 4005.376, 3853.398, 32…After predicting the entire testing set, we have real and predicted body masses. Remember, the model does not have access to these 86 observation when we estimate the parameters. It is as though someone brought along 86 new penguins and asked us to predict the body masses. If we let \(y\) be the true body mass and \(\hat{y}\) be the predicted body mass, then we compute RMSE using Equation (5.3).
#compute RMSE for model
testing_pred %>%
summarize(RMSE=sqrt(mean((body_mass_g-pred_body_mass_g)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 376.If we employ the best-fit line from the training data to predict new testing data, we find a RMSE of about 376. In context, this suggests we can predict the body mass of a Palmer penguin to within 376 grams, on average, if we know its flipper length. This is our best estimate of the model’s performance on new data (penguins). Whether this accuracy is acceptable depends on the opinions of domain experts.
Advise on Results
When interpreting the results of this analysis for domain experts, we might simply provide the equation of the best-fit line along with instructions for its use. Multiply a penguin’s flipper length by 50.66 and subtract 5,974.51. The resulting body mass estimate is accurate to within 376 grams, on average. The domain expert may or may not find this model valuable. Perhaps they are capable of estimating a penguin’s body mass more accurately based on experience alone. If a more accurate model is required, we may consider including additional predictor variables (e.g., bill length). We investigate these multiple linear regression models in the next section. On the other hand, the domain expert may not know whether this accuracy is “good” or not. In that case, it helps if we provide a frame of reference in the form of a null model.
In predictive analysis, the null model represents the prediction we might make with no information at all. Typically, this involves predicting the average response value. We know from previous work that the mean body mass of penguins in the training set is 4,200.10 grams. What would be the RMSE if we predicted the testing set by always guessing 4,200.10 for the body mass?
## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 728.If we use no other information about the penguins and simply guess the mean body mass for all of them, we are off by an average of nearly 728 grams. By using a single piece of information, namely the penguin’s flipper length, we cut that error nearly in half! Comparisons to a null model such as this often assist in describing the value of a trained model to domain experts. If we are asked whether the flipper length model is “good” we can reply that it cuts the error in half compared to no model at all. Of course, we still don’t know how much more accurate the model could be if additional predictors are included.
In terms of limitations, a word of caution regarding extrapolation is warranted. The training set includes penguins with flipper lengths ranging between 172 and 231 mm. The model parameters are estimated based solely on data in that range. It is possible that the association between flipper length and body mass changes for penguins with extremely short or long flippers. Thus, the model should not be applied to such situations. If domain experts desire a more robust model, then a more diverse set of sample data is required.
Answer the Question
Based on a sample of 342 penguins from the Palmer Archipelago in Antarctica, it appears we can predict a penguin’s body mass to within 376 grams, on average, if we know its flipper length. This accuracy, and the associated model, only apply to the Adelie, Chinstrap, and Gentoo species with flipper lengths between 172 and 231 mm. Further study is required to determine if a more accurate model is achievable using additional characteristics of the resident penguins. In order to develop a model with multiple predictors, we require the methods presented in the next section.
5.2.3 Multiple Linear Regression
Previously, we estimated a simple linear regression model using training data and validated its accuracy using testing data. Though the resulting accuracy was superior to simply guessing the mean response (i.e., the null model), it is possible that additional predictor variables improve the model’s accuracy. A linear model with a continuous numerical response and more than one predictor is referred to as a multiple linear regression model. In general, a model with \(p\) predictor variables is defined as in Equation (5.5).
\[\begin{equation} y = \beta_0+\beta_1 x_1+\beta_2 x_2+\cdots+\beta_p x_p \tag{5.5} \end{equation}\]
Similar to the simple linear regression equation, there is a single intercept parameter (\(\beta_0\)). However, there are now multiple slope parameters (\(\beta_1,\beta_2,...,\beta_p\)). The slope for a given predictor represents the change in the response when all other predictors are held constant. That said, estimating and interpreting the value of each slope parameter is primarily in the realm of inference. Our current focus is prediction, so we want to know whether the presence of each predictor increases the accuracy of the model. We investigate the value of multiple predictors using the tidyverse in the example below.
Ask a Question
In Chapter 2.3.4 we demonstrate data cleaning with a sample of player performance values from the National Football League (NFL) scouting combine. With regard to missing values, we notice that some players decline to compete in certain events. Yet, this missing information could be valuable for team executives trying to determine whether to draft a particular player. One solution is to develop a predictive model for the missing event based on the player’s performance in the other events. As an example, we pose the following question: How accurately can we predict an offensive lineman’s forty-yard dash time based on the other five events?
The answer to this question could be of very high interest to teams considering drafting an offensive lineman. The draft value of this position was made famous, in part, by the 2009 movie The Blind Side which highlighted the early career of offensive tackle Michael Oher. Though the facts of the film have more recently been brought into question, the value of the position to football teams remains unquestionably high. In this case study, we assume the forty-yard dash is the missing event and the offensive linemen participate in the other five events. However, the process described here remains the same for other missing events.
Acquire the Data
The data for NFL combines in the years 2000 to 2020 is made available in the file nfl_combine.csv. The offensive line of a football team consists of five players. The center (C) is placed in the middle of the line with offensive guards (OG) to the left and right. Outside of the two guards are offensive tackles (OT) on the far left and far right of the line. Sometimes players are capable of performing in multiple positions and thus are referred to generically as offensive linemen (OL). Below, we isolate these positions and wrangle the combine data.
#import NFL Combine data
combine <- read_csv("nfl_combine.csv") %>%
filter(Pos %in% c("C","OG","OT","OL")) %>%
transmute(Forty=`40YD`,Vertical,Bench=BenchReps,
Broad=`Broad Jump`,Cone=`3Cone`,Shuttle) %>%
na.omit()
#review data structure
glimpse(combine)## Rows: 451
## Columns: 6
## $ Forty <dbl> 4.85, 5.32, 5.23, 5.57, 5.22, 5.24, 5.08, 5.08, 4.91, 5.37, 5…
## $ Vertical <dbl> 36.5, 29.0, 25.5, 27.0, 30.5, 30.0, 30.5, 33.0, 29.5, 25.0, 3…
## $ Bench <dbl> 24, 26, 23, 23, 21, 34, 24, 28, 24, 22, 26, 26, 20, 28, 25, 2…
## $ Broad <dbl> 121, 110, 102, 97, 109, 107, 107, 113, 110, 93, 113, 109, 106…
## $ Cone <dbl> 7.65, 8.26, 7.88, 8.07, 7.58, 8.03, 7.57, 7.91, 7.76, 8.17, 8…
## $ Shuttle <dbl> 4.68, 5.07, 4.76, 4.98, 4.66, 4.87, 4.69, 4.64, 4.62, 5.11, 4…The resulting data frame includes 451 offensive linemen who performed in all six events. Though our goal is to predict forty-yard dash times when they are not present, we need training and testing data where these values are present. Otherwise, we cannot estimate and validate a predictive model. We next randomly split the sample data into 75% training and 25% testing.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(combine),size=floor(0.75*nrow(combine)),replace=FALSE)
#split sample into training and testing
training <- combine[rows,]
testing <- combine[-rows,]As always, our goal when splitting the sample is to have each data set maintain the same distribution. One quality check in this regard is to compute the mean response within the training and testing sets.
## [1] 5.255296## [1] 5.216814The average forty-yard dash times for offensive linemen in the training and testing sets are 5.255 and 5.217 seconds, respectively. Though we would not expect the two values to be exactly the same, the random approach to splitting the data sets should ensure close proximity. In this case, the mean response for both sets is relatively close. Our data is now ready for analysis.
Analyze the Data
When constructing predictive models, we require a baseline accuracy for comparison. Otherwise, it is difficult to assess the value of the model. Typically, the baseline is derived from the null model which consists of predicting the mean response for all observations. In our case, the null model suggests every offensive lineman runs the forty-yard dash in 5.255 seconds. Let’s compute the accuracy of this model against the testing set.
## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.175If we always predict a forty-yard dash time of 5.255 seconds for offensive lineman, we will be off by an average of 0.175 seconds. Can we do better by including information from the other events? Let’s find out by investigating the association between events.
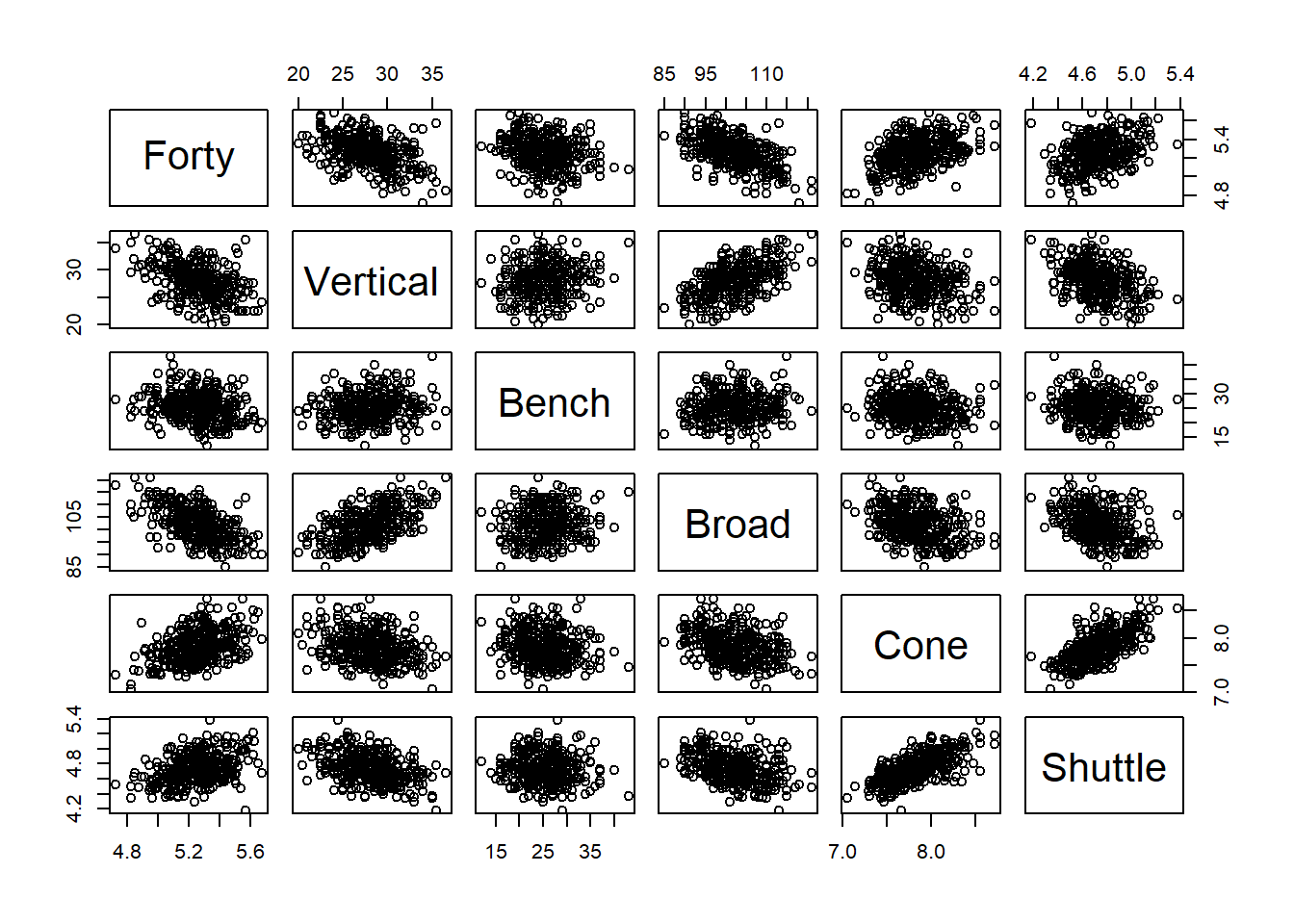
Figure 5.5: Linear Associations between Events
Upon reviewing the top row of the scatter plot matrix in Figure 5.5, we find some clear associations between forty-yard dash time and the other events. The vertical jump, bench press, and broad jump all appear to have negative, linear associations with forty-yard dash time. In other words, the higher or farther a player jumps, the lower (faster) the forty-yard dash time. Similarly, the more repetitions a player bench presses, the faster the time. Meanwhile, the associations with the cone and shuttle drills appear to be positive and linear. The longer a player takes to complete each drill, the longer it takes them to complete the forty-yard dash. Overall, it appears the other five events could provide some predictive value for forty-yard dash time.
As a starting point, we estimate a simple linear regression model with only vertical jump height as the predictor. The model is fit to the training data and evaluated on the testing data. Does this model outperform the null model?
#estimate simple linear regression model
model1 <- lm(Forty~Vertical,data=training)
#estimate accuracy of model
testing %>%
mutate(pred_Forty=predict(model1,newdata=testing)) %>%
summarize(RMSE=sqrt(mean((Forty-pred_Forty)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.155The answer is yes! By applying vertical jump height we reduce the average error of the model from 0.175 to 0.155 seconds. Can we do even better by adding another predictor? We add bench press repetitions to the linear model with a plus sign.
#estimate multiple linear regression model
model2 <- lm(Forty~Vertical+Bench,data=training)
#estimate accuracy of model
testing %>%
mutate(pred_Forty=predict(model2,newdata=testing)) %>%
summarize(RMSE=sqrt(mean((Forty-pred_Forty)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.149Again, the answer is yes! When we use a player’s vertical jump and bench press we can predict forty-yard dash time to within 0.149 seconds, on average. Notice the improvement is smaller than when we transitioned from the null model to the vertical jump model. Based on the scatter plot matrix, this should not be too surprising. The correlation between bench press and forty-yard dash appears weaker than that of vertical jump and forty-yard dash. Yet, we still witness improvement with the additional predictor. What happens to our accuracy if we include all five events?
#estimate multiple linear regression model
model_all <- lm(Forty~.,data=training)
#estimate accuracy of model
testing %>%
mutate(pred_Forty=predict(model_all,newdata=testing)) %>%
summarize(RMSE=sqrt(mean((Forty-pred_Forty)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.137We achieve even further reduction in error down to 0.137 seconds. Notice we use a short-cut in the lm() function this time. The period in the syntax Forty~. includes every other variable in the data frame as a predictor. By using the information provided by the other five events, we can predict an offensive lineman’s forty-yard dash time to within 0.137 seconds. This represents a 22% reduction in error compared to the null model.
In order to provide an actionable prediction model to domain experts, we require estimates for the model parameters. We could simply use the estimated parameters from the training data model. However, common practice to obtain even better parameter estimates is to fit the final model to all of the data.
#estimate parameter values
model_final <- lm(Forty~.,data=combine)
#review parameter estimates
coefficients(summary(model_final))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.169997868 0.262512406 19.694299 1.494712e-62
## Vertical -0.006555840 0.002549351 -2.571572 1.044743e-02
## Bench -0.004435510 0.001296457 -3.421256 6.808712e-04
## Broad -0.008877147 0.001218900 -7.282916 1.495156e-12
## Cone 0.130625002 0.029466497 4.433001 1.171945e-05
## Shuttle 0.055273159 0.046433750 1.190366 2.345372e-01Given the values in the Estimate column, the final multiple linear regression model with five predictors is written as in Equation (5.6).
\[\begin{equation} \text{Forty}=5.170-0.007 \cdot \text{Vertical}-0.004 \cdot \text{Bench}-0.009 \cdot \text{Broad}+\\ 0.131 \cdot \text{Cone}+0.055 \cdot \text{Shuttle} \tag{5.6} \end{equation}\]
Though we base the parameter estimates on the entire sample, the reported accuracy of the model is still based on the training and testing split. This subtle distinction is important! We validate the accuracy of a model by testing it on data that it did not “see” during training. Once we decide which predictors are included in the most accurate model, we estimate the parameters using all available data. We do not compute the RMSE for this final model, because we have no remaining hold-out data. Instead, we rely on the RMSE from the validation process.
Advise on Results
Our predictive model provides a method for NFL team executives to estimate an offensive lineman’s forty-yard dash time when that player declines to participate in the event. The domain expert need only “plug in” the values for the five other events into the multiple linear regression equation and complete the arithmetic to obtain an estimated forty-yard dash time. That estimate is accurate to within 0.137 seconds, on average. Whether this accuracy is sufficient for use in the NFL draft is up to the domain experts. If a more accurate model is required, then we might attempt more advanced non-linear or non-parametric approaches. However, the majority of these approaches are outside the scope of the text.
An important limitation of the model is the assumption that players participate in all five other events. If a player skips the shuttle drill, for example, it is not appropriate to use our current model and simply leave out the shuttle term. The model was trained in the presence of shuttle drill data and that can influence the parameter estimates for the other predictors. If we want a model that excludes the shuttle drill, then we must repeat our training and testing process without it.
#estimate multiple linear regression model
model4 <- lm(Forty~.-Shuttle,data=training)
#estimate accuracy of model
testing %>%
mutate(pred_Forty=predict(model4,newdata=testing)) %>%
summarize(RMSE=sqrt(mean((Forty-pred_Forty)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.137We use another short-cut in the lm() function to exclude shuttle drill from the model. By preceding a predictor with the minus sign, we remove it from the model. The four-variable model without shuttle drill predicts forty-yard dash time to within an average of just over 0.137 seconds. We removed a predictor and witnessed almost no increase in error. One way to interpret this is that the shuttle drill offers almost no additional predictive value when we already have the other four events included. What are the new parameter estimates when we fit the four-variable model to all of the data?
#estimate parameter values
model_final2 <- lm(Forty~.-Shuttle,data=combine)
#review parameter estimates
coefficients(summary(model_final2))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.288807793 0.242911355 21.772584 3.911342e-72
## Vertical -0.007269022 0.002479108 -2.932112 3.539881e-03
## Bench -0.004407247 0.001296845 -3.398438 7.385550e-04
## Broad -0.008962307 0.001217368 -7.362039 8.803704e-13
## Cone 0.152420633 0.023097960 6.598879 1.177380e-10While some of the parameters changed very little, the intercept and the cone drill parameter estimates changed quite a bit. This is due, in part, to the very strong correlation between the cone and shuttle drills depicted in Figure 5.5. With such a strong dependence between the two predictors, the removal of one impacts the estimate of the other. Thus, in a situation where the domain expert is missing the shuttle drill, they should employ this new regression equation rather than the five-variable equation.
Answer the Question
Based on a sample of 451 offensive linemen, it appears we can predict a player’s forty-yard dash time to within 0.137 seconds if we know their performance in the other five events. Even if we are missing the shuttle drill time, we can still predict the forty-yard dash with roughly the same accuracy. Further study is necessary to determine if other factors, such as the player’s height and weight, provide additional predictive value.
A logical extension to this study is to determine which combination of predictors provides the most accurate model. Adding more predictors does not always increase the accuracy of a model. If predictor variables are not correlated with the response, then including them in the model may just introduce “noise” that decreases the model’s effectiveness. Thus, we prefer to find the smallest number of predictors necessary to obtain a sufficiently accurate model. This process of choosing predictors is known as feature selection or variable selection. There are a wide variety of techniques for determining the optimal combination of predictors, such as subset selection, regularization, and dimension reduction. But these approaches are reserved for more advanced texts.
5.2.4 Regression Trees
Thus far we have only considered parametric models for predicting a numerical response. Multiple linear regression is a parametric approach because it consists of estimating parameters (\(\beta_0,\beta_1,\cdots,\beta_p\)) in a linear equation. However, a whole host of non-parametric regression models also exist. Non-parametric models have no particular functional form and instead derive predictions directly from the data. One common example of a non-parametric model is a decision tree. When the response is a numerical variable, we refer to the model as a regression tree. Regression trees consist of a sequence of binary decisions that eventually end with the prediction of a numerical response. Consider the simple example of adopting a new dog. If we want to predict the cost, we might employ a regression tree like that in Figure 5.6.
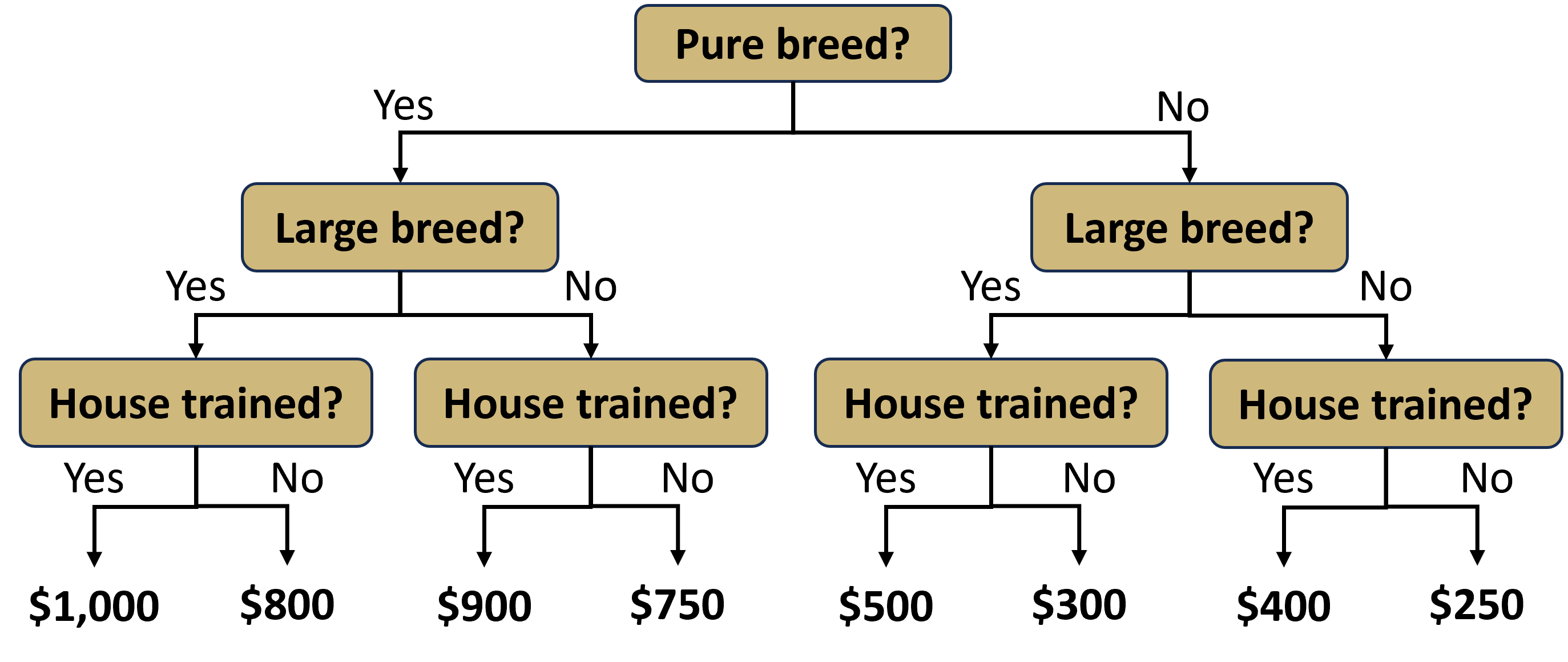
Figure 5.6: Regression Tree to Predict Dog Adoption Cost
Though presented upside-down, the diagram does roughly resemble a tree. At each level of the tree, there exists a binary decision that creates a branch. At the first level, we must decide whether we care to have a pure breed dog or not. If we do not want a pure breed dog, then we take the right branch. At the next level, we are asked whether we want a large dog. Suppose we do want a large breed and take the left branch. Finally, we must decide whether we want the dog to be house trained. If the answer is yes, then we take the left branch again. Having made all of the decisions, we arrive at a terminal leaf of the tree. The associated value of $500 is our prediction for the cost to adopt the dog.
Notice this model requires no calculations to produce a prediction. There are no parameters or equations, just a simple visual diagram. But where did the predicted costs at the bottom of the tree come from? We demonstrate the answer to this question in an example.
Ask a Question
In Chapter 5.2.3, we constructed a multiple linear regression model to predict the forty-yard dash time of an offensive lineman based on their performance in the other scouting combine events. The associated parametric model includes estimates for the coefficients on each predictor value in a linear equation. As a point of comparison, we now construct a non-parametric version of the same model in the form of a regression tree. Rather than coefficient estimates in an equation, the model consists of a sequence of branches in a tree. After navigating the branches of the tree, we arrive at an answer to the following question: How accurately can we predict an offensive lineman’s forty-yard dash time based on the other five events?
Acquire the Data
The performance data for players in the years 2000 to 2020 National Football League (NFL) scouting combine are available in the file nfl_combine.csv. In the code chunk below, we import and wrangle the data before splitting it into training and testing sets.
#import NFL Combine data
combine <- read_csv("nfl_combine.csv") %>%
filter(Pos %in% c("C","OG","OT","OL")) %>%
transmute(Forty=`40YD`,Vertical,Bench=BenchReps,
Broad=`Broad Jump`,Cone=`3Cone`,Shuttle) %>%
na.omit()
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(combine),size=floor(0.75*nrow(combine)),replace=FALSE)
#split sample into training and testing
training <- combine[rows,]
testing <- combine[-rows,]
#compute mean response
mean(training$Forty)## [1] 5.255296The average forty-yard dash time for the 338 offensive linemen in the training set is 5.255 seconds. We use this value in the null model as we initiate our analysis.
Analyze the Data
Prior to developing a prediction model, we require a frame of reference for improvements in accuracy based on root mean squared error (RMSE). In this case, our reference point is the null model consisting of the mean response.
## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.175If we predict 5.255 seconds for every lineman in the testing set, regardless of performance in the other events, we are off by an average of 0.175 seconds. Our goal is to improve this accuracy as much as possible by constructing a decision tree. Conceptually, a decision tree is based on the idea of repeatedly branching (i.e., splitting) the training set into two groups based on the predictor values. For example, suppose we decide to branch on a lineman’s broad jump distance. First we need a broad jump value to branch on. One logical option is to use the mean.
## [1] 102.1568The average lineman jumps 102.157 inches. By branching on this value, we split the linemen into two groups: below average and above average. We often refer to these groups as the left and right branches. Let’s compute the mean forty-yard dash time for our two branches.
#add branch assignments
training_branch <- training %>%
mutate(Branch1=if_else(Broad<102.157,"Left","Right"))
#compute branch means
training_branch %>%
group_by(Branch1) %>%
summarize(avg=mean(Forty)) %>%
ungroup()## # A tibble: 2 × 2
## Branch1 avg
## <chr> <dbl>
## 1 Left 5.33
## 2 Right 5.18Now we see a difference in forty-yard dash performance between linemen with below and above average broad jumping ability. Players that jump shorter distances take longer to complete the forty-yard dash. The opposite is true for players that jump longer distances. We visualize this difference in a scatter plot of broad jump distance versus forty-yard dash time.
#display scatter plot
ggplot(data=training_branch,aes(x=Broad,y=Forty,color=Branch1)) +
geom_point(position="jitter") +
geom_hline(yintercept=5.326,color="red") +
geom_hline(yintercept=5.255) +
geom_hline(yintercept=5.177,color="blue") +
geom_vline(xintercept=102.157,linetype="dashed") +
labs(title="NFL Scouting Combine",
subtitle="Offensive Linemen",
x="Broad Jump (in)",
y="Forty-Yard Dash (sec)") +
scale_x_continuous(limits=c(84,124),breaks=seq(84,124,5)) +
scale_y_continuous(limits=c(4.7,5.7),breaks=seq(4.7,5.7,0.1)) +
scale_color_manual(values=c("red","blue")) +
theme_bw()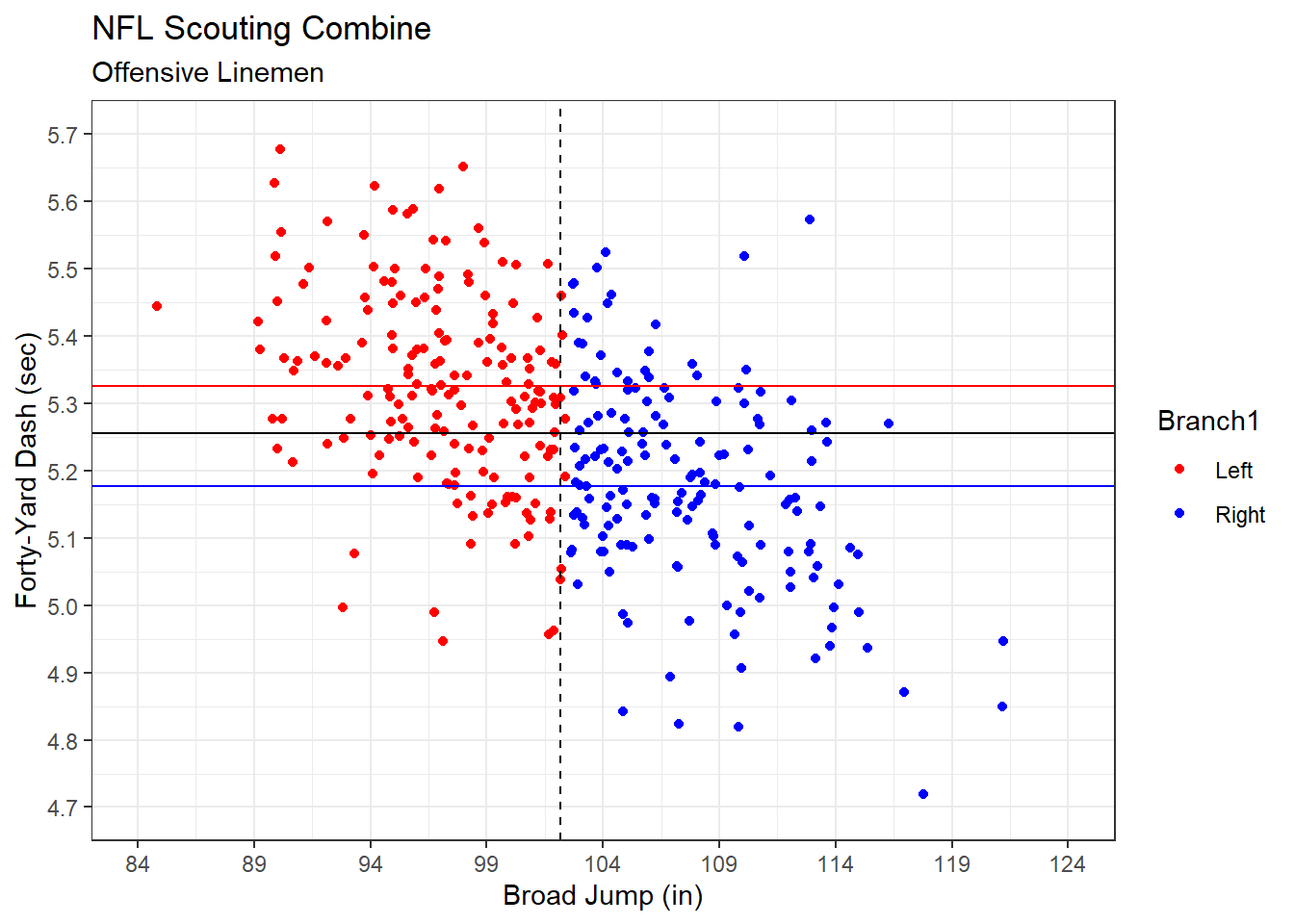
Figure 5.7: Forty-Yard Dash Time Branched on Broad Jump Distance
The horizontal black line in Figure 5.7 indicates the overall mean forty-yard dash time. This is the prediction for our null model that ignores broad jump distance. By instead branching on broad jump distance (vertical dashed line) we achieve more accurate predictions for each branch. The left branch has a greater mean forty-yard dash time (horizontal red line) than that of the right branch (horizontal blue line). So, rather than using a generic prediction for forty-yard dash time, we tailor it to each branch according to the broad jump performance. This should produce more accurate predictions in the testing set.
#compute RMSE for tree model
testing %>%
mutate(Forty_pred=if_else(Broad<102.157,5.326,5.177)) %>%
summarize(RMSE=sqrt(mean((Forty-Forty_pred)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.158Simply by branching on broad jump distance, we reduce our prediction error from 0.175 to 0.158 seconds. What if we branch again? Can we achieve even greater accuracy? We investigate this question by branching on the mean cone drill time.
#compute mean cone drill for each branch
training_branch %>%
group_by(Branch1) %>%
summarize(avg=mean(Cone)) %>%
ungroup()## # A tibble: 2 × 2
## Branch1 avg
## <chr> <dbl>
## 1 Left 7.90
## 2 Right 7.76The left branch (below average broad jump) has an average cone drill time of 7.90 seconds. After splitting on this new predictor we obtain a left-left branch and left-right branch. The right branch (above average broad jump) has an average cone drill time of 7.76 seconds. When we split on this value, we create right-left and right-right branches. Let’s label each lineman in the training set according to these branches.
#add branch assignments
training_branch2 <- training_branch %>%
mutate(Branch2=case_when(
Branch1=="Left" & Cone<7.901 ~ "LL",
Branch1=="Left" & Cone>=7.901 ~ "LR",
Branch1=="Right" & Cone<7.759 ~ "RL",
Branch1=="Right" & Cone>=7.759 ~ "RR"
))
#compute branch means
training_branch2 %>%
group_by(Branch2) %>%
summarize(avg=mean(Forty)) %>%
ungroup()## # A tibble: 4 × 2
## Branch2 avg
## <chr> <dbl>
## 1 LL 5.28
## 2 LR 5.38
## 3 RL 5.14
## 4 RR 5.22Now we have segmented the linemen into four groups. The left-right (LR) branch represents linemen with below average jump distance and above average cone time. In other words, they performed poorly in both events. Consequently, that group has the slowest average forty-yard dash time. By contrast, the right-left (RL) branch includes linemen with above average jump distance and below average cone time. These players can jump far and move fast. Not surprisingly, they have the fastest mean forty-yard dash time. We visualize all four groups in a scatter plot of broad jump versus cone drill.
#display scatter plot
ggplot(data=training_branch2,aes(x=Broad,y=Cone,color=Branch2)) +
geom_point(position="jitter") +
geom_vline(xintercept=102.157,linetype="dashed") +
geom_segment(x=82,xend=102.157,y=7.901,yend=7.901,linetype="dashed",color="black") +
geom_segment(x=102.157,xend=126,y=7.759,yend=7.759,linetype="dashed",color="black") +
labs(title="NFL Scouting Combine",
subtitle="Offensive Linemen",
x="Broad Jump (in)",
y="Cone Drill (sec)") +
scale_x_continuous(limits=c(84,124),breaks=seq(84,124,5)) +
scale_y_continuous(limits=c(7,8.75),breaks=seq(7,8.75,0.25)) +
scale_color_manual(values=c("red","dark red","blue","dark blue")) +
annotate("text",x=86,y=8.6,label="5.379",color="dark red",size=5) +
annotate("text",x=86,y=7.2,label="5.284",color="red",size=5) +
annotate("text",x=120,y=8.6,label="5.220",color="dark blue",size=5) +
annotate("text",x=120,y=7.2,label="5.139",color="blue",size=5) +
theme_bw()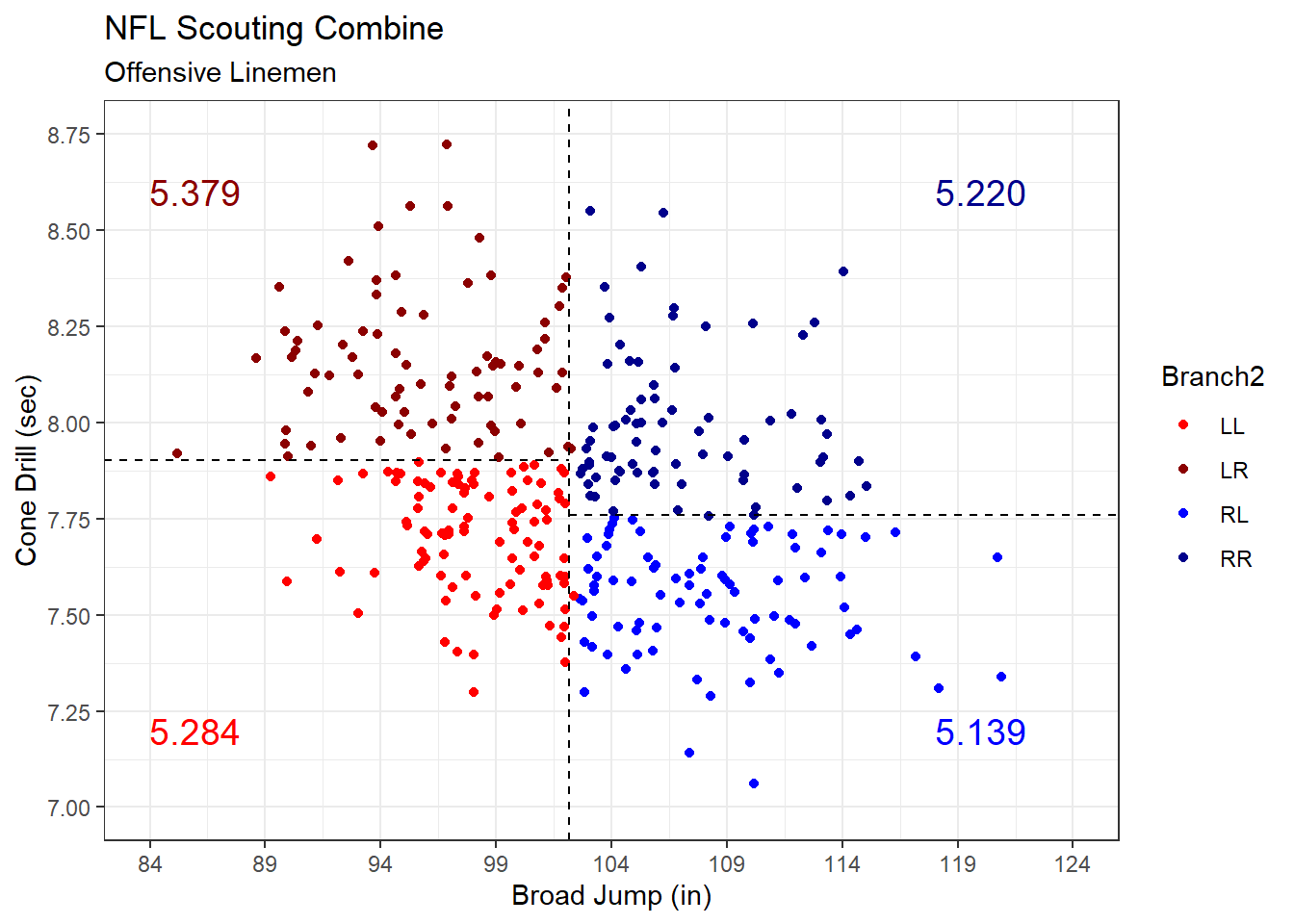
Figure 5.8: Forty-Yard Dash Time Branched on Broad Jump Distance and Cone Drill Time
After branching on two predictors, we have four groups of linemen in Figure 5.8. Given the limitations of visualizing three dimensions, we list the mean forty-yard dash time for each group in text. Once again, by tailoring our forty-yard dash predictions more and more specifically to each sub-group of linemen, we should achieve greater accuracy.
#compute RMSE for tree model
testing %>%
mutate(Forty_pred=case_when(
Broad<102.157 & Cone<7.901 ~ 5.284,
Broad<102.157 & Cone>=7.901 ~ 5.379,
Broad>=102.157 & Cone<7.759 ~ 5.139,
Broad>=102.157 & Cone>=7.759 ~ 5.220
)) %>%
summarize(RMSE=sqrt(mean((Forty-Forty_pred)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.153Though not as dramatic as the first branch, our second branch does reduce the error from 0.158 to 0.153 seconds. We could continue branching on the remaining predictors in a similar manner and ideally achieve a more accurate model. However, there is no need to continue the process manually. The tree package includes functions for growing decision trees that ease the process. In fact, the tree() function works just like the lm() function in terms of notation. Below we use the training data to build a regression tree to predict forty-yard dash time based on the other events. We then display the results in a tree diagram.
#load tree library
library(tree)
#build decision tree
model <- tree(Forty~.,data=training)
#plot decision tree
plot(model)
text(model,cex=0.8,pretty=TRUE)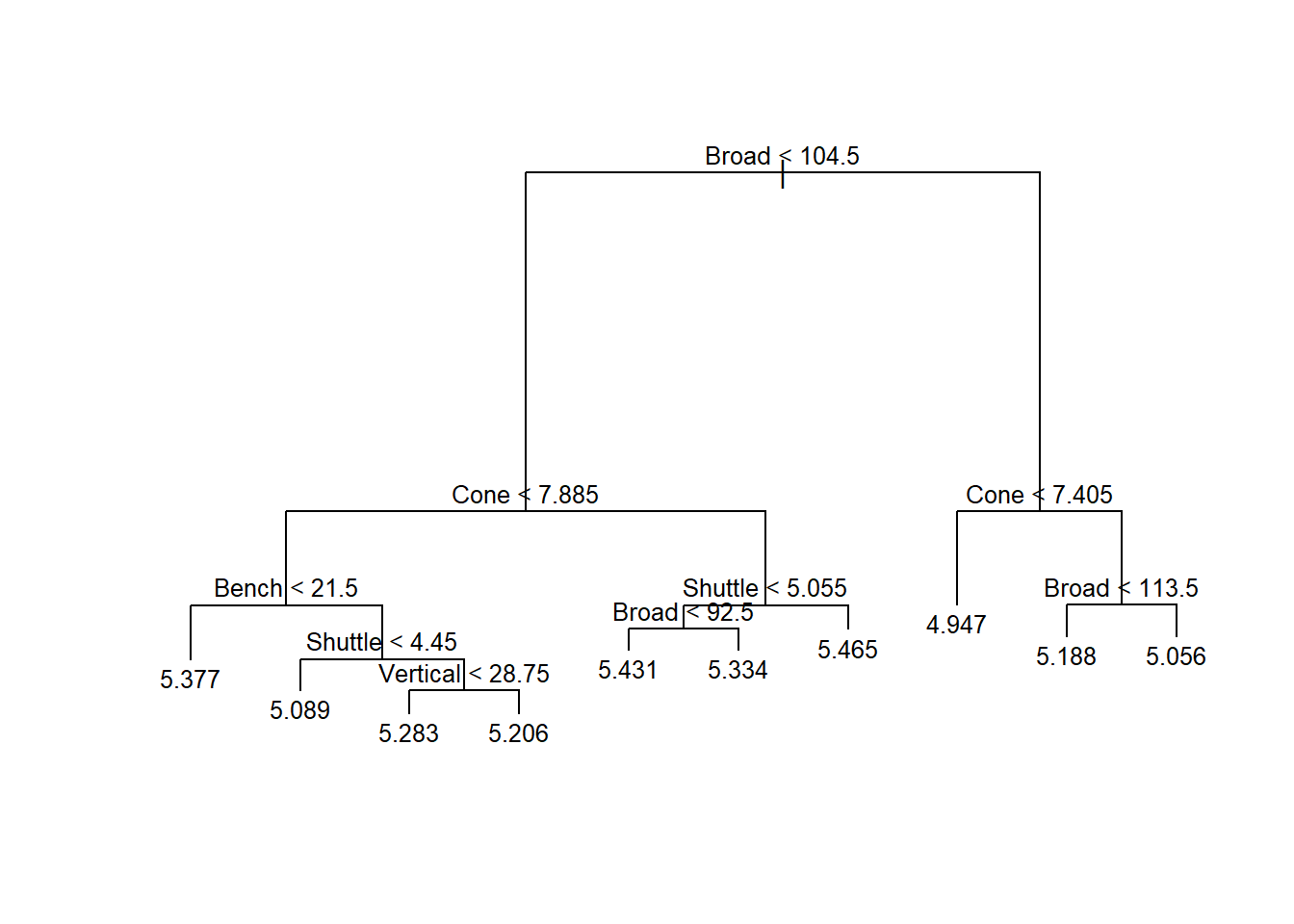
Figure 5.9: Regression Tree to Predict Forty-Yard Dash Time
Figure 5.9 finally displays our model in the form of a tree. However, the algorithm employed to grow the tree is more sophisticated than our manual approach. Rather than branching on the mean value of a randomly-selected predictor, the algorithm uses recursive binary splitting. This method chooses the predictor and branch value that provides the maximum reduction in error at each level of the tree. For the first branch, the algorithm chooses broad jump but splits on 104.5 inches because that value provides a greater reduction in error than the mean value of 102.2 inches. By default, the labels on each branch indicate the left branch. Further down the tree we notice that branches on the same level are not required to split on the same predictor. In fact, the third level of the tree includes bench press, shuttle run, and broad jump again. Such behavior is permitted with recursive binary splitting, because the algorithm chooses the branch that provides the greatest improvement in accuracy.
At the bottom of the tree, the leaves indicate the mean forty-yard dash time for the associated group. After splitting our linemen into 10 distinct groups, let’s see what accuracy the model achieves. As with linear regression models, we simply apply the predict() function to the testing set and compute the RMSE.
#compute RMSE for tree model
testing %>%
mutate(Forty_pred=predict(model,newdata=testing)) %>%
summarize(RMSE=sqrt(mean((Forty-Forty_pred)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 0.150Even with the more sophisticated algorithm, we only achieve another modest decrease in error compared to our manual approach. Using the regression tree, we can predict the forty-yard dash time of an offensive lineman to within 0.150 seconds, on average. Should we recommend this model or our previous multiple linear regression model to stakeholders?
Advise on Results
As with any modeling approach, regression trees have their pros and cons. Compared to multiple linear regression models, decision trees are often less accurate. The linear model of forty-yard dash time presented earlier provides a RMSE of 0.137 seconds. Thus, the decision tree’s RMSE of 0.150 may be rightly perceived as inferior. However, decision trees are far easier to explain and implement for most stakeholders. Imagine a coach wants to predict the forty-yard dash time for the following player.
## # A tibble: 1 × 5
## Vertical Bench Broad Cone Shuttle
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 27 23 97 8.07 4.98The coach needs nothing other than Figure 5.9. Based on the lineman’s performance in the five events, we navigate the branches of the tree by choosing left, right, left, right and arrive at 5.334 seconds. For that particular player, we don’t even need to know their vertical jump or bench press performance. Compare this to the linear model that requires the coach to find a calculator and compute the following:
\[ 5.170-0.007\cdot27-0.004\cdot23-0.009\cdot97+0.131\cdot8.07+0.055\cdot4.98=5.347 \]
To be fair, nearly any stakeholder will be capable of performing the required arithmetic for the linear model with a calculator. However, the tree model is clearly faster and easier to implement. The question is whether the overall reduction in accuracy is unacceptable to the stakeholder. If the difference between a 5.334 second lineman and a 5.347 second lineman is important, then the linear model may be preferred.
Answer the Question
Based on a sample of 451 offensive linemen from the years 2000 to 2020, we can predict forty-yard dash time to within 0.150 seconds based on the performance in the other five events. This accuracy is based on a very intuitive decision tree model that can be implemented without calculations, directly from a diagram. If a greater level of accuracy is required, a multiple linear regression model can reduce the error to 0.137 seconds. However, implementation does require some basic computations using a calculator.
Given the inferior performance of regression trees compared to other modeling approaches, there exist a variety of extensions that can greatly improve prediction accuracy. In practice, many data scientists employ ensemble methods that consist of growing and aggregating multiple decision trees. If we average the predictions from multiple trees, then we tend to get more accurate results. Ensemble methods such as bagging, boosting, and random forests can dramatically decrease the prediction error compared to individual decision trees. However, they represent advanced techniques beyond the scope of this text.
5.2.5 Categorical Predictors
So far in this chapter we have described linear regression models with numerical predictors. In other words, the predictor variables (\(x_1,x_2,\cdots,x_p\)) take on continuous, numerical values. However, we often want to use categorical predictor variables as well. This presents a problem because the levels of a factor are typically words rather than numbers. How do we use words to predict a numerical response in a linear regression model? The answer is to assign a binary numerical variable to each level of the factor. Specifically, if we want to predict numerical response \(y\) based on a categorical predictor \(z\) with \(k\) levels, then we define linear regression model in Equation (5.7).
\[\begin{equation} y = \beta_0+\beta_1 z_1+\beta_2 z_2+\cdots+\beta_{k-1} z_{k-1} \tag{5.7} \end{equation}\]
The predictor \(z_1\) is a binary variable that is set equal to 1 if an observation is assigned the first level of the factor and 0 otherwise. The same is true for \(z_2\) through \(z_{k-1}\). We do not need a binary variable for the last level (\(k\)) of the factor. By process of elimination, if an observation is not assigned one of the first \(k-1\) levels, then is must be assigned the last level. Because a given observation is assigned one and only one level, we know that \(z_1+z_2+\cdots+z_{k-1}\leq1\).
Another way to think about this formulation for categorical predictors is that it simply shifts the intercept (\(\beta_0\)) of the best-fit line. For example, if an observation is assigned the first level, then \(z_1=1\) and \(z_2=z_3=\cdots=z_{k-1}=0\). In that case, Equation (5.7) is reduced to \(y=\beta_0+\beta_1\). Thus, the intercept is shifted by a value of \(\beta_1\). Since the categorical variable is the only predictor in this example, there is no slope parameter. However, we can mix numerical and categorical predictors so that the regression equation includes both intercept and slope parameters. We demonstrate this with a case study using the tidyverse below.
Ask a Question
The ggplot2 package includes a data set called diamonds which describes the appearance, size, and price of over 50 thousand round cut diamonds. Our goal is to predict the price of a diamond based on what are commonly referred to as the 4Cs: carat, cut, color, and clarity. While carat is a numerical measure of a diamond’s weight (1 carat equals 0.2 grams), the other three measures are categorical assignments determined by experts. The cut of a diamond is ranked on a scale from fair to ideal. The color is assigned a letter between Z and D that corresponds to a range between light yellow and colorless. Finally, the clarity of a diamond is ranked on an alpha-numeric scale between I1 and IF that aligns with descriptors from imperfect to flawless. A large, ideal cut, colorless, flawless diamond can be incredibly expensive given its rarity. For our case study, we isolate two of the Cs and investigate the following question: How accurately can we predict the price of a diamond based on its carat and color?
For academic purposes, we increase the specificity of this question even further. We consider only ideal cut, nearly colorless diamonds of less than one carat that are assigned a clarity between VS2 and VVS1. Though this may appear overly-specific, we will be left with more than enough diamonds in our sample. Reducing the scope of the problem decreases some of the variability that otherwise exists in pricing and facilitates the demonstration of our modeling approach. The selected characteristics also represent diamonds that are not too large, but still exhibit very high quality. We begin by acquiring the built-in data.
Acquire the Data
The data we seek is stored in the file diamonds as part of the tidyverse package. We import the data below and isolate the characteristics of interest.
#import diamond data
data(diamonds)
#wrangle diamond data
diamonds2 <- diamonds %>%
filter(carat<1,
cut=="Ideal",
color %in% c("G","H","I","J"),
clarity %in% c("VS2","VS1","VVS2","VVS1")) %>%
transmute(price,carat,
color=factor(color,levels=c("G","H","I","J"),ordered=FALSE)) %>%
droplevels()
#summarize data frame
summary(diamonds2)## price carat color
## Min. : 340 Min. :0.2300 G:2265
## 1st Qu.: 689 1st Qu.:0.3200 H:1232
## Median :1008 Median :0.4100 I: 818
## Mean :1432 Mean :0.4684 J: 278
## 3rd Qu.:1922 3rd Qu.:0.5600
## Max. :6807 Max. :0.9700Despite our narrow focus, we are left with 4,593 diamonds ranging in price from $340 to $6,807. The diamonds weigh between 0.23 and 0.97 carats. The scale for nearly colorless diamonds includes four sub-categories increasing in quality from J to G. Thus we have one numerical predictor (carat) and one categorical predictor (color) with four levels. Next we must split our data into training and testing sets in preparation for analysis.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(diamonds2),size=floor(0.75*nrow(diamonds2)),replace=FALSE)
#split sample into training and testing
training <- diamonds2[rows,]
testing <- diamonds2[-rows,]Our training set includes 3,444 diamonds which we use to estimate the parameters of a predictive model. The accuracy of the resulting model is validated with the 1,149 diamonds that reside in the testing set. As in previous modeling efforts, we compute the mean response for each set to ensure the values do not differ significantly.
## [1] 1431.813## [1] 1431.124In both data sets, the average diamond costs just over $1,431. We are now prepared to train and test our model.
Analyze the Data
Our first step in developing a predictive model is to determine a baseline accuracy using a null model. In this case, the null model is the mean response in the training set of $1,431.81. What is the accuracy of a model that always predicts this price?
## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 984.If we use no information regarding carat and color and simply guess $1,431.81 as the price for every diamond, then we will be off by an average of $984. That is a relatively high error rate. Hopefully, we can develop a much more accurate prediction model by using the other information available to us. Let’s explore the association between a diamond’s carat, color, and price.
#create colored scatter plot
ggplot(data=training,aes(x=carat,y=price,color=color)) +
geom_point(position="jitter",alpha=0.5) +
labs(title="Price of Diamonds less than 1 Carat",
subtitle="Ideal Cut, Very (Very) Slightly Included, Nearly Colorless",
x="Weight (carats)",
y="Price ($US)",
color="Color",
caption="Source: ggplot2 package") +
scale_x_continuous(limits=c(0.2,1),breaks=seq(0.2,1,0.1)) +
scale_y_continuous(limits=c(0,7000),breaks=seq(0,7000,1000)) +
scale_color_manual(values=c("#481567FF","#2D708EFF","#3CBB75FF","#FDE725FF")) +
theme_bw()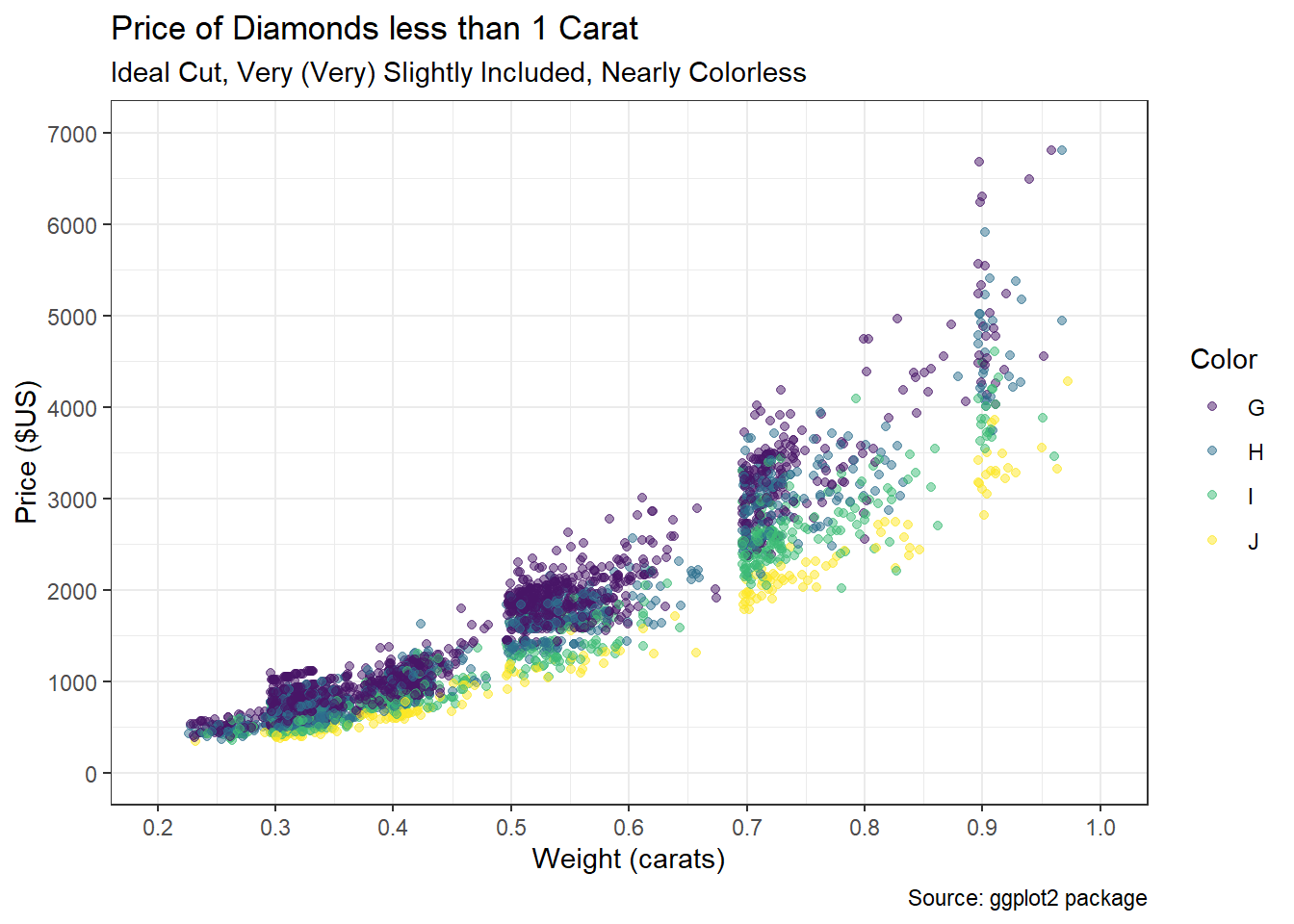
Figure 5.10: Nonlinear Association between Price and Weight
Based on Figure 5.10, there does appear to be an association between color and price. As the levels progress from J to G, the average price increases. There also appears to be a strong, positive, nonlinear association between weight and price. The relationship seems to curve in a concave-up manner. In other words, as weight increases the price increases at a larger and larger rate. We cannot model such an association with linear regression. Thus, we need to transform the response variable in order to linearize the association.
If we think of a diamond’s weight as proportional to its volume, then a cubic relationship may make sense. In essence, each of the three dimensions (length, width, and depth) of a diamond have an associated cost. As a result, the price of a diamond is correlated with cubic units (volume). In order to use a linear model, we need to “undo” the cubic relationship by applying the inverse function (i.e., cube root). Below, we transform the response variable using the cube root.
#create colored scatter plot
ggplot(data=training,aes(x=carat,y=price^(1/3),color=color)) +
geom_point(position="jitter",alpha=0.5) +
labs(title="Price of Diamonds less than 1 Carat",
subtitle="Ideal Cut, Very (Very) Slightly Included, Nearly Colorless",
x="Weight (carats)",
y="Cube-Root Price ($US)",
color="Color",
caption="Source: ggplot2 package") +
scale_x_continuous(limits=c(0.2,1),breaks=seq(0.2,1,0.1)) +
scale_y_continuous(limits=c(5,20),breaks=seq(5,20,2.5)) +
scale_color_manual(values=c("#481567FF","#2D708EFF","#3CBB75FF","#FDE725FF")) +
theme_bw()
Figure 5.11: Linearized Association between Price and Weight
Notice the association between weight and (cube root) price in Figure 5.11 appears linear. In this form, a linear regression model is appropriate. In mathematical notation, we want to estimate the parameters of the model in Equation (5.8).
\[\begin{equation} \sqrt[3]{y} = \beta_0+\beta_1 z_1+\beta_2 z_2+\beta_3 z_3+\beta_4 x \tag{5.8} \end{equation}\]
The binary predictors \(z_1,z_2,z_3\) determine which color level the diamond is assigned. Typically, R excludes the first level in alphabetical order. So, \(z_1,z_2,z_3\) are assigned to H, I, J, respectively. The numerical predictor \(x\) refers to the diamond’s weight in carats. We train and test this model in the same manner as previous case studies.
#estimate linear model
model <- lm(price^(1/3)~carat+color,data=training)
#estimate accuracy of model
testing %>%
mutate(pred_price=predict(model,newdata=testing)^3) %>%
summarize(RMSE=sqrt(mean((price-pred_price)^2)))## # A tibble: 1 × 1
## RMSE
## <dbl>
## 1 226.When the lm() function encounters a categorical predictor, it automatically knows to split it into binary levels. Thus, we can simply add the variable name color to the model without creating the binary variables manually. The resulting accuracy suggests we can predict a diamond’s price to within $226, on average, if we know its carat and color. The calculation of accuracy includes a very important adjustment. Note that we cube the results of the predict() function in the previous code. Due to the required linearization, our model predicts the cube root of price. If we want to return to price itself, we must cube the prediction.
With a RMSE of $226, we reduce our error by 77% compared to the null model. That is a dramatic improvement! For our prediction model to be actionable, we need to estimate the parameters using the entire data set and produce a regression equation.
#estimate final linear model
model_final <- lm(price^(1/3)~carat+color,data=diamonds2)
#review estimated coefficients
coefficients(summary(model_final))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.7700616 0.02368740 201.37550 0.000000e+00
## carat 13.5644849 0.04609404 294.27847 0.000000e+00
## colorH -0.3824592 0.01862011 -20.54012 9.211158e-90
## colorI -0.9300547 0.02156984 -43.11830 0.000000e+00
## colorJ -1.6490977 0.03362910 -49.03782 0.000000e+00Our summary output provides a clear indication of which color levels are included in the model. The baseline level is G, since it is not included. So, when the binary variables associated with H, I, and J are all zero, we know the diamond must be G. We write the estimated regression equation as follows:
\[\begin{equation} \text{Cube-Root Price}=4.77-0.38\cdot \text{H}-0.93 \cdot \text{I}-1.65 \cdot \text{J}+13.56 \cdot \text{Carat} \tag{5.9} \end{equation}\]
The form of Equation (5.9) suggests that the color of the diamond only impacts the intercept, while the slope is connected to the carats. For a diamond with color G, the right-hand side of the equation is reduced to \(4.77+13.56\cdot \text{Carat}\). For a diamond with color J, the equation becomes \(3.12+13.56\cdot \text{Carat}\). Thus, the intercept changes, but the slope remains the same. We depict this graphically in Figure 5.12.
#create scatter plot matrix
ggplot(data=diamonds2,aes(x=carat,y=price^(1/3),color=color)) +
geom_point(position="jitter",alpha=0.25) +
geom_abline(intercept=4.77,slope=13.56,color="#481567FF",linewidth=0.75) +
geom_abline(intercept=4.77-0.38,slope=13.56,color="#2D708EFF",linewidth=0.75) +
geom_abline(intercept=4.77-0.93,slope=13.56,color="#3CBB75FF",linewidth=0.75) +
geom_abline(intercept=4.77-1.65,slope=13.56,color="#FDE725FF",linewidth=0.75) +
geom_segment(x=0.9,xend=0.9,y=4.5,yend=15.3,
linewidth=0.5,linetype="dashed",color="red") +
geom_segment(x=0.17,xend=0.9,y=15.3,yend=15.3,
linewidth=0.5,linetype="dashed",color="red") +
labs(title="Price of Diamonds less than 1 Carat",
subtitle="Ideal Cut, Very (Very) Slightly Included, Nearly Colorless",
x="Weight (carats)",
y="Cube-Root Price ($US)",
color="Color",
caption="Source: ggplot2 package") +
scale_x_continuous(limits=c(0.2,1),breaks=seq(0.2,1,0.1)) +
scale_y_continuous(limits=c(5,20),breaks=seq(5,20,2.5)) +
scale_color_manual(values=c("#481567FF","#2D708EFF","#3CBB75FF","#FDE725FF")) +
theme_bw()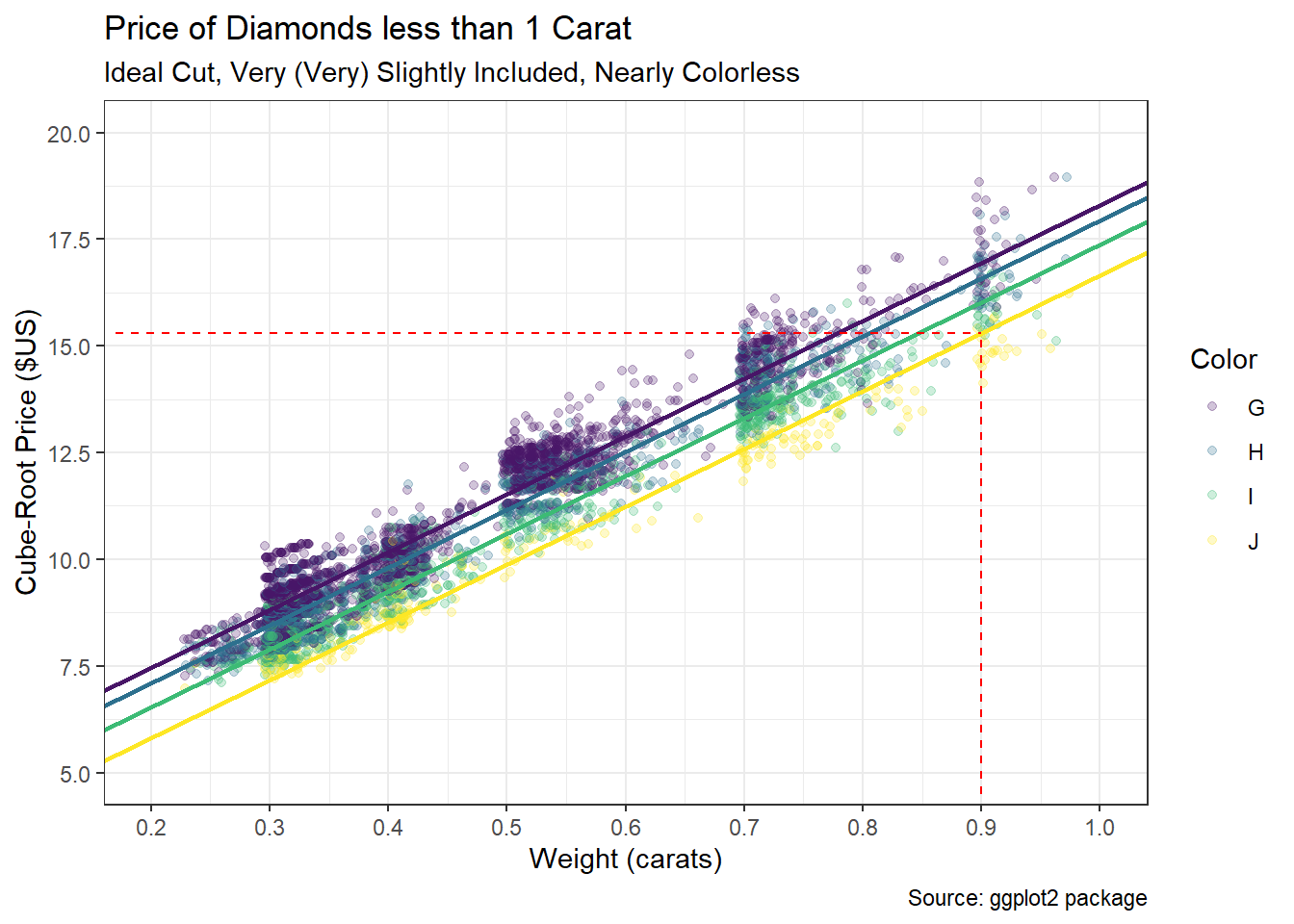
Figure 5.12: Best-Fit Lines between Price and Weight
Given a diamond’s color and carat, we predict its cube-root price based on the appropriate best-fit line. For example, 0.9 carat diamonds with J color have an average cube-root price of about 15.3 (dashed red lines). Consequently, the predicted price is \(15.3^3\) or $3,581.58. Such predictions are accurate to within $226, on average. How might we present these results to stakeholders?
Advise on Results
More complex models often afford us more accurate predictions. By transforming the response variable and mixing both numerical and categorical predictors, we are able to predict the price of certain diamonds to within a couple of hundred dollars. But the trade-off with complex models is the capacity to describe their use to stakeholders. Without some technical experience, it can be difficult to grasp the meaning and purpose behind methods like non-linear transformation and binary decomposition. Yet, good data scientists have the ability to communicate complex methods using common language. In order to apply our prediction model, we might propose the following set of instructions.
- Multiply the diamond’s carats by 13.56.
- Add the following value to the result:
- If color is G, then add 4.77.
- If color is H, then add 4.39.
- If color is I, then add 3.84.
- If color is J, then add 3.12.
- Cube the result to obtain the price.
Clear and concise instructions such as this can ease the implementation of the model for many users. That is not to say that all stakeholders are incapable of digesting a more mathematical representation of the model or a graphic such as Figure 5.12. Some may actually prefer a more technical approach. It is critical to know our stakeholders and advise on analytic results in a manner well-aligned with their background.
Our model does have some limitations based on the specificity of the formulation. It was trained and tested only on ideal cut, nearly colorless, VS2-VVS1 clarity diamonds of less than one carat. The model should not be used to predict prices for diamonds outside of this set of characteristics. It’s possible that the associations between price, carat, and color change for other diamond types. That said, if stakeholders desire a broader model we could repeat a similar analysis for a more diverse set of diamonds.
Answer the Question
Based on a sample of 4,593 round-cut diamonds, we can predict the average price to within $226 if we know the carat and color. This accuracy estimate applies to diamonds with the following characteristics: cut (ideal), color (G-J), clarity (VS2-VVS1), and carat (<1). Diamonds with different characteristics may not achieve the same accuracy level. Further research that considers a broader range of variable values is required to determine the associated accuracy.
How might someone apply the results of this model? One possibility is to use the model as a sanity check on the prices charged for diamonds in the future. Similar to a confidence interval, we can compute what is known as a prediction interval to determine the expected variability around our point estimate. Thus, for a diamond with a particular set of characteristics we can be fairly confident its price should be between the resulting bounds of the interval. If the listed price is outside of those bounds, then we should question the reason. While the margin of error for predicting an individual observation is typically larger than that of the average observation, the insights are nonetheless valuable.
5.3 Classification Models
In Chapter 3.3.4 we explored associations in the context of a logistic regression model. Logistic regression was the appropriate method because the response was a dichotomous (binary) categorical variable. However, our goal in the exploratory analysis was simply to describe the association between variables with a logistic equation. In this chapter, our objective is to predict the likelihood of each binary outcome given a particular set of predictor variable values. The prediction of likelihood is the gateway to classifying response values.
5.3.1 Simple Logistic Regression
One of the most common supervised, parametric, classification models for predicting a binary response value \(y\) is the simple logistic regression model. As with linear regression, the qualifier simple implies there is only one predictor variable. After estimating the parameters \(\beta_0\) and \(\beta_1\) using the maximum likelihood method, we obtain the function shown in Equation (5.10).
\[\begin{equation} \hat{p} = P(y=1) = \frac{1}{1+e^{-(\hat{\beta}_0+\hat{\beta}_1 x)}} \tag{5.10} \end{equation}\]
The form of the logistic function reveals an important difference compared to a linear regression model. Namely, we cannot directly estimate the binary response \(y\). The continuous logistic function produces output values between zero and one, rather than solely equal to zero or one. We interpret the output as the estimated proportion (\(\hat{p}\)) of response values equal to one. Alternatively, the output is often referred to as the probability that the response will be equal to one (\(P(y=1)\)). In a sense, we are measuring the frequency (or likelihood) of response values equal to one when the predictor variable (\(x\)) takes on a particular value. We demonstrate this by returning to the tropical storm data from Chapter 5.2.1.
Ask a Question
In the chapter on simple linear regression, we explored a NOAA data set comprised of tropical storm characteristics in the Atlantic Ocean. Our goal was to establish a predictive relationship between the air pressure in the eye of a storm and its maximum sustained wind speed. According to NOAA, any tropical storm with a maximum sustained wind speed above 74 miles per hour (64.3 knots) is classified as a hurricane. Consequently, if an association exists between a storm’s pressure and wind speed, then there should also be a relationship between pressure and hurricane classification. With this in mind, we pose the following question: How likely is it that a tropical storm will be classified as a hurricane when its air pressure is 980 millibars?
As with our previous tropical storm analysis, there is nothing particularly special about the value 980 millibars. The objective of this chapter is to demonstrate the use of a logistic regression model to predict a likelihood (probability), so it is helpful to choose an exemplar input value. That said, it is an interesting transitive connection to make between air pressure, wind speed, and storm classification. Imagine a scenario in which we only have a barometer to measure air pressure and not an anemometer to measure wind speed. With our intended prediction model, we could establish the likelihood of a hurricane without directly knowing the wind speed. Let’s acquire and analyze the data to see if this is possible.
Acquire the Data
Although tropical storm data remains openly available on the NOAA website, we will once again use the built-in table storms from the dplyr package. Import and wrangle the data using the code below.
#import storm data
data(storms)
#wrangle storm data
storms2 <- storms %>%
transmute(pressure,
hurricane=if_else(status=="hurricane",1,0)) %>%
na.omit()
#review data structure
glimpse(storms2)## Rows: 19,066
## Columns: 2
## $ pressure <int> 1013, 1013, 1013, 1013, 1012, 1012, 1011, 1006, 1004, 1002, …
## $ hurricane <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …The original table includes a variable for status that labels a given storm as a disturbance, depression, hurricane, or other relevant category. Since our current interest is solely whether a storm reaches the magnitude of a hurricane, we create a binary response variable that is equal to one for hurricanes and zero otherwise. Once again, we split our sample into training and testing sets prior to estimating a model.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(storms2),size=floor(0.75*nrow(storms2)),replace=FALSE)
#split sample into training and testing
training <- storms2[rows,]
testing <- storms2[-rows,]After randomly selecting 75% of the storms for training, we can estimate a simple logistic regression model and predict our air pressure value of interest.
Analyze the Data
As we demonstrated in Chapter 3.3.4, it is useful to first visually explore the association between the numerical predictor and binary response. Figure 5.13 displays the relationship between air pressure and hurricane status.
#create scatter plot of pressure versus status
ggplot(data=training,
mapping=aes(x=pressure,y=hurricane)) +
geom_jitter(width=0,height=0.05,alpha=0.2) +
labs(title="Tropical Storm Classification",
subtitle="Training Data",
x="Air Pressure at Storm Center (millibars)",
y="Proportion that are Hurricanes",
caption="Source: NOAA") +
scale_x_continuous(limits=c(880,1030),breaks=seq(880,1030,10)) +
scale_y_continuous(limits=c(0,1),breaks=seq(0,1,0.1)) +
theme_bw()
Figure 5.13: Logistic Association between Pressure and Status
The training data suggests a relatively strong, negative association between the variables. In other words, as the air pressure in the eye of the storm increases, the likelihood of being classified as a hurricane decreases. This makes intuitive sense based on what we learned previously regarding the correlation between air pressure and wind speed. Higher pressures tend to result in lower wind speeds. To further bolster our assessment of the strength of association, we next compute a point-biserial correlation coefficient. Recall, the point-biserial coefficient is mathematically equivalent to Pearson coefficient when one of the variables is binary.
#compute Pearson correlation coefficient
cor(x=training$pressure,
y=training$hurricane,
method="pearson")## [1] -0.7531415The Pearson coefficient confirms a strong, negative association between the variables. Now that we have confirmed a monotonic relationship (both visually and numerically), we can fit a logistic function and estimate the response for an air pressure of 980 millibars.
#create scatter plot of pressure versus status
ggplot(data=training,
mapping=aes(x=pressure,y=hurricane)) +
geom_jitter(width=0,height=0.05,alpha=0.2) +
geom_smooth(method="glm",formula=y~x,se=FALSE,
method.args=list(family="binomial")) +
geom_segment(x=980,xend=980,y=-0.05,yend=0.63,
linewidth=0.75,linetype="dashed",color="red") +
geom_segment(x=870,xend=980,y=0.63,yend=0.63,
linewidth=0.75,linetype="dashed",color="red") +
labs(title="Tropical Storm Classification",
subtitle="Training Data",
x="Air Pressure at Storm Center (millibars)",
y="Proportion that are Hurricanes",
caption="Source: NOAA") +
scale_x_continuous(limits=c(880,1030),breaks=seq(880,1030,10)) +
scale_y_continuous(limits=c(0,1),breaks=seq(0,1,0.1)) +
theme_bw()
Figure 5.14: Logistic Association between Pressure and Status
Based on Figure 5.14, it appears that roughly 63% of storms with a central pressure of 980 millibars are classified as hurricanes. Said another way, if the air pressure in the eye of a storm is 980 millibars, then it is more likely than not to be a hurricane. We still observe plenty of storms at 980 millibars that are not hurricanes (\(y=0\)). But a larger proportion at that pressure are in fact hurricanes (\(y=1\)). Our visual estimate is insightful, but we prefer to have the equation for the logistic function (blue curve).
#estimate logistic regression model
model <- glm(hurricane~pressure,data=training,family="binomial")
#review coefficient estimares
coefficients(summary(model))## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 176.3158885 3.237988965 54.45228 0
## pressure -0.1793509 0.003276915 -54.73162 0Among generalized linear models, the logistic function belongs to the Binomial family and employs the maximum likelihood method. After executing the maximum likelihood method, we obtain the best estimates for our parameters \(\beta_0\) and \(\beta_1\). The resulting simple logistic regression model is shown in Equation (5.11).
\[\begin{equation} \hat{p} = \frac{1}{1+e^{-(176.32-0.18 x)}} \tag{5.11} \end{equation}\]
We could compute the estimated proportion (\(\hat{p}\)) of hurricanes by manually substituting our input pressure (\(x=980\)) and completing the arithmetic. Alternatively, we can predict input values using the predict() function.
## 1
## 0.6346119The resulting proportion confirms the estimated value in the scatter plot. A 980 millibar storm has a 63.5% chance of being classified as a hurricane. Of course, by this point in the textbook we know that a single-value estimate of \(\hat{p}=0.635\) is not ideal. A different sample of storms would likely produce a different estimate, even for the same input value. So, we instead construct a bootstrap confidence interval for the mean response.
#initiate empty data frame
results_boot <- data.frame(prop=rep(NA,1000))
#resample 1000 times and save predictions
for(i in 1:1000){
set.seed(i)
storms_i <- sample_n(training,size=nrow(training),replace=TRUE)
model_i <- glm(hurricane~pressure,data=storms_i,family="binomial")
results_boot$prop[i] <- predict(model_i,
newdata=data.frame(pressure=980),
type="response")
}Via bootstrap resampling, we simulate repeatedly gathering new storm data and predicting the proportion of hurricanes for the same air pressure. The sampling distribution of proportions is depicted in Figure 5.15.
#plot resampling distribution
ggplot(data=results_boot,
mapping=aes(x=prop)) +
geom_histogram(color="black",fill="#CFB87C",bins=32) +
geom_vline(xintercept=quantile(results_boot$prop,0.05),
color="red",linetype="dashed",linewidth=0.75) +
geom_vline(xintercept=quantile(results_boot$prop,0.95),
color="red",linetype="dashed",linewidth=0.75) +
labs(title="Atlantic Ocean Tropical Storms (1975-2021)",
subtitle="Prediction Distribution for 980 millibars Air Pressure",
x="Proportion of Storms Classified as Hurricanes",
y="Count",
caption="Source: NOAA") +
scale_x_continuous(limits=c(0.58,0.68),breaks=seq(0.58,0.68,0.01)) +
theme_bw()
Figure 5.15: Distribution for predicted proportion of hurricanes when air pressure is 980 millibars
Across 1,000 samples of tropical storms, an air pressure of 980 millibars produced hurricane proportions between 58% and 68%. Ninety percent of those samples returned proportions between 61.5% and 65.7% (red dashed lines). Hence, we are 90% confident that between 61.5% and 65.7% of storms with an air pressure of 980 millibars will be classified as hurricanes. Next, we interpret these results for stakeholders.
Advise on Results
The concept of likelihood (probability) can be challenging to interpret. It is difficult enough to accurately articulate among those with a background in statistics, let alone those who do not. The confusion is largely due to the use of a statistic, which is based on many observations, to predict the outcome of a single observation. We might tell a stakeholder that a particular storm has a 63.5% chance of being a hurricane. But that storm will or will not be a hurricane. There is no in between. A tropical storm cannot be 63.5% hurricane and 36.5% not hurricane. Consequently, we are often expected to convert a probability prediction into a binary classification. We must commit! Will it be a hurricane or will it not.
With a probability of 63.5%, we would likely classify the storm as a hurricane. Of course, there is a reasonable chance we will be wrong. In the long run, given many storms with the same air pressure, we only expect to be wrong 36.5% of the time. Unfortunately, analysts are often not afforded enough opportunities for this fact to be revealed to stakeholders. For any individual prediction we are 100% right or 100% wrong. Many predictions (storms) are required for the likelihood of 63.5% to be demonstrated and we may not get that chance if we are wrong a few times in a row. Predictions such as these are based on long-run frequency where it is not uncommon to have streaks of being right or being wrong. But that is often (and understandably) of little interest to stakeholders in the very short term.
One potential remedy for this challenge is a very careful explanation of the difference between long-term frequency and short-term outcomes. For example, based on our model, we would classify a 980 millibar storm as a hurricane. We are not providing a guarantee that the next 980 millibar storm is a hurricane. We are merely stating that the majority of 980 millibar storms do turn out to be hurricanes. Said another way, if we lived to witness 1,000 tropical storms with an air pressure of 980 millibars, then about 635 of them would be hurricanes. Of course, that means 365 of them will not be hurricanes. If it just so happens that the first ten storms we witness are from the non-hurricane group, then bad luck for us. It does not mean our advice is incorrect. This is just a consequence of applying long-run statistics to individual events.
Answer the Question
Based on a training set of 14,299 Atlantic storm measurements between 1975 and 2021, we predict between 61.5% and 65.7% of tropical storms will be classified as hurricanes when the air pressure of the eye is 980 millibars. Thus, storms with an air pressure of 980 millibars are more likely than not to be hurricanes. This prediction is only valid for tropical storms in the Atlantic Ocean and the model should only be applied to central air pressures between 882 and 1,024 millibars. Other air pressure values are outside the range of the training data and require extrapolation.
Just as with regression, the concept of prediction suggests some measure of accuracy across a range of input values. But, given a binary response, a single classification will be either right or wrong. The idea of “closeness” to the actual response value is not appropriate. Instead, we simply want our classifications to be correct as frequently as possible. In the next section, we describe the most common measure of classification accuracy.
5.3.2 Classification Accuracy
In Chapter 5.2.2, we applied root mean squared error (RMSE) as the prediction accuracy metric for regression models. One interpretation of RMSE is that it represents the average deviation between our predictions and the true values of the numerical response. Given a categorical response, the measure of prediction accuracy is more straight-forward. Our predictions for the level (category) assigned to each observation will be either right or wrong. Rather than a deviation for each prediction we obtain a binary indicator \(I(y\neq\hat{y})\) that is equal to 1 when our prediction is incorrect and 0 otherwise. For \(n\) total predictions, we compute the classification error rate (CER) as:
\[\begin{equation} \text{CER}=\frac{\sum I(y\neq\hat{y})}{n} \tag{5.12} \end{equation}\]
In Equation (5.12), the numerator determines the total number of incorrect classifications. We then divide by the total number of predictions to obtain the proportion that are incorrect. Ideally, the CER for our classification models would be as small as possible. However, the overall error rate is not the only mistake we are typically interested in. We also like to know the false positive rate (FPR) and false negative rate (FNR). These values are best demonstrated in an example.
Imagine we develop a classification model to predict whether our favorite team wins each game in the upcoming basketball season. Table 5.1 provides the results at the end of the 80-game season.
| Result | Predicted_Win | Predicted_Loss |
|---|---|---|
| Win | 35 | 15 |
| Loss | 5 | 25 |
Based on the table, we incorrectly predicted 20 out of the 80 games. Thus, our CER is 25%. However, our model is not equally capable of predicting wins and losses. Of our team’s 50 wins, we got 15 wrong. So, our FNR is 30%. In other words, for 30% of the team’s wins we predicted they would lose. On the other hand, we only missed the mark on 5 of the team’s 30 losses. So, our model’s FPR is much lower at about 17%. In predictive modeling, it is important to distinguish between these three types of error. Though our overall error rate is 25%, we know that the model is much better at predicting losses than wins. Let’s incorporate these ideas into a more complex model using functions from the tidyverse.
Ask a Question
To demonstrate classification accuracy, we return to the pumpkin seed research by Koklu et al (Koklu et al. 2021) from Chapter 3.3.4. Recall, the study uses digital imagery to obtain various measurements for two varieties of pumpkin seed. The authors apply advanced modeling techniques to classify the seed variety with between 87-89% accuracy. In this section, we attempt to partially replicate their work with a much simpler model. In the end, we answer the following question: How accurately can we predict the variety of pumpkin seed based on its major axis length?
Acquire the Data
The data from the Koklu et al. study are available in the file pumpkin_seeds.csv. Below, we import and wrangle the data frame to isolate the variables of interest.
#import data
pumpkin <- read_csv("pumpkin_seeds.csv")
#wrangle data
pumpkin2 <- pumpkin %>%
transmute(Type=as.factor(Type),
Length=Major_Axis_Length) %>%
na.omit()
#review data structure
glimpse(pumpkin2)## Rows: 2,500
## Columns: 2
## $ Type <fct> A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, …
## $ Length <dbl> 326.1485, 417.1932, 435.8328, 381.5638, 383.8883, 405.8132, 392…The data consists of 2,500 pumpkin seeds of two types: A and B. Our goal is to use a seed’s length (in pixels) to predict its type. First, we must split our sample into training and testing sets.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(pumpkin2),size=floor(0.75*nrow(pumpkin2)),replace=FALSE)
#split sample into training and testing
training <- pumpkin2[rows,]
testing <- pumpkin2[-rows,]Using the validation set approach, we will train our classification model on 1,875 pumpkins seeds and test the model’s accuracy on the remaining 625 seeds. With regression models, we compute the mean response as a quality check on the distribution within each set. We perform the same check for classification models, but we must choose which binary response value to consider a success (1) versus a failure (0). Here we arbitrarily select Type A to be equal to 1.
## [1] 0.5194667## [1] 0.5216The mean of a binary response provides the proportion of values that are equal to 1. In our case, the training and testing sets are both comprised of roughly 52% Type A seeds. Thus, our split maintained similar distributions in the two sets and we can proceed to the analysis.
Analyze the Data
As always, we require a null model prior to constructing a prediction model. Just as with regression, we employ the mean response in the training set as a basis for the null model. However, we use CER rather than RMSE. The training set is comprised of 51.9% Type A seeds. So, we could simply guess the most prevalent type (Type A) for every seed in the testing set. If we implemented this strategy, we would be correct 52.2% of the time. This is equivalent to a CER of 47.8%, since error is the complement of accuracy. Based on this null model, any prediction model we develop must have a CER less than 0.478 to be useful.
We begin the modeling process by plotting the training data and displaying the best-fit logistic curve.
#create scatter plot of length versus type
ggplot(data=training,aes(x=Length,y=ifelse(Type=="A",1,0))) +
geom_jitter(width=0,height=0.05,alpha=0.2) +
geom_smooth(method="glm",formula=y~x,se=FALSE,
method.args=list(family="binomial")) +
geom_segment(x=400,xend=400,y=-0.05,yend=0.85,
linewidth=0.75,linetype="dashed",color="red") +
geom_segment(x=280,xend=400,y=0.85,yend=0.85,
linewidth=0.75,linetype="dashed",color="red") +
labs(title="Pumpkin Seed Classification",
subtitle="Training Data",
x="Major Axis Length (pixels)",
y="Proportion that are Type A") +
scale_x_continuous(limits=c(320,670),breaks=seq(320,670,50)) +
scale_y_continuous(limits=c(0,1),breaks=seq(0,1,0.1)) +
theme_bw()
Figure 5.16: Logistic Association between Length and Type
Figure 5.16 shows a decreasing association between seed length and type. In other words, the longer a seed the more likely it is not Type A. We could use this graphic to predict new seed types based purely on visual estimation. For example, we see from the dashed red line that about 85% of 400 pixel long seeds are Type A. Said another way, there is an 85% chance that a seed is Type A if its length is 400 pixels. Rather than a visual estimation, we could rely on an algebraic calculation after estimating the parameters of the logistic regression model.
#estimate logistic regression model
model <- glm(Type=="A"~Length,data=training,family="binomial")
#review parameter estimates
coefficients(summary(model))## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 13.70074919 0.660350571 20.74769 1.286236e-95
## Length -0.02999687 0.001455623 -20.60758 2.346664e-94Since we are now applying logistic regression, we require the glm() function along with the Binomial parameter. The maximum likelihood estimates for the model parameters are displayed in the Estimate column of the summary output. Combining the parameter estimates with the general formula for the logistic function, we obtain Equation (5.13).
\[\begin{equation} P(\text{Type A}) = \frac{1}{1+e^{-13.701+0.030 \cdot \text{Length}}} \tag{5.13} \end{equation}\]
From this equation, we find a length of 400 pixels produces a Type A proportion of 0.846. Of course, there is no need to perform these computations manually. We obtain the same solution using the predict() function.
#estimate Type A proportion for 400 pixel length
predict(model,newdata=data.frame(Length=400),type="response")## 1
## 0.8457957When predicting a logistic regression model, it is critical we use the type="response" option. Otherwise, the result will be the log-odds of a seed being Type A, rather than the proportion. Although the predict() function is helpful for a single observation, its true power is the capacity to predict an entire testing set of observations. We predict and review the testing set below.
#estimate Type A proportion for testing set
testing_pred <- testing %>%
mutate(Type_pred=predict(model,newdata=testing,type="response"))
#review structure of predictions
glimpse(testing_pred)## Rows: 625
## Columns: 3
## $ Type <fct> A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, …
## $ Length <dbl> 392.2516, 413.6504, 438.5827, 403.0626, 371.2713, 382.1808, …
## $ Type_pred <dbl> 0.8737386, 0.7845751, 0.6328909, 0.8334296, 0.9284932, 0.903…After predicting the testing set, we arrive at an interesting conundrum. The true values of the response variable are the letters A and B. But the predicted values are numbers between 0 and 1. How do we compare our predictions to reality when they aren’t even the same data type? The answer is we must make the leap from prediction to classification using a classification threshold. Typically, we choose 0.50 as our threshold. In other words, if there is more than a 50% chance that a seed is Type A, then we classify it as Type A. All seeds with a predicted proportion at or below 0.50 are classified as Type B. Let’s enforce this threshold and compute the CER of the testing set.
#classify testing set
testing_class <- testing_pred %>%
mutate(Type_class=ifelse(Type_pred>0.5,"A","B"))
#compute CER for model
testing_class %>%
summarize(CER=mean(Type!=Type_class))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.242When computing CER, the notation Type!=Type_class is equivalent to the binary indicator \(I(y\neq\hat{y})\) from Equation (5.12). Our classification error rate is about 0.24. So, based on 625 classifications, our model is wrong about 24% of the time. That is half the error rate of the null model. Equivalently, our model correctly classifies pumpkin seeds 76% of the time. If we want to determine the other error types, we can produce a table of classifications similar to Table 5.1.
##
## A B
## A 256 70
## B 81 218A table of classifications such as this is often referred to with the unfortunate title of confusion matrix. The rows represent the true pumpkin seed types, while the columns represent the predicted types. The off-diagonal values indicate the classifications we got wrong. So, the model classifies 151 of the 625 seeds (24.2%) incorrectly. However, it is not equally capable of classifying Type A versus B seeds. Of the 326 Type A seeds, the model gets 70 (21.5%) wrong. Since we chose Type A seeds to represent success, this value is the FNR. Meanwhile, 81 (27.1%) of the 299 Type B seeds are incorrectly classified. This is equivalent to the FPR. Consequently, the model is slightly better at identifying Type A seeds compared to Type B.
Advise on Results
When reporting CER, FNR, and FPR to stakeholders, clear and precise communication is critical. These concepts are often confused, even by experienced practitioners. Maybe confusion matrix is an appropriate name after all! The key is to identify the subset of the data to which the error rate refers. The CER is the error rate for all the pumpkin seeds. The FNR is the error rate for only Type A seeds. Finally, the FPR is the error rate for only Type B seeds.
Interestingly, false positive and negative rates are often not the metric stakeholders care about. These rates assume we know a priori whether a seed is Type A or B. But isn’t the entire reason we developed a model because we do not know the seed type? In reality the stakeholder only knows what we predict, not the truth. So, they want to know the chance we are wrong given we predicted a certain seed type. This question refers to the columns of the confusion matrix rather than the rows. Of the 337 seeds predicted to be Type A, our model got 81 (24.0%) wrong. This is referred to as false discovery rate (FDR). Similarly, the model predicted 288 Type B seeds and got 70 (24.3%) wrong. This value is called the false omission rate (FOR). These error rates are more consistent across seed types. Hence, we could inform a stakeholder that regardless of which seed type our model predicts, there is about a 24% chance it is wrong.
Confusion matrices, in one form or another, are common across many different domains. In any situation where a binary decision can be right or wrong, the concept of a confusion matrix exists. The verdict of a legal trial will be right or wrong. The results of a COVID-19 test or pregnancy test will be accurate or inaccurate. Wagers on the result of a sporting event will be correct or incorrect. Due to the pervasive nature of confusion matrices, there are many synonymous terms for the same types of error and accuracy. It is important for data scientists to understand the terminology used within a given domain to ensure results are communicated accurately.
Answer the Question
Based on a sample of 2,500 pumpkin seeds, we can predict the variety (A or B) with roughly 76% accuracy simply by knowing the major axis length. That said, our model is slightly more accurate when classifying Type A seeds (78%) versus Type B seeds (73%). More advanced models in outside research have demonstrated up to 89% accuracy when classifying this data. Thus, it is likely that other characteristics of a seed besides major axis length have significant predictive value. In order to develop a model with multiple predictors, we require the methods presented in the next section.
5.3.3 Multiple Logistic Regression
In the previous section, we classify a binary response variable based on a single predictor. Just as with regression models, it is possible that additional predictor variables improve the classification accuracy. A popular classification approach employing more than one predictor is known as multiple logistic regression. Despite the use of “regression” in the title, logistic models are typically used for classification. That said, the title is appropriate since the initial output of a logistic regression model is a numerical value. In general, a model with \(p\) predictor variables is defined as in Equation (5.14).
\[\begin{equation} P(y=1) = \frac{1}{1+e^{-(\beta_0+\beta_1 x_1+\beta_2 x_2+\cdots+\beta_p x_p)}} \tag{5.14} \end{equation}\]
The response variable \(P(y=1)\) in the logistic function is the proportion of observations with predictor values \(x_1,x_2,\cdots,x_p\) that are expected to have a response value of \(y=1\). Thus, the response is in fact numerical. However, as part of the classification process, we transform the proportions into binary values based on a threshold (typically 0.5). In other words, when \(P(y=1)>0.5\) we classify the observation as \(\hat{y}=1\) and when \(P(y=1)\leq 0.5\) we classify \(\hat{y}=0\). Let’s demonstrate multiple logistic regression with an example.
Ask a Question
Another study by Koklu et al. regards an acoustic fire suppression system (Koklu and Taspinar 2021). The system consists of amplified subwoofer speakers inside a collimator cabinet capable of producing 4,000 Watts of power. The goal of the study is to predict whether a flame will be extinguished by a sound wave produced from the system. Though the paper employs more advanced classification techniques, the case study offers a fantastic application for multiple logistic regression as well. Specifically, we seek an answer to the following question: How accurately can we predict an extinguished flame based on the airflow, decibels, distance, and frequency of a sound wave?
The Koklu study achieves accuracies between 92-97%, depending on the approach. So, in some sense, our question has been answered. However, the paper does not include the simpler approach of multiple logistic regression. As a result, there is still some value in discovering the relative performance of a more straightforward approach. Luckily, the authors make their data openly available to support replication.
Acquire the Data
The fire suppression data is available in the file called fire.csv. We import and wrangle the data in the code chunk below.
#import data
fire <- read_csv("fire.csv")
#wrangle data
fire2 <- fire %>%
select(STATUS,AIRFLOW,DECIBEL,DISTANCE,FREQUENCY) %>%
na.omit()
#review data structure
glimpse(fire2)## Rows: 17,442
## Columns: 5
## $ STATUS <dbl> 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
## $ AIRFLOW <dbl> 0.0, 0.0, 2.6, 3.2, 4.5, 7.8, 9.7, 12.0, 13.3, 15.4, 15.1, 1…
## $ DECIBEL <dbl> 96, 96, 96, 96, 109, 109, 103, 95, 102, 93, 93, 95, 110, 111…
## $ DISTANCE <dbl> 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, …
## $ FREQUENCY <dbl> 75, 72, 70, 68, 67, 66, 65, 60, 55, 52, 51, 50, 48, 47, 46, …The experimental data consists of over 17 thousand observations. Each represents an individual attempt to extinguish the fire using particular settings for airflow (m/sec), decibel (dB), distance (cm), and frequency (Hz). The binary response variable indicates an extinguished fire with a status of 1 and a non-extinguished fire with a status of 0. Prior to developing a model to predict fire status, we must split our sample into training and testing sets.
#randomly select rows from sample data
set.seed(719)
rows <- sample(x=1:nrow(fire2),size=floor(0.75*nrow(fire2)),replace=FALSE)
#split sample into training and testing
training <- fire2[rows,]
testing <- fire2[-rows,]Our random segmentation of the data results in 13,081 observations for training and 4,361 for testing. For purposes of quality control and to establish the relative prevalence of our two statuses, we compute the mean response in both the training and testing sets.
## [1] 0.499656## [1] 0.4923183In both sets, the proportions of extinguished and non-extinguished fires are nearly the same. Based on these proportions, we begin our analysis with a discussion of the null model.
Analyze the Data
The most prevalent response status in the training set is for the fire to not be extinguished. Thus, our null model consists of always predicting that a fire will not be extinguished. When we apply this model to the testing set we are correct 51.8% of the time. Conversely, our classification error rate (CER) for the null model is 49.2%. Our goal is to develop a classification model with a much lower error rate than this.
We begin model development with a simple logistic regression model and then include additional variables one at a time. Let’s visualize the association between the airflow of the sound wave and the status of the fire.
#create scatter plot of length versus type
ggplot(data=training,aes(x=AIRFLOW,y=STATUS)) +
geom_jitter(width=0,height=0.05,alpha=0.2) +
geom_smooth(method="glm",formula=y~x,se=FALSE,
method.args=list(family="binomial")) +
labs(title="Fire Suppression Classification",
subtitle="Training Data",
x="Airflow (m/sec)",
y="Proportion that are Extinguished") +
scale_x_continuous(limits=c(0,18),breaks=seq(0,18,3)) +
scale_y_continuous(limits=c(0,1),breaks=seq(0,1,0.1)) +
theme_bw()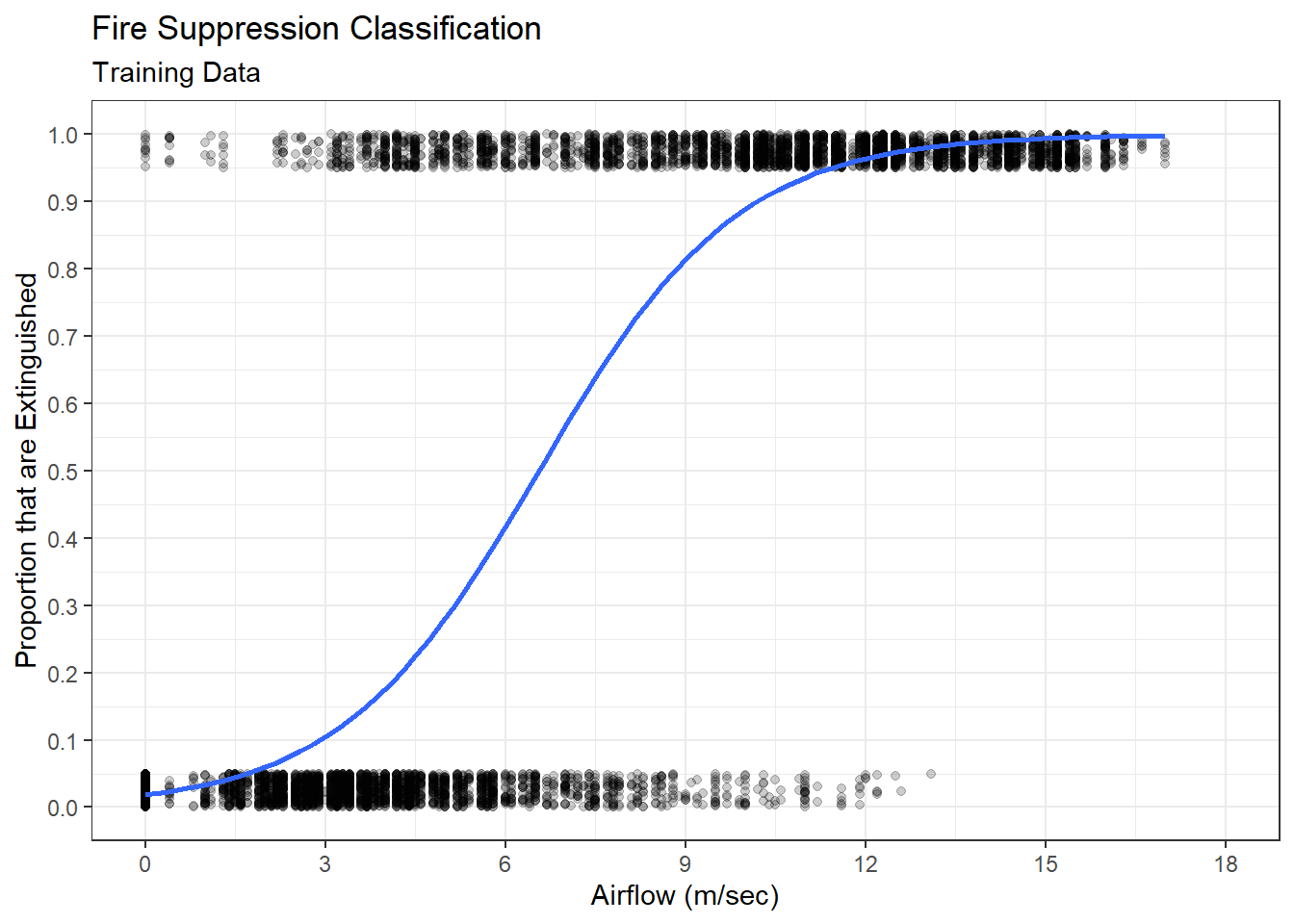
Figure 5.17: Logistic Association between Airflow and Status
Based on Figure 5.17, there is a monotonic increasing association between airflow and the likelihood of extinguishing the fire. This makes intuitive sense, because we would expect a faster rush of air to have a greater chance of putting out the fire. Picture this as blowing out the candles on a birthday cake. The harder you blow, the more likely you put out the candles. Given the relatively strong association between the two variables, it seems plausible that airflow has some predictive value. So, we estimate a logistic regression model using the training data and validate its accuracy on the testing data.
#estimate simple logistic regression model
model1 <- glm(STATUS~AIRFLOW,data=training,family="binomial")
#estimate accuracy of model
testing %>%
mutate(pred_STATUS=predict(model1,newdata=testing,type="response")) %>%
summarize(CER=mean(STATUS!=(pred_STATUS>0.5)))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.141Using a single predictor, we witness a dramatic decrease in CER down to 14.13%. Our null model is barely more accurate than flipping a coin, but the simple logistic regression model correctly classifies the test set nearly 86% of the time. If including one predictor adds that much value, then maybe another will reduce the error even more. Let’s add frequency as another predictor variable.
#estimate multiple logistic regression model
model2 <- glm(STATUS~AIRFLOW+FREQUENCY,data=training,family="binomial")
#estimate accuracy of model
testing %>%
mutate(pred_STATUS=predict(model2,newdata=testing,type="response")) %>%
summarize(CER=mean(STATUS!=(pred_STATUS>0.5)))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.140Although modest compared to the previous improvement, we do again achieve a reduction in error down to 13.96%. Given that we already know the airflow of the sound wave, adding the frequency provides limited benefit. Perhaps the distance predictor variable performs better?
#estimate multiple logistic regression model
model3 <- glm(STATUS~AIRFLOW+FREQUENCY+DISTANCE,data=training,family="binomial")
#estimate accuracy of model
testing %>%
mutate(pred_STATUS=predict(model3,newdata=testing,type="response")) %>%
summarize(CER=mean(STATUS!=(pred_STATUS>0.5)))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.133The CER decreases by more than when we added frequency. Knowing the distance of the sound system from the fire adds some predictive value, even if we already know the airflow and frequency. Yet the improvement in error continues to be modest as we add more information. The decibels is our last remaining variable to include.
#estimate multiple logistic regression model
model4 <- glm(STATUS~AIRFLOW+FREQUENCY+DISTANCE+DECIBEL,data=training,family="binomial")
#estimate accuracy of model
testing %>%
mutate(pred_STATUS=predict(model4,newdata=testing,type="response")) %>%
summarize(CER=mean(STATUS!=(pred_STATUS>0.5)))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.132Decibel decreased the error by the least so far. Keep in mind that the sequence of error reductions does depend on the order in which we add the predictor variables. The improvement provided by each additional variable depends on the existing variables. In the end, our final model is expected to have a CER of only 13.19%. To obtain the best parameter estimates for this model, we fit the final model to the entire data set.
#estimate multiple logistic regression model
model_final <- glm(STATUS~AIRFLOW+FREQUENCY+DISTANCE+DECIBEL,data=fire2,family="binomial")
#review parameter estimates
coefficients(summary(model_final))## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.88540328 0.4412365182 -6.539357 6.178373e-11
## AIRFLOW 0.40466059 0.0115008662 35.185227 3.364305e-271
## FREQUENCY -0.04056614 0.0022923231 -17.696519 4.460372e-70
## DISTANCE -0.02107157 0.0007567537 -27.844688 1.249089e-170
## DECIBEL 0.03737579 0.0057752556 6.471712 9.689862e-11By substituting these parameter estimates into the general logistic function, we obtain Equation (5.15).
\[\begin{equation} P(\text{Extinguish}) = \frac{1}{1+e^{-2.885+0.405 \text{AIR}-0.041 \text{FREQ} -0.021 \text{DIST}+0.037 \text{DEC}}} \tag{5.15} \end{equation}\]
This model predicts the proportion of fires that will be extinguished for particular system settings of airflow, decibel, distance, and frequency. It is expected to correctly classify about 87% of fires when applying a threshold of 0.5. In the next subsection, we discuss methods for presenting these results to stakeholders.
Advise on Results
Our primary focus when assessing a model’s performance is error rate against the testing set. However, the complement to error is accuracy. In some cases, it may be more intuitive to present performance statistics to stakeholders in the positive context of accuracy. But, just as with error, overall accuracy is not the only characteristic we are concerned with. The conditional accuracies represented by true positive rate (TPR) and true negative rate (TNR) are important as well.
In order to demonstrate the calculation of TPR and TNR, let’s construct a confusion matrix for our 4,361 testing set classifications.
#classify testing set
testing_class <- testing %>%
mutate(pred_STATUS=predict(model4,newdata=testing,type="response"),
class_STATUS=ifelse(pred_STATUS>0.5,1,0))
#construct confusion matrix
table(testing_class$STATUS,testing_class$class_STATUS)##
## 0 1
## 0 1962 252
## 1 323 1824The overall accuracy of 87% is computed by dividing the total correct classifications (3,786) by the total number of predictions (4,361). However, our model is not equally capable of classifying extinguished fires compared to non-extinguished fires. Of the 2,147 fires that were actually extinguished, we correctly predicted 1,824 (84.96%). By contrast, we correctly predicted 1,962 (88.62%) of the 2,214 non-extinguished fires. Thus, our TNR is higher than our TPR. Said another way, the model is better at predicting non-extinguished fires compared to extinguished fires.
Of course, these conditional accuracies assume we know the true status of the flame. More often, we do not know the true status of the response variable. That is why we desire a prediction in the first place. From a stakeholder perspective, the more interesting metric is the likelihood our predictions are correct. For example, of the 2,076 fires we predicted to be extinguished, 1,824 (87.86%) actually were. We refer to this accuracy as the positive predictive value (PPV) of the model. On the other hand, we classified 2,285 fires as non-extinguished and 1,962 (85.86%) were correct. This metric is known as negative predictive value (NPV). So, if the model predicts a fire will be extinguished, it is slightly more likely to be correct than if it predicts it will not be extinguished.
The two different perspectives described above may initially appear contradictory. On the one hand, the TNR suggests the model is better at predicting non-extinguished fires. On the other hand, the PPV indicates the model is more likely to be correct when predicting extinguished fires. However, there is no contradiction because the two metrics are conditioned on very different knowledge. The TNR assumes we know the fires true status, while the PPV assumes we only know what was predicted. In general, TNR is more likely to be of interest to the designers of the suppression system, whereas the PPV is of interest to those using the system.
Answer the Question
Based on a sample of 17,442 experimental cases, we can predict a fire’s status (extinguished or not) with 87% accuracy. Additionally, the model is more likely to be correct when predicting extinguished fires (88%) compared to non-extinguished fires (86%). To achieve this performance, we require the suppression system’s airflow, decibel, distance, and frequency settings. While more sophisticated models with more predictors have been shown to produce accuracies as high as 97%, our logistic regression model performs surprisingly well compared to the null model.
As with most models, it is possible that a different combination of predictor variables could provide more accurate classifications. In fact, the best model may not even comprise a parametric method like logistic regression. In the next section, we present a common non-parametric method for classification.
5.3.4 Classification Trees
Multiple logistic regression requires the estimation of model parameters (\(\beta_0,\beta_1,...,\beta_p\)) using the maximum likelihood method. However, there are also non-parametric methods for classifying a binary response. In fact, we can employ the same decision trees that we constructed for the purposes of regression in Chapter 5.2.4. The only difference regards the predicted values at each leaf in the tree. For classification models, the response variable is categorical and, for our purposes, binary. Thus, the mean response prescribed at each leaf is a proportion.
Returning to the dog adoption example, we consider the classification tree in Figure 5.18.
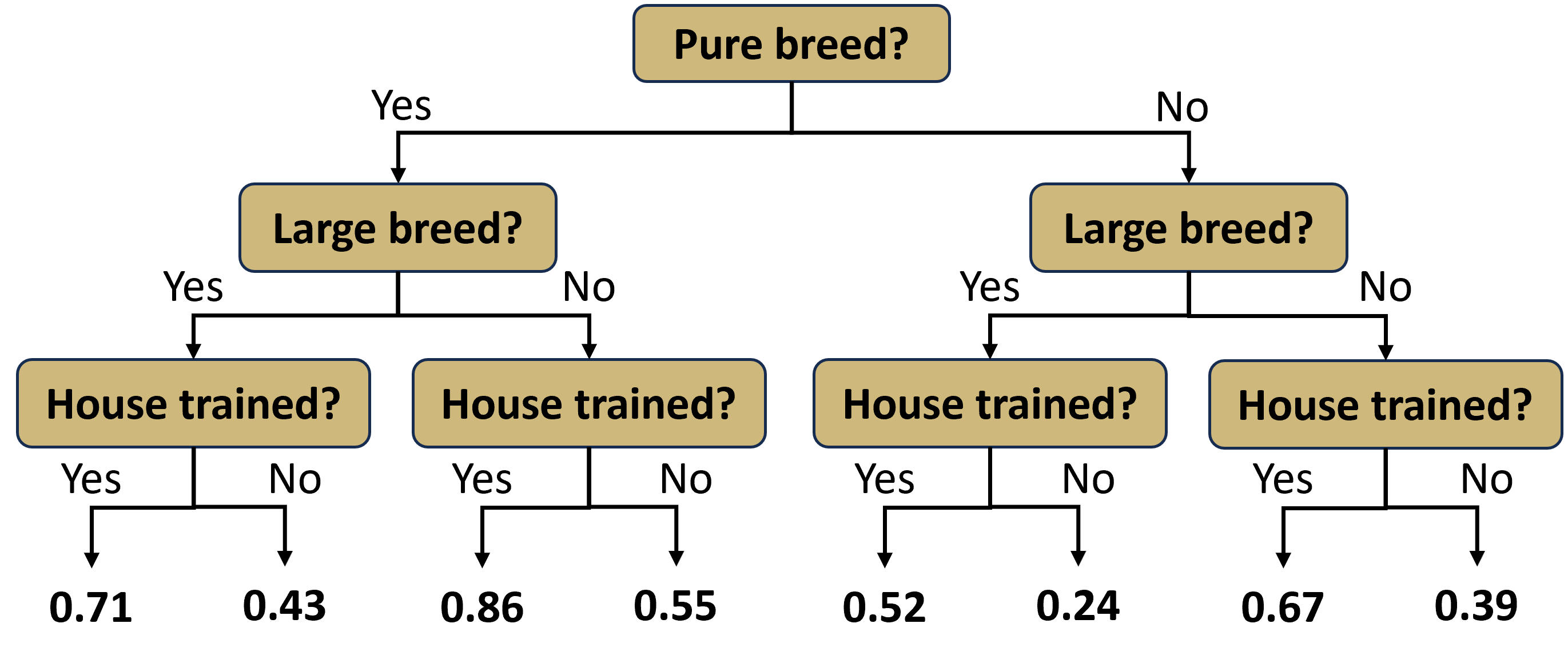
Figure 5.18: Classification Tree to Predict Dog Adoption Cost
Rather than predicting the numerical cost of adopting a dog, suppose we simply want to predict whether the dog will cost more than $500. Hence, our binary response is equal to one if the cost exceeds $500 and zero otherwise. In this example, we use the same set of predictor variables regarding the breed, size, and training for a dog. But the predictions at each leaf are no longer dollar values. Instead they represent proportions. Among pure breed, large, house-trained dogs we predict 71% will cost more than $500. As a result, we would likely classify such a dog as costing more than $500 (i.e., a binary value of one). On the other hand, mixed breed, small, non-trained dogs only include 39% that cost more than $500. Consequently, we would classify such a dog as not costing more than $500 (i.e., a binary value of zero).
Similar to logistic regression, we still rely on a threshold in order to convert proportions to classifications. The difference lies in how we obtain the proportions. Instead of estimating parameters and computing proportions from a logistic function, we grow a decision tree to parse the training data into distinct groupings. We demonstrate this process below using a familiar case study.
Ask a Question
In Chapter 5.3.3, we estimated a multiple logistic regression model to predict whether a flame would be extinguished by a sound wave generated from an acoustic suppression device. The model included parameter estimates associated with the speed, frequency, and decibel of the sound wave, as well as the distance of the suppression device from the flame. Similar to regression models, we can construct non-parametric models for classification purposes. Specifically, we develop a classification tree to answer the following question: How accurately can we predict an extinguished flame based on the airflow, decibels, distance, and frequency of a sound wave?
Acquire the Data
As in the previous section, the fire suppression data is available in the file fire.csv. The code chunk below imports, wrangles, and randomly splits the sample into training and testing sets. We then compute the mean response value in the training set.
#import data
fire <- read_csv("fire.csv")
#wrangle data
fire2 <- fire %>%
select(STATUS,AIRFLOW,DECIBEL,DISTANCE,FREQUENCY) %>%
na.omit()
#randomly select rows from sample data
set.seed(719)
rows <- sample(x=1:nrow(fire2),size=floor(0.75*nrow(fire2)),replace=FALSE)
#split sample into training and testing
training <- fire2[rows,]
testing <- fire2[-rows,]
#compute mean response
mean(training$STATUS)## [1] 0.499656Of the 13,081 experimental trials in the training data, the fire was extinguished 49.97% of the time. We apply this proportion as our null model in the next section.
Analyze the Data
Based on the proportion of extinguished flames in the training data, our null model consists of always predicting a fire will not be extinguished. When we evaluate this model using the testing data, we obtain a maximum acceptable error rate for any future models.
## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.492If we always predict a fire will not be extinguished, then we can expect to be wrong about 49.23% of the time. Our goal is to develop a decision tree model that reduces this error rate. First we must choose a predictor variable and statistic to branch on. Since we already know (from the previous section) that airflow has some predictive value, we choose that variable for the first branch. Purely to demonstrate a different statistic, we will branch on the median rather than the mean.
## [1] 5.8The median airflow of sound waves in the training set is 5.8 meters per second. By branching on this value, we split all of the experimental trials into speeds below 5.8 and speeds above 5.8. Then we compute the proportion of extinguished fires in each branch.
#add branch assignments
training_branch <- training %>%
mutate(Branch1=if_else(AIRFLOW<5.8,"Left","Right"))
#compute branch means
training_branch %>%
group_by(Branch1) %>%
summarize(prop=mean(STATUS)) %>%
ungroup()## # A tibble: 2 × 2
## Branch1 prop
## <chr> <dbl>
## 1 Left 0.134
## 2 Right 0.853When the airflow of the sound wave is below 5.8 m/sec, the fire is put out only 13.44% of the time. By contrast, when the airflow is above 5.8 m/sec the fire is extinguished 85.27% of the time. The airflow appears to be highly valuable information! We visualize the branching in Figure 5.19.
#create scatter plot of length versus type
ggplot(data=training_branch,aes(x=AIRFLOW,y=STATUS,color=Branch1)) +
geom_jitter(width=0,height=0.05,alpha=0.2) +
geom_vline(xintercept=5.8,linetype="dashed") +
geom_hline(yintercept=0.134,color="red") +
geom_hline(yintercept=0.4997) +
geom_hline(yintercept=0.853,color="blue") +
labs(title="Fire Suppression Classification",
subtitle="Training Data",
x="Airflow (m/sec)",
y="Proportion that are Extinguished") +
scale_x_continuous(limits=c(0,18),breaks=seq(0,18,3)) +
scale_y_continuous(limits=c(0,1),breaks=seq(0,1,0.1)) +
scale_color_manual(values=c("red","blue")) +
theme_bw()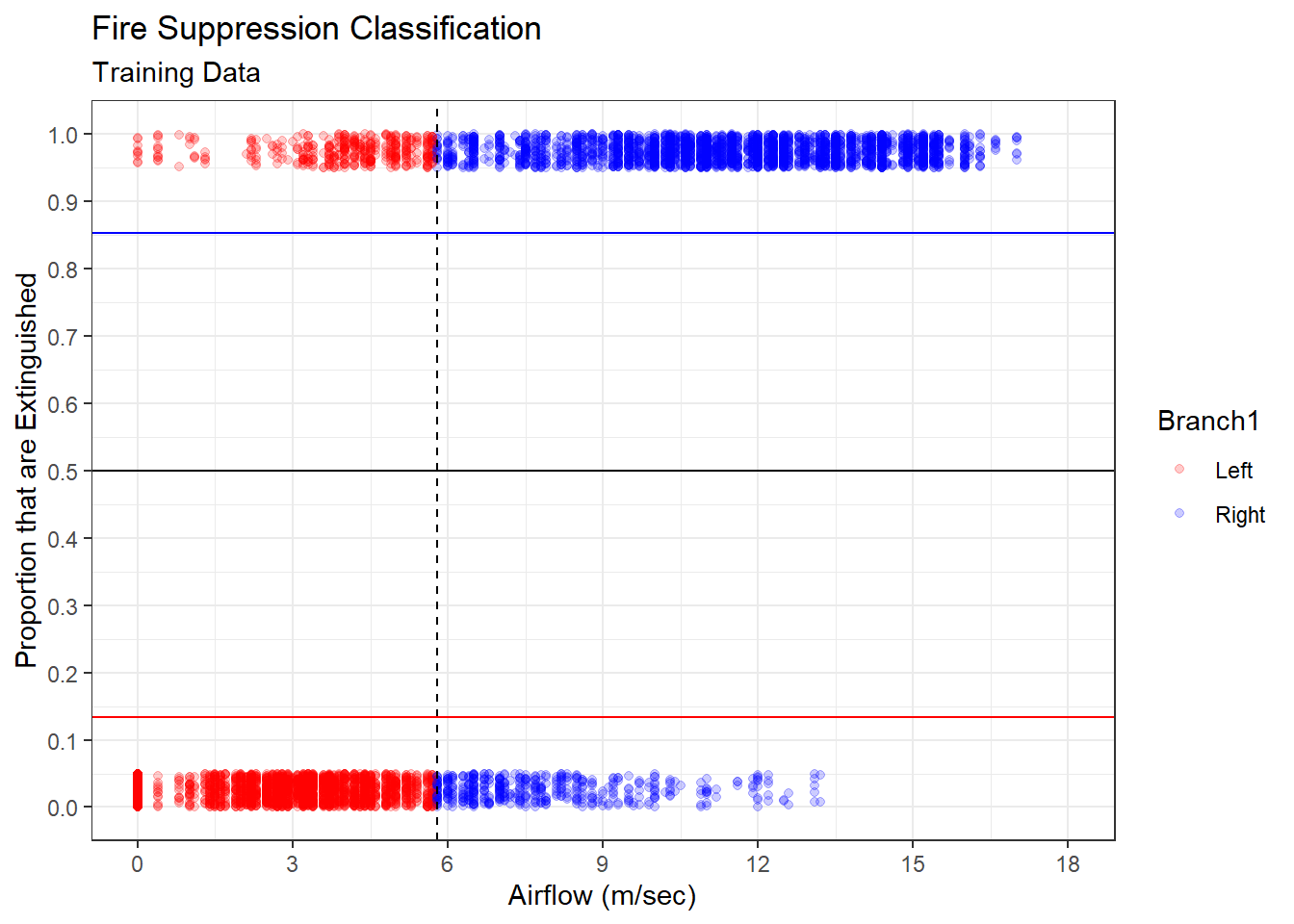
Figure 5.19: Fire Status Branched on Airflow
The horizontal black line represents the overall proportion of extinguished fires, which is roughly 50%. Among trials with an airflow below 5.8 m/sec (red points) the proportion drops to about 13%. It would seem prudent to predict that these sound waves will not extinguish the fire. For airflow values above 5.8 m/sec (blue points) the proportion increases to about 85%. These sound waves likely will extinguish the fire. Thus, the knowledge of airflow dissects our trials into two very different groups in terms of fire status. What impact does this dissection have on the error rate?
#compute CER for tree model
testing %>%
mutate(STATUS_class=ifelse(AIRFLOW<5.8,0,1)) %>%
summarize(CER=mean(STATUS!=STATUS_class))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.147Our error rate plummets from 49% to about 15%. If we ignore all of the available information, our fire predictions are little better than a coin flip. On the other hand, by knowing and applying the airflow of the sound wave we increase our prediction accuracy to 85%. If one branch is this valuable, than perhaps a second branch will be as well. With this in mind, we next branch on the median distance of the device from the flame.
#compute mean distance for each branch
training_branch %>%
group_by(Branch1) %>%
summarize(med_dist=median(DISTANCE)) %>%
ungroup()## # A tibble: 2 × 2
## Branch1 med_dist
## <chr> <dbl>
## 1 Left 150
## 2 Right 60The lower airflow speeds (left branch) have a median distance of 150 cm, while the higher speeds (right branch) have a median of 60 cm. By branching on these distance values, we segment our training data into four groupings. The code chunk below computes the proportion of extinguished flames for each of the groups.
#add branch assignments
training_branch2 <- training_branch %>%
mutate(Branch2=case_when(
Branch1=="Left" & DISTANCE<150 ~ "LL",
Branch1=="Left" & DISTANCE>=150 ~ "LR",
Branch1=="Right" & DISTANCE<60 ~ "RL",
Branch1=="Right" & DISTANCE>=60 ~ "RR"
))
#compute branch means
training_branch2 %>%
group_by(Branch2) %>%
summarize(prop=mean(STATUS)) %>%
ungroup()## # A tibble: 4 × 2
## Branch2 prop
## <chr> <dbl>
## 1 LL 0.208
## 2 LR 0.0673
## 3 RL 0.984
## 4 RR 0.749For the experimental trials with low airflow and large distance (LR branch), only 6.73% extinguished the flame. For these trials, we should predict the flame is not extinguished. Meanwhile, the trials with high airflow and short distance (RL branch) extinguish 98.40%. This combination of airflow and distance will almost certainly extinguish the fire. The other two combinations produce proportions in between. We visualize these results in Figure 5.20.
ggplot(data=training_branch2,aes(x=AIRFLOW,y=DISTANCE,color=Branch2)) +
geom_point() +
geom_vline(xintercept=5.8,linetype="dashed") +
geom_segment(x=0,xend=5.8,y=150,yend=150,linetype="dashed",color="black") +
geom_segment(x=5.8,xend=18,y=60,yend=60,linetype="dashed",color="black") +
labs(title="Fire Suppression Classification",
subtitle="Training Data",
x="Airflow (m/sec)",
y="Distance (cm)") +
scale_x_continuous(limits=c(0,18),breaks=seq(0,18,3)) +
scale_y_continuous(limits=c(0,200),breaks=seq(0,200,25)) +
scale_color_manual(values=c("red","dark red","blue","dark blue")) +
annotate("text",x=3,y=200,label="0.067",color="dark red",size=5) +
annotate("text",x=3,y=0,label="0.208",color="red",size=5) +
annotate("text",x=12,y=200,label="0.749",color="dark blue",size=5) +
annotate("text",x=12,y=0,label="0.984",color="blue",size=5) +
theme_bw()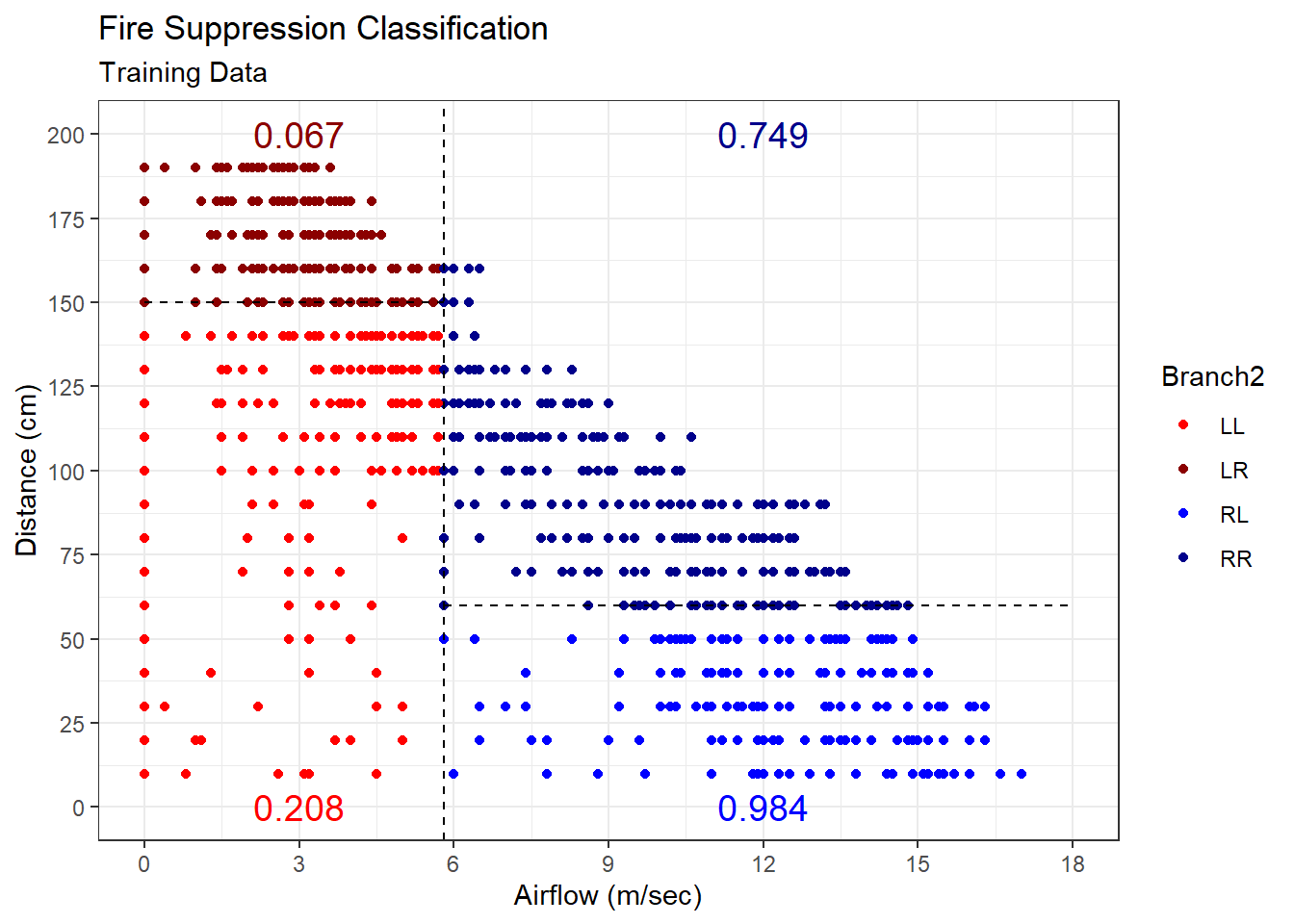
Figure 5.20: Fire Status Branched on Airflow and Distance
Based on the scatter plot, there appears to be a negative correlation between airflow speed and the distance of the suppression device from the flame. This makes intuitive sense if the speed is measured at the flame rather than at the device. All other things being equal, the speed of the sound wave that hits the flame will be lower if it has to travel further. The question remains, is there additional value in knowing the distance of the device from the fire?
#compute CER for tree model
testing %>%
mutate(STATUS_class=case_when(
AIRFLOW<5.8 & DISTANCE<150 ~ 0,
AIRFLOW<5.8 & DISTANCE>=150 ~ 0,
AIRFLOW>=5.8 & DISTANCE<60 ~ 1,
AIRFLOW>=5.8 & DISTANCE>=60 ~ 1
)) %>%
summarize(CER=mean(STATUS!=STATUS_class))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.147The error rate is exactly the same as before. In other words, if we already know the sound wave speed then we gain no value by knowing the distance of the device. This insight has everything to do with the association we observe in Figure 5.20. Since the airflow is largely determined by the distance, we don’t really need both pieces of information. Of course, our analysis so far was based on manually selecting branch variables and constraining our branch value to the median. Let’s try the more sophisticated recursive binary splitting algorithm and see is the error rate improves.
#load tree library
library(tree)
#build decision tree
model <- tree(STATUS~.,data=training)
#plot decision tree
plot(model)
text(model,cex=0.7,pretty=TRUE)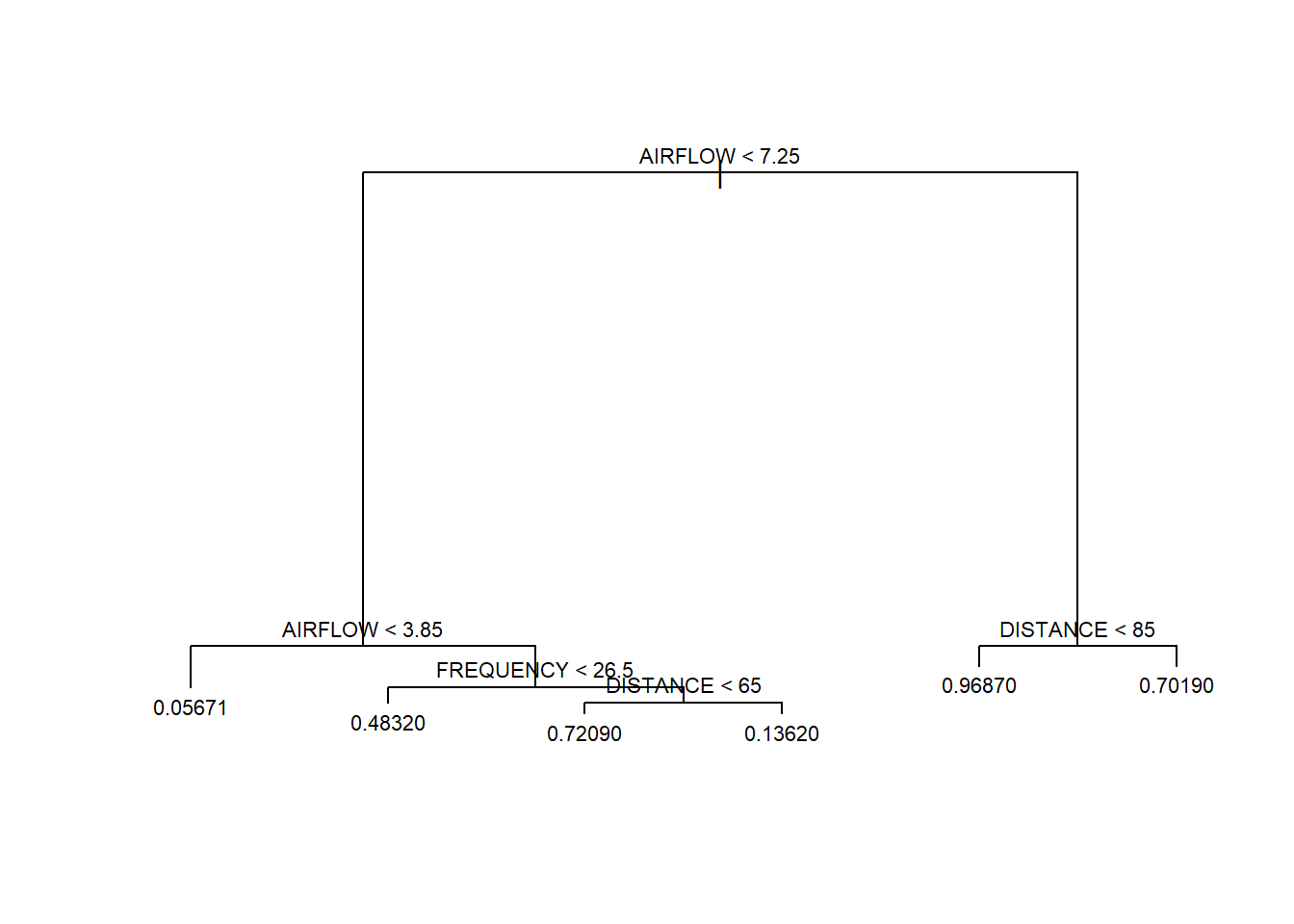
The automated algorithm selected airflow as the first branching variable, but employed a value of 7.25 m/sec rather than the median value of 5.8 m/sec. It must be the case that this larger airflow dissects the training data into more distinct groups. At the second branch, we see an interesting phenomenon. For the left branch (< 7.25 m/sec) we choose the airflow variable a second time and further split the trials above and below 3.85 m/sec. By contrast, the right branch changes to the distance variable and uses a threshold of 85 cm. The frequency variable also makes an appearance lower in the tree, but the algorithm never applies the decibel variable. Ultimately, we obtain six possible predictions (leaves) at the bottom of the tree which we can use to compute the error rate on the testing set.
#classify responses using tree model
testing_class <- testing %>%
mutate(STATUS_pred=predict(model,newdata=testing),
STATUS_class=ifelse(STATUS_pred>0.5,1,0))
#compute CER for tree model
testing_class %>%
summarize(CER=mean(STATUS!=STATUS_class))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.134Using a classification threshold of 0.5, our automated decision tree produces a prediction model with an error rate of only 13.37%. This is a minor improvement over our manual tree, but an improvement nonetheless. Given the airflow, distance, and frequency values for the suppression device, we can navigate the decision tree and produce predictions with about 87% accuracy. Next we must interpret these results for stakeholders.
Advise on Results
An important limitation of our model that should be explained to stakeholders is the classification threshold of 0.50. Any fire with more than a 50% chance of being extinguished is classified as extinguished. While this is common practice, there is no guarantee that the 0.50 threshold produces the most accurate model. If we think of the threshold as the strength of evidence required to classify a fire as extinguished, then certain stakeholders may require a different burden of proof. A lower threshold (e.g., 0.40) implies we are willing to positively classify (\(\hat{y}=1\)) an observation on weaker evidence. On the other hand, a higher threshold (e.g., 0.60) suggests we require stronger evidence to support a positive classification.
Let’s demonstrate the impact of lowering the threshold in our fire suppression model to 0.40. This change means we will classify more fires as extinguished, because we don’t require as strong of evidence to do so.
#classify with new threshold
testing_class2 <- testing %>%
mutate(STATUS_pred=predict(model,newdata=testing),
STATUS_class=ifelse(STATUS_pred>0.4,1,0))
#compute CER for new model
testing_class2 %>%
summarize(CER=mean(STATUS!=STATUS_class))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.134By classifying more fires as extinguished, we increase our error rate only slightly from 13.37% to 13.41%. However, we know that overall accuracy is not the only metric of interest. The false discovery rate (FDR) and false omission rate (FOR) are also important. Let’s compare confusion matrices for the original threshold of 0.5 and the new threshold of 0.4.
#generate confusion matrix for original threshold
table(testing_class$STATUS,testing_class$STATUS_class)##
## 0 1
## 0 2020 194
## 1 389 1758#generate confusion matrix for new threshold
table(testing_class2$STATUS,testing_class2$STATUS_class)##
## 0 1
## 0 1754 460
## 1 125 2022Based on the matrices, the new threshold impacts both the FDR and FOR. The FDR increased from 9.94% to 18.53%. In other words, among fires that we predicted extinguished, we are wrong more often. This makes intuitive sense given that we are predicting “extinguished” for more fires. By contrast, the FOR decreased from 16.15% to 6.65%. For fires that we predicted not extinguished, we are wrong less often. Again, this is logical since we are predicting “not extinguished” for fewer fires. The important point here is that a minor difference in the overall accuracy of the model resulted in relatively significant changes to the conditional accuracies.
Whether or not this change is beneficial depends on the preferences of the stakeholder. Does the stakeholder care more about the model being right when it predicts “extinguished” or “not extinguished”? Let’s imagine for a moment that the context is forest fires. If we predict that the fire is out, then first responders might stop all containment and go home. But if that prediction is a false discovery, then the fire continues to burn. On the other hand, if we predict the fire is not out, then first responders and other resources will continue to be applied to the scene. In the case of false omission, these resources are being wasted and could be applied elsewhere (potentially to another fire). Careful collaboration with stakeholders and domain experts should reveal the appropriate priorities between the two scenarios.
In some cases, we might be willing to accept a small increase in CER to achieve the benefit of a much lower FDR, FOR, FPR, or FNR. In other cases, changing the classification threshold can actually improve the CER. Computational methods exist for determining the optimal threshold, but they are beyond the scope of this text. Regardless, careful collaboration with domain experts to determine the relative importance of CER, FDR, FOR, and the other metrics is critical.
Answer the Question
Based on 17,442 experimental trials, we can predict a fire’s status (extinguished or not) with about 87% accuracy. The model relies solely on knowledge of the distance of the suppression device from the flame and the speed and frequency of the sound wave. These results are similar to those achieved with a parametric model, but with fewer variables and a more intuitive model.
5.3.5 Interaction Predictors
All of the parametric models we have presented thus far, whether linear or logistic, are additive. In other words, the response variable is modeled as purely a sum of the predictor variables. For multiple logistic regression (in log-odds form) the additive model appears in Equation (5.16).
\[\begin{equation} \log\left(\frac{P(y=1)}{P(y=0)} \right)=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_px_p \tag{5.16} \end{equation}\]
In some cases, the accuracy of a model can be improved by including an interaction between two or more predictors. We model interactions using the product of predictor variables. For example, an interaction model between two numerical predictor variables \(x_1\) and \(x_2\) is displayed in Equation (5.17).
\[\begin{equation} \begin{aligned} \log\left(\frac{P(y=1)}{P(y=0)} \right) &= \beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_1x_2 \\ &= \beta_0+\beta_1x_1+(\beta_2+\beta_3x_1)x_2 \end{aligned} \tag{5.17} \end{equation}\]
The interaction model includes a product term (\(x_1x_2\)), along with the associated parameter (\(\beta_3\)). The benefit of including this term is that we can now capture any synergy between the predictors \(x_1\) and \(x_2\). The mathematically-equivalent representation in the second line of Equation (5.17) highlights the synergistic effect. The parenthetical term (\(\beta_2+\beta_3x_1\)) indicates the expected change in log-odds when increasing the predictor \(x_2\). However, this change now depends on the value of \(x_1\). In other words, we have to know the value of one predictor before we can determine the influence of the other predictor on the response.
Synergy between predictors exists in many complex real-world systems. Not only can we model interactions between numerical predictors, but we can also include categorical predictors like those presented in Chapter 5.2.5. We demonstrate this in an example using functions from the tidyverse below.
Ask a Question
Research by W. Nick Street and others at the University of Wisconsin seeks to diagnose breast cancer using predictive modeling (Street et al. 1993). The team’s sample data consists of magnified digital images of cell nuclei extracted from breast tumors using fine-needle aspiration. For each cell, the collected features include the size, shape, and texture of the nucleus. Similar to the original researchers, we hope to use this data to answer the following question: How accurately can we distinguish malignant tumors from benign using characteristics of the cell nucleus?
The Street paper claims a classification accuracy of 97%, which has been confirmed by multiple independent researchers using advanced modeling techniques. Though our research question has been answered, the data offers an opportunity to replicate the authors’ work and add to the validity of their results. Specifically, we seek to classify malignant tumors using logistic regression and only the size and texture of the cell nuclei. As with any study involving human subjects, we must carefully consider the ethical implications of the data collection and security. In this case, the publicly-available data is already anonymized and devoid of any information beyond that of the tumor cells.
Acquire the Data
Among other sources, the data can be acquired from the University of California - Irvine Machine Learning Repository at this link. For simplicity, we offer a reduced version of the data in the file cancer.csv. Import and review the data below.
## Rows: 569
## Columns: 12
## $ id <dbl> 842302, 842517, 84300903, 84348301, 84358402, 8…
## $ diagnosis <chr> "M", "M", "M", "M", "M", "M", "M", "M", "M", "M…
## $ radius_mean <dbl> 17.990, 20.570, 19.690, 11.420, 20.290, 12.450,…
## $ texture_mean <dbl> 10.38, 17.77, 21.25, 20.38, 14.34, 15.70, 19.98…
## $ perimeter_mean <dbl> 122.80, 132.90, 130.00, 77.58, 135.10, 82.57, 1…
## $ area_mean <dbl> 1001.0, 1326.0, 1203.0, 386.1, 1297.0, 477.1, 1…
## $ smoothness_mean <dbl> 0.11840, 0.08474, 0.10960, 0.14250, 0.10030, 0.…
## $ compactness_mean <dbl> 0.27760, 0.07864, 0.15990, 0.28390, 0.13280, 0.…
## $ concavity_mean <dbl> 0.30010, 0.08690, 0.19740, 0.24140, 0.19800, 0.…
## $ concave_points_mean <dbl> 0.14710, 0.07017, 0.12790, 0.10520, 0.10430, 0.…
## $ symmetry_mean <dbl> 0.2419, 0.1812, 0.2069, 0.2597, 0.1809, 0.2087,…
## $ fractal_dimension_mean <dbl> 0.07871, 0.05667, 0.05999, 0.09744, 0.05883, 0.…The original data includes 569 tumor cells (observations) and 30 characteristics (variables) describing the cells. Here we reduce the variables to ten features describing the size, shape, and texture of the cell nuclei. Each nuclei includes a unique identifier (id) and the diagnosis is listed as malignant (M) or benign (B). For the purposes of this academic exercise, we further reduce the variables to a categorical response (diagnosis), numerical predictor (texture), and categorical predictor (size).
#wrangle tumor data
cancer2 <- cancer %>%
transmute(diagnosis=if_else(diagnosis=="M",1,0),
texture=texture_mean,
size=if_else(radius_mean<quantile(cancer$radius_mean,0.25),"small",
if_else(radius_mean>quantile(cancer$radius_mean,0.75),"large",
"medium"))) %>%
na.omit()
#review new data structure
glimpse(cancer2)## Rows: 569
## Columns: 3
## $ diagnosis <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, …
## $ texture <dbl> 10.38, 17.77, 21.25, 20.38, 14.34, 15.70, 19.98, 20.83, 21.8…
## $ size <chr> "large", "large", "large", "small", "large", "medium", "larg…Our binary response now has a value of 1 when the tumor is malignant and 0 when it is benign. The texture of the cell nuclei represents the variation in the grey-scale pixels of the digital imagery. A smaller value indicates less variation and thus a smoother nuclei. Larger values suggest high variation and a rougher texture. For size, we separate the cells into three levels based on the quartiles of the cell radius. The middle 50% of radii are identified as medium sized. Values above this are labeled large and values below this are small.
Our final step prior to analysis is to split the sample into training and testing sets.
#randomly select rows from sample data
set.seed(303)
rows <- sample(x=1:nrow(cancer2),size=floor(0.75*nrow(cancer2)),replace=FALSE)
#split sample into training and testing
training <- cancer2[rows,]
testing <- cancer2[-rows,]We now have 426 randomly-selected cells to train a multiple logistic regression model and another 143 cells to evaluate the model’s accuracy. As always, the baseline accuracy is determined from a null model using the mean response in the training set.
## [1] 0.3849765Roughly 38% of the cells in the training set are malignant. Hence, the null model consists of classifying every new cell as benign. We are more likely to be correct when we choose the more prevalent outcome, which in this case is a cell being benign. Just based on random chance, benign cells happen to be more common in the testing set.
## [1] 0.3356643Our data is now clean, organized, and prepared for analysis. Let’s use this data to train and test a multiple logistic regression model with interactions.
Analyze the Data
The prevalence of benign cells in the testing set suggests our baseline classification error rate (CER) is 33.57%. Said another way, if we blindly classify every cell in the testing set as benign, then we will be wrong about 34% of the time. Our goal is to design a model that reduces this error rate as much as possible. We begin by exploring the training data in a graphic.
#display data in scatter plot
ggplot(data=training,mapping=aes(x=texture,y=diagnosis,
group=size,color=size)) +
geom_jitter(width=0,height=0.05,alpha=0.4) +
geom_smooth(aes(color=size),
method="glm",formula=y~x,se=FALSE,
method.args=list(family="binomial")) +
labs(title="Diagnosis of Breast Tumor Cells",
subtitle="(measurement via digital imagery)",
x="Texture",
y="Proportion that are Malignant",
color="Size",
caption="Source: UCI Machine Learning Repository") +
scale_x_continuous(limits=c(10,40),breaks=seq(10,40,5)) +
scale_y_continuous(limits=c(-0.05,1.05),breaks=seq(0,1,0.1)) +
scale_color_manual(values=c("#481567FF","#3CBB75FF","#FDE725FF")) +
theme_bw()
Figure 5.21: Logistic Association between Texture and Diagnosis for Different Sizes
Figure 5.21 clearly indicates a positive association between the texture of a cell and its diagnosis. The greater (rougher) the texture of a cell, the more likely the tumor is malignant. However, the rate of increase in likelihood depends on the size. As the size increases, so does the rate of increase in likelihood. For small cells (yellow) an increase in texture is associated with a modest increase in the proportion that are malignant. By contrast, large cells (purple) are much more likely to be malignant when the texture increases.
\[\begin{equation} \begin{aligned} \log\left(\frac{P(y=1)}{P(y=0)} \right) &= \beta_0+\beta_1z+\beta_2x+\beta_3zx \\ &= \beta_0+\beta_1z+(\beta_2+\beta_3z)x \end{aligned} \tag{5.18} \end{equation}\]
Equation (5.18) shows that the relationship between texture (\(x\)) and diagnosis (\(y\)) depends on the size (\(z\)) of the cell nucleus. Notice in this formulation the categorical size of the cell adjusts the intercept term (\(\beta_0\)) and the slope term (\(\beta_2\)). Without the interaction, categorical predictors only adjust the intercept. Of course, we learned in Chapter 5.2.5 that categorical predictors must be split into binary indicator variables for each level (minus one). If we let \(z_1\) indicate small cells and \(z_2\) indicate medium cells, then the model becomes:
\[\begin{equation} \log\left(\frac{P(y=1)}{P(y=0)} \right)=\beta_0+\beta_{11}z_1+\beta_{12}z_2+(\beta_2+\beta_{31}z_1+\beta_{32}z_2)x \tag{5.19} \end{equation}\]
Let’s estimate the parameters of this interaction model using the glm() function. The syntax for an interaction is the asterisk symbol (*). This symbol automatically includes the sum of the predictors and their product.
#train logistic regression model
model <- glm(diagnosis~size*texture,data=training,family="binomial")After estimating the parameters of the model using the training set, we evaluate its accuracy using the testing set.
#predict and classify testing set
testing_class <- testing %>%
mutate(pred_diagnosis=predict(model,newdata=testing,type="response"),
class_diagnosis=if_else(pred_diagnosis>0.5,1,0))
#compute CER of model
testing_class %>%
summarize(CER=mean(diagnosis!=class_diagnosis))## # A tibble: 1 × 1
## CER
## <dbl>
## 1 0.168The interaction model reduces the error rate from 34% (null model) to about 17%. We cut the error in half! In other words, if we know the size and texture of a tumor cell, then we can correctly diagnose it around 83% of the time. Even with introductory methods, we can produce powerful models. Although the overall accuracy is surprisingly high, that does not mean the model performs equally well on malignant versus benign tumors. A confusion matrix provides this additional information.
##
## 0 1
## 0 89 6
## 1 18 30Of the 143 cells in the testing set, 24 (17%) are incorrectly classified. There are 6 false positives and 18 false negatives. Thus, the false positive rate (FPR) is about 6% (6/95) and the false negative rate (FNR) is around 38% (18/48). This represents a dramatic difference in performance. The model is much better at identifying benign tumors (\(y=0\)) than it is at identifying malignant tumors (\(y=1\)). Members of the medical community would likely prefer a model that does a better job of detecting malignant tumors.
From the standpoint of a patient, FPR and FNR may not be the most important metric. A patient will not know the true state of the tumor. Instead, they will only know what was predicted. As a result, patients are likely more concerned with the false discovery rate (FDR) and false omission rate (FOR). For our model, the FDR (6/36) and FOR (18/107) are both near 17%. So, regardless of which diagnosis the model provides, a patient can feel confident it is correct about 83% of the time.
The classification accuracy on the testing set provides a good estimate of the model’s performance on future data. However, in order to obtain the most accurate parameter estimates, we use the entire sample.
#estimate final model
model_final <- glm(diagnosis~size*texture,data=cancer2,family="binomial")
#review parameter estimates
coefficients(summary(model_final))## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -6.4976338 2.9051841 -2.2365653 0.02531477
## sizemedium 1.3561574 3.0032652 0.4515610 0.65158527
## sizesmall 0.6234760 3.7811566 0.1648903 0.86903034
## texture 0.5088733 0.1667248 3.0521745 0.00227190
## sizemedium:texture -0.3001327 0.1708492 -1.7567114 0.07896702
## sizesmall:texture -0.4014977 0.2035910 -1.9720798 0.04860050As expected from Equation (5.19), we obtain six parameter estimates in the Estimate column. The glm() function automatically creates the binary indicators (sizesmall and sizemedium) and the products with the numerical predictor (sizesmall:texture and sizemedium:texture). With an accurate model in hand, we are prepared to advise stakeholders and answer the research question.
Advise on Results
When presenting our interaction model to stakeholders in the medical community, it is critical we divulge its limitations. For example, we ignored a large number of variables included in the original data. We only incorporated two of the 30 features collected and we simplified one of them (size) by converting it to a categorical variable. It is likely that valuable information resides in the other variables that could increase the accuracy of our predictions. In fact, it is the inclusion of other predictors that permitted previous researchers to achieve accuracies as high as 97%.
Answer the Question
Based on a sample of 569 cell nuclei, it appears we can correctly diagnose breast tumors as malignant or benign with 88% accuracy. The associated model includes the numerical texture of the cell as well as its categorical size (small, medium, or large). The classification process also employs a threshold of only 0.4 in order to label a tumor as malignant. Although the overall error rate is relatively low, the model does detect benign tumors more accurately than malignant tumors.
5.4 Resources: Predictive Analyses
Below are the learning objectives associated with this chapter, as well as exercises to evaluate student understanding. Afterward, we provide recommendations for further study on the topic of predictive analysis.
5.4.1 Learning Objectives
After completing this chapter, students should be able to:
- Differentiate between supervised and unsupervised statistical learning based on objectives.
- Identify the requirement for regression versus classification models based on the response.
- Recognize parametric versus nonparametric modeling approaches based on the algorithm.
- Explain the concept of over-fitting and how it is reduced by the validation set approach.
- Split a random sample into a training set and a testing set using common ratios.
- Construct multiple linear and logistic regression models with numerical predictors.
- Classify observations using predicted probabilities from a multiple logistic regression.
- Evaluate the accuracies of linear and logistic regression models using test data.
- Construct and interpret linear and logistic regression models with categorical predictors.
- Construct and interpret linear and logistic regression models with interaction predictors.
- Explain the structure and methods for developing regression and classification trees.
- Build and assess decision trees to predict a response using recursive binary splitting.
- Explain the structure and methods for constructing k-nearest neighbors predictive models.
- Build and assess k-nearest neighbors models for regression and classification problems.
- Articulate the pros and cons of non-parametric methods versus linear or logistic regression.
5.4.3 Further Study
In this chapter we describe introductory methods for constructing and evaluating predictive models. But there exists an ever-growing host of parametric and nonparametric methods for building regression and classification models. Below we suggest additional resources for students to pursue further study in predictive modeling.
A fantastic resource for all data scientists is An Introduction to Statistical Learning by Gareth James et al. (James et al. 2013). The authors introduce a much wider variety of predictive modeling techniques than what we describe here. Textbooks are offered online in both R and Python coding languages. Additionally, the authors provide video tutorials discussing both conceptual knowledge and coding skills.
For additional study of unsupervised learning, Alok Malik and Bradford Tuckfield offer Applied Unsupervised Learning with R (Malik and Tuckfield 2019). With a focus on professional applications, the authors provide more details regarding clustering and principal components than we attempt to complete here. They also include additional methods, such as data comparison and anomaly detection, all executed using R.
In terms of supervised learning, Max Kuhn and Kjell Johnson produced the text Applied Predictive Modeling (Kuhn and Johnson 2013). After a brief introduction to the modeling process, the authors outline both regression and classification models. As the title suggests, the focus remains on applications with real-world data for which the primary objective is prediction accuracy. The text employs R as the exemplar coding language.
For a rapid introduction to machine learning, Andriy Burkov offers The Hundred-Page Machine Learning Book (Burkov 2019). The text outlines the most common methods and tools currently employed by practitioners, along with links to deeper study in each topic. Thus, the reader may “choose their own adventure” in terms of the depth of individual topics. Though mathematically dense, the book is well-written and offers a great deal of flexibility in its use.