Chapter 4 Lista de Regressão

4.1 Laboratorio Aula 6

Carregar dados Excel

getwd()

## [1] "C:/Mestrado/Cadernos_Julio"

#library(readxl)

Teste do que tem na memoria

## Rows: 10
## Columns: 2
## $ `Square Feet` <dbl> 1400, 1600, 1700, 1875, 1100, 1550, 2350, 2450, 1425, 17…
## $ `House Price` <dbl> 245, 312, 279, 308, 199, 219, 405, 324, 319, 255

## Rows: 10
## Columns: 2
## $ `Square Feet` <dbl> 1400, 1800, 1700, 1875, 1200, 1480, 2350, 2100, 2000, 17…
## $ `House Price` <dbl> 245, 312, 279, 308, 199, 219, 405, 324, 319, 255

Grafico

par(mfrow=c(2,2))
plot(dadoscenario1$'House Price' ~ dadoscenario1$'Square Feet' , main = "Cenario 1")
plot(dadoscenario2$'House Price' ~ dadoscenario2$'Square Feet' , main = "Cenario 2")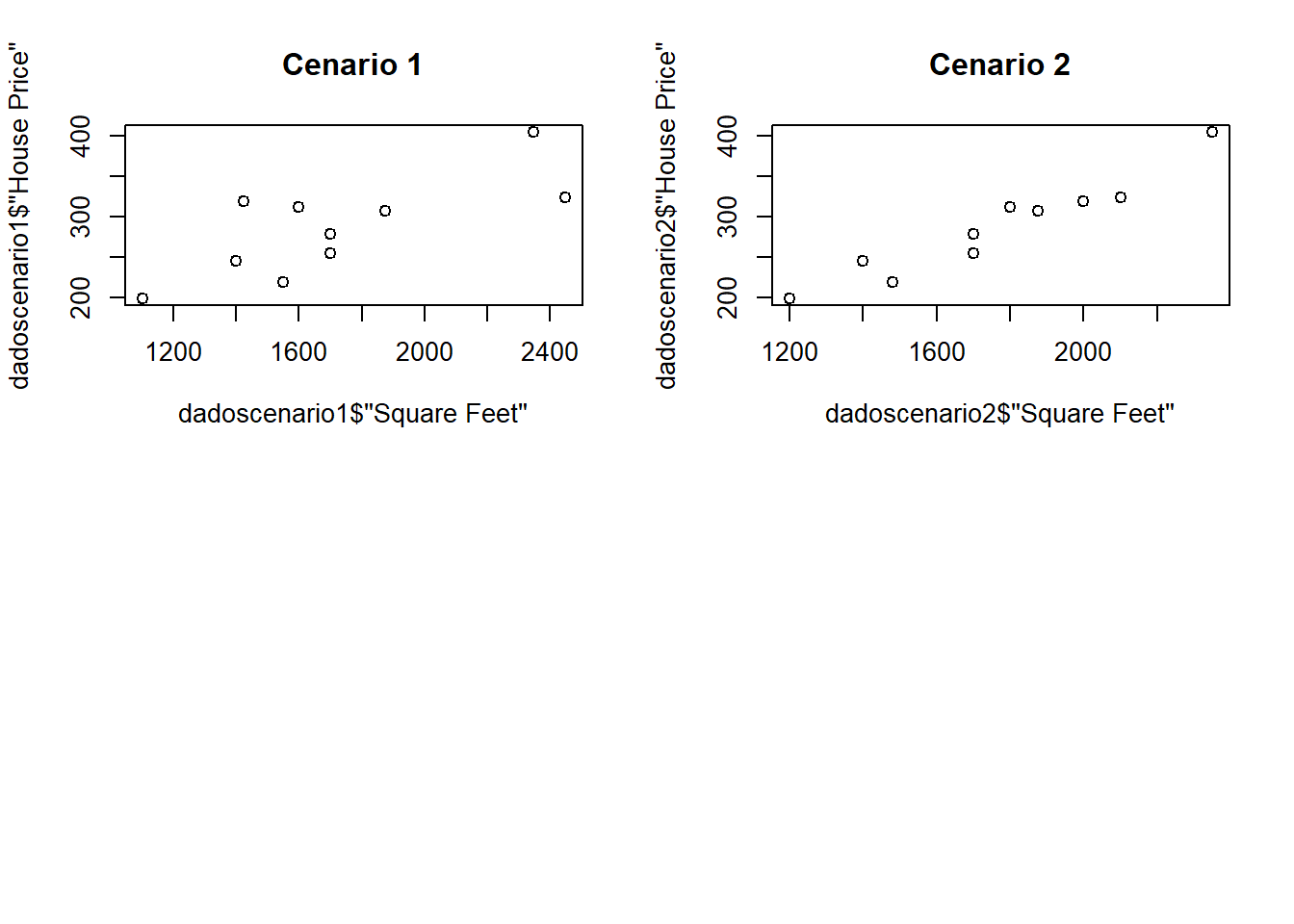

Algumas Estatísticas descritivas - Cenario 1

## Construção do Modelo
mod <- lm(dadoscenario1$'House Price' ~ dadoscenario1$'Square Feet', dadoscenario1)

##Analise Grafica
par(mfrow=c(2,2))

plot(mod)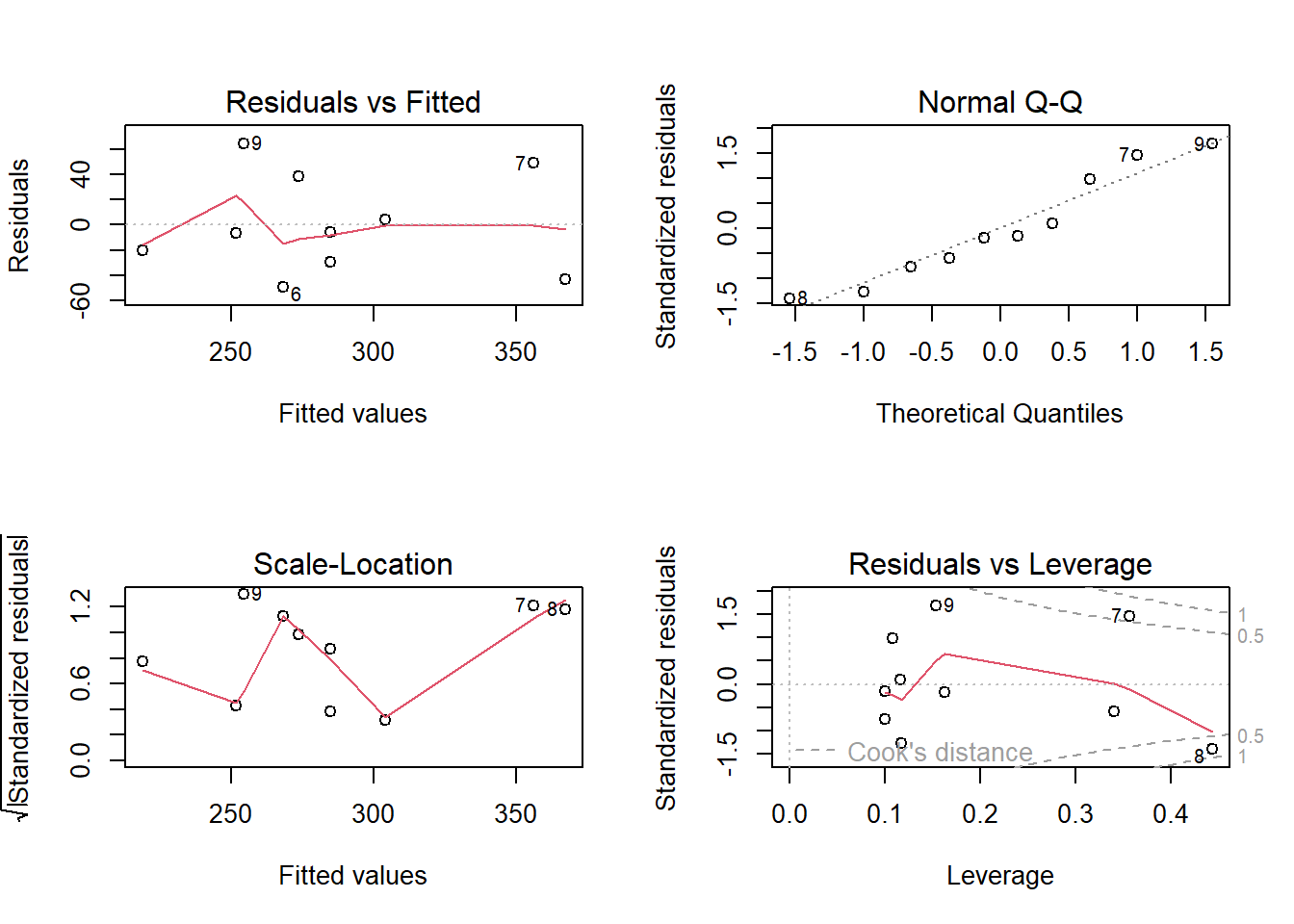

par(mfrow=c(1,1))

##Analise do modelo
summary(mod)

## 
## Call:
## lm(formula = dadoscenario1$"House Price" ~ dadoscenario1$"Square Feet", 
##     data = dadoscenario1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -49.388 -27.388  -6.388  29.577  64.333 
## 
## Coefficients:
##                             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)                 98.24833   58.03348   1.693   0.1289  
## dadoscenario1$"Square Feet"  0.10977    0.03297   3.329   0.0104 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 41.33 on 8 degrees of freedom
## Multiple R-squared:  0.5808, Adjusted R-squared:  0.5284 
## F-statistic: 11.08 on 1 and 8 DF,  p-value: 0.01039

##Normalidade dos residuos:
shapiro.test(mod$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  mod$residuals
## W = 0.93527, p-value = 0.5017

##Outliers nos residuos
summary(rstandard(mod))

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -1.40080 -0.72002 -0.16620 -0.01204  0.75799  1.69182

##Independencia dos residuo
##durbinWatsonTest(mod)

##Homocedasticvidade (Breuch-Pagan)
bptest(mod)

## 
##  studentized Breusch-Pagan test
## 
## data:  mod
## BP = 0.27033, df = 1, p-value = 0.6031

##Grafico Dispersão
ggplot(data = dadoscenario1, mapping = aes(x = dadoscenario1$'House Price', y = dadoscenario1$'Square Feet')) + 
   geom_point() +
  geom_smooth(method = "lm", col = "red") +
  stat_regline_equation(aes(label = paste(..eq.label.., ..adj.rr.label.., 
                                           sep = "*plain(\",\")~~")),
                 label.x = 0, label.y = 40) +
  theme_classic()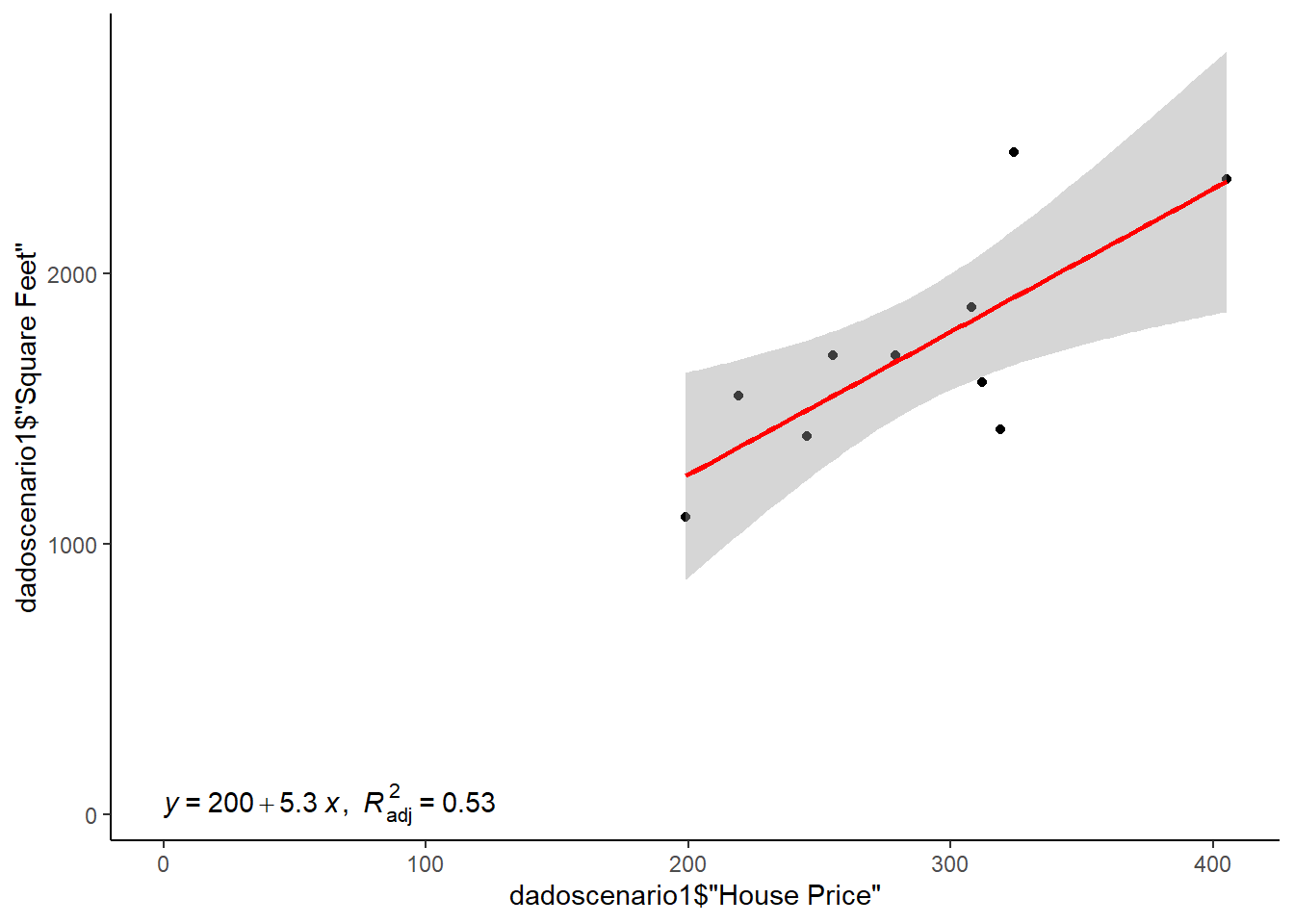

#ARvore de decisao library(rpart) library(rpart.plot) fit <- rpart(species - ., data = iris, method=“clas”) sumamary(fit) prp(fit,)

iris = tibble(iris) irisS = iris[,1:4]

d <- dist(irisS, ethod = “maximum”) grup = hclust(d, method = “ward.D”) plot(grup, cex = 0.6)