Chapter 2 EXERCÍCIOS
2.1 Análise dos preços das casas
Caregando os dados:
# dados01 = read_excel("Dados/04_LABORATORIO REGRESSAO COM DADOS 03_DADOS.xlsx", sheet = 1)
# dados01 = dados01[,1:2]
dados01_cen01 = read_excel("Dados/Data_HousePrice_Area.xlsx", sheet = 1)
dados01_cen02 = read_excel("Dados/Data_HousePrice_Area.xlsx", sheet = 2)Ambos os conjuntos de dados possuem as seguites variáveis:
- House Price: Preço da casa;
- Square Feet: Área da casa.
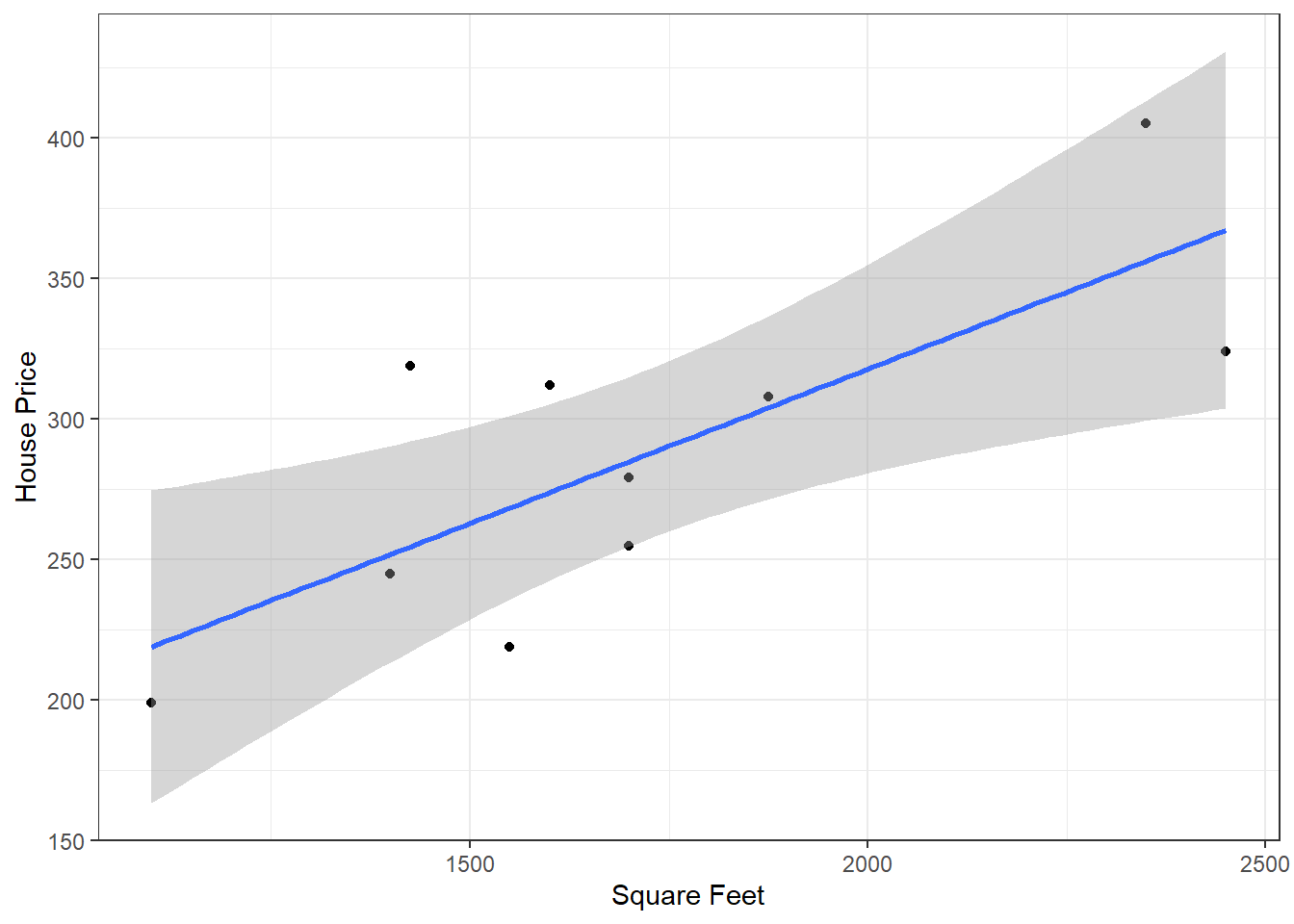
Fazendo um gráfico de dispersão:
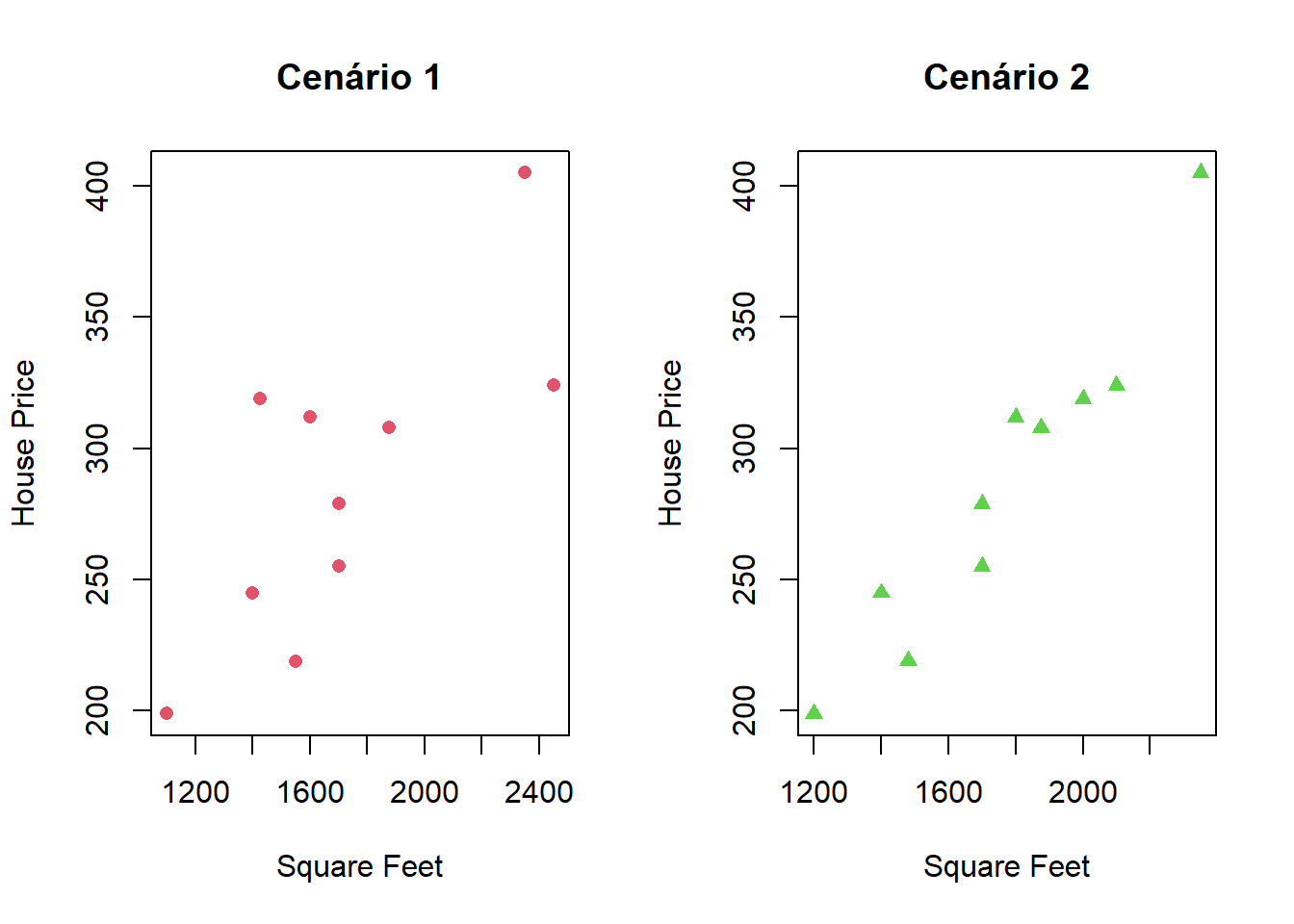
O modelo de regressão linear é
model_Cen1 = lm(`House Price` ~ `Square Feet`, data = dados01_cen01)
summary(model_Cen1)##
## Call:
## lm(formula = `House Price` ~ `Square Feet`, data = dados01_cen01)
##
## Residuals:
## Min 1Q Median 3Q Max
## -49.388 -27.388 -6.388 29.577 64.333
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.24833 58.03348 1.693 0.1289
## `Square Feet` 0.10977 0.03297 3.329 0.0104 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 41.33 on 8 degrees of freedom
## Multiple R-squared: 0.5808, Adjusted R-squared: 0.5284
## F-statistic: 11.08 on 1 and 8 DF, p-value: 0.01039model_Cen2 = lm(dados01_cen02$`House Price` ~ dados01_cen02$`Square Feet`)
summary(model_Cen2)##
## Call:
## lm(formula = dados01_cen02$`House Price` ~ dados01_cen02$`Square Feet`)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.323 -16.654 2.458 15.838 19.336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -9.64509 30.46626 -0.317 0.76
## dados01_cen02$`Square Feet` 0.16822 0.01702 9.886 9.25e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 17.56 on 8 degrees of freedom
## Multiple R-squared: 0.9243, Adjusted R-squared: 0.9149
## F-statistic: 97.73 on 1 and 8 DF, p-value: 9.246e-06Gráfico de dispersão com a reta de regressão:
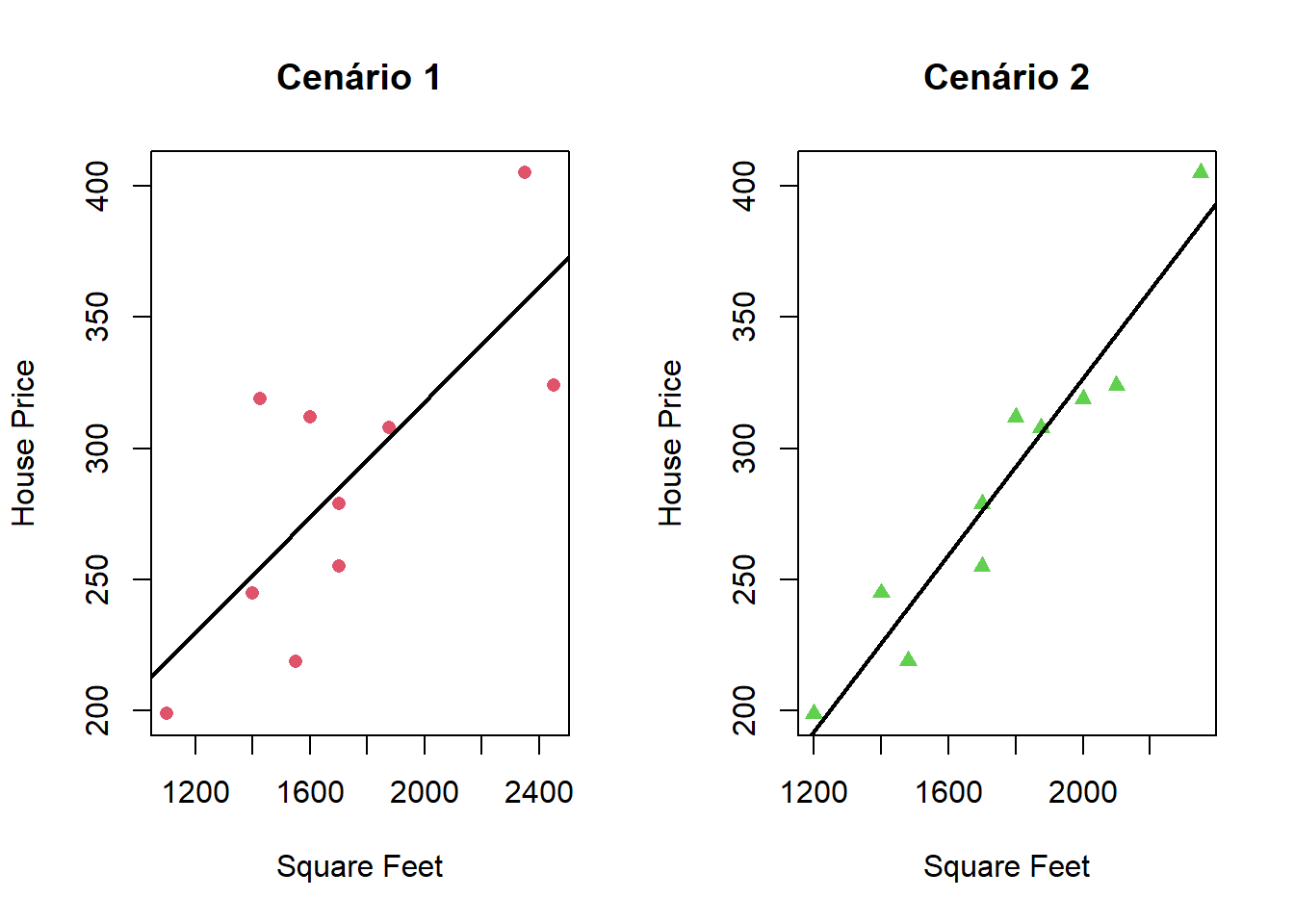
Note que se uma casa possui \(1300 ft^2\) então o preço esperado de acordo com o modelo do cenário 1 é: \(98.25 + 1300 \times 0.11 = 241\).
Já para o cenário 2 temos que o preço esperado é: \(-9.65 + 1300 \times 0.17 = 209\).
vet = 2*2o valor de vet é 4
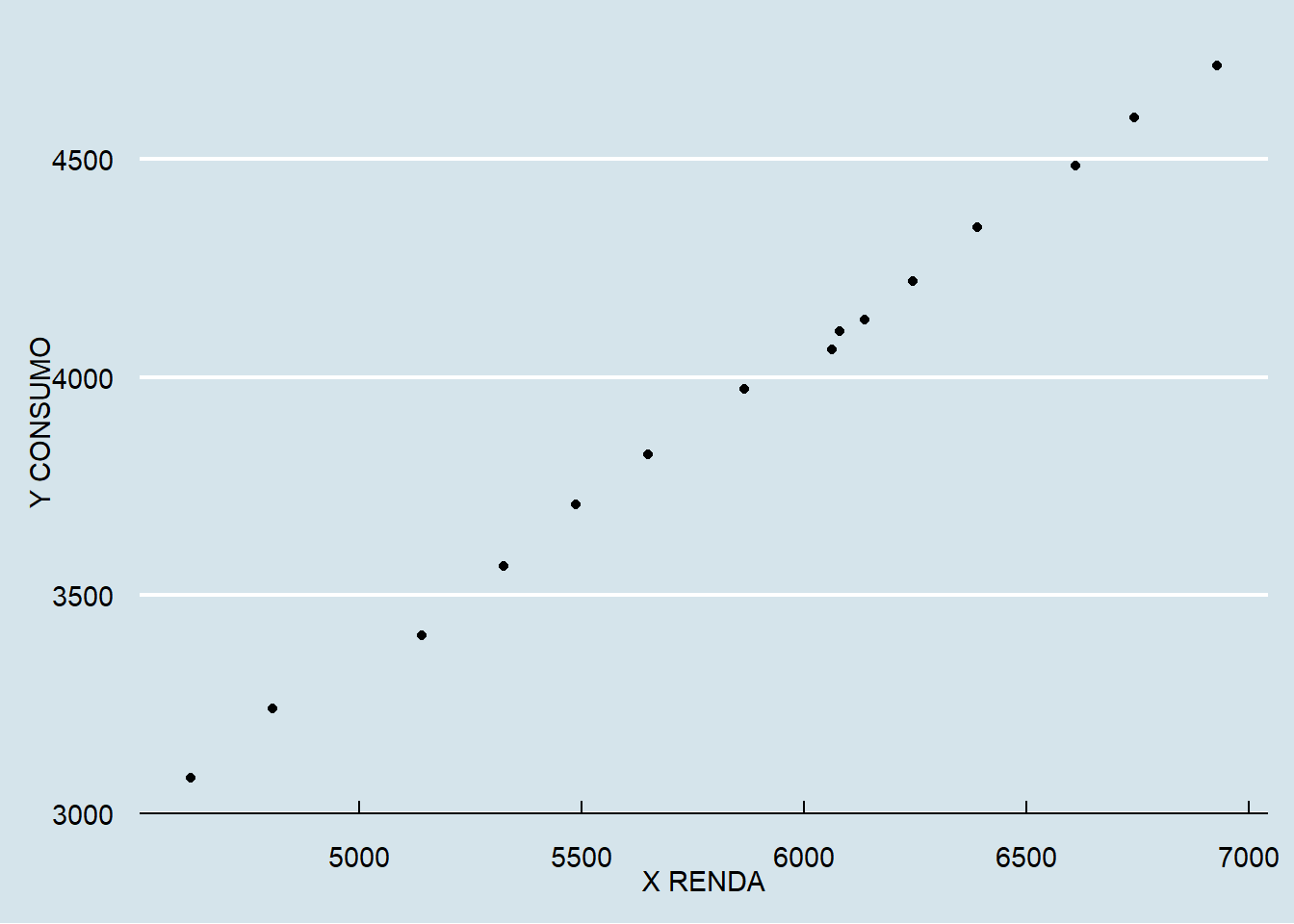
2.2 Análise Extra: Conjunto de Renda X Consumo
Um gráfico da renda e do consumo ao longo dos anos usando ggplot2:
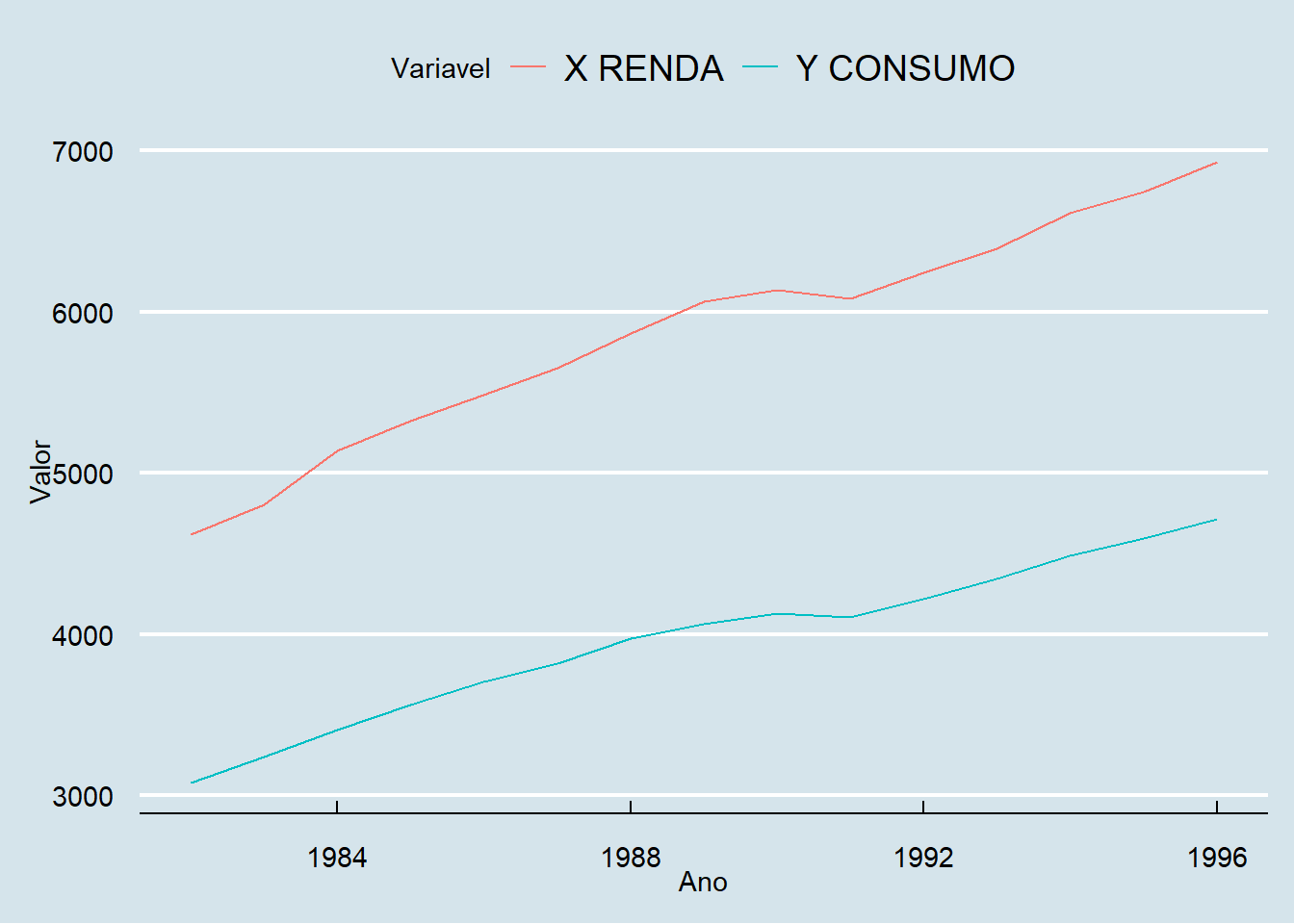
Gráfico da renda x consumo usando ggplot2:
2.3 Análise conjunto energia
## # A tibble: 10 × 2
## `Ajuste na maquina` `Consumo de energia`
## <dbl> <dbl>
## 1 11.2 21.6
## 2 15.7 4
## 3 18.9 1.8
## 4 19.4 1
## 5 21.4 1
## 6 21.7 0.8
## 7 25.3 3.8
## 8 26.4 7.4
## 9 26.7 4.3
## 10 29.1 36.2Um gráfico dos dados:
Ajustando os modelos:
modelEner01 = lm(`Consumo de energia`~`Ajuste na maquina`, data = dados02)
modelEner02 = lm(`Consumo de energia`~`Ajuste na maquina` + I(`Ajuste na maquina`^2), data = dados02)
modelEner03 = lm(`Consumo de energia`~`Ajuste na maquina` + I(`Ajuste na maquina`^2) + I(`Ajuste na maquina`^3), data = dados02)
modelEner04 = lm(`Consumo de energia`~`Ajuste na maquina` + I(`Ajuste na maquina`^2) + I(`Ajuste na maquina`^3)+ I(`Ajuste na maquina`^4), data = dados02) Gráfico do ajuste dos modelos:
x = seq(0,40, 0.1)
y1 = modelEner01$coefficients[1] + modelEner01$coefficients[2]*x
y2 = modelEner02$coefficients[1] + modelEner02$coefficients[2]*x + modelEner02$coefficients[3]*x^2
y3 = modelEner03$coefficients[1] + modelEner03$coefficients[2]*x + modelEner03$coefficients[3]*x^2 + modelEner03$coefficients[4]*x^3
y4 = modelEner04$coefficients[1] + modelEner04$coefficients[2]*x + modelEner04$coefficients[3]*x^2 + modelEner04$coefficients[4]*x^3 + modelEner04$coefficients[5]*x^4
par(mfrow = c(1,1))
plot(`Consumo de energia`~`Ajuste na maquina`, data = dados02, col = 1, pch = 16, xlab = "Ajuste na máquina", ylab = "Consumo de energia", main = "Consumo de energia x Ajuste na máquina", ylim = c(-10, 40))
lines(y1~x, col = 2, lty = 1, lwd = 2)
lines(y2~x, col = 3, lty = 2, lwd = 2)
lines(y3~x, col = 4, lty = 3, lwd = 2)
lines(y4~x, col = 5, lty = 4, lwd = 2)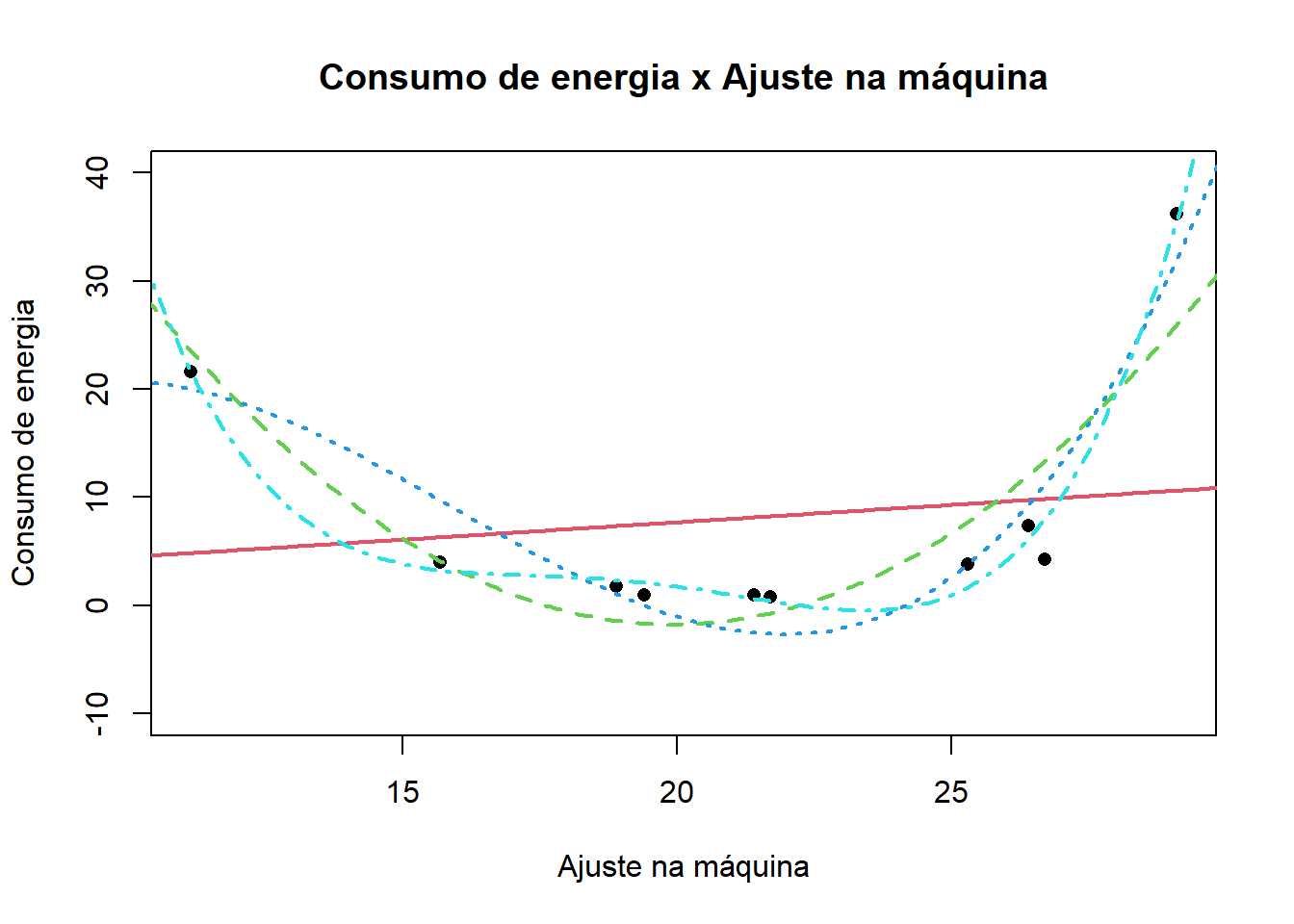
2.4 Análise Conjunto Sales x fontes de publidades
dados03 = read_excel(path = "Dados/04_LABORATORIO REGRESSAO COM DADOS 03_DADOS.xlsx", sheet = 3)
dados03 = dados03[,2:5]
# tail(dados03, 3)
# dados03_t = pivot_longer(dados03, c(2:5))
# names(dados03_t) = c("Indice", "Grupo", "Valor")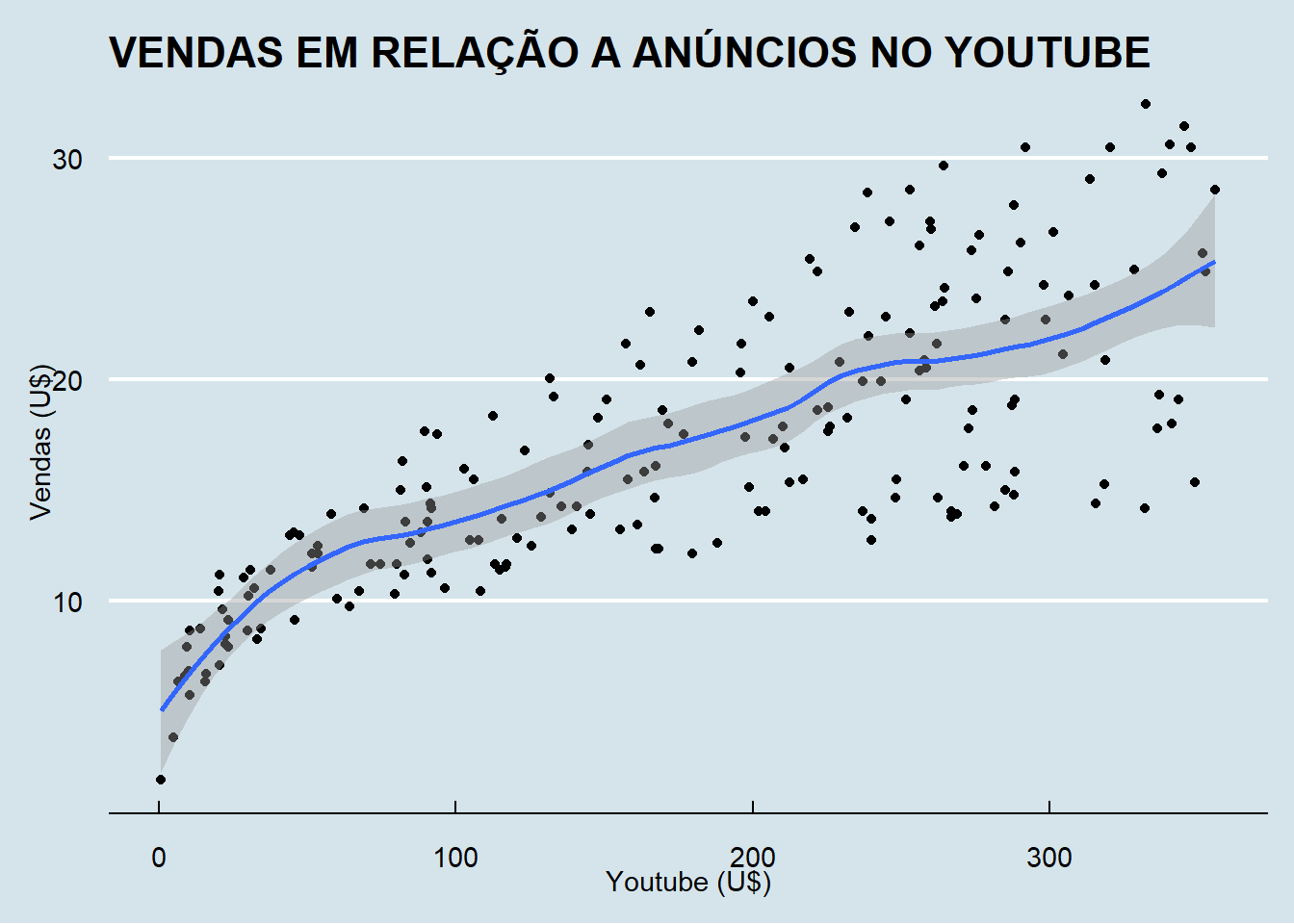
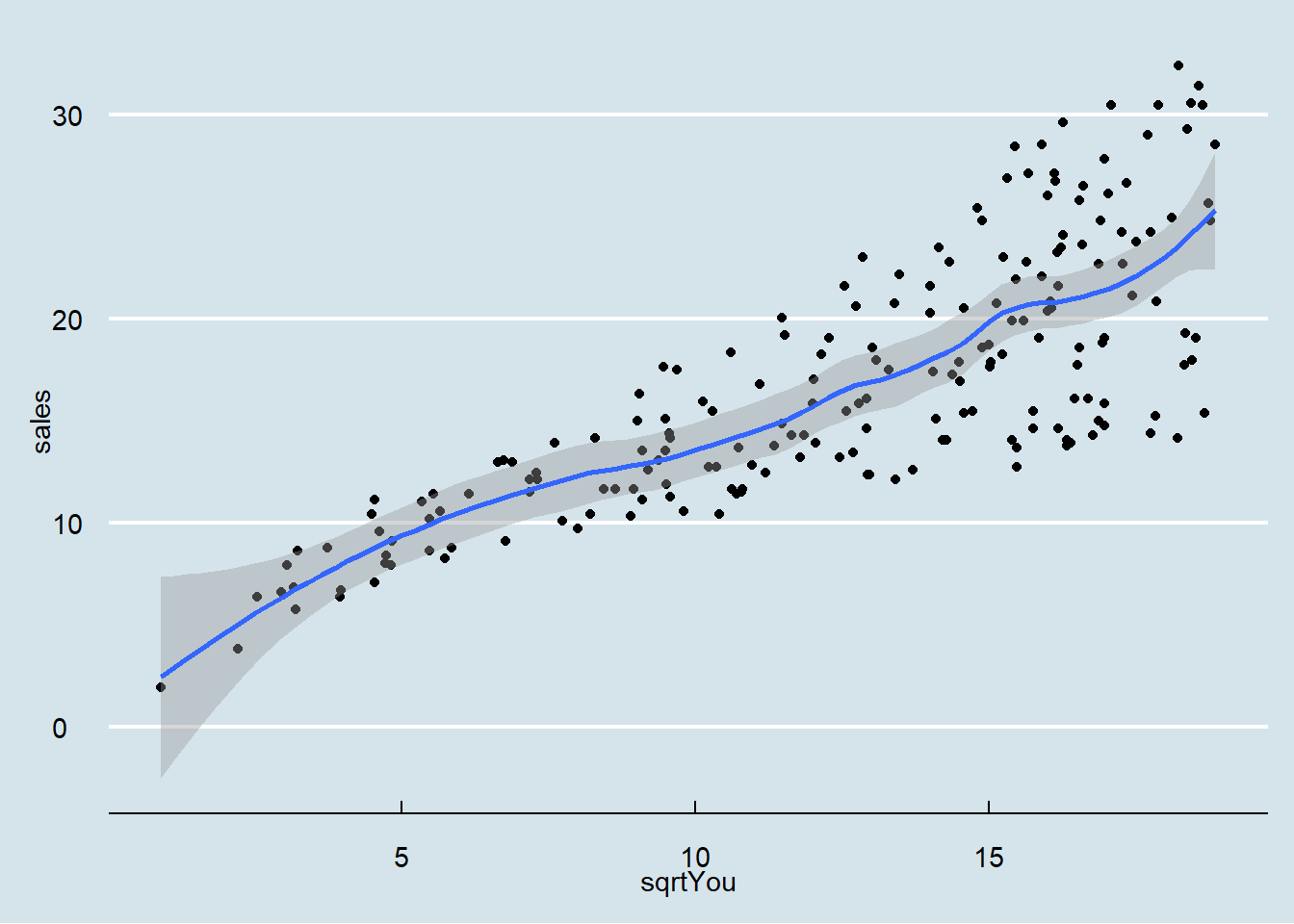
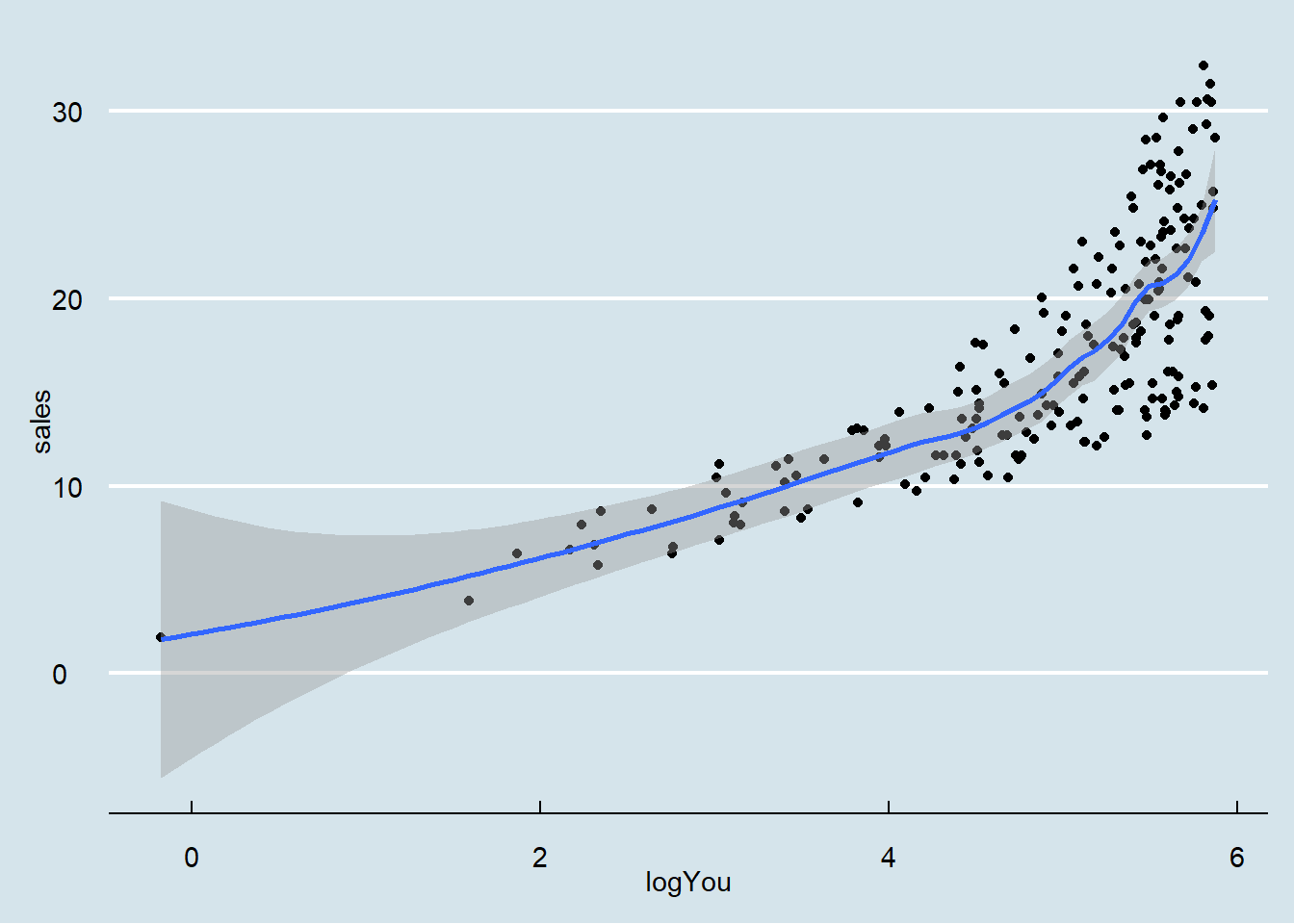
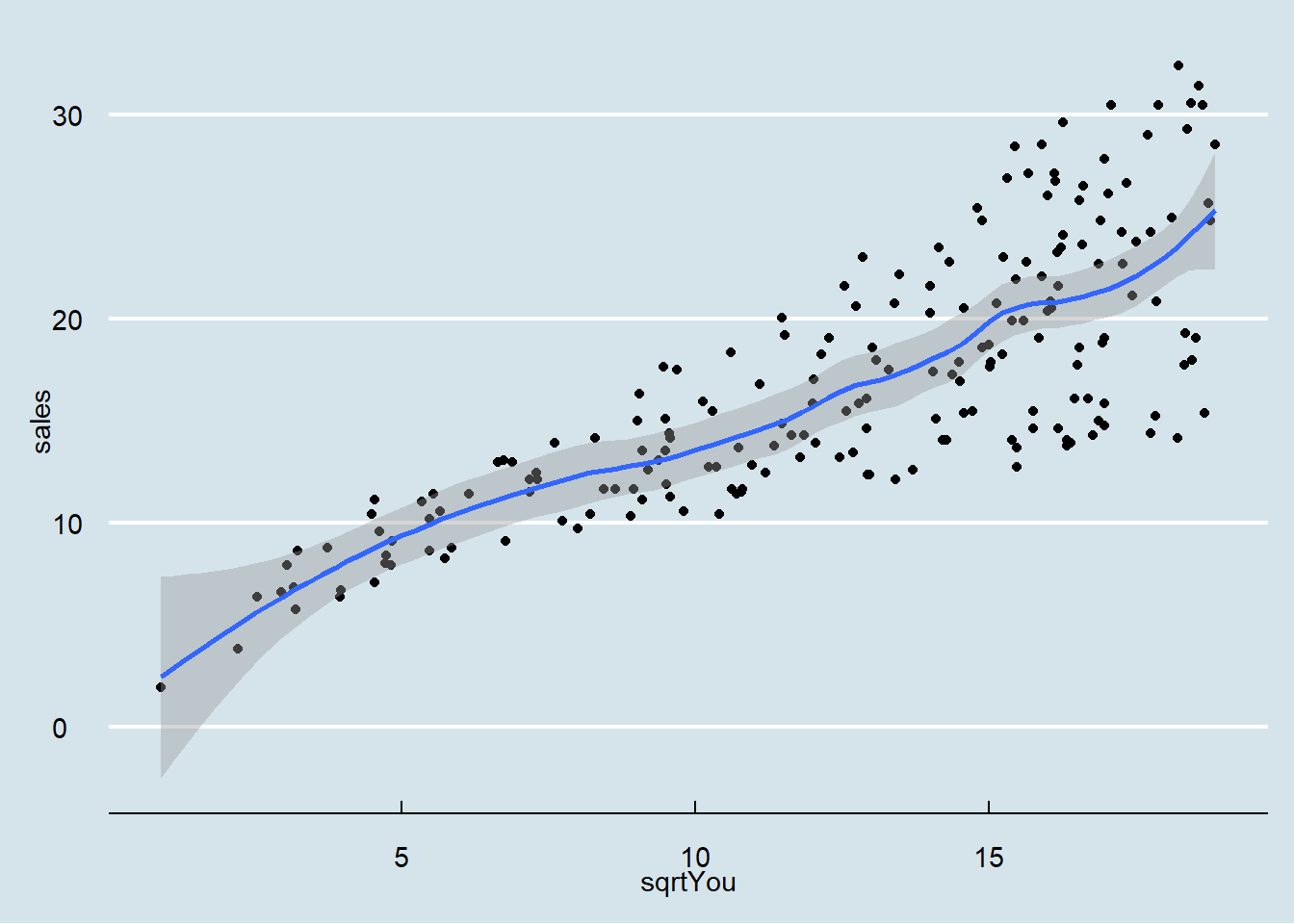
model = lm(sales ~ sqrtYou, data = dados03_mod)
summary(model)##
## Call:
## lm(formula = sales ~ sqrtYou, data = dados03_mod)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.916 -2.344 -0.131 2.326 9.316
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.20688 0.80092 4.004 8.8e-05 ***
## sqrtYou 1.09042 0.06029 18.085 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.854 on 198 degrees of freedom
## Multiple R-squared: 0.6229, Adjusted R-squared: 0.621
## F-statistic: 327.1 on 1 and 198 DF, p-value: < 2.2e-16plot(sales ~ sqrtYou, data = dados03_mod)
abline(model)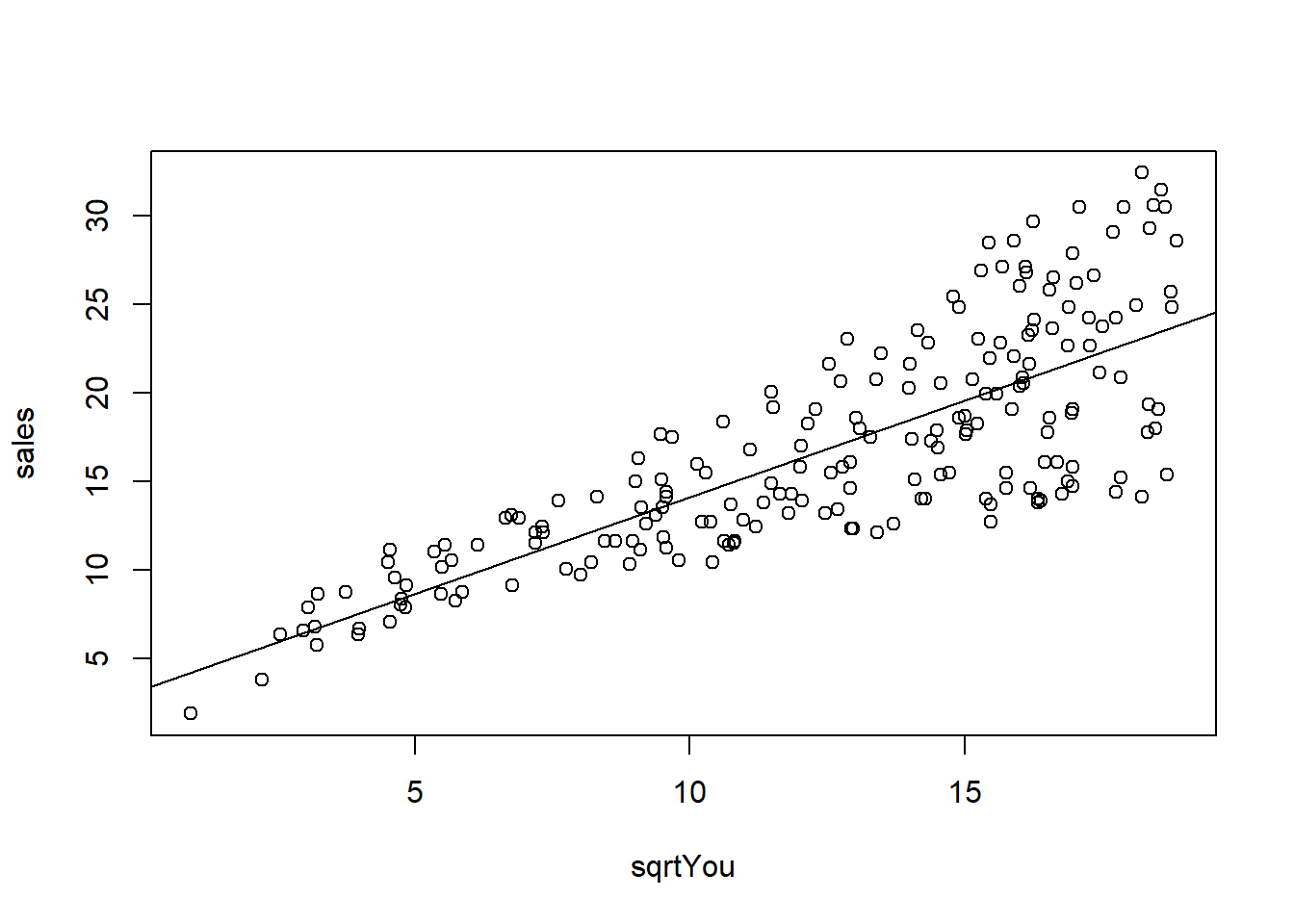
modelMult = lm(sales ~ youtube + facebook + newspaper, data = dados03)
# summary(modelMult)
modelMult2 = lm(sales ~ youtube + facebook, data = dados03)
summary(modelMult2)##
## Call:
## lm(formula = sales ~ youtube + facebook, data = dados03)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10.5572 -1.0502 0.2906 1.4049 3.3994
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.50532 0.35339 9.919 <2e-16 ***
## youtube 0.04575 0.00139 32.909 <2e-16 ***
## facebook 0.18799 0.00804 23.382 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.018 on 197 degrees of freedom
## Multiple R-squared: 0.8972, Adjusted R-squared: 0.8962
## F-statistic: 859.6 on 2 and 197 DF, p-value: < 2.2e-16plot(modelMult2)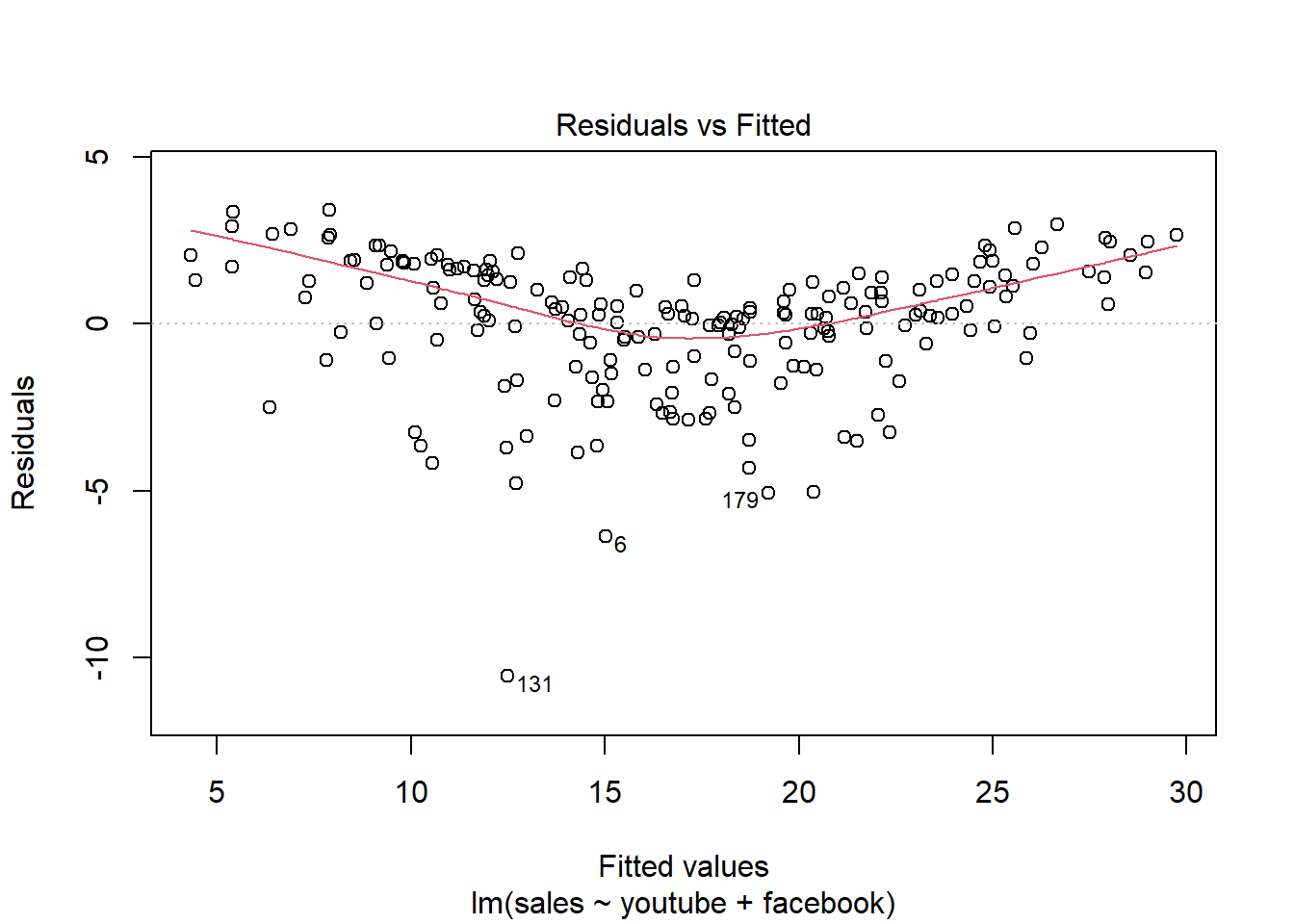
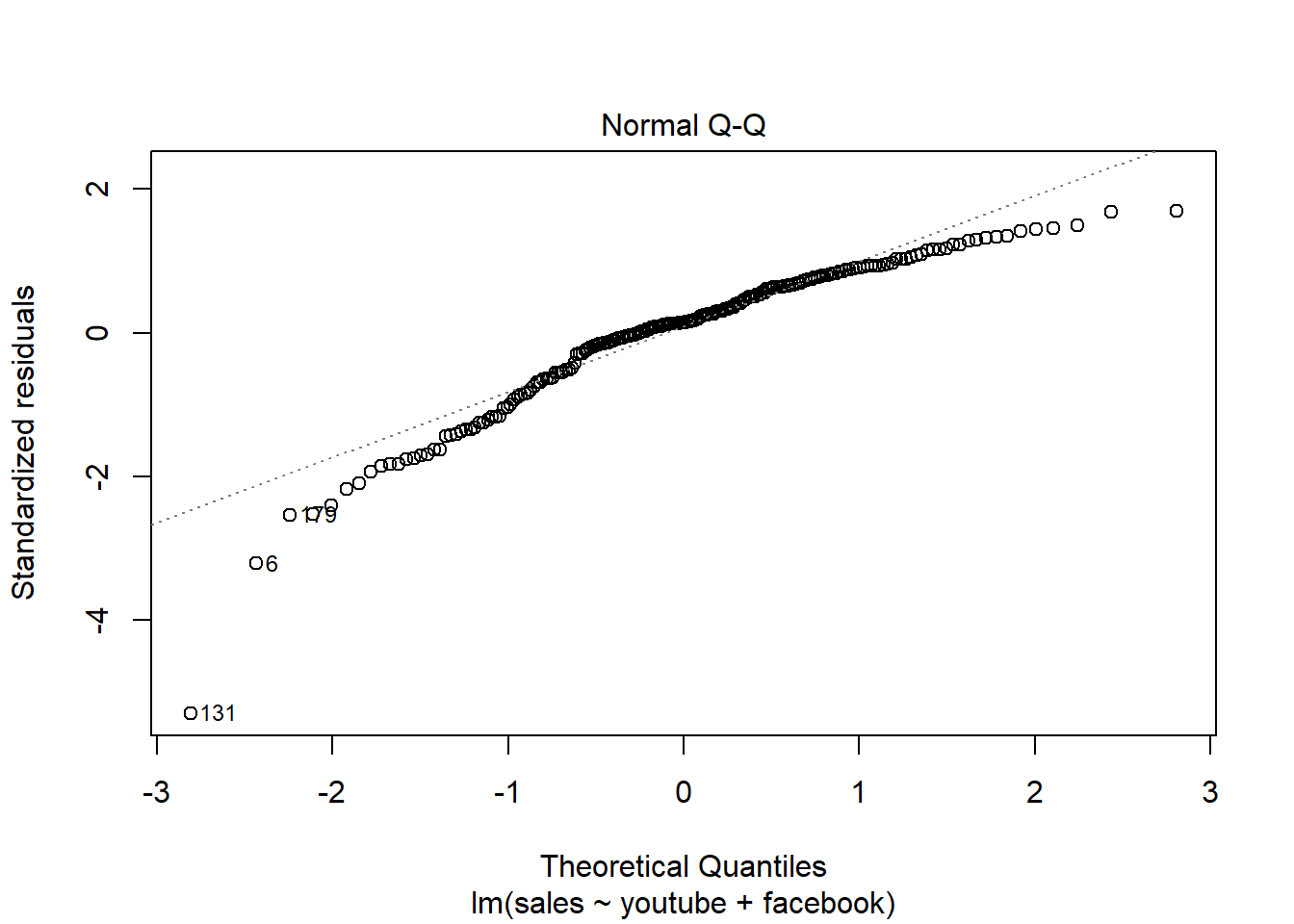
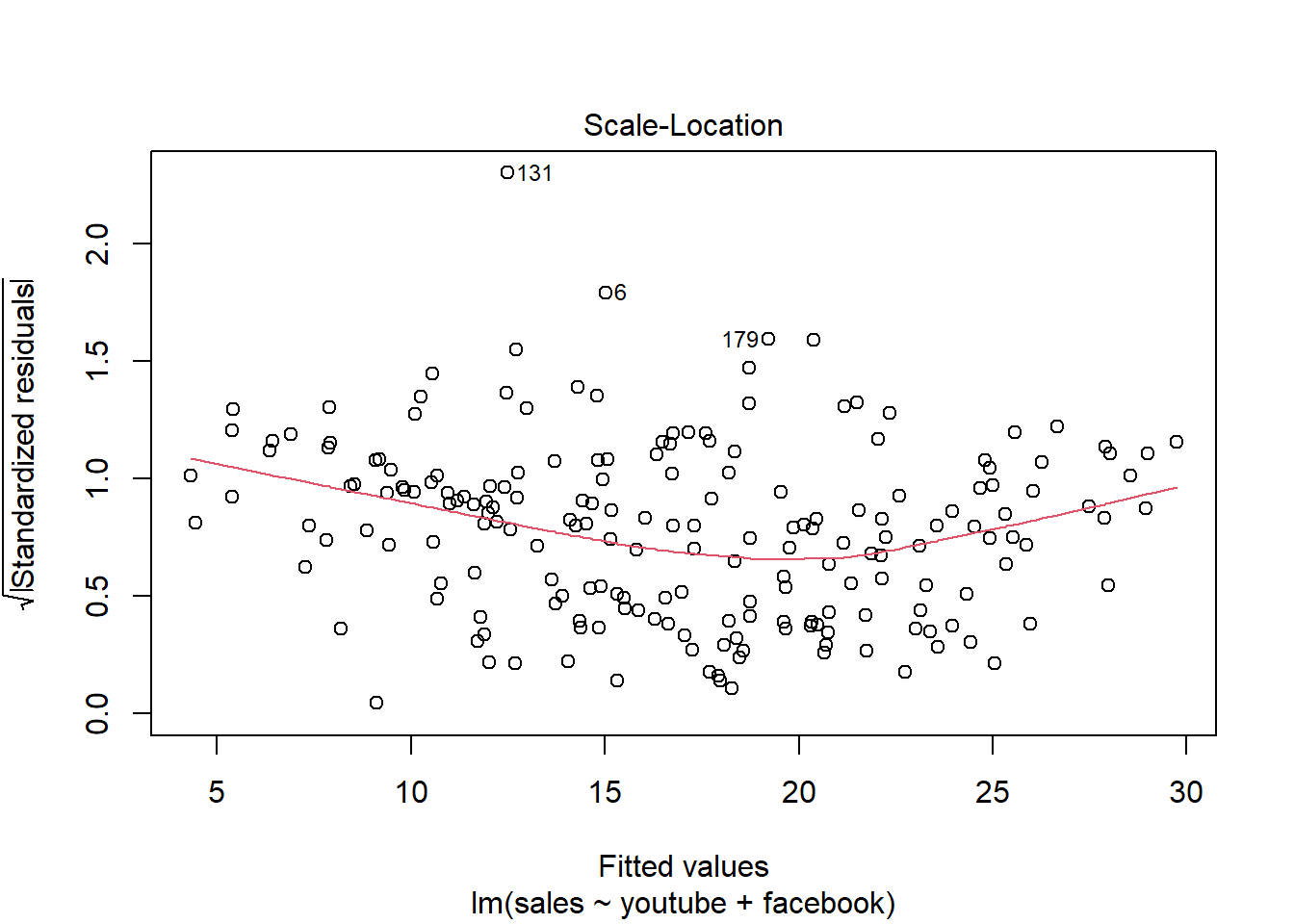
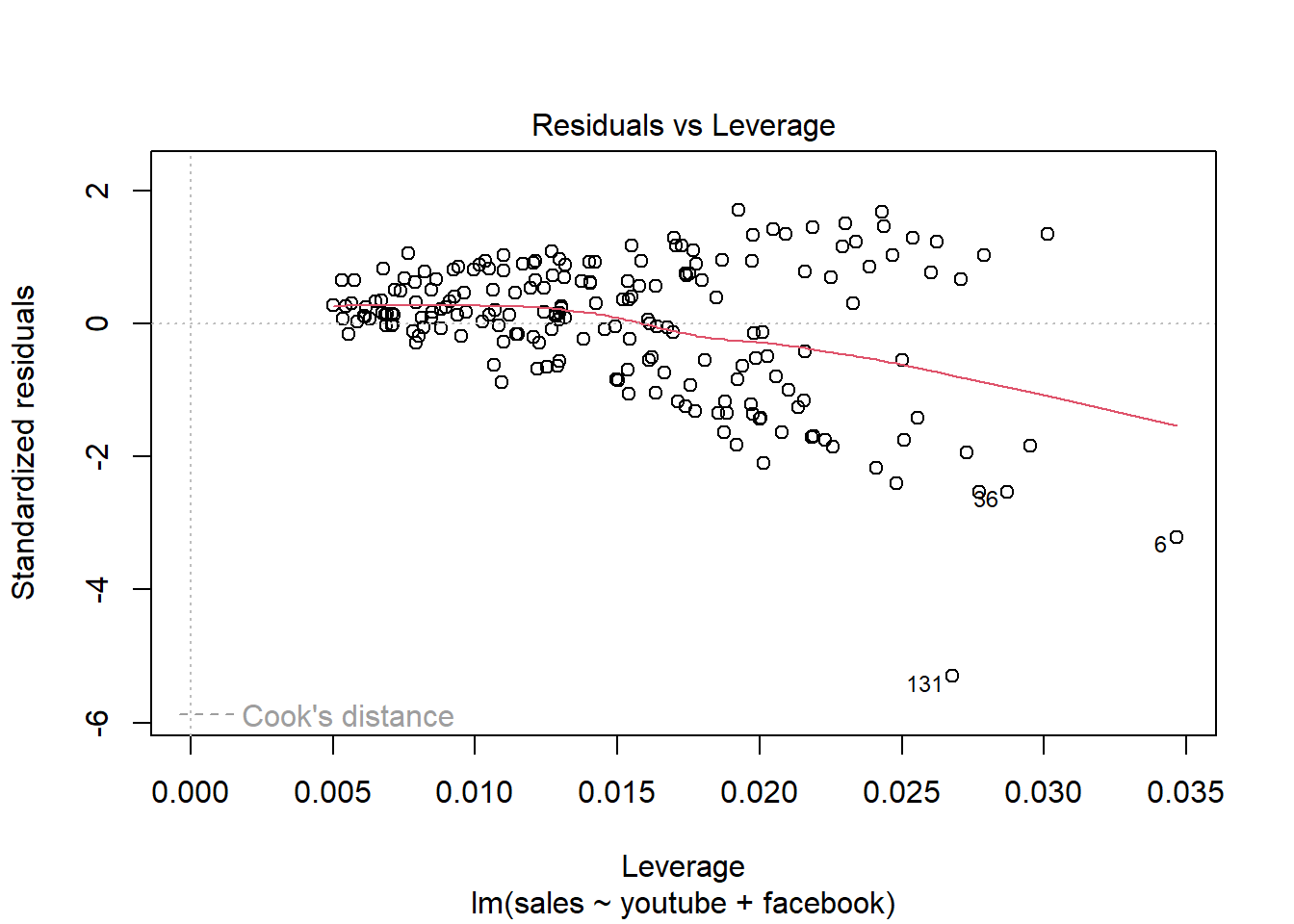
2.5 Análise conjunto ST vs demais variáveis
dados04 = read_excel(path = "Dados/04_LABORATORIO REGRESSAO COM DADOS 03_DADOS.xlsx", sheet = 4)
dados04 = dados04[,18:21]
dados04$ST = factor(dados04$ST)
dados04$VE = factor(dados04$VE)
tail(dados04)plot(dados04$R ~ dados04$ST)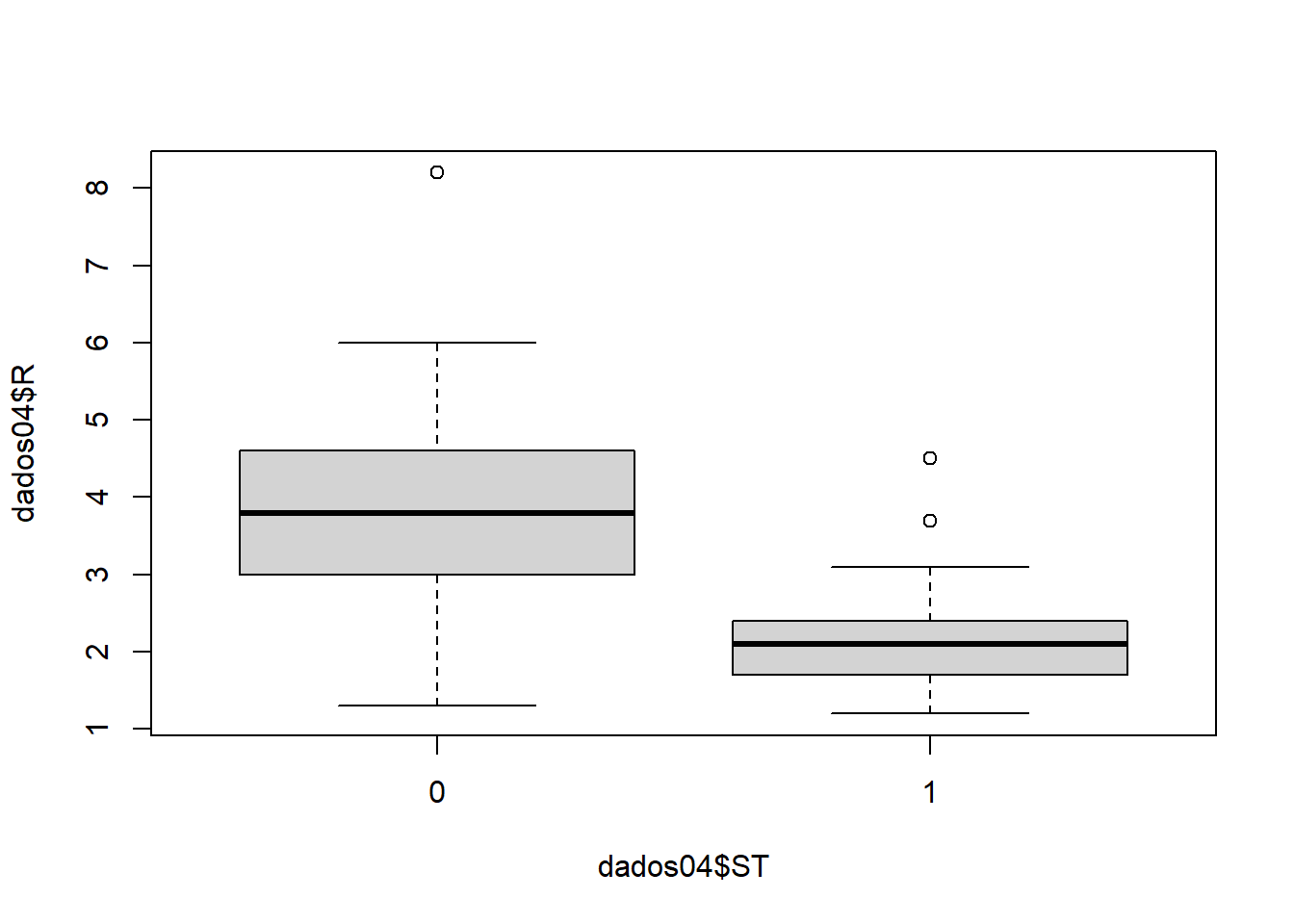
# table(dados04$VE, dados04$ST)O modelo é
\[ \log{\left(\frac{P(y_i=1)}{1-P(y_i=1)}\right)} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \epsilon_i \]
\[ \frac{P(y=1)}{1-P(y=1)} = e^{(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3)} \]
O ajuste é
modelo04 = glm(dados04$ST ~ dados04$R + dados04$ND + dados04$VE, family = binomial(link='logit'))
valoresPredito = predict.glm(modelo04, type = "response")
summary(modelo04)##
## Call:
## glm(formula = dados04$ST ~ dados04$R + dados04$ND + dados04$VE,
## family = binomial(link = "logit"))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6591 -0.2633 -0.0531 0.4187 2.0147
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.1117 1.5725 0.707 0.479578
## dados04$R -1.7872 0.4606 -3.880 0.000105 ***
## dados04$ND 0.9031 0.3857 2.341 0.019212 *
## dados04$VE1 2.9113 0.8506 3.423 0.000620 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 126.450 on 91 degrees of freedom
## Residual deviance: 51.382 on 88 degrees of freedom
## AIC: 59.382
##
## Number of Fisher Scoring iterations: 6Os valores preditos é
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 46 5
## 1 5 36
##
## Accuracy : 0.8913
## 95% CI : (0.8092, 0.9466)
## No Information Rate : 0.5543
## P-Value [Acc > NIR] : 2.554e-12
##
## Kappa : 0.78
##
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.9020
## Specificity : 0.8780
## Pos Pred Value : 0.9020
## Neg Pred Value : 0.8780
## Prevalence : 0.5543
## Detection Rate : 0.5000
## Detection Prevalence : 0.5543
## Balanced Accuracy : 0.8900
##
## 'Positive' Class : 0
##