Chapter 6 KNN Algorithm

The KNN, K Nearest Neighbours, algorithm is an algorithm that can be used for both unsupervised and supervised learning. It can be used in a regression and in a classification context.

6.1 KNN in Classification

The idea behind the KNN algorithm is simple. Suppose a binary classification problem, i.e. the dataset provides a couple of features and a binary target Y-variable. The dataset contains hostorical data.
To predict the value of the target variable for a new observation, based on the values of the features, the distance of the new observation to the observations in the data set is calculated. The K observatioons wtih the lowest distance are filtered. The majority Y-value for these K observations is used as the predicted Y-value for the new observation.

Before this algorithm can be used two important choices must be made: (1) which value of K to use and (2) which distance metric to use.
Besides the choice of a distance metric two important preprocessing steps have to be performed, (1) categorical variables must be transformed into dummy variables and (2) numeric variables must be standardized/ normalized. The first step is necessary, because calculating a distance requires numerical values. The second step is performed, because otherwise the units chosen largely determine the distances.
Different techniques can be used for normalizing the values of a numeric variable. Standardizing the values, i.e. transforming the values in the z-score is an option, z-score = $\frac{x-mean}{SD}$. Another option is standardizing the values using the formula below, x_norm = $\frac{max-x}{max-min}$. As in all classification problems, a choice about the metric to use to assess the model must be made.

6.1.1 Choosing appropriate K value

There is no general rule for the choice of the best K-value. It is most common to divide the data in a training an a test set, test a number of choices for K and check which choice leads to the best result.

6.1.2 Distance metrics

Commonly used distance metrics are (1) Eucledian distance and (2) Manhattan distance. Be aware that there are lots of other distance metrics as well.

Example 1

df <- read_csv("data/uci_diabetes/diabetes_data_upload.csv")

Predicting diabetes
Data set: example from UCI website

The data set consists of 520 observations on 17 features. The target variable is the Class variable which can take on two values, Positive and Negative. All but one of the features are binary. The non binary feature is the Age feature.

Table 1
First Six Observations of the Diabetes Data Set

flextable(head(df)) %>% 
  fontsize(size = 7, part = "all")

Age	Gender	Polyuria	Polydipsia	sudden weight loss	weakness	Polyphagia	Genital thrush	visual blurring	Itching	Irritability	delayed healing	partial paresis	muscle stiffness	Alopecia	Obesity	class
40	Male	No	Yes	No	Yes	No	No	No	Yes	No	Yes	No	Yes	Yes	Yes	Positive
58	Male	No	No	No	Yes	No	No	Yes	No	No	No	Yes	No	Yes	No	Positive
41	Male	Yes	No	No	Yes	Yes	No	No	Yes	No	Yes	No	Yes	Yes	No	Positive
45	Male	No	No	Yes	Yes	Yes	Yes	No	Yes	No	Yes	No	No	No	No	Positive
60	Male	Yes	Yes	Yes	Yes	Yes	No	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Positive
55	Male	Yes	Yes	No	Yes	Yes	No	Yes	Yes	No	Yes	No	Yes	Yes	Yes	Positive

Table 2
Summary of the data

summary(df)
##       Age           Gender            Polyuria          Polydipsia       
##  Min.   :16.00   Length:520         Length:520         Length:520        
##  1st Qu.:39.00   Class :character   Class :character   Class :character  
##  Median :47.50   Mode  :character   Mode  :character   Mode  :character  
##  Mean   :48.03                                                           
##  3rd Qu.:57.00                                                           
##  Max.   :90.00                                                           
##  sudden weight loss   weakness          Polyphagia        Genital thrush    
##  Length:520         Length:520         Length:520         Length:520        
##  Class :character   Class :character   Class :character   Class :character  
##  Mode  :character   Mode  :character   Mode  :character   Mode  :character  
##                                                                             
##                                                                             
##                                                                             
##  visual blurring      Itching          Irritability       delayed healing   
##  Length:520         Length:520         Length:520         Length:520        
##  Class :character   Class :character   Class :character   Class :character  
##  Mode  :character   Mode  :character   Mode  :character   Mode  :character  
##                                                                             
##                                                                             
##                                                                             
##  partial paresis    muscle stiffness     Alopecia           Obesity         
##  Length:520         Length:520         Length:520         Length:520        
##  Class :character   Class :character   Class :character   Class :character  
##  Mode  :character   Mode  :character   Mode  :character   Mode  :character  
##                                                                             
##                                                                             
##                                                                             
##     class          
##  Length:520        
##  Class :character  
##  Mode  :character  
##                    
##                    
##

Data cleaning and Preprocessing

Correct variable names (no spaces)
Preprocessing: normalize Age variable
Transform other variables into dummies
Transform class variable into a factor variable, this is a requirement for the caret::knn3() function
Split data set in training and test set; 70% in training, 30% in test set

names(df) <- make.names(names(df)) %>% 
  toupper() %>% str_replace_all("[\\.]", "_")


df_prep <- df %>% 
  mutate(AGE_NORM = (AGE - min(AGE))/(max(AGE)-min(AGE))) %>% 
  select(AGE_NORM, everything(), -AGE) %>% 
  mutate(GENDER = ifelse(GENDER=="Male", 1, 0))

#variables in column 3-16 are all variables which only take on "Yes" or "No" values; these can be transformed into 0/1 variable with one line of code
df_prep[,3:16] <- apply(df_prep[,3:16], 2, function(x) ifelse(x=="Yes", 1, 0))

#transform CLASS variable into type factor variable
df_prep$CLASS <- factor(df_prep$CLASS, levels = c("Positive", "Negative"),
                        labels = c("POS", "NEG"))

#split in training end test set
set.seed(20210309)
train <- sample(1:nrow(df), size = .7*nrow(df))
df_train <- df_prep[train,]
df_test <- df_prep[-train,]

Generate a knn-model. Choice to make beforehand: value of k; first attempt k = 5

#generate model using class::knn3() function
#forst attempt with k=5 as an arbitrary choice
knn_model_1 <- knn3(CLASS~., data = df_train, k = 5)
knn_model_1

5-nearest neighbor model
Training set outcome distribution:

POS NEG 
234 130

Assess model
Choose metric to assess model: Accuracy
Use model to make predictions for test data
Calculate Accuracy

#make predcitions with the generated model
knn_model_1_preds <- predict(knn_model_1, newdata = df_test, type = 'class')

#construct a confusion matrix
cf_1 <- table(knn_model_1_preds, df_test$CLASS)

#calculate Accuracy
acc_1 <- (cf_1[1,1] + cf_1[2,2]) / sum(cf_1)

Table 3
Confusion Matrix knn_1 model on Test Data Set

cf_1

                 
knn_model_1_preds POS NEG
              POS  77   5
              NEG   9  65

Accuracy = (77 + 65) / (77 + 5 +9 + 65) = 0.91.

confusionMatrix(knn_model_1_preds, df_test$CLASS)

#knn_model_1 <- train(class~., data = df_prep, method = ‘knn’) #knn_model_1

Example 1

Predicting credibility bank customers Data set: example from UCI website
The data set contains the following 23 variables as explanatory variables:

X1: Amount of the given credit (NT dollar): it includes both the individual consumer credit and his/her family (supplementary) credit.
X2: Gender (1 = male; 2 = female).
X3: Education (1 = graduate school; 2 = university; 3 = high school; 4 = others).
X4: Marital status (1 = married; 2 = single; 3 = others).
X5: Age (year).
X6 - X11: History of past payment. We tracked the past monthly payment records (from April to September, 2005) as follows: X6 = the repayment status in September, 2005; X7 = the repayment status in August, 2005; . . .;X11 = the repayment status in April, 2005. The measurement scale for the repayment status is: -1 = pay duly; 1 = payment delay for one month; 2 = payment delay for two months; . . .; 8 = payment delay for eight months; 9 = payment delay for nine months and above.
X12-X17: Amount of bill statement (NT dollar). X12 = amount of bill statement in September, 2005; X13 = amount of bill statement in August, 2005; . . .; X17 = amount of bill statement in April, 2005.
X18-X23: Amount of previous payment (NT dollar). X18 = amount paid in September, 2005; X19 = amount paid in August, 2005; . . .;X23 = amount paid in April, 2005.

There is one binary variable, default payment (Yes = 1, No = 0), as the response variable.

#https://archive.ics.uci.edu/ml/machine-learning-databases/00350/

data <- readxl::read_xls("data/uci_bank/default of credit card clients.xls",
                         col_names = TRUE)  
data <- data[-1,]

6.1.2.1 Example 1: Predicting stockmarket going up or down

Dataset: ISLR:: Smarket.
See ?ISLR::Smarket for more information.
Responsive variable: Direction; two possible values: “Up”, “Down”.
Predictors: Lag1, Lag2, Lag3, Lag4, Lag5.
Choices made:
- distance metric: eucledian distance
- k: comparing different values to find the optimal value
- model assessment metric: accuracy

df <- ISLR::Smarket
#data from 2001 to 2004 as training data
#data from 2005 as test data
df_train <- filter(df, Year < 2005) %>% 
  select(Lag1, Lag2, Lag3, Lag4, Lag5, Direction)
df_test <- filter(df, Year == 2005) %>% 
  select(Lag1, Lag2, Lag3, Lag4, Lag5, Direction)

# model 1: k = 1
model_k1 <- knn(train = df_train[, 1:5],
                test = df_test[, 1:5],
                cl = df_train[, 6],
                k = 1)
table(model_k1, df_test$Direction)

        
model_k1 Down Up
    Down   55 66
    Up     56 75

acc_k1 <- round(sum(model_k1 == df_test$Direction)/nrow(df_test), 1)

# accuracy for various k values

accuracies <- data.frame(K = 1:150, ACCURACY = NA)

for (k in 1:150) {
  model_knn <- knn(train = df_train[, 1:5],
                test = df_test[, 1:5],
                cl = df_train$Direction,
                k = k)
  accuracies[k, 2] <- round(sum(model_knn == df_test$Direction)/nrow(df_test), 3)
}

ggplot(accuracies, aes(x = K, y = ACCURACY)) +
  geom_line() +
  ylim(0.4, 0.65) +
  theme_minimal()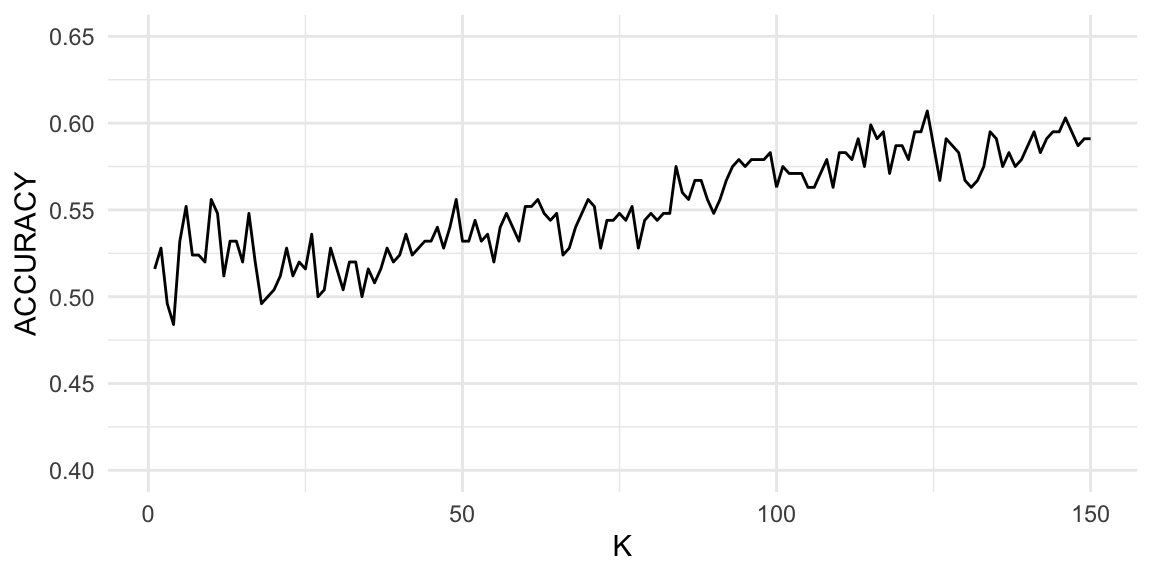

Same example using caret.

knn_model_caret <- train(Direction~.,
                         data = df[, c("Lag1", "Lag2", "Lag3", "Lag4", "Lag5", "Direction")],
                         method = "knn",
                         tuneGrid = data.frame(k = seq(1, 40, 2)))

preds_caret <- predict(knn_model_caret, newdata = df_test)
confusionMatrix(preds_caret, df_test$Direction)

Confusion Matrix and Statistics

          Reference
Prediction Down  Up
      Down   39  37
      Up     72 104
                                          
               Accuracy : 0.5675          
                 95% CI : (0.5038, 0.6295)
    No Information Rate : 0.5595          
    P-Value [Acc > NIR] : 0.425500        
                                          
                  Kappa : 0.092           
                                          
 Mcnemar's Test P-Value : 0.001128        
                                          
            Sensitivity : 0.3514          
            Specificity : 0.7376          
         Pos Pred Value : 0.5132          
         Neg Pred Value : 0.5909          
             Prevalence : 0.4405          
         Detection Rate : 0.1548          
   Detection Prevalence : 0.3016          
      Balanced Accuracy : 0.5445          
                                          
       'Positive' Class : Down

library(tidyverse)
library(openxlsx)
library(flextable)
library(lubridate)
library(caret)
library(tm)
library(e1071)
#options(scipen = 999)

df_train <- tibble(Y = c("POS", "POS","POS" ,"POS" ,"POS",
                         "POS", "NEG","NEG", "NEG", "NEG"),
                   X1 = c(1,1,1,1,0,0,1,0,0,0))

df_train_2 <- tibble(Y = c("POS", "POS","POS" ,"POS" ,"POS",
                         "POS", "NEG","NEG", "NEG", "NEG"),
                     X1 = c(1,1,1,1,0,0,1,0,0,0),
                     X2 = c(1,0,1,0,1,0,1,0,1,0))