Chapter 1 Numbers

1.1 Discrete Numbers

In this module we will explore numbers and ways in which we use numbers. Through history we have slowly increased the different sorts of number that we have, so that we can model the world in which we live. At this link you can get a little bit of history about who invented various numbers

https://www.whoinventedit.net/who-invented-numbers.html

We start off with natural numbers

\[ {\mathbb N} = \{1,2,3,\cdots\}. \]

Interestingly the number 0 was invented much later than others of these numbers, but was used by Indians, Mayans and Egyptians at least.

Negative numbers were invented by the Chinese around 100BC. It is interesting to ask yourself what would have stimulated you to invent a negative number if you did not have to. The set of positive and negative counting numbers is the integers:

\[ {\mathbb Z} = \{\cdots, -2,-1,0,1,1,\cdots\}. \]

The next set of numbers we use is the ratio of integers such as \({1 \over 2}\), \({-3 \over 4}\), \({2 \over -3}\) or \({-4 \over -5}\). We call these the rational numbers (fractions) and denote them by \({\mathbb Q}\). Now you may be wondering why I did not write them down like the others in a list. I encourage you to try and see how you do.

Finally we have numbers which cannot be represented as fractions. These were known about a long time before Pythagoras. Here is an image of a Babylonian tablet YBC792 which has a sexagesimal approximation to the square root of 2:

If you want to know more about this go to

https://en.wikipedia.org/wiki/YBC_7289

1.2 Solving Equations

One way of thinking about how some of these numbers can arise is by thinking about solving equations. For instance we can see that the rational numbers might arise by us trying to solve \[ m x = n, \] where \(m,n \in {\mathbb N}\). In Linear Algebra we think about solving systems of equations of this type (you will have called them simultaneous equations).

In this module we will think about things like quadratic equations, for instance \[ x^2-2=0. \] In the next frame you will see how to plot the function \(y=x^2-2\) using computational tool R. This has become one of the main tools used in industry today, and you should consider developing it in your degree to help the range of jobs you can do.

f <- function(x) {
  x^2 - 2
}

g <-function(x){ 
  0*x
}

  x <- seq(0,3,0.1)
  plot(x,f(x),main="f(x)=x^2-2",
ylab="f(x)",
type="l",
col="blue",
)
  lines(x,g(x),col="red")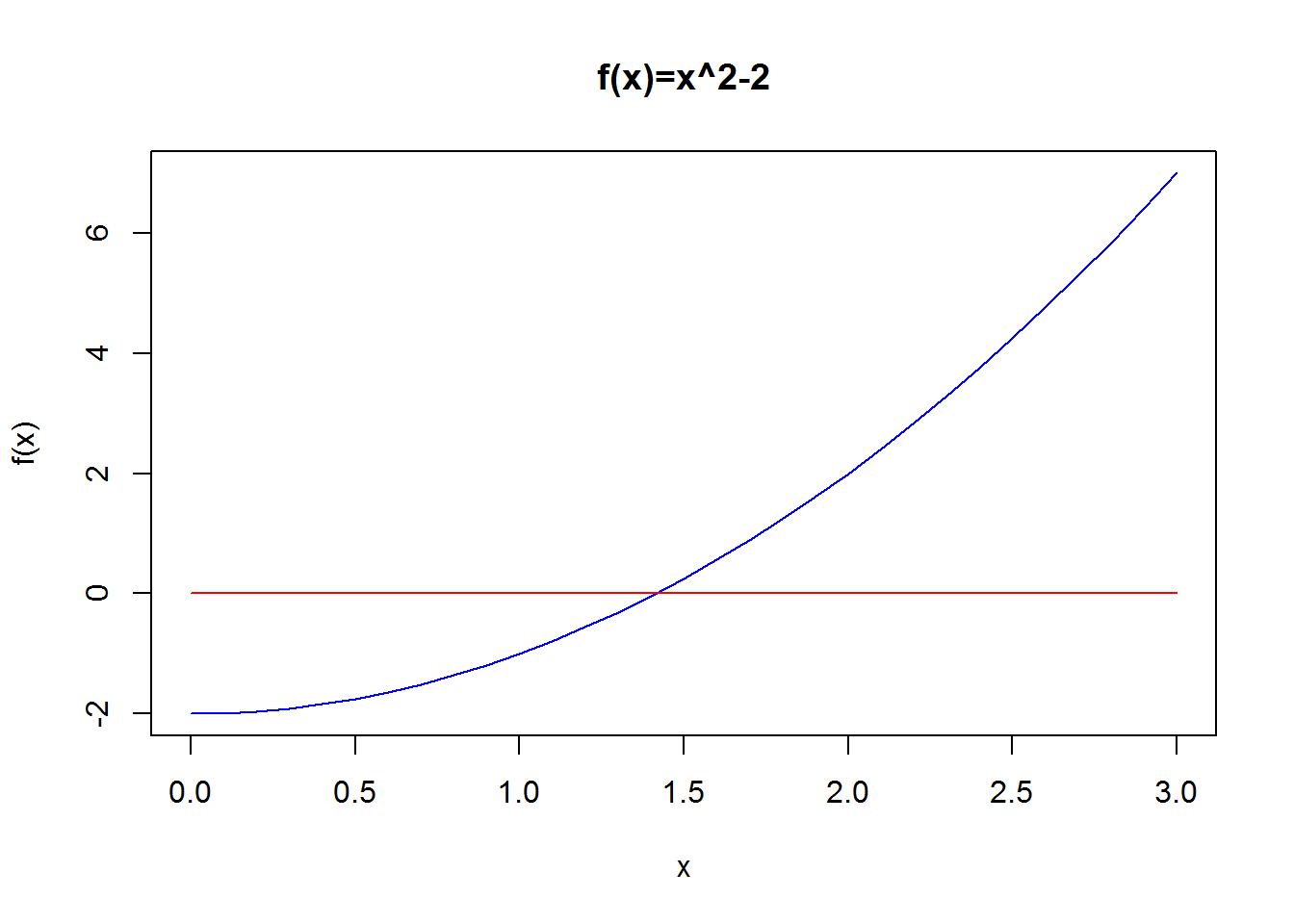

An important question is "How do we know there is a number which solves the equation \(y=x^2\)? One of the most amazing proofs in mathematics is that we can show that it cannot be a rational number, so if there is one, then it is not a fraction.

Theorem 1.1 The solution of the equation \(x^2-2=0\) is not a ratio of the form \({m \over n}\).

Proof: Suppose that the solution \(x={m \over n}\) for some \(m,n \in {\mathbb N}\), where \(m\) and \(n\) have no common factors (why have we said that?). Then we can write \[ \left ({m \over n} \right)^2 = 2, \] in other words \[ {m^2 \over n^2} = 2. \] Multiplying both sides by \(n^2\) we have \[ \hspace{3.5cm} m^2 = 2n^2. \tag{1.1} \] We can conclude from this that \(m\) is even because the right hand side is even, and the square of an odd number is odd. Since we only have odd and even numbers then \(m\) is even. Hence \(m=2p\) for some \(p \in {\mathbb N}\). If we put this into (1.1) we have \[ (2p)^2=4p^2 = 2n^2. \] Cancelling 2 from both sides gives us \[ 2p^2 = n^2. \] By the same argument we now know that \(n\) is even. So both \(n\) and \(m\) are even and we have a common factor of 2, which contradicts our original assumption. \(\Box\)

1.3 Mathematical induction

Induction is a method of proof where we use things that we know already to prove the next thing. Intunitively it is like having a set of dominoes lined up. Watch the video below to get another version of this explanation.

https://www.bing.com/videos/search?q=induction+dominoes&view=detail&mid=D524EACA53AE5BD88DD8D524EACA53AE5BD88DD8&FORM=VIRE

I will now use induction to prove:

Theorem 1.2 Let \(n \in {\mathbb N}\). Then \[ S_n = \sum_{i=1}^n i^2 = {1 \over 6}n (n+1) (2n+1). \]

Proof: Let us try a few cases out first to see if we believe it is true. If \(n=1\) then \[ S_1 = \sum_{i=1}^1 i^2 = 1={1 \over 6}(1) (1+1) (2(1)+1). \] If \(n=2\), \[ S_2 = \sum_{i=1}^2 i^2 = 1+4=5={1 \over 6}(2) (1+2) (2(2)+1). \]

So I think we believe it might be true from a few examples. Now, we assume it is true for \(n=N\) say, and we use this fact to prove it is true for \(n=N+1\) (if I knock down a domino the next one falls). We assume that the following is true \[ \sum_{i=1}^N i^2 = {1 \over 6}N (N+1) (2N+1). \quad (1.2) \] Here is the clever bit. Then \[ \sum_{i=1}^{N+1} i^2 = \sum_{i=1}^{N} i^2 + (N+1)^2. \] Because of our assumption (1.2) we can subtitute \[ \sum_{i=1}^{N+1} i^2 = {1 \over 6}N (N+1) (2N+1) + (N+1)^2. \] If we do some algebra on this (done in Lecture 2) we obtain \[ \sum_{i=1}^{N+1} i^2 = {1 \over 6}(N+1) ((N+1)+1) (2(N+1)+1). \] This is exactly the same formula with \(n=N+1\).

To recap, we have shown that if the equation is true for \(n=N\) then it is true for \(n=N+1\). Now it is true for \(n=1\) because we checked that. Therefore it is true for \(n=2\). Therefore it is true for \(n=3\), and so on. Hence it is true for any natural number. \(\Box\)

This process is called mathematical induction and it is one of the greatest weapons in the armoury of justifying mathematical statements (we call proof).

1.4 Complex numbers

In order to solve differential equations later we are going to need some new numbers, the complex numbers. The idea for complex numbers goes back a long way in history:

https://en.wikipedia.org/wiki/Imaginary_number

They are an invaluable tool in the scientists tool bag, and we give a quick introduction here. The starting point is to have have a square root of \(-1\) because this allows us to solve the equation \[ x^2+1=0. \] Now you might say that this is just not possible and no such number “really” exists. In what sense does the solution of \(x^2-2\) exist? These are interesting philosophical questions. It exists because we have just defined it. This number is called \(i\). The engineers often call it \(j\) so don’t get upset if you see this in some texts. The number \(i\) is referred to as imaginary, but this term was originally used by Descartes in a disparaging way.

A complex number \(z\) has a real and imaginary part \[ z=x+iy. \] We write \(x=\Re(z)\) and \(y=\Im(z)\):

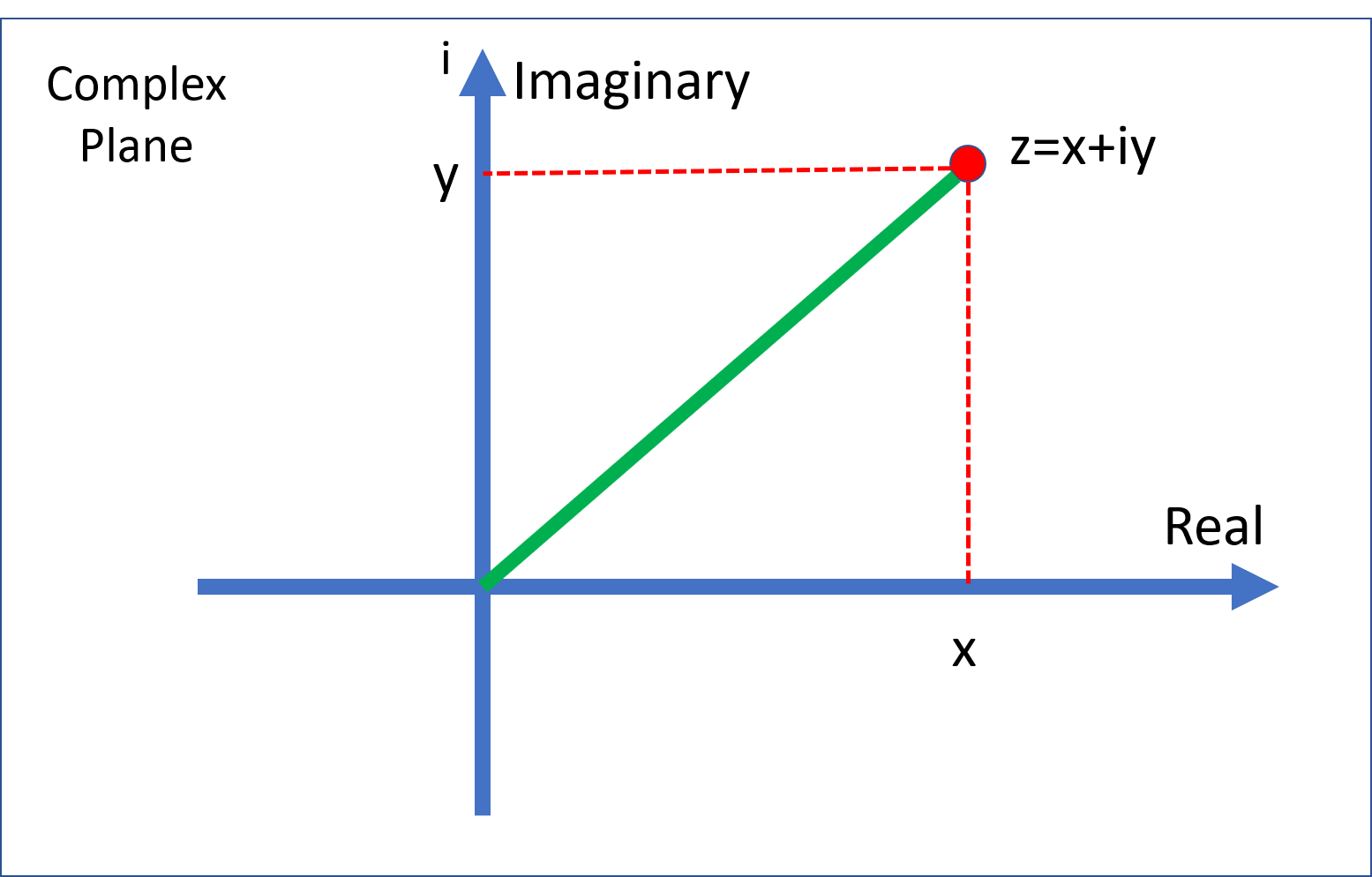
1.4.1 Arithmetic with complex numbers

When \(z_1=x_1+iy_1\) and \(z_2=x_2+iy_2\) the sum is \((x_1+x_2)+i(y_1+y_2)\). The product is \((x_1 x_2 - y_1 y_2)+i(x_1 y_2+x_2 y_1)\).

Example 1.1 Let \(n \in {\mathbb N}\). Then Let \(z_1=3+4i\) and \(z_2=-1+i\). Then \(z_1+z_2=(3+4i)+(-1+i)=(3-2)+i(4+1)=1+5i\). Also \(z_1 z_2=(3+4i)(-1+i)=((3)(-1)-(4)(1)+i((4)(-1)+(3)(1))=-7-i\).

Definition 1.1 Let \(z=x+iy\). The complex number \(\bar z = x-iy\) is called the complex conjugate of \(z\). The length of the complex number is called its modulus and is written \(|z|=\sqrt{x^2+y^2}\) If we multiply \(z \bar z=(x+iy)(x-iy)=x^2+y^2=|z|^2\). If we rearrange this equation we have \[ z^{-1} = {\bar z \over |z|^2}. \] This gives us a way of computing the inverse of a complex number.

Example 1.2 Compute the inverse of \(z=2-4i\). First we have \(|z|^2=2^2+(-4)^2=20\). Also \(\bar z = 2+4i\). Thus \[ z^{-1}={\bar z \over |z|^2}={2+4i \over 20}={1 \over 10}+{i \over 5}. \] You can check this by direct multiplication.

Here is a bit of R code you can use to find the inverse of a number for you to practice.

x <- 2
y <- -4
 
z <- complex(real = x, imaginary = y)

print(1/z)

## [1] 0.1+0.2i

MA1014 Calculus and Analysis