Chapter 2 Integration
Integration is the term we use to describe adding together an infinite number of infinitesimally small bits of something to make up the whole. For instance, in order to work out the length of a curve, we might break it into a lot of straight lines, and then add the lengths of these lines together:
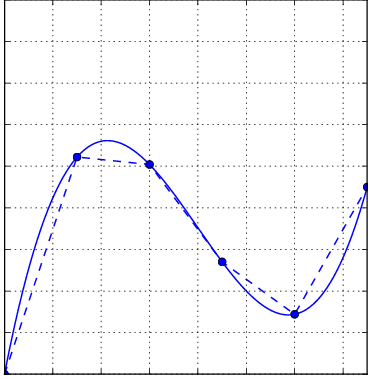
In the next bit of code we estimate the length of a semi circle of radius 1. What answer should we expect?
semicirc <-function(x){
(1-x^2)^(1/2)
}
npts <- 4 # as.integer(readline(prompt="Number of points:"))
div<-2/npts
for (i in 0:npts+1){
x[i] <- -1+(i-1)*div
}
y=x[0:npts+1]
plot(y,semicirc(y),main="f(x)=sqr(1-x^2)",
ylab="f(x)",
type="l",
col="blue")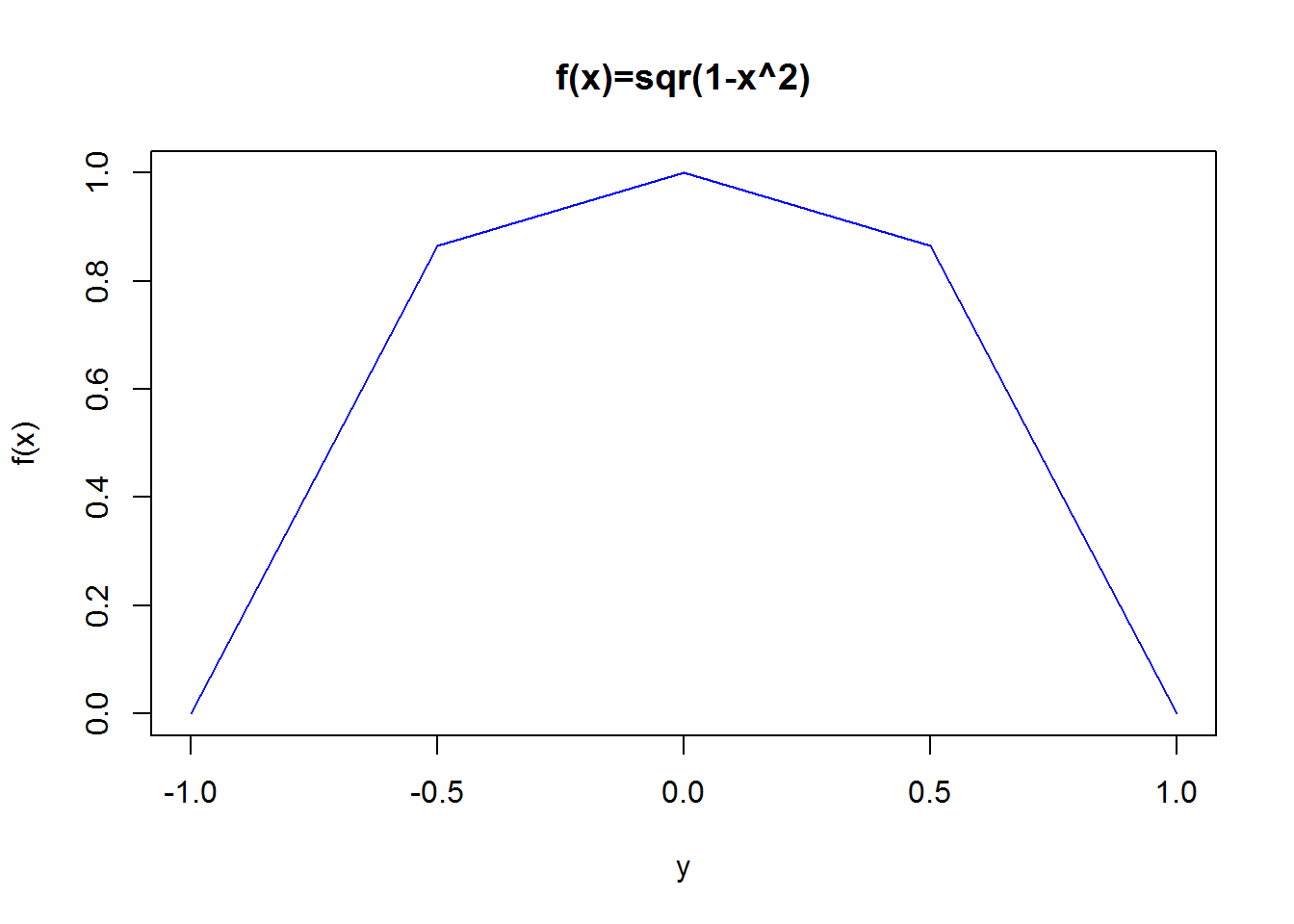
lentot<-0
for (i in 1:npts){
lentot<-lentot+((y[i+1]-y[i])^2+(semicirc(y[i+1])-semicirc(y[i]))^2)^(1/2)
}
print(lentot)## [1] 3.0352762.1 Integration of Polynomials
In this section we will look at the integration of polynomials by approximating the area under the curve by rectangles. Now let us think about the function \(y=1\) on the interval \([0,t]\), for some \(t>0\).

Then the area of the rectangle is \(t\) and we say the integral of \(y=1\) between \(0\) and \(t\) is \(t\), and we write \[ \int_0^t 1 dx = t. \]
Now let us consider the function \(y=x\) on the interval \([0,t]\), for some \(t>0\). Here is a picture.
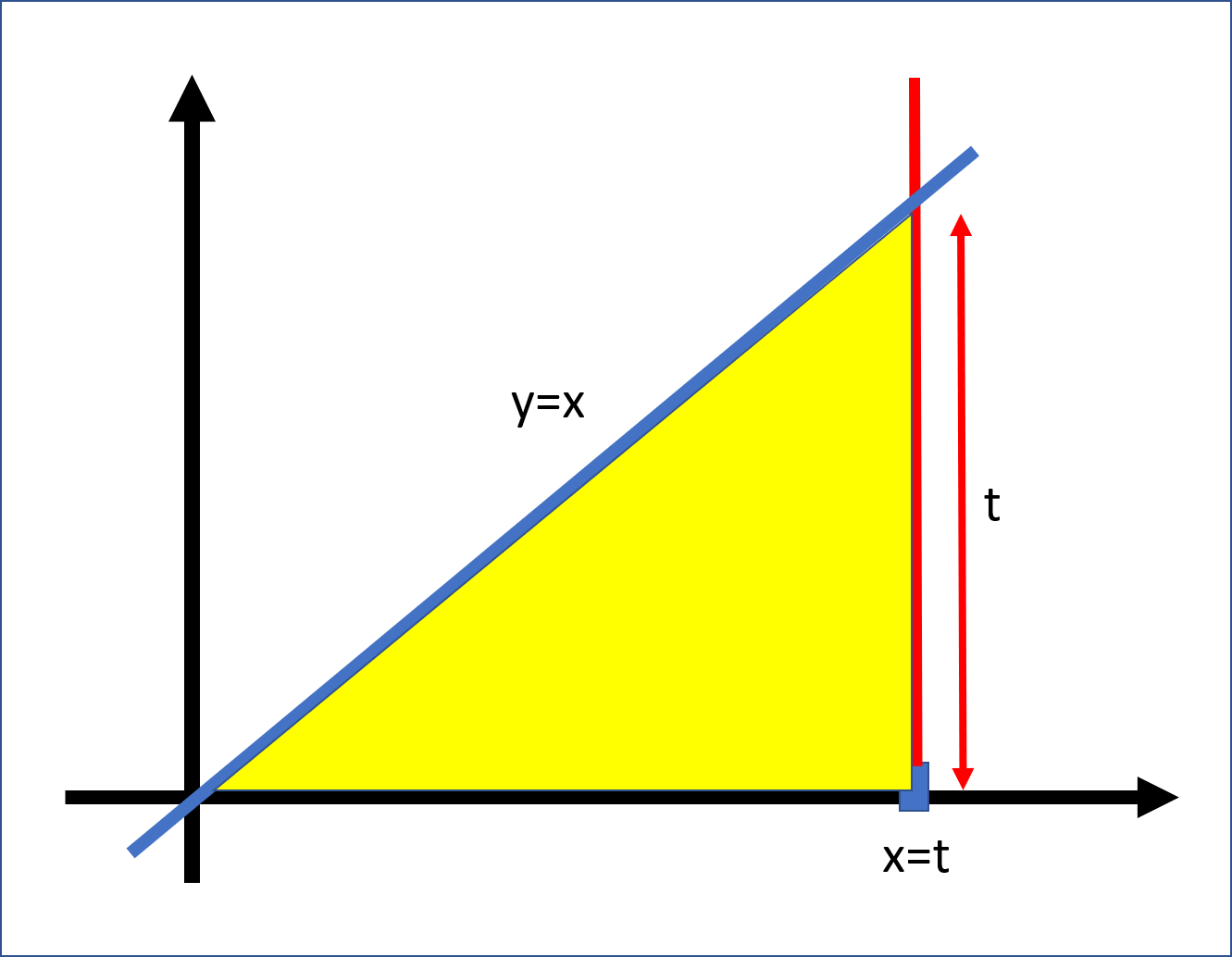
It is clear that the area of this is the area of an isosceles right-angled triangle of side length \(t\) which is \(t^2/2\). Hence, the integral of \(y=x\) between \(0\) and \(t\) is \(t^2/2\). We write this \[ \int_0^t x dx = {t^2 \over 2}. \]
Unfortunately, integrating other functions is not so straightforward. The next bit of code shows how to compute an esimate to the area under \(y=x^2\) using rectangles.
parab <-function(x){
x^2
}
npts <- 16 # as.integer(readline(prompt="Number of points:"))
div<-1/npts
x <- seq(0,1,0.01)
plot(x,parab(x),main="f(x)=x^2",
ylab="f(x)",
type="l",
col="blue")
area<-0
for (i in 1:npts){
area<-area+(i-1)^2/npts^3
rect((i-1)/npts,0,i/npts,(i-1)^2/npts^2,col="red")
}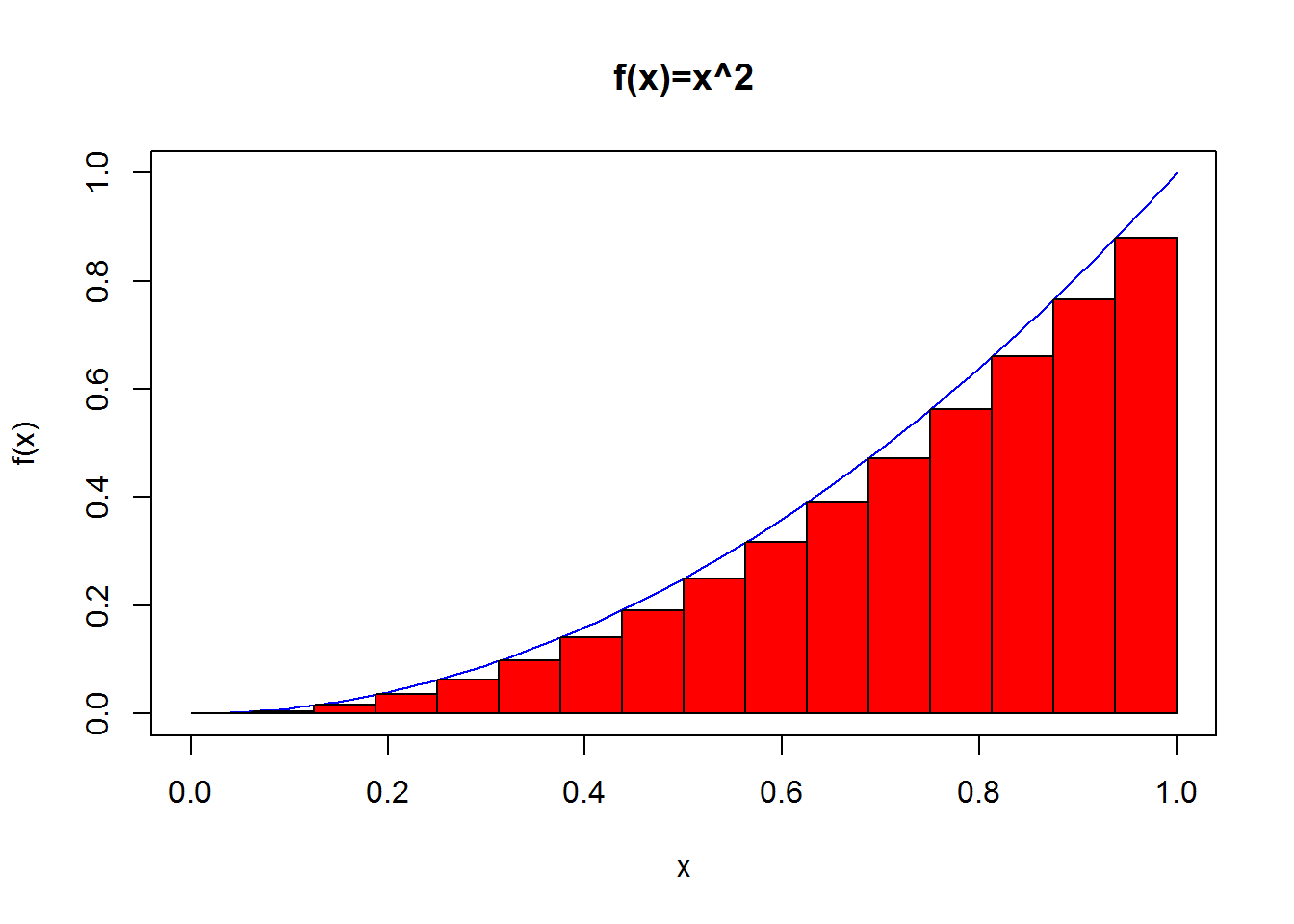
## [1] 0.3027344Proof: Let us divide the interval \([0,t]\) into \(n\) equal parts, each of width \(t/n\). Let us write \(x_i=it/n\), \(i=0,1,\cdots,n\). Then the height of the \(i\)th rectangle is \(x_{i-1}^2\) (the left hand end of the first rectangle is \(x_0=0\)). If we substitute \(x_{i-1}=(i-1)t/n\), we get the height \((i-1)^2t^2/n^2\). Hence the area of the \(i\)th rectangle is \[ R_i = {t \over n}{(i-1)t^2 \over n^2}={t^3 \over n^3} (i-1)^2. \] Thus the total area of the rectangles is \[ A_n = \sum_{i=1}^n R_i = {t^3 \over n^3} \sum_{i=1}^n (i-1)^2 = {t^3 \over n^3} \sum_{i=1}^{n-1} i^2. \tag{2.1} \]
For the moment we will just use the known fact that \[ \sum_{i=1}^m i^2 = {1 \over 6} m(m+1)(2m+1) \] to see that \[ \sum_{i=1}^{n-1} i^2 = {1 \over 6} (n-1)n(2n-1)={1 \over 3}n^3-{1 \over 2}n+{1 \over 6}n. \](We will look at how to prove such relationships in the next section).
Substituting the last equation intp we get \[ A_n = {t^3 \over n^3} \left ( {1 \over 3}n^3-{1 \over 2}n+{1 \over 6}n \right ) = {t^3 \over 3} - {1 \over 2} {t^3 \over n} + { 1 \over 6}{t^3 \over n^2}. \] Now, as \(n \rightarrow \infty\) the second and third terms tend to zero (we will make these terms more precise later in the course), leaving us with the area \[ A = \lim_{n \rightarrow \infty} A_n = {t^3 \over 3}. \Box \]