Part 6 Decision Trees
I built a decision tree in chapter 2 - a decision tree is a kind of flowchart that has a tree-like structure and is used in classification (i.e., our case) and regression problems to reach a conclusion about a target value.
If it helps, you can also think of a decision tree as a series of if-then statements that begin from the tree’s node (i.e., the top of the tree) and continuously branches out into two possible outcomes!
Below is a sample (classification) decision tree I generated using the train() function from the caret package. The data came from dataset ex2018 of the Sleuth3 package; ex2018 contains data on 1995 and later model compact sports utility vehicles that were involved in fatal accidents in the US between 1995 and 1999.
There are 2321 entries in ex2018 with four variables:
Make- this is a factor indicating the type of sports utility vehicle:OtherorFord.VehicleAge- this is the vehicle’s age in years.Passengers- this is the number of passengers in the vehicle during the time of accident.Cause- this is a factor indicating whether or not the accident was caused by the car’s tires:NotTireandTire:
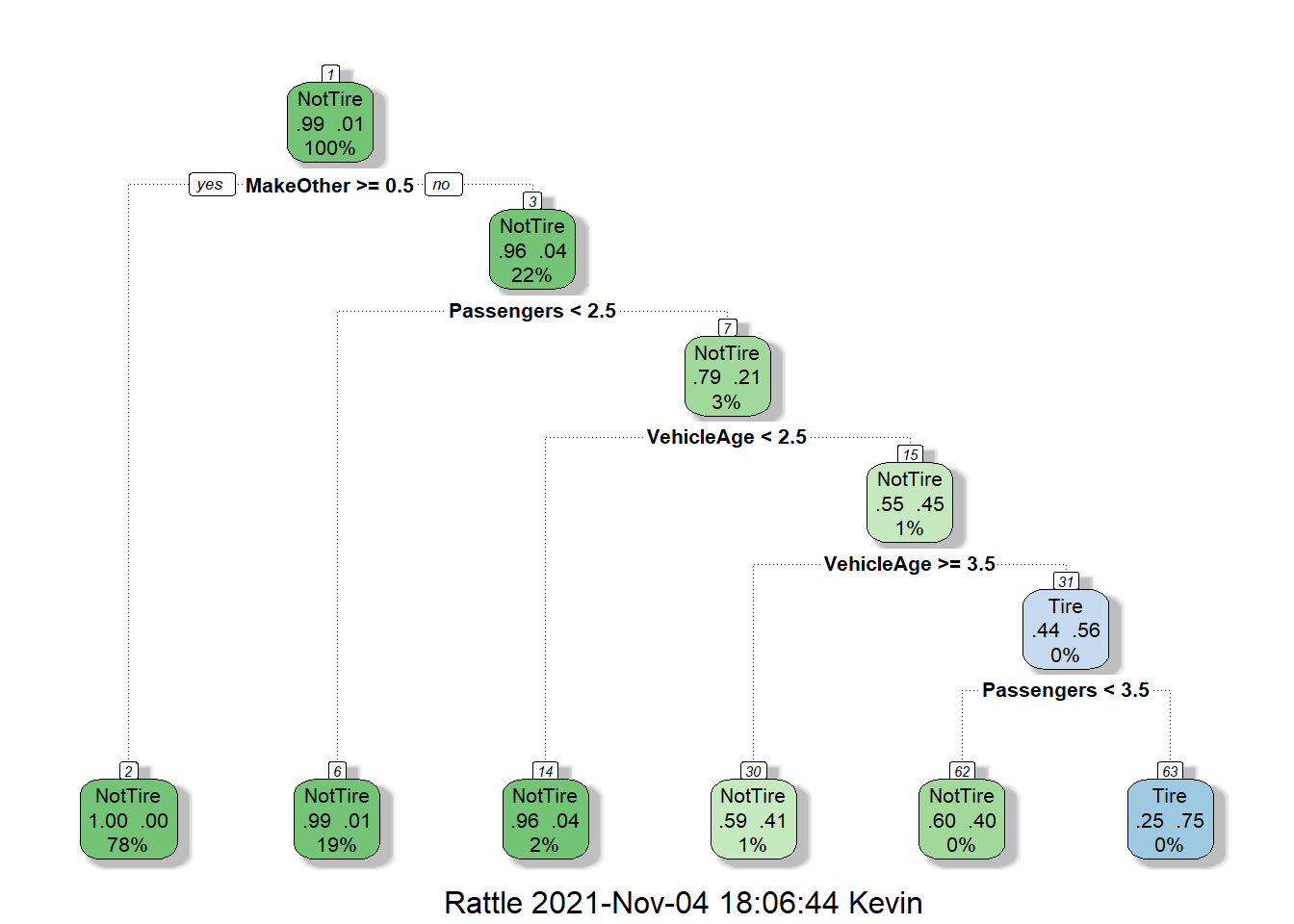
Granted - I did not actually split the data into testing and training sets like I should have, but this was just to demonstrate what a decision tree looks like.
6.1 Some Assumptions for Building a Decision Tree
A decision tree assumes the following:
- The tree will begin with a node (see the above decision tree for reference).
- All features should be categorical - otherwise, they are continuous and will be discretized (divided into categories) prior to building the model.
- Some statistical / mathematical approach should be taken to decide how to construct branches and to place the nodes in a decision tree.
6.1.1 How Does a Decision Tree Actually Work?
When training a decision tree using training data, the training data is first split into multiple, similar subgroups of data before fitting each subgroup with a constant.
These subgroups are then split into branches via a series of yes / no questions - this is done until a criteria of some sort has been met (e.g., the maximum depth of the tree has been reached). In the case of a classification problem, the decision tree makes predictions off the class that has the majority representation.
6.2 The CART Algorithm
There are many models used for making decision trees: however, I have only ever worked with two - the iterative dichotomizer 3 (i.e., ID3) and the Classification and Regression Tree (i.e., CART).
However, since the CART algorithm was used to build the decision trees in chapter 2, I will focus solely on the CART algorithm.
6.2.1 Inner workings of CART
CART is an algorithm that uses binary recursive partitioning to make the splits in a decision tree: the main goal of the binary recursive partitioning in classification problems is to - at each node - minimize the reduction of the Gini Index \(G\):
\[\begin{equation} \sum_{k = 1}^{K}\hat{p}_{jk}(1 - \hat{p}_{jk}) \end{equation}\]
Where \(K\) is the total number of classes in the \(j\)-th region.
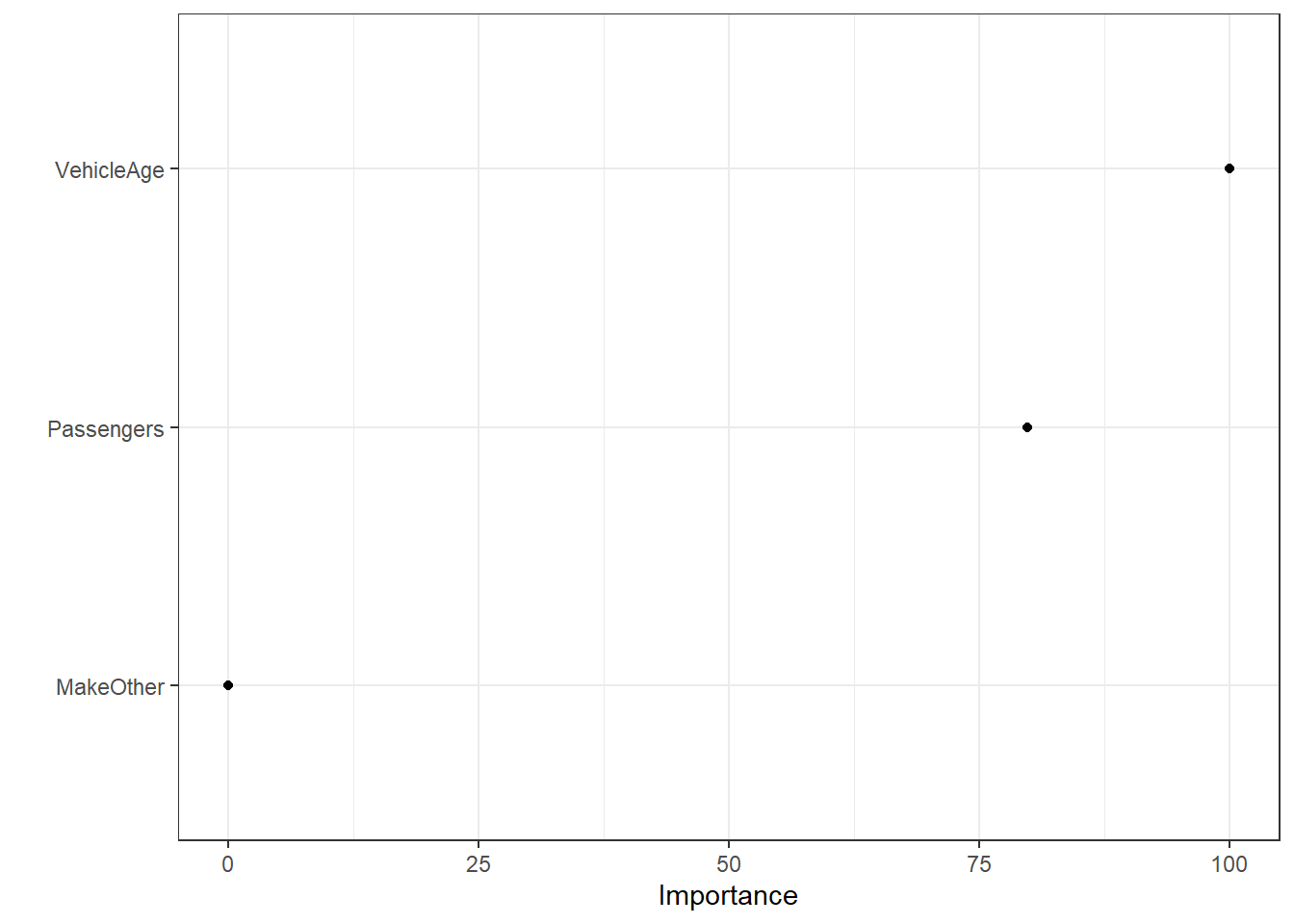
6.3 Variable Importance
Feature or variable importance is a technique whereby input variables are assigned a score of some sort to quantify how “useful” they are at predicting a target variable.
As seen in the decision tree at the beginning of the chapter, the same predictor can be used multiple times throughout different branches of the tree; the total reduction in all splits’ loss functions by that predictor is then summed up and used to calculate the total variable importance.
Using the ex2018 again, one can calculate a feature importance plot using the vip() function from the vip package as such (the more “useful” the variable, the higher its importance) - note that the variable importance of all decision trees trained using the caret package will be automatically scaled to out of 100:
vip(xx, num_features = 10, geom = "point") + theme_bw()