第 6 章 概率论基础
6.1 随机现象与随机试验
6.1.1 随机试验、随机现象和随机事件
随机试验特点:可重复性、不可预知性
随机试验观测到的现象为随机现象
概率论与数理统计研究的对象
概率论研究随机现象的统计规律
数理统计研究随机现象的数据收集与分析
随机试验的某些可能结果组成的集合称为,简称事件
| 序号 | 随机试验 | 事件A | 事件B |
|---|---|---|---|
| (1) | 观测一部手机的通话时间 | 通话时间2h | 通话时间2h |
| (2) | 观测一颗骰(tóu)子的点数 | 点数为奇数 | 点数为偶数 |
| (3) | 某新型药的治疗效果 | 治疗有效 | 治疗无效 |
6.1.2 样本空间与随机事件
样本空间:随机试验所有可能结果的集合称为样本空间。常用\(\Omega\)表示。
样本点:样本空间的元素称为样本点,常用\(\omega\)表示。
| 序号 | 随机试验 | 样本空间 |
|---|---|---|
| (1) | 观测一部手机的通话时间 | \(\Omega=[0,\infty)\) |
| (2) | 观测一颗骰(tóu)子的点数 | \(\Omega=\{1,2,3,4,5,6\}\) |
| (3) | 某新型药的治疗效果 | \(\Omega=\{\text{治疗有效}, \text{治疗无效}\}\) |
有限样本空间:试验(2)和试验(3)
无限样本空间:试验(1)
随机事件是某些样本点组成的集合。
在一次试验中,当试验结果属于事件A时,称这次试验中。否则称。
| 事件类型 | 记号 |
|---|---|
| 必然事件 | \(A=\Omega\) |
| 不可能事件 | \(A=\emptyset\) |
| 基本事件/简单事件 | \(A = \{\omega\}\), \(\omega\in \Omega\) |
| 复合事件 | \(A\subseteq \Omega\) |
例 6.1 在一批含有20件正品,5件次品的产品中随机地抽取2件,可能结果如下:
A={2件全是正品}
B={只有1件是正品}
C={2件全是次品}
在不计次序的假定下,A、B、C是基本事件。
如果考虑次序,B不再是基本事件,它可分解为\(B_1\)和\(B_2\)两个基本事件。
\(B_1\)={第1次抽到正品,第2次是次品}
\(B_2\)={第1次抽到次品,第2次是正品}
事件的关系:
包含: 如果事件A发生,事件B一定发生。则称事件B包含事件A。记为\(A\subset B\)。显然\(A\subset\Omega\)。
相等: \(A=B\Leftrightarrow A\subset B\text{且}B\subset A\)
互斥: \(A\cap B = \varnothing\)
对立:\(A\cap B = \varnothing\)且\(A\cup B=\Omega\),记\(A = \bar{B}\)或者\(B = \bar{A}\)
事件A和B的关系?
事件B和C的关系?
事件C和D的关系?
事件D和E的关系?
事件的运算:交、并、差
\(A\cap B\)或者AB,事件A和B同时发生
\(A\cup B\),事件A和B至少一个发生。若\(A\)和\(B\)互斥, 则\(A\cup B\)可表示为\(A+B\)。
\(A\backslash B\),或表示为\(A-B\),事件A发生但事件B不发生
多个事件的交\(\bigcap_{i=1}^n A_i\),多个事件的并 \(\bigcup_{i=1}^n A_i\)
例 6.3 设\(A\)、B、C为任意三个事件,写出下列事件的表达式:
AC都发生B不发生。
恰有二个事件发生。
至少有一个事件发生。
三个事件同时发生。
三个事件发生。
三个事件发生。
事件的运算法则:
对于任意三个事件A,B,C,满足下列运算:
\(AB=BA\), \(A\cup B=B\cup A\)
\((AB)C=A(BC)\), \((A\cup B)\cup C=A\cup (B\cup C)\)
\(A(B\cup C)=AB\cup AC\), \(A\cup (B\cap C)=(A\cup B)\cap (A\cup C)\)
\(\overline{A\cup B}=\bar{A}\cap \bar{B}\), \(\overline{A\cap B}=\bar{A}\cup \bar{B}\)
\[\overline{\bigcup_{i=1}^n A_i}=\bigcap_{i=1}^n \bar{A}_i,\quad \overline{\bigcap_{i=1}^n A_i}=\bigcup_{i=1}^n \bar{A}_i\]
6.2 概率的定义
频率的定义:设事件\(A\)在\(n\)次试验中出现了\(r\)次,则比值 \(r/n\)称为事件\(A\)在\(n\)次试验中出现的频率。
概率的统计定义:在同一组条件下所作的大量重复试验中,事件\(A\)出现的频率总是在区间\([0,1]\)上的一个确定的常数\(p\)附近摆动,并且稳定于\(p\)(频率的稳定值),则\(p\)称为事件\(A\)的概率,记作\(P(A)\)。
注意:\(P(\)这里面只能为事件!\()\)。如,\(P(\)骰子的点数\()=1/6\)是错误的。
确定概率的古典方法。古典概型的随机试验要求满足下两条件:
有限性。只有有限多个不同的基本事件。
等可能性。每个基本事件出现的可能性相等。
在古典概型中,如果基本事件(样本点)的总数为\(n\),事件\(A\)所包含的基本事件(样本点)个数为\(r(r\le n)\),则定义事件\(A\)的概率\(P(A)\)为\(r/n\)。即
\[P(A)=\frac{r}{n}=\frac{A\mathrm{中包含的基本事件的个数}}{\mathrm{基本事件的总数}}.\]
简单例子:抛均匀的硬币、骰子 思考: 古典概型的取值范围?
解. 设事件A={第\(k\)次取出的球是黄球}。
解法一:考虑第1次到第\(k\)次的取球结果。
\[P(A)=\frac{C_a^1A_{a+b-1}^{k-1}}{A_{a+b}^{k}}=\frac{a}{a+b}.\]
解法二:只考虑第\(k\)次的取球结果。
\[P(A)=\frac{C_a^1}{C_{a+b}^{1}}=\frac{a}{a+b}\]
结论:抽签与顺序无关(如同有放回的情况)!基本事件是相对的!
例 6.5 (m个质点在n个格子中的分布问题) 设有\(m\)个不同质点,每个质点都以概率\(1/n\)落入\(n\)个格子(\(n\ge m\))的每一个之中,求下列事件的概率:
- A: 指定\(m\)个格子中各有一个质点;
- B: 任意\(m\)个格子中各有一个质点;
- C: 指定的一个格子中恰有\(k(k\le m)\)个质点。
例 6.6 (同一天生日问题) 某班级有\(n\)个人,问至少有两个人的生日在同一天的概率为多大?(假设一年有365天)
解. 记\(A=\){\(n\)个人中至少有两个人的生日相同}。\(\bar{A}=\){\(n\)个人中的生日全不相同}, 易知
\[P(\bar{A})=\frac{A_{365}^n}{365^n}=\frac{365!}{365^n(365-n)!}.\] 因此, \[P(A)=1-P(\bar{A})=1-\frac{365!}{365^n(365-n)!}.\]
上述只是对\(n\le 365\)成立。如果\(n>365\),则显然\(P(A)=1\). 联系生日攻击问题
概率的几何定义:平面上有可测的区域\(G\)和\(g\),向\(G\)中随机投掷一点\(M\),设\(M\)必落在\(G\)内。如\(M\)落在\(g\)内的概率只与\(g\)的面积成正比,而与\(g\)的位置和形状无关。这样的随机实验,称为几何概型。点\(M\)落入\(G\)内的部分区域\(g\)的概率为:
\[P = \frac{g\text{的面积}}{G\text{的面积}}.\]
注意:随机投点是指\(M\)落入\(G\)内任一处均是等可能的。
思考: 几何概型的取值范围?
\[P(A) = \frac{24^2-(16^2+18^2)/2}{24^2}\approx 0.4965.\]
例 6.8 (蒲丰投针实验) 蒲丰是几何概率的开创者,并以蒲丰投针问题闻名于世,发表在其1777年的论著《或然性算术试验》中。 由于通过他的投针试验法可以利用很多次随机投针试验算出\(\pi\)的近似值,所以特别引人瞩目,这也是最早的几何概 率问题。并且蒲丰本人对这个实验给予证明。1850年,瑞士数学家沃尔夫在苏黎世,用一根长\(36mm\)的针,平行线间距为\(45mm\),投掷\(5000\)次,得\(\pi\approx3.1596\)。1864年,英国人福克投掷了\(1100\)次,求得\(\pi\approx3.1419\)。1901年,意大利人拉泽里尼投掷了\(3408\)次,得到了准确到6位小数的\(\pi\)值。

George-Louis Leclerc de Buffon (1707.9.7-1788.4.16),法国数学家、自然科学家。
解. 设\(x\)表示针的中点到最近的一条平行线的距离,\(\theta\)表示针与平行线的交角。显然\(0\le x\le a/2\), \(0\le \theta\le \pi\). 为使针与平行线相交,必须\(x\le \frac{\ell}{2}\sin\theta\).
所求的概率为:
\[\frac{\frac \ell 2\int_0^\pi\sin\theta d\theta }{\frac 1 2\pi a}=\frac{2\ell}{\pi a}.\]
若取\(\ell = a/2\),则\(\pi = 1/P.\)
如果是三角形呢?知道边长分别为\(\ell_1,\ell_2,\ell_3\).
统计界的贝叶斯学派认为:一个事件的概率是人们根据经验对该事件发生的可能性所给出的个人信念。
天气预报说“明天下雨的概率为90%”
医生说“手术成功可能性为90%”
我说“考试及格的可能性为99%”
注意区别“主观概率”与“主观臆造”。
前面学了三种概率定义,各有其局限性。
统计概率:要求作大量重复试验。很难观测到稳定值
古典概率:试验结果要求有限、互不相容、等可能。不均匀的硬币
几何概率:落入区域G内任一点是等可能的。高手投飞镖
如何刻画更一般的情况?1900年数学家希尔伯特(Hilbert, 1862–1943)提出要建立概率的公理化定义来解决这个问题,即以最少的几条本质特征出发去刻画概率的概念。1933年苏联数学家柯尔莫戈夫(Kolmogorov, 1903–1987)首次提出了概率的公理化定义,这个定义既概括了历史上几种概率的共同特征,又避免了各自的局限性和含混之处,不管什么随机现象,只要满足该定义的三条公理,才能说它是概率。
6.2 概率的公理化定义
样本空间\(\Omega\),事件域\(\mathcal{F}\),概率测度\(P:\mathcal{F}\to [0,1]\)。由三元组\((\Omega,\mathcal{F},P)\)定义一个概率空间。
事件域\(\mathcal{F}\)是由样本空间的一些子集构成的集合,并满足以下条件:
\(\Omega\in \mathcal{F}\);
如果\(A\in\mathcal{F}\), 则\(\bar{A}\in \mathcal{F}\);
如果\(A_n\in\mathcal{F}\), \(n=1,\dots,\infty\), 则\(\bigcup_{n=1}^\infty A_n\in \mathcal{F}\).
试证明:\(\varnothing \in \mathcal{F}\). 如果\(A_n\in\mathcal{F}\), \(\bigcap_{n=1}^\infty A_n\in \mathcal{F}\).
概率的公理化定义:样本空间\(\Omega\),事件域\(\mathcal{F}\),概率测度\(P:\mathcal{F}\to [0,1]\)。由三元组\((\Omega,\mathcal{F},P)\)定义一个概率空间。
概率测度\(P(A)\)度量事件\(A\in \mathcal{F}\)发生的概率,满足下面三个公理。
公理1(非负性): \(\forall A\in \mathcal{F}\), \(0\le P(A)\);
公理2(规范性): \(P(\Omega)=1\);
公理3(可列可加性): 对可列个两两互斥的事件\(A_1,A_2,\dots,A_n,\dots\)有
\[P\left(\bigcup_{i=1}^\infty A_i\right)=\sum_{i=1}^{\infty}P(A_i).\]
思考:古典概率和几何概率是否符合该公理化定义?
概率的性质:
\(P(\varnothing)=0\)
如果\(A,B\)互斥,则\(P(A+B)=P(A)+P(B)\).
单调性:如果\(A\subset B\),则\(P(A)\le P(B)\).
\(P(\bar{A})=1-P(A)\)
\(P(A\backslash B)=P(A)-P(AB)\)
\(P(A\cup B)=P(A)+P(B)-P(AB)\)
上连续性:如果\(A_1\supset A_2\supset \cdots\supset A_n\cdots\),则 \[P\left(\bigcap_{i=1}^\infty A_i\right)=\lim_{i\to\infty}P(A_i).\]
下连续性:如果\(A_1\subset A_2\subset \cdots\subset A_n\cdots\),则 \[P\left(\bigcup_{i=1}^\infty A_i\right)=\lim_{i\to\infty}P(A_i).\]
半可加性: 对任意两个事件\(A\), \(B\), 有
\[P(A\cup B)\le P(A)+P(B).\]
对任意\(n\)个事件\(A_1,A_2,\dots,A_n\), 有
\[P(\cup_{i=1}^nA_i)\le \sum_{i=1}^{n}P(A_i).\]
例 6.9 证明下列命题:
若\(A_1\)与\(A_2\)同时发生时\(A\)发生,则有\(P(A)\ge P(A_1)+P(A_2)-1\).
证明:因为\(A_1A_2\subset A\),则\(P(A)\ge P(A_1A_2)\). 又 \[\begin{aligned} P(A_1A_2)&=P(A_1)+P(A_2)-P(A_1\cup A_2)\notag\\&\ge P(A_1)+P(A_2)-1.\label{eq:1} \end{aligned}\]
若\(A_1A_2A_3\subset A\),则有\(P(A)\ge P(A_1)+P(A_2)+P(A_3)-2\).
证明:由第一题结论得到\(P(A)\ge P(A_1A_2)+P(A_3)-1\). 再由??可得所需结果。
思考:若\(\bigcap_{i=1}^nA_i\subset A\),则\(P(A)\ge\sum_{i=1}^nP(A_i)-n+1\).
6.3 条件概率与独立性
条件概率是指在某事件\(B\)发生的前提下,求另一事件\(A\)的概率,记为\(P(A|B)\)。
例 6.10 \(A=\){抽到号码为偶数的橙色球}, \(B=\){抽到号码小于4的球}.
\[\begin{aligned} P(A)&=\frac{4}{12}\\ P(B)&=\frac 6 {12}\\ P(AB)&=\frac{1}{12}\\ P(A|B)&= \frac 1 6 = \frac{1/12}{6/12} = \frac{P(AB)}{P(B)}. \end{aligned}\]
不妨考虑更一般的古典概型和几何概型下的条件概率。
条件概率也是概率。
条件概率满足所有概率性质。验证三个公理
条件概率空间\((\Omega,\mathcal{F},P(\cdot|B))\)
若\(A\subset B\), 则\(P(A|B)\ge P(A)\).
若\(B\subset A\), 则\(P(A|B)=1\).
若\(AB=\varnothing\), 则\(P(A|B)=0\).
乘法公式:如果\(P(B)>0\), 则有 \[P(AB)=P(B)P(A|B).\] 更一般地,对于\(n\)个事件\(A_1,\dots,A_n\), 如果\(P(A_1\cdots A_{n-1})>0\), 则有 \[P(A_1\cdots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1\cdots A_{n-1}).\]
解. 设事件\(A_i\)={第\(i\)套系统能正常工作},\(i=1,2\). 即求\(P(A_1\cup A_2)\).
依题意有,\(P(A_1)=0.92\), \(P(A_2)=0.93\), \(P(A_2|\bar{A}_1)=0.85\).
因此, \[\begin{aligned} P(A_1\cup A_2) &=P(A_1)+P(A_2\bar{A}_1)\\ &=P(A_1)+P(A_2|\bar{A}_1)P(\bar{A}_1)\\ &=P(A_1)+P(A_2|\bar{A}_1)(1-P(A_1))\\ &=0.988. \end{aligned}\]例 6.15 (敏感性问题调查) 考虑以下问题:
问题\(A\): 你的生日是否在7月1日之前?
问题\(B\): 你是否逃过课?
问卷调查
全概率公式(原因推结果)
\(B_1,B_2,\dots,B_n\)为一组两两互斥的事件,且
\(B_1+B_2+\dots+B_n=\Omega\);
\(P(B_i)>0\), \(i=1,\dots,n\),
我们称这些\(B_i\)为样本空间的一个划分。 对任意事件\(A\)有 \[P(A)=\sum_{i=1}^nP(A|B_i)P(B_i).\]
注:
该定理可以推广到可列多个的情况
\(B_i\)视为导致事件\(A\)(结果)发生的"原因"
例 6.16 (敏感性问题调查(续)) - 问题\(A\): 你的生日是否在7月1日之前?
- 问题\(B\): 你是否在考试中做过弊?
\(n\)个人参与调查(\(n\)充分大),通过抛硬币决定回答哪个问题。若其中\(k\)个人回答“是”。作弊的比例大概为: \[p\approx 2k/n-0.5.\]
image
它是贝叶斯定理的应用。英国数学家托马斯贝叶斯(Thomas Bayes)在1793年发表的一篇论文中,首先提出了这个定理。
贝叶斯(Bayes)公式(结果推原因)
设\(B_1,B_2,\dots,B_n\)为一组两两互斥的事件,且
\(B_1+B_2+\dots+B_n=\Omega\);
\(P(B_i)>0\), \(i=1,\dots,n\),
则对任意一个具有正概率的事件\(A\)有 \[\bf{P(B_k|A)=P(B_k)\frac{P(A|B_k)}{P(A)}=\frac{P(A|B_k)P(B_k)}{\sum_{i=1}^nP(A|B_i)P(B_i)}}.\]
几点说明:
该定理可以推广到可列多个的情况。
贝叶斯公式广泛用于统计推断:通过观测到的实验数据来推测模型参数,即由结果推断成因。
\(B_k\)可视为“因”,\(A\)视为“果”,\(P(B_k)\)称为"先验概率",即在事件A发生之前,我们对事件\(B_k\)发生概率的一个判断;\(P(B_k|A)\)称为"后验概率",即在事件A发生后,我们对事件\(B_k\)的重新评估。****

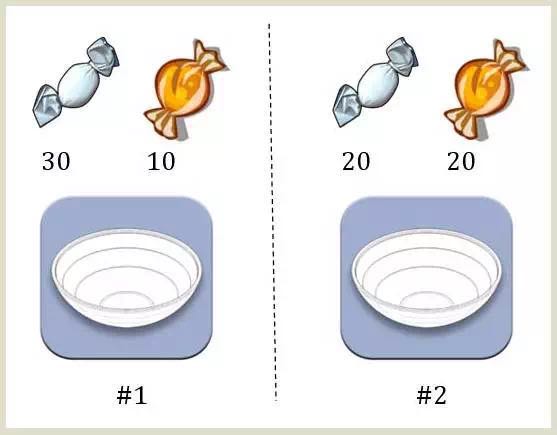
image
设\(H_1\)表示一号碗,\(H_2\)表示二号碗。则\(P(H_1)=P(H_2)\),也就是说,再取出水果糖之前,这两个碗被选中的概率相同。因此,\(P(H_1)=0.5\),我们把这个概率叫做“先验概率",即没有做实验之前,来自一号碗的概率是0.5。再假定,\(E\)表示水果糖,所以问题就变成了在已知\(E\)的情况下,来自一号碗的概率有多少?即求\(P(H_1|E)\)。我们把这个概率叫做”后验概率",即在事件\(E\)发生之后,对\(P(H_1)\)的修正。由贝叶斯公式可求\[P(H_1|E)=\frac{P(H_1)P(E|H_1)}{P(H_1)P(E|H_1)+P(H_2)P(E|H_2)}=\frac{0.5\times(3/4)}{0.5\times(3/4)+0.5\times(1/2)}=0.6,\]也就是说,取出水果糖之后,\(H_1\)事件的可能性得到了增强。
解. 设\(A=\){主持人选中山羊},\(B=\){参赛者第一次选中山羊},\(C=\){参赛者第二次选中汽车}。所求为\(P(C|A)\). 若参赛者换另一扇门,则\(P(C|A)=P(B|A)\),否则
\(P(C|A)=P(\bar{B}|A)=1-P(B|A)\). 已知\(P(B)=2/3\), \(\bf{P(A|\bar{B})=1}\). 由贝叶斯公式得 \[P(B|A)=\frac{P(A|B)P(B)}{P(A|B)P(B)+\bf{P(A|\bar{B})}P(\bar{B})}=\frac{\bf{P(A|B)}(2/3)}{\bf{P(A|B)}(2/3)+1/3}.\]
假定1:主持人知道汽车的位置。如果参赛者第一次没选中汽车,主持人必定开启藏山羊的门。即\(P(A|B)=1\). 所以,换门中奖概率\(P(B|A)=2/3\).
假定2:主持人随机打开一扇门。则\(P(A|B)=1/2\). 所以,换门中奖概率\(P(B|A)=1/2\).
例 6.22 两台机床加工同样的零件,第一台出现废品的概率为\(0.05\),第二台出现废品的概率为\(0.02\),加工的零件混放在一起,若第一台车床与第二台车床加工的零件数为\(5:4\)。求
任意地从这些零件中取出一个合格品的概率;
若已知取出的一个零件为合格品,那么,它是由哪一台机床生产的可能性较大。
例 6.23 某实验室在器皿中繁殖成\(k\)个细菌的概率为 \[p_k = \frac{\lambda^k}{k!}e^{-\lambda}, \lambda>0, k=1,2,\dots.\] 并设所繁殖的每个细菌为甲类菌或乙类菌的概率相等,求下列事件的概率:
器皿中所繁殖的全部是甲类菌的概率;
已知所繁殖的全部是甲类菌,求细菌个数为2的概率;
求所繁殖的细菌中有\(i\)个甲类菌的概率。
解. (1) 设\(A=\){所繁殖的全部是甲类菌},\(B_i=\){器皿中繁殖成\(i\)个细菌}。由全概率公式得 \[P(A)=\sum_{k=1}^\infty P(A|B_k)P(B_k)=\sum_{k=1}^\infty (1/2)^kp_k=e^{-\lambda}\sum_{k=1}^\infty\frac{(\lambda/2)^k}{k!}=e^{-\lambda}(e^{\lambda/2}-1).\]
由贝叶斯公式得 \[P(B_2|A)=\frac{P(A|B_2)P(B_2)}{P(A)}=\frac{(1/2)^2p_2}{e^{-\lambda}(e^{\lambda/2}-1)}=\frac{\lambda^2}{8(e^{\lambda/2}-1)}.\]
设\(A_i=\){所繁殖的细菌中有\(i\)个甲类菌},\(B_i=\){器皿中繁殖成\(i\)个细菌}。则有对于\(k\ge i\), \(P(A_i|B_k)=C_k^i/2^k\). 由全概率公式得 \[\begin{aligned} P(A_i)&=\sum_{k=i}^\infty P(A_i|B_k)P(B_k)=\sum_{k=i}^\infty C_k^i2^{-k}p_k\\&=e^{-\lambda}\sum_{k=i}^\infty\frac{(\lambda/2)^k}{i!(k-i)!} =e^{-\lambda}\frac{(\lambda/2)^i}{i!}\sum_{k=i}^\infty\frac{(\lambda/2)^{k-i}}{(k-i)!} \\&=\frac{\lambda^i}{2^ii!}e^{-\lambda/2}. \end{aligned}\]
注:必然事件及不可能事件与任何事件均是独立的。
如果\(P(A)>0\), 则\(P(B|A)=P(B)\Leftrightarrow\)事件\(A,B\)相互独立。
如果\(P(B)>0\), 则\(P(A|B)=P(A)\Leftrightarrow\)事件\(A,B\)相互独立。
若事件对\(A,B\);\(A,\bar{B}\);\(\bar{A},B\);\(\bar{A},\bar{B}\)中有一对相互独立则其它三对亦相互独立。换言之,这四对事件要么都相互独立;要么都不独立。
设\(n\)个事件\(A_1,A_2,\dots,A_n\)相互独立,那么,把其中任意\(m(1\le m\le n)\)个事件相应换成它们的对立事件,则所得的\(n\)个事件仍然相互独立。
注意:\(A_1,A_2,\dots,A_n\)相互独立可以推出它们两两独立,反之不能!反例?
例 6.24 (一个反例) 同时抛掷两个四面体,每个四面体的四个面分别标有1、2、3、4。定义事件 \(A=\){第一个四面体出现偶数};\(B=\){第二个四面体出现奇数};\(C=\){两个四面体同时出现奇数或同时出现偶数}。
不难发现, \[\begin{aligned} P(A)&=P(B)=P(C)=1/2\\ P(AB)&=P(AC)=P(BC)=1/4\\ P(ABC)&=0. \end{aligned}\] 因此,\(A\)与\(B\)相互独立,\(A\)与\(C\)相互独立,\(B\)与\(C\)相互独立,但\(A,B,C\)不相互独立。解. \(A_i=\){元件\(A_i\)能正常工作},设\(B_i=\){元件\(B_i\)能正常工作}。依题得,**
\(P(A_i)=P(B_i)=r\). \(A_i,B_i\), \(i=1,\dots,n\)相互独立。
\[\begin{aligned} P((A_1A_2\dots A_n)\cup (B_1B_2\dots B_n))&=1-P(\overline{A_1A_2\dots A_n}\cap \overline{B_1B_2\dots B_n})\\ &=1-P(\overline{A_1A_2\dots A_n})P(\overline{B_1B_2\dots B_n}) \\&=1-(1-P(A_1A_2\dots A_n))(1-P(B_1B_2\dots B_n)) \\&=1-(1-r^n)^2=r^n(2-r^n). \end{aligned}\]
设\(A_i=\){元件\(A_i\)能正常工作},设\(B_i=\){元件\(B_i\)能正常工作}。依题得,**
\(P(A_i)=P(B_i)=r\). \(A_i,B_i\), \(i=1,\dots,n\)相互独立。
\[\begin{aligned} P\left(\bigcap_{i=1}^n(A_i\cup B_i)\right)&=\prod_{i=1}^{n}P(A_i\cup B_i) =\prod_{i=1}^{n}(1-P(\bar{A}_i\cap \bar{B}_i)) \\&=(1-(1-r)^2)^n=r^n(2-r)^n. \end{aligned}\]
只需比较\(2-r^n\)与\((2-r)^n\)的大小关系。所以,系统II比系统I更可靠。定义 6.4 (独立试验模型) 设有随机试验\(E_1,E_2,\dots,E_n\). 如果对于\(E_i\)的任意结果(事件)\(A_i\), \(i=1,\dots,n\), 都有 \[P(A_1A_2\cdots A_n)=P(A_1)P(A_2)\cdots P(A_n),\] 则称随机试验\(E_1,E_2,\dots,E_n\)相互独立。
特别地,如果这\(n\)个独立试验的条件相同,可能出现的结果也相同,则称为\(n\)重独立试验。若\(n\)重独立试验中的每个试验都只有两种可能的结果,则称为\(n\)重伯努利(Bernoulli)试验。雅各布\(\cdot\)伯努利(Jacob Bernoulli)
伯努利家族3代人中产生了8位科学家。伯努利家族代表人物之一,数学家。被公认的概率论的先驱之一。他是最早使用“积分”这个术语的人,也是较早使用极坐标系的数学家之一。还较早阐明拉随着试验次数的增加,频率稳定在概率附近。他研究了悬链线,还确定了等时曲线的方程。
1994年第22届国际数学家大会在瑞士的苏黎世召开,瑞士邮政发行的纪念邮票的邮票图案是雅各布\(\cdot\)伯努利的头像,以他名字命名的大数定律及大数定律的几何示意图(即当试验次数无限增大时,事件出现的频率稳定于其出现的概率)。 雅可比\(\cdot\)伯努利在数学方面取得了许多重大成果. 例如:他曾对微积分的发展作出了重要贡献;为常微分方程的积分法奠定理论基础;在研究曲线问题方面,他提出了一系列新概念;他创立了变分法;他还是概率论的早期研究者和奠基人。
洛必达法则是雅各布·伯努利的弟弟约翰\(\cdot\)伯努利(Johann Bernoulli, 1667.7.27–1748.1.1)提出的。

Jacob Bernoulli 1654.12.27–1705.8.16
二项概率公式: 设一次试验中,事件\(A\)出现的概率为\(P(A)=p, (0<p<1)\),则在\(n\)重伯努利试验中,事件\(A\)恰好出现\(k\)次的概率为
\[b(k;n,p)=C_n^k p^k (1-p)^{n-k},\ k=0,\dots,n.\]
注:\(\sum_{k=0}^n b(k;n,p) =\sum_{k=0}^n C_n^k p^k (1-p)^{n-k} = 1\).
十年中你从未中奖很正常嘛!
解. 将每名患者用药治疗作为一次试验,那么\(10\)名患者用药就是\(10\)重伯努利试验,由二项概率公式得,至少有\(6\)人治愈的概率为
\[P=\sum_{k=6}^{10} b(k;10,0.8)=\sum_{k=6}^{10} C_{10}^k 0.8^k0.2^{10-k}\approx 0.97.\]