第 5 章 方差分析
5.1 引言
在工业生产或者实验中经常要比较若干个因素对业务指标的影响。比如,为了比较药物A,B,C对治疗某疾病的疗效,我们将实验对象分成三组,分别记录服用三种药物的治疗效果,得到三组样本
\[X_1,\dots,X_{n_1};\ Y_1,\dots,Y_{n_2};\ Z_1,\dots,Z_{n_3}.\]
通过这些实验数据,我们希望回答:
这三种药物对治疗该疾病有没有显著差异;
如果有差异,哪种药物治疗效果最好?
这个例子中,药物称为因子,A,B,C称为该因子的水平。
由于这个实验只涉及单个因子——“药物”,我们称之为单因子实验。此外,如果比较不同的药物和性别对疗效的影响,这就是两因子实验。不难推广到多因子实验。
本章介绍方差分析方法(Analysis of Variance, ANOVA),研究因子不同水平的差异性,不同因子交互作用的显著性。这些研究有助于搭配有利于指标的不同因子的水平。虽然本章叫做方差分析,但实际上关心的是不同总体的均值比较,而不是它们的方差。
5.2 单因子方差分析
单因子实验设计(one-way layout)在一个因子的不同水平下分别进行独立的观测,是两个独立样本比较方法的推广。
模型假设:考虑一个因子A,有\(r\)个水平\(A_1,\dots,A_r\), \(r\ge 2\). 设在水平\(A_i\)下重复进行了\(n_i\)次实验(\(n_i\ge2\)),数据是\(y_{i1},y_{i2},\dots,y_{in_i}\). 假设这些数据之间相互独立且\(y_{ij}\sim N(\mu_i,\sigma^2)\),其中\(\sigma\)未知。我们关心的问题是\(\mu_i\)是否全相等,即要检验
\[H_0:\mu_1=\dots=\mu_r\ vs.\ H_1:\mu_i\text{不全相等}.\]
令\(n=\sum_{i=1}^r n_i\),
\[\bar y = \frac{1}{n}\sum_{i=1}^r\sum_{j=1}^{n_i}y_{ij},\ \bar y_{i\cdot}=\frac 1{n_i}\sum_{j=1}^{n_i}y_{ij},i=1,\dots,r.\]
这里\(\bar y\)表示所有观测的平均值,\(\bar y_{i\cdot}\)表示水平\(A_i\)下的观测平均值。令
\[S_T^2=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar y )^2,\ S_e^2=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar y_{i\cdot} )^2,\]
\[S_A^2 = \sum_{i=1}^r n_i(\bar y_{i\cdot} -\bar y)^2.\]
其中,\(S_T^2\)刻画全部数据的波动程度,\(S_e^2\)刻画组内数据的波动程度,\(S_A^2\)刻画不同组均值的差异引起的波动程度。这三者满足以下三角分解:
\[S_T^2 = S_e^2+S_A^2.\]
这是由于
\[\begin{align*} S_T^2&=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar y_{i\cdot}+\bar y_{i\cdot}-\bar y )^2\\ &=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar y_{i\cdot})^2+\sum_{i=1}^r\sum_{j=1}^{n_i}(\bar y_{i\cdot}-\bar y )^2+2\sum_{i=1}^r(\bar y_{i\cdot}-\bar y )\sum_{j=1}^{n_i}(y_{ij}-\bar y_{i\cdot})\\ &=S_e^2+S_A^2. \end{align*}\]
这表明,总的平方和等于组内平方和加上组间平方和。注意到\(\bar y_{i\cdot}\)是\(\mu_i\)的无偏估计,如果\(H_0\)成立,\(\bar y_{i\cdot}\)应该接近,那么\(S_A^2\)相对\(S_e^2\)小得多。也就意味着两者的比值\(S_A^2/S_e^2\)大到一定程度就有理由拒绝\(H_0\). 为给出确切的拒绝域, 我们需要知道在\(H_0\)成立下,\((S_A^2, S_e^2)\)的分布。
定理 5.1 考虑上述模型假设,有\(S_e^2/\sigma^2\sim \chi^2(n-r)\)且\(S_e^2\)与\(S_A^2\)独立。如果\(H_0:\mu_1=\dots=\mu_r\)成立,则有
\[\frac{S_A^2}{\sigma^2}\sim \chi^2(r-1),\ F=\frac{S_A^2/(r-1)}{S_e^2/(n-r)}\sim F(r-1,n-r).\]
证明. 由单个正态总体的抽样分布定理有,
\[V_i:=\frac{1}{\sigma^2} \sum_{j=1}^{n_i}(y_{ij}-\bar y_{i\cdot} )^2\sim \chi^2(n_i-1).\]
由于\(y_{ij}\)之间独立, 所以\(V_i\)相互独立。由卡方分布的可加性,我们有\(S_e^2/\sigma^2=\sum_{i=1}^r V_i\sim \chi^2(n-r)\). 此外,\(\{V_1,\dots,V_r\}\)与\((\bar y_{1\cdot},\dots,\bar y_{r\cdot})\)独立。注意到\(S_A^2\)为\(\bar y_{i\cdot}\)的函数,所以\(S_e^2\)与\(S_A^2\)独立。 当\(\mu_1=\dots=\mu_r=\mu\)成立时,\(\bar y_{i\cdot}\stackrel{iid}{\sim} N(\mu,\sigma^2/n_i)\). 令\(x_i = \sqrt{n_i}(\bar y_{i\cdot}-\mu)/\sigma\stackrel{iid}\sim N(0,1)\). 注意到,
\[\begin{align*} S_A^2&=\frac{\sum_{i=1}^rn_i(\bar y_{i\cdot} -\bar y)^2}{\sigma^2}\\ &=\frac{\sum_{i=1}^r(\sqrt{n_i}\bar y_{i\cdot} -\sqrt{n_i}\sum_{j=1}^r \frac{n_j}{n}\bar y_{j\cdot} )^2}{\sigma^2}\\ &=\frac{\sum_{i=1}^r[\sqrt{n_i}(\bar y_{i\cdot}-\mu) -\sqrt{n_i}\sum_{j=1}^r \frac{n_j}{n}(\bar y_{j\cdot}-\mu) ]^2}{\sigma^2}\\ &=\sum_{i=1}^r(x_i-\sqrt{n_i}\sum_{j=1}^r \frac{\sqrt{n_j}}{n}x_j)^2\\ &=\sum_{i=1}^rx_i^2-(\sum_{i=1}^r\sqrt{n_i/n} x_i)^2\\ &=||x_{1{:}r}||^2-(\alpha^\top x_{1{:}r})^2, \end{align*}\] 其中\(\alpha=(\sqrt{n_1/n},\dots,\sqrt{n_r/n})^\top\). 注意到\(||\alpha||=1\),参考定理1.4的证明,可以构造一个正交矩阵\(A\)使得\(A\)的第一行为\(\alpha^\top\)。令\(z_{1{:}r}=Ax_{1{:}r}\sim N(0,I_r)\),此时,\(||z_{1{:}r}||^2=||x_{1{:}r}||^2\), \(z_1=\alpha^\top x_{1{:}r}\). 所以,
\[S_A^2=||z_{1{:}r}||^2-z_1^2=\sum_{i=2}^r z_i^2\sim \chi^2(r-1).\]
由于\(S_e^2\)与\(S_A^2\)独立,所以\(F\sim F(r-1,n-r).\)为此,我们采用F检验,拒绝域为\(W=\{F>F_{1-\alpha}(r-1,n-r)\}\). 这种方法为方差分析法,是R. A. Fisher在1923年提出来的。在实践中常用以下方差分析表格。
| 来源 | 自由度 | 平方和 | 均方和 | \(F\)值 | P值 |
|---|---|---|---|---|---|
| 因子A | \(r-1\) | \(S_A^2=\sum_{i=1}^r n_i(\bar y_{i\cdot} -\bar y)^2\) | \(S_A^2/(r-1)\) | \(\frac{S_A^2/(r-1)}{S_e^2/(n-r)}\) | |
| 误差 | \(n-r\) | \(S_e^2=\sum_{i=1}^r\sum_{j=1}^{n_i}(y_{ij}-\bar y_{i\cdot} )^2\) | \(S_e^2/(n-r)\) | ||
| 总和 | \(n-1\) | \(S_T^2=\sum_{i=1}^I\sum_{j=1}^{n_i}(y_{ij}-\bar y )^2\) | \(S_T^2/(n-1)\) |
| 菌型 | 存 | 活 | 天 | 数 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 3 | 2 | 4 | 7 | 7 | 2 | 2 | 5 | 4 | |
| 2 | 5 | 6 | 8 | 5 | 10 | 7 | 12 | 12 | 6 | 6 | ||
| 3 | 7 | 11 | 6 | 6 | 7 | 9 | 5 | 5 | 10 | 6 | 3 | 10 |
方差分析R的关键命令为aov(model,data....)与lm类似,详细如下:
library(ggplot2)
mouse <- data.frame(
X = c(2, 4, 3, 2, 4, 7, 7, 2, 2, 5, 4,
5, 6, 8, 5, 10, 7, 12, 12, 6, 6,
7, 11, 6, 6, 7, 9, 5, 5, 10, 6, 3, 10),
A = factor(rep(1:3,c(11,10,12)))
)
ggplot(mouse,aes(A,X,fill=A)) + geom_boxplot()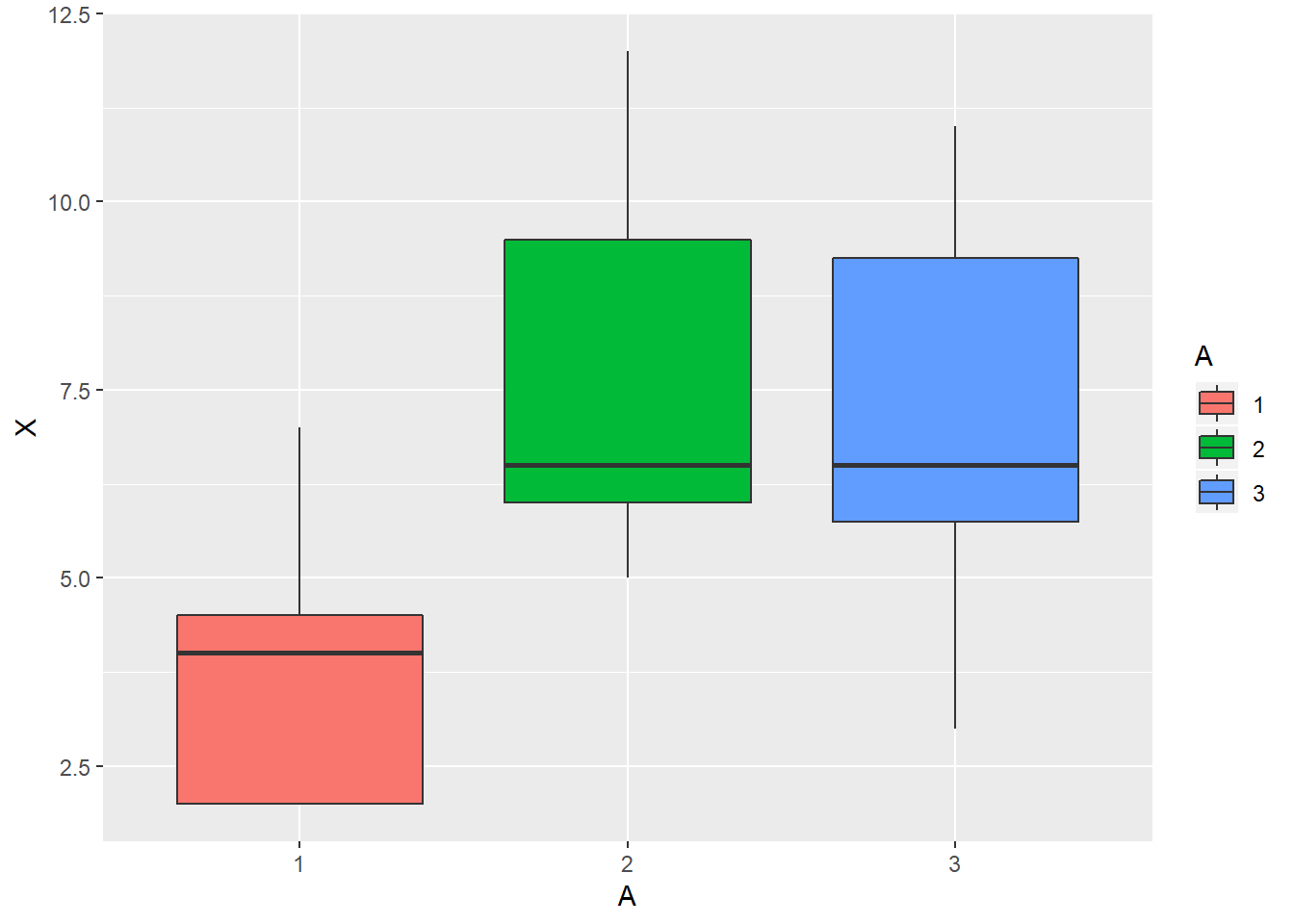
图 5.1: 箱线图
## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 94.3 47.1 8.48 0.0012 **
## Residuals 30 166.7 5.6
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1从中发现,\(p=0.0012\),在显著水平\(\alpha=0.05\)下拒绝\(H_0\),即认为注射三种菌型后的平均存活天数有显著差异。
5.3 两因子方差分析
两因子实验设计(two-way layout)研究两个因子在不同水平下的交互作用。
模型假设:考虑因子A有\(r\)个水平:\(A_1,\dots,A_r\), \(r\ge 2\),因子B有\(s\)个水平:\(B_1,\dots,B_s\), \(s\ge 2\)。 设在水平\((A_i,B_j)\)下重复进行了\(n_{ij}\)次实验(\(n_{ij}\ge2\)),数据是\(y_{ij1},y_{ij2},\dots,y_{ijn_{ij}}\). 假设这些数据之间相互独立且\(y_{ijk}\sim N(\mu_{ij} ,\sigma^2)\),其中\(\sigma\)未知。为分析各个因子对指标的影响,令
\[\mu = \frac{1}{rs}\sum_{i=1}^r\sum_{j=1}^s \mu_{ij},\]
\[\alpha_i = \frac 1 s\sum_{j=1}^s \mu_{ij}-\mu,\ i=1,\dots,r,\]
\[\beta_j = \frac 1 r \sum_{i=1}^r \mu_{ij}-\mu,\ j=1,\dots,s,\]
\[\lambda_{ij} = \mu_{ij}-\mu-\alpha_i-\beta_j.\]
于是,模型可以表示为
\[y_{ijk} = \mu+ \alpha_i+\beta_j +\lambda_{ij}+\epsilon_{ijk},\ \epsilon_{ijk}\stackrel{iid}{\sim}N(0,\sigma^2),\]
其中\(\alpha_i\)表示因子A的第\(i\)个水平\(A_i\)的“主效应”,\(\beta_j\)表示因子B的第\(j\)个水平\(B_j\)的“主效应”,\(\lambda_{ij}\)表示\(A_i\)和\(B_j\)下的交互作用的效应。
我们关心因子A或者因子B或者它们的交互作用(记为\(A\times B\))对指标有没有影响。对应的检验问题为
\[H_0:\alpha_1=\dots=\alpha_r=0\ vs.\ H_1:\alpha_i\text{不全为0},\]
\[H_0:\beta_1=\dots=\beta_s=0\ vs.\ H_1:\beta_j\text{不全为0},\]
\[H_0:\lambda_{11}=\dots=\lambda_{rs}=0\ vs.\ H_1:\lambda_{ij}\text{不全为0}.\]
记\(n_{i\cdot} = \sum_{j=1}^s n_{ij},\ n_{\cdot j} =\sum_{i=1}^r n_{ij},\ n = \sum_{i=1}^r\sum_{j=1}^s n_{ij}\). 类似地,我们有相应的方差分析表:
| 来源 | 自由度 | 平方和 | \(F\)值 | P值 |
|---|---|---|---|---|
| A | \(r-1\) | \(S_A^2=\sum_{i=1}^r n_{i\cdot}(\bar y_{i\cdot\cdot} -\bar y)^2\) | \(\frac{S_A^2/(r-1)}{S_e^2(n-rs)}\) | |
| B | \(s-1\) | \(S_B^2=\sum_{j=1}^s n_{\cdot j}(\bar y_{\cdot j\cdot} -\bar y)^2\) | \(\frac{S_B^2/(s-1)}{S_e^2/(n-rs)}\) | |
| \(A\times B\) | \((r-1)(s-1)\) | \(S_{AB}^2=\sum_{i=1}^r\sum_{j=1}^s n_{ij}(\bar y_{ij\cdot} -\bar y)^2\) | \(\frac{S_{AB}^2/[(r-1)(s-1)]}{S_e^2/(n-rs)}\) | |
| 误差 | \(n-rs\) | \(S_e^2=\sum_{i=1}^r\sum_{j=1}^{s}\sum_{k=1}^{n_{ij}}(y_{ijk}-\bar y_{ij\cdot})^2\) | ||
| 总和 | \(n-1\) | \(S_T^2=\sum_{i=1}^r\sum_{j=1}^{s}\sum_{k=1}^{n_{ij}}(y_{ijk}-\bar y )^2\) |
| \(A_1\) | \(A_2\) | \(A_3\) | |
|---|---|---|---|
| \(B_1\) | 23, 25, 21, 14, 15 | 28, 30, 19, 17, 22 | 18, 15, 23, 18, 10 |
| \(B_2\) | 20, 17, 11, 26, 21 | 26, 24, 21, 25, 26 | 21, 25, 12, 12, 22 |
| \(B_3\) | 16, 19, 13, 16, 24 | 19, 18, 19, 20, 25 | 19, 23, 22, 14, 13 |
| \(B_4\) | 20, 21, 18, 27, 24 | 26, 26, 28, 29, 23 | 22, 13, 12, 22, 19 |
tree <- data.frame(
Y = c(23, 25, 21, 14, 15,
28, 30, 19, 17, 22,
18, 15, 23, 18, 10,
20, 17, 11, 26, 21,
26, 24, 21, 25, 26,
21, 25, 12, 12, 22,
16, 19, 13, 16, 24,
19, 18, 19, 20, 25,
19, 23, 22, 14, 13,
20, 21, 18, 27, 24,
26, 26, 28, 29, 23,
22, 13, 12, 22, 19),
A = gl(3,5,60,labels = paste0("A",1:3)),
B = gl(4,15,60,labels = paste0("B",1:4))
)
tree.aov <- aov(Y~A*B,tree)
summary(tree.aov)## Df Sum Sq Mean Sq F value Pr(>F)
## A 2 353 176.3 8.96 0.00049 ***
## B 3 88 29.2 1.48 0.23108
## A:B 6 72 12.0 0.61 0.72289
## Residuals 48 944 19.7
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1| A | mean | variance |
|---|---|---|
| A1 | 19.55 | 20.37 |
| A2 | 23.55 | 15.63 |
| A3 | 17.75 | 22.09 |
由此可得,在显著水平\(\alpha=0.05\)下,树种效应\(A\)是显著的,地理位置效应\(B\)及相互效应\(A\times B\)并不显著。由于树种效应是显著的,所以选择什么树种对树的生长很重要,计算树种因子的平均值,如上表所示。从中可以看出,第二种树种对生长有利。同样地,我们可以计算地理位置因子的平均值,只不过该因子对生长有没有显著的影响。
5.4 小结
本章主要介绍了方差分析法来研究因子是否显著影响指标。如果发现某因子影响显著,我们可以进一步分析该因子的哪些水平存在差异性,哪些有利于指标。此时就要两两比较不同水平的差异性,如第三章提到的两样本t检验方法。
此外,本章考虑的是全面实验的情形,即各个因子的所有水平组合都安排实验,得到相应的观测数据。然而,当因子比较多,水平数量比较多时,这种全面实验就不合适了,因此需要合理设计实验,挑选出一些有代表性的组合进行实验,这属于实验设计的内容。感兴趣可以参考陈家鼎等编著的教材的第五章。