Chapter 18 补充3:效应量和元分析
18.1 效应量简介
我们今天讲的内容,是在本科心理统计学没有讲的一个很重要的统计学概念——效应量。
今天的这个课程是给大家打一些基础,关于效应量和元分析的一些基础知识。并不是说上完这门课之后,大家就会有一个分析或者说能够熟练的去计算各种各样的效应量。因为大家后面会看到效应量的软件分析,其实很依赖整个研究问题和context。所以如何去解读效应不是一个技术的问题,这既需要懂得统计的方法,也需要你对研究领域很熟悉。提到效应量大家一定会想到Cohen’s
d,实际上对效应量的定义是,研究者感兴趣的任何的效应量,只要研究者对它感兴趣,觉得它有意义,就可以认为它是研究中得效应量。所以效应量本质上就是效应的量(effects)。
心理学研究中的效应量通常是Cohen’s
d,因为很多时候是比较不同组之间的差异,而不同组之间的差异进行比较的时候,我们希望摆脱它原始单位的影响,使之成为某种程度上没有单位的标准化统计量。而在其他的领域,很多时候关注点不一定在这种标准化的效应量。比方说,我们有的时候会看到,家庭的背景如何影响子女的教育成就。教育学的研究者不会关心标准化的效应量是多少。汇报Cohen’s
d等于0.2或者0.4很难去解读它的实际意义。在这种情况下,变化家庭的收入,如每个月多1000元,子女的教育年限会如何增加,就可以把子女的教育用受教育的年份来进行一个量化,把家庭背景用诸如收入水平来进行量化。最后考察的是家庭收入对子女接受教育年限的影响,用年份或学位进行量化。这种研究直接以实际的这个生活中的这个效应作为效应量,而不是以quantity或者相关系数为效应量。所以首先大家一定要明确,效应量不是一个统计的指标,而是一个大家感兴趣的量。
在心理学的研究当中的话常常会碰到三大效应量:
- d-family(difference family):如Cohen’s d, Hedges’ g
- r-family(correlation family):如Pearson r, \(R^2\), \(\eta^2\), \(\omega^2\), & f
- OR-family(categorical family):如odds ratio (OR), risk ratio(RR)
这些指标既说明两个变量之间有怎样的相关,也说明了某一个效应所解释的变异在总体的变异当中占多大的比例。不同的研究领域用的效应量也不一样。相对来说相关系数是最通用的,它会比d-family更加通用。如果大家看
Psychological Bulletin,心理学领域元分析发表很多的期刊,影响力非常高,它上面很多元分析都是以相关系数做为effect
size。
2011年General of Experimental Psychology
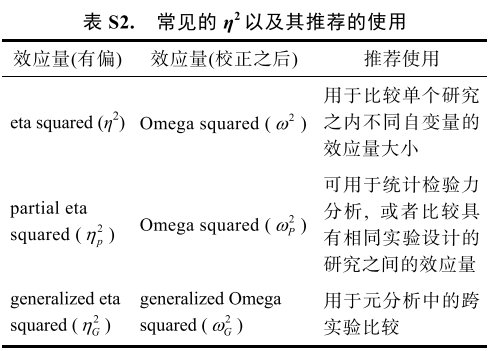
General杂志专门回顾了发表的文章中报告的效应量。其中发现了一个非常有趣的效应,报告最多的其实是Partial
\(\eta\) Squared,即\(\eta^{2}_{p}\),很重要的原因是SPSS输出这个效应量。
Lakens, D. (2013). Calculating and reporting effect sizes to
facilitate cumulative science: A practical primer for t-tests and
ANOVAs. Frontiers in Psychology, 4, 863. 这篇文章报告了各种不同Cohen’s
d的计算方式
推荐在研究中既报告效应量,也报告这个效应量的置信区间
- SPSS提供\(\eta^{2}_{p}\)
- JASP提供Cohen’s d,\(\eta^{2}_{p}\),\(\eta^{2}_{G}\)
Lakens(Lakens,2013)提供了基于excel的计算程序,帮助心理学家方便的得到不同的效应量及其置信区间。
Gpower也可以计算效应量,但其输出的\(\eta^{2}_{p}\)与SPSS是不一样的,需要转换。
效应量的估计最终回归到了统计中一个非常重要的概念:点估计。存在点估计也就不得不提到区间估计。所以说有效应量的点估计就会有95%的自行区间
这个参数估计啊或者点估计 在2012年的时候Cumming(Cumming, 2012)
在一本书讲到,我们应该不仅仅使用P值 还要使用effect size,confidence
interval和meta-analysis这三个统计指标。它们都有一个共同特点——estimation
based,即专门基于估计。
与传统的基于P值二分法相比,基于估计的指标不仅可以看到效应量是否显著,也能看到效应量的具体大小,是把心理学研究和现实的因素关联的很重要的点。例如某个效应很显著,但是其效应量非常微弱,它在社会层面便没有任何意义。有时一个非常小的效应,没有任何坏处且成本很低,当它被实施,会改变一部分人的命运,这个时候或许可以考虑把这个方法应用到现实世界。在解读效应量的时候,注意避免简单的使用所谓的small,medium和large等effect size对Cohen’s d评价,不管它的效应、样本量、研究背景等等。
18.2 算法实现
如何去计算单个研究中或单个样本中的效应量、置信区间以及如何将它们综合起来。下面先给出公式:
独立样本t-test:
\[Cohen's \ d_s = \frac{X_1 - X_2}{\sqrt{SD_{pool}}} = \frac{X_1 - X_2}{\sqrt{\frac{(n_1 -1)SD_1^2 + (n_2-1)SD_2^2)}{n_1+n2-2}}}\]
\[Hedges's \ g_s = Cohen's \ d_s \times (1 - \frac{3}{4(n_1 + n_2) - 9}) \]
配对样本t-test:
\[Cohen's \ d_{rm} = \frac{M_{diff}}{\sqrt{SD_1^2 + SD_2^2 -2 \times r \times SD_1 \times SD_2}} \times \sqrt{2(1-r)} \]
\[Cohen's \ d_{av} = \sqrt{ \frac {M_{diff}} {(SD_1 + SD_2)/2}} \]
接下来尝试计算Cohen’s d,以match数据为例 选定感兴趣的效应量:
Match条件下好我与好人的平均反应时间差异,即自我在好的情况下,它的优势效应
首先还是导入数据:
rm(list = ls())
if (!requireNamespace("pacman", quietly = TRUE)) {
install.packages("pacman") } # # 检查是否已安装 pacman, 如果未安装,则安装包
pacman::p_load("tidyverse", "easystats") # 使用p_load来载入需要的包
df.mt.raw <- read.csv('./data/match/match_raw.csv', # load data:
header = T, sep=",", stringsAsFactors = FALSE)应用11章的预处理数据:
# from chapter 11, Chunk 3
df.mt.rt.subj <- df.mt.raw %>%
dplyr::filter(ACC == 1 & RT > 0.2) %>%
tidyr::extract(Shape, into = c("Valence", "Identity"),
regex = "(moral|immoral)(Self|Other)", remove = FALSE) %>%
dplyr::mutate(Valence = case_when(Valence == "moral" ~ "Good",
Valence == "immoral" ~ "Bad"),
RT_ms = RT * 1000) %>%
dplyr::mutate(Valence = factor(Valence, levels = c("Good", "Bad")),
Identity = factor(Identity, levels = c("Self", "Other"))) %>%
dplyr::group_by(Sub, Match, Identity, Valence) %>%
dplyr::summarise(RT_mean = mean(RT_ms)) %>%
dplyr::ungroup()
head(df.mt.rt.subj, 5)## # A tibble: 5 × 5
## Sub Match Identity Valence RT_mean
## <int> <chr> <fct> <fct> <dbl>
## 1 7302 match Self Good 694.
## 2 7302 match Self Bad 702.
## 3 7302 match Other Good 598.
## 4 7302 match Other Bad 666.
## 5 7302 mismatch Self Good 755.对于我们感兴趣的效应量,计算需要知道五个变量:条件1的主水平RT、条件2主水平RT、条件1的主水平SD、条件2的主水平SD以及相关系数(可以用每个被试在两个条件之间的反应时间做一个相关)。
# from chapter 11, Chunk 3
df.mt.rt.subj.effect <- df.mt.rt.subj %>%
dplyr::filter(Match == "match" & Valence == "Good") %>%
dplyr::group_by(Identity) %>%
dplyr::summarise(mean = mean(RT_mean),
sd = sd(RT_mean))
df.mt.rt.subj.effect.wide <- df.mt.rt.subj %>%
dplyr::filter(Match == "match" & Valence == "Good") %>%
tidyr::pivot_wider(names_from = "Identity", values_from = "RT_mean")
corr_est <- cor(df.mt.rt.subj.effect.wide$Self, df.mt.rt.subj.effect.wide$Other)得到变量后,将Cohen’s drm公式转化为代码:
Cohens_d_manu <- ((df.mt.rt.subj.effect$mean[1] - df.mt.rt.subj.effect$mean[2])/sqrt(df.mt.rt.subj.effect$sd[1]**2 + df.mt.rt.subj.effect$sd[2]**2 - 2*corr_est*df.mt.rt.subj.effect$sd[1]*df.mt.rt.subj.effect$sd[2]))*sqrt(2*(1-corr_est))
Cohens_d_manu## [1] -0.56768也可以使用其他方法计算,发现得到不同的效应量,原因是公式并不一致。
SelfOther_diff <- t.test(df.mt.rt.subj.effect.wide$Self, df.mt.rt.subj.effect.wide$Other, paired = TRUE)
effectsize::effectsize(SelfOther_diff, paired = TRUE)## d | 95% CI
## ----------------------
## -0.48 | [-0.80, -0.17]所以在调用R包时一定要注意查看其内部公式!
18.4 元分析简介
想象你自己做了一个治疗研究,在平均主义这个框架之下,我们会通常认为真实的世界中存在对于该研究特定的效应量。假如这个研究被一万次重复,就会得到一万个效应,且这一万个效应会趋向于一个真实的情况,你的治疗方法是不是比没有治疗过程或选用其他的旧的治疗方法更有效率。 虽然说这个假定可能不合理,但是平均主义就是这样的假定。
假如说有很多人同时在不同地方做类似实验,把这些效应拿过来,对它们进行综合。本质上,某种程度这些实验关注着同一个效应,综合之后应该能够得到一个对真实的更好的估计,在统计过程当中是这样。所以就有了一个对效应量的综合方法——元分析。
元分析是一个统计方法,从这个角度来讲,是对已经存在的多个效应量,通过统计的方法把它进行综合。综合时需要效应量,相关系数R或者是Cohen’s d, 同时我们也需要效应量的估计误差作为权重。接下来都是技术的问题。
怎么去算这个权重呢? 在不同的方法里面或者不同的模型里面,会有自己的具体计算公式。很多时候,如果大家不想了解细节的话,可以不用去管它。如果想了解细节的话,可以去看权重到底是如何确定的。一般来说传统的元分析模型,是通过效应量变异大小的导数对它进行加权。例如对标准差的平方求导数,然后进行加权。当然还会有其他的方法,这里就不细致的展开。
元分析也是一种文章类型,例如之前提到的psychological bulletin,具有很高的影响因子。但也存在问题,有的时候元分析不被认为是实证的研究,因为其没有太多的创新性。
18.5 元分析实现
下面展示一下如何在自己已有的数据中,用R来做一个简单元分析:
把数据分成两部分, 一部分21名被试,一部分23名被试。
subjs <- unique(df.mt.rt.subj$Sub)
set.seed(1234)
subj_ls1 <- sample(subjs, 21)
df.mt.rt.subj.ls1 <- df.mt.rt.subj %>%
dplyr::filter(Sub %in% subj_ls1)
df.mt.rt.subj.ls2 <- df.mt.rt.subj %>%
dplyr::filter(!(Sub %in% subj_ls1))假定两组数据分别为实验1a与实验1b,并计算两个实验同样条件下的效应量。 与上文中计算效应量的方式一致,首先计算均值等所需变量:
## effect size of group 1
df.mt.rt.subj.effect.ls1 <- df.mt.rt.subj.ls1 %>%
dplyr::filter(Match == "match" & Valence == "Good") %>%
dplyr::group_by(Identity) %>%
dplyr::summarise(mean = mean(RT_mean),
sd = sd(RT_mean)) %>%
dplyr::ungroup() %>%
tidyr::pivot_wider(names_from = Identity,
values_from = c(mean, sd))
colnames(df.mt.rt.subj.effect.ls1) <- c("Self_RT_M_mean","Other_RT_M_mean",
"Self_RT_M_sd", "Other_RT_M_sd")
df.mt.rt.subj.effect.ls1.wide <- df.mt.rt.subj.ls1 %>%
dplyr::filter(Match == "match" & Valence == "Good") %>%
tidyr::pivot_wider(names_from = "Identity", values_from = "RT_mean")
corr_est.ls1 <- cor(df.mt.rt.subj.effect.ls1.wide$Self, df.mt.rt.subj.effect.ls1.wide$Other)
df.mt.rt.subj.effect.ls1$Sample_size <- length(unique(df.mt.rt.subj.ls1$Sub))
df.mt.rt.subj.effect.ls1$ri <- corr_est.ls1## effect size of group 2
df.mt.rt.subj.effect.ls2 <- df.mt.rt.subj.ls2 %>%
dplyr::filter(Match == "match" & Valence == "Good") %>%
dplyr::group_by(Identity) %>%
dplyr::summarise(mean = mean(RT_mean),
sd = sd(RT_mean)) %>%
dplyr::ungroup() %>%
tidyr::pivot_wider(names_from = Identity,
values_from = c(mean, sd))
colnames(df.mt.rt.subj.effect.ls2) <- c("Self_RT_M_mean","Other_RT_M_mean",
"Self_RT_M_sd", "Other_RT_M_sd")
df.mt.rt.subj.effect.ls2.wide <- df.mt.rt.subj.ls2 %>%
dplyr::filter(Match == "match" & Valence == "Good") %>%
tidyr::pivot_wider(names_from = "Identity", values_from = "RT_mean")
corr_est.ls2 <- cor(df.mt.rt.subj.effect.ls2.wide$Self, df.mt.rt.subj.effect.ls2.wide$Other)
df.mt.rt.subj.effect.ls2$Sample_size <- length(unique(df.mt.rt.subj.ls2$Sub))
df.mt.rt.subj.effect.ls2$ri <- corr_est.ls2合并数据,计算效应量和效应量的误差,调用R包metafor:
# and nrow with 1
df.mt.meta <- rbind(df.mt.rt.subj.effect.ls1, df.mt.rt.subj.effect.ls2)
df.es <- metafor::escalc(
measure = "SMCRH",
#standardized mean change using raw score standardization with heteroscedastic population variances at the two measurement occasions (Bonett, 2008)
m1i = Self_RT_M_mean,
m2i = Other_RT_M_mean,
sd1i = Self_RT_M_sd,
sd2i = Other_RT_M_sd,
ni = Sample_size,
ri = ri,
data = df.mt.meta
) %>%
dplyr::mutate(unique_ID = c("study1a", "study1b"))我们此时得到了两组数据的效应量以及其误差(Y1:-0.42712,Y2:-0.91145,V1:0.08473,V2:0.12716)
接着建立随机效应模型:
此处应该添加chapter-13meta结果与forest plot
这是最简单的可视化,在发表时还应考虑将图表绘制的更加直观与美观。
其中有许多细节,例如22的实验中,效应量数量为C82=28,在报告时需要选择合适的效应;选择的计算方法(效应量公式)也值得考虑,是手动输入还是函数中自带的公式;在一些报告中只会提供均值与标准差,而不提供相关系数,那么就只能依赖于作者报告的数据选择。
元分析还可以应用于自己的研究中:
- 如果自己手中有许多实验,对这些实验进行效应量计算的工作,能使得实验更加准确(mini metaanalysis)
- 在做预实验时发现效应不够显著,又做了正式实验,可以通过元分析的方式将样本量增加,也能通过元分析判断效应量是否稳定。
在使用Mini Meta-Analysis时不能只把显著的效应综合起来,只把显著效应综合起来的话,效应就被高估了*