Chapter 14 第十三讲：基于网络模型的心理学研究
杜新楷
今天和大家探讨一下基于网络模型的心理学研究。 今天先和大家介绍一下基于潜变量模型的心理学研究，以及经过长时间发展，潜变量模型已经相对成熟，为什么我们还要使用一种新的模型，可以给我们带来什么新的视角和独特的思路？然后介绍基于网络的心理学理论，给大家讲一讲怎么估计、选择网络模型，以及在R中如何实现。最后介绍在网络模型发展的情况下，潜变量模型还有什么意义。
14.1 基于潜变量的心理学研究
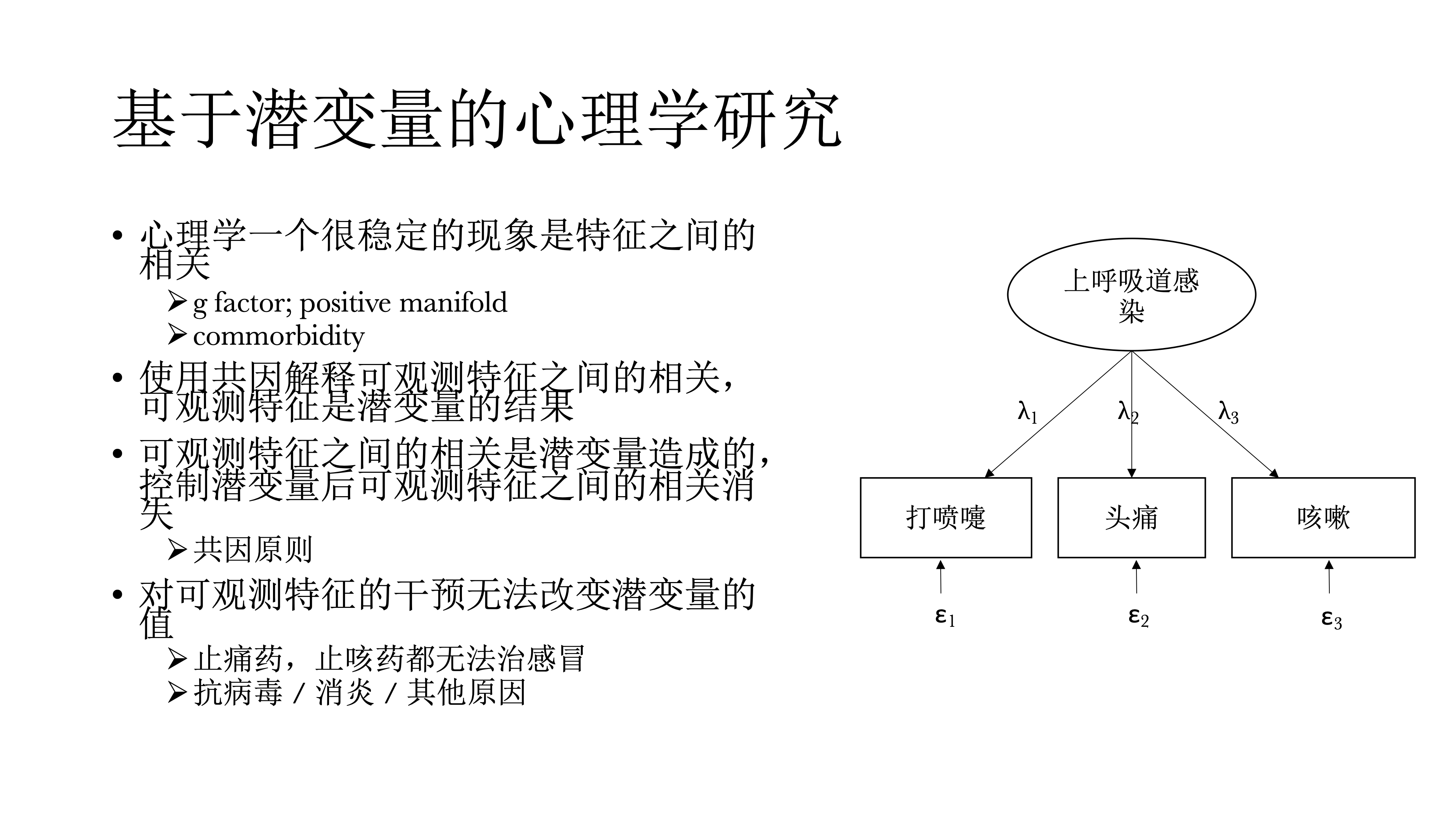
首先，心理学有一个很稳定的现象是什么东西之间都有相关，比如说，在智力的研究中，存在g factor，一个非常稳定的现象是positive manifold，测量智力的所有东西，哪怕测量的是不同的东西，比如测量数学能力、英语能力，他们之间也会有正相关，而且这个正相关非常普遍，他们也是在解释掉这些潜变量，低阶的潜变量之后还会发现一些没有被解释的变异，因而就提出了一个潜变量模型，然后就叫p factor model。在精神病理学里面，也有一种非常常见的现象，就是commorbidity，是指并发症的意思，指精神科病人往往不只有一个病，有抑郁的人往往有焦虑，而有焦虑的人往往有抑郁，很少说一个人只有焦虑或抑郁，单一的诊断其实非常少见。过去基于潜变量的心理学使用共因来解释观测到的特征之间的相关，认为这些可观测的特征是潜变量的结果；可观测特征之间的相关是潜变量造成的，在控制潜变量之后，这些可观测特征之间的相关应该是消失的，这个是根据因果推断中的共因原则。另外对可观测特征的干预是没有办法改变潜变量的值的。比如在感冒的时候，我们往往会打喷嚏还头疼，还咳嗽，这个时候我们不能说吃止痛药或者是吃止咳药都无法治疗感冒，这些只能减轻症状，但不能让感冒好起来，最终还是需要诊断来确定感冒是病毒性感冒还是其他原因，然后针对具体的感冒类型选择治疗方案，如抗病毒或是消炎，这是我们不需要治疗打喷嚏或咳嗽。打喷嚏、咳嗽等就是可观测的特征其实没有意义。
14.2 潜变量模型在心理学的困境
但是这种范式在心理学研究中的困境时，心理学研究对象往往是概念，比如人格之类，是看不见摸不到的东西——如果依据潜变量定义的话。另外，在可观测的潜变量特征之间是存在有意义的因果关系才导致他们之间存在相关。比如说睡不着会导致没精神，而没精神又会导致注意力不集中，而注意力不集中又导致自责，而自责之后又导致睡不着，然后又没精神，从而产生恶性循环，最终可能会导致抑郁。这其实也是网络模型的视角。
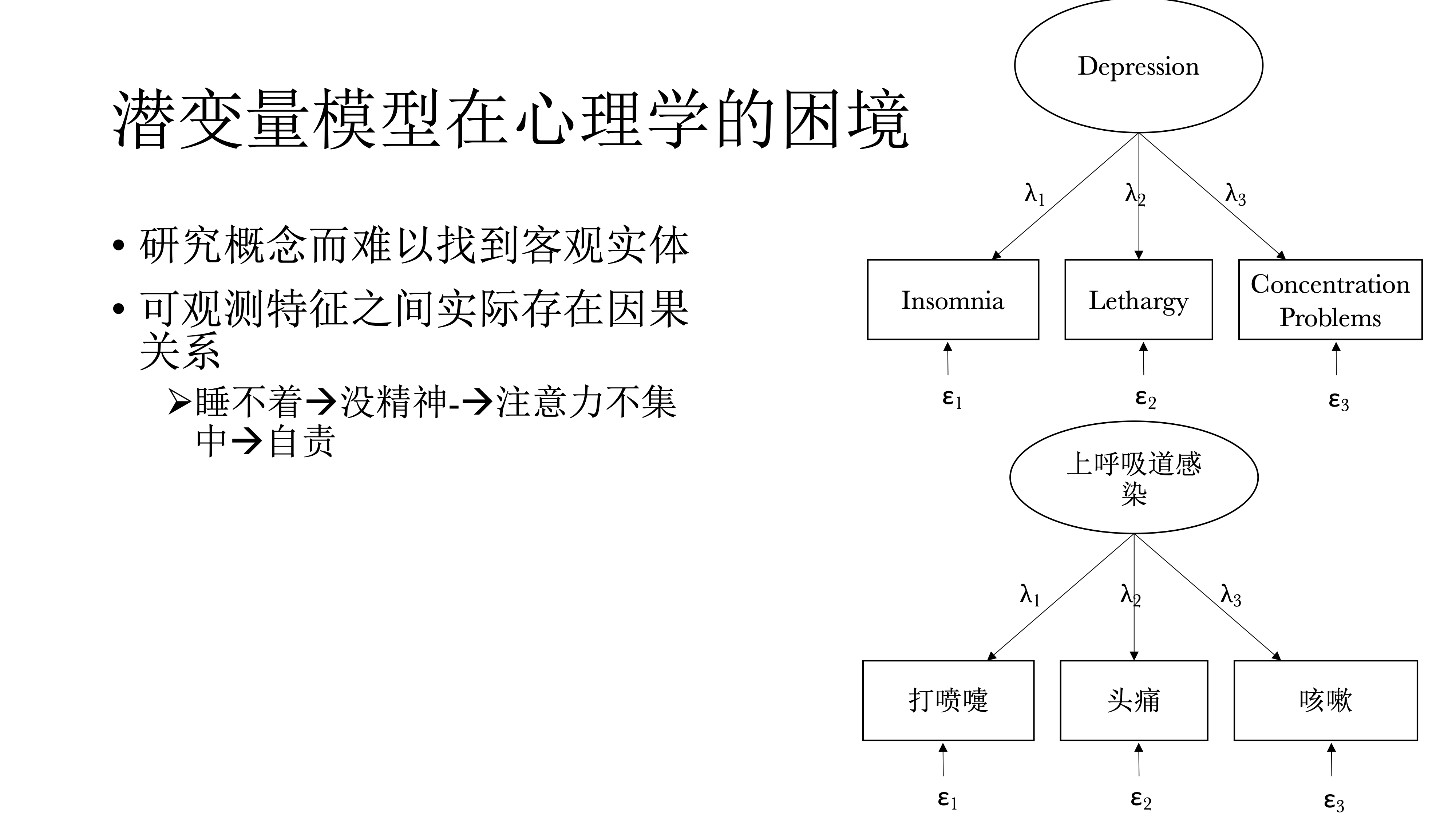
14.3 基于网络的心理学视角
在基于网络的心理学视角中，可观测特征之间的关系是有意义的，对可观测特征的干预也是有效果的。比如对病人的分析发现很多疾病的源头是睡不着觉，就可以给病人开安眠药，然后他可能发现睡眠质量提升一个星期后，其他症状也会有明显改善；比如发现一些人没什么朋友，或者想谈恋爱但是他谈不了，这时可以鼓励他和别人交流，多参加社交场合，有机会认识更多的人。所以说基于网络的心理学视角会关注可观测特征，探索他们之间的因果，关注可观测特征之间的相互作用。网络分析中可观测特征和心理学概念之间的关系与潜变量是相反的：潜变量在因果方向上是从潜变量到可观测的特征，但是在网络分析的视角中，则是可观测变量间相互作用，然后浮现到具体的心理学现象
14.4 如果寻找可观测特征的因果关系
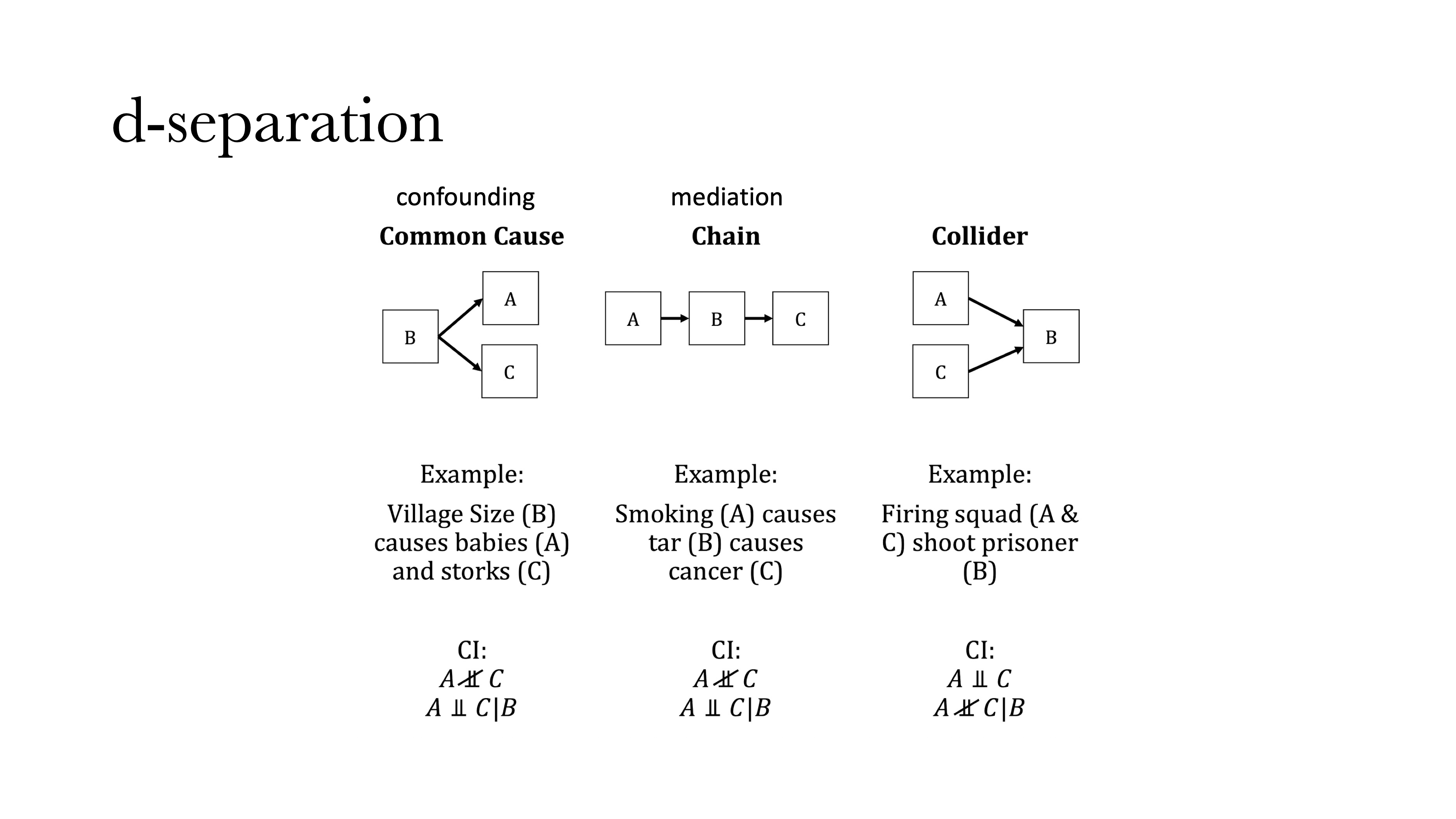
那么我们如何寻找可观测特征之间的因果关系呢？这方面的研究则要归功于Judea Pearl，他做了非常多的有关因果推断的工作，发现我们其实可以从变量之间的偏相关中推断变量间因果关系，这个称为d-separation rule。他发现三种原始的因果图示，所有的偏相关推断因果都归纳为三种基本的图式（共因、链、对撞因子）。
### d-separation
第一个是共因。顾名思义，是两个变量具有共同原因B：如果在没有B的情况下，A和B之间存在相关，但一旦引入并控制B时，A和C的相关就会消失。B还有另外一个名字叫干扰变量(confounding)，和心理学中很多的“假发现”有关系，我们发现两个变量之间存在相关可能是“假相关”，是由于没有控制另外一个变量（B）导致的。举一个例子，一个村子中小孩的数量和鸟的数量存在正相关，但这并不是因为孩子会生鸟或鸟会生孩子，这是因为无论鸟的数量还是孩子的数量都与村子大小有关——村子更大会使得孩子和鸟都会更多。在下方图中，B到A和C都有一个箭头，而这个箭头则反应因果的方向。
另外一个情况叫链（Chain），也叫中介。比如吸烟会导致癌症，但吸烟本身不会导致癌症，而是烟里面的焦油会致癌，因此如果将烟里面的焦油给过滤掉，那么烟的致癌率会大大下降。这也是我们在做中介分析中会做的事情，就是说先分析A和C之间的相关，然后引入B之后，看A和C之间的相关会不会消失或变小。
第三种情况是对撞(Collider)，这种情况大家相对陌生，是指A和C之间本来没有相关，但是在引入B之后会产生相关，而且这种相关永远是负相关。举一个例子，A和C两个人去射击，如果已知A开枪或没开抢，这个信息对于知道C是否开枪是没有任何帮助的；但如果A和C是要处决B，且B已经死亡，即控制第三个变量（即B是否死亡），这个时候就可以通过A是否开枪来判断C是否开枪，因为这时如果不是A开的枪那么就一定是C开的枪，这是A和C之间就会产生负相关。
14.5 DAG（贝叶斯网络）
上面其实体现了有向无环图的构建。在图中，圆圈内的字母表示某一可观测的特征，称之为节点(node)，而不同圆圈（可观测特征）之间的连线称之为边(edge)，而而边上的箭头则表示因果关系的方向，因而成为有向无环图(Directed Acyclic Graph)。
DAG通过拼接因果关系的图示来寻找边，起点永远是一个偏相关网络；可以发现对撞因子是有唯一解的——如果A和C之间没有相关，但是引入B之后存在相关，就可以推断出某个因子一定是对撞因子，也一定知道方向一定是从A到B，从C到B。但如果是Common Cause或Chain的时候，这两个偏相关模式是一样的，没有办法进行区分——比如对于Common Cause来说，B到A和A到B在统计上是没有办法区分的，这也会导致DAG有非常多等价模型问题，好处是在模型有唯一解的情况下，可以很直接的看到因果关系的方向。
也可以通过总结的方式来进行观察，在多少个循环里面、或在多少个样本里面方向到底如何，但具体确认还是很困难。在R中可以使用bnlearn进行实现，教程见下面的引用文献。
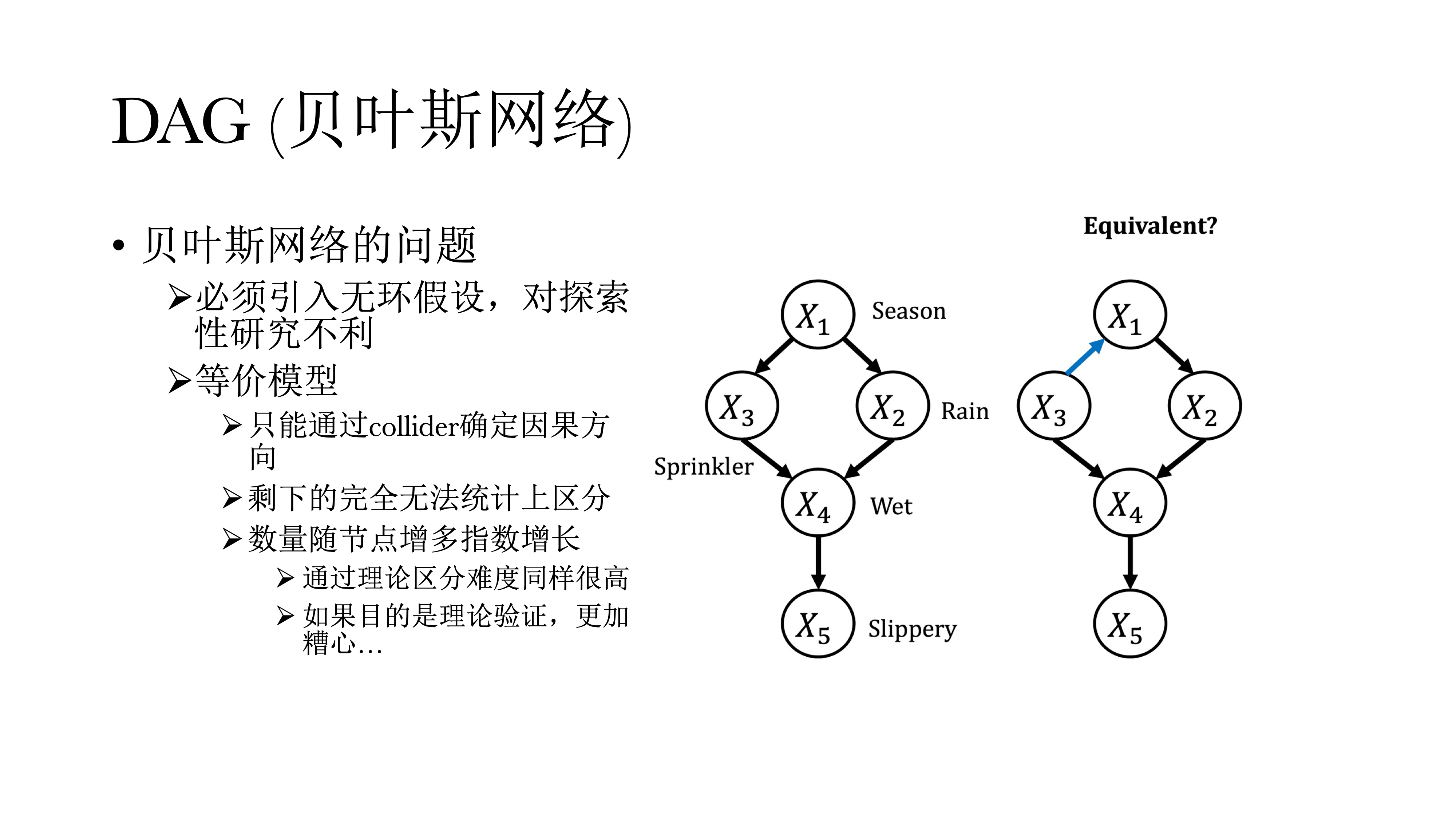
除了等价模型的问题，还有一个假设即无环假设，因为如果在模型中引入双向因果，则模型无法识别，必须无环假设来对模型进行估计。但这是一个强假设，在心理学中正反馈与负反馈是非常常见的，这也对探索性研究非常不利。
此外，还有个问题是，如果模型中的节点越多，其等价模型也就越多，几乎没有办法进行判断应选择哪个模型
14.6 高斯图模型（GGM）
因此，我们经常退一步，选择偏相关矩阵代表网络，这也是PC-algorithm的起点；在高斯图模型中，我们放弃了因果推断的方向，而使用理论或常识来自行判断来做探索性的研究。由于放弃了因果方向，因而模型有唯一解，同时没有无环假设，可以以此来指导哪两个变量之间存在正反馈或负反馈的关系。同时它也有一个很fancy的名字叫马尔科夫随机场，因为偏相关矩阵具有马尔科夫特性。
14.7 易辛模型Ising model
另外一个是易辛模型，适用于变量为二元变量。它实际上是一个物理模型，用来判断电磁场的能量，现在也被应用于心理学中来做模型推演和理论推导和数据分析。
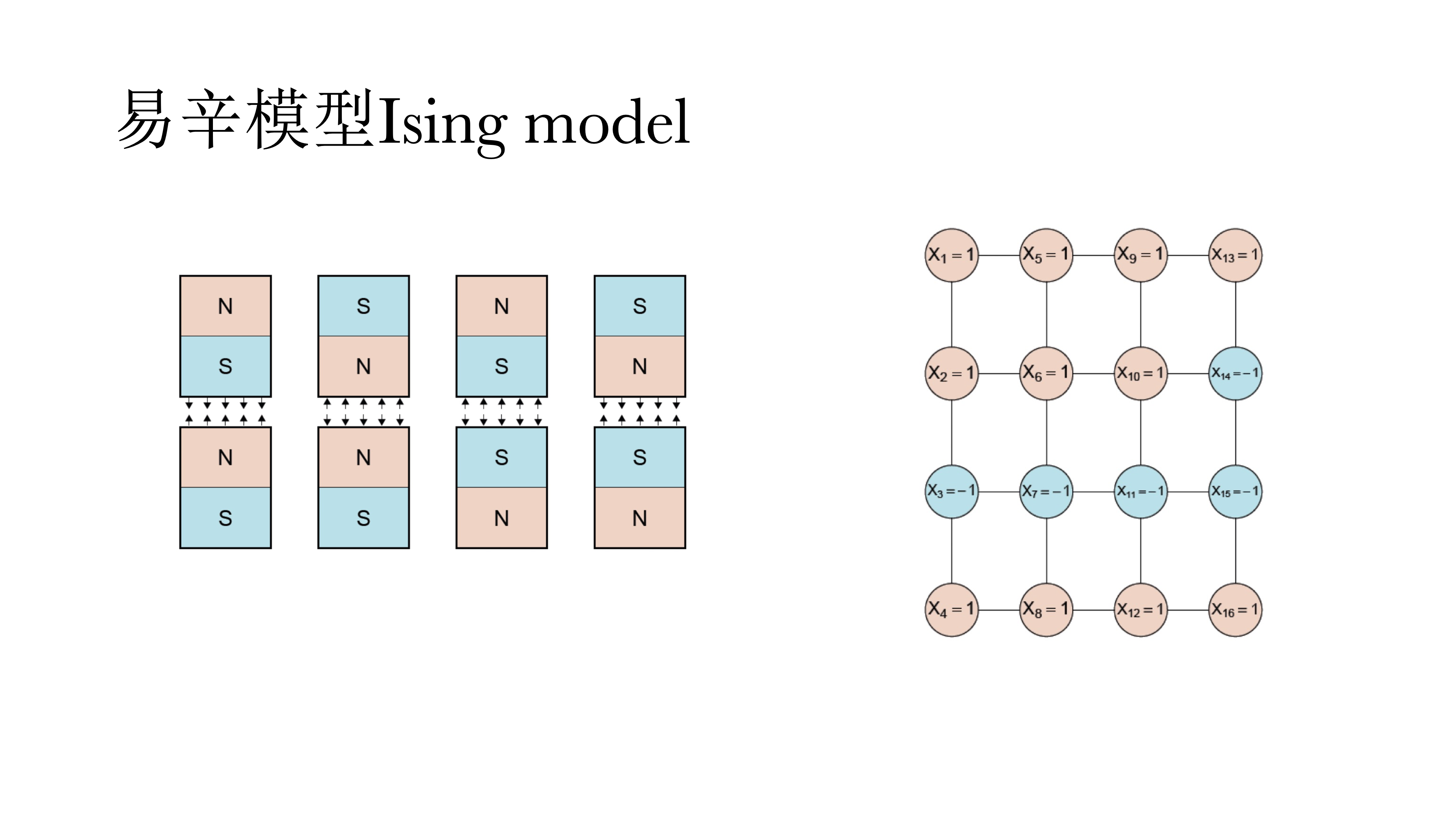
易辛模型在数学上与IRT 模型是等价的。网络模型和潜变量模型在数学上是等价的，它的好处在于可以复现同样的数据，也少了潜变量的假设。
14.8 心理网络的估计
14.8.1 高斯图模型
对于高斯图模型，有两种估计方式。
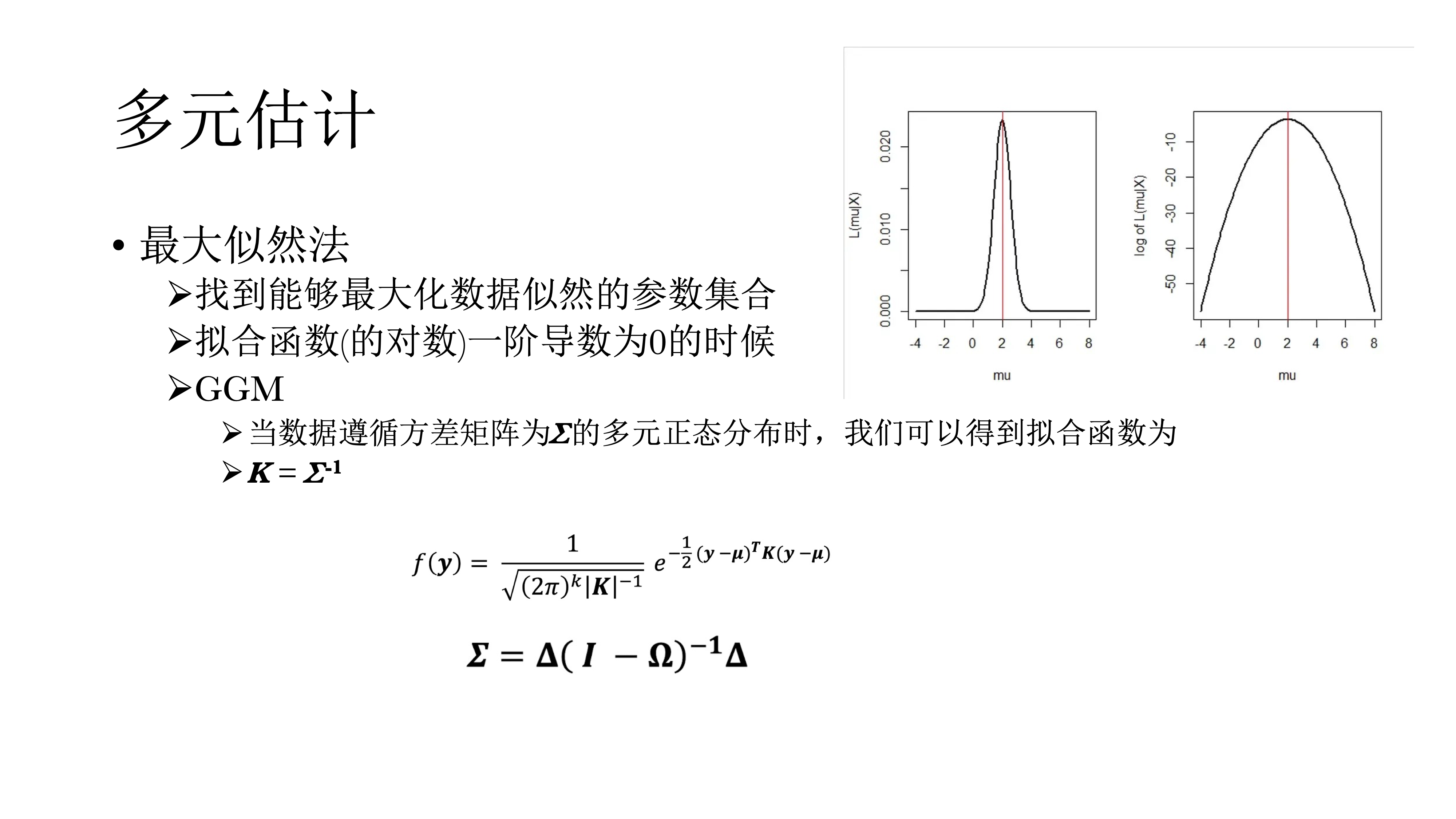
如果一次性将网络中所有的点和边都估计出来，叫做多元估计，通常使用最大似然法。
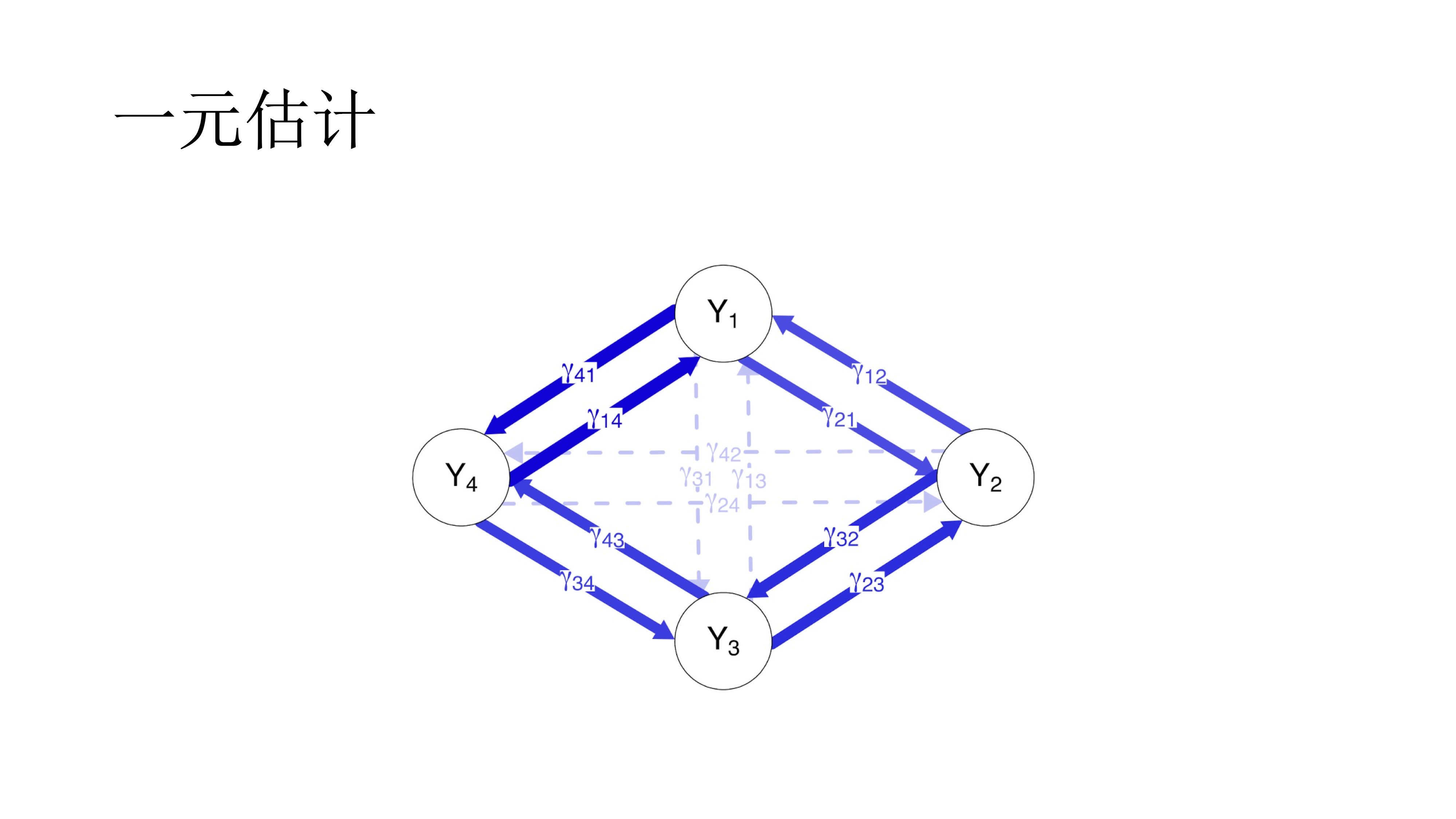
如果一个一个的估计，即使用多个多元回归，一次使用一个节点作为因变量，其他所有节点作为自变量，最后对结果取平均数，即一元估计。
14.8.2 多元估计
14.8.4 代码实现
14.8.4.1 bootnet包
# load libraries
pacman::p_load(bootnet, qgraph, psychonetrics, tidyverse, BGGM)
# load data
data("bfi")
# preprocessing -----------------------------------------------------------
# only use the first 25 items
bfi <- bfi[, 1:25]
bfi_na.rm <- na.omit(bfi)
# estimate unconstrained networks -----------------------------------------
##-----------
## bootnet
##-----------
# estimate
net_boot <- bootnet::estimateNetwork(data = bfi_na.rm, default = "pcor")
## defalut 为估计网络的方法，这里使用偏相关，别的方法可参考帮助文档
# store the ggm
graph_boot <- net_boot$graph
# Item descriptions
Names <- scan("http://sachaepskamp.com/files/BFIitems.txt",
what = "character", sep = "\n")
# Form item clusters
Traits <- rep(c(
'Agreeableness',
'Conscientiousness',
'Extraversion',
'Neuroticism',
'Opennness' ),each=5)
# plot the network
qgraph(graph_boot,
layout = "spring",
theme = "colorblind",
groups = Traits,
nodeNames = Names,
legend.cex = 0.4) 14.8.4.2 psychonetrics包
##-----------------
## psychonetrics
##-----------------
# FIML(full information likelihood maximum)
# FIML handles missing data
net_psy <- psychonetrics::ggm(bfi, estimator = "FIML") %>% runmodel
### 注意这里typeof(net_psy) 为S4对象，提取信息不用$，而是用@
### 比如net_psy@submodel查看使用什么模型
# store ggm
graph_psy <- psychonetrics::getmatrix(net_psy, "omega")
# plot the network
qgraph(graph_psy,
layout = "spring",
theme = "colorblind",
groups = Traits,
nodeNames = Names,
legend.cex = 0.4)14.8.4.3 BGGM
##--------
## BGGM
##--------
# handles missing data with mice imputation by default
net_bggm <- BGGM::explore(bfi)
## 也可使用estimate
graph_bggm <- net_bggm$pcor_mat
qgraph(graph_bggm,
layout = "spring",
theme = "colorblind",
groups = Traits,
nodeNames = Names,
legend.cex = 0.4)
# compare the three networks
L <- averageLayout(graph_boot, graph_psy, graph_bggm)
layout(t(1:3))
qgraph(graph_boot, title = "bootnet", layout = L)
qgraph(graph_psy, title = "psychonetrics", layout = L)
qgraph(graph_bggm, title = "bggm", layout = L)
dev.off()
# compare parameter estimations
plot(c(graph_boot), c(graph_psy), xlab = "bootnet", ylab = "psychonetrics")
abline(coef(lm(c(graph_boot) ~ c(graph_psy)))[1], coef(lm(c(graph_boot) ~ c(graph_psy)))[2])
plot(c(graph_bggm), c(graph_psy), xlab = "bggm", ylab = "psychonetrics")
abline(coef(lm(c(graph_bggm) ~ c(graph_psy)))[1], coef(lm(c(graph_boot) ~ c(graph_psy)))[2])14.9 模型选择
以上模型都是饱和模型，都没有经过选择，即每一个观测都会都应一个参数，不仅很难解释，而且会导致过多的假阳性，很多的相关都不显著，因而需要对模型进行选择。
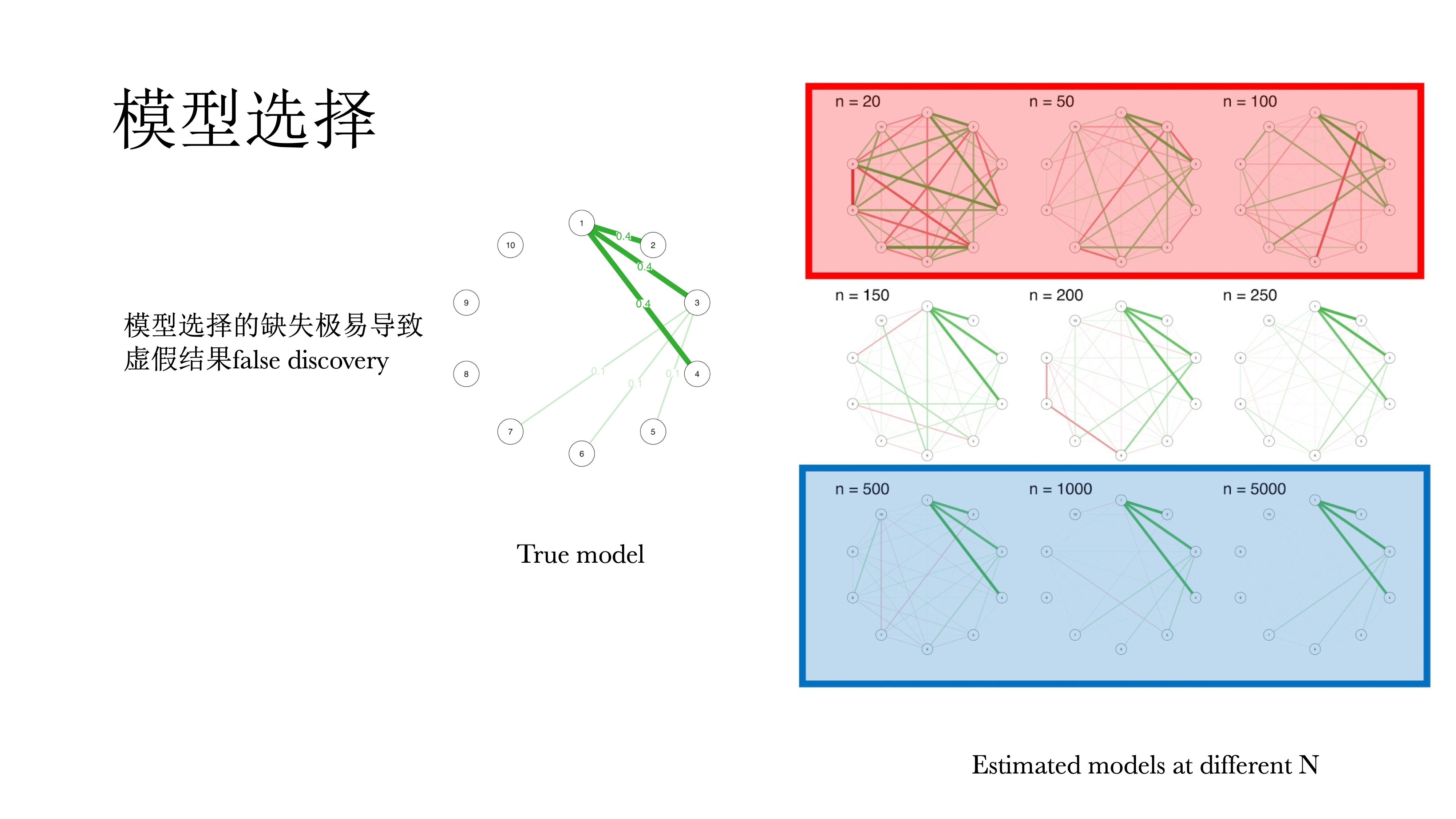
在模型选择中有一个原则称为奥卡姆剃刀，即在拟合相似模型中选择最简单的，因为其推广性最好，也容易解释。在网络模型中基本上都要去做模型选择来简化模型，留下有解释意义的参数。
14.9.1 模型选择的方式
模型选择有很多方式：阈值法、剪枝法、正则发和模型搜索法
14.9.1.1 阈值法&剪枝法
阈值法与剪枝法比较像，但是有一些区别。
阈值法是将某些不符合标准的连接直接给藏起来，但也仅仅只是藏起来，并不会重新估计这个模型；而剪枝法会将不符合标准的连接设置为0，并对模型进行重新估计。
而对标准来说，不仅可以是P值，也可以是bootstrapped的P值，或是经过矫正的，或是贝叶斯因子；在一元估计中的AND/OR规则也可以用与模型选择。
模型选择的结果会有一些不同，大家在解释的时候可以看一看哪一些发现比较稳定。阈值与剪枝的有点在于速度快，不需要估算很多的模型；可以有固定的假阳性率，是实际可控的（与正则法相比）；其估计值是无偏的，即期望值等于真值；比较保守，假阳性率不高。
缺点在于：阈值法本身不是一种模型选择，只是把边给藏起来了；在小样本时不够精确。
14.9.1.2 正则法
正则法在似然函数中添加罚项\(\lambda\)，会把很大的偏相关给惩罚掉(即LASSO，Least Absolute Shrinkage and Selection Operator)，让0多一点。而控制惩罚程度(罚项)的参数\(\lambda\)也可以使用EBIC(Extended Bayesian Information Criterion)来选择，即\(\lambda\)控制罚项，而\(\gamma\)控制\(\lambda\)，\(\gamma\)越大，对模型复杂度的惩罚越大，网络也就越稀疏（EBICglasso）。
在一元回归的时候，同样可以使用LASSO回归来惩罚偏相关；也可以使用交叉验证的方法。
正则法的优点是同样很快；另外一个独特的优点是非常适合小样本，阈值与剪枝两种方法并不适合小样本，在模拟数据中，N = 50时就能还原出很不错的网络；结果也很清晰，将不太显著的边直接压缩为0。
但是这种方法在大样本时表现差；同样正则法假设网络本身是稀疏的，如果使用正则法，它永远会将一些边压缩为0，哪怕这些边的真值不为0，如果我们的理论假设是这个网络应该是密集网络，这时就不应该使用正则法；最后，正则法没有固定的假阳性率，不同于前面两种方法，具体假阳性率是未知的。
14.9.1.3 模型搜索
模型搜索的方法应该是最好的方法，但也是最慢的，由于时间限制今天就不演示。其逻辑是使用不带正则的最大似然估计不停调整并重新估计模型，直到选择最优解。比如简单的step-up ，如下图所示，首先从空模型开始，然后加一个modification index（结构方程模型中的调整系数），每次把调整系数最大的连接给加上，然后再重新估算一次模型，并且比较模型拟合是否有提升；然后再在新的模型中找到新的调整系数，再计算、比较模型，直到模型拟合不再提升。
psychonetrics::modelsearch更加麻烦，具体算法见下图。
qgraph::ggmModSelect与modelsearch很相似，但是是从正则化网络出发的。
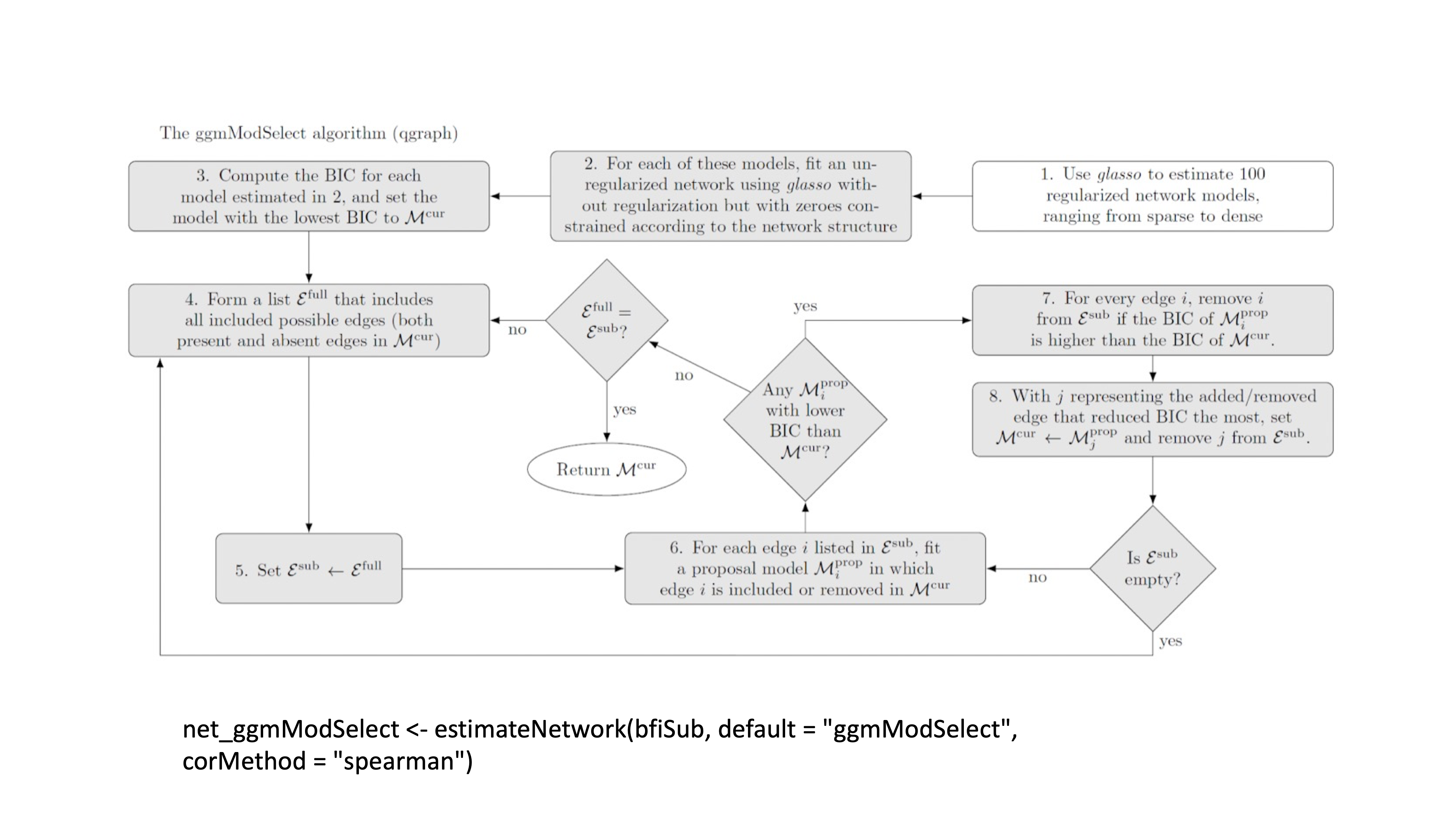
14.9.2 总结
阈值/剪枝法
将饱和模型中不合标准的edge隐藏 / 设置为0再重新估计
好处：快速，有固定的假阳性率，无偏估计
缺点：阈值法并不选择模型，小样本时不稳定，不一定能converge到真模型
正则法
在最大似然中惩罚模型复杂度
好处：快速，小样本时表现好，结果更易解释
缺点：估计永远是biased的，大样本下表现不好
模型搜索
- 依次添加或去除edge来优化某项指标（e.g., BIC）
- 好处：同时照顾power和假阳性,-无偏估计，因为检查的模型多更可能converge 到真模型
- 坏处：很慢，小样本时表现糟糕
小样本使用正则化方法，而单样本使用模型搜索
14.9.3 代码实现
14.9.3.1 阈值法&剪枝法
##----------------
## Thresholding （阈值法）
##----------------
#------------------- bootnet -----------------------#
# bootnet: sig(依据p值选择，具体threshold参数见帮助文档)
net_boot_thresh_sig <- estimateNetwork(bfi,
default = "pcor",
threshold = "sig",
alpha = 0.01)
qgraph(net_boot_thresh_sig$graph,
layout = L,
title = "threshold alpha = .01")
qgraph(net_boot$graph, layout = L)
## 或者可以先估计，再选择
# bootnet: boot
## nCores设置使用CPU核心数，nBoots设置重抽样数量，默认1000
net_boot_booted <- bootnet::bootnet(net_boot,
nCores = parallel::detectCores(),
nBoots = 100)
net_boot_thresh_boot <- bootnet::bootThreshold(net_boot_booted, alpha = 0.01)
qgraph(net_boot_thresh_boot$graph,
layout = L,
title = "threshold boot .01")
#------------------- BGGM -----------------------#
# BGGM: threshold with credible interval(使用select函数)
net_bggm_thresh_ci <- BGGM::estimate(bfi) %>% select
qgraph(net_bggm_thresh_ci$pcor_adj,
layout = L,
title = "bggm threshold ci")
## 注意select.estimate和select.explore不一样
## select.estimate 根据95%CI进行选择，即删去包含0的边
## select.explore根据贝叶斯因子小于3的标准进行排除
# BGGM: threshold with BF
net_bggm_thresh_bf <- BGGM::explore(bfi) %>% select
qgraph(net_bggm_thresh_bf$pcor_mat,
layout = L,
title = "bggm threshold bf")
##-----------
## pruning （剪枝法）
##-----------
net_psy_prune <- psychonetrics::ggm(bfi, estimator = "FIML") %>%
## recursive 可以设置是否迭代进行
psychonetrics::prune(alpha = 0.01, recursive = TRUE) %>%
runmodel
qgraph(getmatrix(net_psy_prune, "omega"),
layout = L,
title = "psychonetrics pruned")14.9.3.2 正则化(EBICglasso)
##------------------
## regularization
##------------------
net_boot_reg <- estimateNetwork(bfi_na.rm,
default = "EBICglasso",
tuning = 0.5)
## 注：对于不同的模型估计时tuning默认值不同，见帮助文档
## 这里运行时提示Warning，提示选择了密集网络
## EBICglasso会假设网络是稀疏网络，但也可能真实网络确实是密集的
qgraph(net_boot_reg$graph,
layout = L,
title = "bootnet EBICglasso")14.9.3.3 模型选择
## 从零模型开始搜索(step-up)
mod <- psychonetrics::ggm(bfi_na.rm, omega = "zero") %>%
runmodel %>%
stepup
net <- getmatrix(mod,"omega")
## 从被剪枝后的模型开始搜索(modelsearch)
mod <- psychonetrics::ggm(bfi_na.rm) %>%
runmodel %>%
prune(alpha = .01) %>%
stepup
## ggModSelect
net_ggmModSelect <- estimateNetwork(bfi_na.rm,
default = 'ggmModSelect',
corMethod = 'spearman')14.10 心理网络的挑战
心理网络本身也面临一些挑战。
首先我们讲了网络理论不等于网络模型，就是刚才所说的上升啊，因果之类的。到底DAG还是GGM，或者是更新的的模型更符合心理学理论，这个问题是值得讨论的。
还有就是Collider比较麻烦，它会在网络里面表现出一些虚假的边，因此如果大家的网络里面如果出现一些负连接一定要小新，在解释的时候要看它符不符合逻辑。
在选择样本的时候，一定不能使用提前选择后的样本，比如只看有精神疾病的对象（e.g. 只去量表中得分超过10分的人），这会人为的引入collider effect。但最近有文章在估计时可以纠正这种Berkon’s bias，因此这么做也可以。
心理网络的中心度其实是有问题的，所以今天也没有将具体中心度计算，在社会网路中中心度有着比较可靠的解释或数据基础，但在心理网络中，中心度并不好解释，如betweenness 和 closeness的可重复性并不太好，唯一一个比较好的可能就是degree centrality。
使用高斯图因果推断也有问题，因为在使用时并不知道ggm对应的真正的因果产生机制(真模型)是什么——由于ggm牺牲了方向，因而真正的因果方向是不知道的。也有一些替代ggm的办法，但可靠性值得研究。
14.11 是否还需要潜变量模型
答案是确定的。很多人觉得使用网络模型就很讨厌潜变量模型，这其实是一个很不好的刻板印象。
潜变量模型首先对测量误差的估计是无可替代的，可以在研究时控制住测量误差，其他任何方法都不行，只有基于潜变量模型才可以。
同时，潜变量模型需要更小的样本，而网络模型需要的样本量就大多了。
对于IRT，对于量表中题项的评估也是无法被代替的；同样，基于IRT的计算机自适应测验的方式在网络模型中也没有被发展出来。
基于Network的心理测量其实也不是很全面，大家可以看看下面两个人的文章（见下图）——基于网络的心理测量应该怎么做，定义是什么样，其实都不太一样。基于网络模型的量表，跟基于潜变量模型的量表也不太一样。
什么时候用网络模型：
在数据探索时，试图想要发现一些稳定的现象时，网络分析是一个不需要什么前提理论的方法、
当研究对象是可观测特征之间的动态关系时，如做临床的人通过网络模型，可以直接看出治疗效果在哪一个症状上体现出来，这种动态的关系是否发生改变。这时网络分析所显示出的结果要比潜变量模型要多很多。
当有理论来支持可观测特征之间的英国关系时，这时候用网络模型更好