Chapter 16 补充1：如何进行基本的数据分析: 相关与回归
16.1 什么是相关
相关分析是一种统计技术，用于测量两个变量之间线性关系的强度和方向。它涉及计算相关系数，相关系数的取值为[-1, 1]，其中-1表示两个变量完全呈负相关，0表示无相关，1表示完全正相关。 Pearson(皮尔逊)相关 Pearson相关系数是最常用的方法之一，用于衡量两个变量之间的线性相关程度，取值范围为-1到1之间，其值越接近于1或-1表示两个变量之间的线性相关程度越强，而越接近于0则表示两个变量之间线性相关程度越弱或不存在线性相关性。皮尔逊相关系数适用场景是呈正态分布的连续变量，当数据集的数量超过500时，可以近似认为数据呈正态分布 Spearman(斯皮尔曼)相关 Spearman等级相关系数用于衡量两个变量之间的关联程度，但不要求变量呈现线性关系，而是通过对变量的等级进行比较来计算它们之间的相关性。 与皮尔逊相关系数相比，斯皮尔曼相关系数没有那些限制，比如要符合正态分布、样本容量要超过一定数量(比如30个). Kendall(肯德尔)相关 Kendall秩相关系数也用于衡量两个变量之间的关联程度，其计算方式与Spearman等级相关系数类似，但它是基于每个变量的秩来计算它们之间的相关性。 肯德尔相关系数，又称肯德尔秩相关系数，它也是一种秩相关系数，不过，它的目标对象是有序的类别变量，比如名次、年龄段等。 假想问题 在penguin数据中，参与者压力和自律水平的相关水平？
16.2 相关-代码实现
# 检查是否已安装 pacman
if (!requireNamespace("pacman", quietly = TRUE)) {
install.packages("pacman") } # 如果未安装，则安装包
# 使用p_load来载入需要的包
pacman::p_load("tidyverse", "bruceR", "performance")
# 或者直接使用 easystats这个系列
pacman::p_load("tidyverse", "bruceR", "easystats")检查工作路径 - 导入原始数据
## [1] "C:/Users/30258/Desktop/R/Practice/transcript2024inRMD_test/qht_R4psyBook"#读取数据
df.pg.raw <- read.csv('./data/penguin/penguin_rawdata.csv',
header = T,
sep=",",
stringsAsFactors = FALSE)首先需要将数据导入R中，并进行数据清洗和转换。可以使用Tidyverse包中的函数来选择和转换数据。在进行反向计分后，使用mutate函数来计算每个问卷的得分。 然后选择性别、压力和自我控制这三个变量，并使用Bruce R中的相关分析方法来计算它们之间的相关性。 需要注意的是，当有多个变量需要进行两两相关性分析时，需要进行P值的多重性校正。这里最后得到的是一个宽数据，需要在此基础上进行进一步的分析。
df.pg.corr <- df.pg.raw %>%
dplyr::filter(sex > 0 & sex < 3) %>% # 筛选出男性和女性的数据
dplyr::select(sex,
starts_with("scontrol"),
starts_with("stress")) %>% # 筛选出需要的变量
dplyr::mutate(across(c(scontrol2, scontrol3,scontrol4,
scontrol5,scontrol7, scontrol9,
scontrol10,scontrol12,scontrol13,
stress4, stress5, stress6,stress7,
stress9, stress10,stress13),
~ case_when(. == '1' ~ '5',
. == '2' ~ '4',
. == '3' ~ '3',
. == '4' ~ '2',
. == '5' ~ '1',
TRUE ~ as.character(.)))
) %>% # 反向计分修正
dplyr::mutate(across(starts_with("scontrol")
| starts_with("stress"),
~ as.numeric(.))
) %>% # 将数据类型转化为numeric
dplyr::mutate(stress_mean =
rowMeans(select(.,starts_with("stress")),
na.rm = T),
scontrol_mean =
rowMeans(select(., starts_with("scontrol")),
na.rm = T)
) %>% # 根据子项目求综合平均
dplyr::select(sex, stress_mean, scontrol_mean)使用head查看一下前五行
bruceR::Corr()
results.Corr <- capture.output({
bruceR::Corr(data = df.pg.corr[,c(2,3)],
file = "./output/chp8/Corr.doc")
})
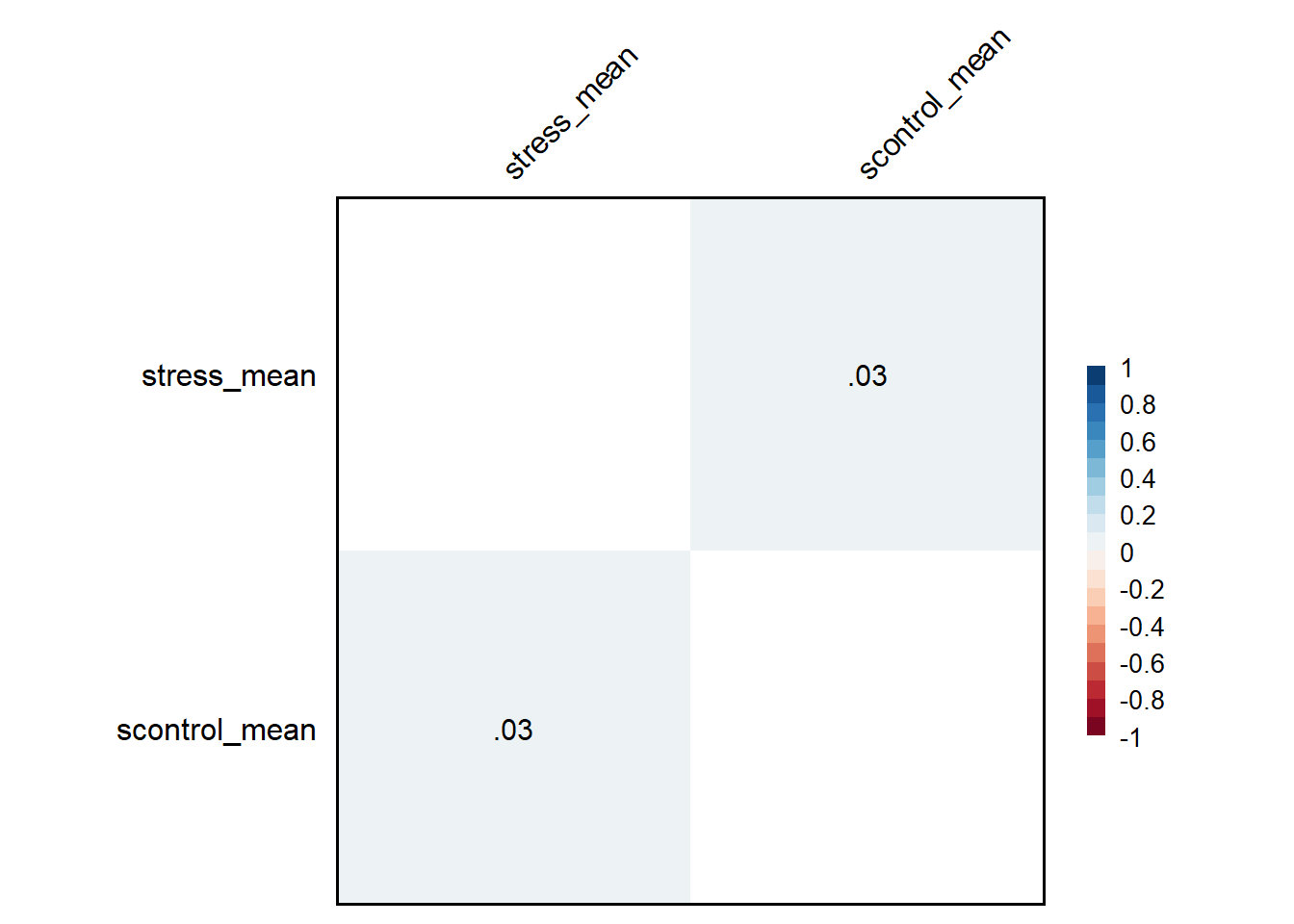
Bruce R默认采用pearson相关，也可以选择使用spearman或者kendall。如果有多个即两个以上的个变量，两两之间计算相关，往往还需要对P值进行多重校正。如果只有两个变量，就不需要了。
在保存文件时，要注意文件名和文件类型的后缀。
也可以用散点图来展示变量之间的相关性。
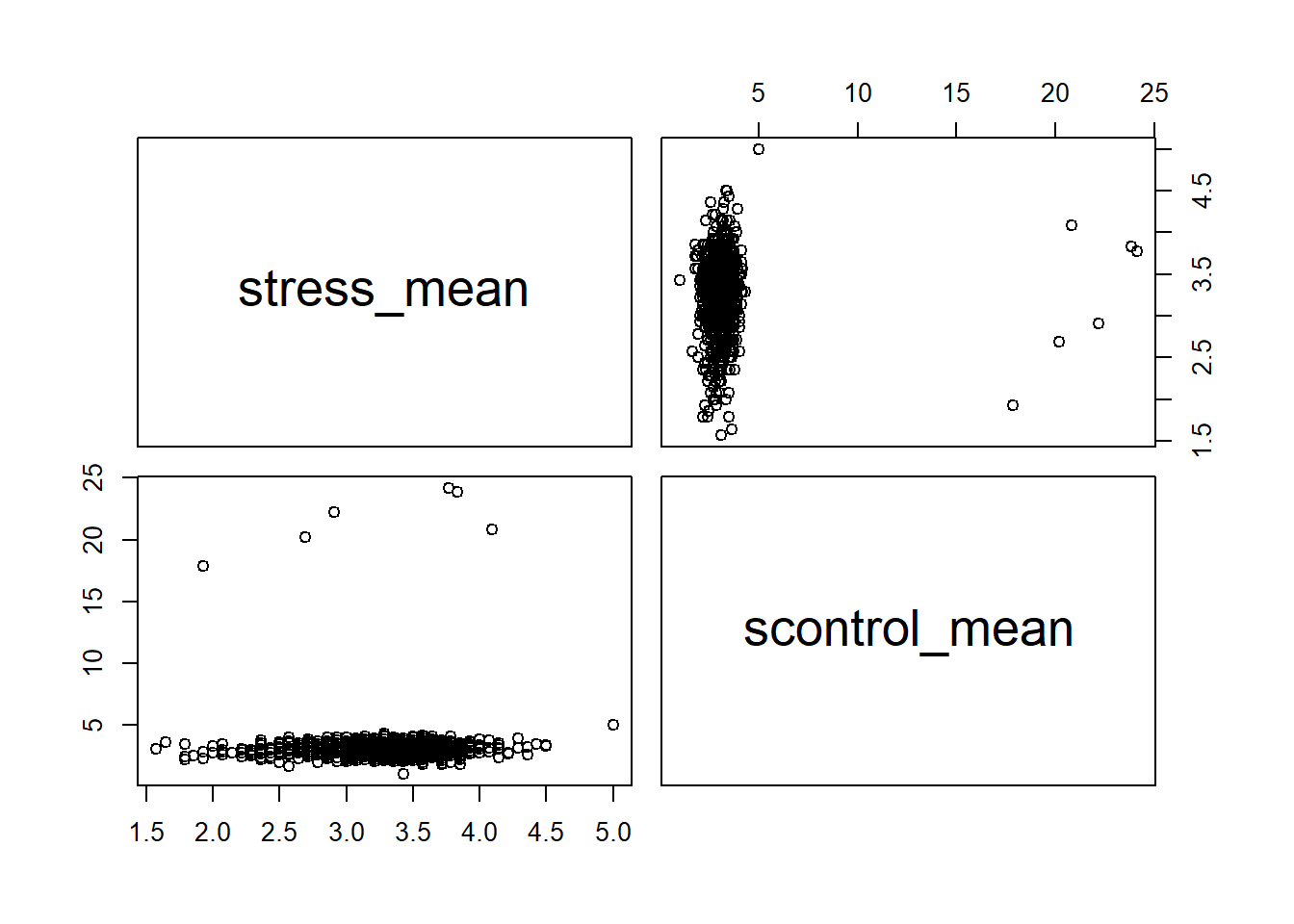RStudio有4个panel，最右下角的面板是用来画图的，有时运行画图命令之后图没有输出，可能就是由于这个面板的区域留得不够大，导致图无法呈现；这种情况下只需要把面板拖拽至合适的大小即可。
成功之后会自动输出一张图，图上是stress_mean和control_mean这两个变量的相关矩阵。 图的右侧是从-1到1的legend图例，颜色越深相关越高、颜色越浅相关越低；矩阵中的数字即为两个变量的相关系数，这里的值为0.05，可见这两个变量相关性很弱；如果相关显著，在相关系数的右上角会自动呈现星号，这个图中没有出现，表明二者相关并不显著。 结果也可以输出为word文档 但是需要精确地指出所需要的变量，也就是对应的columns。如果不指定，它会将所有变量两两组合计算相关；例如计算性别和一个连续变量之间的相关，但是这种情况下不能使用pearson。 如果一个二分变量（如性别）和一个连续变量进行相关分析，不应该使用pearson，应该用点二列相关，或者直接使用t检验。
在ezstates中有一个类似的包correlation，它的好处在于它会输出更多的信息，因此很适用于探索性的分析的阶段（这个时候对于变量之间的关系没有大概的了解，需要探索一下）。 它就会以一个可视的形式展现变量间的关系，便于快速发现哪两个变量之间相关变强，哪两个变量相对弱。
16.3 什么是回归
回归模型是通过对观测数据进行拟合来描述变量之间的关系。回归允许我们估计因变量如何随着自变量的变化而变化。 很多经典统计（T-test,方差分析,相关,回归分析）都有共同的技术，GLM。 广义线性模型（Generalized Linear Model，GLM）, 或者线性混合模型（Generalized Linear Mixed Model）,本质上就是Y=A+BX。通常会将Y作为预测项，有时候会在预测项上加上一个误差，这是可以扩展的，我们也可以假设他是一个非线性的关系，当它是线性的时候，我们实际上是在预测一个正态分布的均值，如果我们不是预测均值，我们可以通过一个转换，使用一个链接函数，转化后的参数仍然能用这种方法来组合预测，这个自变量或者因变量可以是非连续的变量。 ## 回归-代码实现
\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \epsilon\]
假想的问题 “在penguin数据中，我们希望找到参与者压力和自律水平关于性别的回归？”
# 数据预处理
df.pg.lm <- df.pg.corr %>%
# 将sex变量转化为factor类型
mutate(sex = as.factor(sex)) %>%
# 自变量为scontrol和sex
group_by(scontrol_mean,sex) %>%
# 根据分组获得stress的平均值，。groups属性保留了之前的group_by
summarise(stress_Mean = mean(stress_mean),.groups = 'keep')希望找到压力，自律以及性别之间的关系。 在此之前，首先做了correlation。 在数据预处理阶段，把性别转换为factor类型,然后再把数据进行group by。 数据预处理之后,可以做一个探索分析，先用ggPlot画一个图，用不同的颜色分别表示男性和女性的数据。 绘制散点之后继续绘制趋势线时，使用了geom_smooth(), 这里自动使用了formula,y ~ x，表示用x来预测y。这里y即为strength， x即为self-control。两条线看起来是交叉的。图中呈现的粗略的结果支持在女性中存在相关, 在男性当中不存在，之后可以对它进行检验。
# 使用ggplot()画图
ggplot(df.pg.lm, aes(x = scontrol_mean, y = stress_Mean, color = sex)) +
geom_point() +
geom_smooth(method = "lm") +
scale_color_discrete(name = "Gender",
labels = c("Female", "Male")) +
theme_minimal()## `geom_smooth()` using formula = 'y ~ x'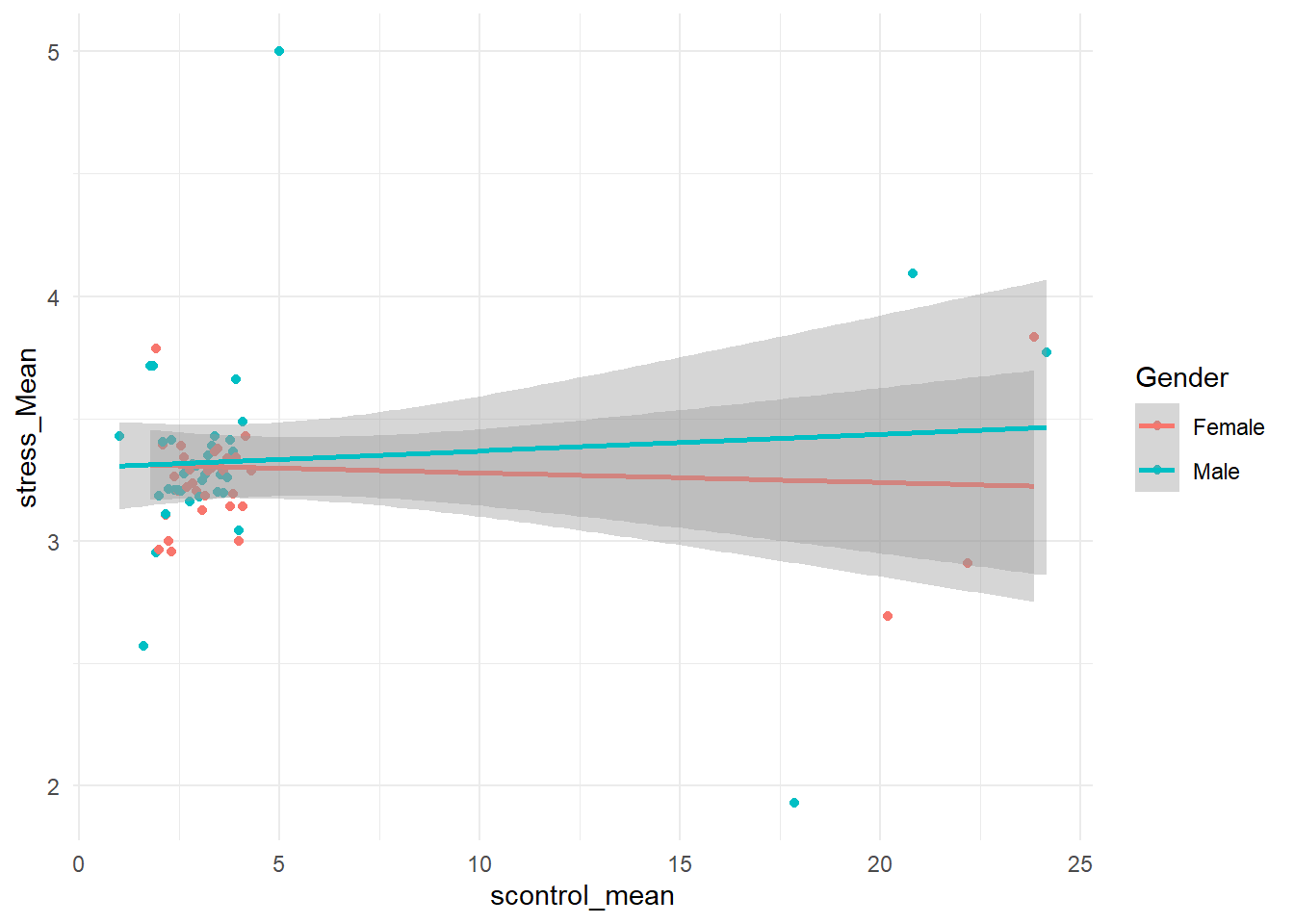
直接使用lm linear model，它是base中的一个函数。这里是R中进行回归常用的公式写法, 也就是左边为因变量，右边为自变量, 运行后R就自动输出结果。 因此在R中因变量自变量要选择清楚。
这个例子中因变量是主观压力stress，三个自变量分别是sex性别、scontrol_mean、以及二者的交互作用（因为sex和scontrol_mean之间可能存在交互作用），那么代码就可以写成mod <- lm(stress_Mean ~ scontrol_mean + sex + scontrol_mean:sex, df.pg.lm)。
如果后续需要做线性回归及相关的分析，需要掌握这种写法。
公式会作为第一个参数被输入到函数中，也可以更完善的补全它的argument，也就是formula=之后的内容，在这个例子中其他的argument被省略了、为默认值。
运行代码之后,线性回归的结果被保存在变量mod中，然后可以用mod_summary将结果提取出来。
# 建立回归模型
mod <- lm(stress_Mean ~ scontrol_mean + sex + scontrol_mean:sex, df.pg.lm)
# 使用bruceR::model_summary()输出结果
result.lm <- capture.output({
model_summary(mod,
std = T,
file = "./output/chp8/Lm.doc")
})
writeLines(result.lm, "./output/chp8/Lm.md") 输出的结果中包括显著性检验，可以看到selfcontrol、sex以及它们之间的交互作用是否显著。
整个模型的一个决定系数指这个模型解释了多少变异,adjusted是调整之后的数据。
number of observations 为53。
推荐一个很好的包：performance,它可以进行常用的统计模型分析,包括Anova、T-test等。它会检查模型的各个方面,比如posterior predictive check，inlinearity，方差齐性，共线性，正态性检验等等。 它可以告诉你数据是否符合做这个模型的假定的assumption。 它还可以进行模型比较,比如我们有模型1是有交互作用的,模型2是没有交互作用的，它可以对模型1和模型2进行比较，告诉你哪个模型能够更合理地解释数据的变异,可以用model comparison这个函数来对三个模型进行比较,这个在easy state里面有。
在这一部分,有两个内容需要强调。 首先是需要掌握公式如何写,尤其是对于第一次在R中接触回归模型的同学,需要注意这个固定的写公式套路。 其次是如果需要做简单的回归分析,那么使用LM就可以；在心理统计学中,一个变量对另外一个变量的预测作用、多个变量对一个变量的预测作用、变量为二分变量这些情况，LM都可以适用。
可以自己试着编写一条进行回归模型比较的函数，并把相关指标建议附在控制台的输出结果中
P_anova<- function(model1, model2, file = NULL){
if(is.null(file)){
cat("\033[1;32m
Tips by P：
AIC：Lower values indicate better fit for model comparison.
BIC：Lower values indicate better fit for model comparison.
liglik: The smaller the absolute value of logLik, the better the model fits.
deviance: The smaller the deviance value, the better the model fit.
Chisq: chi-square value(χ²) of likelihood ratio test.
Pr(>Chisq): P-value of likelihood ratio test.
\033[0m\n")
cat("\033[1;32m
Model Comparison Table
\033[0m\n")
result<-anova(model1,model2)
print_table(result)
}else{
cat("\033[1;32m
Tips by P：
AIC：Lower values indicate better fit for model comparison.
BIC：Lower values indicate better fit for model comparison.
liglik: The smaller the absolute value of logLik, the better the model fits.
deviance: The smaller the deviance value, the better the model fit.
Chisq: chi-square value(χ²) of likelihood ratio test.
Pr(>Chisq): P-value of likelihood ratio test.
\033[0m\n")
cat("\033[1;32m
Model Comparison Table
\033[0m\n")
result<-anova(model1,model2)
print_table(result)
print_table(table, file = file)
}
}可以自己试着写一条建立回归模型的函数，基lmerTest、bruceR和一些数据清理的包，这行代码可以输出两个模型（可以是：lm、glm（二项分布、泊松分布、高斯分布）、lmer）的方差分析表、回归系数、标准化系数、(随机效应)、随机效应的显著性检验、输出各自模型的三线表到word文档、两个模型之间的比较（AIC、BIC、LogLik以及似然比检验 /F 检验的结果）。Tips: compare.except指模型二与模型一相比剔除的解释变量，暂不支持对多层线性模型随机斜率的比较。
P_regress<- function(formula,
data,
family = NULL,
compare.except = NULL,
digits = 3,
nsmall = digits,
robust = FALSE,
cluster = NULL,
test.rand = FALSE,
file1 = NULL,
file2 = NULL,
file3 = NULL){
if(is.null(compare.except)){
if (class(formula) == "formula" & grepl("\\|", deparse(formula))){
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand)
model1 = lmer(formula = formula, data = data)
if(!is.null(file1)){
print_table(model1,file = file1)}
ranova = ranova(model1)
cat("\033[1;37m
The significance test of random effects
\033[0m\n")
print_table(ranova)
}else if(class(formula) == "formula" & grepl("family", deparse(formula))){
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand)
if(family == "binomial"){
model1 = glm(formula = formula, data = data,family = binomial())
if(!is.null(file1)){
print_table(model1, file = file1)}
}else if(family == "gaussian"){
model1 = glm(formula = formula, data = data,family = gaussian())
if(!is.null(file1)){
print_table(model1, file = file1)}
}else{
model1 = glm(formula = formula, data = data,family = poisson())
if(!is.null(file1)){
print_table(model1, file = file1)}
}
}else{
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand)
model1 = lm(formula = formula, data = data)
if(!is.null(file1)){
print_table(model1, file = file1)}
}
}else{
if (class(formula) == "formula" & grepl("\\|", deparse(formula))){
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand)
model1 = lmer(formula = formula, data = data)
if(!is.null(file1)){
print_table(model1, file = file1)}
ranova = ranova(model1)
cat("\033[1;37m
The significance test of random effects
\033[0m\n")
print_table(ranova) # model1 ranova
string<- formula_paste(formula)
string1<-gsub(" ", " \\\\+ ", compare.except)
new_string <- gsub(string1, "", string)
formula = as.formula(new_string)
model2 = lmer(formula = formula, data = data)
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand) #model2
ranova = ranova(model2)
cat("\033[1;37m
The significance test of random effects
\033[0m\n")
print_table(ranova)
if(!is.null(file2)){
print_table(model2, file = file2)} #model2 ranova
P_anova(model1, model2,file = file3)#模型比较
}else if(class(formula) == "formula" & grepl("family", deparse(formula))){
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand) #model1
if(family == "binomial"){
model1 = glm(formula = formula, data = data,family = binomial())
if(!is.null(file1)){
print_table(model1, file = file1)}
string<- formula_paste(formula)
string1<-gsub(" ", " \\\\+ ", compare.except)
new_string <- gsub(string1, "", string)
formula = as.formula(new_string)
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand) #model2
if(!is.null(file2)){
print_table(model2, file = file2)}
P_anova(model1, model2,file = file3)
}else if(family == "gaussian"){
model1 = glm(formula = formula, data = data,family = gaussian())
if(!is.null(file1)){
print_table(model1, file = file1)}
string<- formula_paste(formula)
string1<-gsub(" ", " \\\\+ ", compare.except)
new_string <- gsub(string1, "", string)
formula = as.formula(new_string)
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand) #model2
if(!is.null(file2)){
print_table(model2, file = file2)}
P_anova(model1, model2,file = file3)
}else{
model1 = glm(formula = formula, data = data,family = poisson())
if(!is.null(file1)){
print_table(model1, file = file1)}
string<- formula_paste(formula)
string1<-gsub(" ", " \\\\+ ", compare.except)
new_string <- gsub(string1, "", string)
formula = as.formula(new_string)
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand) #model2
if(!is.null(file2)){
print_table(model2, file = file2)}
if(!is.null(file3)){
P_anova(model1, model2,file = file3)}
}
}else{
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand)
model1 = lm(formula = formula, data = data)
if(!is.null(file1)){
print_table(model1, file = file1)}
string<- formula_paste(formula)
string1<-gsub(" ", " \\\\+ ", compare.except)
new_string <- gsub(string1, "", string)
formula = as.formula(new_string)
regress(formula = formula,
data = data,
family = family,
digits = digits,
nsmall = digits,
robust = robust,
cluster = cluster,
test.rand = test.rand) #model2
if(!is.null(file2)){
print_table(model2, file = file2)}
P_anova(model1, model2,file = file3)
}
}
}可以自己试着编写一条回归分析中简单斜率检验的函数，并输出简单斜率检验图。适用于绝大多数调节模型。
P_simpleslopes<- function(y,x,mod,mod2 = NULL, data, main.title = "Simple Slope Test Graph", way = 2){
P_dif<- function(x){
return(length(unique(x)))
}
if(is.null(mod2)){
datamod = unlist(select(data, mod))
if(P_dif(datamod) == 2){
a = paste(x,mod, sep = " * ")
formula = paste(y,a,sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 1 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Formula :", paste(formula), "\033[0m\n")
data = rename(data, "y" = y, "x" = x, "mod" = mod)
model = lm(formula = y ~ x * mod, data = data)
result<- sim_slopes(model, pred = x, modx = mod, jnplot = T)
data1 = result$slopes
names(data1)[1] = mod
names(data1)[2] = "Effect"
names(data1)[6] = "t"
cat("\033[1;37m
Simple slope:\033[0m\n")
print_table(data1)
interact_plot(model,
pred = x,
modx = mod,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}else{
a = paste(x,mod, sep = " * ")
formula = paste(y,a,sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 1 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Formula :", paste(formula), "\033[0m\n")
data = rename(data, "y" = y, "x" = x, "mod" = mod)
model = lm(formula = y ~ x * mod, data = data)
result<- sim_slopes(model, pred = x, modx = mod, jnplot = T)
data1 = result$slopes
a = data1[,1]
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data1[,1] = a
names(data1)[1] = mod
names(data1)[2] = "Effect"
names(data1)[6] = "t"
cat("\033[1;37m
Simple slope:\033[0m\n")
print_table(data1)
interact_plot(model,
pred = x,
modx = mod,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}
}else{
if(way == 3){
datamod = unlist(select(data, mod))
datamod2 = unlist(select(data, mod2))
if(P_dif(datamod) == 2){
if(P_dif(datamod2) == 2){
a = paste(x, mod, mod2,sep = " * ")
c = paste(y , a, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 3 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 0.00 :\033[0m\n")
print_table(data1)
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 1.00 :\033[0m\n")
print_table(data2)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}else{
a = paste(x, mod, mod2,sep = " * ")
c = paste(y , a, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 3 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
data3 = data.table(slopes[[3]])
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
sd = sd(unlist(select(data, mod2)))
mean = round(mean(unlist(select(data, mod2))),3)
b = round(mean - sd,3)
c = round(mean + sd,3)
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(b), "(- 1 SD):\033[0m\n")
print_table(data1)
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(mean), "(Mean):\033[0m\n")
print_table(data2)
names(data3)[1] = paste(mod,"(mod)",sep = " ")
names(data3)[2] = "Effect"
names(data3)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(c), "(+ 1 SD):\033[0m\n")
print_table(data3)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}
}else{
if(P_dif(datamod2) == 2){
a = paste(x, mod, mod2,sep = " * ")
c = paste(y , a, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 3 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
a = unlist(data1[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data1[,1] = a
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 0.00 :\033[0m\n")
print_table(data1)
a = unlist(data2[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data2[,1] = a
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 1.00 :\033[0m\n")
print_table(data2)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}else{
a = paste(x, mod, mod2,sep = " * ")
c = paste(y , a, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 3 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
data3 = data.table(slopes[[3]])
a = unlist(data1[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data1[,1] = a
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
sd = sd(unlist(select(data, mod2)))
mean = round(mean(unlist(select(data, mod2))),3)
b = round(mean - sd,3)
c = round(mean + sd,3)
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(b), "(- 1 SD):\033[0m\n")
print_table(data1)
a = unlist(data2[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data2[,1] = a
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(mean), "(Mean):\033[0m\n")
print_table(data2)
a = unlist(data3[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data3[,1] = a
names(data3)[1] = paste(mod,"(mod)",sep = " ")
names(data3)[2] = "Effect"
names(data3)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(c), "(+ 1 SD):\033[0m\n")
print_table(data3)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}
}
}else{
datamod = unlist(select(data, mod))
datamod2 = unlist(select(data, mod2))
if(P_dif(datamod) == 2){
if(P_dif(datamod2) == 2){
a = paste(x, mod, sep = " * ")
b = paste(x, mod2, sep = " * ")
ab = paste(a, b, sep = " + ")
c = paste(y , ab, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 2 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod + x * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 0.00 :\033[0m\n")
print_table(data1)
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 1.00 :\033[0m\n")
print_table(data2)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}else{
a = paste(x, mod, sep = " * ")
b = paste(x, mod2, sep = " * ")
ab = paste(a, b, sep = " + ")
c = paste(y , ab, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 2 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod + x * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
data3 = data.table(slopes[[3]])
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
sd = sd(unlist(select(data, mod2)))
mean = round(mean(unlist(select(data, mod2))),3)
b = round(mean - sd,3)
c = round(mean + sd,3)
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(b), "(- 1 SD):\033[0m\n")
print_table(data1)
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(mean), "(Mean):\033[0m\n")
print_table(data2)
names(data3)[1] = paste(mod,"(mod)",sep = " ")
names(data3)[2] = "Effect"
names(data3)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(c), "(+ 1 SD):\033[0m\n")
print_table(data3)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}
}else{
if(P_dif(datamod2) == 2){
a = paste(x, mod, sep = " * ")
b = paste(x, mod2, sep = " * ")
ab = paste(a, b, sep = " + ")
c = paste(y , ab, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 2 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod + x * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
a = unlist(data1[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data1[,1] = a
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 0.00 :\033[0m\n")
print_table(data1)
a = unlist(data2[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data2[,1] = a
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) = 1.00 :\033[0m\n")
print_table(data2)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}else{
a = paste(x, mod, sep = " * ")
b = paste(x, mod2, sep = " * ")
ab = paste(a, b, sep = " + ")
c = paste(y , ab, sep = " ~ ")
cat("\033[37m
PROCESS Model Code : 2 (Hayes, 2018; www.guilford.com/p/hayes3)\033[0m\n")
cat("\033[34m- Outcome (Y) :", paste(y), "\033[0m\n")
cat("\033[34m- Predictor (X) :", paste(x), "\033[0m\n")
cat("\033[34m- Moderator variable 1 (M) :", paste(mod), "\033[0m\n")
cat("\033[34m- Moderator variable 2 (M) :", paste(mod2), "\033[0m\n")
cat("\033[34m- Formula :", paste(c), "\033[0m\n")
data = rename(data, "y" = y, "mod" = mod, "x" = x, "mod2" = mod2)
model = lm(formula = y ~ x * mod + x * mod2, data = data)
result<- sim_slopes(model, pred = x, modx = mod, mod2 = mod2, jnplot = T)
slopes = result$slopes
data1 = data.table(slopes[[1]])
data2 = data.table(slopes[[2]])
data3 = data.table(slopes[[3]])
a = unlist(data1[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data1[,1] = a
names(data1)[1] = paste(mod,"(mod)",sep = " ")
names(data1)[2] = "Effect"
names(data1)[6] = "t"
sd = sd(unlist(select(data, mod2)))
mean = round(mean(unlist(select(data, mod2))),3)
b = round(mean - sd,3)
c = round(mean + sd,3)
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(b), "(- 1 SD):\033[0m\n")
print_table(data1)
a = unlist(data2[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data2[,1] = a
names(data2)[1] = paste(mod,"(mod)",sep = " ")
names(data2)[2] = "Effect"
names(data2)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(mean), "(Mean):\033[0m\n")
print_table(data2)
a = unlist(data3[,1])
a = round(a, 3)
a[1] = paste(a[1], "(- SD)", sep = " ")
a[2] = paste(a[2], "(Mean)", sep = " ")
a[3] = paste(a[3], "(+ SD)", sep = " ")
data3[,1] = a
names(data3)[1] = paste(mod,"(mod)",sep = " ")
names(data3)[2] = "Effect"
names(data3)[6] = "t"
cat("\033[1;37m
While",paste(mod2), "(mod2) =",paste(c), "(+ 1 SD):\033[0m\n")
print_table(data3)
interact_plot(model,
pred = x,
modx = mod,
mod2 = mod2,
interval = TRUE, x.label = x, y.label = y ,colors = "seagreen",main.title = main.title)
}
}
}
}
}