Chapter 9 第八讲：回归模型(一)
我们之前讨论的内容主要分为两方面。首先是学习R语言的一些基本知识，另一方面则是使用R代码来帮助我们解决描述性统计问题。如果大家还记得心理统计学中的内容，它分为描述统计和推断统计两部分。我们使用数据来进行统计推断，而R语言则可以帮助我们更灵活地实现各种统计方法。
纯粹的R代码学习 → 使用R语言来实现统计知识。当然，这种灵活性既有好处也有坏处。好处是我们有很多选择，坏处则是面对众多选择，我们可能会不知道如何选择。但是，如果我们能够度过刚开始不知道如何选择的阶段，后面就能更好地运用统计知识。另外，在接下来的课程中，我们将重点讨论回归模型，例如回归模型一、回归模型二和回归模型三。
我们之所以关注回归模型，是因为我们希望借此机会将大家在心理学、社会科学研究中常用的统计检验统一到回归框架下。这也是近年来一些研究者推荐的做法。实际上，心理学使用的统计方法与其他学科并没有本质区别，只是大家的偏好问题。在心理学领域中，最常用的方法便是各种回归模型的特例。
9.1 研究问题
我们从研究问题开始，先来回顾一下人类企鹅计划的关键变量。其中一个是恋爱状态，另一个是核心温度，还有一个是社交复杂程度，以及赤道距离。在刚开始进行数据分析时，我们可能没有特别明确的假设，但我们想要了解社会关系，尤其是亲密关系，是否会影响我们的体温，是否能帮助我们调节核心温度。
我们可以使用我们知道的统计方法进行一些探索性分析，比如检验恋爱状态和赤道距离之间是否存在交互作用。大家还记得中介模型吗？其中一个变量是社交复杂程度，另一个是核心温度，中间有一个变量是赤道距离。研究发现，在不同的情侣关系群体中，这三个变量之间的关系是不一样的。
在接下来的课程中，我们将回顾一些关键概念，并进行一些常用的统计检验，包括t检验和方差分析。我们还将介绍为什么t检验和方差分析实际上是线性回归的特例。关于第一个研究问题，我们主要关注恋爱状态是否会影响核心体温。我们会比较两组不同的人，看他们的核心体温是否有差异。
基于恋爱状态，我们可以将数据分为两组：一组是处于恋爱或亲密关系中的人，另一组是没有处于亲密关系的人。我们想要比较这两组之间是否存在差异，通常会采用独立样本t检验。这是我们在学习过程中接触过的统计方法，大家应该都不陌生。
(引自9.2 t-test作为回归模型的特例
9.2.1 独立样本t检验(independent t-test)
当然，我们需要了解一些基础知识，比如独立样本t检验。第一，我们需要满足正态性假设，即两个样本都来自正态总体。我们也知道，如果样本量足够大，即使不严格服从正态分布，使用t检验也是没有问题的。第二，我们还需要满足方差同质性假设，即两个样本的方差应该是类似的。第三，两个样本应该是独立的。
在进行独立样本t检验时，我们的零假设是这两个独立样本在某个变量上的均值没有差异，即μ1等于μ2。而我们的备择假设则是它们的总体均值是有差异的，即μ1不等于μ2。接下来，我们需要计算t值，这是进行t检验时通常需要用到的一个公式。
\[t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]
在R语言中，如果我们要进行t检验，首先我们需要进行数据预处理。这包括清洗数据，处理缺失值，选择我们感兴趣的变量，以及生成新的变量等。
首先，我们可能需要为数据集生成一些新的变量，比如在原始数据中可能没有被试编号，我们可以随机生成。然后，我们选择自己在分析中关心的问题，使用dplyr函数选择我们感兴趣的变量。
在处理数据时，我们需要注意缺失值。在初步分析时，我们一般选择忽略缺失值，直接将其剔除，以便快速查看结果。此外，还需要将一些变量转换为因子，比如将是否处于亲密关系的变量转换为因子，并赋予两个水平：恋爱和单身。
接下来，我们关注的因变量是被试的体温，我们想知道在两组之间是否有差异。在原始数据中，有两次测量体温的数据，我们可以选择将两次测量的平均值作为新的变量，这可以通过R语言中的行函数实现。具体来说，我们可以创建一个新的变量，这个变量是以temperature字符串开头的列的平均值。
这些步骤都是数据预处理的一部分，是进行t检验之前必要的步骤。
df.penguin <- bruceR::import(here::here('data', 'penguin', 'penguin_rawdata.csv')) %>%
dplyr::mutate(subjID = row_number()) %>%
dplyr::select(subjID,Temperature_t1, Temperature_t2, socialdiversity,
Site, DEQ, romantic, ALEX1:ALEX16) %>% # 选择变量
dplyr::filter(!is.na(Temperature_t1) & !is.na(Temperature_t2) & !is.na(DEQ)) %>% # 处理缺失值
dplyr::mutate(romantic = factor(romantic, levels = c(1,2), labels = c("恋爱", "单身")), # 转化为因子
Temperature = rowMeans(select(., starts_with("Temperature"))), # 计算两次核心温度的均值
ALEX4 = case_when(TRUE ~ 6 - ALEX4),
ALEX12 = case_when(TRUE ~ 6 - ALEX12),
ALEX14 = case_when(TRUE ~ 6 - ALEX14),
ALEX16 = case_when(TRUE ~ 6 - ALEX16),
ALEX = rowSums(select(., starts_with("ALEX")))) # 反向计分后计算总分要在R语言中进行t检验，我们可以使用自带的stats包中的t.test函数。这是一个非常常用的t检验函数。在使用t.test函数时，我们需要输入一些参数。第一个参数是经过筛选的数据框，第二个参数是我们感兴趣的自变量（如temp），第三个参数是分组变量（如romantic）。此外，我们还可以假定两组的方差是相等的。运行t.test函数后，我们可以得到结果，包括t值、自由度（df）和p值。在这个例子中，t值为0.34664，自由度为1425，而p值较大，表示在恋爱组和非恋爱组之间的体温差异不显著。从结果来看，恋爱状态对体温的影响似乎并不大。
stats::t.test(data = df.penguin, # 数据框
Temperature ~ romantic, # 因变量~自变量
var.equal = TRUE) %>%
capture.output() # 将输出变整齐## [1] ""
## [2] "\tTwo Sample t-test"
## [3] ""
## [4] "data: Temperature by romantic"
## [5] "t = -0.34664, df = 1425, p-value = 0.7289"
## [6] "alternative hypothesis: true difference in means between group 恋爱 and group 单身 is not equal to 0"
## [7] "95 percent confidence interval:"
## [8] " -0.0555949 0.0388971"
## [9] "sample estimates:"
## [10] "mean in group 恋爱 mean in group 单身 "
## [11] " 36.38498 36.39333 "
## [12] ""当然，除了t.test函数，还有其他方法可以进行类似的分析。不过，在这个简单的示例中，t.test已经足够满足我们的需求。
我们说t检验是一个特殊的线性回归模型，这是因为在R语言中，它们的编写方式非常相似。在回归模型中，我们将自变量放在前面，因变量放在后面。为了理解这个概念，我们需要简要回顾一下线性回归模型。
线性回归模型是一种统计方法，用于研究一个或多个变量能否预测或解释另一个变量。我们将用来预测的变量称为预测变量或自变量，而被预测的变量称为因变量或响应变量。线性回归的核心是通过拟合一条直线来表示两个变量之间的关系，使得直线与每个数据点之间的距离最小。这样，我们便可以利用这条直线来进行预测。
我们通常会用一个方程或等式来表示线性回归模型，如y = β0 + β1x1 + β2x2 + … + ε。其中y是我们关心的因变量，x1、x2等是自变量，β0、β1、β2等是回归系数，而ε是误差项。
\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \epsilon\]
在学习线性回归时，我们通常关注连续变量之间的关系。这意味着x和y都是连续变量。而在t检验中，我们关注的是分组变量，这似乎与线性回归有所不同。然而，在特定情况下，我们可以将t检验视为线性回归的一个特例。当我们分析的自变量是一个二分类变量时，线性回归模型实际上等同于独立样本t检验。所以，虽然它们在某些方面有所不同，但t检验确实可以看作是线性回归的一个特殊情况。
9.2.2 线性回归(linear regression)
在t检验中，我们的因变量，比如体温，是连续的，而自变量，比如是否处于亲密关系，是二分类的。这似乎与我们通常的线性回归模型有所不同，因为在线性回归中，我们通常关注的是连续变量之间的关系。然而，实际上，当我们的自变量是二分类变量时，我们也可以将其视为线性回归模型的一个特例。
想象一下，我们在图上有两堆数据点，一堆是处于亲密关系的人的体温，另一堆是非恋爱状态的人的体温。在这两堆数据点之间，我们可以拟合出一条回归线，这条线可以帮助我们进行预测。当x=1（处于亲密关系）时，我们预测的y值（体温）是多少？当x=2（非恋爱状态）时，我们预测的y值是多少？
在常规的线性回归中，x可以有很多值，y也可以有很多值。然而，在t检验中，x只有两个值，一个是1，一个是2（或者0和1）。我们要做的预测也是，当x=1时，y是多少？当x=2时，y是多少？这就是为什么我们说独立样本t检验是线性回归模型的一个特例，特别是当我们的自变量是二分变量时。
在R语言中，我们可以通过代码来验证这个观点。无论我们是使用t.test函数进行t检验，还是使用lm函数进行线性回归，我们得到的结果应该是一样的。这是因为在这种特殊情况下，这两种方法本质上是在做同样的事情。
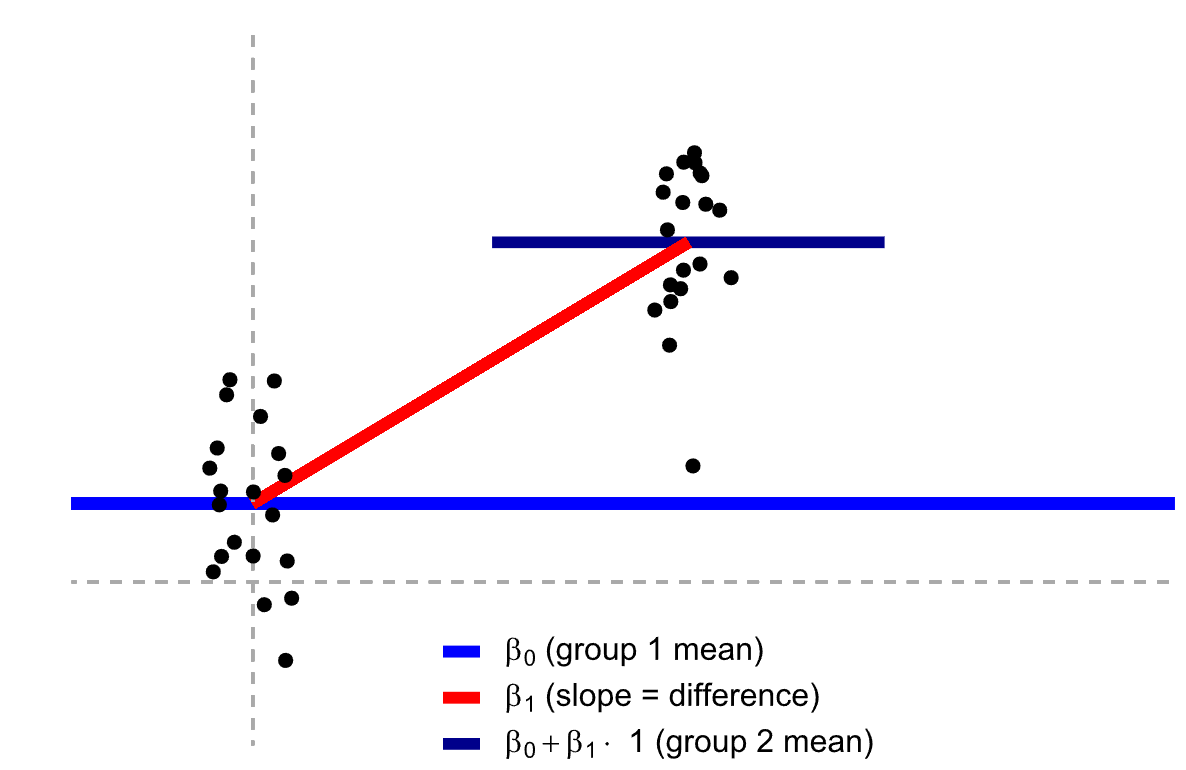
实际上，在进行线性回归时，我们可以采用不同的编码方法来表示分类变量。比如，对于二分类变量，我们可以将其编码为0和1。当我们采用这种编码方式时，线性回归方程为y = β0 + β1x1。其中，x1只有两个可能的取值：0和1。当x1 = 0时，y = β0。当x1 = 1时，y = β0 + β1。这样，我们可以看到，β1实际上表示了两组之间的差异。当然，这只是一种方便我们理解的编码方式。在实际应用中，我们可能会遇到更复杂的编码方法，比如虚拟变量编码、效应编码等。这些编码方法在处理多分类变量时尤为有用。
总之，独立样本t检验实际上可以看作是线性回归模型的一个特例，特别是当我们的自变量是二分变量时。无论我们是使用t.test函数进行t检验，还是使用lm函数进行线性回归，我们得到的结果应该是一样的。这是因为在这种特殊情况下，这两种方法本质上是在做同样的事情。
首先，我们进行预处理数据。这个过程相对简单，大家应该都能理解。接下来，我们来看一下t检验。假设我们不对结果进行整理，而是直接查看原始输出，那么我们会看到以下内容：t值是多少，df值是多少，以及p值是多少。我们之前提到过，t检验实际上是一种特殊的回归。
# t检验
stats::t.test(
data = df.penguin,
Temperature ~ romantic,
var.equal = TRUE) %>%
capture.output() # 将输出变整齐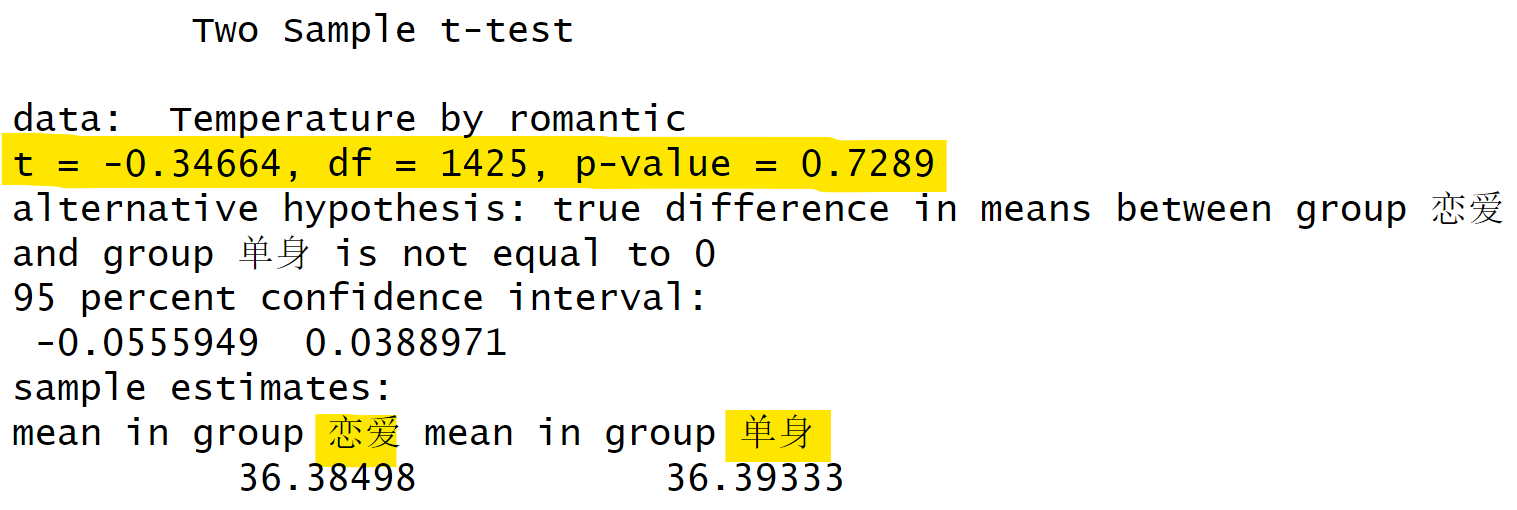
我们继续讨论回归模型。在R语言中，线性回归模型的常用函数是lm。我们可以通过比较t检验和线性回归模型得到的t值、df值和p值来判断它们是否相同。
在这个地方，大家可以看到我们使用的是stats包的lm代码，这个代码代表线性回归模型。我们在这里还是采用同样的数据，然后使用回归模型的公式。在这个公式中，temp是我们的因变量y，而romantics是我们的自变量x。这个x是一个因子，我们需要将其转换为因子。在编写这个公式时，我们只需在因变量前加上一个波浪号，然后加上自变量。接下来，lm函数会自动帮助我们处理因子变量在回归分析中的一些后续处理。最后，它会给我们一个结果。
# 线性回归
model.inde <- stats::lm(
data = df.penguin,
formula = Temperature ~ 1 + romantic
)
summary(model.inde)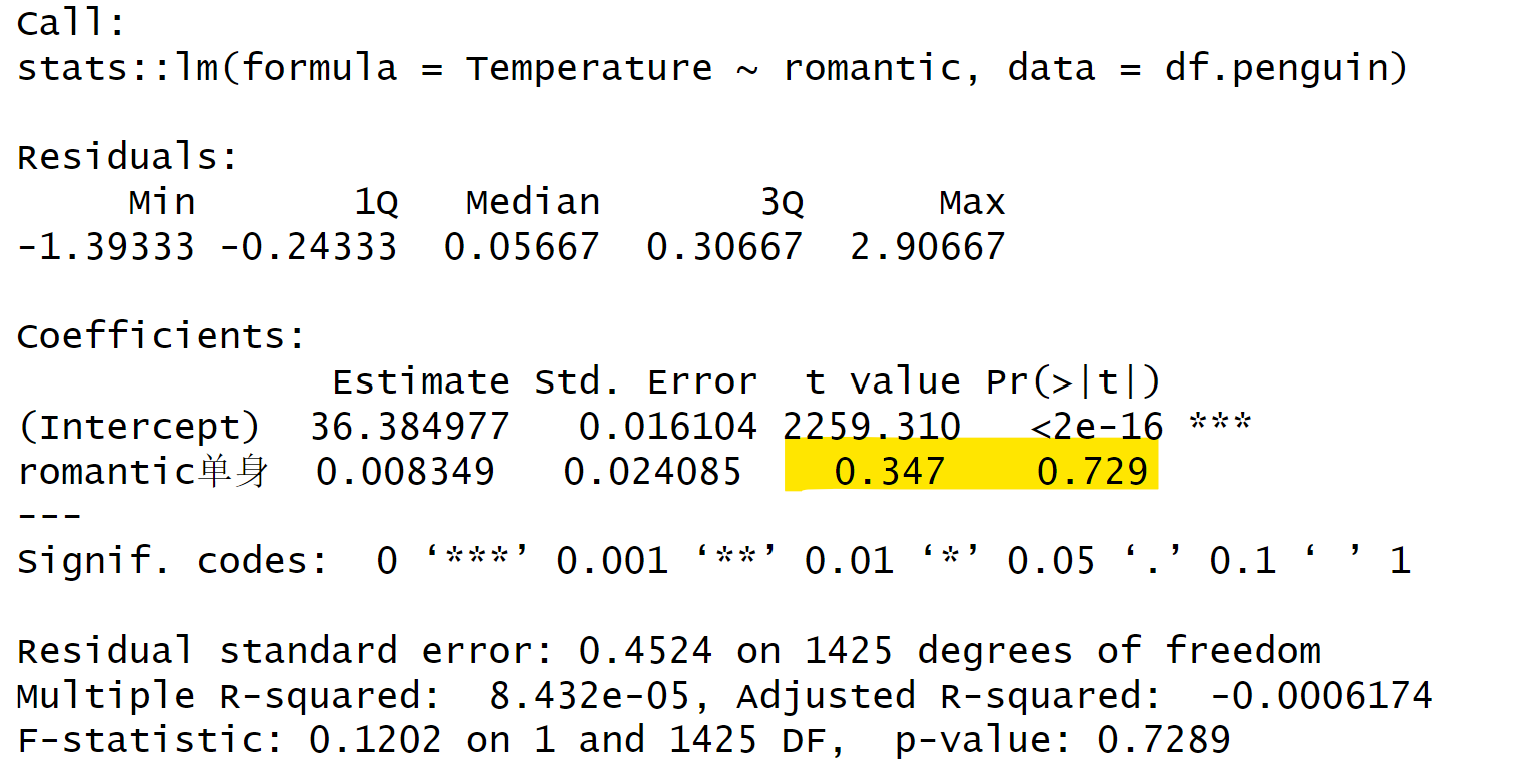
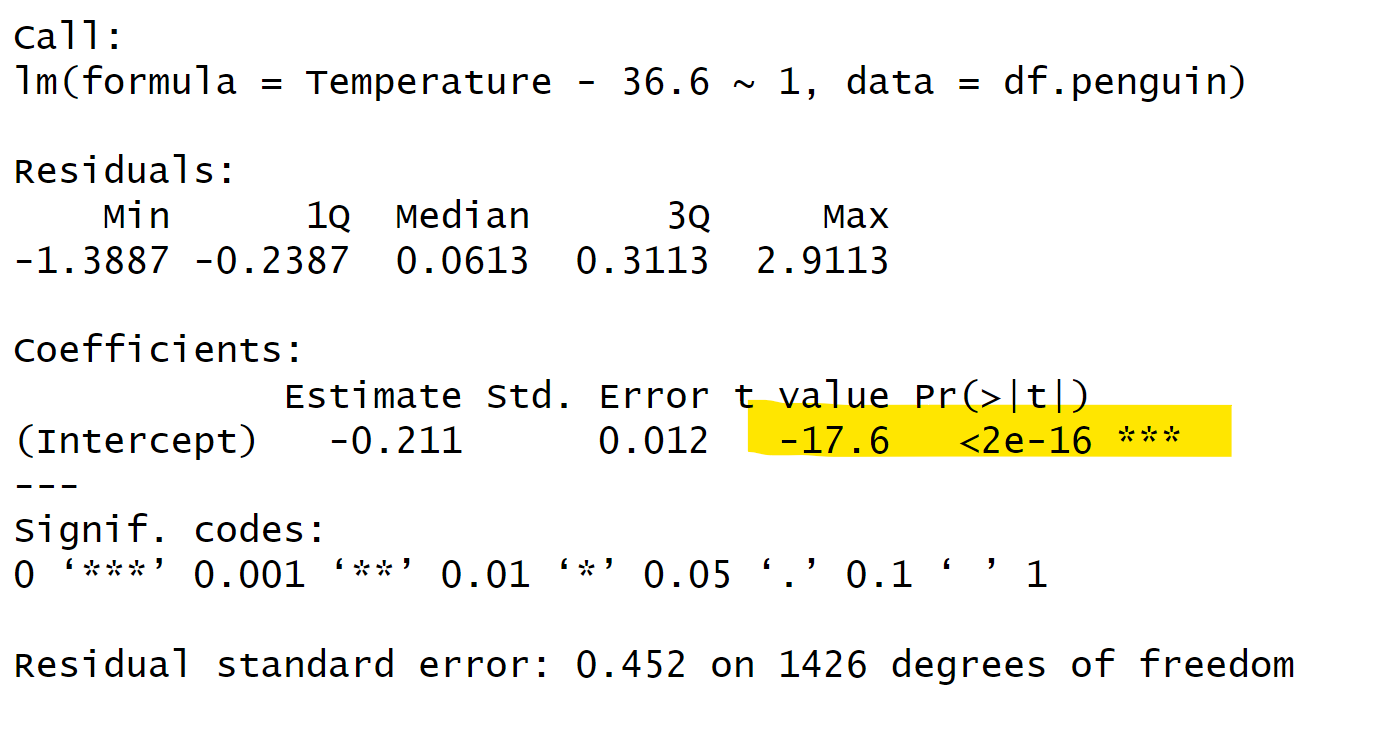
我们可以看到，这里的t值、p值与我们之前的结果基本相同（t值为0.347，p值为0.729）。这是因为我们主要关注的是单身对结果的影响。因此，我们可以得出这样的结论：两组之间的差异在t检验和回归模型中表现得相当一致。在回归模型中，可能还会有一个intercept，但我们通常不会关注它。斜率slope代表的含义是当x从一个单位变化到另一个单位时，我们的因变量y会发生多少变化。而对于我们这种只有二分变量的自变量的情况，就代表两组之间的差异。
因此，我们可以说，二分变量的t检验与回归模型之间存在密切关系。我们关注的是回归系数，它的统计检验值与t检验中的值完全相同。这就是我们希望展示的结果。所以，在心理学中常用的t检验实际上是线性回归的一种特殊情况。
那当然，这里涉及到一个知识点，我们没有详细展开讲，但大家以后感兴趣的话可以去了解。这个知识点就是编码方法。因为我们的数据有两个水平，可能有多种编码方法。例如，我们可以把一个水平编码为0，另一个水平编码为1。那么我们的公式可以表示为：y = β0 + β1 * x1。在这个情况下，x1只有两种取值：0和1。当x=0时，y等于β0；当x=1时，y等于β0 + β1。所以这个时候我们可以看出β1就是两组之间的区别。
当然，这只是一种方便我们理解的方法。另外一种常用的编码方法是将x1编码为-0.5和0.5。在这种情况下，对β的解读就不一样了。大家可以将这种编码带入公式后，自己去观察一下。我们在这里就不展开详细讲解了，因为我们主要想向大家介绍这个概念。大家可以在R语言中多探索一下这个知识点，以便更好地理解和应用。
9.2.3 单样本t检验(one sample t-test)
那么同理，一系列的t检验其实都可以认为是回归模型的特例。例如，我们来看单样本t检验。虽然我们平时很少使用单样本t检验，但在某些情况下，它还是有用的。比如，我们想要判断某个班级的成绩是否属于全校成绩的总体。在这种情况下，我们实际上是在比较这个班级的成绩均值和全校的总体均值。
在单样本t检验中，我们关心的是一个样本的均值是否等于某个特定值。例如，在“在penguin数据中，全体被试的核心体温(Temperature)是否等于36.6？”这个例子中，我们关心的是全体被试的核心温度是否等于正常人的温度。单样本t检验的计算公式可以不用深究，关键是理解其背后的逻辑。
\[t = \frac{\bar{X} - \mu}{s / \sqrt{n}}\]
\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_p x_p + \epsilon\]
单样本t检验中，仅截距不为0。此时公式为：
\[y = \beta_0\] \[H_0: \beta_0 = 0\] 如图所示，这里有一群点，我们想要比较的是这些点的均值（例如用菱形表示）与某条线（特定值）之间是否存在显著性差异，或者说这些点的均值与这条线是否来自同一个总体。在这种情况下，我们可以构建一个只包含截距项β0的回归模型，即y = β0。我们也可以使用回归模型进行统计检验。
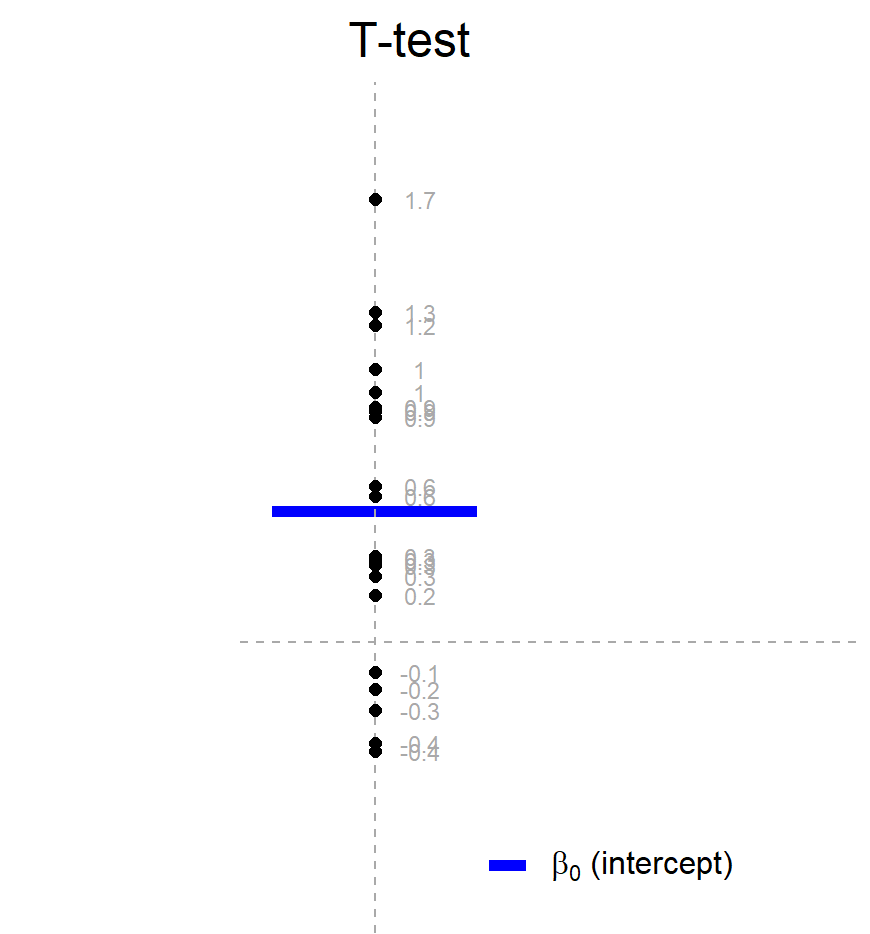
当我们进行单样本t检验时，我们需要稍微调整公式。我们将因变量（temperature）减去我们想要比较的特定值（例如30），然后考虑减去特定值后的因变量均值是否属于一个以0为均值的正态分布。在这个回归模型中，我们加入一个截距项，用于进行t检验。
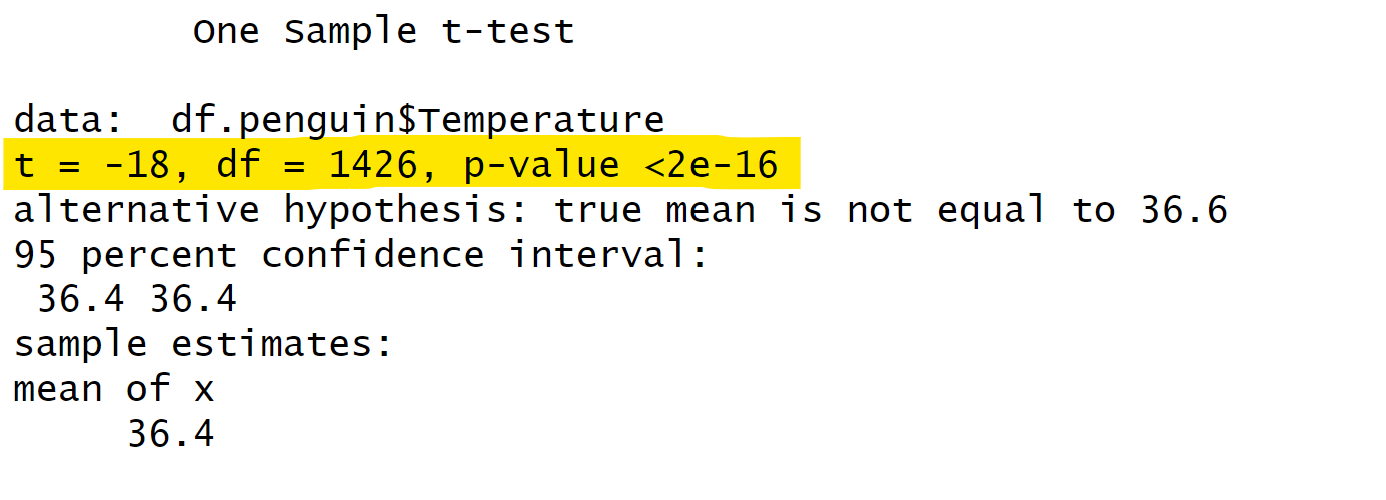
当然，在实际应用中，我们可以直接使用单样本t检验，将观测值x与某个特定值进行比较。这样，我们就可以判断样本数据的均值是否与特定值之间存在显著性差异，从而得出结论。总之，无论是单样本t检验还是回归模型，它们都可以帮助我们解决实际问题。在具体分析过程中，我们可以根据需要选择合适的方法。
9.2.4 配对样本t检验(paired t-test)
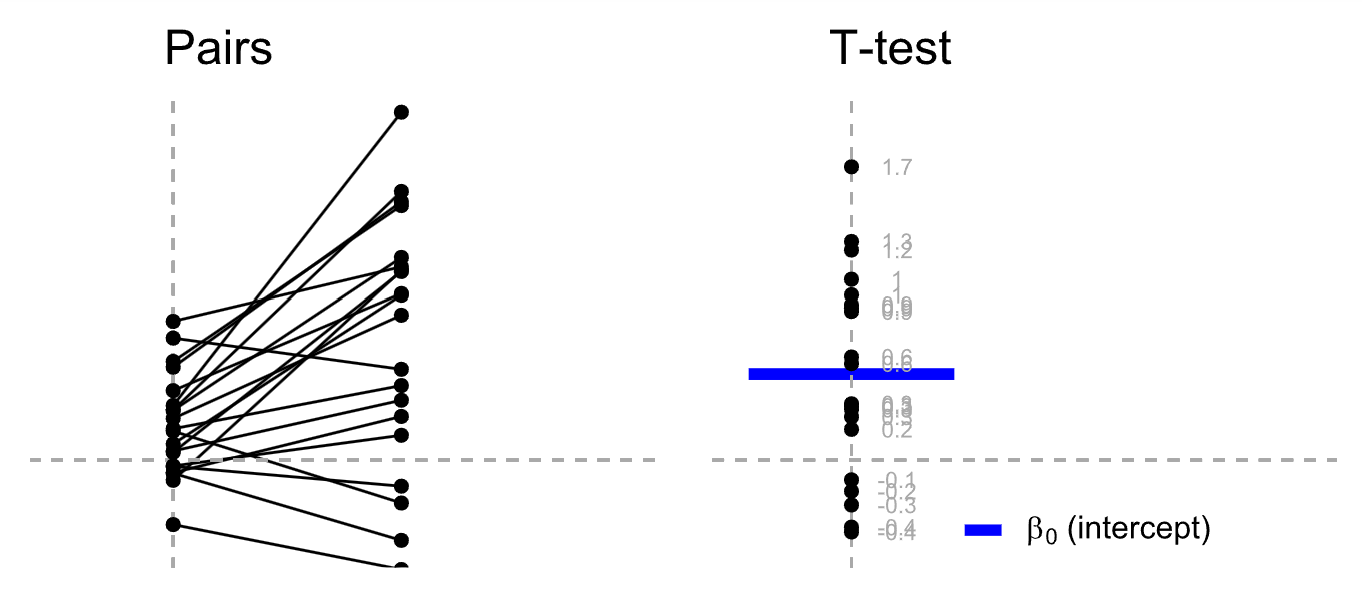
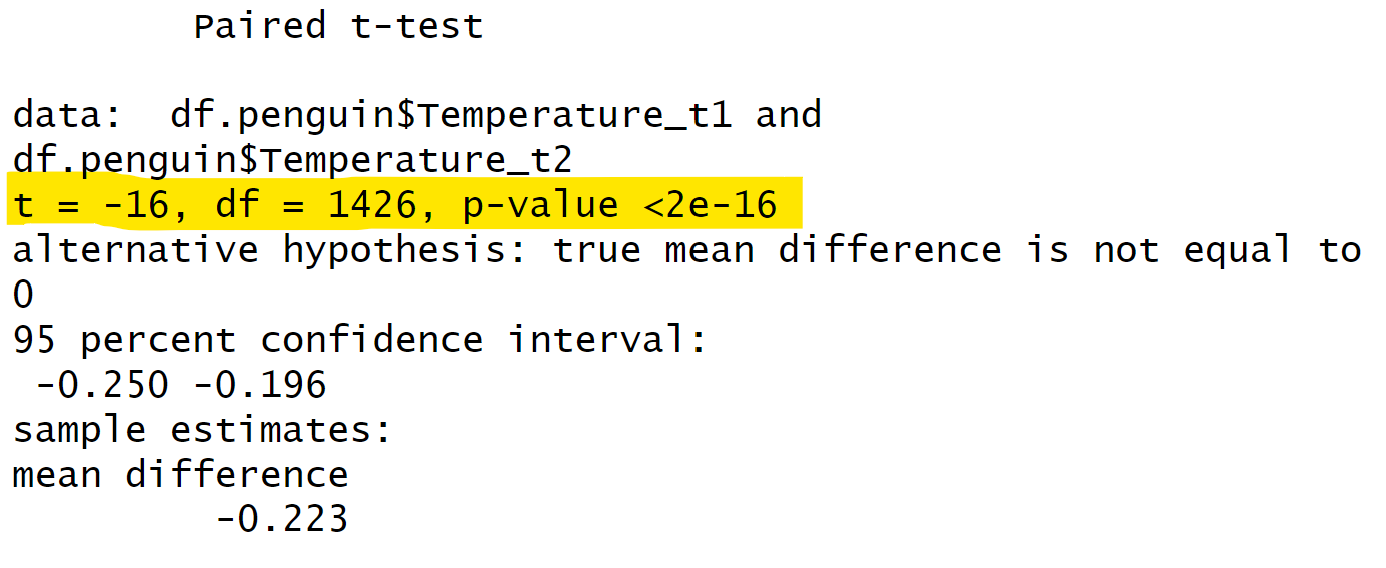
那么，对于配对样本t检验，我们其实可以把它看作是单样本t检验。因为配对样本t检验中的数据是一一对应的，我们可以通过一个简单的操作，即将两列配对数据相减，得到一列新的数据。然后，我们可以将这列新数据进行单样本t检验。
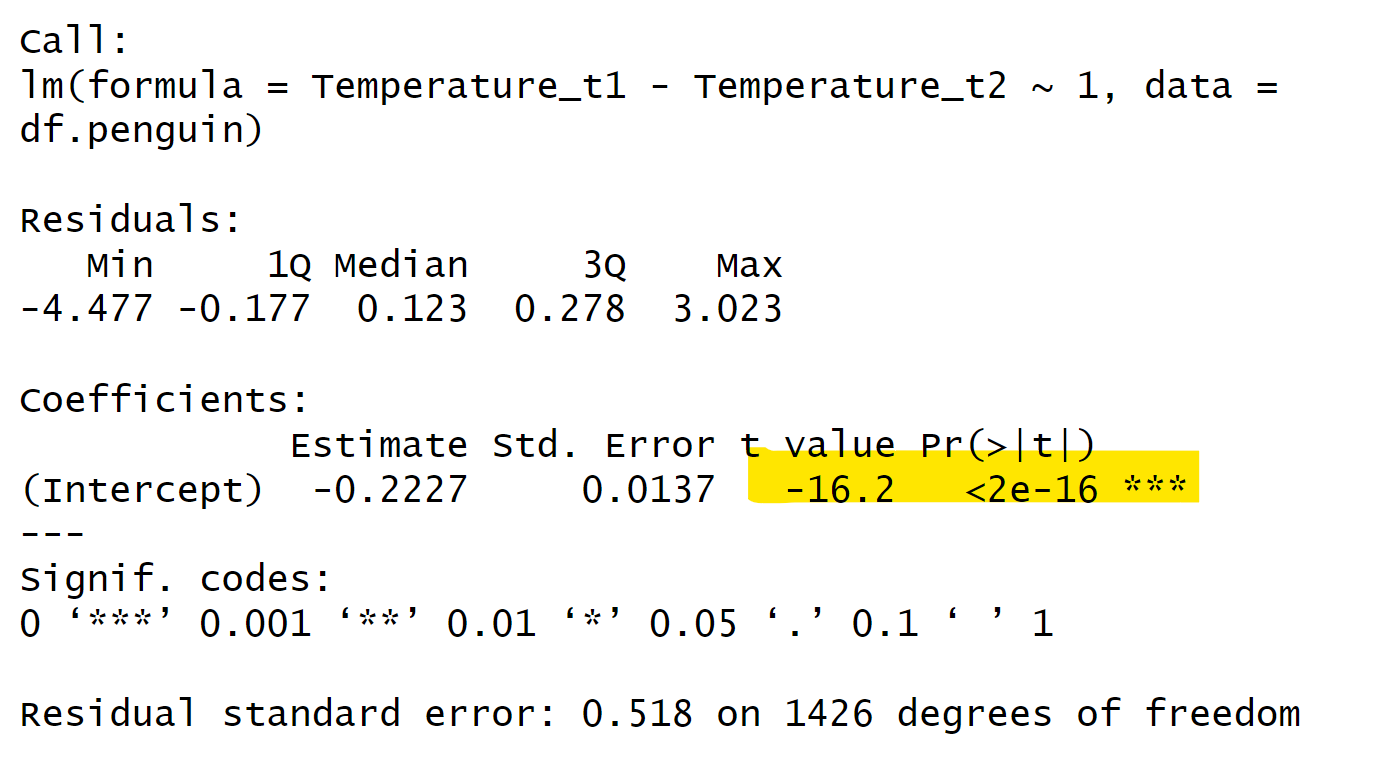
\[t = \frac{\bar{X} - \mu}{s / \sqrt{n}}\] 这里的前提条件我们就不详细讲了。简单来说，对于配对样本t检验，我们可以先将两个值相减，得到他们的差值。然后，我们检验这个差值是否显著地不同于零。如果差值的分布明显不同于零，那么我们就可以认为两者之间存在显著的差异。 \[y_1 - y_2 = \beta_0 \] \[H_0: \beta_0 = 0 \] 我们之所以能这样做，是因为在配对样本t检验中，每个被试都有两个数据点，这两个数据点是一一对应的。但是，对于独立样本t检验，由于数据点之间没有形成配对关系，我们不能直接相减。
同样，对于配对样本t检验，我们也可以使用回归方法进行检验。方法类似于独立样本t检验，我们只需将两个值相减，然后检验这个差值的均值是否等于零。在R语言中，我们可以使用t.test函数来进行配对样本t检验。我们只需将两列数据分别作为x和y输入，然后设置参数paired为TRUE，表示这两列数据是配对的，就可以进行配对样本t检验了。
在前面我们讲了关于亲密关系和非亲密关系的两组人在体温上是否有区别的问题。我们可以使用配对样本t检验来进行检验，而配对样本t检验实际上是一个特殊的回归模型。同样地，对于所有其他类型的t检验，它们也都可以看作是特定的回归模型。因此，t检验与线性模型的本质是相同的。
9.2.5 bruceR::TTEST
这里，我们可以介绍一下bruceR包中的t检验功能，它涵盖了我们前面提到的各种t检验，并且输出结果非常方便。如果大家下载了我们的课件，可以看到关于bruceR包中t检验各种参数的介绍。bruceR包基本上涵盖了所有类型的t检验，包括独立样本t检验、配对样本t检验和单样本t检验。它的输出结果通常是一个三线表，方便大家查看和理解。
[单样本t检验]
bruceR::TTEST(
data = df.penguin, # 数据
y = "Temperature", # 确定变量
test.value = 36.6, # 固定值
test.sided = "=") # 假设的方向
[配对样本t检验]
stats::t.test(
x = df.penguin$Temperature_t1, #第1次
y = df.penguin$Temperature_t2, #第2次
paired = TRUE)
bruceR::TTEST(
data = df.penguin, # 数据
y = c("Temperature_t1",
"Temperature_t2"), # 变量为两次核心体温
paired = T) # 配对数据，默认是FALSE
无论是使用bruceR包中的t检验功能，还是R语言自带的t检验功能，我们都可以发现它们得到的结果与线性回归模型的结果是一模一样的。这再次证实了t检验与线性回归模型之间的密切关系。在实际研究中，我们可以根据问题的具体情况选择合适的方法，无论是t检验还是线性回归模型。同时，理解它们之间的关系有助于我们更好地掌握统计分析的原理和技巧。
9.2.6 总结
我们来做一个简单的总结。对于t检验，我们可以使用R自带的t.test函数。虽然语法上略有不同，但实际上，线性模型和t检验在本质上是一致的。单样本t检验可以看作是一个仅有截距的线性模型；独立样本t检验是一个仅有截距和一个斜率的线性模型；而配对样本t检验则是一个基于差值的仅有截距的线性模型。
独立样本t检验也可以看作是一个自变量为二分变量的线性回归模型。要理解为什么仅有截距的回归模型与t检验相关，我们可能需要回顾正态分布、抽样分布等概念，以及为什么我们使用t值这个分布来进行检验。然而，我们在这里没有足够的时间来展开这个话题。如果大家对此感兴趣，可以自行深入学习，也很推荐大家关注包寒吴霜老师的专栏。
9.3 ANOVA & linear regression
接下来我们讨论方差分析，这也是心理学中常用的一种统计方法。在学习统计时，我们会花很多时间学习如何进行方差分解。
9.3.1 研究问题
以Penguin数据为例，我们刚才发现恋爱状态对体温没有太大影响。但我们可以进一步探讨它是否与距离赤道的距离有交互作用。因为我们知道，离赤道越远，气温就越寒冷。有时候，我们可能会发现某个自变量没有影响，但实际上它可能受到另一个自变量的调节。例如，在这个例子中，我们可以检验恋爱状态是否在较寒冷的地方影响体温，而在较暖和的地方则不需要调节。要检验这种交互作用，我们通常会想到使用双因素方差分析。
9.3.2 代码实操 & 知识回顾
双因素方差分析通常是我们在讨论方差分析时所指的完全随机方差分析。但在这里，我们需要注意我们使用的是双因素的重复测量方差分析，而不是完全随机的。也就是说，不同距离赤道的人以及处于不同恋爱状态的人并非随机分配。我们无法将某人随机分配到离赤道较近的恋爱状态这一组，因为这是一个横断数据。然而，我们仍然可以使用方差分析来进行数据分析。
在学习方差分析时，我们可能会了解到它的历史以及它所检验的假设。对我们来说，检验的假设是关键。也就是说，在各因素的各个水平下，因变量的均值是否完全相同。原假设认为各因素各水平下的因变量均值完全相同，而备择假设则认为各因素各水平下的因变量均值并不完全相同。通常情况下，只要有一个水平的因变量均值不同，方差分析就能探测出来。
当然，方差分析的使用也有一些前提假设，包括随机性、正态性、独立性和方差齐性等。这些内容我们在这里就不再详细展开了。
9.3.3 ANOVA代码实操|数据预处理
在R中实现方差分析的关键是选择合适的函数。当我们想进行多因素方差分析时，R中有一些常用的函数可以帮助我们实现。在进行方差分析之前，我们需要对数据进行一些预处理。
以距离赤道的距离为例，我们发现它是一个连续的数值变量。但为了进行方差分析，我们可以将其分为三个水平：热带、温带和寒温带。我们可以根据纬度的区别设定分隔点，例如，赤道到23.5度为热带，35度到40度为暖温带，40度到50度为中温带（统称为温带），50度以上为寒温带。我们可以使用R中的cut函数将连续性的数据划分为不同的段，并赋予不同的值。同时，我们可以为这个新变量命名为climate。 [vars]
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.293 34.433 39.912 39.842 51.317 60.391# 设定分割点
# [0-23.5 热带， 23.5-35 亚热带]， [35-40 暖温带， 40-50 中温带]， [50-66.5 寒温带]
breaks <- c(0, 35, 50, 66.5)
# 设定相应的标签
labels <- c('热带', '温带', '寒温带')
# 创建新的变量
df.penguin$climate <- cut(df.penguin$DEQ,
breaks = breaks,
labels = labels)
summary(df.penguin$climate)## 热带 温带 寒温带
## 396 592 439[tidy data]
9.3.4 代码实操|正态性检验
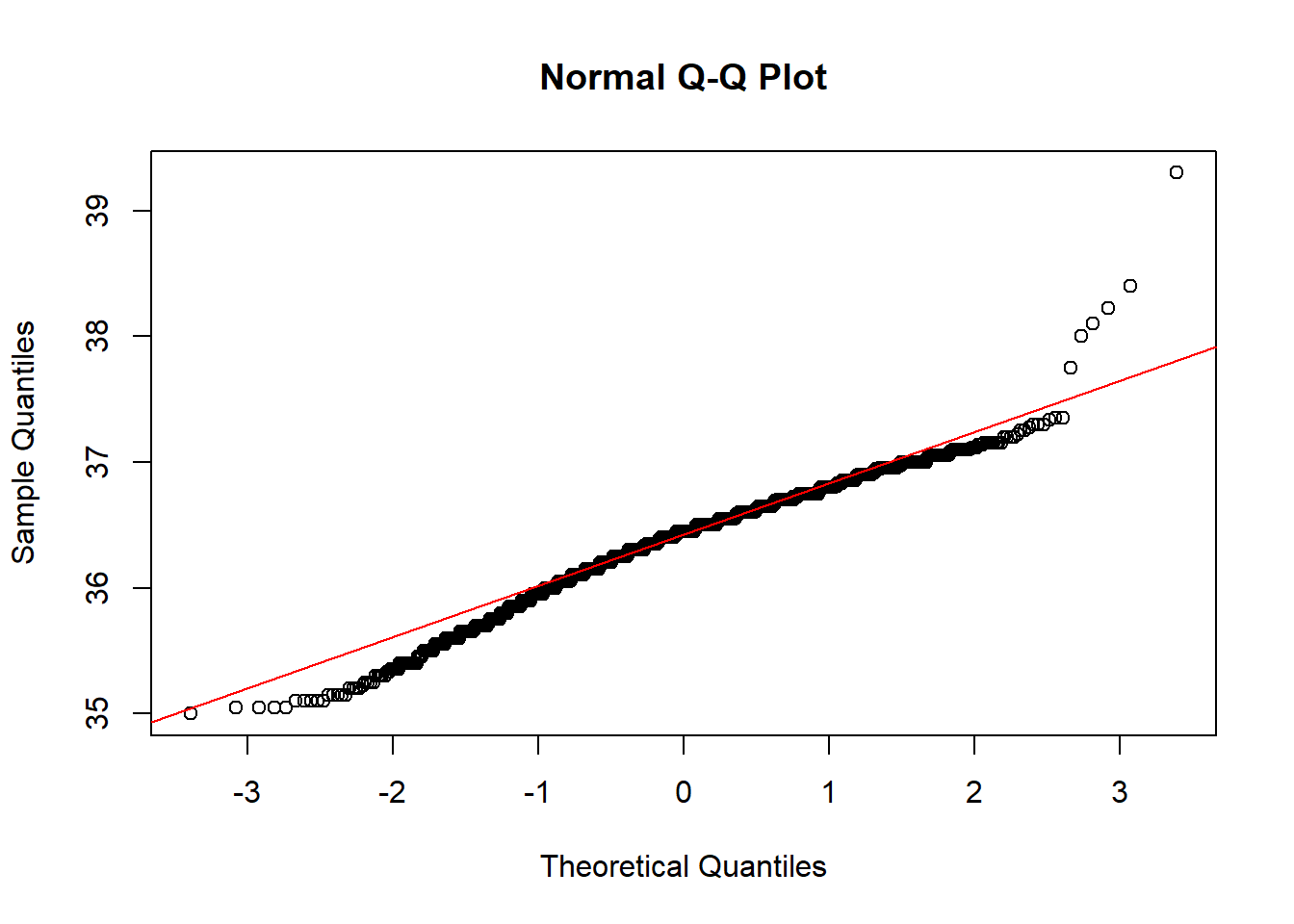
在进行方差分析前，我们还需要检验数据的正态性。R中有一些方法可以帮助我们检验正态性，例如KS检验和QQ图。通过这些方法，我们可以观察数据的分布情况。虽然数据可能不是完全正态分布的，但接近正态分布的数据也是可以接受的。
##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: df$Temperature
## D = 1, p-value < 0.00000000000000022
## alternative hypothesis: two-sided##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: df$Temperature_log
## D = 0.99981, p-value < 0.00000000000000022
## alternative hypothesis: two-sided[qq图]
ggplot(df, aes(Temperature)) +
geom_histogram(aes(y =..density..), color='black', fill='white', bins=30) +
geom_density(alpha=.5, fill='red')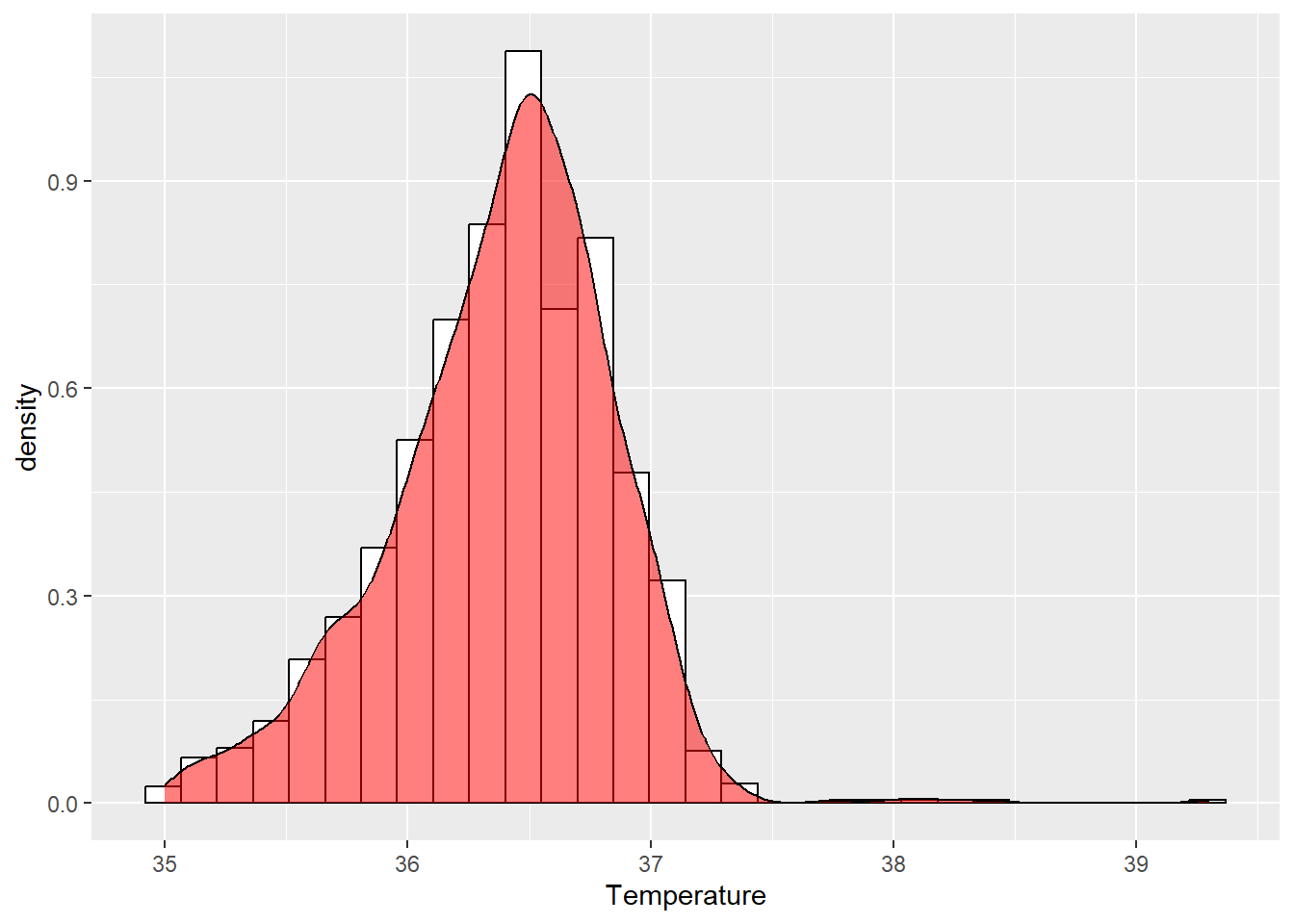
9.3.5 代码实操|双因素被试间方差分析
在R中实现方差分析，我们通常会用到aov函数，这是R自带的一个函数。实际上，这个函数来自于stats包，同样的，t.test函数和lm函数也是来源于这个包。在进行方差分析时，我们采用的语法与t检验非常相似，仍然是线性回归的写法。我们将因变量放在前面，自变量放在后面，中间用一个波浪号连接。然后，我们指定使用的数据。
在方差分析的语法中，我们使用乘号 * 来表示主效应及其交互作用。例如，我们可以写成climate * romantic，这表示考虑climate和romantic的主效应以及它们之间的交互作用。在R中，这样的写法非常常见，前面的波浪号表示因变量与自变量之间的关系，而乘号表示考虑主效应及交互作用。
实际上，这种线性方程有多种写法。例如，在t检验中，我们只关注romantic；而在方差分析中，我们加入了climate的主效应以及它们之间的交互作用。在R中最基础的包里，当我们进行方差分析时，实际上沿用了线性模型的语法。通过这种语法，我们可以得到方差分析的一些统计值，如F值、P值以及我们熟悉的平方和（SS，Sum of Squares）。
如果我们对方差分析的结果使用summary函数进行查看，我们会看到熟悉的方差分析表。在这个表中，我们可以看到两个主效应（romantic和climate）以及它们之间的交互作用。同时，表格中还包含了残差（Residuals）信息。这些信息有助于我们了解各个因素对因变量的影响程度和显著性。
## Df Sum Sq Mean Sq F value Pr(>F)
## climate 2 18.82 9.408 49.392 < 0.0000000000000002 ***
## romantic 1 0.24 0.244 1.280 0.25807
## climate:romantic 2 1.91 0.955 5.014 0.00676 **
## Residuals 1421 270.65 0.190
## ---
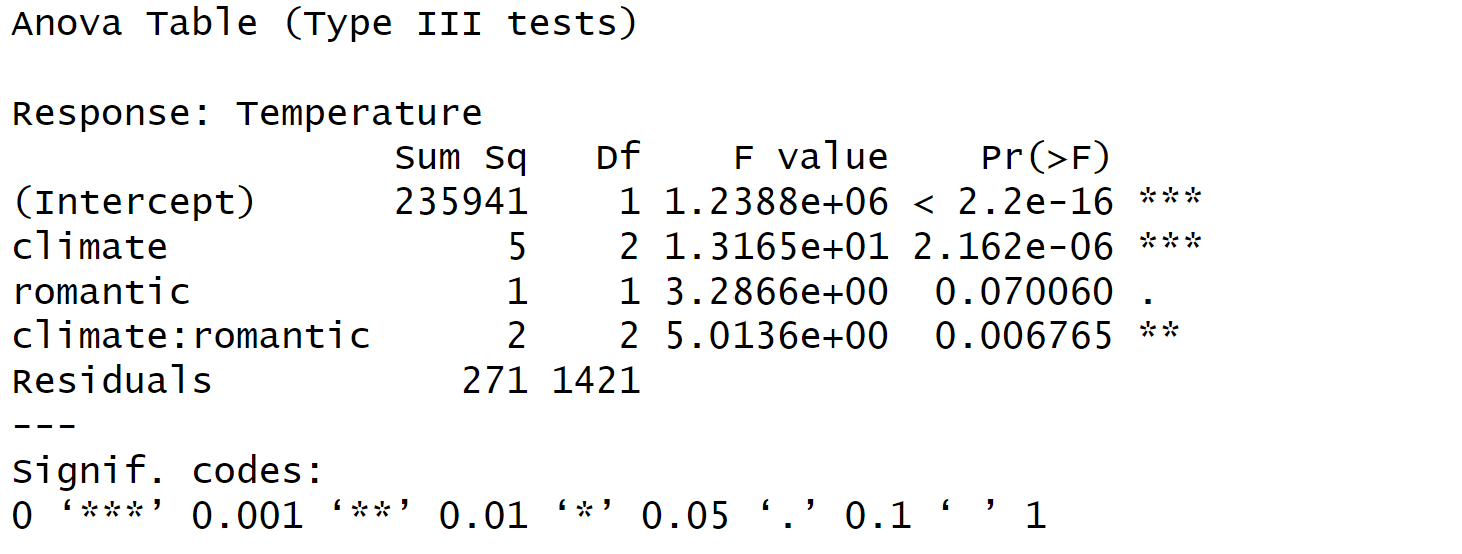
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1在进行方差分析时，有时我们会发现，在R中进行的分析结果与在SPSS中进行的结果不完全一样。例如，climate的F值在R中为49.39，而在SPSS中为50.88。这种情况下，我们可能会感到困惑，不知道是否可以信任R的结果，甚至可能会认为R的分析方法不靠谱。
[SPSS]
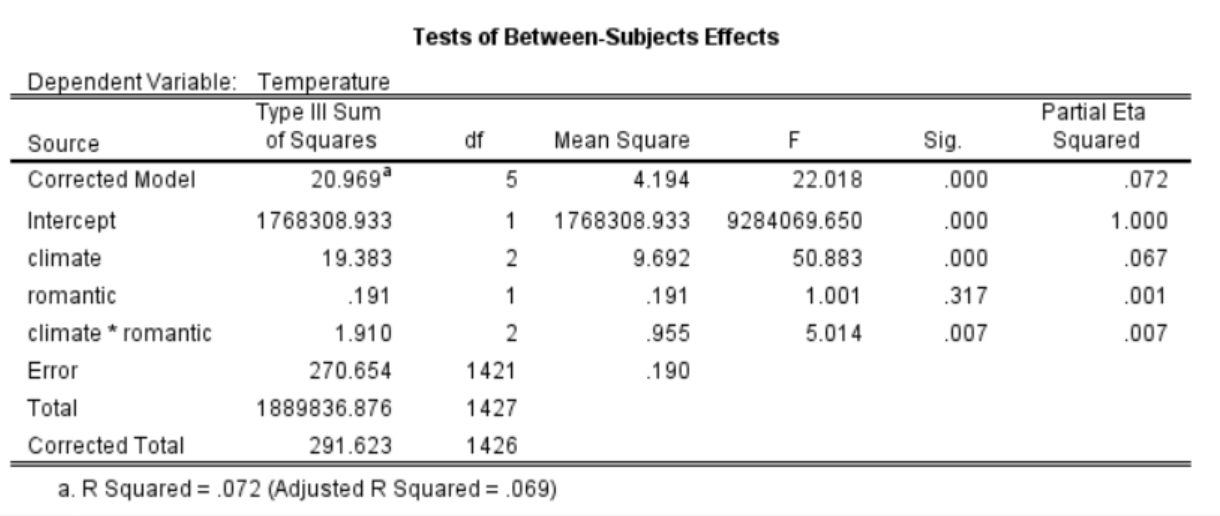实际上，这种差异的出现很可能是因为在R和SPSS中使用的方法或某些设置不同。这可能导致在相同的数据和看似相同的方法下，得到不同的分析结果。在这里，我们需要讨论一个问题：为什么方差分析这样一个看似简单的方法（我们在本科阶段就学过并且很熟悉），会在不同软件中产生不同的结果呢？
9.3.6 代码实操|平方和(SS)的计算
在进行方差分析时，可能会涉及到平方和计算方法的问题。在平衡设计下，即每个条件下的样本量相同时，三类平方和的结果是没有差别的。但在不平衡设计下，即每个条件下的样本量不同时，就需要进行一些调整。
这里的不平衡设计是指，比如我们有两个变量，climate有三个水平，romantic有两个水平，那么组合之后就有六个条件，但这六个条件下的被试数量可能是不同的。理论上，最好的情况是每个条件下的被试数量是一样的，这样的设计被称为平衡设计。在平衡设计中，三种类型的平方和的结果会很清晰，并且方差分析的结果独立于平方和的类型。但在实际情况中，这种设计可能较难实现，从而导致不平衡设计。
在不平衡设计下，计算方差时就会出现问题，因为我们需要将不同组的方差进行合并。尤其是当各组样本量差距较大时，三种类型的平方和计算结果可能会不同。在这种情况下，我们需要进行一些调整，需要根据具体研究设计和问题来选择使用哪一种类型的平方和。这就产生了三类平方和。SPSS默认使用的是第三类平方和，而在R中，aov函数默认使用的是第一类平方和。因此，当我们使用R进行方差分析时，可能会发现结果与SPSS有所不同。
这种情况下，我们需要更深入地理解平方和的计算方法，以便正确解读R的输出结果。这也是我们在使用R进行统计分析时，需要不断强化统计知识的一个重要原因。因为相比于SPSS这类点击式操作的软件，R提供了更多的选项，而正确理解和使用这些选项，就需要我们对统计学有更深入的理解。
我们是否能得到完全相同的结果呢？实际上，这是完全可能的。例如，我们可以使用afex这个包，这是在2017或2018年后出现的一个包。afex是为了满足实验心理学家进行方差分析的需求而设计的，其中包含了各种方差分析的功能。如果我们按照这样的写法，即将被试的identity写在这里，然后将类型设置为三，我们就能得到完全相同的结果。我们也可以在其他地方使用同样的方法，同样能得到一模一样的结果。
[car::Anova()]
# 结果不一致，原因PPT显示不全，请回到rmd文档查看
aov1 <- car::Anova(stats::aov(Temperature ~ climate * romantic, data = df))
aov1## Anova Table (Type II tests)
##
## Response: Temperature
## Sum Sq Df F value Pr(>F)
## climate 19.034 2 49.9680 < 0.00000000000000022 ***
## romantic 0.244 1 1.2801 0.258072
## climate:romantic 1.910 2 5.0136 0.006765 **
## Residuals 270.654 1421
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1我们是否能得到完全相同的结果呢？实际上，这是完全可能的。例如，我们可以使用afex这个包，这是在2017或2018年后出现的一个包。afex是为了满足实验心理学家进行方差分析的需求而设计的，其中包含了各种方差分析的功能。如果我们按照这样的写法，即将被试的identity写在这里，然后将类型设置为三，我们就能得到完全相同的结果。我们也可以在其他地方使用同样的方法，同样能得到一模一样的结果。
## $contrasts
## unordered ordered
## "contr.treatment" "contr.poly"# 从输出结果可知，无序默认为contr.treatment()，有序默认为contr.poly()
# factor()函数来创建无序因子，ordered()函数创建有序因子
is.factor(df$climate)## [1] TRUE## [1] FALSE# climate是无序因子
# 创建一个3水平的因子的基准对比
c1 <- contr.treatment(3)
# 创建一个新的对比，这个编码假设分类水平之间的差异被等分，每一个水平与总均值的差异等于1/3
my.coding <- matrix(rep(1/3, 6), ncol=2)
# 将对比调整为每个水平与第一个水平的振幅减去1/3
# 可能的原因：除了关心每个水平对应的效果，同时也关心水平与水平之间的效果
my.simple <- c1-my.coding
my.simple## 2 3
## 1 -0.3333333 -0.3333333
## 2 0.6666667 -0.3333333
## 3 -0.3333333 0.6666667# 更改climate的对比
contrasts(df$climate) <- my.simple
# 将数据集df的romantic列的对比设为等距对比，它假设分类水平之间的差异为等距离
contrasts(df$romantic) <- contr.sum(2)/2
# 方差分析
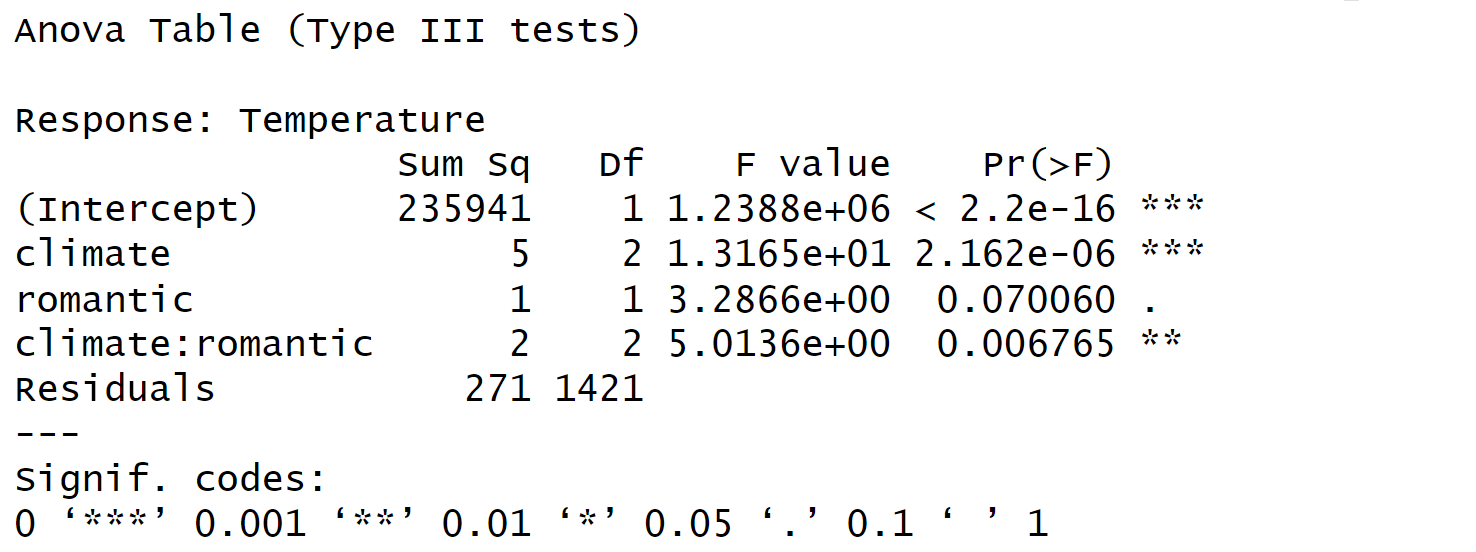
aov1 <- car::Anova(lm(Temperature ~ climate * romantic, data = df),
type = 3)
aov1## Anova Table (Type III tests)
##
## Response: Temperature
## Sum Sq Df F value Pr(>F)
## (Intercept) 1768309 1 9284069.6498 < 0.00000000000000022 ***
## climate 19 2 50.8832 < 0.00000000000000022 ***
## romantic 0 1 1.0006 0.317336
## climate:romantic 2 2 5.0136 0.006765 **
## Residuals 271 1421
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1[afex::aov_ez()]
afex::aov_ez(id = "subjID",
dv = "Temperature",
data = df,
between = c("climate", "romantic"),
type = 3)## Contrasts set to contr.sum for the following variables: climate, romantic## Anova Table (Type 3 tests)
##
## Response: Temperature
## Effect df MSE F ges p.value
## 1 climate 2, 1421 0.19 50.88 *** .067 <.001
## 2 romantic 1, 1421 0.19 1.00 <.001 .317
## 3 climate:romantic 2, 1421 0.19 5.01 ** .007 .007
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1# afex中的其他函数可以得到同样的结果
afex::aov_car(Temperature ~ climate * romantic + Error(subjID), data = df, type = 3)## Contrasts set to contr.sum for the following variables: climate, romantic## Contrasts set to contr.sum for the following variables: climate, romantic也就是说，如果我们使用最常见的R代码，很可能会得到与SPSS不同的结果。同样的现象也可能发生在我们习惯使用AMOS进行结构方程模型（SEM）的情况下。当你使用R的某些包进行结构方程模型时，即使是同样的数据和结构，可能会得到不同的结果。这可能是因为它们内部设定的不同。因此，我们需要去了解它们内部的设定是什么。
9.4 线性回归
我们刚刚讨论的是t检验，它是一种特定的回归模型。而对于ANOVA（方差分析），从它的表示方法来看，我们可以很明显地看出它实际上也是一个回归模型。因为它的方程表示形式与线性模型非常相似，包括一些自变量以及它们之间是否存在交互作用。在实际应用中，我们经常会遇到单因素方差分析和多因素方差分析。
在这种情况下，两因素方差分析也是一个特殊的回归模型。它的特殊之处在于我们的自变量是分类变量，也可以称为离散变量。因此，在进行方差分析时，我们需要注意处理这些分类变量或离散变量。
假设我们这里有一个2×2的设计，也就是有四个条件，这四个条件可以视为四组。每一组被试在某一因变量上都会有自己的取值。我们需要检验的是这四组被试的均值是否完全相同，即它们是否有偏离总体均值的情况。这就是我们进行方差分析的一个核心目标。在线性模型上，我们也在检验同样的问题。
比如说，我们可以通过某种方式对自变量进行编码，然后观察各组的均值与其他组之间的差异是否达到显著水平。举个例子，这里我们展示的是一种非常简单的编码方式，我们以某一条件下的值作为零点，比如第一组，然后其他所有的系数都是其他组的均值与这个零点的差异，也就是我们斜率的比较对象。
可能这么说有点抽象，让我们以一个具体的例子来说明。假设我们有一个变量叫”romantic”，我们可以把它编码为0和1。同样地，我们也可以把其他变量编码为0和1。如果我们简化这两种情况，就更容易理解了。
在这里，我们可以看到如果有一个组合为0和0，那么在我们的回归模型中，这个部分就变成了β0。在这种编码方式下，β0代表的就是某个条件下的均值。通过这种方式，我们可以看到β1可能代表的是某种条件下的值，比如当某个变量取值为1或0时的情况。同样，β2可能代表的是另一个变量在取值为1、0或者两个变量都为1时的情况。
所有这些回归系数都可以被理解为组间的差异值。我们的回归模型的目标就是去检验这些差异是否显著。在做回归模型时，我们检验显著性的方式可能有所不同。在这种最简化的情况下，我们可以看到，我们的2×2的两因素方差分析完全可以对应成为一个离散变量的回归模型。
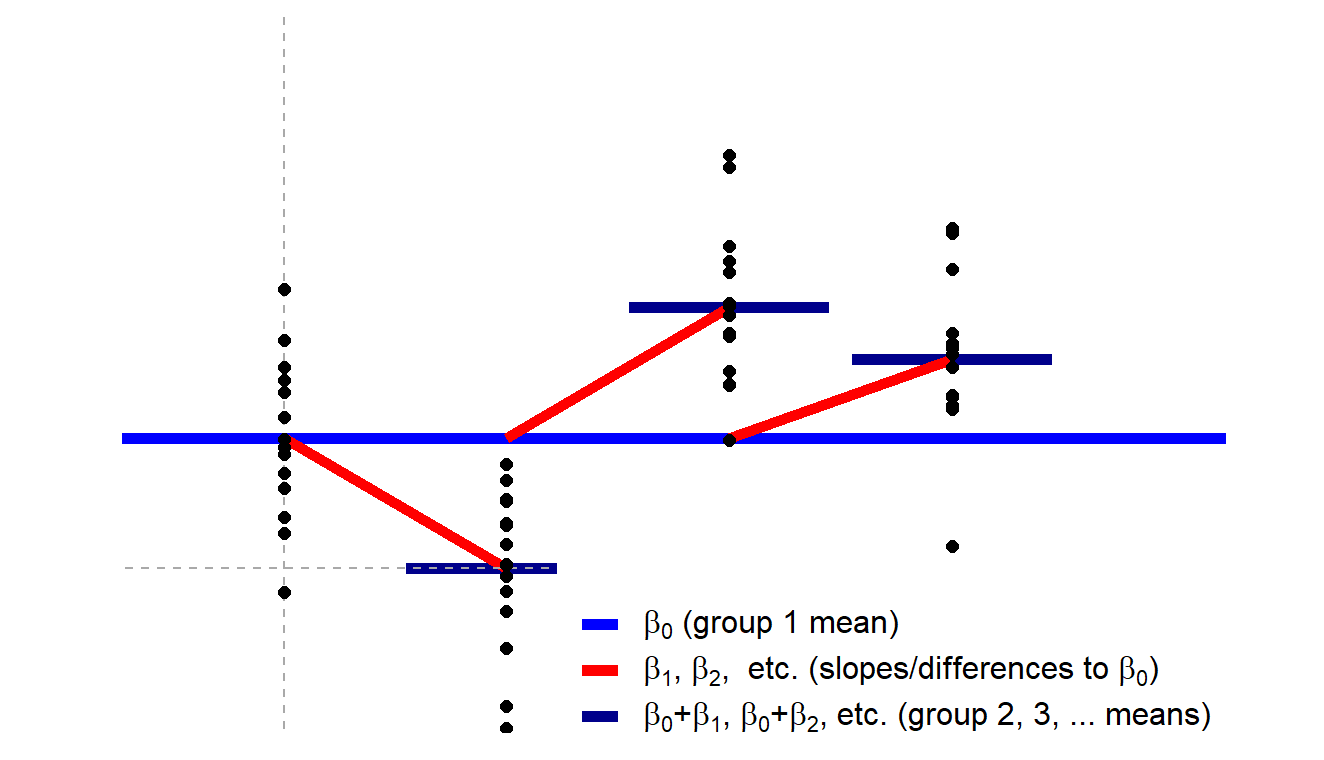
如果我们采用ANOVA或者线性模型，并且我们的设定是一样的，那么得到的结果将会是完全一样的。可能我讲得有点快，大家可能需要回顾一下自己学的线性回归的知识。因为我不确定其他的统计老师在讲线性回归的时候是否已经将其与ANOVA或t检验进行了关联。但大家可以这样理解，它们本质上都是一样的。如果大家理解了，ANOVA其实就是线性回归的一个特定模式，那么你们就已经把握了其要点。
在实际研究中，即使我们知道ANOVA与线性回归有相似之处，但我们仍然需要报告传统的方差分析结果。在这种情况下，我们推荐使用bruceR包的mANOVA函数，它是一个非常强大的函数，基本上涵盖了我们在心理学中常用的所有ANOVA类型。使用mANOVA函数可以大大简化心理学研究者使用这个方法的门槛。
关于mANOVA函数的主要参数，我们不再详细讲解，大家可以查阅相关资料。该函数非常全面，而且有一个非常好的特点，就是它可以直接将结果保存为三线表格，方便我们将结果粘贴到Word文档中进行报告。
以我们刚才讲解的例子为例，我们要对climate和romantic进行方差分析，我们可以调用mANOVA函数，设置dependent variable为temperature，参数设为between表示主间变量。这里有两个主间变量。大家可以看到，得到的结果与SPSS是完全相同的，如50.88。
与SPSS不同之处在于mANOVA函数会输出Generalized Eta Squared（广义η²），这是方差分析的一个效应量指标，有助于我们更好地理解结果。关于效应量的指标，对于传统心理学来说，我们通常只关注p值。但实际上，最近的趋势是大家会更加关注效应量有多大，而不仅仅是p值是否显著。换句话说，我们不仅关心结果是否显著，还关心效应量是否足够大。
在方差分析中，我们经常会进行进一步的简单效应分析和事后多重比较。这里的操作比较灵活。例如，如果你使用的是纯粹的重复测量设计，那么在没有交互作用的情况下，我们可能会进行多重比较，也就是比较某一条件下不同水平之间是否存在差异。然而，如果存在交互作用，我们可能需要重新检查在某一自变量的水平下，另一个自变量是否具有效应。这种情况下，我们称之为简单效应。简单效应分析可以帮助我们深入了解在某一特定条件下，不同水平之间的差异，以便更好地解释和理解我们的研究结果。
## [1] "Anova Table (Type III tests)"
## [2] ""
## [3] "Response: Temperature"
## [4] " Effect df MSE F ges p.value"
## [5] "1 climate 2, 1421 0.19 50.88 *** .067 <.001"
## [6] "2 romantic 1, 1421 0.19 1.00 <.001 .317"
## [7] "3 climate:romantic 2, 1421 0.19 5.01 ** .007 .007"
## [8] "---"
## [9] "Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1"在这个例子中，我们可以看到，我们对climate和romantic进行了方差分析，试图查看在不同的romantic条件下（即单身或非单身），climate是否有影响。这就是简单效应分析。
在R中，我们可以看到mANOVA函数的输出结果。首先，它会输出描述性统计结果，包括climate和romantic的各个水平的均值、标准差和样本量。然后，它会给出方差分析表，包括climate的主效应、romantic的主效应和它们的交互作用的效应。我们可以看到，climate的主效应是显著的，这与我们的预期一致。即在不同气候带的人们体温存在差异，其p值非常小，F值也比较大。此外，我们也发现climate和romantic的交互作用是显著的，这也与我们的预期相符。
原先，我们试图通过t检验来查看不同romantic状态下的人们体温是否有区别，但我们并没有发现显著差异。然后，我们怀疑这可能是因为人的体温受到climate的影响，这个效应可能掩盖了romantic的影响。因此，我们引入了climate这个因素，然后再次检验romantic和climate的交互作用。结果显示，这个交互作用是显著的，这也就验证了我们的猜想。
在mANOVA中，它会输出各种效应量指标，如η²和广义η²（Generalized Eta Squared）。通常情况下，在做方差分析时，我们会报告广义η²。实际上，关于方差分析的效应量指标是一个重要且不容易掌握的知识点。在mANOVA中，它还会输出其他效应量指标，如Cohen’s f和方差同质性检验结果。这些输出结果非常符合心理学研究者的使用习惯。
当我们发现交互作用时，我们通常需要进一步了解这个交互作用代表什么。在这种情况下，我们可以使用emmeans（estimated marginal means）函数来查看不同条件下的结果。这个函数可以帮助我们查看在不同条件下，climate和romantic之间的简单效应。通过emmeans函数，我们可以得到一个三线表，展示了在不同romantic条件下，climate的简单效应。在这个表格中，我们可以看到，在不同的romantic条件下，climate都具有显著效应。这些信息有助于我们更深入地了解交互作用背后的实际情况。
在这个分析过程中，我们首先在恋爱和单身的条件下分别看了climate的影响，并发现climate在两种情况下都有显著影响，虽然效应量可能会有所不同。然后，我们进一步进行了post-hoc比较，比较了恋爱和单身状态下，不同climate的体温差异，结果显示基本上所有的差异都是显著的。
然后，我们通过改变分组条件，看了在不同climate下，恋爱关系是否有影响。结果显示，在热带和温带，恋爱关系没有显著影响，但在寒带，恋爱关系则有显著影响。这个结果与我们的预期相符，表明在较冷的气候下，恋爱关系对体温有调节作用。
此外，我们还进行了F检验，实际上是在热带、温带和寒带三种条件下进行了单因素方差分析。由于只有两个水平（恋爱和单身），所以这个F检验的结果与后面的t检验结果基本一致。这是因为在只有两个水平的情况下，F检验和t检验的结果是一样的。如果你对这个有兴趣，你可以进一步查看t值和F值之间的关系。
sim_eff <- res1 %>%
bruceR::EMMEANS("climate", by = "romantic") %>%
bruceR::EMMEANS("romantic", by = "climate")—— EMMEANS (effect = “climate”) ——
Joint Tests of “climate”: ───────────────────────────────────────────────────────────────── Effect “romantic” df1 df2 F p η²p [90% CI of η²p] ───────────────────────────────────────────────────────────────── climate 恋爱 2 1421 13.165 <.001 *** .018 [.008, .031] climate 单身 2 1421 41.817 <.001 *** .056 [.037, .075] ───────────────────────────────────────────────────────────────── Note. Simple effects of repeated measures with 3 or more levels are different from the results obtained with SPSS MANOVA syntax.
Univariate Tests of “climate”:
───────────────────────────────────────────────────────────────
Sum of Squares df Mean Square F p
───────────────────────────────────────────────────────────────
恋爱: “climate” 5.015 2 2.507 13.165 <.001
单身: “climate” 15.929 2 7.965 41.817 <.001
Residuals
───────────────────────────────────────────────────────────────
Note. Identical to the results obtained with SPSS GLM EMMEANS syntax.
Estimated Marginal Means of “climate”: ───────────────────────────────────────────────────── “climate” “romantic” Mean [95% CI of Mean] S.E. ───────────────────────────────────────────────────── 热带 恋爱 36.510 [36.446, 36.575] (0.033) 温带 恋爱 36.393 [36.346, 36.440] (0.024) 寒温带 恋爱 36.296 [36.245, 36.347] (0.026) 热带 单身 36.590 [36.532, 36.648] (0.029) 温带 单身 36.356 [36.303, 36.409] (0.027) 寒温带 单身 36.182 [36.114, 36.250] (0.035) ─────────────────────────────────────────────────────
Pairwise Comparisons of “climate”: ──────────────────────────────────────────────────────────────────────────────────────── Contrast “romantic” Estimate S.E. df t p Cohen’s d [95% CI of d] ──────────────────────────────────────────────────────────────────────────────────────── 温带 - 热带 恋爱 -0.117 (0.041) 1421 -2.879 .012 * -0.268 [-0.491, -0.045] 寒温带 - 热带 恋爱 -0.214 (0.042) 1421 -5.111 <.001 *** -0.490 [-0.720, -0.260] 寒温带 - 温带 恋爱 -0.097 (0.035) 1421 -2.741 .019 * -0.222 [-0.417, -0.028] 温带 - 热带 单身 -0.234 (0.040) 1421 -5.853 <.001 *** -0.536 [-0.756, -0.317] 寒温带 - 热带 单身 -0.409 (0.046) 1421 -8.969 <.001 *** -0.936 [-1.186, -0.686] 寒温带 - 温带 单身 -0.174 (0.044) 1421 -3.966 <.001 *** -0.400 [-0.641, -0.158] ──────────────────────────────────────────────────────────────────────────────────────── Pooled SD for computing Cohen’s d: 0.436 P-value adjustment: Bonferroni method for 3 tests.
Disclaimer:
By default, pooled SD is Root Mean Square Error (RMSE).
There is much disagreement on how to compute Cohen’s d.
You are completely responsible for setting sd.pooled.
You might also use effectsize::t_to_d() to compute d.
—— EMMEANS (effect = “romantic”) ——
Joint Tests of “romantic”: ──────────────────────────────────────────────────────────────── Effect “climate” df1 df2 F p η²p [90% CI of η²p] ──────────────────────────────────────────────────────────────── romantic 热带 1 1421 3.287 .070 . .002 [.000, .008] romantic 温带 1 1421 1.055 .305 .001 [.000, .005] romantic 寒温带 1 1421 6.966 .008 ** .005 [.001, .013] ──────────────────────────────────────────────────────────────── Note. Simple effects of repeated measures with 3 or more levels are different from the results obtained with SPSS MANOVA syntax.
Univariate Tests of “romantic”:
──────────────────────────────────────────────────────────────────
Sum of Squares df Mean Square F p
──────────────────────────────────────────────────────────────────
热带: “romantic” 0.626 1 0.626 3.287 .070 .
温带: “romantic” 0.201 1 0.201 1.055 .305
寒温带: “romantic” 1.327 1 1.327 6.966 .008 **
Residuals 271
──────────────────────────────────────────────────────────────────
Note. Identical to the results obtained with SPSS GLM EMMEANS syntax.
Estimated Marginal Means of “romantic”: ───────────────────────────────────────────────────── “romantic” “climate” Mean [95% CI of Mean] S.E. ───────────────────────────────────────────────────── 恋爱 热带 36.510 [36.446, 36.575] (0.033) 单身 热带 36.590 [36.532, 36.648] (0.029) 恋爱 温带 36.393 [36.346, 36.440] (0.024) 单身 温带 36.356 [36.303, 36.409] (0.027) 恋爱 寒温带 36.296 [36.245, 36.347] (0.026) 单身 寒温带 36.182 [36.114, 36.250] (0.035) ─────────────────────────────────────────────────────
Pairwise Comparisons of “romantic”: ───────────────────────────────────────────────────────────────────────────────────── Contrast “climate” Estimate S.E. df t p Cohen’s d [95% CI of d] ───────────────────────────────────────────────────────────────────────────────────── 单身 - 恋爱 热带 0.080 (0.044) 1421 1.813 .070 . 0.183 [-0.015, 0.382] 单身 - 恋爱 温带 -0.037 (0.036) 1421 -1.027 .305 -0.085 [-0.247, 0.077] 单身 - 恋爱 寒温带 -0.115 (0.043) 1421 -2.639 .008 ** -0.262 [-0.458, -0.067] ───────────────────────────────────────────────────────────────────────────────────── Pooled SD for computing Cohen’s d: 0.436 No need to adjust p values.
Disclaimer:
By default, pooled SD is Root Mean Square Error (RMSE).
There is much disagreement on how to compute Cohen’s d.
You are completely responsible for setting sd.pooled.
You might also use effectsize::t_to_d() to compute d.
9.5 知识延申|单因素方差分析示例
在本节课中，我们讲解了单因素方差分析和多因素方差分析，并重点讲解了多因素方差分析。我们提到了R中自带的函数以及其他一些适合心理学研究者使用的包，如PR和fx。这些包的输出结果与SPSS的输出结果非常相似，因此可以让老师和同学们更加放心地使用R进行分析。
##
## ====== ANOVA (Between-Subjects Design) ======
##
## Descriptives:
## ─────────────────────────────
## "climate" Mean S.D. n
## ─────────────────────────────
## 热带 36.555 (0.411) 396
## 温带 36.377 (0.401) 592
## 寒温带 36.255 (0.504) 439
## ─────────────────────────────
## Total sample size: N = 1427
##
## ANOVA Table:
## Dependent variable(s): Temperature
## Between-subjects factor(s): climate
## Within-subjects factor(s): –
## Covariate(s): –
## ───────────────────────────────────────────────────────────────────────
## MS MSE df1 df2 F p η²p [90% CI of η²p] η²G
## ───────────────────────────────────────────────────────────────────────
## climate 9.408 0.192 2 1424 49.106 <.001 *** .065 [.045, .085] .065
## ───────────────────────────────────────────────────────────────────────
## MSE = mean square error (the residual variance of the linear model)
## η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
## ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
## η²G = generalized eta-squared (see Olejnik & Algina, 2003)
## Cohen’s f² = η²p / (1 - η²p)
##
## Levene’s Test for Homogeneity of Variance:
## ──────────────────────────────────────────────
## Levene’s F df1 df2 p
## ──────────────────────────────────────────────
## DV: Temperature 18.207 2 1424 <.001 ***
## ──────────────────────────────────────────────9.6 知识延申|总结
此外，我们还讨论了线性模型与t检验之间的关系。可能有些同学在理解这部分内容时会感到困惑，这时候建议大家回顾一下本科阶段的教材，加深对回归模型和t检验之间关系的理解。学习代码和应用是很重要的，但要正确地使用它们，还需要掌握背后的统计知识。
总之，通过学习本节课的内容，我们可以更好地理解方差分析的原理和应用，并能够在R中使用相应的函数进行实际分析。同时，我们也要意识到，在学习和使用R进行统计分析时，理解和掌握背后的统计知识是非常重要的。
课堂总结
在今天的课程中，我们讨论了方差分析的原理和应用，并在R中使用了相关函数进行实际分析。我们还提到了一个国外博客，这个博客指出许多常见的统计检验都是线性模型的特例。这可以帮助大家更好地理解这些统计方法之间的联系。
最后，我们留了一个思考题：对于重复测量设计（within-subject design），如何用回归模型进行分析？此外，我们还给出了一些课堂练习，建议大家尝试自己编写代码来完成这些练习，以加深对课程内容的理解。
本节课在此结束。感谢大家的参与，如果有任何问题，请随时提问。