Chapter 10 第十讲:回归模型(三):广义线性模型
10.1 前章回顾和本章数据预处理
上节课我们讲解了如何把T检验和方差分析用回归模型的方式来进行解读。接着我们从认知心理学最常见的反应时数据出发,从层级模型的角度将数据分解为整体的水平(group level),以及每个被试个体试次的水平(trial level),层级模型可以提高统计检验力并且为研究者提供十分丰富的信息,因此也是学界越来越推荐的一种统计方法。
让我们先对本章数据进行预处理,这里用到的还是之前的认知实验的数据,我们先对正确率进行预处理。
这里需要注意一下我们对于正确率ACC的处理,实际上我们的认知实验数据当中包含了其他两种反应,这里我们直接删除了另外两种情况,只保留了正确和错误的反应,即0和1,当然也有一些实验会将1之外的所有反应归到0中做处理。另外我们筛选去除了反应在1500ms以上和200ms以下的反应时,因为这在经验上是不符合人类的反应速度的。
## `summarise()` has grouped output by 'Sub', 'Valence'. You can override using the `.groups` argument.上面是我们通常所做的操作:将不同条件下的反应正确率做一个平均,然后进行方差分析。
(知识补充:easystats系统包是过去五六年快速发展起来的一个包系列,适用于统计分析,特别是心理学相关背景的统计分析,具体使用可以参考我们在B站上传的视频(链接如下)。https://www.bilibili.com/video/BV1rz421D7iJ/?spm_id_from=333.337.search-card.all.click)
让我们再来看一下正确率的原始数据。
可以发现其只存在0和1两种取值,这种分布显然不服从正态分布,因此我们不能简单地用前一章提到的一般线性模型进行处理。在传统的方差分析中,我们对正确率数据的处理是求出每个条件下的平均正确率再进行统计分析。这个平均正确率的取值作为一个连续数据,可以被放在坐标轴上形成一个分布,其与以0为原点,向两端无限延伸的标准正态分布也存在差异。因此我们需要对一般线性模型进行拓展,这也就是我们这一章所要讲的广义线性模型(Generalized Linear Model, GLM)。
10.2 广义线性模型
10.2.1 回归方程和普通线性模型
下面是线性模型的一个基本的形式:首先可以看到一个截距b0;假设我们有p个自变量,每一个自变量都会有一个它的斜率b;最后的残差\(\epsilon\)是无法被这个回归解释的一个部分。
\[Y = b_0 + b_{1}X_{1} + b_{2}X_{2} +... + b_{p}X_{p} + \epsilon\] -\(Y\): 因变量,Dependent variable - \(X_i\) : 自变量,Independent (explanatory) variable - \(b_0\) : 截距,Intercept - \(b_i\) : 斜率,Slope - \(\epsilon\) : 残差,Residual (error)
当然我们也可以用更加一般化的方法来书写上面的线性回归方程,以下这个方程包含了依然一个截距,并且我们将所有自变量用求和符号相加,以及最后相应残差项。方程右边除去残差项的内容,就是该方程的预测项,左边的y则是对应的观测项。
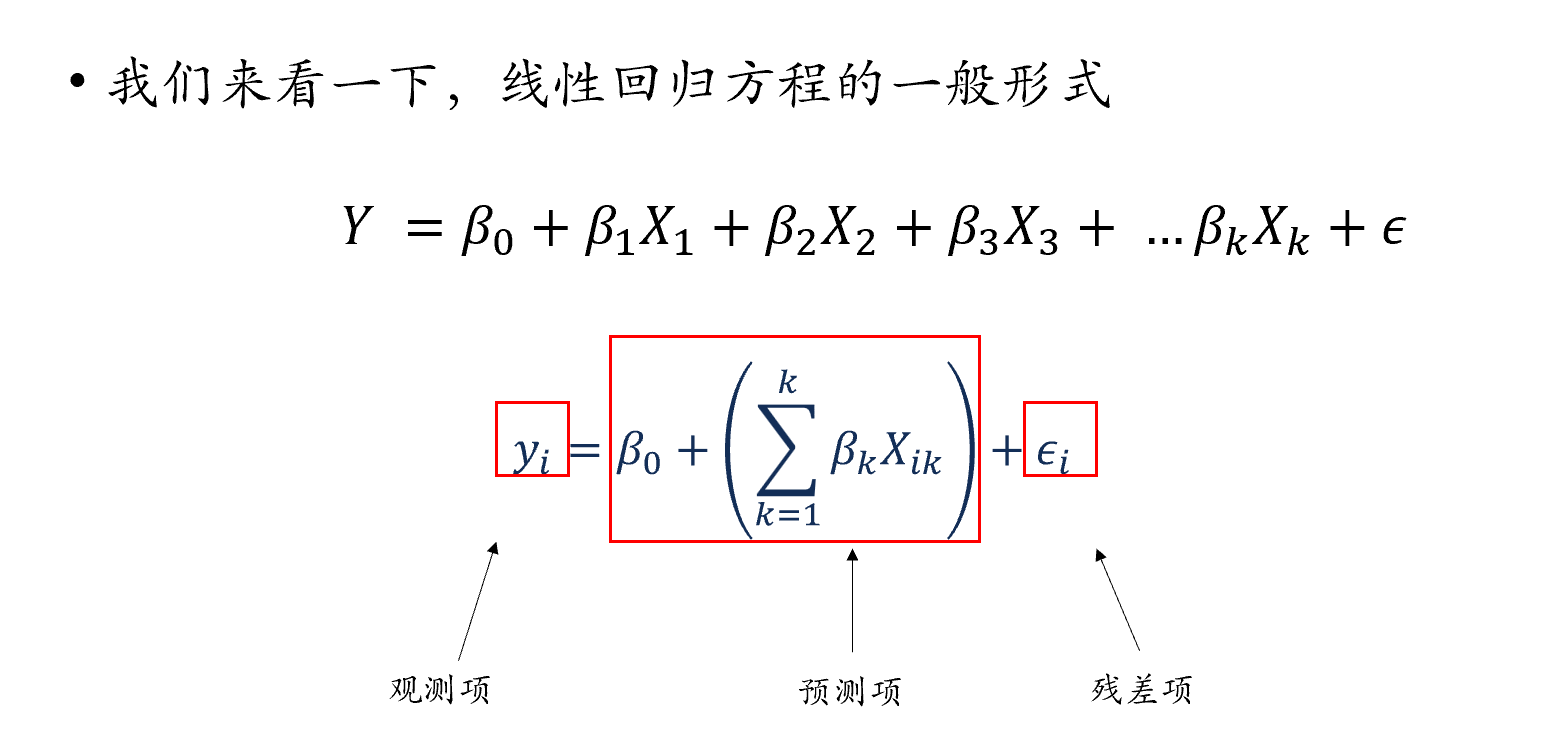
当我们在x轴上选择一个具体取值的时候,y轴上对应的是一系列可能的y值,这些y值组成了每一个x值下对应的y的正态分布,这个正态分布的中心就是对应x的观测值。
另外还有一些其他的回归方程写法,贴在下方供读者参考。
-简单线性回归: \[Y = b_0+b_1 X_1+ b_2 X_2+…+b_p X_p + \epsilon\] -线性代数表达:\[y_i = b_0 + b_1 X_{i1} + b_2 X_{i2} + … + b_p X_{ip} + \epsilon\] -矩阵表达: \[Y= X\beta + \epsilon\] -代码表达(r):\[Y \sim X_1 + X_2 + ... + X_n\]
我们也可以用一种更为简单的形式来写回归公式,因为我们观测到的y实际上是一个分布,所以我们用”~“来表示分布的含义。分布y中包含了预测项\(\mu\)和误差项\(\epsilon\)这两个参数。因此如果从数据分布的角度来看,线性回归实际上是在根据预测项推导出相应的分布,这也是为什么我们在进行线性回归的时候要假定数据呈正态分布,因为只有这样观测项才等于这个分布中数据的均值。
- 回归模型形式:观测项 = 预测项 + 误差项
- 假定观测项是正态分布,上述公式可以重新表达为:
\[y \sim N(\mu, \epsilon)\]
- 其中,\(\mu\)为预测值,即 \[μ = \beta_0 + \beta_1 x\]
- 观测值服从以预测项为均值的正态分布,观测值与预测值之间的差值就是残差。
10.2.2 连接函数和广义线性模型
那么如果因变量不服从正态分布,如何构建回归模型?
当x无法直接去预测y的时候,我们就要通过一个连接函数,将x对应的线性组合值z,映射到q上,然后再将q作为一个预测值去预测y的分布。
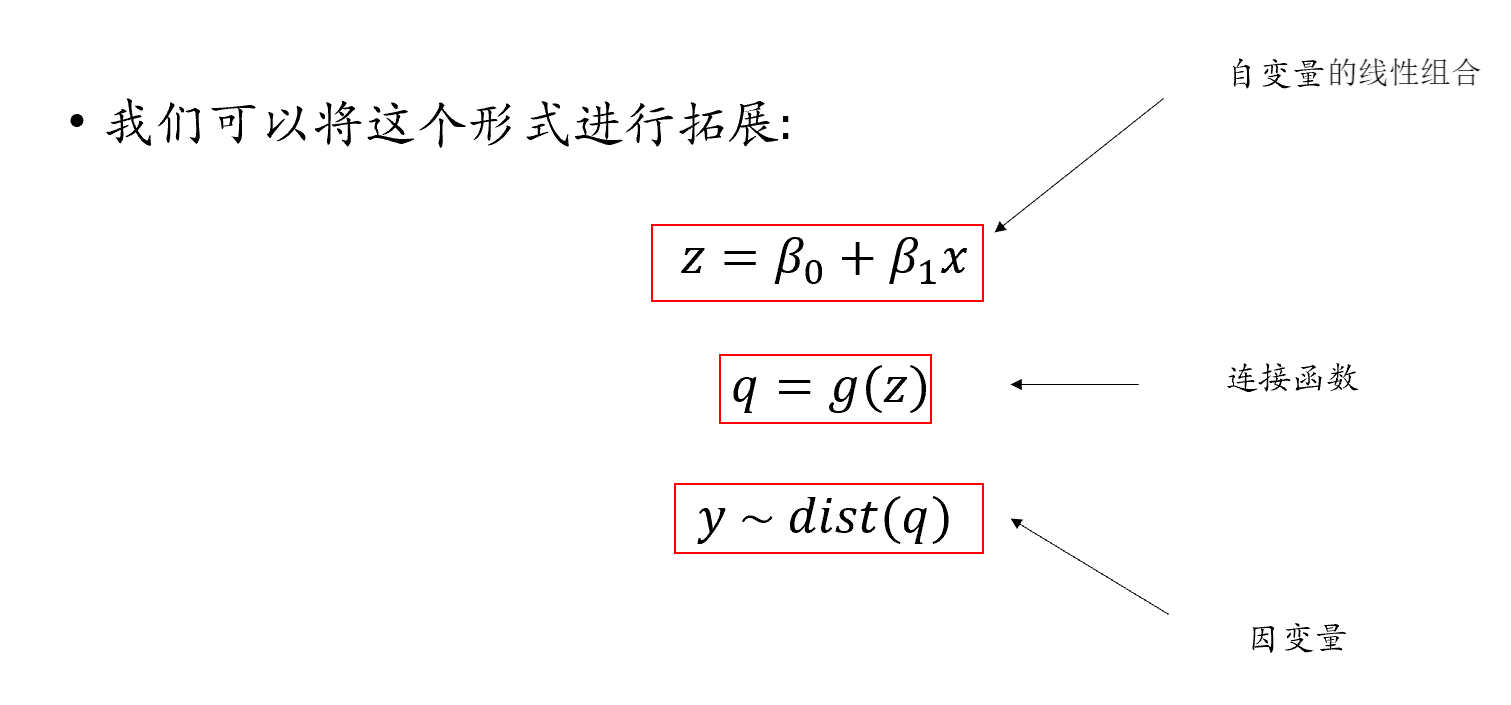
具体而言,连接函数的作用就是将原本不能用于预测y的z转换为可以预测的值q。
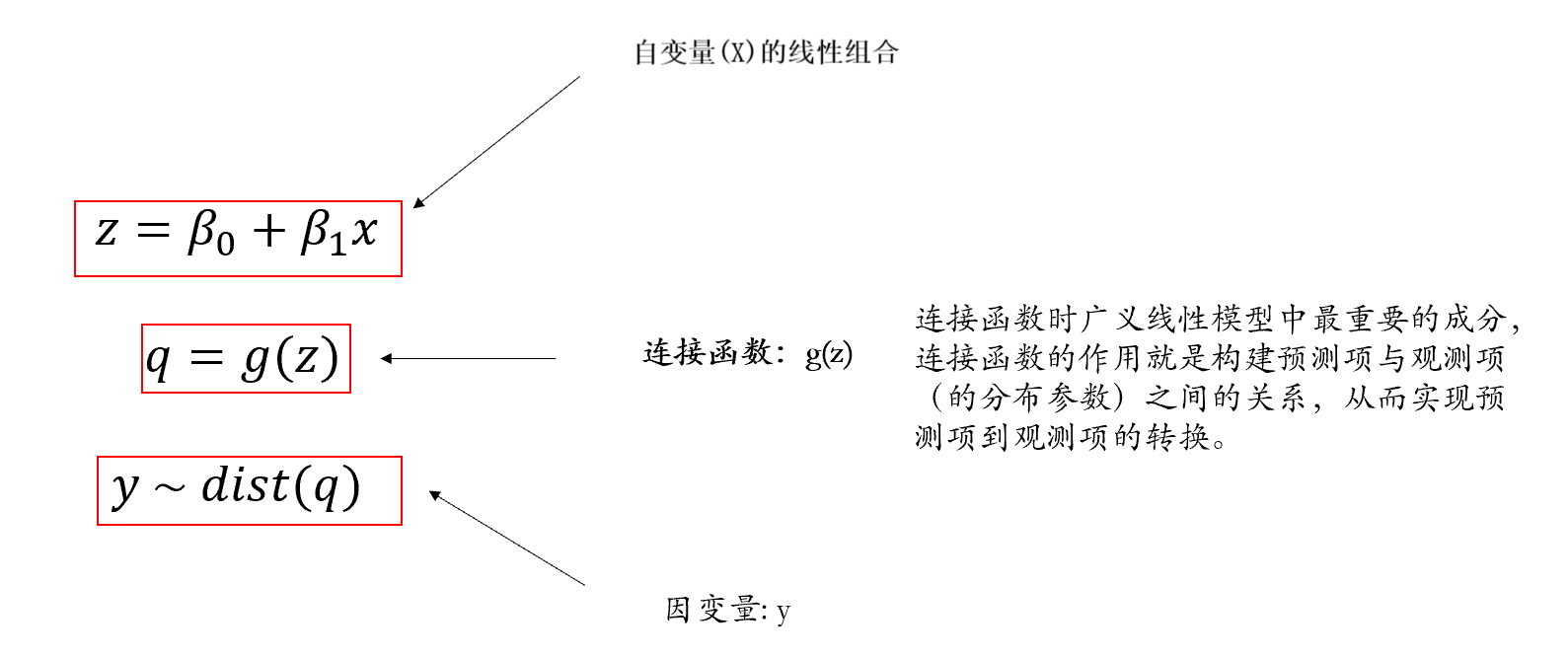
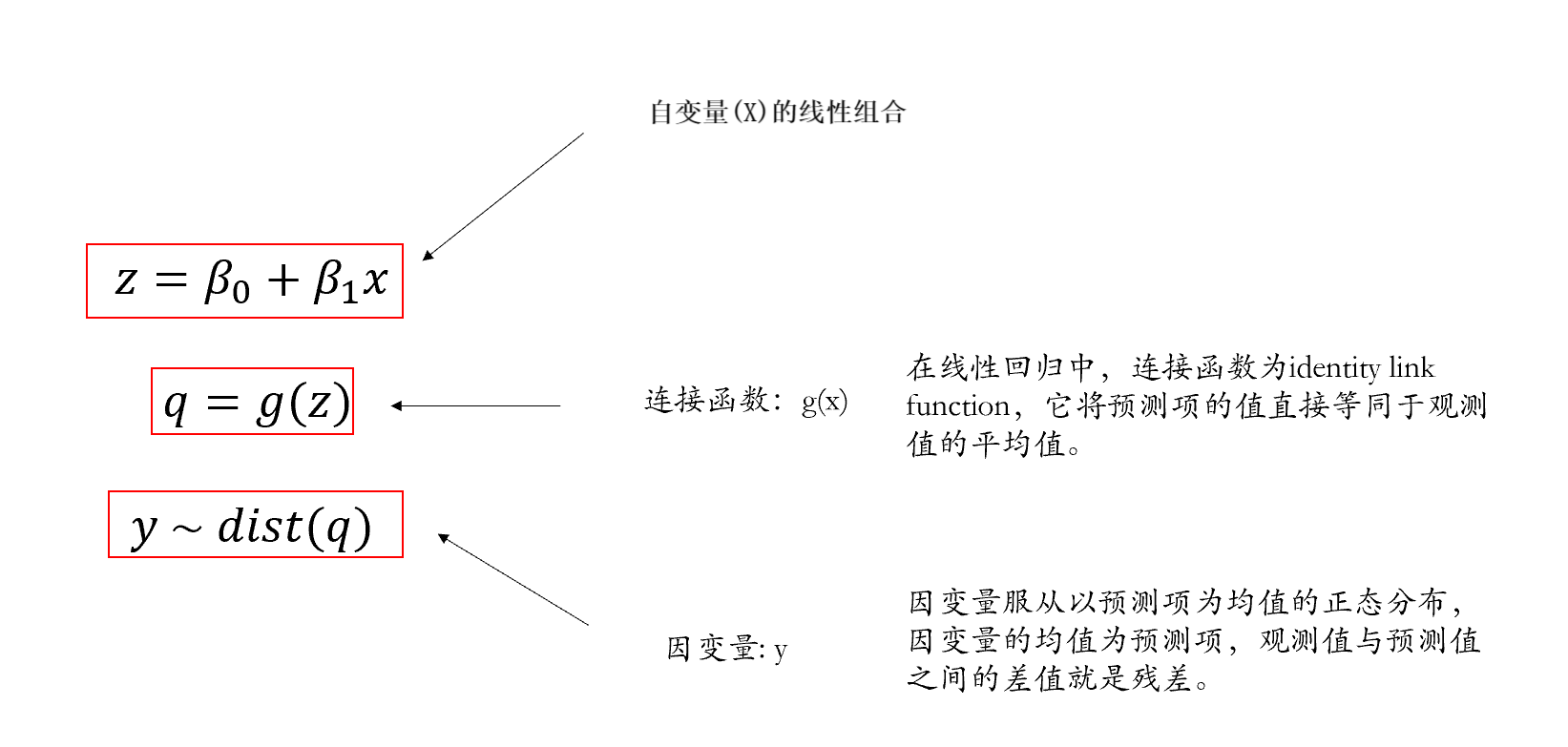
这里我们就可以看到之前所讲的简单线性模型的非常特殊的点:简单线性模型可视为GLM的特殊形式,预测项的连接函数等于它本身(即不需要使用连接函数进行转换,写代码是有时候会写的”identity”就是不需要转换的意思),观测项为正态分布。
而在广义线性模型中:观测项不一定是正态分布(残差不一定是正态分布),连接函数不等于其自身,这也使得广义线性模型能够对非正态分布的因变量进行建模。
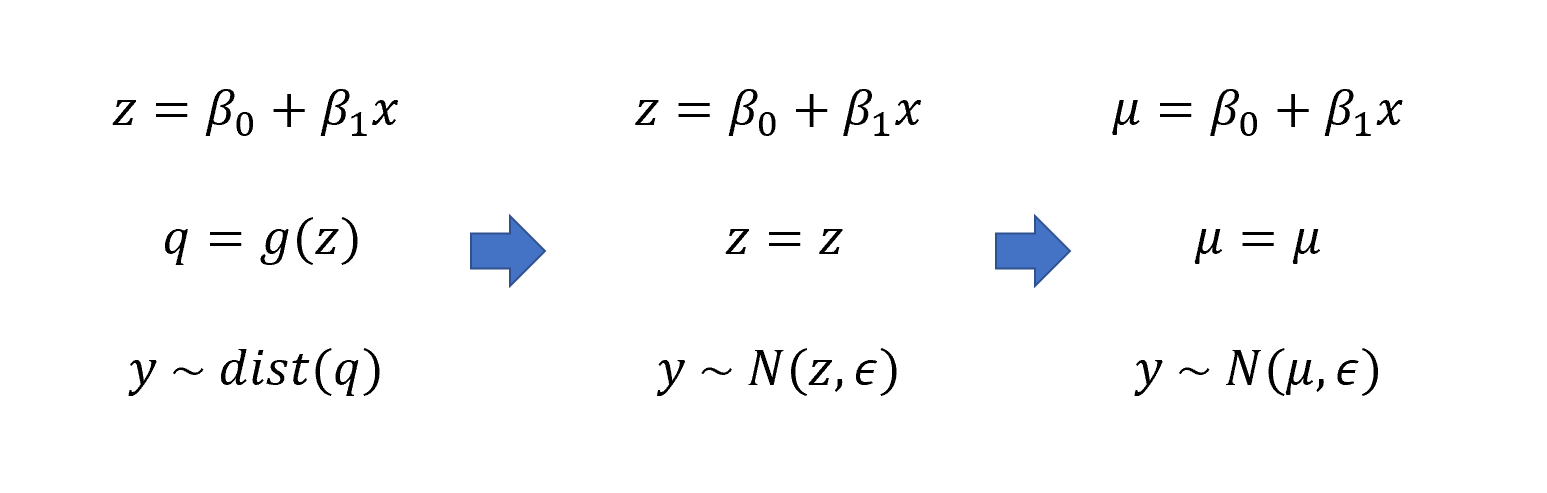
10.3 二项分布
10.3.1 伯努利实验
我们前面提到了正确率这种数据,其可能存在的取值只有0和1。事实上我们在抛硬币的游戏中也经常也涉及到类似的情况,也就是抛硬币只存在正面或者反面朝上两种情况。用统计学上的书面话语来讲,就叫”伯努利实验”。伯努利实验是一种在同样的条件下重复地、相互独立地进行的随机试验;该随机试验只有两种可能结果:发生或者不发生。假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验(n-fold bernoulli trials)。
而n次独立重复的伯努利试验的概率分布服从二项分布(Binomial Distribution),二项分布的公式如下。
\[P(X=k )=𝐶_𝑛^𝑘 𝑝^𝑘 𝑞^{𝑛−𝑘}= 𝐶_𝑛^𝑘 𝑝^𝑘 (1−𝑝)^{𝑛−𝑘}\] \[𝐶_𝑛^𝑘= 𝑛!/𝑘!(𝑛−𝑘)! \]
其中,p表示每次试验中事件A发生的概率;X表示n重伯努利试验中事件A发生的次数,X的可能取值为0,1,…,n;对每一个k(0 ≤ k ≤ n),事件{X = k} 指”n次试验中事件A恰好发生k次”;随机变量X服从以n, p为参数的二项分布,写作 \(X \sim B(n, p)\),\(p \in [0,1]\),\(n \in N\)
还是以抛硬币来举例,假如我们抛十次硬币,十次全部正面朝上的概率就是二分之一的十次方,我们用到的两个参数就是正面朝上的概率以及抛的次数,如果我们只知道抛了几次,或者只知道正面朝上的概率,都不足以算出具体的概率。因此对于二项分布,我们要知道的两个参数分别为实验次数n,以及事件发生的概率p。
我们可以在R中来模拟一下抛硬币的实验。首先我们先写一个模拟抛硬币的函数。
我们让若干人每人抛若干次硬币,首先让5个人每人抛10次硬币。理论上来说,对于一枚公平的硬币,正面朝上次数为5的应该是最多的。
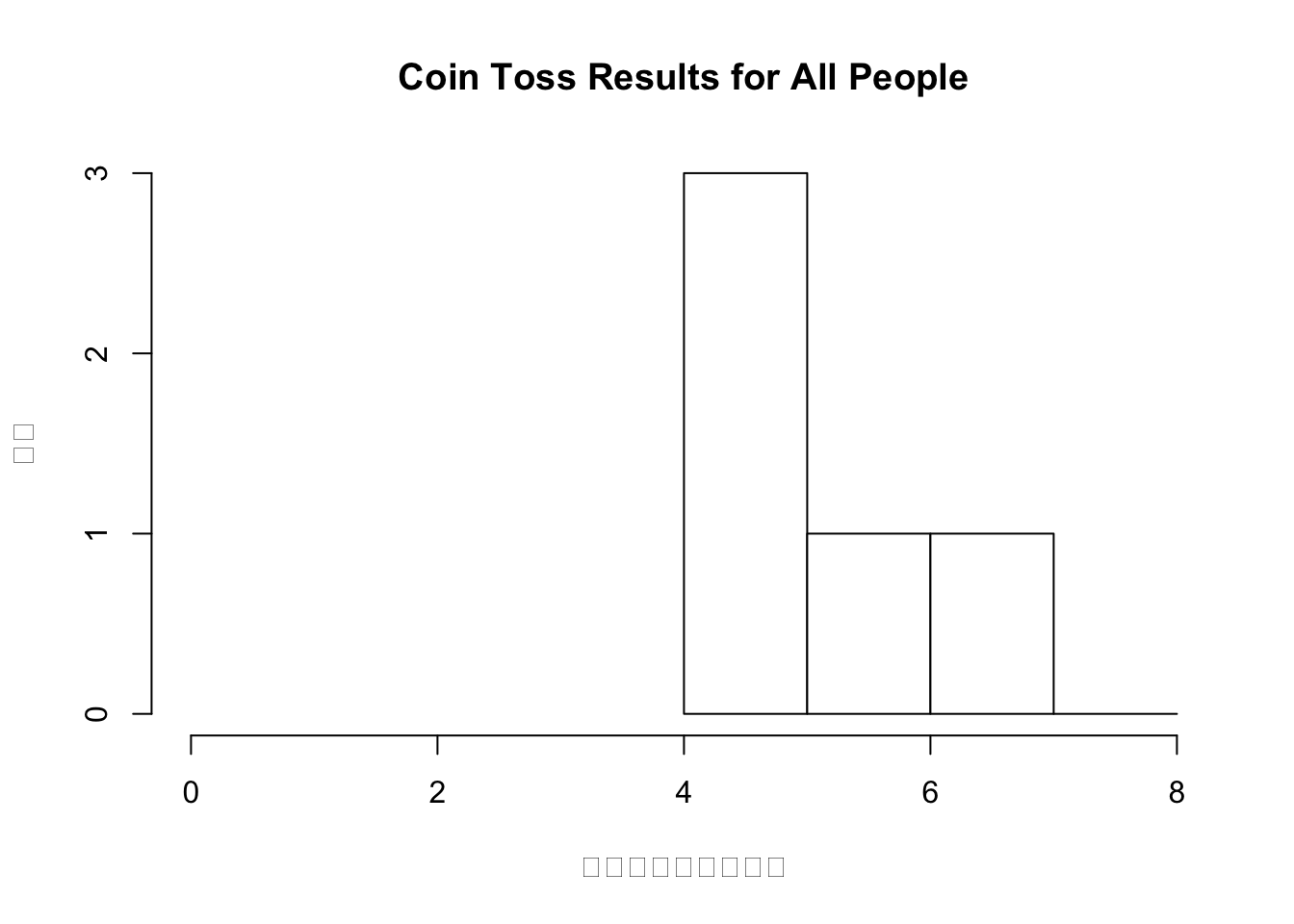
但是事实上我们模拟出来发现小于5的反而更多一点,这好像在暗示我们这是一枚不公平的硬币。但是如果我们把人数n增多呢?以下模拟的是10人每人抛10次。
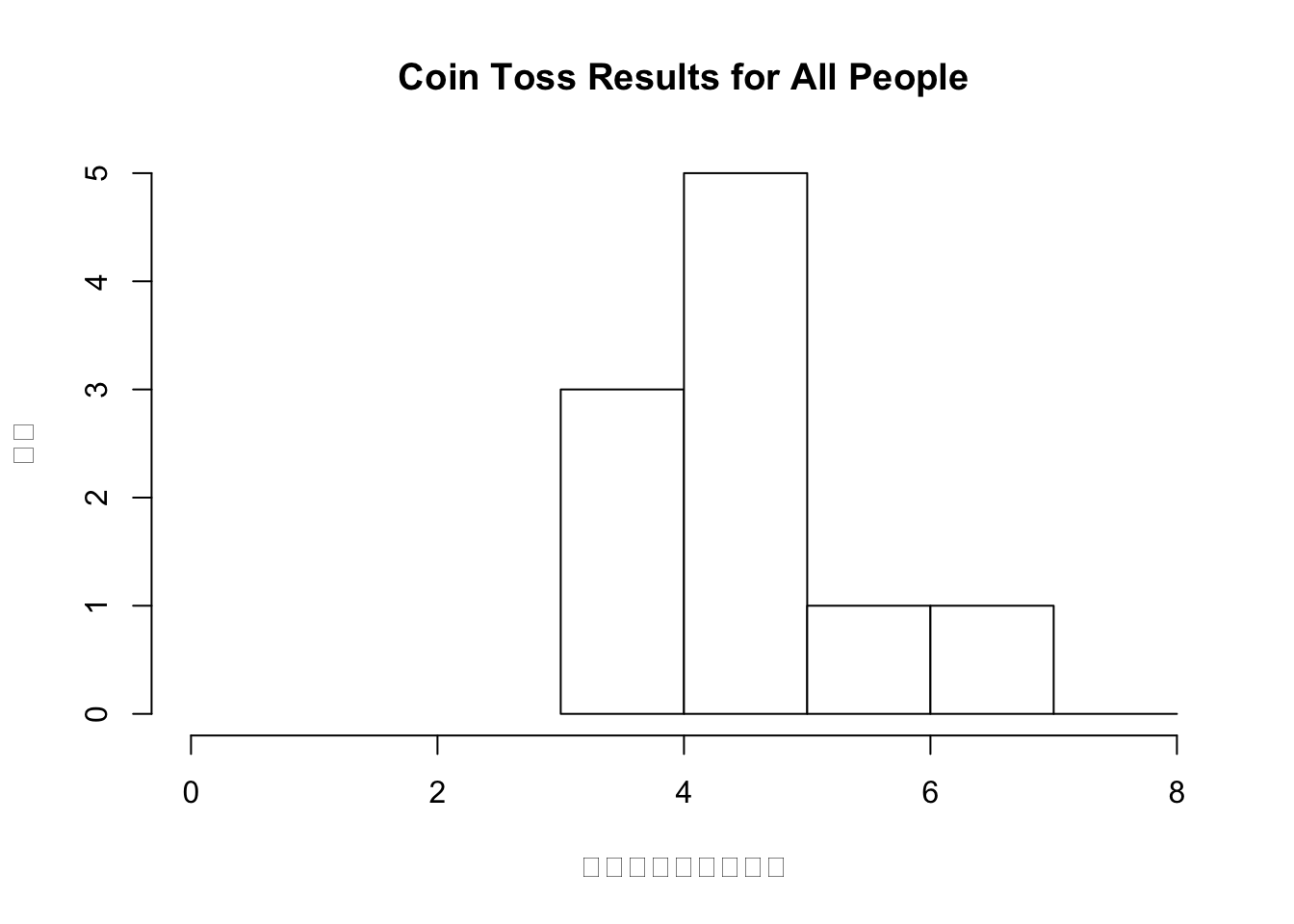
emmmm,似乎还是一枚不太公平的硬币。我们再将人数n增加到1000人。
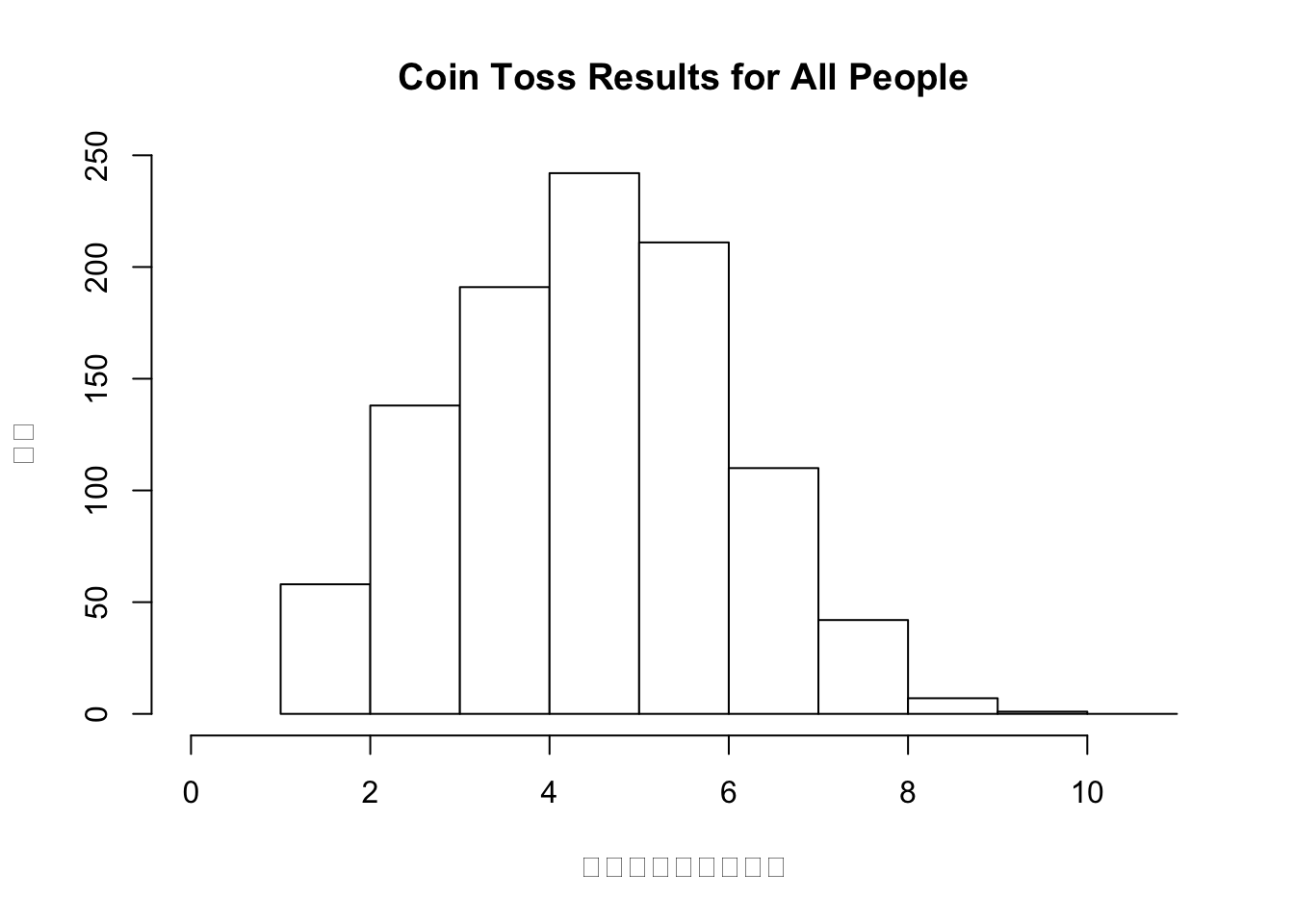
这时候我们就可以看到数据呈现一个非常好的正态分布,此时正面朝上次数为5次的确实是最多的。
这里主要想让大家直观了解一下参数n对于事件发生次数分布的影响。让我们总结一下,已知一次试验中的每次尝试中事件A发生的概率\(p\),共进行\(n\)次独立重复的伯努利试验,假如事件A在一次试验中出现k次,事件A在n次试验中出现次数的平均数为: \[(𝑘_1+𝑘_2+𝑘_3+...+𝑘_𝑛/𝑛)\] 当n → ∞,\(p\) ≠ \(q\),\(np\) ≥ 5且\(nq\) ≥ 5,事件A在\(n\)次试验中出现次数的平均数为: \[\mu = np\] 事件A出现次数所属分布的标准差: \[ \sigma = \sqrt{𝑛𝑝𝑞}\] 也就是说,当n趋于无穷的时候,事件发生次数的分布就会慢慢地逼近正态分布,它会存在均值np,我们也可以算出它相应的标准差。
假如我们想用大五人格分数来预测正确率,我们会先将分数标准化为\(z\),那么如何将\(z\)与正确率这一二分变量进行连接呢?我们需要先将\(z\)映射到(0,1)之间再作为预测项,例如使用如下转换函数: \[\frac{1}{1+exp(-z)}\] 接着我们需要找到一个分布,能根据(0,1)之间的值转成二分变量,例如伯努利分布。
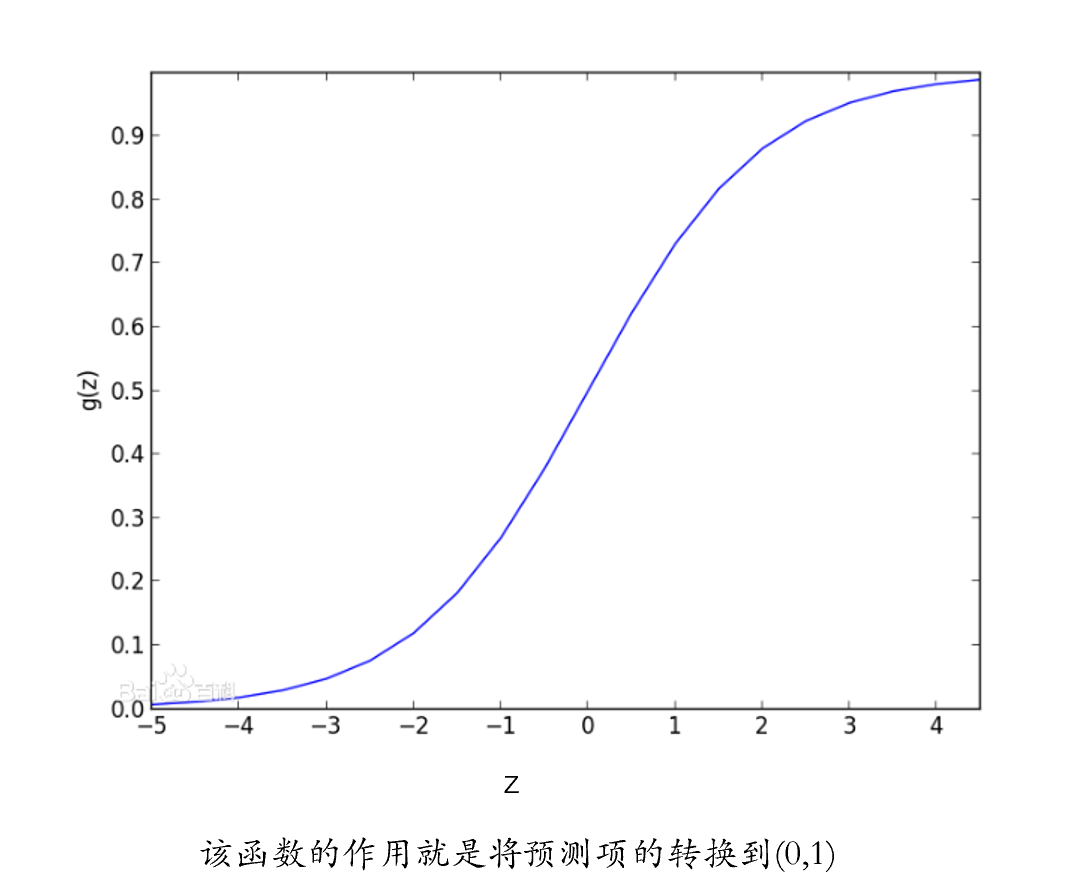
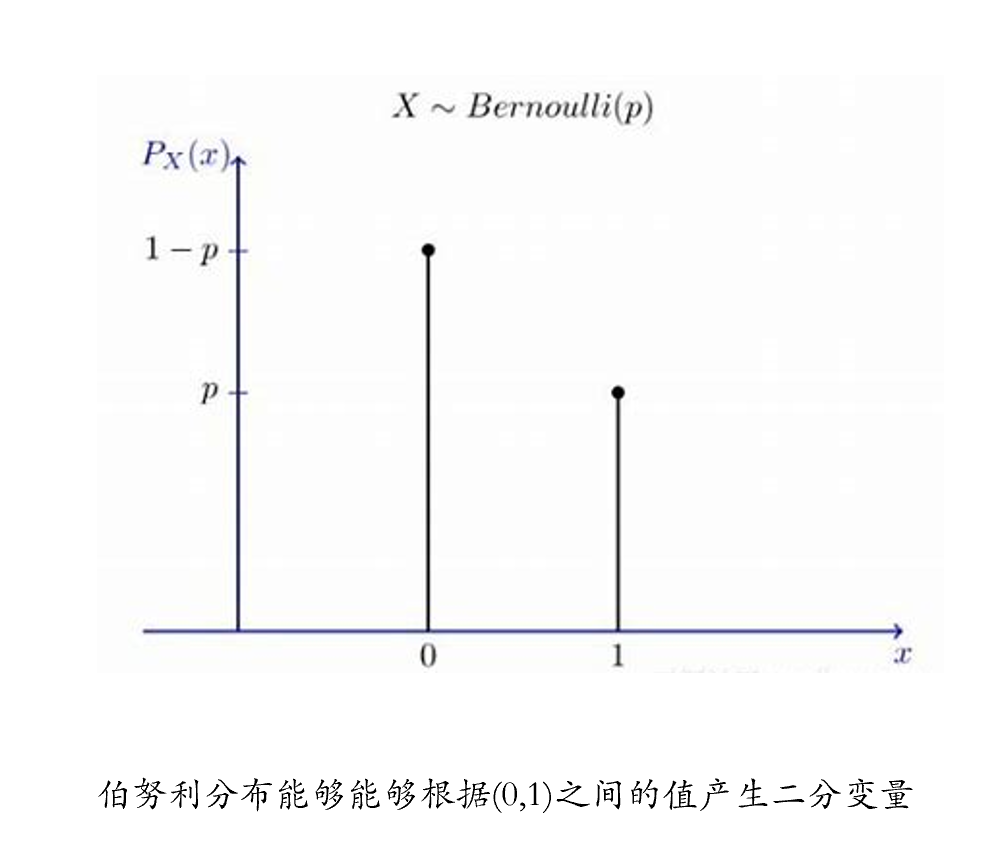
我们再次回到开头讲的线性模型的三部分,第一部分是将自变量通过线性组合得到z值,第二部分我们使用连接函数将连续的数值z映射到p的空间内,第三部分就是用p所属的一个分布去预测因变量。

这里会涉及到参数求解的问题,对于logit回归,我们可以使用极大似然估计对其进行求解,该求解过程比较复杂,一般由计算机自动完成,我们绝大部分都不需要了解。
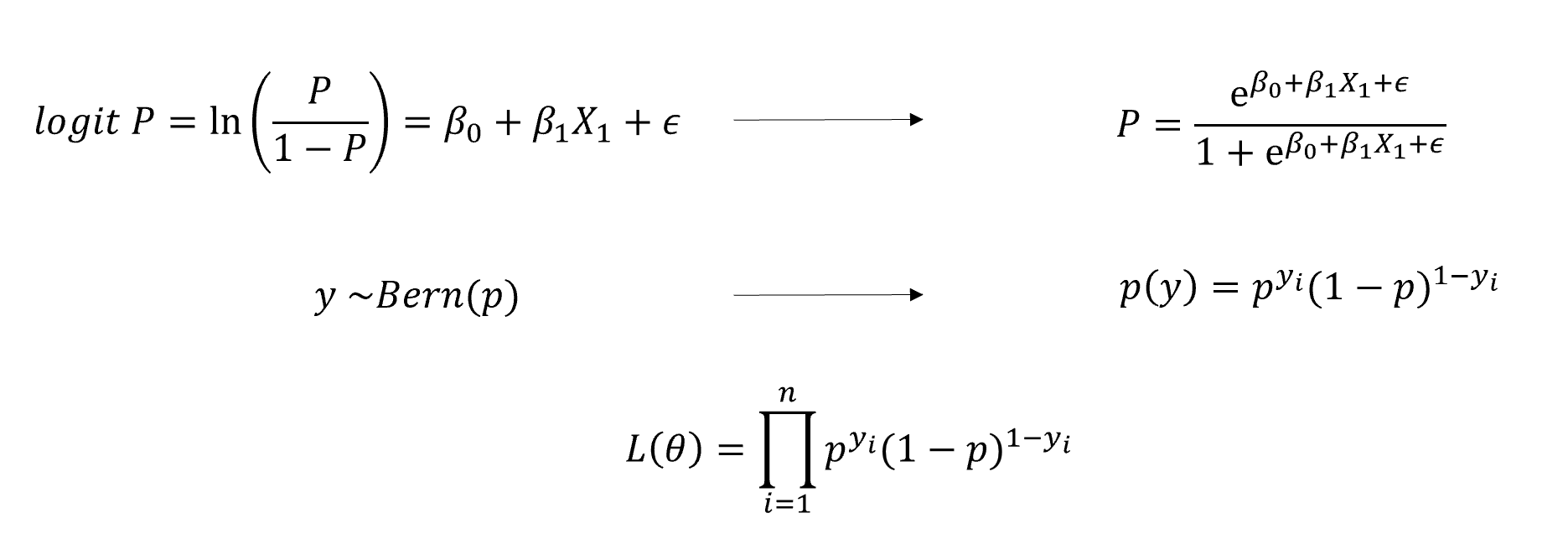
10.3.2 GLM代码实操
虽然我们前面提到了非常复杂和抽象的数学运算,但是在R中我们可以用非常简单的几行代码来实现广义线性模型。在公式部分和前一章是一致的,1是截距,后面放上实验的两个自变量,因变量是正确率ACC。我们所做的改动主要是在前面将函数改成了glm,并且加上了family这个参数,让其等于binomial。
这里我们可以明显地看到当我们使用广义线性模型之后,相较于传统的方差分析,我们可以对单个被试进行数据分析,这也意味着我们依然可以像前一章那样建立层级模型。以下是对单个被试进行glm建模的代码。
df.match.7304 <- df.match %>%
dplyr::filter(Sub == 7304) #选择被试7304
mod_7304_full <- stats::glm(data = df.match.7304, #数据
formula = ACC ~ 1 + Identity * Valence, #模型
family = binomial) #因变量为二项分布
summary(mod_7304_full) %>% #查看模型信息
capture.output() %>% .[c(6:11,15:19)] #课堂展示重要结果## [1] "Coefficients:"
## [2] " Estimate Std. Error z value Pr(>|z|) "
## [3] "(Intercept) 4.30 1.01 4.28 0.000019 ***"
## [4] "IdentityOther -2.69 1.05 -2.56 0.0106 * "
## [5] "Valenceimmoral -2.77 1.05 -2.64 0.0083 ** "
## [6] "IdentityOther:Valenceimmoral 2.10 1.13 1.86 0.0628 . "
## [7] "(Dispersion parameter for binomial family taken to be 1)"
## [8] ""
## [9] " Null deviance: 254.02 on 290 degrees of freedom"
## [10] "Residual deviance: 228.32 on 287 degrees of freedom"
## [11] "AIC: 236.3"建立层级模型意味着我们需要对总体和单个被试的效应都进行比较,通常我们会建立多个模型,然后对不同的模型进行比较。首先我们建立一个只有被试随机效应而没有群体固定效应的模型。
#无固定效应
mod_null <- lme4::glmer(data = df.match, #数据
formula = ACC ~ (1 + Identity * Valence|Sub), #模型
family = binomial) #因变量二项分布
#performance::model_performance(mod_null)
summary(mod_null) %>%
capture.output()%>% .[c(7:8,14:24)]## [1] " 9378.8 9460.2 -4678.4 9356.8 11999 "
## [2] ""
## [3] " Groups Name Variance Std.Dev. Corr "
## [4] " Sub (Intercept) 1.53 1.24 "
## [5] " IdentityOther 2.52 1.59 -0.86 "
## [6] " Valenceimmoral 2.40 1.55 -0.85 0.83 "
## [7] " IdentityOther:Valenceimmoral 3.34 1.83 0.69 -0.87 -0.82"
## [8] "Number of obs: 12010, groups: Sub, 41"
## [9] ""
## [10] "Fixed effects:"
## [11] " Estimate Std. Error z value Pr(>|z|) "
## [12] "(Intercept) 2.014 0.114 17.7 <0.0000000000000002 ***"
## [13] "---"接着我们建立一个随机效应只包含截距的模型。
#随机截距,固定斜率
mod <- lme4::glmer(data = df.match, #数据
formula = ACC ~ 1 + Identity * Valence + (1|Sub), #模型
family = binomial) #因变量二项分布
#performance::model_performance(mod)
summary(mod) %>%
capture.output() %>% .[c(7:8,14:24,28:32)]## [1] " 9639.0 9675.9 -4814.5 9629.0 12005 "
## [2] ""
## [3] " Groups Name Variance Std.Dev."
## [4] " Sub (Intercept) 0.237 0.487 "
## [5] "Number of obs: 12010, groups: Sub, 41"
## [6] ""
## [7] "Fixed effects:"
## [8] " Estimate Std. Error z value Pr(>|z|) "
## [9] "(Intercept) 2.4964 0.1015 24.60 < 0.0000000000000002 ***"
## [10] "IdentityOther -0.7161 0.0839 -8.53 < 0.0000000000000002 ***"
## [11] "Valenceimmoral -0.9474 0.0818 -11.58 < 0.0000000000000002 ***"
## [12] "IdentityOther:Valenceimmoral 0.8230 0.1085 7.58 0.000000000000034 ***"
## [13] "---"
## [14] " (Intr) IdnttO Vlncmm"
## [15] "IdenttyOthr -0.519 "
## [16] "Valencemmrl -0.533 0.641 "
## [17] "IdnttyOth:V 0.401 -0.773 -0.753"
## [18] NA最后我们建立一个包含了所有固定效应和随机效应的全模型。
#随机截距,随机斜率
mod_full <- lme4::glmer(data = df.match, #数据
formula = ACC ~ 1 + Identity * Valence + (1 + Identity * Valence|Sub), #模型
family = binomial) #因变量二项分布
##performance::model_performance(mod_full)
summary(mod_full) %>%
capture.output() %>% .[c(6:8,13:18,21:26,30:34)]## [1] " AIC BIC logLik deviance df.resid "
## [2] " 9355.9 9459.4 -4664.0 9327.9 11996 "
## [3] ""
## [4] "Random effects:"
## [5] " Groups Name Variance Std.Dev. Corr "
## [6] " Sub (Intercept) 0.972 0.986 "
## [7] " IdentityOther 1.770 1.331 -0.79 "
## [8] " Valenceimmoral 1.028 1.014 -0.75 0.75 "
## [9] " IdentityOther:Valenceimmoral 2.305 1.518 0.54 -0.82 -0.74"
## [10] "Fixed effects:"
## [11] " Estimate Std. Error z value Pr(>|z|) "
## [12] "(Intercept) 2.772 0.178 15.55 < 0.0000000000000002 ***"
## [13] "IdentityOther -0.870 0.234 -3.72 0.00020 ***"
## [14] "Valenceimmoral -1.150 0.189 -6.07 0.0000000013 ***"
## [15] "IdentityOther:Valenceimmoral 0.988 0.272 3.64 0.00027 ***"
## [16] "Correlation of Fixed Effects:"
## [17] " (Intr) IdnttO Vlncmm"
## [18] "IdenttyOthr -0.801 "
## [19] "Valencemmrl -0.782 0.740 "
## [20] "IdnttyOth:V 0.571 -0.820 -0.746"我们在运行全模型的时候可以明显感受到运行时间相较于之前变长了。当我们的模型内参数越多,模型越复杂的时候,计算机就需要花更多时间去拟合模型,也会有些时候因为找不到合适的参数而导致模型无法拟合。习惯了SPSS的读者可能会难以忍受,但实际上我们在后面处理一些大数据或者跑机器学习的时候,等待会是一件很常见的事情。这就提示我们合理分配时间,把要运行的代码提前运行起来,然后去做别的工作。
在这里,我们也可以根据结果来判断R语言对我们自变量的编码方式,可以看到结果中除了截距外的第一项为”Identityother”,由此我们可以判断R将”Identityself”编码为了基线,并据此来计算相应的回归系数和估计值,下面的其他结果也类似。
接下来我们对上述三个模型进行比较。
## Data: df.match
## Models:
## mod: ACC ~ 1 + Identity * Valence + (1 | Sub)
## mod_null: ACC ~ (1 + Identity * Valence | Sub)
## mod_full: ACC ~ 1 + Identity * Valence + (1 + Identity * Valence | Sub)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## mod 5 9639 9676 -4814 9629
## mod_null 11 9379 9460 -4678 9357 272.1 6 < 0.0000000000000002 ***
## mod_full 14 9356 9459 -4664 9328 28.9 3 0.0000023 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1可以发现全模型(mod_full)的效果是最好的,但当我们更换一种模型比较方法的时候,可能会得到不一样的结论,如下。
## Some of the nested models seem to be identical and probably only vary in their random effects.
让我们输出全模型的结果,尝试进行解读。
## [1] "Fixed effects:"
## [2] " Estimate Std. Error z value Pr(>|z|) "
## [3] "(Intercept) 2.772 0.178 15.55 < 0.0000000000000002 ***"
## [4] "IdentityOther -0.870 0.234 -3.72 0.00020 ***"
## [5] "Valenceimmoral -1.150 0.189 -6.07 0.0000000013 ***"
## [6] "IdentityOther:Valenceimmoral 0.988 0.272 3.64 0.00027 ***"
## [7] "---"在结果里面显示的估计值,并不直接等于p值,我们要根据前面转换函数的逆运算来讲其转换为p值,转换公式如下。
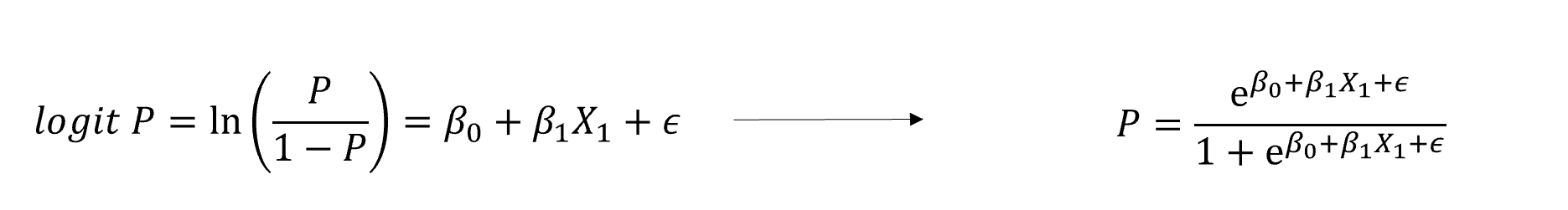
代入之后我们便可以求出不同实验条件下各自的p值。
MoralSelf: \(P=\frac{e^{2.73}}{1+e^{2.73}} = 0.939\)
ImmoralSelf: \(P=\frac{e^{2.73-1.10 }}{1+e^{2.73-1.10}} = 0.836\)
MoralOther: \(P=\frac{e^{2.73-0.76 }}{1+e^{2.73-0.76 }} = 0.878\)
ImmoralOther: \(P=\frac{e^{2.73-0.76-1.10+0.89}}{1+e^{2.73-0.76-1.10+0.89}} = 0.853\)
我们可以使用cat_plot()函数将模型预测的结果快速地展示出来。
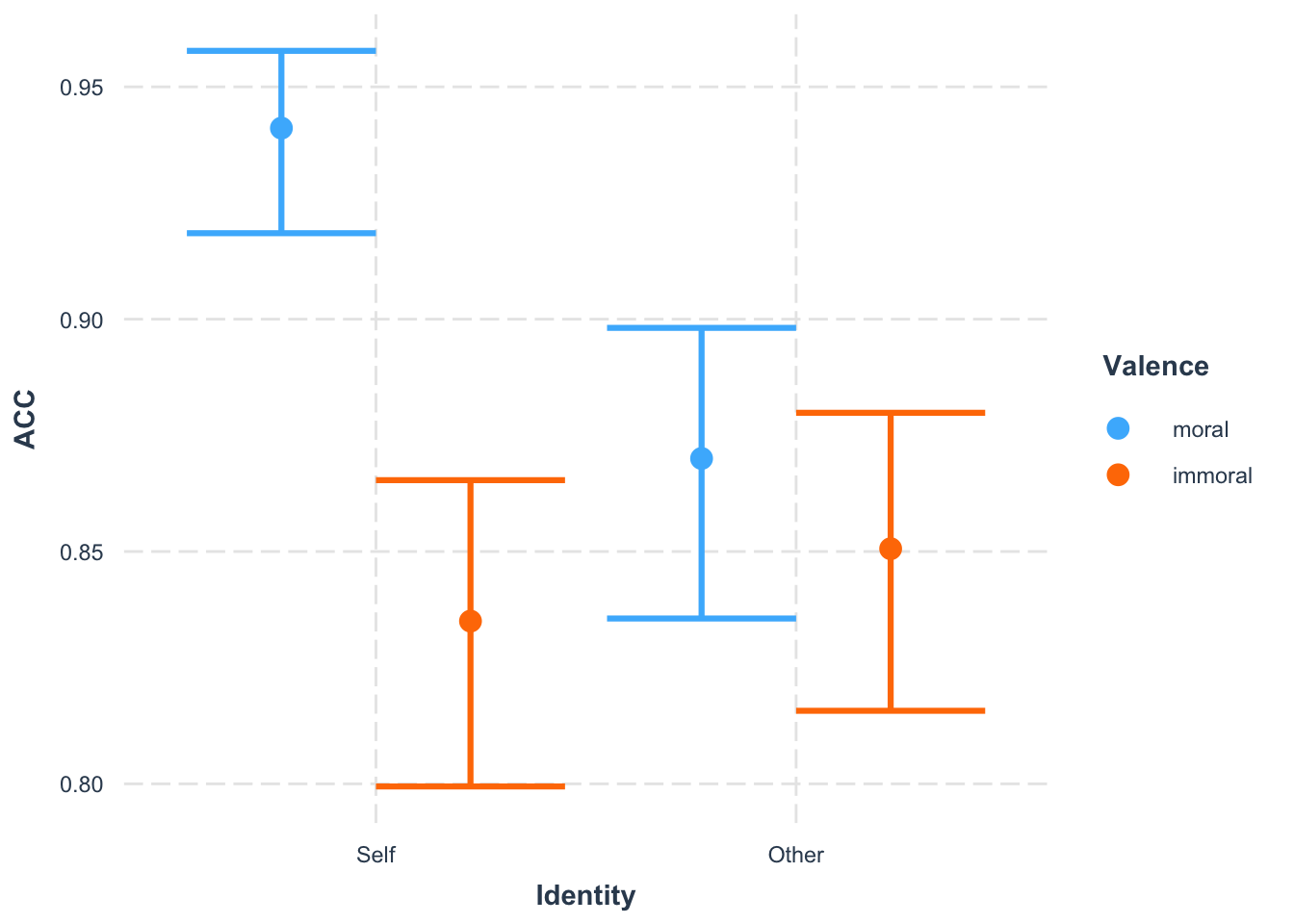
这里可以看到很明显的交互作用,也就是当我们把不同颜色的柱子连线就会发现二者的交叉。
10.4 不同方法比较
10.4.1 不同的建模方法
接下来我们对正确率不同的分析方法做一个比较。首先是传统的方差分析,方差分析实际上就是一个线性模型。以下是对正确率进行方差分析的代码。
res <- bruceR::MANOVA(data = df.match.aov, #数据
subID = 'Sub', # 被试编号
dv= 'mean_ACC', # 因变量
within = c('Identity', 'Valence')) #自变量(被试内)##
## * Data are aggregated to mean (across items/trials)
## if there are >=2 observations per subject and cell.
## You may use Linear Mixed Model to analyze the data,
## e.g., with subjects and items as level-2 clusters.## [1] "Response: mean_ACC"
## [2] " Effect df MSE F ges p.value"
## [3] "1 Identity 1, 40 0.01 3.08 + .017 .087"
## [4] "2 Valence 1, 40 0.01 16.26 *** .068 <.001"
## [5] "3 Identity:Valence 1, 40 0.01 8.52 ** .038 .006"
## [6] "---"我们可以得到一个f值,并且因为研究的被试量比较大,我们可以发现这里呈现的主效应以及交互作用,和后面用glm或者层级模型做出来的结果有一样的趋势。我们可以用EMMAMNS()函数来查看模型的一些具体值。
## [1] "------ EMMEANS (effect = \"Valence\") ------"
## [2] ""
## [3] "Joint Tests of \"Valence\":"
## [4] "────────────────────────────────────────────────────────────────"
## [5] " Effect \"Identity\" df1 df2 F p η²p [90% CI of η²p]"
## [6] "────────────────────────────────────────────────────────────────"
## [7] " Valence Self 1 40 35.614 <.001 *** .471 [.282, .610]"
## [8] " Valence Other 1 40 0.412 .525 .010 [.000, .114]"
## [9] "────────────────────────────────────────────────────────────────"
## [10] "Note. Simple effects of repeated measures with 3 or more levels"
## [11] "are different from the results obtained with SPSS MANOVA syntax."
## [12] ""
## [13] "Estimated Marginal Means of \"Valence\":"
## [14] "───────────────────────────────────────────────────"
## [15] " \"Valence\" \"Identity\" Mean [95% CI of Mean] S.E."
## [16] "───────────────────────────────────────────────────"
## [17] " moral Self 0.916 [0.885, 0.947] (0.015)"
## [18] " immoral Self 0.814 [0.776, 0.852] (0.019)"
## [19] " moral Other 0.844 [0.809, 0.879] (0.017)"
## [20] " immoral Other 0.829 [0.794, 0.864] (0.017)"
## [21] "───────────────────────────────────────────────────"
## [22] ""
## [23] "Pairwise Comparisons of \"Valence\":"
## [24] "────────────────────────────────────────────────────────────────────────────────────────"
## [25] " Contrast \"Identity\" Estimate S.E. df t p Cohen’s d [95% CI of d]"
## [26] "────────────────────────────────────────────────────────────────────────────────────────"
## [27] " immoral - moral Self -0.102 (0.017) 40 -5.968 <.001 *** -0.736 [-0.985, -0.487]"
## [28] " immoral - moral Other -0.015 (0.024) 40 -0.642 .525 -0.111 [-0.459, 0.238]"
## [29] "────────────────────────────────────────────────────────────────────────────────────────"
## [30] "Pooled SD for computing Cohen’s d: 0.139"
## [31] "No need to adjust p values."
## [32] ""
## [33] "Disclaimer:"
## [34] "By default, pooled SD is Root Mean Square Error (RMSE)."
## [35] "There is much disagreement on how to compute Cohen’s d."
## [36] "You are completely responsible for setting `sd.pooled`."
## [37] "You might also use `effectsize::t_to_d()` to compute d."
## [38] ""接下来是包括所有固定效应和随机效应的全模型的结果。
## Analysis of Variance Table
## npar Sum Sq Mean Sq F value
## Identity 1 0.2 0.2 0.2
## Valence 1 26.8 26.8 26.8
## Identity:Valence 1 13.6 13.6 13.6下面我们在求出每个被试的正确率之后,将其当作层级模型来进行处理的结果,和上面其他模型得到的也比较类似。
mod_anova <- lme4::lmer(data = df.match,
formula = ACC ~ 1 + Identity * Valence + (1 + Identity * Valence|Sub))
stats::anova(mod_anova)## Analysis of Variance Table
## npar Sum Sq Mean Sq F value
## Identity 1 0.42 0.42 3.70
## Valence 1 3.17 3.17 27.70
## Identity:Valence 1 0.98 0.98 8.54我们还可以用线性模型来做出类似于方差分析的结果,但由于二者算法并不完全相同,因此结果也存在一些细微的差异。
mod_mean <- lme4::lmer(data = df.match.aov,
formula = mean_ACC ~ 1 + Identity * Valence + (1|Sub) + (1|Identity:Sub) + (1|Valence:Sub))
stats::anova(mod_mean)## Analysis of Variance Table
## npar Sum Sq Mean Sq F value
## Identity 1 0.0272 0.0272 3.08
## Valence 1 0.1410 0.1410 15.93
## Identity:Valence 1 0.0769 0.0769 8.6910.4.2 不同的模型比较方法
在建立了上述所有模型之后,我们想要知道的是,层级模型是否就是一个最好的模型呢?我们可以用默认的模型比较方法对上述模型进行比较。

performance()结果会把比较好的模型排在上面,总体而言anova模型更好。不过我们可以看到一些参数,R2表示模型解释的变异,ICC反映的是个体变异的内容,这两个参数都是层级模型更优。我们再用anova()对模型做一次比较。
## refitting model(s) with ML (instead of REML)## Data: df.match
## Models:
## mod_full: ACC ~ 1 + Identity * Valence + (1 + Identity * Valence | Sub)
## mod_anova: ACC ~ 1 + Identity * Valence + (1 + Identity * Valence | Sub)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## mod_full 14 9356 9459 -4664 9328
## mod_anova 15 8396 8507 -4183 8366 962 1 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1在结果的参数中,AIC的值一般是越小越好,我们会发现anova的模型反而是更好的。总体而言,两种方法似乎都提示我们传统的方差分析是更优的。
接着我们还用机器学习的方法对层级模型和方差分析模型进行了比较,70%的数据作为训练集,剩余的30%作为测试集,以此比较二者的模型预测效果。
# 设置种子以确保结果的可重复性
set.seed(456)
# 随机选择70%的数据作为训练集,剩余的30%作为测试集
train_index <- caret::createDataPartition(df.match$Sub, p = 0.7, list = FALSE)
train_data <- df.match[train_index, ]
test_data <- df.match[-train_index, ]
# 根据训练集生成模型
model_full <- lme4::glmer(data = train_data,
formula = ACC ~ 1 + Identity * Valence + (1 + Identity * Valence|Sub),
family = binomial)
model_anova <- lme4::lmer(data = train_data,
formula = ACC ~ 1 + Identity * Valence + (1 + Identity * Valence|Sub))
# 使用模型进行预测
pre_mod_full <- stats::predict(model_full, newdata = test_data, type = 'response')
pre_mod_anova <- stats::predict(model_anova, newdata = test_data)我们对二者的预测性能进行比较。
# 计算模型的性能指标
performance_mod_full <- c(RMSE = sqrt(mean((test_data$ACC - pre_mod_full)^2)),
R2 = cor(test_data$ACC, pre_mod_full)^2)
# 打印性能指标
print(performance_mod_full)## RMSE R2
## 0.342402 0.074985# 计算模型的性能指标
performance_mod_anova <- c(RMSE = sqrt(mean((test_data$ACC - pre_mod_anova)^2)),
R2 = cor(test_data$ACC, pre_mod_anova)^2)
# 打印性能指标
print(performance_mod_anova)## RMSE R2
## 0.342263 0.075676RSME表示的是模型预测值和实际值之间的差异,可以发现二者的区别并不是很大。我们接下来还使用了混淆矩阵和ROC曲线的方法对模型性能进行比较,具体的代码和结果可以参考如下内容。
# 将预测概率转换为分类结果
predicted_classes <- ifelse(pre_mod_full > 0.5, 1, 0)
# 计算混淆矩阵
confusion_matrix <- caret::confusionMatrix(as.factor(predicted_classes), as.factor(test_data$ACC))## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 37 27
## 1 499 3037
##
## Accuracy : 0.854
## 95% CI : (0.842, 0.865)
## No Information Rate : 0.851
## P-Value [Acc > NIR] : 0.33
##
## Kappa : 0.095
##
## Mcnemar's Test P-Value : <0.0000000000000002
##
## Sensitivity : 0.0690
## Specificity : 0.9912
## Pos Pred Value : 0.5781
## Neg Pred Value : 0.8589
## Prevalence : 0.1489
## Detection Rate : 0.0103
## Detection Prevalence : 0.0178
## Balanced Accuracy : 0.5301
##
## 'Positive' Class : 0
## ## Setting levels: control = 0, case = 1## Setting direction: controls < cases##
## Call:
## roc.default(response = test_data$ACC, predictor = pre_mod_full)
##
## Data: pre_mod_full in 536 controls (test_data$ACC 0) < 3064 cases (test_data$ACC 1).
## Area under the curve: 0.699# 绘制ROC曲线
plot(roc_result, main = "ROC Curve", col = "blue", lwd = 2)
abline(a = 0, b = 1, lty = 2) # 添加对角线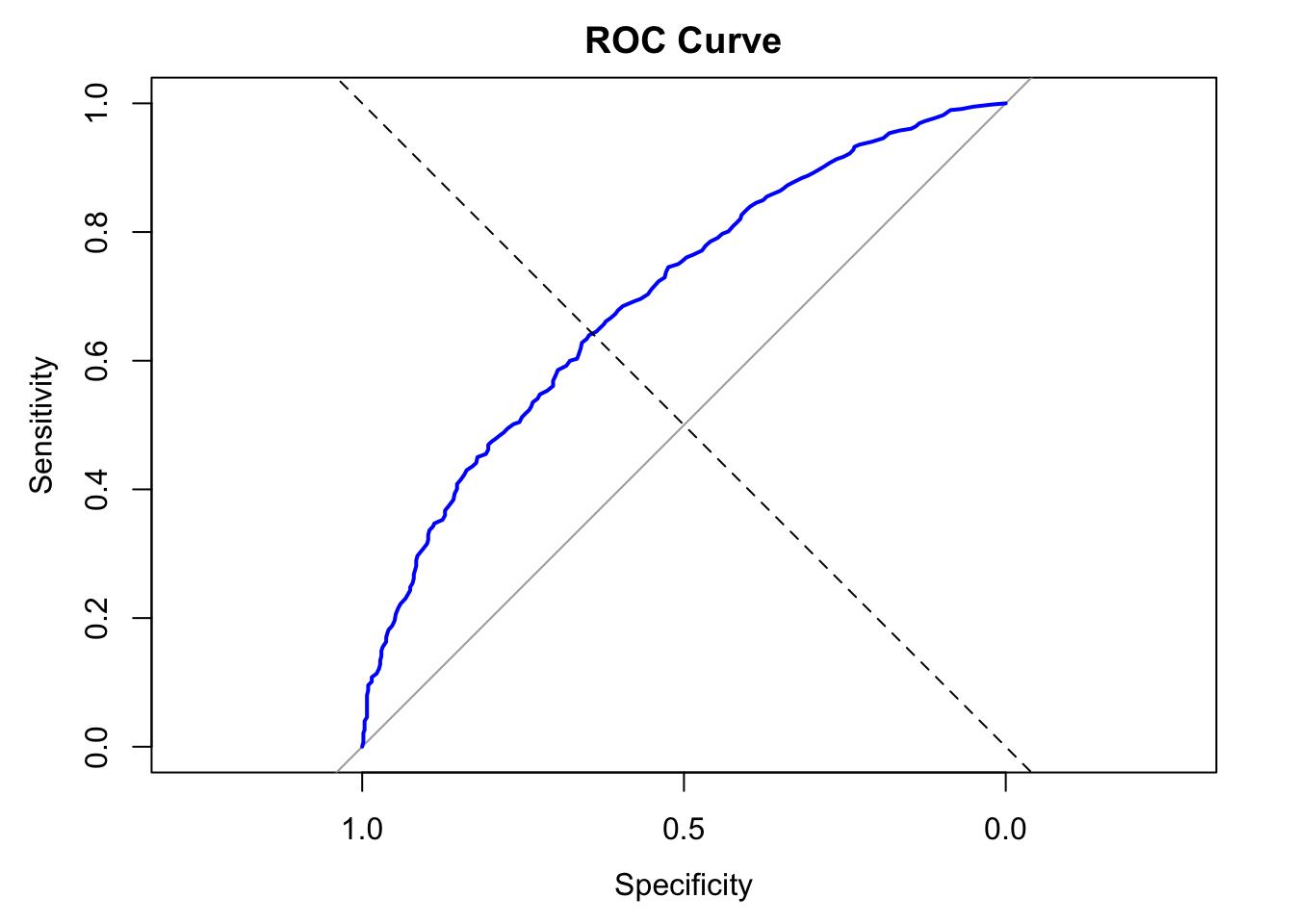
ROC的结果会返回一个指标”area under the curve”(AUC,曲线下面积),这个值一般越大说明模型越好。可以发现anova的曲线下面积值低于glm,也就是说glm优于anova。
在进行了上述的模型比较之后,我们发现不同的方法得到的结果是不一致的。我们一般认为当模型越符合数据特征的时候,模型的表现应该会更好,这是我们的直觉。glm使用二项分布去捕捉正确率这一因变量的数据,这是更符合数据特征的,但是这种更符合数据特征的模型效果居然更差,这和我们的直觉冲突。
这是因为有一些模型比较的方法是只适合于线性模型的,对于广义线性模型进行比较的时候就会出现问题,所以我们用一些传统的模型比较指标会发现anova更优或者二者没有差异。但我们用glm去预测不同被试在不同条件下被试的反应的时候,我们通常会发现glm的效果比anova更好。
不管怎样,这也提示我们建立完模型之后,对于如何比较不同的模型,选择什么样的比较指标和方法也要去花费一定的心思,而不能拿来就用。
本章至此一直在介绍如何对正确率这种分类的变量进行层级模型的建模分析,那么我们为什么不使用传统的方差分析呢? 2008年的一篇文章(jager, 2008)提到,我们对正确率进行anova时,会产生难以解释的结果:假设在10个回答中,正确回答8次,错误回答2次,此时95%CI为[0.52,1.08] ( = 0.8 ± 0.275),我们发现方差不齐,不满足方差分析基本假设。 \[\mu = np\] \[𝜎 = √(𝑛𝑝𝑞 )\] \[𝜎_p^2 = \frac{p(1-p)}{n}\] Jaeger, T. F. (2008). Categorical data analysis: Away from ANOVAs (transformation or not) and towards logit mixed models. Journal of Memory and Language, 59(4), 434-446. doi:http://dx.doi.org/10.1016/j.jml.2007.11.007
《Journal of Memory and Language》看上去好像是关于记忆和语言的期刊,但实际上上面有很多方法学,包括混合线性模型方法的介绍,读者可以关注该期刊。
10.5 其他分布
参照本章之前的思路,只要y和x之间可以通过线性转换和连接函数建立关系,就可以去对各式各样的数据类型进行建模分析。例如泊松分布(Poisson distribution),这是一种在医学或者流行病学领域研究中常见的数据分布类型。泊松分布是指在固定时间间隔或空间区域内发生某种事件的次数的概率,它适用于事件以恒定平均速率独立发生的情况,例如电话呼叫、网站访问、机器故障等。 \[P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}\] - λ:事件在给定时间或空间内的平均发生率(或平均数量)。 - k:可能的事件发生次数,可以是0, 1, 2, …
下面我们用代码来模拟一下泊松分布。
set.seed(123) # 设置随机种子以获得可重复的结果
random_samples <- rpois(1000, lambda = 5)
hist(random_samples,col = 'white', border = 'black',)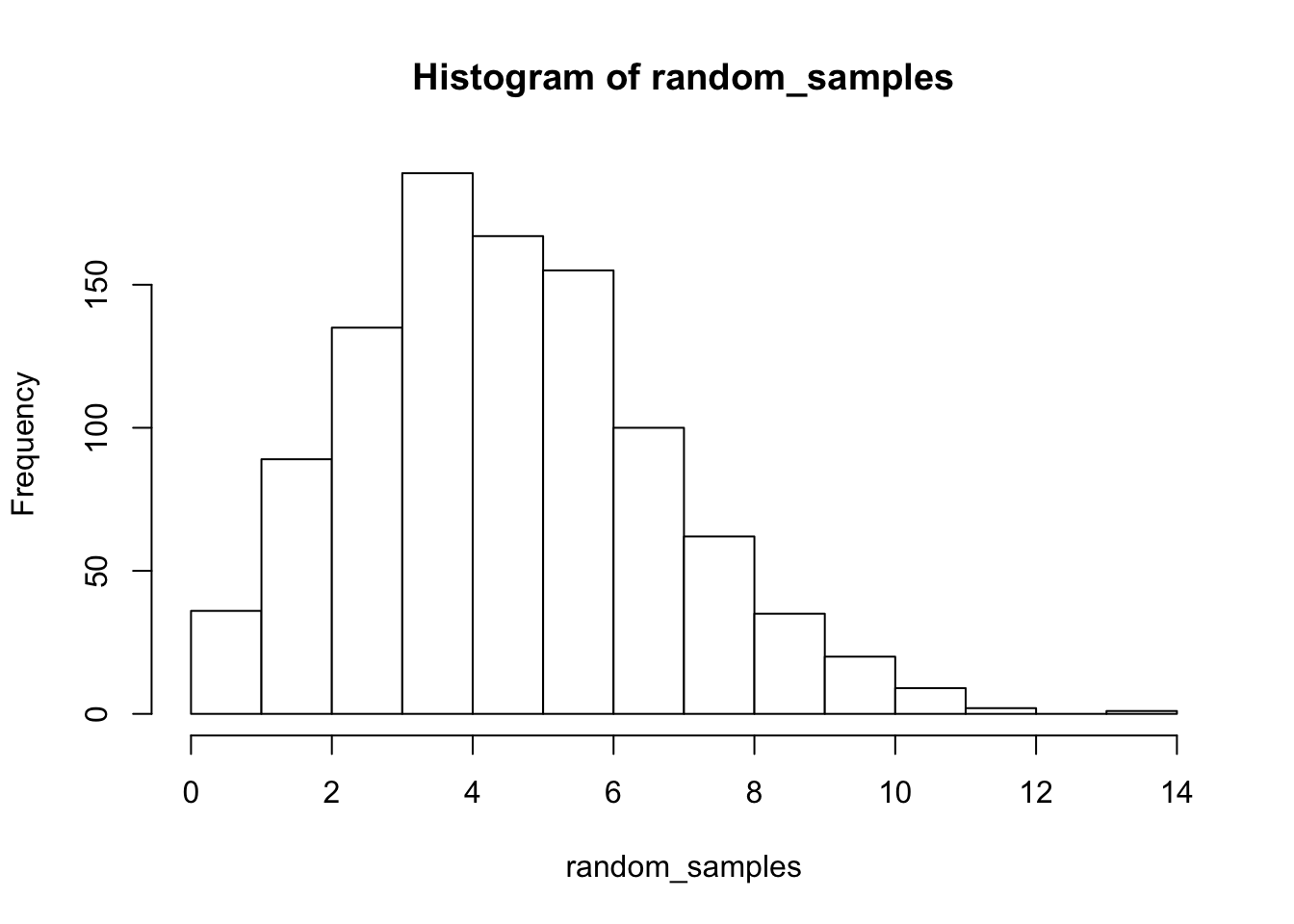
同样我们可以通过连接函数对其进行广义线性模型的建模。
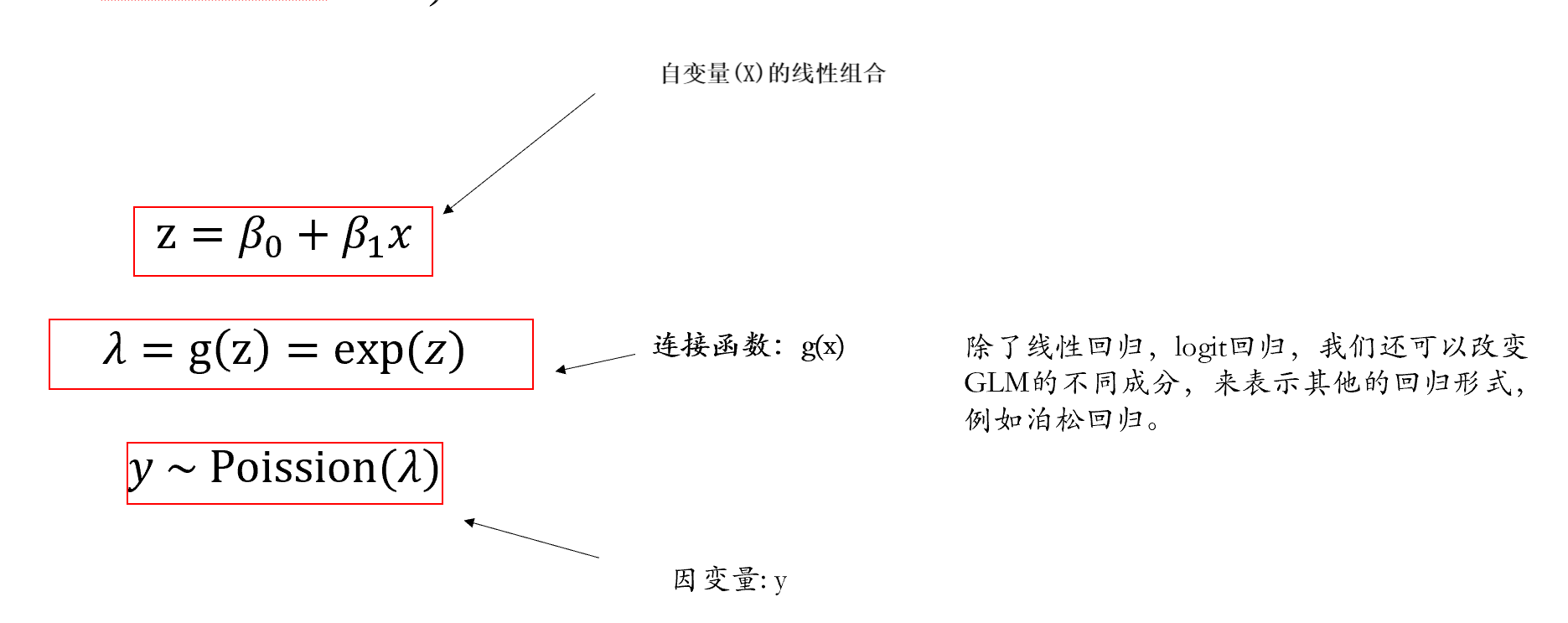 另外一些常见的分布还包括伽马分布(Gamma
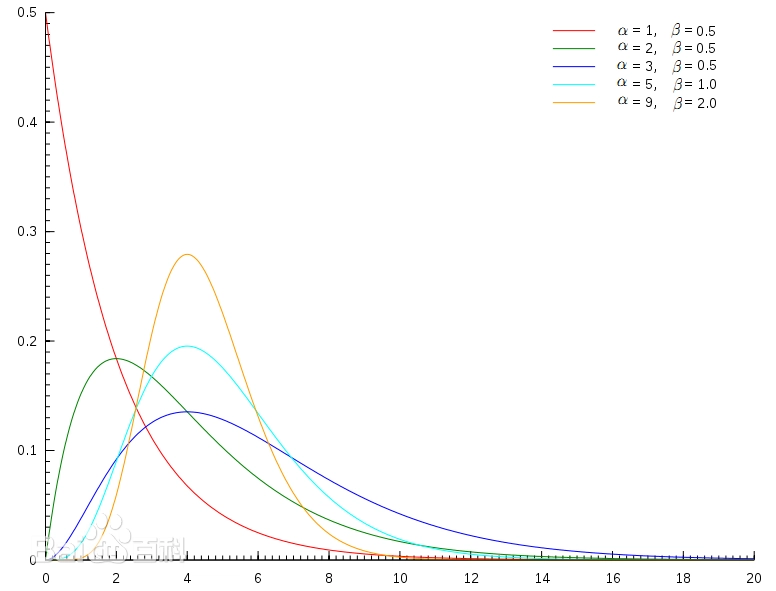
Distribution),这是统计学的一种连续概率函数,是概率统计中一种非常重要的分布。“指数分布”和”卡方分布”都是伽马分布的特例。
\[f(x | \alpha, \beta) = \frac{\beta^\alpha x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)}\] -
α:形状参数(shape
parameter),决定了分布的曲线形态,尤其是峰值的位置和曲线的尖峭程度。 -
β:尺度参数(scale
parameter),影响分布的宽度;当尺度参数增大时,分布会变得更宽且矮平;尺度参数减小时,分布会变得更窄且高耸。
另外一些常见的分布还包括伽马分布(Gamma
Distribution),这是统计学的一种连续概率函数,是概率统计中一种非常重要的分布。“指数分布”和”卡方分布”都是伽马分布的特例。
\[f(x | \alpha, \beta) = \frac{\beta^\alpha x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)}\] -
α:形状参数(shape
parameter),决定了分布的曲线形态,尤其是峰值的位置和曲线的尖峭程度。 -
β:尺度参数(scale
parameter),影响分布的宽度;当尺度参数增大时,分布会变得更宽且矮平;尺度参数减小时,分布会变得更窄且高耸。
下面是伽马分布的示意图。
总体而言,本章介绍的广义线性模型可以将我们能够处理的数据拓展到正态分布以外,给我们提供了一个更好的工具。另外,请读者朋友们可以思考一下,信号检测论是否可以用广义线性模型分析?大家可以思考后在网上搜到相关的资料,这里不再赘述。