Chapter 9 第九讲:回归模型(二):分层线性模型
# Packages
if (!requireNamespace('pacman', quietly = TRUE)) {
install.packages('pacman')
}
pacman::p_load(
# 本节课需要用到的 packages
here, tidyverse,
# ANOVA & HLM
bruceR, lmerTest, lme4, broom, afex, interactions, knitr)
options(scipen=99999,digits = 5)9.1 回顾
大家晚上好,我们开始上课,上节课我们介绍了使用r语言分析数据,以我们最常见的或者说我们心理学当中,最常见的两种方法ttest和ANOVA,但是我们给它加了一个标题,叫做回归模型或者线性模型一,然后我们在介绍完如何使用常规的R代码来实现这些功能之后,我们又给大家讲解了一下,为什么t-test和ANOVA实际上是线性模型的特例,那么这个是如果要运行我们Rmarkdown的话一定要提前准备一下这个代码。我们上节课是以这个表结尾的,也就是说我们常见的这个t-test,包括单样本、独立样本和配对样本的ttest以及单因素的方差分析和多因素的方差分析,基本上都可以用R里面的最基本的这个space,就是统计学的这个包里面的lm (linear model)来实现,而且我们也可以从线性模型的角度对它进行解读。比方说我们发现这个t-test,它可能就是一个自变量是二分变量的一个回归模型然后还有其他的我们在这里都有讲解。
| R自带函数 | 线性模型 | 解释 | |
|---|---|---|---|
| 单样本t | t.test(y, mu = 0) | lm(y ~ 1) | 仅有截距的回归模型 |
| 独立样本t | t.test( \(y_1\), \(y_2\)) | lm(y ~ 1 + \(G_2\)) | 自变量为二分变量的回归模型 |
| 配对样本t | t.test( \(y_1\), \(y_2\), paired=T) | lm( \(y_1\) - \(y_2\) ~ 1) | 仅有截距的回归模型) |
| 单因素ANOVA | aov(y ~ G) | lm(y ~ 1 + \(G_1\) + \(G_2\) + …) | 一个离散自变量的回归模型 |
| 多因素ANOVA | aov(y ~ G * S) | lm(y ~ \(G_1\) + \(G_2\) + … + \(S_1\) + \(S_2\) + …) | 多个离散自变量的回归模型 |
那么上节课给大家在讲解的时候,我们用的是penguin那个数据,在这里也可能会涉及到对一些离散变量的虚拟编码的问题,对离散变量的这个虚拟编码dummycoding,它其实有很多种方式,在这个space这个包里面,它专门有一个叫做controltreatment这样一个方式来对我们的离散变量怎么进入回归方程进行编码,有各种各样的方式,大家如果感兴趣呢,可以去参考一些相关的资料。
首先就是大家注意不同的软件或者不同软件包,它的默认的编码方式可能是不一样的,这里面可能会有一些区别,所以有可能比方说由于这个默认的编码方式不一样,最后会导致一个你看到的统计的结果是不一样的。在第八课我们在课后做了一点点小的修改,就是我们不仅仅可以采用,比方说FX那个包来去达到一模一样的一个回归,我们可以采用多种方式来实现跟方差分析一模一样的结果,其中一个方式,就是改变controltreatment改变编码方式。大家如果把我们那个最新的rmarkdown拉下去回顾的话,看一下我们上节课的课件。
[预处理]
df.penguin <- bruceR::import(here::here("Book",'data', 'penguin', 'penguin_rawdata.csv')) %>%
dplyr::mutate(subjID = row_number()) %>%
dplyr::select(subjID,Temperature_t1, Temperature_t2, socialdiversity,
Site, DEQ, romantic, ALEX1:ALEX16) %>%
dplyr::filter(!is.na(Temperature_t1) & !is.na(Temperature_t2) & !is.na(DEQ)) %>%
dplyr::mutate(romantic = factor(romantic, levels = c(1,2),
labels = c("恋爱", "单身")), # 转化为因子
Temperature = rowMeans(select(., starts_with("Temperature"))))
# 设定相应的标签
breaks <- c(0, 35, 50, 66.5)
labels <- c('热带', '温带', '寒温带')
# 创建新的变量
df.penguin$climate <- cut(df.penguin$DEQ,
breaks = breaks,
labels = labels)在结果上面,这个treatment,我们的现在这种编码方式,实际上就是以其中的一个条件,比方说我们上节课讲到了不同的这个气温带,那么我们实际上就是以热带作为基线,另外的这种回归系数它分别其实表示的是另外两种条件跟它的一个差值,这里我们其实可以从这个这个统计数据上面能够看得出来。
[虚拟编码]
# 比较不同气候条件下个体的体温是否存在差异:
## 虚拟编码
contrasts(df.penguin$climate) <- stats::contr.treatment(unique(df.penguin$climate))
### contr.treatment本质上创建了一个矩阵
### 由于3个分组,所以矩阵为2列
## 建立回归模型
lm_temp <- stats::lm(Temperature ~ climate,data = df.penguin)[结果]
## # A tibble: 3 × 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 36.6 0.022
## 2 climate寒温带 -0.178 0.028
## 3 climate温带 -0.299 0.03## 可以看到回归的结果以热带为基准,系数则为均值之差
df.penguin %>%
group_by(climate) %>%
summarise(mean = mean(Temperature)) %>%
as.data.frame() ## climate mean
## 1 热带 36.555
## 2 温带 36.377
## 3 寒温带 36.255虚拟编码方式很多,可参考这里
9.2 重复测量方差分析
那这是我们上节课的一个结果,上节课我们回答了一个问题,对于这种有重复测量的这种情况怎么办?在我们心理学当中另外一个非常常见的一个现象,或者说使用的一个方法,就是用重复测量的方差分析。那比方说我们检验某一种干预,某种心理干预也好,或者是药物干预也好,它有没有效果,一般我们会设计一个干预前进行一次测量,干预之后再进行测量,不仅如此,可能还有实验组和控制组,有组间变量,有组内的变量,它就是前后测,前后测的时候就涉及到了一个重复测量的问题。所以在我们心理学当中,尤其在实验研究当中,我们非常常用的,就是重复测量的方差分析。那么我们上节课既然讲到了ttest和方差分析,组间的方差分析,它是一个线性模型的话,那么重复测量的方差分析,它是不是也是一个线性模型呢?我们这个时候以我们在课堂上经常采用的另外一个例子,就是我们那个实验matching的这个数据为例,这个数据,它是一个典型的认知心理学的实验,采用的是完全的被试内设计,我们有2*2的这个实验设计,也就是说我们有两种自变量,一个是刺激他的身份,另外一个是道德上的效价,是积极的moral还是消极的immoral,那么这两个自变量的话,它就组合成为4个条件,每一个被试在实验当中,都要经历所有的4种条件处理。我们通过之前学到的bruceR,然后用here这个包,在我们的这个课件的所在文件夹内部,可以通过这种方式把它读取进来,读取进来之后的话,我们可以看一下,我们先做了一个处理,在实验设计中,我们有两个自变量,但是在我们的这个数据里面我们当时是用一个变量shape来表示这两个自变量,就是两个自变量的各种组合,我们这里先把它进行了一个拆分,实际上是用的这个tidyr里面的一个函数,这是数据预处理的部分。大家有可能以后也会经常碰到这种字符的处理tidyr里面有一些函数是比较方便的。处理完了之后可以看到它这个数据,每一个被试,有他的年龄性别,还有他的左右利手,然后还有这个实验的信息,原来是一个变量,这个试次他这个形状代表的是什么,拆分之后的,它就拆分成了两个变量,一个叫做Valence,一个叫做Identity。
[预处理]
mt_raw <- bruceR::import(here::here("Book",'data','match','match_raw.csv'))
mt_raw <- mt_raw %>%
tidyr::extract(Shape,
into = c("Valence", "Identity"),
regex = "(moral|immoral)(Self|Other)",
remove = FALSE)[数据展示]
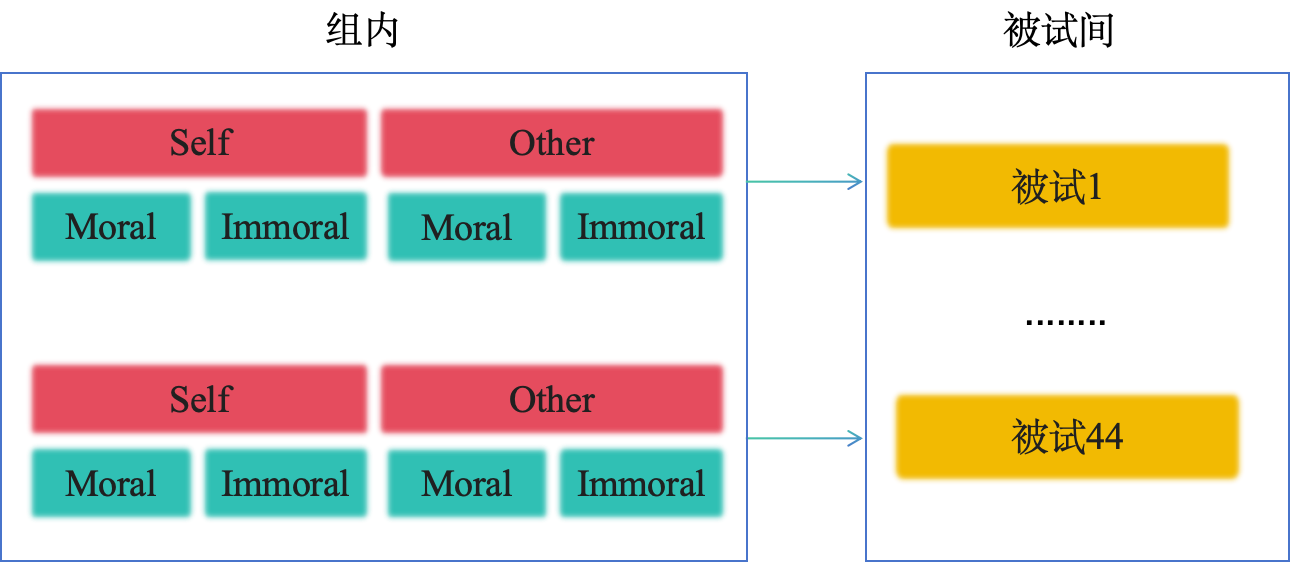
以match_raw.csv为例,一个2x2的被试内实验设计(Identity:Self vs.Other) x Valence:Moral vs.Immoral)),我们希望知道这两种条件之下被试的反应时是否存在显著差异然后我们就发现,这个数据实际上是有很多的,每个被试还有很多个试次,那么这种情况的话,大家通常做法是怎么做呢?如果通常我们用常规的这个重复测量方差分析,大家怎么做呢?比方说有40多个被试,然后有四种条件,我们最后会算出每个被试在每种条件下,比方说我们关心反应时间的话,就是反应时间的一个均值,那么最后我们得到比方说44个被试他们的这个反应时间的均值,然后呢我们就把它输入到SPSS里面,然后进行一个重复测量方差分析,然后把它对应好,这是我们常规的做法,它数理结构基本上就是这样的。每一个被试有自我有他人,自我和他人下面又有moral和immoral两个条件,other的也有moral和immoral。 这样的话,如果说我们在本科阶段我们讲方差分析的时候,我们就会告诉大家,这里面会进行方差的分解,我们把它分解为,不同条件之间的变异,或者不同的自变量引起的变异,以及这个被试的个体差异,我们主要关注的,比方说就是这个自变量它引起的变异在总体的变异当中的比值,然后根据这个比值去计算f值等等等等,计算MSE就是谁的,这是本科的或大概考研的时候,可能会涉及到内容,那么在SPSS里面,大家可能也看到过,类似的这个实现的方式,那么在r里面也很方便的进行实现.

那我们先按照常规的方式,先进行一个预处理,比方说我们一般看反应时间的时候,我们主要看的就是正确的反应试次的反应时间,我们把没有反应的和这个错误的都剔除掉,那么在这里我们还有一点额外处理,我们先还有一个条件,就是这个图片和这个文字是不是匹配的,我们这个时候只关心这个匹配的,因为我们上课做一个演示,简化一点,那么所以我们筛选出的是匹配的,这个试次的数据,因为我们关心反应时间,所以我们选出了全部为正确试次的一个反应,那么然后我们就通过这个group_by,在数据预处理里面我们提到的这个函数,以被试的ID、identity和valence三个作为分组变量,然后通过summarise去求他们的均值,这都是我们前面学到的内容,然后这样的话我们就得到了非常熟悉的这种数据。但这个时候如果大家想要,把它输到SPSS进行预处理的话,我们还要把它从长型的数据转成宽型的数据,但是在r里面我们其实没有必要转,我们可以直接使用bruceR里面的这个ANOVA,然后把被试的ID放进来,然后DV,dependent variable等于RT,很方便,这个within就表示是within-subject,应该是independent variable,我们这里有两个就是identity和valence那么到这里其实整个r里面就输完了,我们这里只不过是把它的结果,后面这个部分的话是为了显示结果,所以前面的这个部分,就是大家可能会比较关心的。如果你自己在r里面你就选择这段代码运行的话,你会在那个rmarkdown里面直接看到它全部的输出,那么我们看多少里面最重要的输出,或者我们最关心的输出可能就是这个方差分析表,那么这里面我们可以看到identity valence,它们分别的主效应和它们的交互作用,这时候我们可以看到很明显的,比方说这里有p值、f值这是大家都很喜欢的。
[ANOVA-bruceR]
mt_mean <- mt_raw %>%
dplyr::filter(!is.na(RT) & Match == "match" & ACC == 1) %>%
dplyr::group_by(Sub,Identity,Valence) %>%
dplyr::summarise(RT = mean(RT)) %>%
dplyr::ungroup()## `summarise()` has grouped output by 'Sub', 'Identity'. You can override using the `.groups` argument.## 本例为长数据
## RUN IN CONSOLE!
## 球形检验输出:
bruceR::MANOVA(data = mt_mean,
subID = 'Sub', # 被试编号
dv= 'RT', # dependent variable
within = c('Identity', 'Valence')) %>% capture.output() %>% .[c(33:37)]##
## * Data are aggregated to mean (across items/trials)
## if there are >=2 observations per subject and cell.
## You may use Linear Mixed Model to analyze the data,
## e.g., with subjects and items as level-2 clusters.## [1] "Levene’s Test for Homogeneity of Variance:"
## [2] "No between-subjects factors. No need to do the Levene’s test."
## [3] ""
## [4] "Mauchly’s Test of Sphericity:"
## [5] "The repeated measures have only two levels. The assumption of sphericity is always met."然后还有大家可能没有那么常用的、现在越来越推荐报告的,比方说这个eta-square,叫伊塔方,反映的是效应量的一个指标。那么bruceR里面有一个好处,就是它会输出多个效应量的指标,包括partialeta-squared,偏伊塔方,包括generalized eta-squared,这是一个更加推荐的效应量的指标还有cohen’s f²,这也是以前会有一些元分析的时候,大家会用到的一些指标。那么从这里顺便可以稍微多讲一句,就是当实验设计是ANOVA的时候,大家有的时候可能会想,我如何用它来规划样本量,把什么作为一个效应量,输入到g*power里面而这里要有一个非常值得注意的问题,就是大家如果是完全被试内实验设计,千万不要说我用g*power做了这个样本量的规划或者power analysis,因为g*power做不了这个事情,如果你审稿的稿件里写这么一句的话,审稿人如果有经验的话,就一下看到你可能就是表演了一下power analysis。
[ANOVA-bruceR(输出)]
bruceR::MANOVA(data = mt_mean,
subID = 'Sub',
dv = 'RT',
within = c('Identity', 'Valence')) %>%
capture.output() %>% .[c(15:31)]##
## * Data are aggregated to mean (across items/trials)
## if there are >=2 observations per subject and cell.
## You may use Linear Mixed Model to analyze the data,
## e.g., with subjects and items as level-2 clusters.## [1] "ANOVA Table:"
## [2] "Dependent variable(s): RT"
## [3] "Between-subjects factor(s): –"
## [4] "Within-subjects factor(s): Identity, Valence"
## [5] "Covariate(s): –"
## [6] "─────────────────────────────────────────────────────────────────────────────────"
## [7] " MS MSE df1 df2 F p η²p [90% CI of η²p] η²G"
## [8] "─────────────────────────────────────────────────────────────────────────────────"
## [9] "Identity 0.008 0.003 1 43 2.554 .117 .056 [.000, .198] .009"
## [10] "Valence 0.128 0.002 1 43 64.374 <.001 *** .600 [.440, .706] .131"
## [11] "Identity * Valence 0.033 0.002 1 43 14.364 <.001 *** .250 [.085, .417] .037"
## [12] "─────────────────────────────────────────────────────────────────────────────────"
## [13] "MSE = mean square error (the residual variance of the linear model)"
## [14] "η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)"
## [15] "ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)"
## [16] "η²G = generalized eta-squared (see Olejnik & Algina, 2003)"
## [17] "Cohen’s f² = η²p / (1 - η²p)"然后这是bruceR里面的输出,我们可以看到bruceR,实际上是对另外一个很方便的包,进行了一个封装,就是afex,我们其实之前也见过这个包,那么在afex里面我们可以得到同样的结果,这里我们就不再展示了,那么通常如果说我们做这个方差分析,到这里我们看到交互作用,接下来就进行简单效应分析,就像我们上节课结尾的时候,上节课我们用emmeans去查看不同条件下,比方说在不同的identity条件下面不同valence的效应,或者反过来不同的valence下面identity的效应,这里就不展开了,因为跟上节课是一模一样的,大家可以借用上节课的一个代码来做同样的事情。
[ANOVA-afex]
## bruceR::MANOVA 是对afex的封装
m_aov <- afex::aov_ez(
data = mt_mean,
id = 'Sub',
dv = 'RT',
within = c('Identity', 'Valence'))
m_aov## Anova Table (Type 3 tests)
##
## Response: RT
## Effect df MSE F ges p.value
## 1 Identity 1, 43 0.00 2.55 .009 .117
## 2 Valence 1, 43 0.00 64.37 *** .131 <.001
## 3 Identity:Valence 1, 43 0.00 14.36 *** .037 <.001
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1那么我们今天想要讲的是,从这个方差分析,它可能对于做实验的同学来说非常熟悉,在R里面也非常简单实现,那它到底有没有问题,或者说是不是有更好的做法,以及为什么我们可以认为它是一个线性模型的一个特例。 首先,我们看到的基本上就是,所有的效应都是叫做主水平的效应,如果大家去仔细回顾一下方差分解的逻辑,会发现在整个方差分解的过程中,我们关注的都是不同条件下主水平的一个均值,每个数据点和这个均值的偏移到底是什么样,从这个角度来讲的话,我们会发现在重复测量方差分析里面,我们基本上完全忽略了个体的差异,当然在我们大部分的认知实验当中,我们也都是不太关注个体差异的,我们可能更多的关注的是这个效应,也就是不同条件之间的一个差异,然后另外这个缺失值的处理,也是非常严格的,比方说我们有2*2四个条件,如果说我们有一个条件上,有一个缺失值的话,那整个被试的数据就没办法再使用了,你如果采用更加老一点的做法,不管你是用SPSS还是用EZ这个R包,当你的数据不平衡的时候,它直接就没有办法出结果,会报错,那么你只有把有缺失值的整个被试的数据完成删除掉,你的数据才能够运行。但是他会带来一个问题,即便这个被试可能缺失了一个条件,但他还有三个条件的数据,这三个条件数据其实也是有信息的,还有他会对这个数据类型有要求,比方说我们现在看到的这个自变量他是分类的条件,假如我们自变量是个连续的数据,我们这个时候就很难用这个重复测量的方差分析了,然后还有我们对每一个被试的整个数据,其实利用率是比较低的,我们可以回过头来看一下,我们这个数据,我们在看到这个原始数据的时候,每个被试在每个条件上都有很多个试次,每个试次下面都会有自己的反应时间,但是我们在做重复测量方差分析的时候,我们先把它求了一个均值,我们用的是一个每个被试,比方说它有60个trial,60个试次或者70个试次,最后我们就把它平均起来,当然你平均之后,每一个被试的每一个试次有一定的信息可以用起来,但是可能还有很多信息都被丢失掉了,这带来了数据的一个浪费,试次的一个浪费。
重复测量方差分析有没有局限性?
个体间差异同样无法估计;
处理缺失值只能将整行观测删除,会导致标准误增加、功效降低;
对因变量(连续)和自变量(分类)的类型有要求;
对每一个试次中数据利用率低,造成试次的浪费
重复测量方差分析有没有局限性?

因此,现在越来越多的期刊推荐使用多层线性回归(Hierarchical Linear Model) ,如Neuron。 那么在脑电的这个数据当中,其实有的时候你需要权衡到底每一个被试做多少次,以及做多少人,你才能够比较有比较强的统计检验力把你关注的这个效应看出来,那么每个被试做多少试次和被试的人数之间的权衡,其实这两年关注的人也很多,包括前段时间我们在OpenScience的公众号,邀请了新加坡国立大学的一个课题组他们介绍的就是在fMRI中扫描的时间被试的数量之间如何达到一个平衡,因为你增加扫fMRI扫描时间,你也能够提高这个数据的质量或者说信号的强度,所以这里会涉及到很多如何充分使用这个数据的问题,以及提高我们的统计功效statistical power,那么正是因为这个原因,其实这两年在一些期刊上面,我们也能够明显的看到,就是大家开始推荐不再完全依赖于t-test和ANOVA,而是采用mixed model,比方混合线型模型,我们这里举的是Neuron这两年发的一篇,叫做Premier,类似教程吧就是两年之前的,再加上Neuron,是如果大家做神经成像偶尔就会发现,Neuron实际上是我们整个神经科学领域,不仅仅包括认知神经科学,包括神经生物学领域,非常顶级的一个期刊也说这种主流的期刊也都开始推荐使用这种更加合理的方式,这就是我们今天,要跟大家简单介绍一下的,多层线性模型。

它实际上就是用来处理这种多层嵌套类型的数据,我们之前说过,我们的这个数据是有有嵌套的,整个实验的数据,它是分成在一个一个的被试,每一个被试下面又有不同的条件,每个条件下面又有不同的试次,所以它是有这种嵌套的结构的,那么如果我们以前的这个方法,它就是有一些信息的浪费,所以现在很多人在推荐使用,这个层级模型,或者叫做分层模型,或者叫多层模型,它的名字非常多啊,比方说Hierarchy Model,或者叫做Hierarchical Linear Model,或者叫做Multi-level Model,或者叫做Linear Mixed Model等等等等,就是名字很多,Random Effect Model啊,大家知道它本质上就是,我们要去处理这种多层线性模型,多层的这种数据结构,那么我们如何去考虑层级之间的一个相互影响,另外我们就比方说比考虑,它的效应在不同层级之间的一个变化,这个主要就是多层线性模型或者分层线性模型的一个核心,或者层级线性模型。
9.3 分层线性模型/多层线性模型(HLM):
用于处理”多层嵌套数据”,在一个以上层次上变化参数的线性模型。但多层线性模型的名字非常多,不同学科称呼不同,有许多“近义词”:]
- 层级/分层模型(Hierarchical Model,HM)
- 多水平模型(Multilevel Model,MLM)
- 线性混合模型(Linear Mixed Model)
- 混合效应模型(Mixed Effects Model)
- 随机效应模型(Random Effects Model)
- 随机系数模型(Random Coefficients Model).....但在注意与多元回归(multiple regression)进行区分,即逐步引入自变量到回归模型中,以检验每个自变量对因变量的影响是否独立于其他自变量。
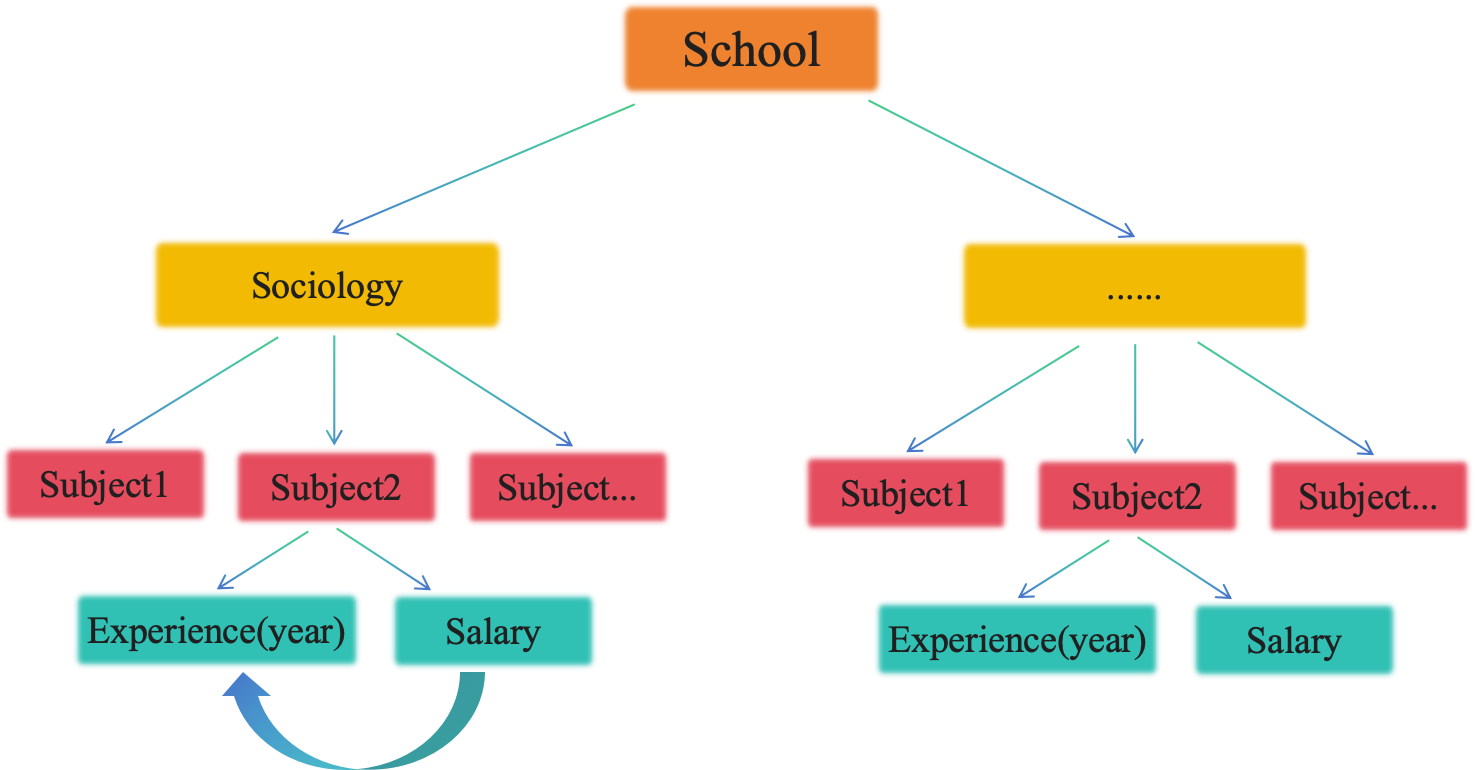
那么可能在有一些领域,它可能根据多层线性模型的思路,它发展出了一些新的,特异于处理某一些特定类型的数据的方法,那么它还会给它一些叠加一些其他的名字,最重要的就是你要看到它本质是什么,它是不是比方说用以线性模型,或是广义线性模型,广义线性模型我们下节课会讲以线性模型作为最核心的一个模型,然后去考虑他的这个数据的层级结构,或层次结构,如果他有做这样做,基本上你就可以确定,他的原理上,可能就是跟我们这里讲的是差不多的,这里跟多元回归是完全不一样,多元回归是说有多个自变量,但他是没有考虑这个层级的结构的,那么在这个多层线型模型或者层级线型模型当中,有两个很重要的概念,我们先给大家简单的说一下,因为我们这里的层级模型,它都是以回归模型,就是以正态分布为核心的,那么在这种现行的层级模型当中,一般我们会考虑,从截距和斜率这两个效应上面去考虑我们这些效应,那么层级模型当中,它最关注两个效应就是固定效应和随机效应,一个叫fixed effect,一个叫random effect,这个所谓的固定和随机,这个名字本身非常不好理解,那我这里也不去跟大家把这个做非常细致的展开,大家如果感兴趣的话,可以去看知乎上的一个博客,包寒吴霜老师写的,那个博客对随机效应做了一个比较详尽的一个梳理,那么我们就通过一个例子来给大家展示一下,什么叫做固定效应和随机效应,那比方说我们看一个非常简单明了的一个层级数据,比方说工龄和薪水之间的一个关系,我们想要调查高校老师的工龄和工资之间有没有关系,那么从某一个学校里面,随机抽取出5个学院,然后获得他们的工资和工龄之间的关系,这是一个网上的数据,这里有数据来源,大家如果拿到rmarkdown,可以点击这个来源,然后这个数据结构大家可以看到,它基本上是这么一个嵌套的结构,首先你整个大学或者你整个学校,然后它有不同的departments,它有不同的学院或者系,每个系下面有不同的人,你调查的时候,实际上就是在不同的学院下面,去搜不同的人,然后再去从这个每个人身上,找到两个数据,一个是他工作多少年,另外一个是他的这个工资,然后你关心的是工资,和他的工作年限之间关系。
在回归模型中一般会在截距和斜率上分别讨论固定效应和随机效应。
例如,关于研究教师的工龄(Experience)与薪水(Salary)之间是否存在关系。在某校随机抽取了5个学院的教师信息,具体数据如下:]
数据来源见(https://github.com/mkfreeman/hierarchical-models/blob/master/generate-data.R) 问题:是否可用工龄预测某个学校员工的工资?
## `geom_smooth()` using formula = 'y ~ x'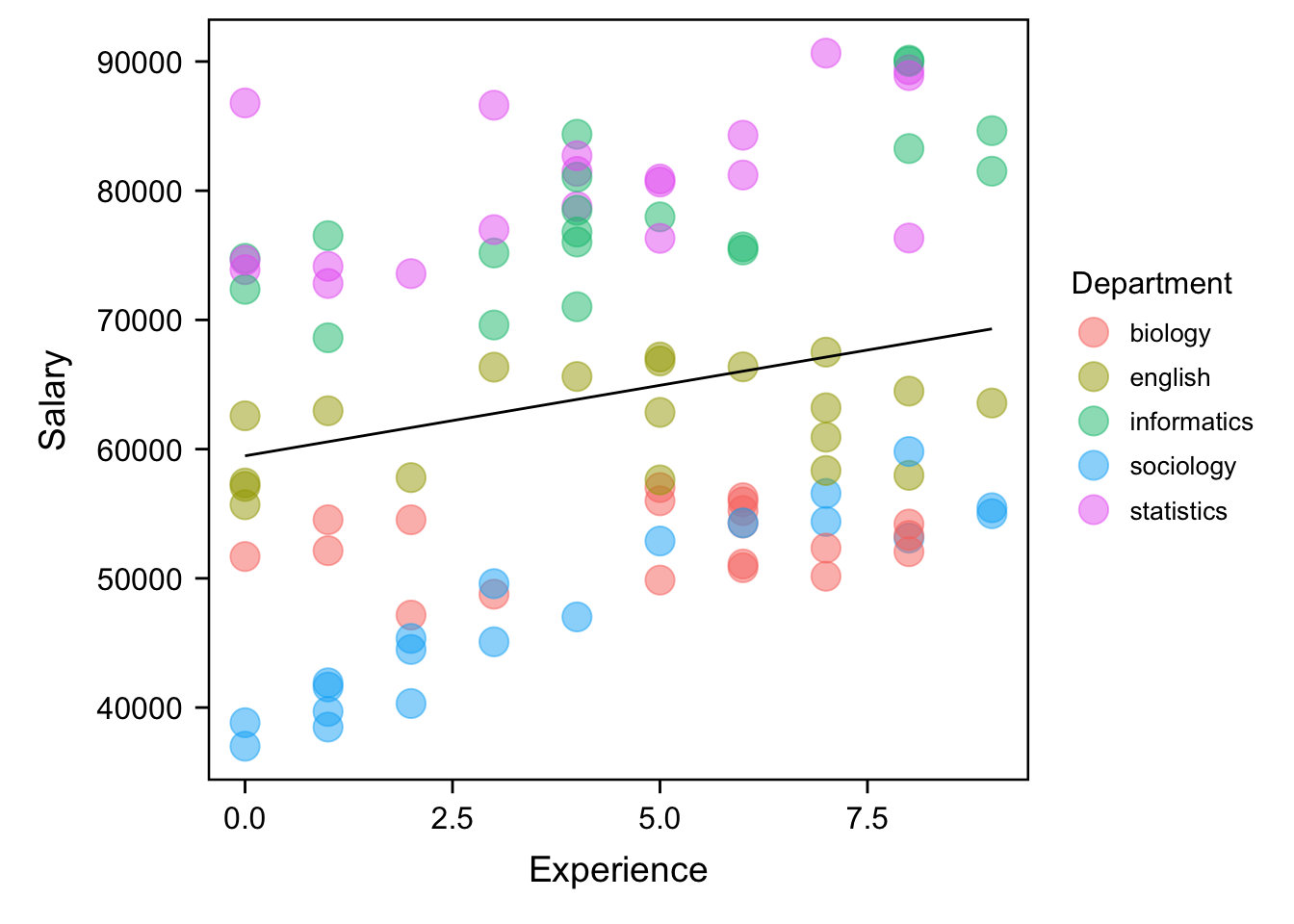
那么如果我们不考虑他的这个嵌套结构的话,我们可能就把所有信息都放在一起,就做一个总体上的一个回归模型,然后做一个简单的线性回归,那么在这个情况之下我们可以看到,x就是我们的这个这个工作年龄,然后y就是他的工资,那么从这个角度讲的话,看起来似乎在工资和工作能力之间是有一个微弱相关的,但是我们这个时候假如说把不同的department,把他们不同的这个学院用不同的颜色标出来的话,我们可以看到这个线他到底有没有捕捉到任何一个学院的信息你看起来好像其实它跟表面上看它似乎捕捉到了某种关系,但是仔细观察,和每个学院的模式似乎都很不一样。在这种情况下,我们可以看到,如果我们不区分数据的层级结构,那么最终得到的回归线或者说预测关系可能就不太有用,尤其是当我们已经掌握了学院的信息时的情况下。因此,在这里,我们可以明显看到两个问题:
不同学院的底薪有可能存在差异(存在/不存在)
不同学院间间,工资与工龄的关系存在差异(存在/不存在)
首先,当我们的工龄为0时,大家的起点实际上是有所不同的,不同的颜色区别是非常明显的,回归线的起点似乎反映了一个综合的情况。其次,在不同的学院之间,工龄和工资的关系也存在差异。有的情况下,随着工龄的增加,工资似乎呈上升趋势,而有的情况下,可能看不到明显的趋势,比如粉红色的。我们要去做回归的时候,会不会有两个这种院之间的差异是完全没有考虑到的,一个是是他们的底薪或起薪不同,第二个是不同学院内工资和工龄之间的关系在学员之间是存在明显差异的。我们不能够用一个总体的趋势去捕捉到每个学院内部的工作年龄和工资之间的关系,那说明我们的模型可能就没有那么有用了。 另外,我们还需要考虑四种不同的模型。如果你认为所有不同学院的底薪或起薪都没有差异,对于回归线来说,它的起薪类似于我们这里的直线和y轴的交点,就是我们的截距,你认为这个截距在不同学院之间没有变化,认为这个截距是固定的,这就是所谓的固定截距。此外,如果你也认为工资和工龄的关系在不同学院之间以同样的速率变化,也就是说他们之间的关系在不同学院之间也是固定的,那么在我们的回归线上的表现就是固定斜率。那这样我们这个相对是一个比较简单的回归中这个线,它的斜率代表是什么?是x每增加一个单位,基本上对应的y要增加多少。也就是斜率越大的话表示工龄每增加一年,工资增加得越多。所以回归线的斜率表示x和y之间的关系,在这种情况下,当你认为在不同学院之间,工资和工龄的关系是完全一模一样的时候,是固定的时候,那么回归线的斜率也是被固定下来的,这种情况就称为固定截距、固定斜率的模型。
这意味有可能会出现四种情况
对应在图中,则会在截距与斜率之间出现差异:
1.不同学院的底薪相同,工资涨幅也相同;(固定截距,固定斜率)
2.不同学院间底薪不同,但工资涨幅相同;(随机截距,固定斜率)
3.不同学院间底薪相同,但工资涨幅不同;(固定截距,随机斜率)
4.不同学院间底薪和工资涨幅都不相同。(随机截距,随机斜率)
画图看看.
[fixI-fixS]
## `geom_smooth()` using formula = 'y ~ x'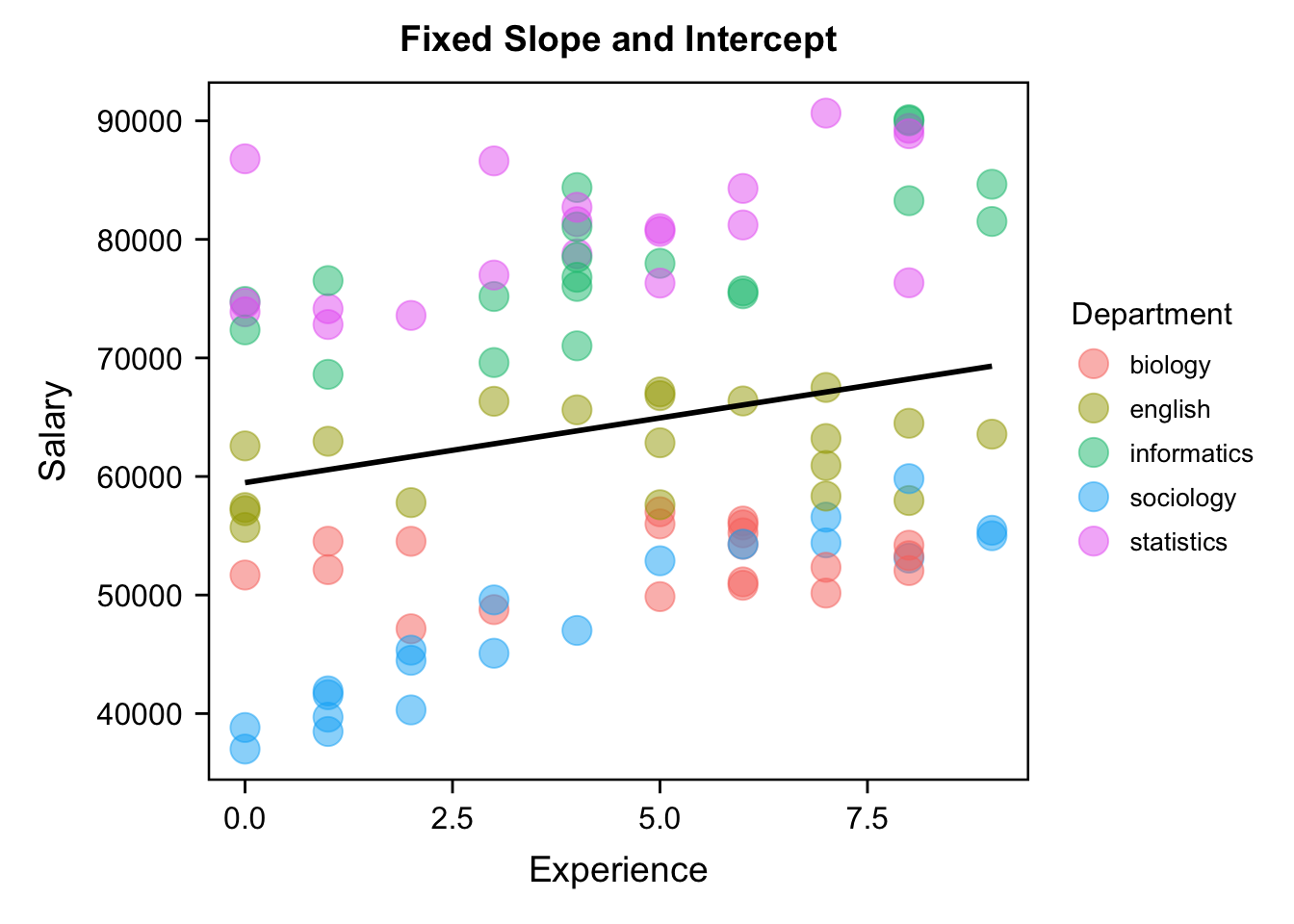
所以我们的最开始不管学院,把所有的数据放在一起,然后做一个简单的回归就完了,但是还有其他的可能性.比方说我们认为截距,也就是起薪,在不同学院之间是不一样的,但是假定每个学院工资的涨幅,也就是随着工龄的增加,你的工资增加的速率是相同的,也就是说在不同学院之间是保持一致的。那么就会出现这种情况,每一个学院他的起薪,它的起点是不一样的,但是看这个斜线,它的斜率都是一模一样的,这个就叫做固定的截距,随机的斜率。随机的意思是,斜率在不同的组之间,在群体当中不同的组之间,它是在进行变化的,vary,但它并不一定是随机的在变动。所以为什么随机效应这个词刚开始让人很容易误解,它是说某一个特定效应在组成这个总体的不同的组当中他是在变化的。我们现在看到的这个直线的起点在不同学院之间是在变化的,如果我们在0这个地方画一条垂线,那么这个斜线和这个0和y轴的交界点它就是在变化的,这就是我们说的变化的截距,intercept。但是工作年限每增加一个单位,我们的回归线基本上都是一模一样。这个时候我们可以看到,他其实也不一定能够捕捉到每一个学院的特点。比方说我们还是看这个粉红的线,这个粉红线,它看起来更应该是一个平的,而不是这个斜斜的一个增长的方式,但是因为我们在建这个模型的时候,我们没有让它进行变化,我们强制的让每一个学院的回归线的斜率都是一模一样的,把它固定住了,那么这个时候,我们看到的就是这么一个拟合的效果。
[ranI-fixS]
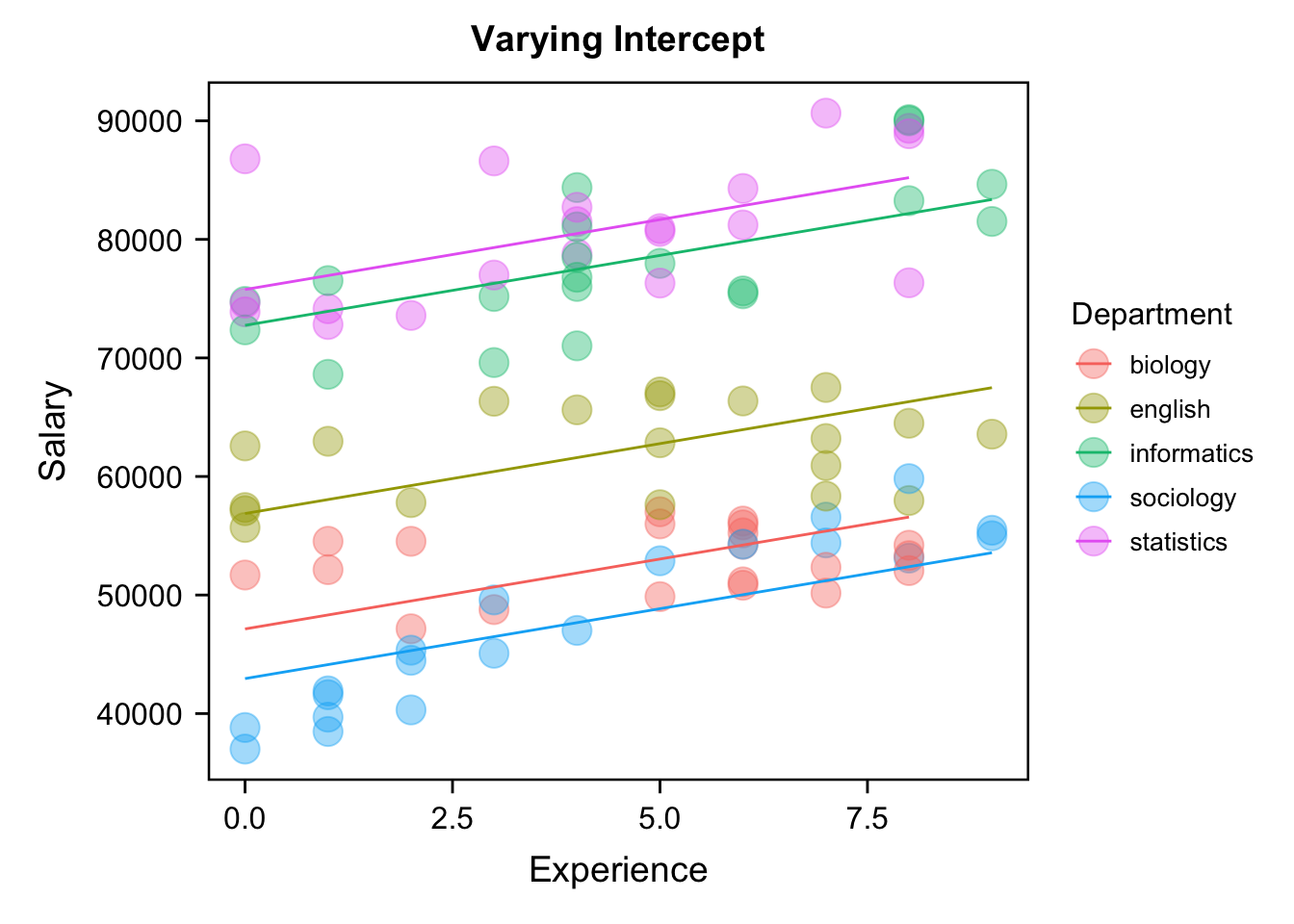
还有一说是我们认为底薪是相同的,但是工资的涨幅是不一样的,这个就叫做固定截距、随机斜率的情况。那么最后就是这两个都是不同的,它的起薪也不一样,斜率也不一样。我们刚刚看到这个其实比较少见,它的截距是固定的,但斜率是不一样的,这个其实很不符合现状。
[fixI-ranS]
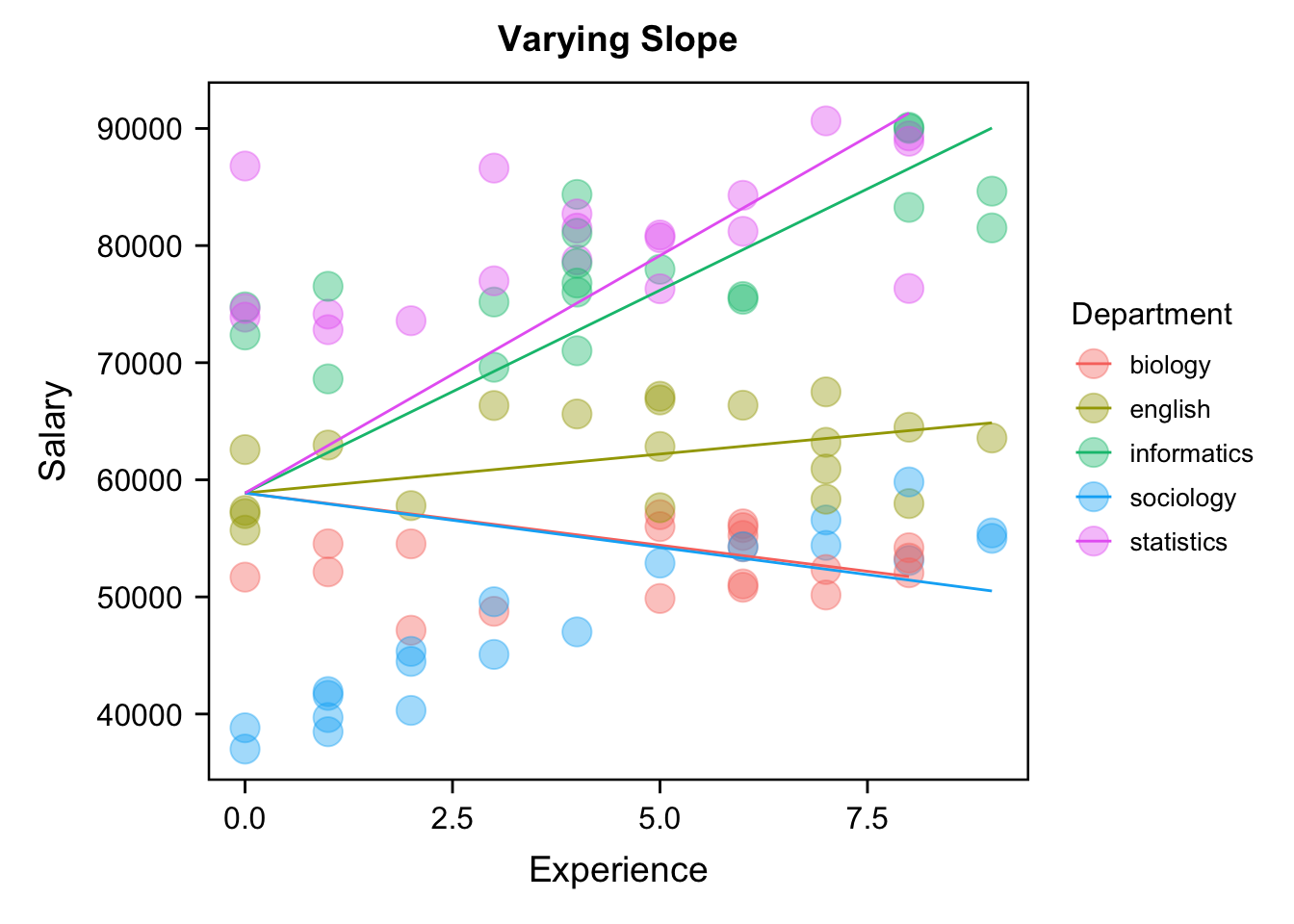
最后一个就是说这个intercept和slope,截距和斜率都是在变化的,这个时候我们看到它的拟合的效果,就是比较好的。比方说我们看到这个粉红的线,它的起薪比这个蓝色的要高,但是它一直没有什么太大的变化,蓝色的起薪比较低但它可能一直在变化,所以通过这个情况我们就能够捕捉到一个比较好的特点。这五条线反映出来的就是我们的所说的veryeffect,或者叫做变化的或者叫做随机的效应。有一些研究者更加喜欢使用very effect就是是变化的这个效应而不是random effect。
[ranI-ranS]
## `geom_smooth()` using formula = 'y ~ x'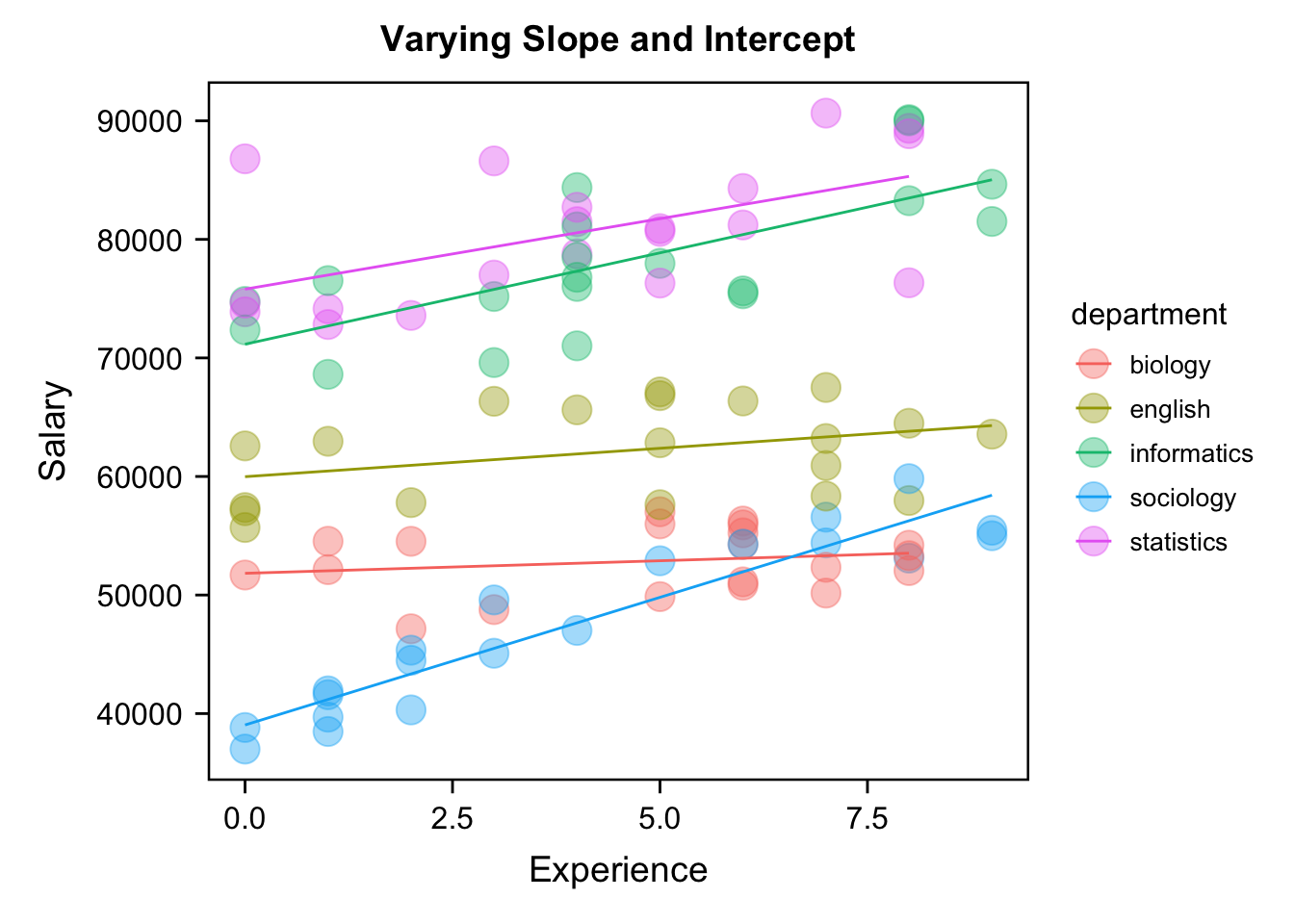
那我们现在再把这个四个图给大家看一下,这个时候都固定,所有的都是一模一样的;这个斜率是固定的,但截距是变化的,这5条线是平行的,但起点不一样。那么这个起点都是一样的,但斜率都不一样,这种情况很少,很少有人会去建这样的模型。这个情况就是两个都在变化,不管是截距还是斜率都在变化,这就是我们在混合线性模型里面经常会碰到的随机效应,也就是在我们现有回归的模型里面,当我们做这种层级模型的时候,我们有可能有两个效应在变化,一个是intercept,一个是slope,这个slope就对应着我们自变量对应变量的影响。 那么如果大家对刚才这两个概念基本上清楚的话,因为刚才说这个数据仅仅是用来展示两种随机效应,那么对于我们的这个数据来说,我们回到我们那个反应时的数据,我们这个数据其实也有一个嵌套关系,每一个变量都嵌套在每一个被试当中,每一个被试它自己可能就存在一个类似于我们刚才观察的这个回归线,每一个被试它的每一个条件下面还有很多个试次,每一个试次又是一个数据点。所以在这里的两种效益,固定效益代表的就比方说在总体上的不同条件下的一个差异,比方说在我们的match这个实验当中有两个自变量,这两个自变量identity和valence,它们对反应时间的整体的影响就是我们说的固定效应。每个被试身上的identity和valence的影响可能跟总体的是有偏差的,那么每个被试身上identity和valence的影响就是一个very effect,是在变化的一个随机的效应。那么它反映的这种不管是被试个体差异也好,还是说被试是对identity和valence是一种特异性的反应也好,它都在跟总体上面identity和valence的效应产生偏差,这个偏差有可能是有意义的。这个时候我们就能够把它通过这种层级模型捕捉到。
无论在我们的数据中,还是刚才的数据中,其实都出现了层级或嵌套关系;只是对于match数据,每个变量都嵌套在一个被试中,而每个被试都可视为一条回归线。
[两种效应]
固定效应代表了实验中稳定的、总体水平上的效应,即它们在不同个体、群体或条件之间的影响是一致的,如match数据中Identity和Valence的效应
随机效应则表示了数据中的随机变异或个体间的差异的程度,以及这种变异程度如何随着特定分组因素的变化而变化。
[match_data]
[shcool]
我们可以看一下,对于我们Naisen的数据来说,每个被试都做一个数据它下面嵌套了自我、他人,然后自我和他人下面又嵌套了moral和immoral,然后在这下面又嵌套了有60个试次或者50个试次,这下面有50个试次,同样对其他被试来说也是如此。


那么他们这个数据类型的嵌套方式,其实我们也可以把它跟我们刚刚看这个数据做一个类比,我们这里可以再加一个整体上的一个效应,我们好像在平时实验当中我们很少去看,不同的这个实验处理,或者不同的自变量,在个体的身上是不是有差异。可以想象,可能每一个被试自身的反应速度就会有很大的差异,有的被试很快,不管做什么反应都很快,因为他的基线的反应是就是非常快的,那么另一些他的反应就是整个就比较慢,不管是说自我的还是他人的,moral还是immoral他都慢。这种反映的类似于截距上的一个差别,他的总体基线就会比别人更快一点或者更慢一点。
对于match数据,类比与学校员工薪水数据,我们也可以设想:
不同被试总体上会不会存在反应时上的差异:有些个体普遍反应速度更快,而有些反应速度普遍更慢(随机截距)
在自我条件下,两种Valence的差异是否完全相同?还是会有个体差异?(随机斜率)
画图尝试一下,计算被试平均反应时后进行排序,选取首尾的几名被试:
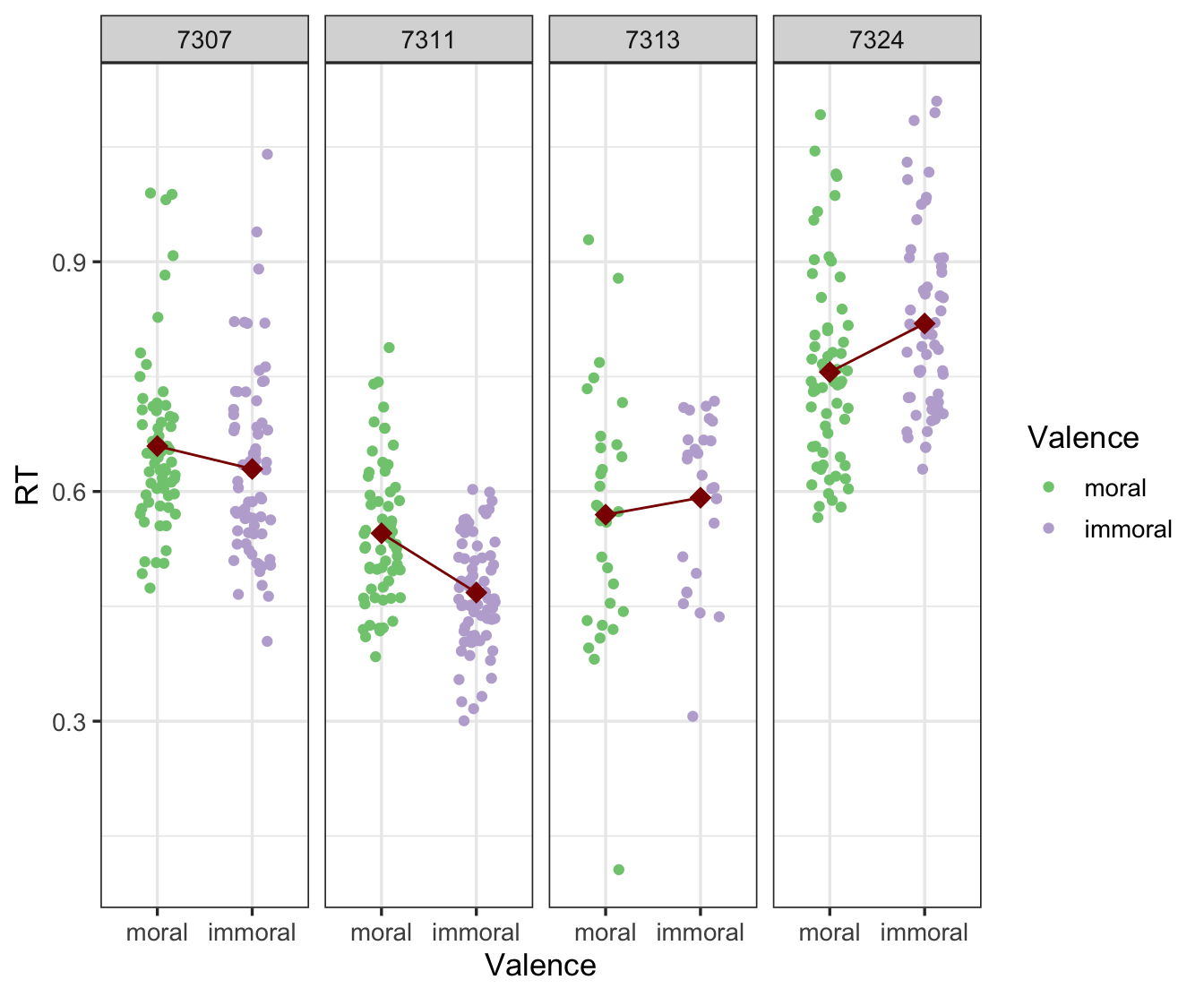
我们在这里展示的4个被试的数据,大家可以看到,像这个被试,他的反应时间整体上面就会比其他的要低,当然他每一个试次上面可能会有快有慢,但是整体上这个被试他会比这个被试快很多,这个就是我们说的在反应时间上面可能存在这样的一个随机的截距,一些被试平均的反应时间就会要更快一点或者更慢一点。另外我们刚才说到我们这个实验有两个自变量,一个是valence,一个是identity在这里举一个例子,比方说在自我条件下面两种不同的valence的差异是不是相同的。 再看重复测量方差分析的简单应的时候,我们也是这么做的,自我条件下面moral和immoral它之间的差异是多少,我们最后甚至可以把它量化出一个Cohen’sd,这个时候我们量化出的cohen’sd,在自我条件下这两种不同条件的差异就是什么我们通常所说的fixeffect,固定的效应。但即使我们可以通过重复测量方差分析把固定效应算出来,每一个被试之间的差异是完全不知道的,那么有没有差异呢?我们可以看到是有明显差异的。我们这里画的是在自我条件下moral和immoral之间有没有差异,可以看到对于被试7307来说,moral比immoral要慢一点,可以看到这个斜线从左往右是向下倾斜的,7311这个被试就更显眼了,moral是比immoral要慢的,但7313和7324两个被试呈现了一种相反的趋势,moral要比immoral更快。整体上可能有更多的被试表现出了右边两个被试的情况,moral要比immoral更快,所以整体上我们可能发现moral要比immoral反应时更短。我们可以很明显地看到被试的个人差异,在JEG2021年左右有一篇文章专门强调需要去考虑实验处理的异质性,这里我们就看到了实验处理的异质性,在不同被试身上实验处理的效应是不一样的,我们以往是完全不关心的,但其实是需要关心的,如果我们认为我们的测量工具或者认知任务可以在某种程度上对被试内在的不可测量的认知能力进行测量的话,我们应该关注这些个体差异。 刚刚我们通过对原始数据的可视化发现,原始数据有很多的数据点,可能出现随机截距和随机斜率两种情况,也就是说在每个被试身上反应时的效应是会发生变化的,如果我们发现确实存在这个问题,有什么更推荐的方式去实现它呢?实际上在过去的大概十多年间,围绕线性模型,或者说层级模型这一类的方法开发出了很多系列的包,lme4应该算是目前使用的最广泛的一个包,至少是最广泛之一,如果光看它的语句,其实是很简单的。首先就是这个这个包的名字,然后做这个沉积模型的这个函数就是lmer,后面就输入代码数据,然后就是这个format,实际上是跟线性模型是类似的.如果你按照顺序的话可以把这个formula就直接不用写,它也能够识别出来。
9.4 多层线性模型的应用
我们使用lme4包对多层线性模型建模,具体语句形式如下:
fit <- lme4::lmer(
data = ,
formula = DV ~ Fixed_Factor + (Random_intercept + Random_Slope | Random_Factor)) #<<注:
但在建立模型之前,需要考虑好在我们的数据中,随机效应和固定效应分别是什么。一般都会添加随机截距,而随机斜率的加入应当考虑是否有充足理由;
另外,由于随机效应是从某些总体中抽样的离散单位,因而本质上是分类变量
这个公式跟之前的线形模型是类似的,这个波浪号前面是dependent variable,因变量。这个公式分两个部分,一部分就是括号括起来的,另外一个是括号之外的,跟以前的线型模型是一样的,也就是说以前的线性模型只关注了fixed effect,回顾一下刚刚说的四种可能的模型,固定截距和固定斜率实际上就是传统的简单回归,所以固定效应的这些变量就放在括号外面,随机的截距和斜率就放在这里,random effect就是我们说的分组变量,比方说要用什么来对数据进行分组,看每个组上有不同的效应。一般random intercept,随机的截距用跟我们前面写的回归实际上是一样的,然后随机的斜率加上自变量的名字就可以了。
这可能是很多同学第一次接触分层模型,也是第一次接触随机效应和固定效应,所以很难去思考到底应该怎么去加等等等等,这里先跟大家说一下,实际上这个模型的建立,把什么样的变量纳入到随机效应之中,实际上是需要仔细思考的,想一想到底有没有这种可能性,要有充足的理由,一般来说大家都会加随机的截距,随机的斜率的加入目前来说是有争论的,至少我看到的一些文章中是有争论的。另外,随机效应一般是从总体中的一些离散单位,本质上是一个分类的变量。关于刚刚说的争论,比方说应不应该把所有的自变量加到随机斜率里,现在不同的研究者是有不同的看法的,大家目前来说可以暂时不用管它,在对层级模型越来越熟悉之后可以去考虑这些比较细致的知识点。
刚才说的是在r里面用lme4这个包去建分层模型的一个基本语法结构,在这里我们可以把数据带入进来,数据就是我们刚才说的原始的数据,前面是RT,我们有两个自变量,一个是identity,一个是valence。这里大家可以看到有一个加号,后面加了随机的效应,这个竖线的左边就是你的公式是什么,你要让那些效应有变化,右边是变化的效应是在那些组织间以什么样的标准进行分组,然后进行变化的,这里表示每个被试的截距是不一样的,换成更易懂的话来说,每个被试基本的反应时间是有快有慢的。当我们建了这么一个模型后,它代表我们可能认为,identity和valence这两个效应在主水平上是要进行检验的,但我们并没有检验它在每个个体上的差异,也就是说我们认为identity和valence在每个被试身上的效应和在总体上都是类似的。当然我们也可以认为identity和valence在不同被试间是有变化的,和刚才的相比,我们可以看到公式的变化就是在括号里把identity和valence都加进来了,这个星号一般在r里表示乘号,它实际上表示两个变量间所有可能的组合,比方说identity*valence实际上表示identity的主效应加上valence的主效应,再加上它们之间的交互作用,交互作用是由冒号来表示的,目前这种用一个乘号来表示自变量之间所有可能的写法是很常见的,在r和python中至少我观测到的主流的方法都采用这种方式了。
[ranI]
Identity*Valence: *表示两变量间所有可能的形式,等同与Identity + Valence + Identity:Valence
(1|Sub): 1表示随机截距(0则表示固定截距); 管道(|)右侧Sub为随机因子
在这个随机的模型中,1表示随机截距,有时候我们也可以认为它没有随机的截距,把它固定下来,这个时候一定要写上0,0加上什么什么,我们在写固定效应的时候,没有写1加上identity乘以valence,是因为在r里面,默认的就有一个1加什么什么,但在随机的效应里必须写出来,也就是说如果我们认为它没有随机的截距,也得写出来。在前面的这个公式里面,如果我们认为他没有截距的话,我们也可以就写0加上什么什么,这个公式基本上都是通用的,当然随着模型越来越复杂,大家感兴趣的话可以查一下这个公式中很多其他符号的写法对于心理学院来说,我们最常用的可能就是这里解释的乘号,还有它们之间表现交互作用的冒号,还有括号里加竖线表示的随机效应。 假如我们用现在的这个数据建了两个模型,一个是随机截距、随机斜率,另一个是随机截距、固定斜率,这时候就存在一个问题,这两个模型可能都能跑出来,那么我们到底要看哪个结果?实际上当我们采用层级模型的时候,或者当我们把线性的回归模型当作一种模型来处理的时候,我们会发现它的结果远远比我们在心理统计学中学到的t检验、方差分析以及之后的一系列分析要更复杂,因为它的模型首先有很多个。大家可以看看到这里标注的公式,RT这个是identity*valence,假如我们不变固定效应的这部分,那么对于随机效应的部分我们还可以变换吗?我们这里可能给出了一个很全面的随机效应,大家想一想它还能继续变化吗?我们可不可以拿掉其中一个?比如拿掉valence,随机效应里就变成1+identity,可不可以?也是可以的,至少是可以运行的。或者把identity拿掉只留valence,只认为不同被试在valence这个自变量上面的效应有差异,在identity上认为它是一模一样的,这也是可行的。或者认为它们两个主效应都在,但没有交互作用,这也是可行的。所以我们发现可以建好几个模型,这时候你需要想清楚到底哪个模型是makesense的,是合理的,因为有些模型可以凭经验发现是不合理的,那你就不应该用这个数据去建这个模型。在你把这个模型建起来之后,它在r里跑也可以给你结果,但这个结果对你来说可能是没有意义的,你需要用你的专家经验只是去筛选那些模型是合理的,是值得把它跑出来,去test的。 当你觉得这几个模型好像都差不多,需要通过数据本身来告诉我哪个模型是更加合适的,在这种情况下,我们可能需要借助一些模型比较的方法,可以直接对这些模型进行比较,哪些模型能够更好地拟合数据,这个模型更能捕捉到数据内部的一些特点,这就涉及到模型比较的问题,模型比较的问题基本上在所有的统计学中都会涉及到,当我们使用层级模型的时候我们可能也会用模型比较的方法去选择模型。在认知计算建模里我们也会用模型比较的方法去选择模型,在SEM,结构方程模型里也有很多模型选择的标准,如果大家仔细去看mplus或者spss或者mos里的输出的话,也是需要对不同模型进行比较的。 [ranI ranS]
## 随机截距 随机斜率
model_full <- lme4::lmer(data = mt_raw,
RT ~ Identity * Valence + (1 + Identity * Valence|Sub)) [模型比较]
## refitting model(s) with ML (instead of REML)## [1] "Data: mt_raw"
## [2] "Models:"
## [3] "model: RT ~ Identity * Valence + (1 | Sub)"
## [4] "model_full: RT ~ Identity * Valence + (1 + Identity * Valence | Sub)"
## [5] " npar AIC BIC logLik deviance Chisq Df Pr(>Chisq) "
## [6] "model 6 -29173 -29124 14592 -29185 "
## [7] "model_full 15 -30024 -29902 15027 -30054 869 9 <0.0000000000000002 ***"
## [8] "---"
## [9] "Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1"注:模型比较的指标、计算方法及其优劣请参考《认知建模中模型比较的方法》
在我们这个层级模型里,我们这里简单展示用spaceANOVA的函数比较两个模型,我们刚刚建了两个模型,一个是基本的模型,只有一个random intercept,另外一个不仅有random intercept,还有random slope,随机的斜率,当然如果你自己在r里面看结果,直接用输前面这部分就可以了,我们这里是把它给打出来了,我们可以看到它会给一个输出。大家可以看到这个地方是它一系列模型比较的指标,这里就有两个模型,一个是model,一个是model_full,这个npar表示它的parameters的数量,我们可以看到简单的模型里面只有6个,full里面有16个参数,这个是AIC——一个模型比较的指标,BIC——一个模型的指标,这个是Log likelyhood,这个是deviance,还有对模型比较之间用卡方做的一个检验,然后发现两个模型拟合之间是有差异的,,如果按照卡方的标准发现它是显著的,这个时候我们可以推断有随机截距和随机斜率的模型对数据的拟合更好,那么接下来我们就会选择它作为解读的对象。这里有一篇preprint的文章,是两个年轻的博士生跟我一起写的,我是主要是跟他们学习,大家感兴趣可以去看一下。
在这里我们基本可以说在重复测量方差分析的基础上又做了一个层级模型,并且假定我们做了几个潜在可能的模型,都对它进行了拟合,然后再通过ANOVA进行了选择,选择之后要对模型的输出进行解读,去看感兴趣的自变量的效应在主水平是不是存在,在个体层面是不是有很大的变异,或者这个变异到底有多大,我们应该如何去解释这个变异。所以我们要去对这个结果进行一个解读,那么我们怎么去查看这个结果呢?这里肯定要涉及到模型比较的事项,加入我们要去看一下固定效应是不是显著的,那么我们怎么查看显著呢?我们可以通过刚才ANOVA的模型比较的方式,去对两个模型进行比较,一个模型是没有固定效应的,一个模型是由固定效应的,这两个模型之间的差异就是一个有固定效应一个没有,如果有固定效应的模型比没有固定效应的模型显著地更好,那它可能说明了这些固定的效应就应该放到这些模型里,我们可以认为它是显著的。所以我们需要借没有固定效应的模型作基线,然后把我们刚刚已经跑完的有固定效应也有随机效应的模型,和这个只有随机效应没有固定效应的模型进行比较,比较完发现有固定效应的模型确实更好,这基本上就可以帮助我们判断,我们加入进来的固定效应,就是identity和valence,以及它们之间的交互作用,肯定是有作用的.
在建立模型后,我们希望知道固定效应大小是否显著,但由于多层线性模型中对于自由度的估计有多种方法,比较复杂,所以lme4::lmer()中没有提供显著性。
[anova]
# 建立没有固定效应的“空模型”
model_null <- lme4::lmer(data = mt_raw,
RT ~ (1 + Identity*Valence|Sub))
## 根据似然比进行模型比较
stats::anova(model_full, model_null)## refitting model(s) with ML (instead of REML)## Data: mt_raw
## Models:
## model_null: RT ~ (1 + Identity * Valence | Sub)
## model_full: RT ~ Identity * Valence + (1 + Identity * Valence | Sub)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## model_null 12 -29992 -29894 15008 -30016
## model_full 15 -30024 -29902 15027 -30054 38.1 3 0.000000026 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1我们也可以用FX,FX这个包我们经常介绍它,我们也可以用它的mix函数来进行检验。我们比方说就直接用他的这个mix把这个数据输入进来,然后大家可以看到这个地方的回归方程和我们刚刚在lme4里看到的是一模一样的,也就是说我们在FX里建了一个多层模型,然后通过它里面LRT这个算法来进行检验,它输出的结果和我们传统的方差分析很像,它会给出主效应和交互作用,如果想查看固定效应,也可以用FX的mix这个函数来查看固定效应。
在模型非常复杂时(多层嵌套),如果仅仅只想对固定效应进行检验,可以使用afex::mixed(),设置method 参数为 LRT(Likelihood-ratio tests)
## Contrasts set to contr.sum for the following variables: Identity, Valence## REML argument to lmer() set to FALSE for method = 'PB' or 'LRT'## Fitting 4 (g)lmer() models:
## [..## .## .]## Mixed Model Anova Table (Type 3 tests, LRT-method)
##
## Model: RT ~ Identity * Valence + (1 + Identity * Valence | Sub)
## Data: mt_raw
## Df full model: 15
## Effect df Chisq p.value
## 1 Identity 1 1.73 .188
## 2 Valence 1 30.27 *** <.001
## 3 Identity:Valence 1 12.03 *** <.001
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1第三个方法是我们我们可以用叫做lmertest这个包,这个包实际上是跟lme4兼容的一个包,主要就是对混合效应模型,或者说层级模型进行假设检验,这里就包含了lmer这个函数,lmer和我们前面用到的lme4基本上名字都是一样的,就是不同的包,它的一个主要特点就是会报告显著性,它在这里使用它自己的一些算法。我们在用lmer这个函数的时候,这里的语法的输入跟我们在lme4里基本是一模一样的,然后我们可以通过summary来去看它的结果。我们第一个看到的是它随机效应的相关矩阵,这里主要关注不同的随机效应间有没有相关性,但绝大部分的时候我们可能不会太关注这些信息,然后我们可能更多的看的是两个,第一个就是把这个固定效应,就是类似两个自变量有没有主效应和交互效应,另外一个我们有时候也会专门去看变化的随机效应,这里我们可能没有展示。
lmerTest是一个与lme4包兼容的包,主要用于对混合效应模型进行假设检验;其中也包含了lmerTest::lmer()函数,与lme4::lmer()不同的是,其结果报告了显著性(使用Satterthwaite分母自由)
lmer_model <- lmerTest::lmer(data = mt_raw,
RT ~ Identity * Valence + (1 + Identity * Valence|Sub))
# summary(lmer_model)
# 如果使用lmerTest包进行建模,可以使用bruceR::HLM_summary()进行输出
## RUN IN CONSOLE
# HLM_summary(lmer_model)[随机效应] 注意: - 相关矩阵会体现自变量效应在个体上的差异,尤其是第一列(截距与斜率的相关),而具体的解释也应考虑对应固定效应系数本身的正负;
- 有可能会提供天花板与地板效应的相关信息,如任务过于简单,数据变化较小,有可能出现截距与斜率为负相关。
## [1] "Random effects:"
## [2] " Groups Name Variance Std.Dev. Corr "
## [3] " Sub (Intercept) 0.00425 0.0652 "
## [4] " IdentitySelf 0.00147 0.0383 -0.24 "
## [5] " Valencemoral 0.00219 0.0468 -0.22 0.49 "
## [6] " IdentitySelf:Valencemoral 0.00510 0.0714 -0.02 -0.53 -0.80"
## [7] " Residual 0.01801 0.1342 "
## [8] "Number of obs: 25920, groups: Sub, 44"[固定效应]
## [1] "Fixed effects:"
## [2] " Estimate Std. Error t value"
## [3] "(Intercept) 0.72328 0.00997 72.52"
## [4] "IdentitySelf 0.01329 0.00624 2.13"
## [5] "Valencemoral -0.00913 0.00744 -1.23"
## [6] "IdentitySelf:Valencemoral -0.04150 0.01128 -3.68"比如说在这个模式里面,我们应该是可以把每一个被试在identity上的效应提取出来,看它在被试间是怎样一个变化,以及比方说valence的效应,或者它们之间的交互作用,我们也可以对它进行一个可视化,这个可视化是个非常简陋的可视化,这里全部采用的是默认值,比方说顺序就是他人和自我,道德也是moral和immoral,跟我们之前呈现的顺序不一样,在讲完了这个统计模型之后,我们会专门讲怎么在gPlot里面,对这种最后要呈现的结果进行精细的打磨。那么实际上在现在有很多包,包括像interaction这样的包,它能够帮助我们迅速地把一些我们关注的效应进行可视化,让我们看到它们之间是什么样的情况,比方说这里我们可以看到是一个比较明显的交互作用,在other的条件之下的immoral和moral的差别,肯定是要比在自我条件下的差别是要小的,所以在这里我们可以非常明显的看到交互作用的存在。
[交互效应的可视化]
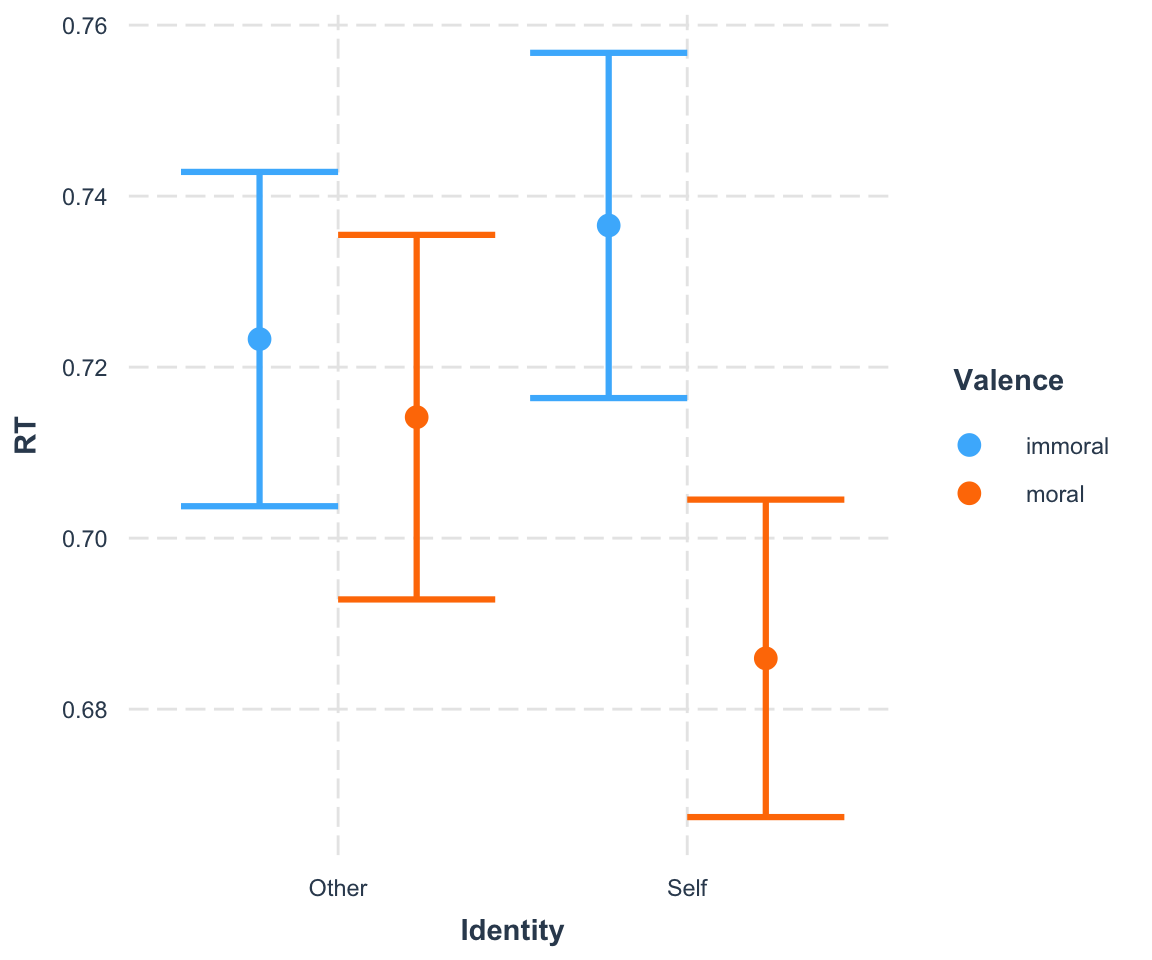
我们前面讲不同模型之间是等价的,我们也说从重复测量方差分析是一个特定的混合陷阱模型,那么它们到底能不能做到完全等价,或者说几乎是相同的呢?大家觉得能做到吗?我们可以先看一看。我们这里直接把之前的重复测量方差分析的结果打印出来。 我们可以仔细看一下它的这个值,对Valence来说,效应是f值是64.37,p值是很小的,另外一个f值是14.36;然后还有identity它的f值是2.55,df都是143,这个跟我们在心理统计学上学到的重复测量方差分析是很像的。
[anova]
## Anova Table (Type 3 tests)
##
## Response: RT
## Effect df MSE F ges p.value
## 1 Identity 1, 43 0.00 2.55 .009 .117
## 2 Valence 1, 43 0.00 64.37 *** .131 <.001
## 3 Identity:Valence 1, 43 0.00 14.36 *** .037 <.001
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1我们可以看一下lme4,我们刚才建了好多个模型,然后我们选出最合适的一个,那么我们看一下最合适这个是不是跟我们的重复测量方式分析是一样的呢?我们直接看的话,用anova这个函数,用fullmodel把它的方差分析表打出来,我们就会看到它的f值,有三个f值,identity是0.74,跟我们的2.55不一样,第二个是45.00,跟我们的64.37也不要太一样,第三个也不太一样,但总体趋势差不多,总体趋势就是identity很小,valence比较大,它们的交互作用也比较大。
[lme4]
## Analysis of Variance Table
## npar Sum Sq Mean Sq F value
## Identity 1 0.013 0.013 0.74
## Valence 1 0.811 0.811 45.00
## Identity:Valence 1 0.244 0.244 13.54我们再看一下lmertest的fullmodel,因为它是给出显著性的,所以我们可以看看它会不会得到类似结果,可以看到跟lme4得到类似的结果,但是模式也都是一样的,identity比较小,valence比较大,identity和valence的交互作用处于中间,下面两个都是显著的,所以我们发现重复测量的方差分析和常规的层级模型,其实好像不太一样。
[lmerTest]
## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## Identity 0.031 0.031 1 43.0 1.73 0.19574
## Valence 0.765 0.765 1 43.3 42.46 0.000000063 ***
## Identity:Valence 0.244 0.244 1 43.0 13.54 0.00065 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1其实这个刚开始我也是比较困惑的,也找了很多解决方案,后来发现它需要以一种很特定的方式来建构层级模型,才能达到跟它很一致的结果。 因为我们今年一直采用matching_data的反应时的数据,我们用它来跟前面进行对比,这里大家可以看到我们用的是mt_mean,我们在数据上做到了一样,前面那里还有个问题,就是它们的数据是不太一样的,比如这里的mt_mean,它用的是一个原始的数据应不应该在这里使用?因为我们这个数据量很大,所以有一些没有清理的数据不影响整体的趋势但假如你自己做数据分析,数据预处理这里一定是要再考虑考虑的。当然这里我们也试过了,用一模一样的数据,也是用mt_mean来做层级模型,它得到的结果也也是不一样的,跟这里是同样的一个趋势。那么假如我们采用mt_mean这种方式去去建立这个模型,它最有可能得到跟重复测量方差分析一样的结果了,这个模型是比较特别的,首先它有identity和valence的主效应,然后它有被试间的random intercept,每一个被试在每一个identity下面会有一个独特的intercept,同样对每一个被试来说,在每一个valence上也有一个独特的random intercept。在这种情况之下,我们得到的结果是最接近的,是59.89,接近60,这个是15.36,跟64.37和14.36是最接近的,但还是没有达到一模一样,还有个问题大家可以看他的这个df,它的自由度,第一个自由度是一模一样的,所以它这里达到了一样的值,143和2.55,这个地方也是2.55,但后面两个自由度和F值不一样,如果大家有兴趣仔细去扒为什么出现这个问题,实际上是因为使用这两个不同函数的人是有不同的习惯的,或者说有不同的重视的点,对于做传统的重复测量方差分析的人来说,很重视方差的分解,然后如何去求f值,这方面会做的很精细,不同的包之间也是能达到精确的一致性的,对于绝大多数做lmer的人来说,他都是从线性模型的角度,他不会在把这个模型做完之后,再去做一个方差分析,然后看它跟重复测量方差分析是不是一模一样的结果。
# http://www.dwoll.de/rexrepos/posts/anovaMixed.html#two-way-repeated-measures-anova-rbf-pq-design
model_aov <- mt_mean %>%
# dplyr::filter(!is.na(RT) & Match == "match" & ACC == 1) %>%
lmerTest::lmer(
data = .,
RT ~ Identity * Valence + (1|Sub) + (1|Identity:Sub) + (1|Valence:Sub)
)## boundary (singular) fit: see help('isSingular')## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## Identity 0.0055 0.0055 1 43 2.55 0.11735
## Valence 0.1282 0.1282 1 86 59.89 0.000000000018 ***
## Identity:Valence 0.0329 0.0329 1 86 15.36 0.00018 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 19.5 HLM的应用
在这种情况之下,我们就发现,它相对这个借助的计算的方法,是没有优化的,也就是说现在这个lmer这个包,或者lme4,它更多的是去建线性的模型,而不是说如何把线性模型的结果转化为传统意义上的方差分析。这个模型是本身比较复杂的,所以如果你要让这个模型的转换,得到一模一样的数值上的结果,其实需要做很多软件工程的工作了,你要写很多代码,然后把各种条件加上判断,然后就达到一致的结果。从我目前找到的资料看,很少用lme4这一类模型的开发者会在意这个问题,就是说一定要把它转化为跟传统的方差分析一模一样,所以这样的代码没有人去写。这个跟我们去年上课的时候的结果也不太一样,去年上课的时候我们写了这个代码之后,其实能够得到跟重复测量方差分析基本上一样的结果,只在小数点后面有差别,这里还有一个可能
就是说我们的这个模型本身,可能会有一些warnings,会有一些警告,如果大家跑自己在电脑跑的时候,会有一些warnings的,有个叫做similarity的一个问题,这里我就不展开了,这是属于模型最后拟合求解的时候的一个问题。也就是说因为我们这个数据存在这个问题,所以最后我们直接用这个方法的时候,它可能就没有办法得到跟重复测量方差分析在数字上一模一样的结果。原则上,这个公式应该是跟我们重复测量方差分析是一样的,但数字上面确实可能会出现不一样的结果,
在这里我稍微总结一下,借这个公式,也就是说我们在心理统计学上学到的常用统计方法,包括我们上节课讲到的ttest和方差分析,它是线性模型的一个特例,那么我们传统意义上用到的重复测量方差分析,它也是另外一个特例,它就是一个嵌套结构的,层级模型模型的一个特例,那么在你的数据和你求解的方法,各方面比较理想的状况下的话,应该是能够得到一模一样的结果的。
我们在这里看这个lme4的结果的时候,它是比较丰富的,大家也可以找一些更加最先进开发的包,去看能不能更好的帮助我们查看这个模型的结果。为什么呢?因为这个模型的结果建出来之后,我们这里看到这个model_full,这个文件本身是很大的,里面包含了很多的信息,肯定有很多信息是值得去提取出来的,我们这里讲到的只是最简单的,一个是fixeffect,如何把它里面固定的项提取出来,但我们在前面讲到了,随机的效应其实有的时候很关键,它也是可以被提取出来的,我们这里没有细讲,主要是时间不太够。另外一个需要说明的是,层级模型是一个很复杂的大的框架,我们仅仅是以重复测量方差分析为例,以我们常用的反应时间,这种非常特定的嵌套结构的数据来介绍了层级模型,但是其实看到的很多数据分析都是在这个框架之下的,它可以适合很多这种具有嵌套和层级结构的数据的,这里举了几个嵌套结构的例子。

元分析其实也是一个特例,元分析大家可能听说过,你看某一个领域的文献的时候,你肯定会想这里面有没有元分析告诉我,这个效应它的效应总体上是多大,实际上它本质上也是一个层级模型,那么它这个层级模型,比方说最高的就是我们总体的效应,然后就是不同的研究、不同的实验,甚至可以再给加1层,比方说不同的课题组或者不同的文章,不同文章里面有不同的实验,不同的实验项目有不同条件,所以它也是这么一层一层一层的,嵌套下的。当我们做元分析的时候,其实是建了一个特定的层级模型,我们用的是这种描述性的统计数据,而没有用原始数据,有原始数据的时候,其实我们可以把所有实验室的原始数据拿到一起,直接用一个大的层级模型,把它进行一个效应量的综合,这也是可以的。这个是比方说大家在看元分析时经常会看到一个图,这个森林图不同的效应从小到大进行排列,最后会出现一个什么样的结果,然后针对原本性的这个结果,检查他的异质性等等各方面的,还有做元回归,很多很多这样的一些内设统计方法。但它本质上讲,也就是我们今天讲的层级模型里面一个非常特殊的例子。

 ## 可能遇到的问题
## 可能遇到的问题
我们在使用层级模型的时候,可能会碰到很多问题,我们今天讲的是一个非常简单的一个入门,但是我们这个入门也基本上回应了前面我们将为什么要学习r语言的时候,说当我们学习r语言之后,就可以开始使用这些比较复杂的模型,它会引出我们更多值得学习的东西。同样如此,对于这个层级模型来说,当我们开始使用层级模型之后,我们就会碰到很多这种可能存在的问题,这些问题就会让我们进行进一步的去学习层级模型里面的一些技术细节,比方说模型收敛的问题,有可能你的模型很复杂,最后发现它不给你出任何结果,这个时候可能就是存在收敛的问题。然后还有自由度的问题,我们刚才其实已经碰到自由度的问题,当我们试图把层级模型和重负测量方差分析进行完全对应的时候,它的自由度的计算就会有一些技术细节的问题。还有我们讲了统计的固定效应和随机效应还有包括像是固定效应、主效应、简单效应,后面这两个都包寒吴霜老师在知乎上的帖子里,大家可以去看看,这也都是非常值得去关注的。大家如果做发展心理学,有一些比方说交叉滞后模型等等,交叉滞后也是我们碰到的层级模型的一个特例。 所以今天我们只是给大家开了个头,希望大家能够感受到大的统计框架的魅力。但是我们还有一个问题,就是大家可以想一想,我们今天其实是在刻意的,回避了一些数据,就像我们上节课的时候刻意回避了重复测量方差分析,引出了这节课内容,那么我们今天这个思考是要引出下一节课内容,就是当我们这个数据它不服从正态分布,你都没办法去假设他是服从正态分布的时候,怎么办?比方说我们碰到这个正确率的数据,在这个实验当中假如我们考虑每个试次,其实就是0和1,要么就是错了0,要么就对了1,大家可以想想我们以前是用什么样的统计方法来去对这个证据进行检验,它肯定是很确定的不服从正态分布的情况,这种情况之下,比方说有很多的试次,我们最后算出了它的平均的正确率,之后我们把它做t检验或者方差分析,也可以接受,那么有没有更好的办法,或者有没有更加适合的办法,这个可能就是我们下节课要讲的内容。