Chapter 8 Reporting your findings

A discussion of how to interpret and report sensitivity analyses

8.1 Methods

We propose a short checklist to ensure adequate reporting of the sensitivity analysis. The following items can be included in the “methods” section of a scientific manuscript, or in an attached supplement:

  • Description of each MNAR mechanism to be tested

  • DAG that includes MAR and MNAR mechanisms to be tested

  • List of assumptions that accompany each posited MNAR mechanism

  • Description of complete case, multiple imputation, and pattern-mixture model methods

  • Explanation of why additive and/or multiplicative offsets were tested

  • Explanation of how and why offset values were selected

8.2 Results

Scenario 3 (MNAR mechanism dependent on outcome \(Y\))

For scenario 3 (MNAR mechanism dependent on \(Y\)), we suggest that the following table, figure and interpretations can be used to more effectively communicate findings from the sensitivity analysis. These can be included in the main results of the manuscript or an attached supplement. Sample output is included below (more examples can be found in Section 5)

Tabular output

Scale parameter RR se PAA (mean) PAA (sd)
-32 -0.014 0.002 -4.45 14.41
-16 -0.014 0.001 -1.99 10.37
-8 -0.014 0.001 -0.76 9.08
-4 -0.013 0.001 -0.14 8.73
-2 -0.013 0.001 0.16 8.64
-1 -0.013 0.001 0.32 8.62
0 -0.013 0.001 0.47 8.61
1 -0.013 0.001 0.62 8.62
2 -0.013 0.001 0.78 8.64
4 -0.013 0.001 1.08 8.73
8 -0.013 0.001 1.70 9.08
16 -0.013 0.001 2.93 10.36
32 -0.013 0.002 5.39 14.39

Graphical output

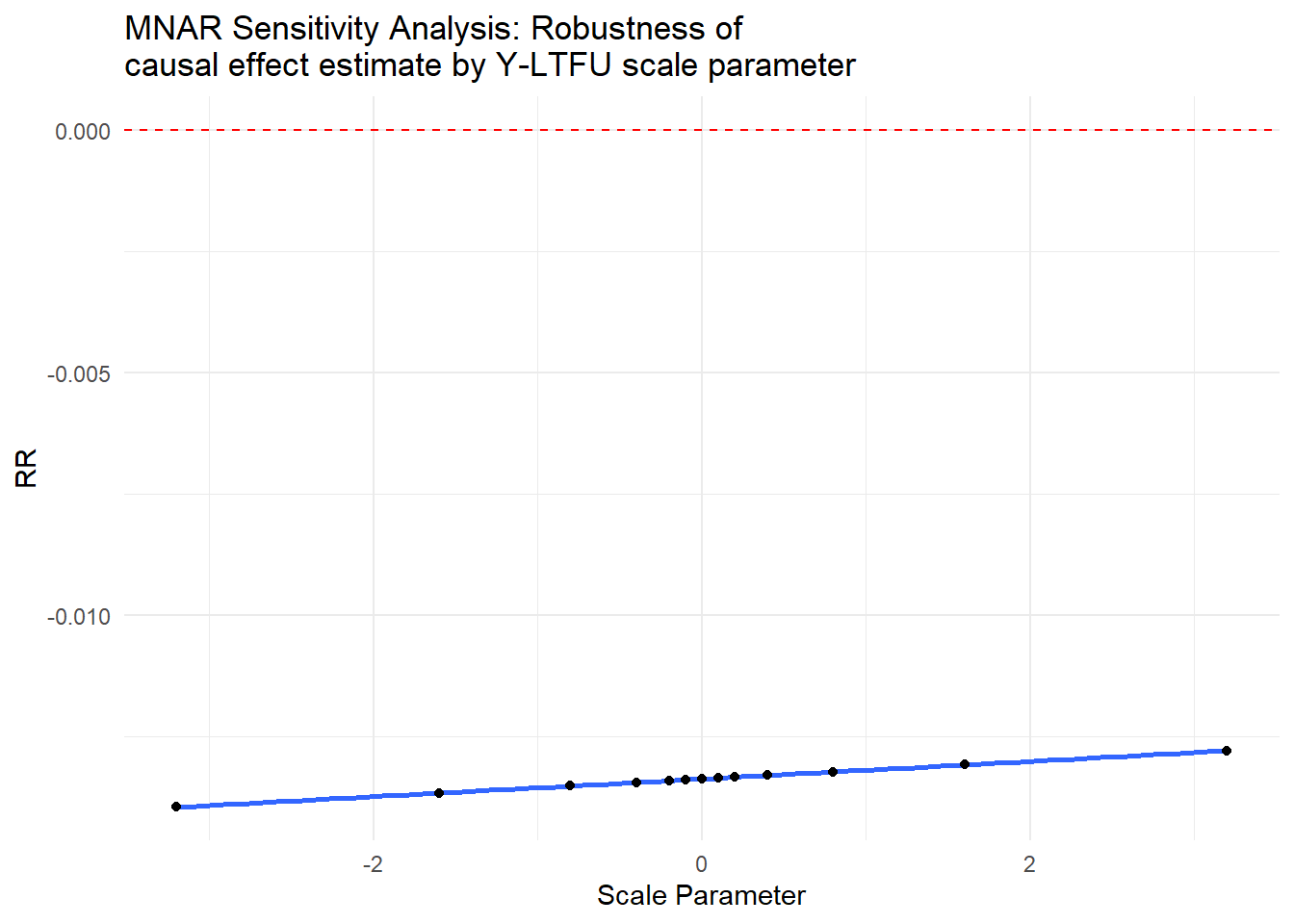
Scenario 4 (MNAR mechanism dependent on unmeasured confounder \(U\))

For MNAR scenarios in which LTFU is dependent on an unmeasured confounder \(U\), we suggest a parallel set of tables and figures that can be used to more effectively communicate findings from the sensitivity analysis. We further recommend reporting the magnitude of association between the generated “unmeasured” U, exposure, and disease, as follows, as shown at the end of this section.

Tabular output

Unmeasured variable Scale parameter RR se PAA (mean) PAA (sd)
U1 -3.2 -0.003 0.002 -1.34 15.35
U1 -1.6 -0.008 0.001 -0.43 9.43
U1 -0.8 -0.011 0.001 0.02 8.06
U1 -0.4 -0.012 0.001 0.24 8.09
U1 -0.2 -0.013 0.001 0.36 8.29
U1 -0.1 -0.013 0.001 0.41 8.44
U1 0.0 -0.013 0.001 0.47 8.61
U1 0.1 -0.014 0.001 0.53 8.81
U1 0.2 -0.014 0.001 0.58 9.03
U1 0.4 -0.015 0.001 0.70 9.54
U1 0.8 -0.016 0.001 0.92 10.78
U1 1.6 -0.018 0.002 1.37 13.83
U1 3.2 -0.023 0.003 2.28 20.99
U2 -3.2 0.004 0.003 -1.56 24.68
U2 -1.6 -0.005 0.002 -0.54 12.86
U2 -0.8 -0.009 0.001 -0.04 8.69
U2 -0.4 -0.011 0.001 0.22 7.99
U2 -0.2 -0.012 0.001 0.34 8.14
U2 -0.1 -0.013 0.001 0.41 8.34
U2 0.0 -0.013 0.001 0.47 8.61
U2 0.1 -0.014 0.001 0.53 8.95
U2 0.2 -0.014 0.001 0.60 9.36
U2 0.4 -0.015 0.001 0.72 10.32
U2 0.8 -0.018 0.002 0.98 12.69
U2 1.6 -0.022 0.003 1.48 18.33
U2 3.2 -0.030 0.004 2.50 30.83
U3 -3.2 0.010 0.005 -1.78 34.67
U3 -1.6 -0.001 0.002 -0.65 17.22
U3 -0.8 -0.007 0.001 -0.09 9.99
U3 -0.4 -0.010 0.001 0.19 8.10
U3 -0.2 -0.012 0.001 0.33 8.03
U3 -0.1 -0.013 0.001 0.40 8.25
U3 0.0 -0.013 0.001 0.47 8.61
U3 0.1 -0.014 0.001 0.54 9.11
U3 0.2 -0.015 0.001 0.61 9.72
U3 0.4 -0.016 0.002 0.75 11.20
U3 0.8 -0.019 0.002 1.03 14.81
U3 1.6 -0.025 0.003 1.59 23.14
U3 3.2 -0.037 0.006 2.72 40.99

Graphical output

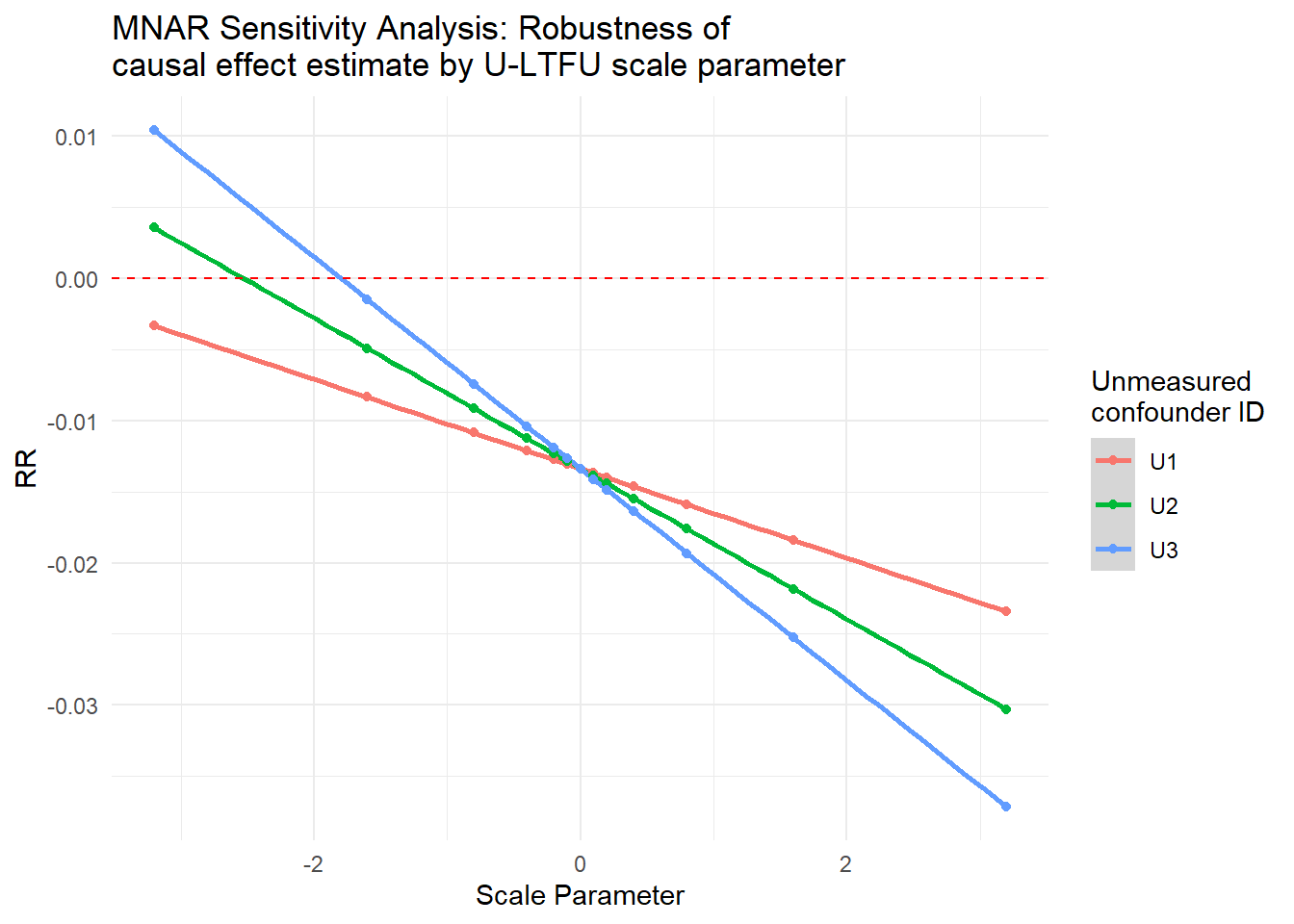
Reporting of \(U-A\) and \(U-Y\) relationship

Table 8.1: Risk Ratios, U-A relationship
variable RR std.error
U1 -0.7520250 0.0625914
U2 -0.4529040 0.0375505
U3 -0.3240197 0.0268205
Table 8.1: Risk Ratios, U-Y relationship
variable RR std.error
U1 0.6667669 8.3e-06
U2 0.4000362 3.0e-06
U3 0.2857328 1.5e-06