8.1 Motivational examples - Symmetries
Before even giving the definition of a group, we’ll look at several examples of symmetries of objects, so that the formal definition will make more sense when we come to it.
Exactly what we mean by a “symmetry” will vary from example to example, and sometimes there’s more than one sensible notion for the same object, so rather than giving a general definition, we’ll clarify what we mean in each example, and the common features should become clear.
8.1.1 Permutations of a set
Let us consider the set of three elements. Imagine them arranged in a line:

Figure 8.1: three points on a line
We can rearrange them, putting them in a different order. For example, we could swap the two elements furthest to the right:

Figure 8.2: the three points above but with the second and third swapped
This leaves us with exactly the same picture, so we’ll regard this as a “symmetry” in this context.
Now let’s label the elements and put both pictures next to each other to see how the elements have been permuted.
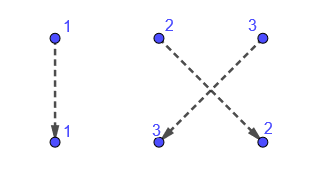
Figure 8.3: showing how we permuted the elements
This picture (Figure 8.3) brings to mind the function \(f:\{1,2,3\}\to\{1,2,3\}\) defined by \(\{(1,1),(2,3),(3,2)\}\) (i.e. \(f(1)=1,f(2)=3\) and \(f(3)=2\)).
Or if we cyclically permuted the elements as follows: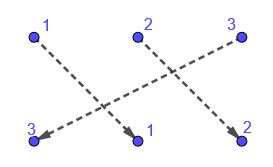
Figure 8.4: a cyclic permutation
this (Figure 8.4) would correspond to the function \(f:\{1,2,3\}\to\{1,2,3\}\) defined by \(\{(1,2),(2,3),(3,1)\}\) (i.e. \(f(1)=2, f(2)=3\) and \(f(3)=1\)).

Figure 8.5: not a permutation
gives a different pattern. Therefore we need the function \(f\) to be bijective.
Let \(X\) be a set. A permutation of the set \(X\) is a bijection \(f:X\to X\).
Let’s look in more detail at the permutations of a set \(X=\{1,2,3\}\) with three elements. It’s easy to check that there are just six of these, which we’ll denote by \(e,f,g,h,i,j\): see Figure 8.6, where we just show the position the three elements end up.
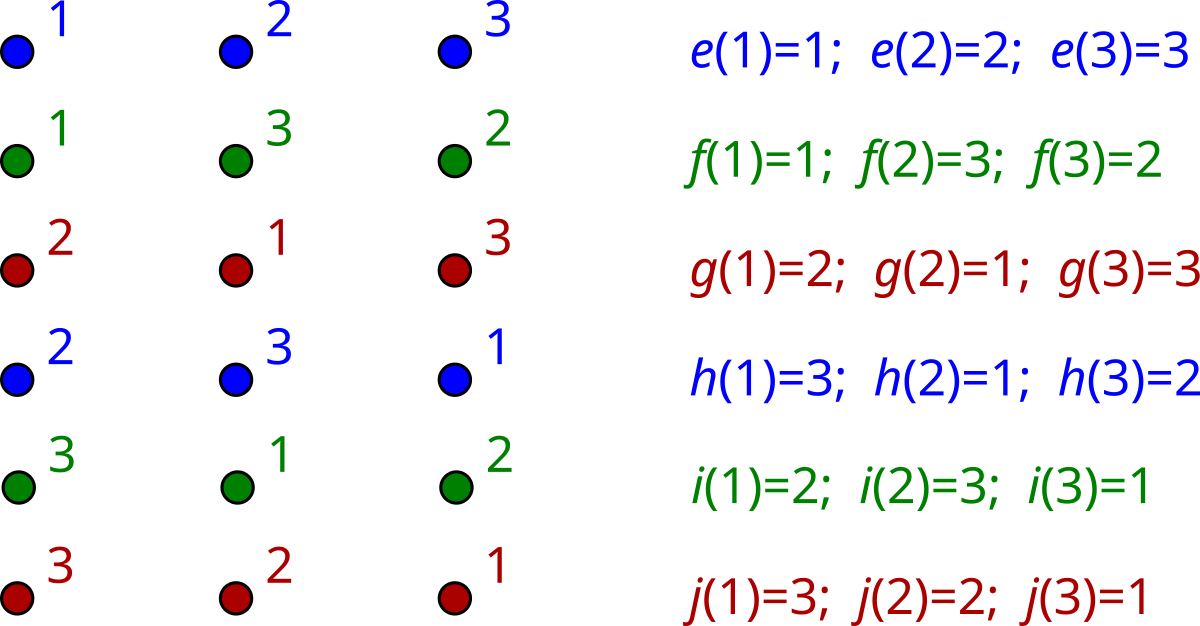
Figure 8.6: the six permutations of three elements
Notice that the function \(e\) is the identity function, and likewise it is called the identity permutation.
Now we can look at what happens when we perform one permutation followed by another. For example, if we do \(f\) (swap the two elements furthest to the right) and then \(g\) (swap the two elements that are now furthest to the left), then we are just taking the composition \(g\circ f\) of the two functions. This gives \(g(f(1))=g(1)=2\), \(g(f(2))=g(3)=3\) and \(g(f(3))=g(2)=1\), so \(g\circ f =i\).
For simplicity, we’ll leave out the composition symbol \(\circ\) and write \(gf\) instead of \(g\circ f\). Let’s see what \(fg\) is: \(f(g(1))=f(2)=3\), \(f(g(2))=f(1)=1\) and \(f(g(3))=f(3)=2\), so \(fg=h\).
When we come to define groups, we’ll think of “composition” as an operation to combine permutations or other kinds of symmetry (if \(f\) and \(g\) are symmetries of an object, then \(gf\) is the symmetry “do \(f\) and then \(g\)”), much as ``multiplication’’ is an operation to combine numbers. In fact we’re using pretty much the same notation: compare \(gf\) for permutations with \(xy\) for numbers. Let’s explore this analogy further with permutations of a set \(X\).
Note that since the composition of two bijections is a bijections, we have that the composition of two permutations is a permutation. This is similar to axioms (A1) and (A7).
We have seen that composition of functions is associative (see Proposition 6.17 ), hence if \(a,b,c\) are permutation, we have \(a(bc)=(ab)c\). This is similar to axioms (A2) and (A8).
We always have an identity permutation, \(e:X\to X\) defined by \(e(x)=x\) for all \(x\in X\). Let \(f\) be any other permutation of \(X\), then for all \(x\in X\) we have \[ef(x)=e(f(x))=f(x)=f(e(x))=fe(x),\] i.e. \(ef=f=fe\). This is similar to axioms (A4) and (A10).
We know that a bijective function is invertible, so for all permutation \(f:X\to X\), there exists \(f^{-1}\) such that \(ff^{-1}=e=f^{-1}f\). This is similar to axioms (A5) and (A11).
[You can check in the permutations of \(\{1,2,3\}\) that \(e^{-1}=e; f^{-1}=f; g^{-1}=g; h^{-1}=i; i^{-1}=h\) and \(j^{-1}=j\)]
Note that we can’t have anything similar to axioms (A3) or (A9) as we have seen an example of two permutations \(f,g\) of \(\{1,2,3\}\) such that \(fg\neq fg\).
8.1.2 Symmetries of polygons
Consider a regular \(n\)-sided polygon (for example, if \(n=3\) an equilateral triangle, or if \(n=4\) a square). Examples of symmetries are:
A rotation through an angle of \(2\pi/n\) (an \(n\)th of a revolution).
A reflection in a line that goes through the centre of the polygon and one of its vertices.
There are many ways to make precise what we mean by a symmetry. For example, considering the polygon as a subset \(X\) of \(\mathbb{R}^2\), we could look at bijections \(f:X\to X\) that preserve distance: i.e., such that the distance between \(f(x)\) and \(f(y)\) is the same as the distance between \(x\) and \(y\). It’s not hard to see that this implies that \(f\) must send vertices to vertices, and moreover must send adjacent vertices to adjacent vertices. To keep things simple, we’ll use this as our definition of a symmetry:
Note that for \(n=3\), every pair of vertices is adjacent, so in that case every permutation of the vertices is a symmetry, and so we are just looking at permutations of a set of three elements as in the last section.
In the case \(n=4\), we have a square. Let’s label the vertices as follows: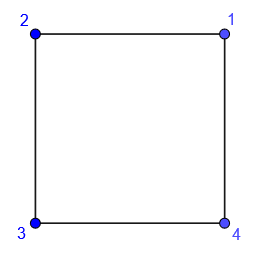
Figure 8.7: the four vertices labelled
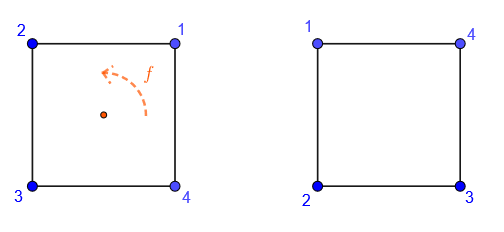
Figure 8.8: rotating the square
While if we reflect in the line of symmetry going from top right to bottom left (let’s call this symmetry \(g\)) we get (Figure 8.9):
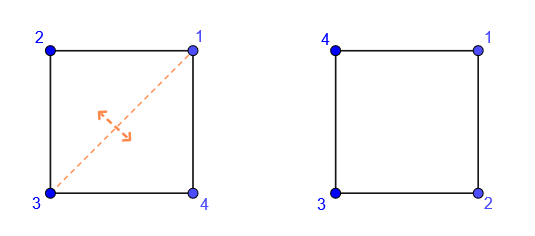
Figure 8.9: reflecting the square
However the following does not represent a symmetry as vertices \(1\) and \(2\) have not remained adjacent (Figure 8.10):
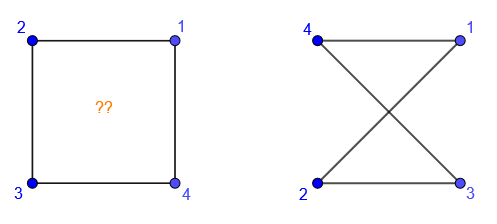
Figure 8.10: not a symmetry
As with permutations, we can compose symmetries together and get a new symmetry. In fact, the analogues of (A1)/(A7), (A2)/(A8), (A4)/(A10) and (A5)/(A11) all hold (Prove that the composition of two bijections that preserves adjacency is a bijection that preserves adjacency, and that the inverse of a function that preserve adjacency is a function that preserves adjacency.)
Let’s look at what happens when we compose the symmetries \(f\) and \(g\) (Figure 8.11).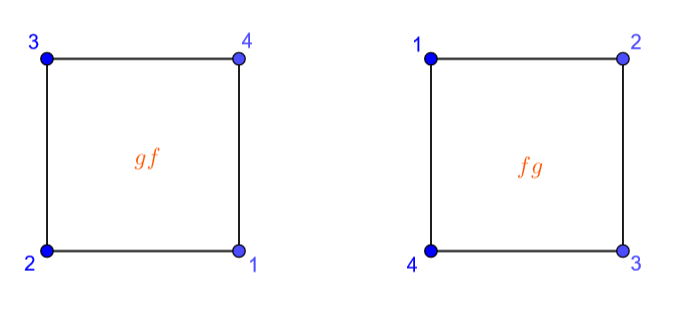
Figure 8.11: composing the two previous symmetries
We see that \(gf\) is a reflection in the horizontal line of symmetry while \(fg\) is a reflection in the vertical line of symmetry. So here again we have \(gf\neq fg\).
8.1.3 Symmetries of a circle
We can look at bijections from a circle to itself that preserve distances between points. It’s not too hard to see that these symmetries are either rotations (through an arbitrary angle) or reflections (in an arbitrary line through the centre).
Again, if \(f\) and \(g\) are symmetries, then usually \(fg\neq gf\).
8.1.4 Symmetries of a cube
We can look at the eight vertices of a cube, and define a symmetry to be a permutation of the set of vertices that preserves adjacency (as we did with a polygon). There are \(48\) symmetries: most are either rotations or reflections, but there is also the symmetry that takes each vertex to the opposite vertex.
8.1.5 Rubik’s Cube
A Rubik’s cube has \(54\) coloured stickers (\(9\) on each face), and we could define a “symmetry” to be a permutation of the stickers that we can achieve by repeatedly turning faces (as one does with a Rubik’s cube). It turns out that there are \(43,252,003,274,489,856,000\) symmetries. Again we can compose symmetries (do one sequence of moves and then another), and every symmetry has an inverse symmetry.