8.4 Dihedral Groups

As we study group theory, it will be useful to have a supply of examples of groups to think about. Of course, no single example will be ideal for everything, but some are more helpful than others. Some of the more “arithmetic” groups, such as \((\mathbb{Z},+)\) and \((\mathbb{R}\setminus\{0\},\times)\), have the advantage of being very familiar, but the disadvantage of being rather untypical because they’re abelian. If you have a “standard example” that you like to think about, then it will be much less misleading if it’s non-abelian.

A good first family of examples are the “dihedral groups”, which are the symmetry groups of regular polygons, and are non-abelian, but still fairly uncomplicated. In the next section we will look at a second important family of examples, the “symmetric groups”.

Let \(X\) be a regular \(n\)-sided polygon, with vertices labelled anticlockwise \(1,2,\dots,n\). Recall that by a symmetry of \(X\) we mean a permutation of the vertices that takes adjacent vertices to adjacent vertices.

For example, we can send vertex \(1\) to any other vertex by an appropriate rotation. If \(f\) is a symmetry sending vertex \(1\) to vertex \(i\), then, since it preserves adjacency, it must send vertex \(2\) to one of the two vertices adjacent to vertex \(i\), and once we know \(f(1)\) and \(f(2)\), then \(f(3)\) is determined as the other vertex adjacent to \(f(2)\), and so on around the polygon for \(f(4),\dots,f(n)\).

So the total number of symmetries is \(2n\) (since there are \(n\) choices for \(f(1)\) and for each of these there are two choices for \(f(2)\)). This explains the following choice of notation.

Definition 8.15:

The dihedral group \(D_{2n}\) of order \(2n\) is the group of symmetries of a regular \(n\)-sided polygon.

Remark:

Some books use the symbol \(D_n\) where we use \(D_{2n}\) (i.e., they label the group with the size of the polygon rather than the size of the group), although at least the \(D\) is fairly standard.

Let’s fix some notation for two particular symmetries.

Notation:

We set \(a\in D_{2n}\) to be a rotation anticlockwise through an angle of \(2\pi/n\). We set \(b\in D_{2n}\) to be a reflection in the line through vertex \(1\) and the centre of the polygon.

So \[ a(1)=2, a(2)=3, \ldots, a(n-1)=n, a(n)=1, \] and \[ \ldots, b(n-1)=3, b(n)=2, b(1)=1, b(2)=n, b(3)=n-1, \ldots \]

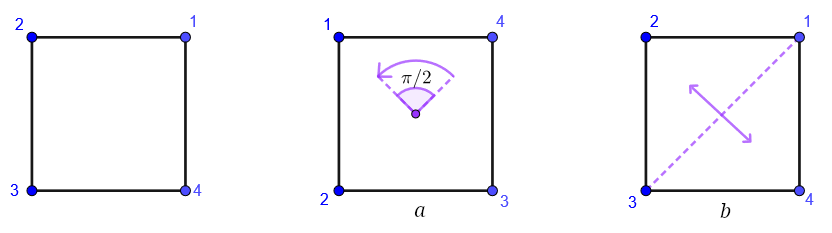
Figure 8.12: The symmetries a and b on \(D_8\)

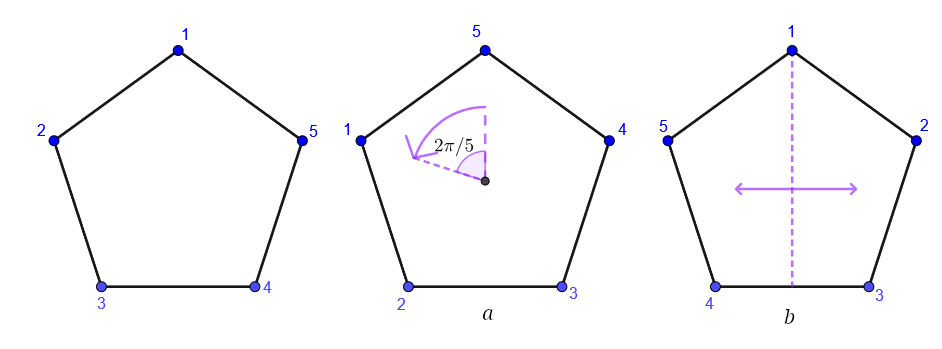
Figure 8.13: The symmetries a and b on \(D_{10}\)

Now consider the symmetries \(a^i\) and \(a^ib\) for \(0\leq i<n\). These both send vertex \(1\) to vertex \(1+i\), but \(a^i\) sends vertices \(2,3,\dots,n\) to the vertices following anticlockwise around the polygon, whereas \(a^ib\) sends them to the vertices following clockwise around the polygon. So all of these symmetries are different, and every symmetry is of this form, and so every element of \(D_{2n}\) can be written in terms of \(a\) and \(b\).

Proposition 8.16:

We have \(D_{2n}=\{e,a,a^2,\dots,a^{n-1},b,ab,a^2b,\dots,a^{n-1}b\}\).

Let \(G\) be a group with a finite number of elements: its multiplication table (often also called the Cayley table) has one row and one column for each element of the group, and the entry in row \(x\) and column \(y\) is the product \(xy\). So the table displays the group operation.

Example:

The Cayley table for \(D_6 = \{e,a,a^2,b,ab,a^2b\}\) is as follows:

	\(e\)	\(a\)	\(a^2\)	\(b\)	\(ab\)	\(a^2b\)
\(e\)	\(e\)	\(a\)	\(a^2\)	\(b\)	\(ab\)	\(a^2b\)
\(a\)	\(a\)	\(a^2\)	\(a^3\)	\(ab\)	\(a^2b\)	\(a^3b\)
\(a^2\)	\(a^2\)	\(a^3\)	\(a^4\)	\(a^2b\)	\(a^3b\)	\(a^4b\)
\(b\)	\(b\)	\(ba\)	\(ba^2\)	\(b^2\)	\(bab\)	\(ba^2b\)
\(ab\)	\(ab\)	\(aba\)	\(aba^2\)	\(ab^2\)	\(abab\)	\(aba^2b\)
\(a^2b\)	\(a^2b\)	\(a^2ba\)	\(a^2ba^2\)	\(a^2b^2\)	\(a^2bab\)	\(a^2ba^2b\)

History:

Arthur Cayley was an English mathematician (1821 - 1895) who gave the first abstract definition of a finite group in 1854. It is around then that he showed that a group is determined by its multiplication table (i.e., its Cayley table), and gave several examples of groups that were not symmetric groups. However, at the time the mathematical community did not pursue this further, preferring to stick to studying the concrete symmetric groups. It wasn’t until 1878 when he re-introduced his definition that other mathematicians refined it and an agreed formal definition of a group emerged.

As we can see in the Cayley graph above, we have expressions such as \(ba\) or \(a^{-1}\) appearing, but they are not in our list of standard form for elements. So, we must be able to work out how to write elements such as \(ba\) or \(a^{-1}\) into standard form.

There are three basic rules that let us easily do calculations.

Proposition 8.17:

We have \(a^n=e\).

This is clearly true, as it just says that if we repeat a rotation through an angle of \(2\pi/n\) \(n\) times, then this is the same as the identity.

Note that this means that \(a(a^{n-1})=e\) and so by uniqueness of inverses \[a^{-1}=a^{n-1},\] which allows us to write any power (positive or negative) of \(a\) as one of \(e,a,\dots,a^{n-1}\).

Proposition 8.18:

We have \(b^2=e\).

This is clearly true, as repeating a reflection twice gives the identity.

This implies, by uniqueness of inverses again, that \(b^{-1}=b\), and so any power of \(b\) is one of \(e\) or \(b\).

What about \(ba\)? Well \(a(1)=2\) and \(b(2)=n\), so \(ba(1)=n\), similarly \(ba(2)=n-1\) and so the other vertices follow clockwise. This is the same as \(a^{n-1}b\), or \(a^{-1}b\).

Proposition 8.19:

We have \(ba=a^{n-1}b=a^{-1}b\).

We’ll see that these three rules allow us to simplify any expression.

For example, \[ba^{-1}=ba^{n-1}=baa^{n-2}=a^{-1}ba^{n-2}=a^{-1}baa^{n-3}=a^{-1}a^{-1}ba^{n-3}=\dots=a^{-n+1}b=ab,\] where we repeatedly “swap” a \(b\) with an \(a\) or \(a^{-1}\), changing the \(a\) into \(a^{-1}\) or the \(a^{-1}\) into \(a\).

We get the following rules for multiplying expressions in standard form.

Theorem 8.20:

Fix \(n\in \mathbb{Z}\). In \(D_{2n}\), for \(0\leq i,j<n\),

\[\begin{align*} a^{i}a^{j}&=\begin{cases}a^{i+j}&\text{ if } i+j<n\\a^{i+j-n}&\text{ if } i+j\geq n\end{cases}\\ a^{i}(a^{j}b)&=\begin{cases}a^{i+j}b&\text{ if } i+j<n\\a^{i+j-n}b&\text{ if } i+j\geq n\end{cases}\\ (a^{i}b)a^{j}&=\begin{cases}a^{i-j}b&\text{ if } i-j\geq0\\a^{i-j+n}b&\text{ if } i-j<0\end{cases}\\ (a^{i}b)(a^{j}b)&=\begin{cases}a^{i-j}&\text{ if } i-j\geq0\\a^{i-j+n}&\text{ if } i-j<0\end{cases} \end{align*}\]

You are encouraged to practice some calculations with the dihedral group, especially with \(n=3\) and \(n=4\), as we’ll frequently be using these as examples.

Example:

We rewrite The Cayley table for \(D_6 = \{e,a,a^2,b,ab,a^2b\}\) (check the calculation yourself):

	\(e\)	\(a\)	\(a^2\)	\(b\)	\(ab\)	\(a^2b\)
\(e\)	\(e\)	\(a\)	\(a^2\)	\(b\)	\(ab\)	\(a^2b\)
\(a\)	\(a\)	\(a^2\)	\(e\)	\(ab\)	\(a^2b\)	\(b\)
\(a^2\)	\(a^2\)	\(e\)	\(a\)	\(a^2b\)	\(b\)	\(ab\)
\(b\)	\(b\)	\(a^2b\)	\(ab\)	\(e\)	\(a^2\)	\(a\)
\(ab\)	\(ab\)	\(b\)	\(a^2b\)	\(a\)	\(e\)	\(a^2\)
\(a^2b\)	\(a^2b\)	\(ab\)	\(b\)	\(a^2\)	\(a\)	\(e\)

Remark:

The cancellation properties which we previously found have a nice interpretation in terms of Cayley tables:

The left cancellation proposition just says that all the entries in each row are different: if two entries \(xy\) and \(xz\) in row \(x\) are the same, then \(xy=xz\) and so \(y=z\). Similarly the right cancellation property says that all the entries in each column are different. This can be a useful method for deducing information about a group from a partial multiplication table.

Observe that these hold with the Cayley table above.

Remark:

When \(n=3\), all vertices of a regular \(n\)-sided polygon (i.e., an equilateral triangle) are adjacent to one another, so \(D_6\) contains all permutations of \(\{1,2,3\}\). But this doesn’t apply for larger \(n\).