6.2 Injective, surjective and bijective
We now introduce three important properties that a function may or may not have.
We say a function \(f:X\to Y\) is injective (or one-to-one, or an injection) if for all \(x_1,x_2\in X\), we have that if \(x_1\not=x_2\) then \(f(x_1)\not=f(x_2)\).
Using the contrapositive, an alternative definition is that a function \(f:X \to Y\) is injective if for all \(x_1,x_2 \in X\), we have if \(f(x_1)=f(x_2)\) then \(x_1 = x_2\).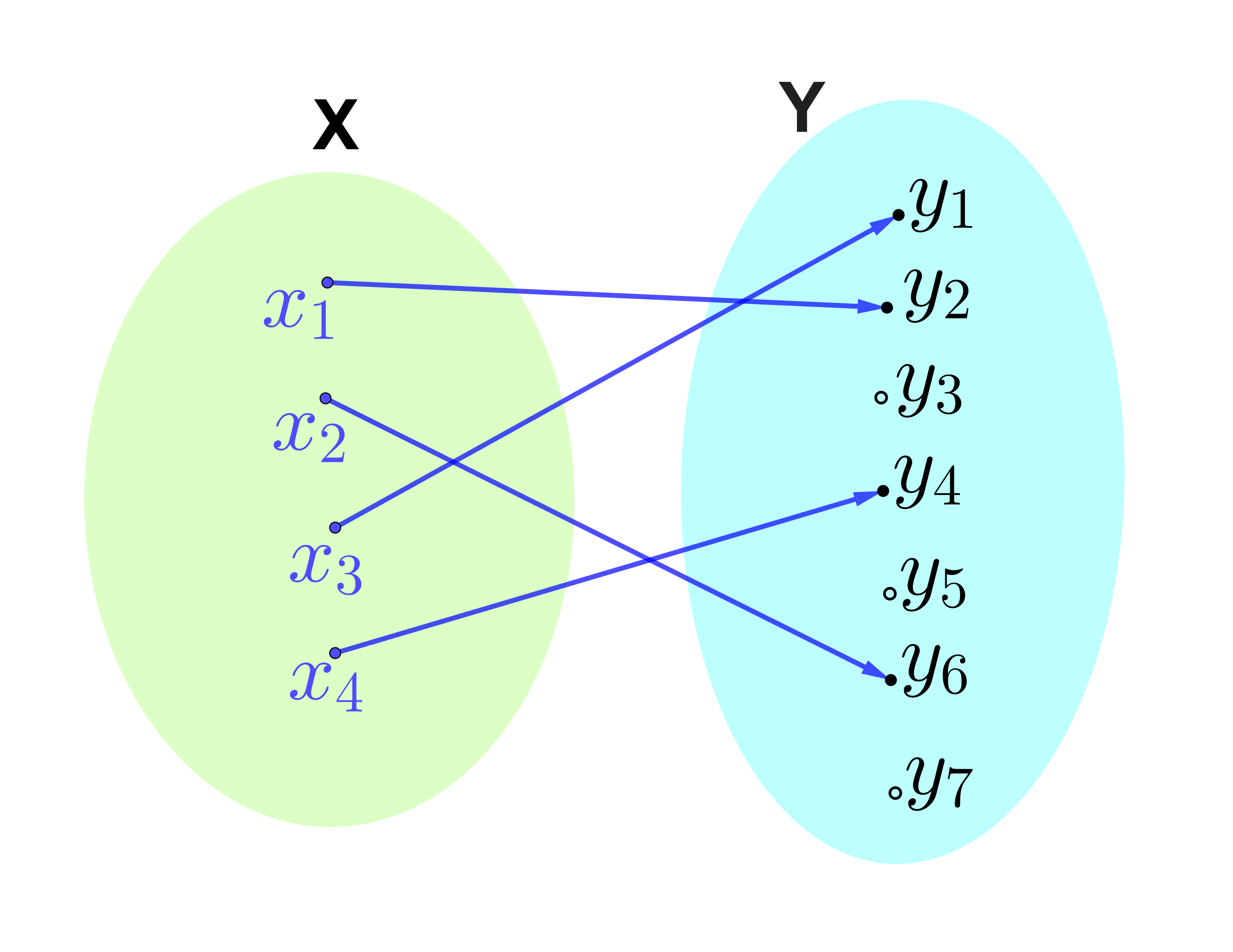
Figure 6.1: An injective function from \(X\) to \(Y\), there are at most one arrow going to any point in \(Y\). However the function is not surjective as there are some points in \(Y\) with no arrow going to it. Figure made with Geogebra.
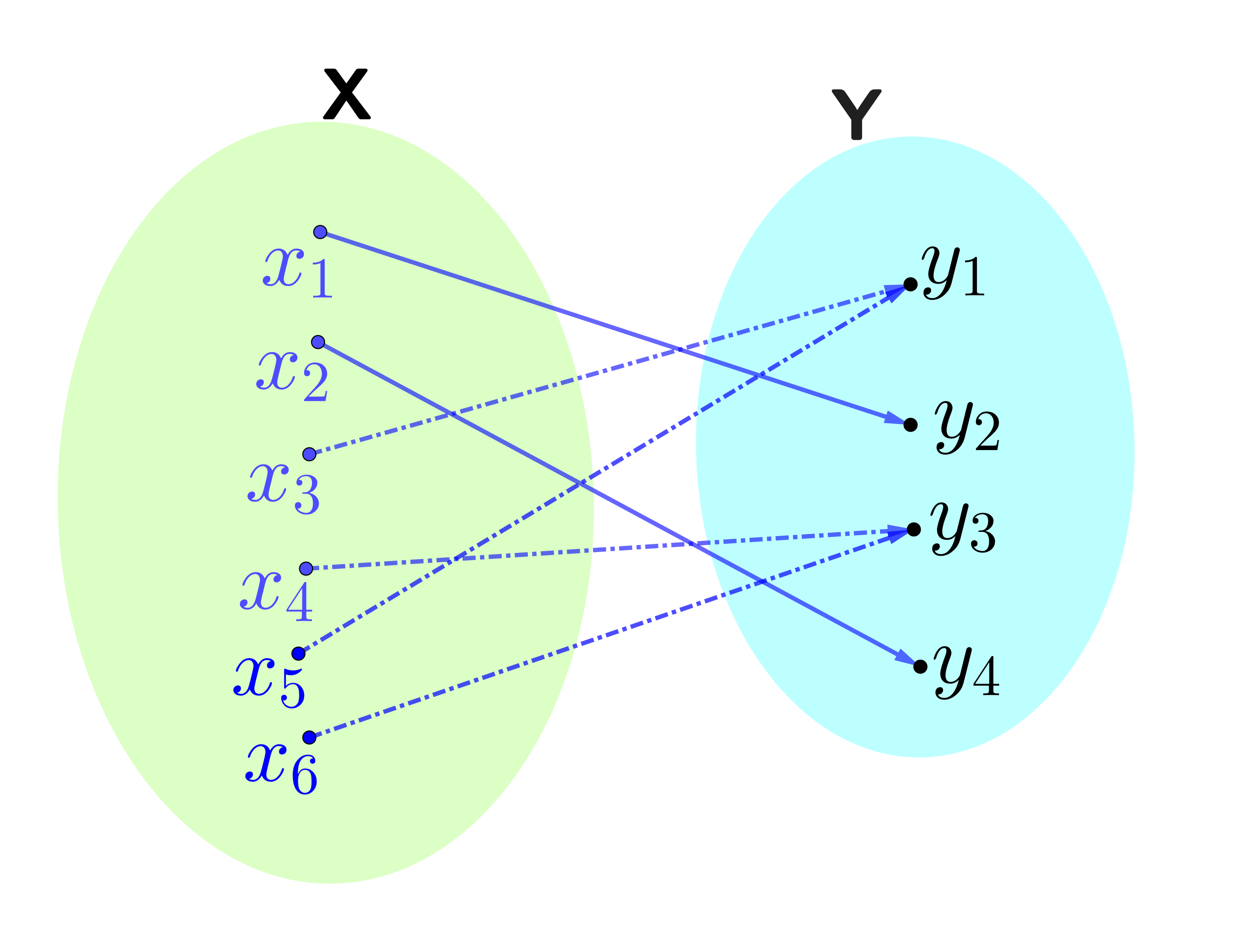
Figure 6.2: A surjective function from \(X\) to \(Y\), every point in \(Y\) has at least one arrow going to it. However the function is not injective as there are some points in \(Y\) with at least two arrows going to it. Figure made with Geogebra
Define \(f:\mathbb{R}\times \mathbb{R}\to \mathbb{R}\times\mathbb{R}\) by \(f((m,n))=(m+n,m-n),\) for all \(m,n\in\mathbb{R}\). We want to show that \(f\) is bijective.
We first show it is injective by using the contrapositive. Let \((m_1,n_1), (m_2,n_2)\in \mathbb{R}\times\mathbb{R}\) (the domain) be such that \(f((m_1,n_1))=f((m_2,n_2))\). That is \((m_1+n_1,m_1-n_1) = (m_2+n_2,m_2-n_2)\), i.e. \(m_1+n_1 = m_2+n_2\) and \(m_1-n_1 = m_2-n_2\). Therefore, \(2m_1 = (m_1+n_1)+(m_1-n_1)=(m_2+n_2)+(m_2-n_2)=2m_2\). Since \(2\neq 0\), we can divide by \(2\) to deduce \(m_1 = m_2\). Hence \(m_1+n_1=m_2+n_2=m_1+n_2\) means \(n_1=n_2\). Therefore \((m_1,n_1)=(m_2,n_2)\) and \(f\) is injective.
We next show that \(f\) is surjective. We begin by choosing \((u,v)\in\mathbb{R}\times\mathbb{R}\) [the co-domain].
[Scratch work: We want to find \((m,n)\in\mathbb{R}\times\mathbb{R}\) such that \(f(m,n)=(u,v)\). So we need to find \((m,n)\in\mathbb{R}\times \mathbb{R}\) such that \(m+n=u\) and \(m-n=v\). Hence, we must have \(m=u-n\) and \(m=v+n\). Then \(u-n=v+n\), or equivalently, \(u-v=2n\), or equivalently, \(\frac{u-v}{2}=n\). If we have \(\frac{u-v}{2}=n\) and \(m=u-n\), then \(m=u-\frac{u-v}{2}=\frac{u+v}{2}.\)]
We set \(m=\frac{u+v}{2}\) and \(n=\frac{u-v}{2}\). Then \((m,n)\in\mathbb{R}\times\mathbb{R}\) [the domain], and \[f(m,n)=(m+n,m-n)=\left(\frac{u+v}{2}+\frac{u-v}{2},\frac{u+v}{2}-\frac{u-v}{2}\right)=(u,v).\] It follows that \(f\) is surjective.
Since \(f\) is injective and surjective, it is bijective.Let \(f_1:\mathbb{Z}_+\to\mathbb{Z}_+\) be defined by \(f_1(n) = n^2\) for all \(n\in \mathbb{Z}_+\). We claim that \(f_1\) is injective but not surjective.
We first show \(f_1\) is injective. Let \(n_1,n_2 \in \mathbb{Z}_+\) be such that \(n_1\neq n_2\). Without loss of generality, we assume \(n_1<n_2\). Note that \(n_1,n_2>0\) by definition, so \(n_1<n_2\) means \(n_1^2<n_2n_1\) and similarly, \(n_1n_2<n_2^2\). Combining these two inequalities together, we get \(n_1^2<n_1n_2<n_2^2\), i.e. \(f_1(n_1)<f_1(n_2)\) so \(f(n_1)\neq f(n_2)\). So \(f_1\) is injective.
We next show \(f_1\) is not surjective. We take \(2 \in \mathbb{Z}_+\) and claim that for all \(n\in \mathbb{Z}_+\) we have \(f_1(n)=n^2 \neq 2\). For a contradiction, suppose such an \(n\) exists, i.e. \(n^2 = 2\). Note that \(n>1\) since \(1^1 = 1<2\). However, if \(n\geq 2\), then \(n^2 \geq 4 >2\) which is not possible. Hence \(1<n<2\), but there are no natural numbers between \(1\) and \(2\). Hence \(n\) does not exists and \(f_1\) is not surjective.Consider \(f:X\to Y\). Then we have that \(f\) is injective if and only if for all\(y\in f[X]\), there exists a unique \(x\in X\) such that \(f(x)=y\).
We show the two implications separately.
\(\Rightarrow\)). Suppose that \(f\) is injective, and take \(y\in f[X]\). Hence, \(\exists x_1\in X\) such that \(f(x_1)=y\). Now, suppose \(\exists x_2\in X\) such that \(x_2\not=x_1\). Since \(f\) is injective, we have that \(f(x_1)\not=f(x_2)=y.\) Hence, \(\forall y\in f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\).
\(\Leftarrow\)). Suppose that \(\forall y\in f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\). Take \(x_1,x_2\in X\) such that \(x_1=x_2\) and let \(y=f(x_1).\) By assumption, \(x\) is the only element of \(X\) that \(f\) maps to \(y\). Then \(y\not=f(x_2),\) so \(f(x_1)\not=f(x_2).\) Hence, we have shown that for \(x_1,x_2\in X\) with \(x_1\not=x_2\), we have that \(f(x_1)\not=f(x_2)\). Therefore, \(f\) is injective.
It follows that \(f\) is injective if and only if \(\forall y\in f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\).□
Caution! Note that the converse of the above definition is, “for all \(x\in X\), there exists a unique \(y\in Y\) such that \(f(x)=y\)”, which is the definition of a function.
So do not confuse the definition of injectivity with the definition of a function. In particular, one definition can be true without the other being true.
For example, consider \(f=\{(y^2,y):\ y\in\mathbb{Z}\ \}\subseteq \mathbb{Z}\times \mathbb{Z}\). We have that for each \(y\in\mathbb{Z}\), there exists a unique \(x\in \mathbb{Z}\) such that \((x,y)\in f\) (namely \(x=y^2\)) so \(f\) satisfies the definition of being injective. However \(f\) is not a function since, for example, \((4,2), (4,-2) \in f\) (so it doesn’t make sense to talk about whether \(f\) is injective or not).Consider \(f:X\to Y\). Then \(f\) is surjective if and only if \(f[X]=Y\).
We show the two implications separately.
\(\Rightarrow\)). Suppose \(f\) is surjective, we will show \(f[X]=Y\) by showing \(f[X]\subseteq Y\) and \(Y\subseteq f[X]\). Note that by definition \(f[X] = \{y\in Y: \exists x\in X \text{ with } f(x)=y\} \subseteq Y\).
Take \(y_0 \in Y\). Since \(f:X\to Y\) is surjective, there exists \(x_0 \in X\) so that \(f(x_0)=y_0\). Thus \(y_0 \in f[X]\). As \(y_0\) was arbitrary, we have \(\forall y_0 \in Y\), \(y_0\in f[x]\). Hence \(Y\subseteq f[X]\).
\(\Leftarrow\)). Suppose \(f[X]=Y\). Choose \(y_0 \in Y = f[X]\). By definition of \(f[X]\), there exists \(x_0 \in X\) such that \(y_0 = f(x_0)\). This argument holds for all \(y_0 \in Y\), hence \(f\) is surjective.□
Consider \(f:X\to Y\). Then we have that \(f\) is bijective if and only if \(\forall y\in Y\), \(\exists !\, x\in X\) such that \(f(x)=y\).
We show the two implications separately.
\(\Rightarrow\)). Suppose \(f\) is bijective, then it is surjective so by Proposition 6.9 \(Y=f[X]\). We also have \(f\) is injective, so by Proposition 6.8 we have \(\forall y\in f[X]=Y\), \(\exists !\, x\in X\) such that \(f(x)=y\) as required.
\(\Leftarrow\)). Suppose that \(\forall y\in Y\), \(\exists ! x\in X\) such that \(f(x)=y\). In particular, \(\forall y\in Y\), \(\exists x\in X\) such that \(f(x)=y\), i.e. by definition \(f\) is surjective. By Proposition 6.9 \(Y=f[X]\), so our assumption becomes \(\forall y\in Y=f[X]\), \(\exists ! x\in X\) such that \(f(x)=y\). Hence by Proposition 6.8, \(f\) is injective. Since we have shown \(f\) is surjective and injective, we deduce \(f\) is bijective.□
The words injective, surjective and bijective all have the same ending “-jective”. This comes from the Latin verb jacere which means “to throw”.
Injective has the prefix in, a Latin word meaning “in, into”. This gave rise to the medical term “injection” where we throw some medecine into the body. An injective function is one that throws the set \(X\) into the set \(Y\) (every elements of \(X\) stay distincts once they are in \(Y\).)
Surjective has the prefix sur a French word meaning “over”, itself coming from the Latin super which means “(from) above”. A surjective function is one that covers the whole of \(Y\) (in the sense \(X\) is thrown from above to cover \(Y\)).
Bijective has the prefix bi, a Latin word meaning “two”. Once we talk about inverse functions, it will become clear that a bijection is a function that works in two directions.
Consider \(f:X\to Y\) and let \(X=U\cup V\). Then
\(f[X]=f[U]\cup f[V]\).
if \(f\) is injective and \(U\cap V=\emptyset\), then \(f[U]\cap f[V]=\emptyset\).
a.) Since \(U,V\subseteq X\), we have that \(f[U], f[V]\subseteq f[X]\), so \(f[U]\cup f[V]\subseteq f[X]\). On the other hand, take \(x\in X\). Then \(x\in U\) or \(x\in V\), so \(f(x)\in f[U]\) or \(f(x)\in f[V]\). Therefore \(f(x)\in f[U]\cup f[V]\). Since this holds for all \(x\in X\), we have \(f[X]\subseteq f[U]\cup f[V]\). Hence, \(f[X]=f[U]\cup f[V]\).
b.) Suppose that \(f\) is injective and \(U\cap V=\emptyset\). To the contrary, suppose that there exists some \(y\in f(U)\cap f(V)\). Hence, there exists some \(u\in U\) such that \(y=f(u)\), and there exists some \(v\in V\) such that \(y=f(v)\). It follows that \(f(u)=y=f(v)\). Since \(f\) is injective, we have that \(u=v\). Hence, \(u\in U\cap V\), which contradicts our initial assumption. It follows that \(f(U)\cap f(V)=\emptyset.\)□
Suppose that \(f:X\to Y\) is bijective, and let \(A\subseteq X\) and \(B=X\setminus A\). Then \(f[A]\cap f[B]=\emptyset\) and \(f[A]\cup f[B] = Y\).
Since \(f\) is bijective it is surjective and \(Y=f[X]\). We also note that \(A\cup B = X\), so we satisfy the hypothesis of the above theorem and deduce \(f[A] \cup f[B] = f[X] =Y\).
Furthermore since \(f\) is bijective, it is injective and we have \(A\cap B = \emptyset\). Hence we satisfy the hypothesis of part b.) of the above theorem and can deduce that \(f[A]\cap f[B]=\emptyset\).□