4 Övningskompendium Sannolikhetslära och Inferens
4.1 Sannolikhetslära
Uppgift 5
choose(n,k) räknar ut \({n\choose k}\)
choose(8,3) #a)
## [1] 56
choose(8,5) #b)
## [1] 56
choose(5,3)*choose(3,2) #c)
## [1] 30Uppgift 28
Funktionen dbinom har tre argument, x,p och n och räknar ut
p(x) = choose(n, x) p^x (1-p)^(n-x)
det vill säga \[p(x) = {n \choose x} p^x(1-p)^{n-x}\]
- Låt \(X\) vara \(Bi(5, 0.2)\). Bestäm \(Pr(X = 2)\)
dbinom(x = 2, size=5, prob=0.2)
## [1] 0.2048- Låt \(X\) vara \(Bi(5, 0.8)\). Bestäm \(Pr(X = 3)\)
dbinom(x = 3, size=5, prob=0.8)
## [1] 0.2048- Låt \(X\) vara \(Bi (8, 0.4)\). Bestäm \(Pr(X \le 3)\) Nu har vi \(\leq\) istället för \(=\), vilket gör att vi måste summera
dbinom(x = 0, size=8, prob=0.4)+
dbinom(x = 1, size=8, prob=0.4)+
dbinom(x = 2, size=8, prob=0.4)+
dbinom(x = 3, size=8, prob=0.4)
## [1] 0.5940864
# Enklare:
sum(dbinom(x = 0:3, size=8, prob=0.4))
## [1] 0.5940864- Låt \(X\) vara \(Bi(20, 0.3)\). Bestäm \(Pr(X > 5)\)
1- sum(dbinom(x = 0:5, size=20, prob=0.3))
## [1] 0.5836292- Låt \(X\) vara \(Bi (10, 0.6)\). Bestäm \(Pr(X \le 5)\)
1 - sum(dbinom(x = 0:4, size=10, prob=0.4))
## [1] 0.3668967Uppgift 39
Här är kod för att själv skapa en normal-kurva. Du kan ändra det skuggade området genom att ändra på lower.x och upper.x. Du kan också ändra standarddavvikelse och medelvärde genom att ändra på sigma respektive mu i funktionen skugga(). Detta är också ett exempel på hur man själv kan skapa en enkel funktion i R, men det är överkurs.
skugga <- function(lower.x, upper.x, mu=0, sigma=1,col="grey",density=NULL){
step <- (upper.x - lower.x) / 100
bounds <- c(mu-3*sigma, mu+3*sigma)
cord.x <- c(lower.x,seq(lower.x,upper.x,step),upper.x)
cord.y <- c(0,dnorm(seq(lower.x,upper.x,step),mu,sigma),0)
curve(dnorm(x,mu,sigma),xlim=bounds,xlab = "",ylab = "",bty="n")
polygon(cord.x,cord.y,col=col,density = density)
}Återskapa de fyra kurvorna i uppgift 39 med
skugga(lower.x = 0, upper.x = 1) # i
skugga(lower.x = 1, upper.x = 2) # ii
skugga(lower.x = -1, upper.x = 2) # iii
skugga(lower.x = -3, upper.x = -1) # iv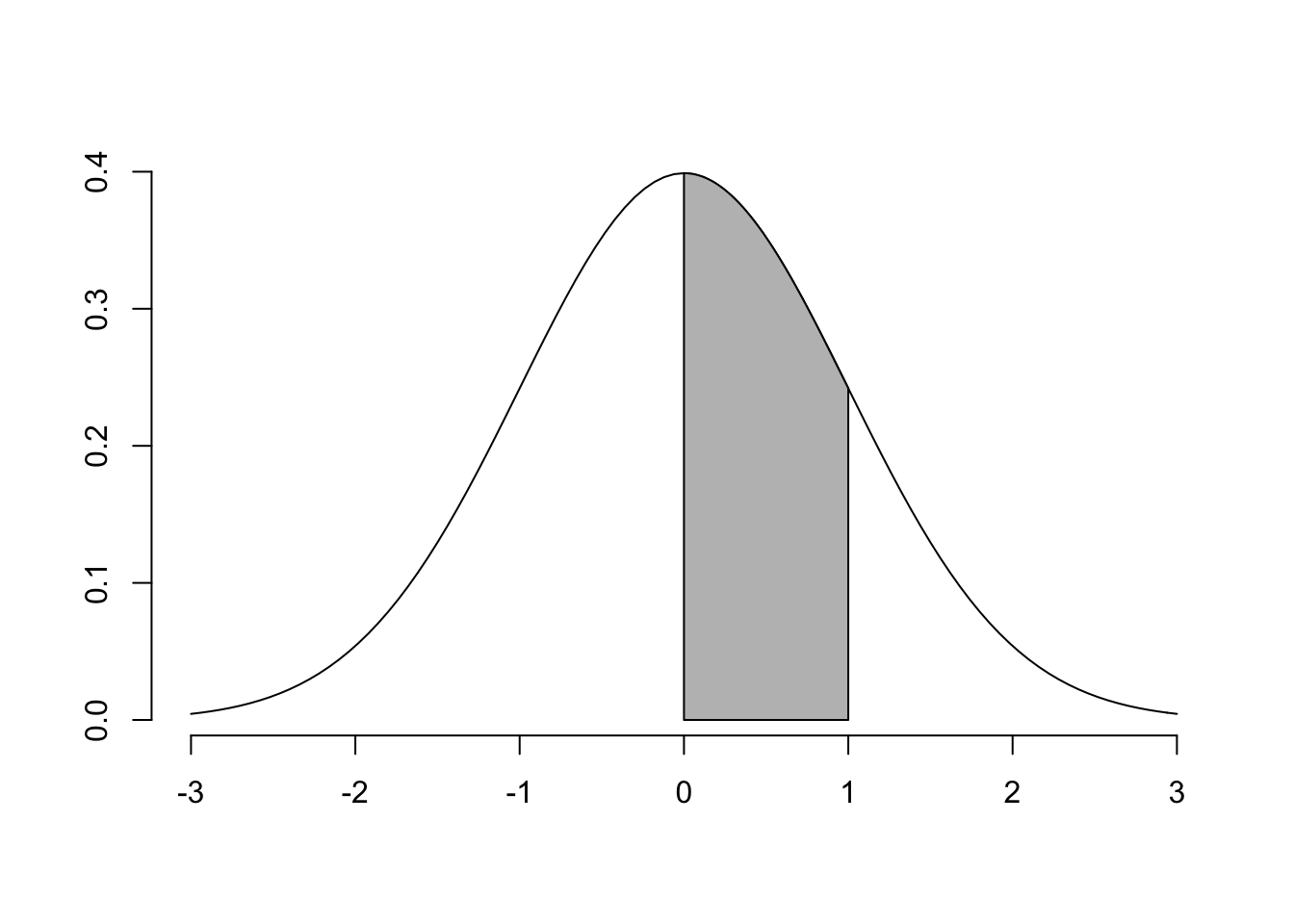
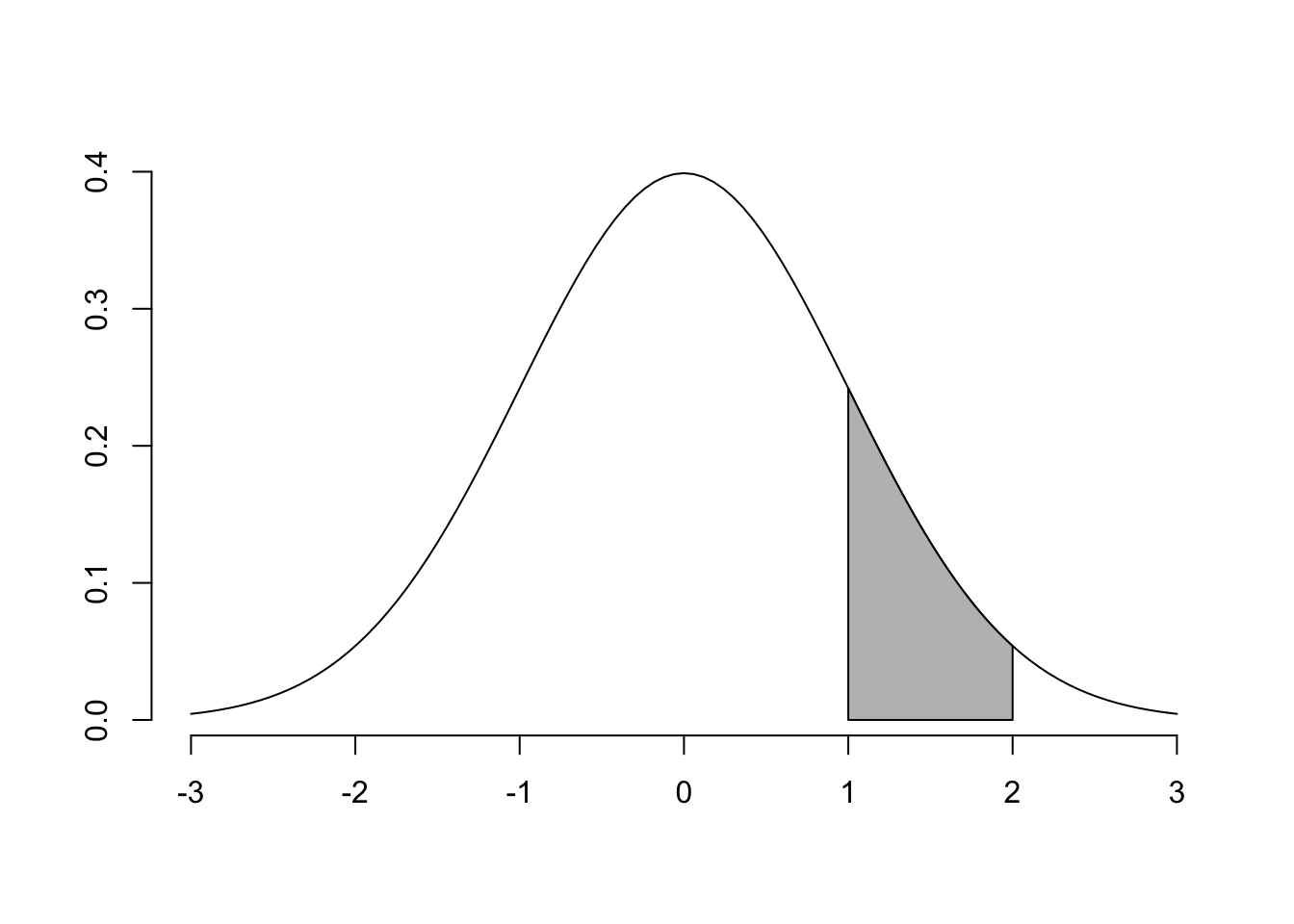
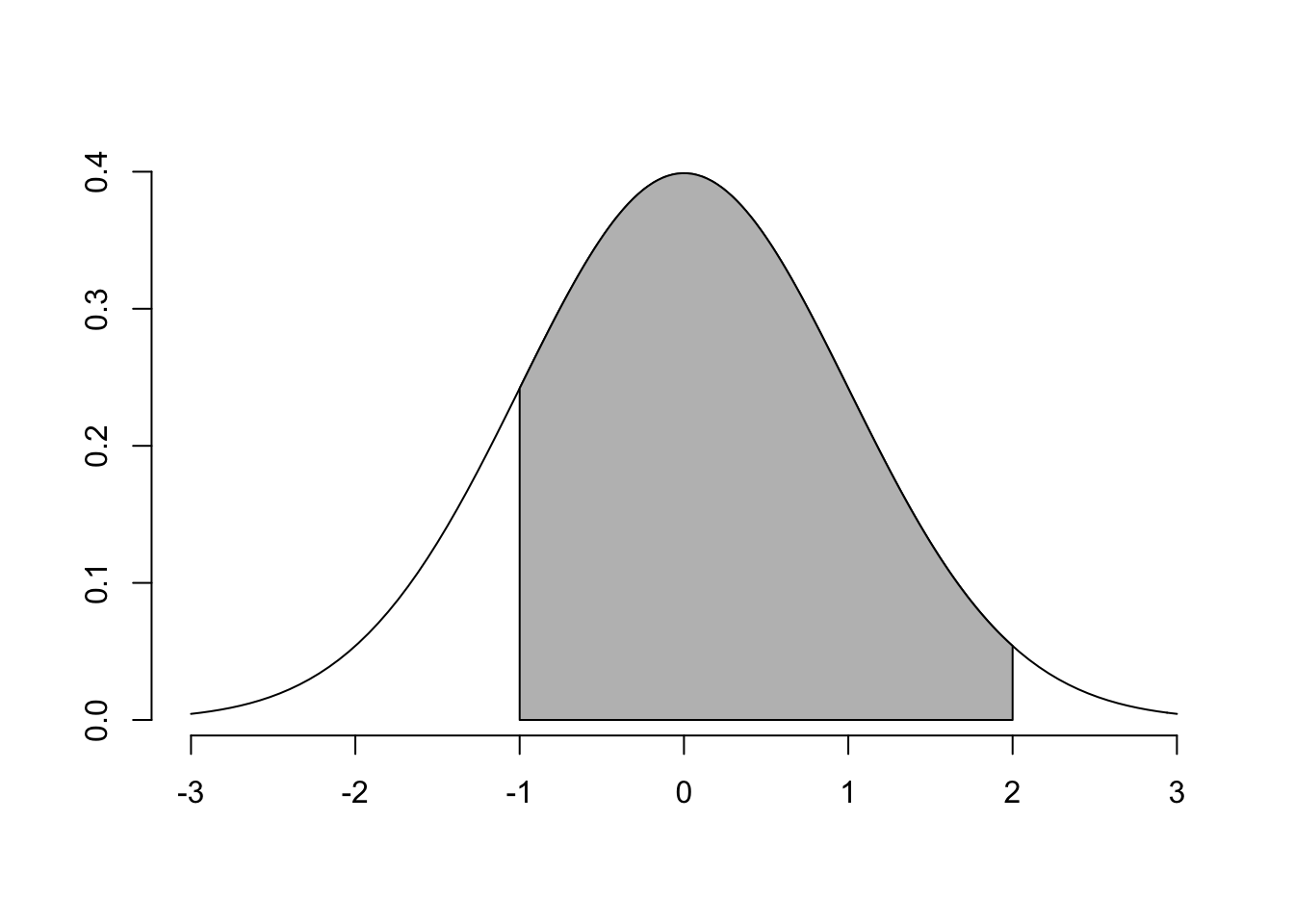
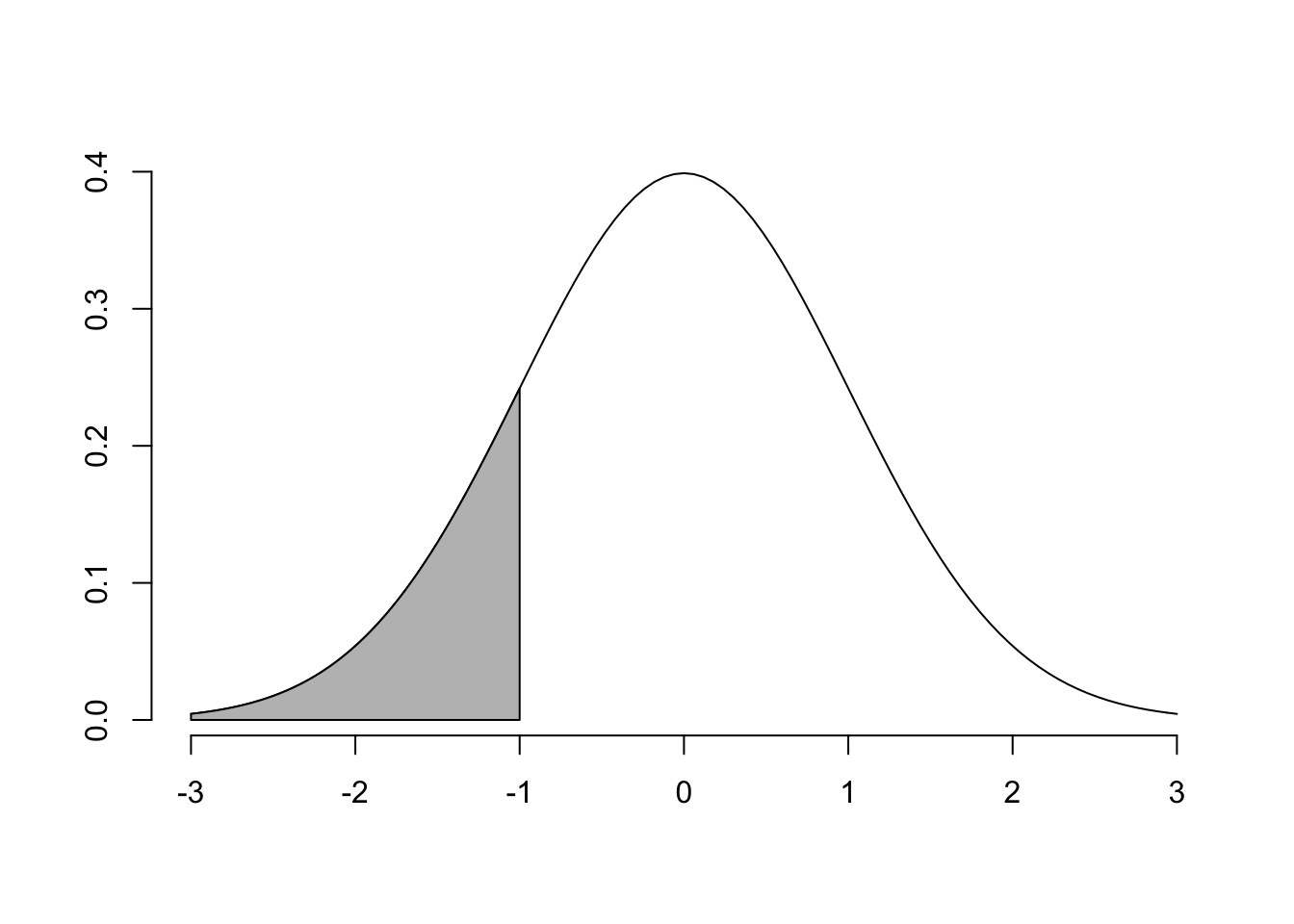
Dessa kurvor är väldigt bra hjälp för att förstå vad man bör göra för trix för att få fram rätt svar. I a) är vi intresserade av \[Pr(0<Z<1)\] Vi är alltså ute efter den blåa skuggade delen av Figur 4.1.
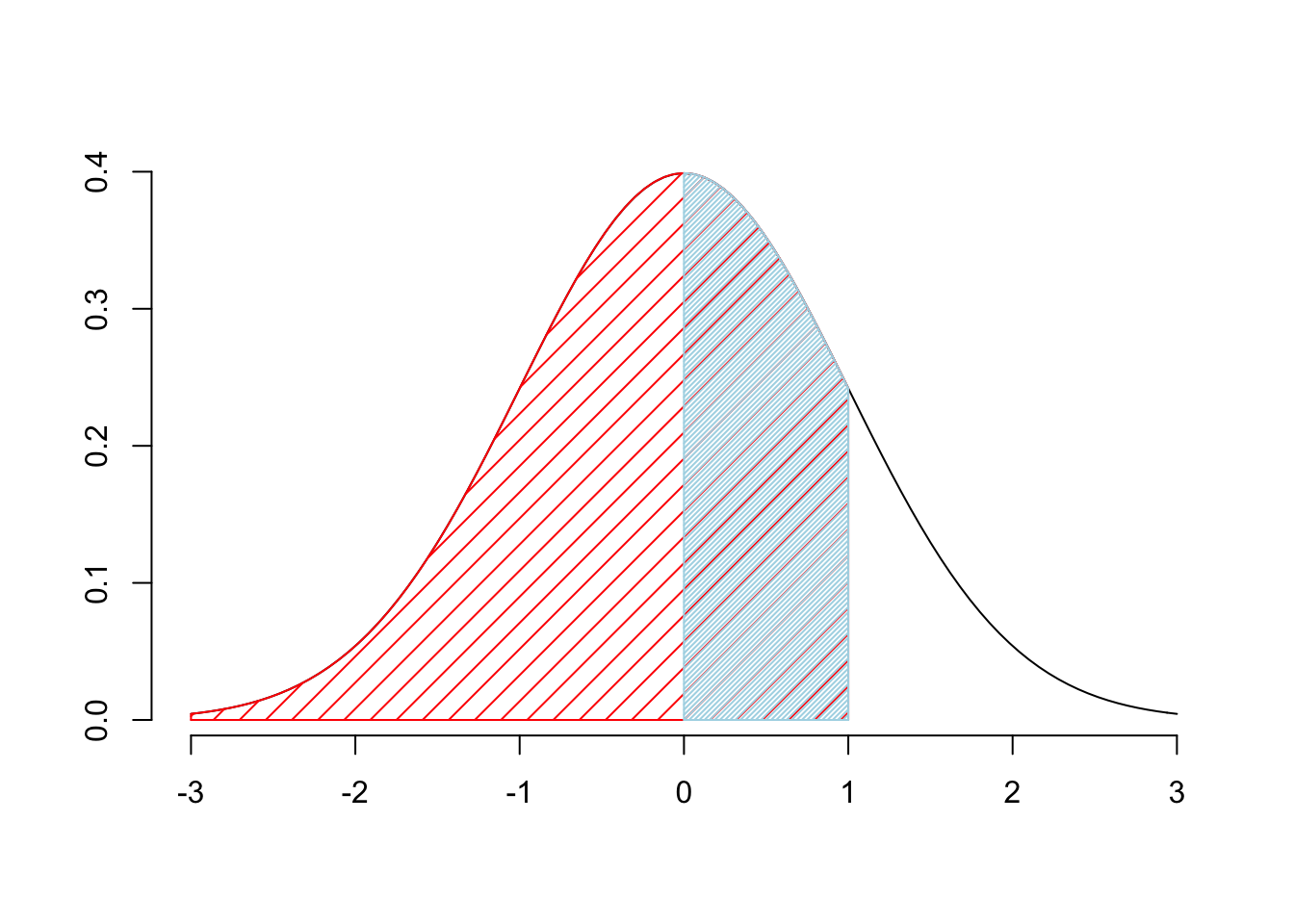
Figure 4.1: \(Pr(0<Z<1)\)
Första steget är att räkna ut skuggan under hela den skuggade delen, för att sedan subtrahera den röda skuggade delen. Kvar blir bara arean under den blåa skuggade delen.
det vill säga \[Pr(0<Z<1) \,=\, Pr(Z<1) \,- \,Pr(Z<0)\] eller
pnorm(1,mean = 0, sd = 1) - pnorm(0,mean = 0,sd = 1)
## [1] 0.3413447Faktum är att vi inte ens behöver specifiera mean=0 och sd=1 eftersom funktionen antar att du menar standard normal om inget annat anges
pnorm(2) - pnorm(1) # (ii)
## [1] 0.1359051
pnorm(2) - pnorm(-1) # (iii)
## [1] 0.8185946
pnorm(-1) # (iv)
## [1] 0.1586553Uppgift 40
Även detta är väldigt enkelt i R. Observera att om du tänkt att läsa om än bara en enda högskolepoäng mer än vad som krävs i statistik så är det lika bra att du här och nu memorerar att Z-värdet som har \(97,5 \%\) av arean till vänster om sig är \(1,96\). Slösa aldrig dyrbar tenta-tid till att gå till Tabell 5.2.B för att hitta 1,96. Eller 1.645 heller för den delen (\(95 \%\))
qnorm(0.975)
## [1] 1.959964
# Vi kan använda round() för att avrunda till önskat antal decimaler
round(qnorm(0.975), digits = 2)
## [1] 1.96
round(qnorm(0.33), digits = 2)
## [1] -0.44Uppgift 42
Vi använder oss återigen av pnorm()
I och med att normalfördelningne är symmetrisk så räcker det med att vi tittar på ena sidan och multiplicerar arean med två, precis som i facit. Det vill säga, vi hittar följande area och multiplicerar med två
skugga(-5,0,mu=10,sigma=4)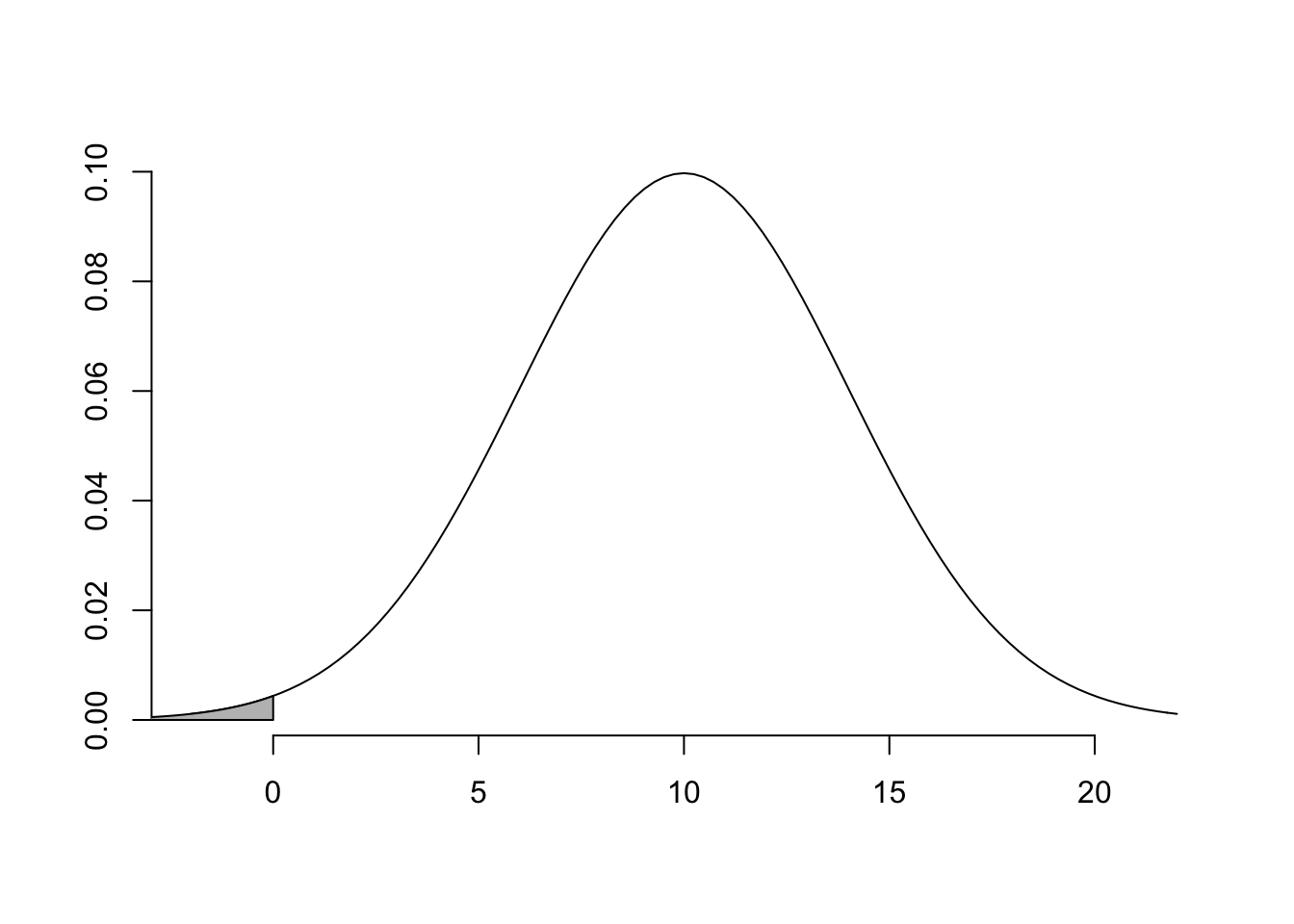
round(pnorm(0,mean=10,sd=4)*2,4)
## [1] 0.0124skugga(6,15,mu = 10, sigma = 4)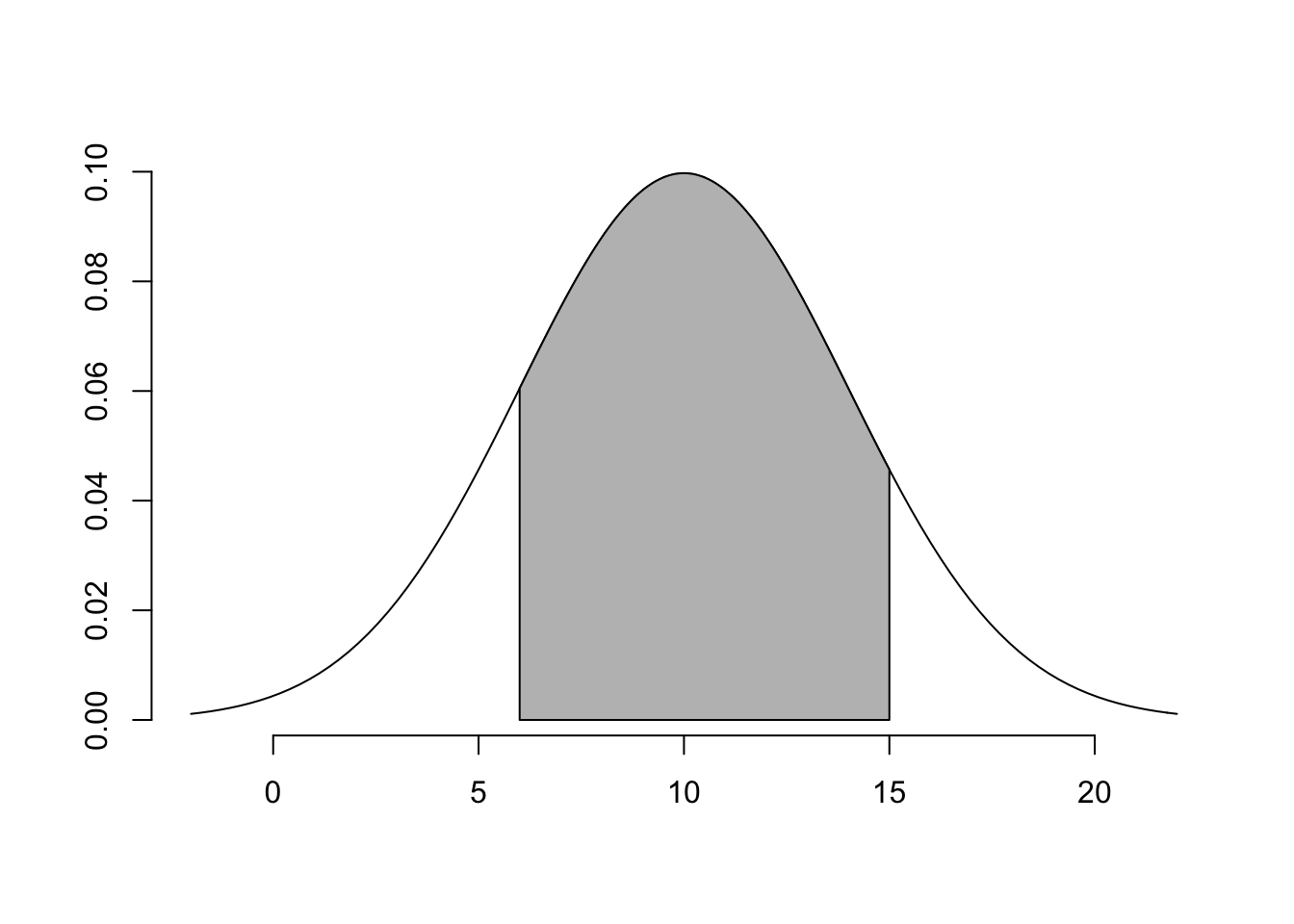
pnorm(15,10,4)-pnorm(6,10,4)
## [1] 0.7356954.2 Statistisk Inferens
Uppgift 11
Vi har ett stickprov om 8 hissåkare, och vi kan anta att vikten i populationen är normalfördelad. Vi kan således använda formeln
\[ \bar{x} \pm t_{n-1,\alpha/2}\frac{s}{\sqrt{n}} \]
stickprov <- c(71, 85, 68, 72, 58, 76, 74, 80)
xbar <- mean(stickprov) # stickprovsmedelvärde
n <- length(stickprov) # stickprovsstorlek
s = sd(stickprov) # stickprovsstandardavvikelse
t = qt(0.975, df = n-1) # t-förd. med n-1 frihetsgrader
xbar - t * s/sqrt(n)
## [1] 66.2376
xbar + t * s/sqrt(n)
## [1] 79.7624Uppgift 17
\[H_0 \: : \mu=9.75 \\ H_1 \: : \mu<9.75\]
stickprov <- c(9.0, 9.2, 9.5, 10.1, 9.8, 9.3, 9.7, 9.6, 10.0 ,9.2)
t.test(stickprov,
mu=9.75, # Noll-hypotesen
alternative = "less", # Vad för slags mothypotes har vi?
conf.level = 0.95) # Vilken signifikansnivå?
##
## One Sample t-test
##
## data: stickprov
## t = -1.8156, df = 9, p-value = 0.05141
## alternative hypothesis: true mean is less than 9.75
## 95 percent confidence interval:
## -Inf 9.752022
## sample estimates:
## mean of x
## 9.54Vi ser att \(t_{obs} = -1.8156\) och eftersom p-värdet inte är mindre än \(0.05\) så kan vi ej förkasta noll-hypotesen, då vår förvalda signifikansnivå var \(5 \%\).