Capítulo 3 Desarrollo del tema
3.1 Tratamiento de los datos
Para realizar el trabajo en cuestión, comenzaremos cargando la base de datos, la cual incluye el PIB trimestral en base 2013, los flujos de inversión extranjera directa en México, la tasa de referencia y la prima de riesgo país, la cual es el diferencial respecto a nuestra tasa y la tasa de fondos de la reserva federal.
Primero, cargalos las librerias correspondientes.
library(ggplot2)
library(dplyr)
library(stats)
library(MASS)
library(strucchange)
library(zoo)
library(sandwich)
library(urca)
library(lmtest)
library(vars)
library(echarts4r)
library(readxl)Leemos la base de datos:
basefinaltempo <- read_excel("basefinalstempo.xlsx")
head(basefinaltempo)## # A tibble: 6 x 6
## Periodo `PIB base 2013 … `Flujos de inve… `Tasa de refere…
## <dttm> <dbl> <dbl> <dbl>
## 1 2000-01-01 00:00:00 12725022. 4599101. 15.9
## 2 2000-04-01 00:00:00 12994569. 4857389. 15.6
## 3 2000-07-01 00:00:00 13008792. 3056946. 13.7
## 4 2000-10-01 00:00:00 13003302. 5733667 13.0
## 5 2001-01-01 00:00:00 12796119. 3597736. 14.2
## 6 2001-04-01 00:00:00 12967530. 5218830. 16.1
## # … with 2 more variables: `Tasa fondos federales` <dbl>, `Prima de
## # riesgo` <dbl>Ahora, los datos que tenemos respecto a la tasa de referencia y la prima de riesgo son mesuales a diferencia de los datos que tenemos para el PIB y los flujos de inversión, por lo que debemos hacer una transformación trimestral a estos datos de la siguiente manera:
# Leemos la base
attach(basefinaltempo)
# Convertimos a series de tiempo
tspib <- ts(na.omit(`PIB base 2013 (millones pesos)`), frequency = 4, start = 2000)
tsinver <- ts(na.omit(`Flujos de inversión (miles dolares)`), frequency = 4, start = 2000)
tstasa <- ts(`Tasa de referencia`, frequency = 12, start = 2000)
tsriesgo <- ts(`Prima de riesgo`, frequency = 12, start = 2000)
# Cambiamos la frecuencia de la prima de riesgo y la tasa de referencia
tstasatrim <- aggregate.ts(tstasa, nfrequency = 4, FUN = mean)
tsriesgotrim <- aggregate.ts(tsriesgo, nfrequency = 4, FUN = mean)
# Creamos otro data frame
basefinal <- data.frame(na.omit(Periodo), tspib, tsinver, tstasatrim, tsriesgotrim)3.2 Gráficas de las series
Ahora podemos comenzar a graficar los datos anteriormente obtenidos. En este caso, para poder hacer una gráfica dinámica haremos uso del paquete echarts4r
basefinal %>%
e_charts(x = na.omit.Periodo.) %>%
e_datazoom(
type = "slider",
toolbox = TRUE,
bottom = -5
) %>%
e_tooltip() %>%
e_title("PIB trimestral", "Millones de pesos") %>%
e_x_axis(na.omit.Periodo., axisPointer = list(show = TRUE)) %>%
e_line(tspib)basefinal %>%
e_charts(x = na.omit.Periodo.) %>%
e_datazoom(
type = "slider",
toolbox = TRUE,
bottom = -5
) %>%
e_tooltip() %>%
e_title("Flujos de inversión trimestrales", "Miles de dólares") %>%
e_x_axis(na.omit.Periodo., axisPointer = list(show = TRUE)) %>%
e_line(tsinver)basefinal %>%
e_charts(x = na.omit.Periodo.) %>%
e_datazoom(
type = "slider",
toolbox = TRUE,
bottom = -5
) %>%
e_tooltip() %>%
e_title("Tasa de referencia trimestral", "Porcentaje") %>%
e_x_axis(na.omit.Periodo., axisPointer = list(show = TRUE)) %>%
e_line(tstasatrim)basefinal %>%
e_charts(x = na.omit.Periodo.) %>%
e_datazoom(
type = "slider",
toolbox = TRUE,
bottom = -5
) %>%
e_tooltip() %>%
e_title("Prima de riesgo", "Porcentaje") %>%
e_x_axis(na.omit.Periodo., axisPointer = list(show = TRUE)) %>%
e_line(tsriesgotrim)Ahora, podemos graficar un gráfico con los logaritmos y las diferencias logaritmicas de las series:
# Logaritmos
logtspib <- log(tspib)
logtsinver <- log(tsinver)
logtstasatrim <- log(tstasatrim)
logtsriesgotrim <- log(tsriesgotrim)
baselog <- data.frame(na.omit(Periodo), logtspib, logtsinver, logtstasatrim, logtsriesgotrim)
# Gráfico de logaritmos
baselog %>%
e_charts(x = na.omit.Periodo.) %>%
e_datazoom(
type = "slider",
toolbox = TRUE,
bottom = -5
) %>%
e_tooltip() %>%
e_title("Logaritmos", "De las series") %>%
e_x_axis(na.omit.Periodo., axisPointer = list(show = TRUE)) %>%
e_line(logtspib) %>%
e_line(logtsinver) %>%
e_line(logtsriesgotrim) %>%
e_line(logtstasatrim) # Diferencias logarítmicas
dltspib <- diff(log(tspib, base = exp(1)),
lag = 1,
differences = 1)
dltsinver <- diff(log(tsinver, base = exp(1)),
lag = 1,
differences = 1)
dltstasatrim <- diff(log(tstasatrim, base = exp(1)),
lag = 1,
differences = 1)
dltsriesgotrim <- diff(log(tsriesgotrim, base = exp(1)),
lag = 1,
differences = 1)
Periodo1 <- Periodo[2:82]
basediflog <- data.frame(Periodo1, dltspib, dltsinver, dltstasatrim, dltsriesgotrim)
# Gráfico de las diferencias logaritmicas
basediflog %>%
e_charts(x = Periodo1) %>%
e_datazoom(
type = "slider",
toolbox = TRUE,
bottom = -5
) %>%
e_tooltip() %>%
e_title("Diferencias", "Logaritmicas de las series") %>%
e_x_axis(Periodo1, axisPointer = list(show = TRUE)) %>%
e_line(dltspib) %>%
e_line(dltsinver) %>%
e_line(dltstasatrim) %>%
e_line(dltsriesgotrim)3.3 Cointegración
En este punto nos hacemos la siguiente pregunta: Suponiendo que encontremos información significativa para el VAR que vayamos a realizar, ¿realmente hay una relación entre las series? o ¿es una mera casualidad? Para poder responder a esto vamos a hacer un análisis de cointegración, el cual nos permitirá averiguar si existe una relación de largo plazo entre las series.
Comencemos haciendo pruebas de raíces unitarias para las respectivas series:
# PIB en niveles
summary(ur.df(logtspib, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.179310 -0.007865 0.001527 0.011813 0.040671
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.1545006 2.6901434 1.173 0.245
## z.lag.1 -0.1928248 0.1648917 -1.169 0.246
## tt 0.0007999 0.0008874 0.901 0.370
## z.diff.lag1 0.2744328 0.2097310 1.308 0.195
## z.diff.lag2 0.1159183 0.1831685 0.633 0.529
## z.diff.lag3 -0.1861053 0.1788130 -1.041 0.302
## z.diff.lag4 0.7872838 0.1761046 4.471 2.94e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02724 on 70 degrees of freedom
## Multiple R-squared: 0.5568, Adjusted R-squared: 0.5188
## F-statistic: 14.66 on 6 and 70 DF, p-value: 9.249e-11
##
##
## Value of test-statistic is: -1.1694 1.3262 1.9708
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(logtspib, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.176184 -0.007386 0.002020 0.011237 0.040061
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.76102 0.43008 1.769 0.0811 .
## z.lag.1 -0.04607 0.02601 -1.771 0.0808 .
## z.diff.lag1 0.16638 0.17187 0.968 0.3363
## z.diff.lag2 0.04729 0.16637 0.284 0.7771
## z.diff.lag3 -0.24460 0.16640 -1.470 0.1460
## z.diff.lag4 0.76038 0.17333 4.387 3.91e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0272 on 71 degrees of freedom
## Multiple R-squared: 0.5516, Adjusted R-squared: 0.52
## F-statistic: 17.47 on 5 and 71 DF, p-value: 3.051e-11
##
##
## Value of test-statistic is: -1.7713 1.5872
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(logtspib, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.184885 -0.007287 0.000936 0.010281 0.047849
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -4.861e-05 2.368e-04 -0.205 0.8379
## z.diff.lag1 1.231e-01 1.726e-01 0.713 0.4780
## z.diff.lag2 6.650e-03 1.672e-01 0.040 0.9684
## z.diff.lag3 -2.833e-01 1.674e-01 -1.693 0.0948 .
## z.diff.lag4 7.393e-01 1.755e-01 4.214 7.18e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0276 on 72 degrees of freedom
## Multiple R-squared: 0.5332, Adjusted R-squared: 0.5008
## F-statistic: 16.45 on 5 and 72 DF, p-value: 8.457e-11
##
##
## Value of test-statistic is: -0.2053
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# PIB en diferencias
summary(ur.df(dltspib, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.176614 -0.008254 0.001882 0.011541 0.040284
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0090056 0.0072283 1.246 0.2170
## z.lag.1 -0.4078993 0.5554038 -0.734 0.4652
## tt -0.0002306 0.0001457 -1.583 0.1179
## z.diff.lag1 -0.4436276 0.5170188 -0.858 0.3938
## z.diff.lag2 -0.4368171 0.3994173 -1.094 0.2779
## z.diff.lag3 -0.7045915 0.3051397 -2.309 0.0239 *
## z.diff.lag4 0.0401435 0.2123606 0.189 0.8506
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02768 on 69 degrees of freedom
## Multiple R-squared: 0.8248, Adjusted R-squared: 0.8096
## F-statistic: 54.15 on 6 and 69 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -0.7344 1.3361 1.6415
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(dltspib, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.185571 -0.007359 0.001589 0.010122 0.047926
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.0004195 0.0041445 -0.101 0.9197
## z.lag.1 -0.4872476 0.5590610 -0.872 0.3864
## z.diff.lag1 -0.3549675 0.5194811 -0.683 0.4967
## z.diff.lag2 -0.3704724 0.4014666 -0.923 0.3593
## z.diff.lag3 -0.6596773 0.3070715 -2.148 0.0352 *
## z.diff.lag4 0.0669193 0.2139528 0.313 0.7554
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02798 on 70 degrees of freedom
## Multiple R-squared: 0.8185, Adjusted R-squared: 0.8055
## F-statistic: 63.11 on 5 and 70 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -0.8715 0.7348
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(dltspib, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.186129 -0.007517 0.001235 0.009943 0.047317
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -0.52305 0.42994 -1.217 0.2278
## z.diff.lag1 -0.32389 0.41610 -0.778 0.4389
## z.diff.lag2 -0.34850 0.33537 -1.039 0.3023
## z.diff.lag3 -0.64531 0.27037 -2.387 0.0197 *
## z.diff.lag4 0.07257 0.20509 0.354 0.7245
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02778 on 71 degrees of freedom
## Multiple R-squared: 0.8187, Adjusted R-squared: 0.806
## F-statistic: 64.13 on 5 and 71 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -1.2165
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# Flujos de inversión en niveles
summary(ur.df(logtsinver, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.10350 -0.16301 -0.01761 0.20770 1.02691
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 21.437599 4.931883 4.347 4.59e-05 ***
## z.lag.1 -1.385382 0.319756 -4.333 4.83e-05 ***
## tt 0.007356 0.002865 2.568 0.0124 *
## z.diff.lag1 0.355276 0.282406 1.258 0.2126
## z.diff.lag2 -0.032128 0.236120 -0.136 0.8922
## z.diff.lag3 -0.014432 0.168719 -0.086 0.9321
## z.diff.lag4 0.037743 0.120154 0.314 0.7544
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4094 on 70 degrees of freedom
## Multiple R-squared: 0.6008, Adjusted R-squared: 0.5665
## F-statistic: 17.56 on 6 and 70 DF, p-value: 2.755e-12
##
##
## Value of test-statistic is: -4.3326 6.4633 9.5161
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(logtsinver, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.09628 -0.20635 0.01363 0.21066 1.08177
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.01041 3.82347 3.403 0.00110 **
## z.lag.1 -0.82783 0.24378 -3.396 0.00112 **
## z.diff.lag1 -0.10518 0.22659 -0.464 0.64392
## z.diff.lag2 -0.39663 0.19597 -2.024 0.04675 *
## z.diff.lag3 -0.22663 0.15278 -1.483 0.14238
## z.diff.lag4 -0.07081 0.11682 -0.606 0.54631
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4252 on 71 degrees of freedom
## Multiple R-squared: 0.5632, Adjusted R-squared: 0.5324
## F-statistic: 18.31 on 5 and 71 DF, p-value: 1.246e-11
##
##
## Value of test-statistic is: -3.3957 5.9314
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(logtsinver, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.05094 -0.23111 0.01631 0.30899 1.21582
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 0.001649 0.003315 0.497 0.620357
## z.diff.lag1 -0.783575 0.115325 -6.794 2.64e-09 ***
## z.diff.lag2 -0.904422 0.136036 -6.648 4.89e-09 ***
## z.diff.lag3 -0.520934 0.134871 -3.862 0.000243 ***
## z.diff.lag4 -0.207349 0.117492 -1.765 0.081839 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4554 on 72 degrees of freedom
## Multiple R-squared: 0.492, Adjusted R-squared: 0.4567
## F-statistic: 13.95 on 5 and 72 DF, p-value: 1.583e-09
##
##
## Value of test-statistic is: 0.4975
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# Flujos de inversión en diferencias
summary(ur.df(dltsinver, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.04752 -0.22730 0.00812 0.24239 1.17570
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0549324 0.1162170 0.473 0.63794
## z.lag.1 -3.2868395 0.5954211 -5.520 5.55e-07 ***
## tt -0.0007657 0.0024238 -0.316 0.75302
## z.diff.lag1 1.5188940 0.5188720 2.927 0.00463 **
## z.diff.lag2 0.6277492 0.4006748 1.567 0.12175
## z.diff.lag3 0.1457140 0.2471626 0.590 0.55742
## z.diff.lag4 -0.0366458 0.1243675 -0.295 0.76914
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4628 on 69 degrees of freedom
## Multiple R-squared: 0.8072, Adjusted R-squared: 0.7905
## F-statistic: 48.16 on 6 and 69 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -5.5202 10.1627 15.237
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(dltsinver, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.04260 -0.22211 0.02101 0.24507 1.20439
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.02232 0.05301 0.421 0.67508
## z.lag.1 -3.27737 0.59083 -5.547 4.84e-07 ***
## z.diff.lag1 1.51072 0.51488 2.934 0.00452 **
## z.diff.lag2 0.62207 0.39769 1.564 0.12228
## z.diff.lag3 0.14283 0.24540 0.582 0.56243
## z.diff.lag4 -0.03733 0.12355 -0.302 0.76340
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4598 on 70 degrees of freedom
## Multiple R-squared: 0.807, Adjusted R-squared: 0.7932
## F-statistic: 58.52 on 5 and 70 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -5.5471 15.392
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(dltsinver, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.01914 -0.19992 0.04098 0.26505 1.22503
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -3.25319 0.58461 -5.565 4.37e-07 ***
## z.diff.lag1 1.49037 0.50963 2.924 0.00463 **
## z.diff.lag2 0.60626 0.39361 1.540 0.12795
## z.diff.lag3 0.13402 0.24309 0.551 0.58313
## z.diff.lag4 -0.04127 0.12248 -0.337 0.73715
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4571 on 71 degrees of freedom
## Multiple R-squared: 0.8065, Adjusted R-squared: 0.7929
## F-statistic: 59.19 on 5 and 71 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -5.5647
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# Tasa de referencia en niveles
summary(ur.df(dltstasatrim, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.40354 -0.03091 0.00398 0.03292 0.35563
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.0282839 0.0290058 -0.975 0.332909
## z.lag.1 -0.7615884 0.1978204 -3.850 0.000261 ***
## tt 0.0005120 0.0006027 0.850 0.398508
## z.diff.lag1 0.2327629 0.1827570 1.274 0.207072
## z.diff.lag2 0.0806992 0.1579235 0.511 0.610981
## z.diff.lag3 0.0250045 0.1305281 0.192 0.848646
## z.diff.lag4 0.1957784 0.1142476 1.714 0.091086 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1039 on 69 degrees of freedom
## Multiple R-squared: 0.3649, Adjusted R-squared: 0.3097
## F-statistic: 6.609 on 6 and 69 DF, p-value: 1.498e-05
##
##
## Value of test-statistic is: -3.8499 5.2131 7.8192
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(dltstasatrim, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.42331 -0.03125 0.00230 0.03424 0.34759
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.005862 0.012009 -0.488 0.626961
## z.lag.1 -0.688931 0.178023 -3.870 0.000242 ***
## z.diff.lag1 0.177139 0.170287 1.040 0.301809
## z.diff.lag2 0.038621 0.149657 0.258 0.797114
## z.diff.lag3 -0.003375 0.125930 -0.027 0.978695
## z.diff.lag4 0.178080 0.112109 1.588 0.116690
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1037 on 70 degrees of freedom
## Multiple R-squared: 0.3583, Adjusted R-squared: 0.3125
## F-statistic: 7.817 on 5 and 70 DF, p-value: 6.844e-06
##
##
## Value of test-statistic is: -3.8699 7.4885
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(dltstasatrim, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.42989 -0.03621 -0.00305 0.02764 0.34336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -0.677287 0.175469 -3.860 0.000247 ***
## z.diff.lag1 0.169099 0.168577 1.003 0.319221
## z.diff.lag2 0.032946 0.148403 0.222 0.824947
## z.diff.lag3 -0.007302 0.124997 -0.058 0.953582
## z.diff.lag4 0.175651 0.111396 1.577 0.119283
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1031 on 71 degrees of freedom
## Multiple R-squared: 0.3562, Adjusted R-squared: 0.3109
## F-statistic: 7.858 on 5 and 71 DF, p-value: 6.211e-06
##
##
## Value of test-statistic is: -3.8599
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# Tasa de referencia en diferencias
summary(ur.df(dltstasatrim, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.40354 -0.03091 0.00398 0.03292 0.35563
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.0282839 0.0290058 -0.975 0.332909
## z.lag.1 -0.7615884 0.1978204 -3.850 0.000261 ***
## tt 0.0005120 0.0006027 0.850 0.398508
## z.diff.lag1 0.2327629 0.1827570 1.274 0.207072
## z.diff.lag2 0.0806992 0.1579235 0.511 0.610981
## z.diff.lag3 0.0250045 0.1305281 0.192 0.848646
## z.diff.lag4 0.1957784 0.1142476 1.714 0.091086 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1039 on 69 degrees of freedom
## Multiple R-squared: 0.3649, Adjusted R-squared: 0.3097
## F-statistic: 6.609 on 6 and 69 DF, p-value: 1.498e-05
##
##
## Value of test-statistic is: -3.8499 5.2131 7.8192
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(dltstasatrim, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.42331 -0.03125 0.00230 0.03424 0.34759
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.005862 0.012009 -0.488 0.626961
## z.lag.1 -0.688931 0.178023 -3.870 0.000242 ***
## z.diff.lag1 0.177139 0.170287 1.040 0.301809
## z.diff.lag2 0.038621 0.149657 0.258 0.797114
## z.diff.lag3 -0.003375 0.125930 -0.027 0.978695
## z.diff.lag4 0.178080 0.112109 1.588 0.116690
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1037 on 70 degrees of freedom
## Multiple R-squared: 0.3583, Adjusted R-squared: 0.3125
## F-statistic: 7.817 on 5 and 70 DF, p-value: 6.844e-06
##
##
## Value of test-statistic is: -3.8699 7.4885
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(dltstasatrim, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.42989 -0.03621 -0.00305 0.02764 0.34336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -0.677287 0.175469 -3.860 0.000247 ***
## z.diff.lag1 0.169099 0.168577 1.003 0.319221
## z.diff.lag2 0.032946 0.148403 0.222 0.824947
## z.diff.lag3 -0.007302 0.124997 -0.058 0.953582
## z.diff.lag4 0.175651 0.111396 1.577 0.119283
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1031 on 71 degrees of freedom
## Multiple R-squared: 0.3562, Adjusted R-squared: 0.3109
## F-statistic: 7.858 on 5 and 71 DF, p-value: 6.211e-06
##
##
## Value of test-statistic is: -3.8599
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# Prima de riesgo en niveles
summary(ur.df(logtsriesgotrim, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.43430 -0.06524 0.00411 0.05942 0.32200
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.2999399 0.0842834 3.559 0.000674 ***
## z.lag.1 -0.2142459 0.0492489 -4.350 4.53e-05 ***
## tt 0.0003024 0.0007017 0.431 0.667798
## z.diff.lag1 0.5738764 0.1059068 5.419 8.03e-07 ***
## z.diff.lag2 -0.1435294 0.1260817 -1.138 0.258841
## z.diff.lag3 0.1516195 0.1193351 1.271 0.208100
## z.diff.lag4 0.2037718 0.1099860 1.853 0.068140 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.132 on 70 degrees of freedom
## Multiple R-squared: 0.4294, Adjusted R-squared: 0.3805
## F-statistic: 8.781 on 6 and 70 DF, p-value: 3.907e-07
##
##
## Value of test-statistic is: -4.3503 6.7103 10.0224
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(logtsriesgotrim, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.44273 -0.06050 0.00710 0.06343 0.31496
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.31749 0.07337 4.327 4.85e-05 ***
## z.lag.1 -0.21725 0.04847 -4.482 2.77e-05 ***
## z.diff.lag1 0.57956 0.10448 5.547 4.68e-07 ***
## z.diff.lag2 -0.13941 0.12500 -1.115 0.2685
## z.diff.lag3 0.15438 0.11848 1.303 0.1968
## z.diff.lag4 0.21050 0.10825 1.945 0.0558 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1313 on 71 degrees of freedom
## Multiple R-squared: 0.4279, Adjusted R-squared: 0.3876
## F-statistic: 10.62 on 5 and 71 DF, p-value: 1.215e-07
##
##
## Value of test-statistic is: -4.4821 10.0882
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(logtsriesgotrim, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.53842 -0.02311 0.02504 0.06919 0.34755
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -0.01193 0.01105 -1.079 0.284
## z.diff.lag1 0.57841 0.11663 4.959 4.56e-06 ***
## z.diff.lag2 -0.30602 0.13275 -2.305 0.024 *
## z.diff.lag3 0.11458 0.13186 0.869 0.388
## z.diff.lag4 0.06011 0.11444 0.525 0.601
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1466 on 72 degrees of freedom
## Multiple R-squared: 0.2789, Adjusted R-squared: 0.2288
## F-statistic: 5.57 on 5 and 72 DF, p-value: 0.0002156
##
##
## Value of test-statistic is: -1.079
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.61# Prima de riesgo en diferencias
summary(ur.df(dltsriesgotrim, type = "trend", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.47762 -0.05078 0.00212 0.04681 0.41022
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.0280815 0.0357609 -0.785 0.43499
## z.lag.1 -0.7632659 0.1674280 -4.559 2.17e-05 ***
## tt 0.0006204 0.0007473 0.830 0.40927
## z.diff.lag1 0.3386916 0.1598163 2.119 0.03767 *
## z.diff.lag2 0.1003025 0.1436841 0.698 0.48748
## z.diff.lag3 0.0943359 0.1180070 0.799 0.42680
## z.diff.lag4 0.3050209 0.1085843 2.809 0.00646 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1383 on 69 degrees of freedom
## Multiple R-squared: 0.409, Adjusted R-squared: 0.3576
## F-statistic: 7.958 on 6 and 69 DF, p-value: 1.551e-06
##
##
## Value of test-statistic is: -4.5588 6.9743 10.4424
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47summary(ur.df(dltsriesgotrim, type = "drift", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression drift
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.50085 -0.04303 0.00853 0.05118 0.39658
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.001486 0.015861 -0.094 0.92562
## z.lag.1 -0.728498 0.161746 -4.504 2.6e-05 ***
## z.diff.lag1 0.314097 0.156698 2.004 0.04889 *
## z.diff.lag2 0.081915 0.141652 0.578 0.56493
## z.diff.lag3 0.082325 0.116857 0.704 0.48346
## z.diff.lag4 0.296293 0.107834 2.748 0.00763 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.138 on 70 degrees of freedom
## Multiple R-squared: 0.4031, Adjusted R-squared: 0.3604
## F-statistic: 9.453 on 5 and 70 DF, p-value: 6.416e-07
##
##
## Value of test-statistic is: -4.504 10.1619
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau2 -3.51 -2.89 -2.58
## phi1 6.70 4.71 3.86summary(ur.df(dltsriesgotrim, type = "none", lags = 4))##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.50247 -0.04449 0.00704 0.04962 0.39526
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -0.72753 0.16028 -4.539 2.25e-05 ***
## z.diff.lag1 0.31346 0.15546 2.016 0.04754 *
## z.diff.lag2 0.08148 0.14058 0.580 0.56404
## z.diff.lag3 0.08201 0.11599 0.707 0.48187
## z.diff.lag4 0.29603 0.10704 2.766 0.00724 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.137 on 71 degrees of freedom
## Multiple R-squared: 0.4034, Adjusted R-squared: 0.3614
## F-statistic: 9.603 on 5 and 71 DF, p-value: 4.951e-07
##
##
## Value of test-statistic is: -4.539
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.6 -1.95 -1.613.4 Resumen de las pruebas ADF.
A partir de los datos anteriores podemos hacer la siguiente tabla resumen de las pruebas Dickey-Fuller aumentadas para saber si existe estacionariedad:
| Variable | ¿Es estacionaria? (al 5% de confianza) |
|---|---|
| PIB (niveles, trend) | No |
| PIB (niveles, drift) | No |
| PIB (niveles, none) | No |
| PIB (diferencias, trend) | No |
| PIB (diferencias, trend) | No |
| PIB (diferencias, trend) | Si |
| Flujos de inversion (niveles, trend) | Si |
| Flujos de inversion (niveles, drift) | No |
| Flujos de inversion (niveles, none) | No |
| Flujos de inversion (diferencias, trend) | Si |
| Flujos de inversion (diferencias, drift) | Si |
| Flujos de inversion (diferencias, none) | Si |
| Tasa referencia (niveles, trend) | No |
| Tasa referencia (niveles, drift) | Si |
| Tasa referencia (niveles, none) | Si |
| Tasa referencia (diferencias, trend) | No |
| Tasa referencia (diferencias, drift) | Si |
| Tasa referencia (diferencias, none) | Si |
| Prima de riesgo (niveles, trend) | Si |
| Prima de riesgo (niveles, drift) | Si |
| Prima de riesgo (niveles, none) | No |
| Prima de riesgo (diferencias, trend) | Si |
| Prima de riesgo (diferencias, drift) | Si |
| Prima de riesgo (diferencias, none) | Si |
Por lo que podemos observar, para algunas variables se requirió hacer una diferenciación, ignorar las tendencias, etc, para que pudiesen considerarse estacionarias, por lo que éstas últimas van a ser consideradas para el modelo en base a la siguiente idea: Si la variable era estacionaria en un primer instante, entonces se tomará esa, si no, se pasará a la variable siguiente (sin tendencia, en diferencia, etc).
3.5 El modelo VAR(p).
En este punto vamos a hacer un modelo VAR(p), pero para eso vamos a considerar las variables que son estacionarias de la siguiente manera:
Basecoint <- data.frame(cbind(dltspib, logtsinver, dltstasatrim, logtsriesgotrim))
Basecoint <- ts(Basecoint[2:82, ],
start = c(2000, 2),
freq = 4)Seleccionamos el VAR(p) ideal para el modelo:
#Quitamos notación científica
options(scipen = 999)
# Escogemos el VAR(p)
VARselect(Basecoint, lag.max = 12, type = "const")## $selection
## AIC(n) HQ(n) SC(n) FPE(n)
## 12 2 2 4
##
## $criteria
## 1 2 3
## AIC(n) -17.54739346245873 -18.429897451539542 -18.479934763352038
## HQ(n) -17.29048196854497 -17.967456762494784 -17.811964879176273
## SC(n) -16.89982635967691 -17.264276666532279 -16.796260296119321
## FPE(n) 0.00000002397209 0.000000009967673 0.000000009598002
## 4 5 6
## AIC(n) -18.59474261135750 -18.33978483369043 -18.25161912163087
## HQ(n) -17.72124353205073 -17.26075655925265 -16.96706165206209
## SC(n) -16.39301446189933 -15.62000300200681 -15.01378360772179
## FPE(n) 0.00000000875761 0.00000001174154 0.00000001359248
## 7 8 9
## AIC(n) -18.5128444945599 -18.44800413359683 -18.4527857364244
## HQ(n) -17.0227578298601 -16.75238827376604 -16.5516406814627
## SC(n) -14.7569552984253 -14.17406125523685 -13.6607891758390
## FPE(n) 0.0000000113868 0.00000001366708 0.0000000159816
## 10 11 12
## AIC(n) -18.40317982206268 -18.39414117897857 -19.10199246270616
## HQ(n) -16.29650557196988 -16.08193773375477 -16.58425982235136
## SC(n) -13.09312957925180 -12.56603725394224 -12.75583485544438
## FPE(n) 0.00000002089618 0.00000002834107 0.00000002090364¿Qué nos dicen estos resultados? A partir de ellos, si consideramos el criterio de Akaike entonces podemos decir que el mejor VAR para nuestro modelo es aquel que incluye 12 rezagos, es decir, que el valor actual va a depender del valor observado 12 periodos \(t-12\) en el pasado, por tanto, estimamos el VAR con 12 rezagos y constante de la siguiente manera:
VAR_p <- VAR(Basecoint, p = 12, type = "cons")
summary(VAR_p)##
## VAR Estimation Results:
## =========================
## Endogenous variables: dltspib, logtsinver, dltstasatrim, logtsriesgotrim
## Deterministic variables: const
## Sample size: 69
## Log Likelihood: 463.392
## Roots of the characteristic polynomial:
## 1.207 1.113 1.113 1.013 1.009 1.009 0.9878 0.9878 0.981 0.981 0.9617 0.9617 0.9601 0.9601 0.9591 0.9591 0.9549 0.9549 0.9508 0.9508 0.9508 0.9508 0.9417 0.9417 0.9383 0.9383 0.9317 0.9317 0.9301 0.9301 0.9252 0.9252 0.9196 0.9196 0.9192 0.9192 0.9152 0.9152 0.9107 0.9107 0.91 0.91 0.9054 0.9054 0.8901 0.8901 0.7589 0.7589
## Call:
## VAR(y = Basecoint, p = 12, type = "cons")
##
##
## Estimation results for equation dltspib:
## ========================================
## dltspib = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + dltspib.l5 + logtsinver.l5 + dltstasatrim.l5 + logtsriesgotrim.l5 + dltspib.l6 + logtsinver.l6 + dltstasatrim.l6 + logtsriesgotrim.l6 + dltspib.l7 + logtsinver.l7 + dltstasatrim.l7 + logtsriesgotrim.l7 + dltspib.l8 + logtsinver.l8 + dltstasatrim.l8 + logtsriesgotrim.l8 + dltspib.l9 + logtsinver.l9 + dltstasatrim.l9 + logtsriesgotrim.l9 + dltspib.l10 + logtsinver.l10 + dltstasatrim.l10 + logtsriesgotrim.l10 + dltspib.l11 + logtsinver.l11 + dltstasatrim.l11 + logtsriesgotrim.l11 + dltspib.l12 + logtsinver.l12 + dltstasatrim.l12 + logtsriesgotrim.l12 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 -0.2014646 0.6587126 -0.306 0.7629
## logtsinver.l1 -0.0140711 0.0196565 -0.716 0.4824
## dltstasatrim.l1 0.1011515 0.1785532 0.567 0.5774
## logtsriesgotrim.l1 -0.0473480 0.1208393 -0.392 0.6993
## dltspib.l2 0.4812716 0.7003510 0.687 0.4999
## logtsinver.l2 0.0126077 0.0196132 0.643 0.5276
## dltstasatrim.l2 -0.1146006 0.1729110 -0.663 0.5150
## logtsriesgotrim.l2 0.0366936 0.2119637 0.173 0.8643
## dltspib.l3 0.0029690 0.7860964 0.004 0.9970
## logtsinver.l3 -0.0196186 0.0187858 -1.044 0.3088
## dltstasatrim.l3 -0.1134883 0.1850000 -0.613 0.5465
## logtsriesgotrim.l3 0.0774171 0.2171794 0.356 0.7252
## dltspib.l4 0.2771942 0.8149467 0.340 0.7373
## logtsinver.l4 0.0147803 0.0230140 0.642 0.5280
## dltstasatrim.l4 0.1538001 0.1860306 0.827 0.4181
## logtsriesgotrim.l4 -0.1581222 0.2239581 -0.706 0.4883
## dltspib.l5 0.3658659 0.6562986 0.557 0.5834
## logtsinver.l5 -0.0380227 0.0217873 -1.745 0.0963 .
## dltstasatrim.l5 0.1641704 0.1938593 0.847 0.4071
## logtsriesgotrim.l5 -0.0175691 0.2278782 -0.077 0.9393
## dltspib.l6 -0.1548308 0.6313542 -0.245 0.8088
## logtsinver.l6 0.0113402 0.0221399 0.512 0.6141
## dltstasatrim.l6 -0.1796952 0.1886054 -0.953 0.3521
## logtsriesgotrim.l6 0.2154486 0.2181657 0.988 0.3352
## dltspib.l7 0.5527996 0.6482971 0.853 0.4039
## logtsinver.l7 0.0001234 0.0219229 0.006 0.9956
## dltstasatrim.l7 -0.0677084 0.1830464 -0.370 0.7153
## logtsriesgotrim.l7 -0.0657139 0.2416458 -0.272 0.7885
## dltspib.l8 0.4757907 0.5963839 0.798 0.4344
## logtsinver.l8 0.0045977 0.0207473 0.222 0.8269
## dltstasatrim.l8 0.0529604 0.1801831 0.294 0.7718
## logtsriesgotrim.l8 -0.1604342 0.2340763 -0.685 0.5010
## dltspib.l9 0.2394839 0.5808831 0.412 0.6845
## logtsinver.l9 -0.0035940 0.0205717 -0.175 0.8631
## dltstasatrim.l9 0.0089926 0.1644485 0.055 0.9569
## logtsriesgotrim.l9 0.1006606 0.2347576 0.429 0.6727
## dltspib.l10 -0.1810058 0.6026095 -0.300 0.7670
## logtsinver.l10 -0.0105844 0.0212855 -0.497 0.6244
## dltstasatrim.l10 0.0286168 0.1638772 0.175 0.8631
## logtsriesgotrim.l10 -0.0350576 0.2327684 -0.151 0.8818
## dltspib.l11 -0.1781911 0.6194266 -0.288 0.7766
## logtsinver.l11 -0.0043432 0.0207043 -0.210 0.8360
## dltstasatrim.l11 -0.2115231 0.1510459 -1.400 0.1767
## logtsriesgotrim.l11 0.1635062 0.2199520 0.743 0.4659
## dltspib.l12 0.8414786 0.5802109 1.450 0.1625
## logtsinver.l12 0.0085095 0.0205216 0.415 0.6828
## dltstasatrim.l12 0.0173716 0.0684724 0.254 0.8023
## logtsriesgotrim.l12 -0.1583343 0.1251712 -1.265 0.2204
## const 0.6585434 0.6894683 0.955 0.3509
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.03663 on 20 degrees of freedom
## Multiple R-Squared: 0.7592, Adjusted R-squared: 0.1812
## F-statistic: 1.313 on 48 and 20 DF, p-value: 0.2569
##
##
## Estimation results for equation logtsinver:
## ===========================================
## logtsinver = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + dltspib.l5 + logtsinver.l5 + dltstasatrim.l5 + logtsriesgotrim.l5 + dltspib.l6 + logtsinver.l6 + dltstasatrim.l6 + logtsriesgotrim.l6 + dltspib.l7 + logtsinver.l7 + dltstasatrim.l7 + logtsriesgotrim.l7 + dltspib.l8 + logtsinver.l8 + dltstasatrim.l8 + logtsriesgotrim.l8 + dltspib.l9 + logtsinver.l9 + dltstasatrim.l9 + logtsriesgotrim.l9 + dltspib.l10 + logtsinver.l10 + dltstasatrim.l10 + logtsriesgotrim.l10 + dltspib.l11 + logtsinver.l11 + dltstasatrim.l11 + logtsriesgotrim.l11 + dltspib.l12 + logtsinver.l12 + dltstasatrim.l12 + logtsriesgotrim.l12 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 -5.10034 6.79667 -0.750 0.46174
## logtsinver.l1 0.19820 0.20282 0.977 0.34014
## dltstasatrim.l1 -0.74598 1.84233 -0.405 0.68984
## logtsriesgotrim.l1 0.32227 1.24683 0.258 0.79868
## dltspib.l2 21.37290 7.22630 2.958 0.00778 **
## logtsinver.l2 -0.24048 0.20237 -1.188 0.24863
## dltstasatrim.l2 -2.01912 1.78411 -1.132 0.27114
## logtsriesgotrim.l2 1.15781 2.18706 0.529 0.60236
## dltspib.l3 1.90768 8.11103 0.235 0.81645
## logtsinver.l3 0.15340 0.19383 0.791 0.43801
## dltstasatrim.l3 0.07129 1.90885 0.037 0.97058
## logtsriesgotrim.l3 -1.73466 2.24088 -0.774 0.44793
## dltspib.l4 5.71269 8.40871 0.679 0.50469
## logtsinver.l4 -0.20007 0.23746 -0.843 0.40946
## dltstasatrim.l4 1.78310 1.91948 0.929 0.36399
## logtsriesgotrim.l4 -0.14668 2.31082 -0.063 0.95002
## dltspib.l5 6.55094 6.77176 0.967 0.34490
## logtsinver.l5 -0.12247 0.22480 -0.545 0.59193
## dltstasatrim.l5 1.75343 2.00026 0.877 0.39111
## logtsriesgotrim.l5 -0.52109 2.35127 -0.222 0.82686
## dltspib.l6 7.87652 6.51438 1.209 0.24073
## logtsinver.l6 0.25888 0.22844 1.133 0.27051
## dltstasatrim.l6 -3.46985 1.94605 -1.783 0.08977 .
## logtsriesgotrim.l6 2.73769 2.25106 1.216 0.23808
## dltspib.l7 8.67589 6.68920 1.297 0.20940
## logtsinver.l7 -0.03521 0.22620 -0.156 0.87786
## dltstasatrim.l7 2.01722 1.88869 1.068 0.29822
## logtsriesgotrim.l7 -2.74371 2.49333 -1.100 0.28422
## dltspib.l8 -1.42667 6.15355 -0.232 0.81901
## logtsinver.l8 0.22757 0.21407 1.063 0.30043
## dltstasatrim.l8 -0.82223 1.85915 -0.442 0.66304
## logtsriesgotrim.l8 1.35593 2.41522 0.561 0.58076
## dltspib.l9 13.85140 5.99361 2.311 0.03162 *
## logtsinver.l9 -0.06491 0.21226 -0.306 0.76292
## dltstasatrim.l9 0.85280 1.69680 0.503 0.62074
## logtsriesgotrim.l9 -0.74023 2.42225 -0.306 0.76307
## dltspib.l10 -6.72771 6.21779 -1.082 0.29212
## logtsinver.l10 0.26213 0.21963 1.194 0.24663
## dltstasatrim.l10 -2.46548 1.69090 -1.458 0.16034
## logtsriesgotrim.l10 2.79064 2.40173 1.162 0.25894
## dltspib.l11 6.64998 6.39131 1.040 0.31054
## logtsinver.l11 -0.04112 0.21363 -0.193 0.84929
## dltstasatrim.l11 0.94912 1.55851 0.609 0.54938
## logtsriesgotrim.l11 -3.93468 2.26949 -1.734 0.09836 .
## dltspib.l12 2.22642 5.98668 0.372 0.71388
## logtsinver.l12 0.31389 0.21174 1.482 0.15381
## dltstasatrim.l12 0.95375 0.70651 1.350 0.19211
## logtsriesgotrim.l12 1.51848 1.29153 1.176 0.25351
## const 4.18443 7.11401 0.588 0.56298
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.378 on 20 degrees of freedom
## Multiple R-Squared: 0.7952, Adjusted R-squared: 0.3035
## F-statistic: 1.617 on 48 and 20 DF, p-value: 0.1209
##
##
## Estimation results for equation dltstasatrim:
## =============================================
## dltstasatrim = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + dltspib.l5 + logtsinver.l5 + dltstasatrim.l5 + logtsriesgotrim.l5 + dltspib.l6 + logtsinver.l6 + dltstasatrim.l6 + logtsriesgotrim.l6 + dltspib.l7 + logtsinver.l7 + dltstasatrim.l7 + logtsriesgotrim.l7 + dltspib.l8 + logtsinver.l8 + dltstasatrim.l8 + logtsriesgotrim.l8 + dltspib.l9 + logtsinver.l9 + dltstasatrim.l9 + logtsriesgotrim.l9 + dltspib.l10 + logtsinver.l10 + dltstasatrim.l10 + logtsriesgotrim.l10 + dltspib.l11 + logtsinver.l11 + dltstasatrim.l11 + logtsriesgotrim.l11 + dltspib.l12 + logtsinver.l12 + dltstasatrim.l12 + logtsriesgotrim.l12 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 0.610438 1.433734 0.426 0.6748
## logtsinver.l1 -0.026648 0.042784 -0.623 0.5404
## dltstasatrim.l1 0.021024 0.388634 0.054 0.9574
## logtsriesgotrim.l1 0.294675 0.263015 1.120 0.2758
## dltspib.l2 0.974156 1.524363 0.639 0.5300
## logtsinver.l2 -0.016323 0.042690 -0.382 0.7062
## dltstasatrim.l2 0.375484 0.376353 0.998 0.3303
## logtsriesgotrim.l2 -0.701968 0.461354 -1.522 0.1438
## dltspib.l3 0.604945 1.710994 0.354 0.7274
## logtsinver.l3 -0.110236 0.040889 -2.696 0.0139 *
## dltstasatrim.l3 0.205875 0.402665 0.511 0.6148
## logtsriesgotrim.l3 0.344277 0.472706 0.728 0.4749
## dltspib.l4 -0.365250 1.773789 -0.206 0.8389
## logtsinver.l4 0.059687 0.050091 1.192 0.2474
## dltstasatrim.l4 -0.089317 0.404909 -0.221 0.8277
## logtsriesgotrim.l4 0.190131 0.487461 0.390 0.7006
## dltspib.l5 1.136101 1.428480 0.795 0.4358
## logtsinver.l5 -0.008681 0.047422 -0.183 0.8566
## dltstasatrim.l5 -0.046441 0.421948 -0.110 0.9135
## logtsriesgotrim.l5 -0.179790 0.495993 -0.362 0.7208
## dltspib.l6 0.664065 1.374187 0.483 0.6342
## logtsinver.l6 0.049436 0.048189 1.026 0.3172
## dltstasatrim.l6 0.212579 0.410513 0.518 0.6103
## logtsriesgotrim.l6 -0.359897 0.474853 -0.758 0.4573
## dltspib.l7 -0.769490 1.411064 -0.545 0.5916
## logtsinver.l7 -0.029784 0.047717 -0.624 0.5396
## dltstasatrim.l7 -0.100585 0.398413 -0.252 0.8033
## logtsriesgotrim.l7 0.654279 0.525959 1.244 0.2279
## dltspib.l8 0.829468 1.298072 0.639 0.5301
## logtsinver.l8 -0.032467 0.045158 -0.719 0.4805
## dltstasatrim.l8 0.026347 0.392181 0.067 0.9471
## logtsriesgotrim.l8 -0.395402 0.509483 -0.776 0.4468
## dltspib.l9 0.072709 1.264333 0.058 0.9547
## logtsinver.l9 0.045763 0.044776 1.022 0.3190
## dltstasatrim.l9 -0.079931 0.357934 -0.223 0.8256
## logtsriesgotrim.l9 0.209295 0.510967 0.410 0.6864
## dltspib.l10 0.260033 1.311622 0.198 0.8448
## logtsinver.l10 0.084801 0.046329 1.830 0.0821 .
## dltstasatrim.l10 -0.045006 0.356690 -0.126 0.9009
## logtsriesgotrim.l10 -0.245571 0.506637 -0.485 0.6331
## dltspib.l11 0.147895 1.348225 0.110 0.9137
## logtsinver.l11 0.052809 0.045064 1.172 0.2550
## dltstasatrim.l11 -0.016047 0.328762 -0.049 0.9616
## logtsriesgotrim.l11 0.140900 0.478741 0.294 0.7716
## dltspib.l12 -0.540866 1.262870 -0.428 0.6730
## logtsinver.l12 0.042355 0.044667 0.948 0.3543
## dltstasatrim.l12 -0.202684 0.149035 -1.360 0.1890
## logtsriesgotrim.l12 -0.018629 0.272444 -0.068 0.9462
## const -1.658911 1.500676 -1.105 0.2821
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.07974 on 20 degrees of freedom
## Multiple R-Squared: 0.8365, Adjusted R-squared: 0.4441
## F-statistic: 2.132 on 48 and 20 DF, p-value: 0.03369
##
##
## Estimation results for equation logtsriesgotrim:
## ================================================
## logtsriesgotrim = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + dltspib.l5 + logtsinver.l5 + dltstasatrim.l5 + logtsriesgotrim.l5 + dltspib.l6 + logtsinver.l6 + dltstasatrim.l6 + logtsriesgotrim.l6 + dltspib.l7 + logtsinver.l7 + dltstasatrim.l7 + logtsriesgotrim.l7 + dltspib.l8 + logtsinver.l8 + dltstasatrim.l8 + logtsriesgotrim.l8 + dltspib.l9 + logtsinver.l9 + dltstasatrim.l9 + logtsriesgotrim.l9 + dltspib.l10 + logtsinver.l10 + dltstasatrim.l10 + logtsriesgotrim.l10 + dltspib.l11 + logtsinver.l11 + dltstasatrim.l11 + logtsriesgotrim.l11 + dltspib.l12 + logtsinver.l12 + dltstasatrim.l12 + logtsriesgotrim.l12 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 -0.24349 1.92796 -0.126 0.9008
## logtsinver.l1 -0.05813 0.05753 -1.010 0.3244
## dltstasatrim.l1 -0.39923 0.52260 -0.764 0.4538
## logtsriesgotrim.l1 1.71893 0.35368 4.860 0.0000949 ***
## dltspib.l2 -1.13626 2.04983 -0.554 0.5855
## logtsinver.l2 -0.06851 0.05741 -1.193 0.2467
## dltstasatrim.l2 0.60814 0.50609 1.202 0.2435
## logtsriesgotrim.l2 -1.26676 0.62039 -2.042 0.0546 .
## dltspib.l3 -0.87718 2.30080 -0.381 0.7070
## logtsinver.l3 -0.12895 0.05498 -2.345 0.0294 *
## dltstasatrim.l3 -0.24995 0.54147 -0.462 0.6493
## logtsriesgotrim.l3 0.76069 0.63565 1.197 0.2454
## dltspib.l4 -0.05930 2.38524 -0.025 0.9804
## logtsinver.l4 0.04253 0.06736 0.631 0.5349
## dltstasatrim.l4 -0.64798 0.54449 -1.190 0.2480
## logtsriesgotrim.l4 0.15798 0.65550 0.241 0.8120
## dltspib.l5 1.98555 1.92090 1.034 0.3136
## logtsinver.l5 0.02495 0.06377 0.391 0.6998
## dltstasatrim.l5 -0.34870 0.56740 -0.615 0.5458
## logtsriesgotrim.l5 -0.29271 0.66697 -0.439 0.6655
## dltspib.l6 1.86167 1.84789 1.007 0.3257
## logtsinver.l6 0.02680 0.06480 0.414 0.6836
## dltstasatrim.l6 0.85544 0.55202 1.550 0.1369
## logtsriesgotrim.l6 -1.05840 0.63854 -1.658 0.1130
## dltspib.l7 -1.24795 1.89748 -0.658 0.5182
## logtsinver.l7 -0.01556 0.06417 -0.243 0.8108
## dltstasatrim.l7 0.25962 0.53575 0.485 0.6332
## logtsriesgotrim.l7 1.01470 0.70726 1.435 0.1668
## dltspib.l8 2.05665 1.74554 1.178 0.2525
## logtsinver.l8 -0.02512 0.06072 -0.414 0.6835
## dltstasatrim.l8 0.03859 0.52737 0.073 0.9424
## logtsriesgotrim.l8 -0.37190 0.68511 -0.543 0.5932
## dltspib.l9 -0.29318 1.70017 -0.172 0.8648
## logtsinver.l9 0.04526 0.06021 0.752 0.4610
## dltstasatrim.l9 -0.31547 0.48132 -0.655 0.5197
## logtsriesgotrim.l9 0.59313 0.68710 0.863 0.3982
## dltspib.l10 1.09670 1.76376 0.622 0.5411
## logtsinver.l10 0.14999 0.06230 2.408 0.0258 *
## dltstasatrim.l10 -0.01565 0.47965 -0.033 0.9743
## logtsriesgotrim.l10 -0.61013 0.68128 -0.896 0.3811
## dltspib.l11 2.10045 1.81298 1.159 0.2603
## logtsinver.l11 0.04686 0.06060 0.773 0.4484
## dltstasatrim.l11 0.01023 0.44209 0.023 0.9818
## logtsriesgotrim.l11 0.46442 0.64377 0.721 0.4790
## dltspib.l12 -1.94542 1.69820 -1.146 0.2655
## logtsinver.l12 0.06804 0.06006 1.133 0.2707
## dltstasatrim.l12 -0.06051 0.20041 -0.302 0.7658
## logtsriesgotrim.l12 -0.21063 0.36636 -0.575 0.5717
## const -1.56027 2.01798 -0.773 0.4485
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.1072 on 20 degrees of freedom
## Multiple R-Squared: 0.9737, Adjusted R-squared: 0.9106
## F-statistic: 15.42 on 48 and 20 DF, p-value: 0.000000008422
##
##
##
## Covariance matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 0.00134202 0.00009607 0.001457 0.0008971
## logtsinver 0.00009607 0.14287579 0.007433 0.0038369
## dltstasatrim 0.00145734 0.00743320 0.006358 0.0070629
## logtsriesgotrim 0.00089715 0.00383690 0.007063 0.0114965
##
## Correlation matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 1.000000 0.006938 0.4989 0.22840
## logtsinver 0.006938 1.000000 0.2466 0.09467
## dltstasatrim 0.498918 0.246629 1.0000 0.82613
## logtsriesgotrim 0.228404 0.094672 0.8261 1.00000Dados los resutados anteriores, no encontramos que haya variables significativas, por lo que en este caso vamos a utilzar el criterio de FPE y solo haremos uso de dos rezagos, tal que:
VAR_p <- VAR(Basecoint, p = 4, type = "cons")
summary(VAR_p)##
## VAR Estimation Results:
## =========================
## Endogenous variables: dltspib, logtsinver, dltstasatrim, logtsriesgotrim
## Deterministic variables: const
## Sample size: 77
## Log Likelihood: 336.154
## Roots of the characteristic polynomial:
## 0.9695 0.9578 0.9578 0.848 0.848 0.8462 0.8462 0.7018 0.7018 0.6915 0.6915 0.6193 0.6141 0.6141 0.5859 0.5859
## Call:
## VAR(y = Basecoint, p = 4, type = "cons")
##
##
## Estimation results for equation dltspib:
## ========================================
## dltspib = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 -0.0117156 0.2169478 -0.054 0.9571
## logtsinver.l1 -0.0097205 0.0086699 -1.121 0.2667
## dltstasatrim.l1 0.1040366 0.0712635 1.460 0.1495
## logtsriesgotrim.l1 -0.0920087 0.0527518 -1.744 0.0862 .
## dltspib.l2 -0.1130931 0.2137237 -0.529 0.5987
## logtsinver.l2 0.0006624 0.0086995 0.076 0.9396
## dltstasatrim.l2 -0.0625886 0.0864087 -0.724 0.4717
## logtsriesgotrim.l2 0.1567672 0.1036434 1.513 0.1356
## dltspib.l3 -0.3963185 0.2305794 -1.719 0.0908 .
## logtsinver.l3 -0.0070270 0.0080872 -0.869 0.3884
## dltstasatrim.l3 -0.0118137 0.0720188 -0.164 0.8703
## logtsriesgotrim.l3 -0.1097246 0.1045912 -1.049 0.2983
## dltspib.l4 0.5849384 0.2377680 2.460 0.0168 *
## logtsinver.l4 -0.0081518 0.0079557 -1.025 0.3096
## dltstasatrim.l4 0.0241823 0.0327199 0.739 0.4627
## logtsriesgotrim.l4 0.0302155 0.0530320 0.570 0.5710
## const 0.4039127 0.2633387 1.534 0.1303
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.02812 on 60 degrees of freedom
## Multiple R-Squared: 0.5951, Adjusted R-squared: 0.4872
## F-statistic: 5.512 on 16 and 60 DF, p-value: 0.0000005301
##
##
## Estimation results for equation logtsinver:
## ===========================================
## logtsinver = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 0.35028 3.06149 0.114 0.909292
## logtsinver.l1 0.04459 0.12235 0.364 0.716812
## dltstasatrim.l1 -0.41960 1.00564 -0.417 0.677989
## logtsriesgotrim.l1 0.70980 0.74441 0.954 0.344161
## dltspib.l2 7.43215 3.01599 2.464 0.016612 *
## logtsinver.l2 -0.14641 0.12276 -1.193 0.237728
## dltstasatrim.l2 -1.24411 1.21937 -1.020 0.311689
## logtsriesgotrim.l2 0.29910 1.46258 0.205 0.838652
## dltspib.l3 2.64714 3.25385 0.814 0.419125
## logtsinver.l3 0.08492 0.11412 0.744 0.459713
## dltstasatrim.l3 1.81737 1.01630 1.788 0.078790 .
## logtsriesgotrim.l3 -2.16232 1.47595 -1.465 0.148133
## dltspib.l4 -4.68795 3.35529 -1.397 0.167505
## logtsinver.l4 0.09372 0.11227 0.835 0.407128
## dltstasatrim.l4 0.42329 0.46173 0.917 0.362945
## logtsriesgotrim.l4 1.15869 0.74837 1.548 0.126811
## const 14.47574 3.71614 3.895 0.000249 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.3968 on 60 degrees of freedom
## Multiple R-Squared: 0.3808, Adjusted R-squared: 0.2156
## F-statistic: 2.306 on 16 and 60 DF, p-value: 0.0103
##
##
## Estimation results for equation dltstasatrim:
## =============================================
## dltstasatrim = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 1.130461 0.773269 1.462 0.149
## logtsinver.l1 -0.002904 0.030902 -0.094 0.925
## dltstasatrim.l1 0.353763 0.254005 1.393 0.169
## logtsriesgotrim.l1 -0.002988 0.188024 -0.016 0.987
## dltspib.l2 1.227401 0.761777 1.611 0.112
## logtsinver.l2 0.037107 0.031008 1.197 0.236
## dltstasatrim.l2 0.177187 0.307987 0.575 0.567
## logtsriesgotrim.l2 -0.312412 0.369417 -0.846 0.401
## dltspib.l3 0.033006 0.821856 0.040 0.968
## logtsinver.l3 -0.027742 0.028825 -0.962 0.340
## dltstasatrim.l3 -0.272792 0.256697 -1.063 0.292
## logtsriesgotrim.l3 0.451490 0.372795 1.211 0.231
## dltspib.l4 -0.335074 0.847479 -0.395 0.694
## logtsinver.l4 0.031617 0.028357 1.115 0.269
## dltstasatrim.l4 0.146742 0.116624 1.258 0.213
## logtsriesgotrim.l4 -0.235369 0.189023 -1.245 0.218
## const -0.468128 0.938621 -0.499 0.620
##
##
## Residual standard error: 0.1002 on 60 degrees of freedom
## Multiple R-Squared: 0.4427, Adjusted R-squared: 0.294
## F-statistic: 2.978 on 16 and 60 DF, p-value: 0.001133
##
##
## Estimation results for equation logtsriesgotrim:
## ================================================
## logtsriesgotrim = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 0.47836 1.01045 0.473 0.63763
## logtsinver.l1 0.02903 0.04038 0.719 0.47506
## dltstasatrim.l1 -0.47806 0.33191 -1.440 0.15497
## logtsriesgotrim.l1 1.68812 0.24569 6.871 0.00000000415 ***
## dltspib.l2 1.05956 0.99543 1.064 0.29140
## logtsinver.l2 0.03470 0.04052 0.857 0.39512
## dltstasatrim.l2 0.46557 0.40245 1.157 0.25193
## logtsriesgotrim.l2 -1.35124 0.48273 -2.799 0.00688 **
## dltspib.l3 -0.84207 1.07394 -0.784 0.43607
## logtsinver.l3 -0.02952 0.03767 -0.784 0.43630
## dltstasatrim.l3 -0.56164 0.33543 -1.674 0.09926 .
## logtsriesgotrim.l3 0.98453 0.48714 2.021 0.04774 *
## dltspib.l4 -1.22934 1.10742 -1.110 0.27139
## logtsinver.l4 0.02050 0.03705 0.553 0.58214
## dltstasatrim.l4 0.18740 0.15239 1.230 0.22361
## logtsriesgotrim.l4 -0.52188 0.24700 -2.113 0.03878 *
## const -0.56604 1.22651 -0.461 0.64611
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.131 on 60 degrees of freedom
## Multiple R-Squared: 0.8937, Adjusted R-squared: 0.8653
## F-statistic: 31.51 on 16 and 60 DF, p-value: < 0.00000000000000022
##
##
##
## Covariance matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 0.00079077 0.00001045 0.0006397 0.000142
## logtsinver 0.00001045 0.15747313 -0.0029951 -0.006892
## dltstasatrim 0.00063969 -0.00299512 0.0100462 0.011111
## logtsriesgotrim 0.00014198 -0.00689176 0.0111112 0.017154
##
## Correlation matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 1.0000000 0.0009363 0.2270 0.03855
## logtsinver 0.0009363 1.0000000 -0.0753 -0.13260
## dltstasatrim 0.2269562 -0.0753026 1.0000 0.84640
## logtsriesgotrim 0.0385488 -0.1325998 0.8464 1.00000summary(VAR_p, equation = "dltspib")##
## VAR Estimation Results:
## =========================
## Endogenous variables: dltspib, logtsinver, dltstasatrim, logtsriesgotrim
## Deterministic variables: const
## Sample size: 77
## Log Likelihood: 336.154
## Roots of the characteristic polynomial:
## 0.9695 0.9578 0.9578 0.848 0.848 0.8462 0.8462 0.7018 0.7018 0.6915 0.6915 0.6193 0.6141 0.6141 0.5859 0.5859
## Call:
## VAR(y = Basecoint, p = 4, type = "cons")
##
##
## Estimation results for equation dltspib:
## ========================================
## dltspib = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 -0.0117156 0.2169478 -0.054 0.9571
## logtsinver.l1 -0.0097205 0.0086699 -1.121 0.2667
## dltstasatrim.l1 0.1040366 0.0712635 1.460 0.1495
## logtsriesgotrim.l1 -0.0920087 0.0527518 -1.744 0.0862 .
## dltspib.l2 -0.1130931 0.2137237 -0.529 0.5987
## logtsinver.l2 0.0006624 0.0086995 0.076 0.9396
## dltstasatrim.l2 -0.0625886 0.0864087 -0.724 0.4717
## logtsriesgotrim.l2 0.1567672 0.1036434 1.513 0.1356
## dltspib.l3 -0.3963185 0.2305794 -1.719 0.0908 .
## logtsinver.l3 -0.0070270 0.0080872 -0.869 0.3884
## dltstasatrim.l3 -0.0118137 0.0720188 -0.164 0.8703
## logtsriesgotrim.l3 -0.1097246 0.1045912 -1.049 0.2983
## dltspib.l4 0.5849384 0.2377680 2.460 0.0168 *
## logtsinver.l4 -0.0081518 0.0079557 -1.025 0.3096
## dltstasatrim.l4 0.0241823 0.0327199 0.739 0.4627
## logtsriesgotrim.l4 0.0302155 0.0530320 0.570 0.5710
## const 0.4039127 0.2633387 1.534 0.1303
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.02812 on 60 degrees of freedom
## Multiple R-Squared: 0.5951, Adjusted R-squared: 0.4872
## F-statistic: 5.512 on 16 and 60 DF, p-value: 0.0000005301
##
##
##
## Covariance matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 0.00079077 0.00001045 0.0006397 0.000142
## logtsinver 0.00001045 0.15747313 -0.0029951 -0.006892
## dltstasatrim 0.00063969 -0.00299512 0.0100462 0.011111
## logtsriesgotrim 0.00014198 -0.00689176 0.0111112 0.017154
##
## Correlation matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 1.0000000 0.0009363 0.2270 0.03855
## logtsinver 0.0009363 1.0000000 -0.0753 -0.13260
## dltstasatrim 0.2269562 -0.0753026 1.0000 0.84640
## logtsriesgotrim 0.0385488 -0.1325998 0.8464 1.00000summary(VAR_p, equation = "logtsinver")##
## VAR Estimation Results:
## =========================
## Endogenous variables: dltspib, logtsinver, dltstasatrim, logtsriesgotrim
## Deterministic variables: const
## Sample size: 77
## Log Likelihood: 336.154
## Roots of the characteristic polynomial:
## 0.9695 0.9578 0.9578 0.848 0.848 0.8462 0.8462 0.7018 0.7018 0.6915 0.6915 0.6193 0.6141 0.6141 0.5859 0.5859
## Call:
## VAR(y = Basecoint, p = 4, type = "cons")
##
##
## Estimation results for equation logtsinver:
## ===========================================
## logtsinver = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 0.35028 3.06149 0.114 0.909292
## logtsinver.l1 0.04459 0.12235 0.364 0.716812
## dltstasatrim.l1 -0.41960 1.00564 -0.417 0.677989
## logtsriesgotrim.l1 0.70980 0.74441 0.954 0.344161
## dltspib.l2 7.43215 3.01599 2.464 0.016612 *
## logtsinver.l2 -0.14641 0.12276 -1.193 0.237728
## dltstasatrim.l2 -1.24411 1.21937 -1.020 0.311689
## logtsriesgotrim.l2 0.29910 1.46258 0.205 0.838652
## dltspib.l3 2.64714 3.25385 0.814 0.419125
## logtsinver.l3 0.08492 0.11412 0.744 0.459713
## dltstasatrim.l3 1.81737 1.01630 1.788 0.078790 .
## logtsriesgotrim.l3 -2.16232 1.47595 -1.465 0.148133
## dltspib.l4 -4.68795 3.35529 -1.397 0.167505
## logtsinver.l4 0.09372 0.11227 0.835 0.407128
## dltstasatrim.l4 0.42329 0.46173 0.917 0.362945
## logtsriesgotrim.l4 1.15869 0.74837 1.548 0.126811
## const 14.47574 3.71614 3.895 0.000249 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.3968 on 60 degrees of freedom
## Multiple R-Squared: 0.3808, Adjusted R-squared: 0.2156
## F-statistic: 2.306 on 16 and 60 DF, p-value: 0.0103
##
##
##
## Covariance matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 0.00079077 0.00001045 0.0006397 0.000142
## logtsinver 0.00001045 0.15747313 -0.0029951 -0.006892
## dltstasatrim 0.00063969 -0.00299512 0.0100462 0.011111
## logtsriesgotrim 0.00014198 -0.00689176 0.0111112 0.017154
##
## Correlation matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 1.0000000 0.0009363 0.2270 0.03855
## logtsinver 0.0009363 1.0000000 -0.0753 -0.13260
## dltstasatrim 0.2269562 -0.0753026 1.0000 0.84640
## logtsriesgotrim 0.0385488 -0.1325998 0.8464 1.00000summary(VAR_p, equation = "dltstasatrim")##
## VAR Estimation Results:
## =========================
## Endogenous variables: dltspib, logtsinver, dltstasatrim, logtsriesgotrim
## Deterministic variables: const
## Sample size: 77
## Log Likelihood: 336.154
## Roots of the characteristic polynomial:
## 0.9695 0.9578 0.9578 0.848 0.848 0.8462 0.8462 0.7018 0.7018 0.6915 0.6915 0.6193 0.6141 0.6141 0.5859 0.5859
## Call:
## VAR(y = Basecoint, p = 4, type = "cons")
##
##
## Estimation results for equation dltstasatrim:
## =============================================
## dltstasatrim = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 1.130461 0.773269 1.462 0.149
## logtsinver.l1 -0.002904 0.030902 -0.094 0.925
## dltstasatrim.l1 0.353763 0.254005 1.393 0.169
## logtsriesgotrim.l1 -0.002988 0.188024 -0.016 0.987
## dltspib.l2 1.227401 0.761777 1.611 0.112
## logtsinver.l2 0.037107 0.031008 1.197 0.236
## dltstasatrim.l2 0.177187 0.307987 0.575 0.567
## logtsriesgotrim.l2 -0.312412 0.369417 -0.846 0.401
## dltspib.l3 0.033006 0.821856 0.040 0.968
## logtsinver.l3 -0.027742 0.028825 -0.962 0.340
## dltstasatrim.l3 -0.272792 0.256697 -1.063 0.292
## logtsriesgotrim.l3 0.451490 0.372795 1.211 0.231
## dltspib.l4 -0.335074 0.847479 -0.395 0.694
## logtsinver.l4 0.031617 0.028357 1.115 0.269
## dltstasatrim.l4 0.146742 0.116624 1.258 0.213
## logtsriesgotrim.l4 -0.235369 0.189023 -1.245 0.218
## const -0.468128 0.938621 -0.499 0.620
##
##
## Residual standard error: 0.1002 on 60 degrees of freedom
## Multiple R-Squared: 0.4427, Adjusted R-squared: 0.294
## F-statistic: 2.978 on 16 and 60 DF, p-value: 0.001133
##
##
##
## Covariance matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 0.00079077 0.00001045 0.0006397 0.000142
## logtsinver 0.00001045 0.15747313 -0.0029951 -0.006892
## dltstasatrim 0.00063969 -0.00299512 0.0100462 0.011111
## logtsriesgotrim 0.00014198 -0.00689176 0.0111112 0.017154
##
## Correlation matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 1.0000000 0.0009363 0.2270 0.03855
## logtsinver 0.0009363 1.0000000 -0.0753 -0.13260
## dltstasatrim 0.2269562 -0.0753026 1.0000 0.84640
## logtsriesgotrim 0.0385488 -0.1325998 0.8464 1.00000summary(VAR_p, equation = "logtsriesgotrim")##
## VAR Estimation Results:
## =========================
## Endogenous variables: dltspib, logtsinver, dltstasatrim, logtsriesgotrim
## Deterministic variables: const
## Sample size: 77
## Log Likelihood: 336.154
## Roots of the characteristic polynomial:
## 0.9695 0.9578 0.9578 0.848 0.848 0.8462 0.8462 0.7018 0.7018 0.6915 0.6915 0.6193 0.6141 0.6141 0.5859 0.5859
## Call:
## VAR(y = Basecoint, p = 4, type = "cons")
##
##
## Estimation results for equation logtsriesgotrim:
## ================================================
## logtsriesgotrim = dltspib.l1 + logtsinver.l1 + dltstasatrim.l1 + logtsriesgotrim.l1 + dltspib.l2 + logtsinver.l2 + dltstasatrim.l2 + logtsriesgotrim.l2 + dltspib.l3 + logtsinver.l3 + dltstasatrim.l3 + logtsriesgotrim.l3 + dltspib.l4 + logtsinver.l4 + dltstasatrim.l4 + logtsriesgotrim.l4 + const
##
## Estimate Std. Error t value Pr(>|t|)
## dltspib.l1 0.47836 1.01045 0.473 0.63763
## logtsinver.l1 0.02903 0.04038 0.719 0.47506
## dltstasatrim.l1 -0.47806 0.33191 -1.440 0.15497
## logtsriesgotrim.l1 1.68812 0.24569 6.871 0.00000000415 ***
## dltspib.l2 1.05956 0.99543 1.064 0.29140
## logtsinver.l2 0.03470 0.04052 0.857 0.39512
## dltstasatrim.l2 0.46557 0.40245 1.157 0.25193
## logtsriesgotrim.l2 -1.35124 0.48273 -2.799 0.00688 **
## dltspib.l3 -0.84207 1.07394 -0.784 0.43607
## logtsinver.l3 -0.02952 0.03767 -0.784 0.43630
## dltstasatrim.l3 -0.56164 0.33543 -1.674 0.09926 .
## logtsriesgotrim.l3 0.98453 0.48714 2.021 0.04774 *
## dltspib.l4 -1.22934 1.10742 -1.110 0.27139
## logtsinver.l4 0.02050 0.03705 0.553 0.58214
## dltstasatrim.l4 0.18740 0.15239 1.230 0.22361
## logtsriesgotrim.l4 -0.52188 0.24700 -2.113 0.03878 *
## const -0.56604 1.22651 -0.461 0.64611
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.131 on 60 degrees of freedom
## Multiple R-Squared: 0.8937, Adjusted R-squared: 0.8653
## F-statistic: 31.51 on 16 and 60 DF, p-value: < 0.00000000000000022
##
##
##
## Covariance matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 0.00079077 0.00001045 0.0006397 0.000142
## logtsinver 0.00001045 0.15747313 -0.0029951 -0.006892
## dltstasatrim 0.00063969 -0.00299512 0.0100462 0.011111
## logtsriesgotrim 0.00014198 -0.00689176 0.0111112 0.017154
##
## Correlation matrix of residuals:
## dltspib logtsinver dltstasatrim logtsriesgotrim
## dltspib 1.0000000 0.0009363 0.2270 0.03855
## logtsinver 0.0009363 1.0000000 -0.0753 -0.13260
## dltstasatrim 0.2269562 -0.0753026 1.0000 0.84640
## logtsriesgotrim 0.0385488 -0.1325998 0.8464 1.000003.6 Pruebas de diagnóstico
Ahora, en este punto haremos uso de pruebas de diagnóstico para saber si existe normalidad, no hay autocorrelación, hay homocedasticidad, etc.
# Tests de diagnóstico
# Normalidad:
normality.test(VAR_p)## $JB
##
## JB-Test (multivariate)
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 3080.6, df = 8, p-value < 0.00000000000000022
##
##
## $Skewness
##
## Skewness only (multivariate)
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 250.59, df = 4, p-value < 0.00000000000000022
##
##
## $Kurtosis
##
## Kurtosis only (multivariate)
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 2830, df = 4, p-value < 0.00000000000000022# Autocorrelacion Serial:
serial.test(VAR_p, lags.bg = 1, type = "BG")##
## Breusch-Godfrey LM test
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 18.115, df = 16, p-value = 0.3172serial.test(VAR_p, lags.bg = 2, type = "BG")##
## Breusch-Godfrey LM test
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 40.964, df = 32, p-value = 0.1331serial.test(VAR_p, lags.bg = 3, type = "BG")##
## Breusch-Godfrey LM test
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 62.78, df = 48, p-value = 0.07449serial.test(VAR_p, lags.bg = 4, type = "BG")##
## Breusch-Godfrey LM test
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 87.948, df = 64, p-value = 0.02524# Homocedasticidad
arch.test(VAR_p, lags.multi = 2)##
## ARCH (multivariate)
##
## data: Residuals of VAR object VAR_p
## Chi-squared = 275.66, df = 200, p-value = 0.0003106Hasta este punto encontramos dos problemas principales, los cuales son:
- La varianza de la serie conjunta no es homocedastica.
- No hay normalidad en las observaciones.
Además de encontrar autocorrelación serial de orden 4, sin embargo, considerando que nuestro modelo es un VAR(p) de órden 4, entonces podemos hacer caso omiso de la autocorrelación. Por otra parte, el objetivo de esta investigación se centra más en analizar el impulso respuesta de la serie, más que el VAR(p) en si, por lo que vamos a obviar por el momento las pruebas que no pasa el modelo y continuaremos analizando el impulso respuesta a continuación.
3.7 Impulso respuesta
En este caso queremos saber la respuesta que generarían las variables en 12 periodos en el futuro (3 años a futuro, considerando que tenemos datos trimestrales), por lo que hacemos lo siguiente:
# Impulso respuesta
# Primer ecuación
IR_dltspib <- irf(VAR_p, n.ahead = 12, boot = TRUE,
ci = 0.95, response = "dltspib")
IR_dltspib##
## Impulse response coefficients
## $dltspib
## dltspib
## [1,] 0.0281206996
## [2,] 0.0015690235
## [3,] -0.0007481169
## [4,] -0.0122286307
## [5,] 0.0174922111
## [6,] 0.0036117430
## [7,] 0.0037076068
## [8,] -0.0124467551
## [9,] 0.0120993566
## [10,] 0.0037272017
## [11,] 0.0057871554
## [12,] -0.0120427665
## [13,] 0.0072132576
##
## $logtsinver
## dltspib
## [1,] 0.0000000000
## [2,] -0.0030464509
## [3,] -0.0011215891
## [4,] -0.0012968599
## [5,] -0.0018187583
## [6,] -0.0022550907
## [7,] 0.0006155434
## [8,] -0.0008147708
## [9,] -0.0008727427
## [10,] -0.0021558898
## [11,] 0.0003963214
## [12,] -0.0004333519
## [13,] -0.0003153344
##
## $dltstasatrim
## dltspib
## [1,] 0.0000000000
## [2,] -0.0001467543
## [3,] 0.0015265014
## [4,] -0.0048462242
## [5,] -0.0009836208
## [6,] -0.0011896839
## [7,] 0.0032688128
## [8,] -0.0027496127
## [9,] -0.0005237674
## [10,] -0.0008684296
## [11,] 0.0042545097
## [12,] -0.0007431342
## [13,] 0.0001175243
##
## $logtsriesgotrim
## dltspib
## [1,] 0.0000000000
## [2,] -0.0060778869
## [3,] -0.0003096003
## [4,] -0.0018860688
## [5,] -0.0008027568
## [6,] -0.0050740646
## [7,] -0.0012015531
## [8,] -0.0009398889
## [9,] 0.0013530169
## [10,] -0.0029567815
## [11,] -0.0002115661
## [12,] -0.0001450671
## [13,] 0.0023764225
##
##
## Lower Band, CI= 0.95
## $dltspib
## dltspib
## [1,] 0.0122213698
## [2,] -0.0042674838
## [3,] -0.0074752956
## [4,] -0.0194034580
## [5,] 0.0060905750
## [6,] -0.0036148741
## [7,] -0.0021542965
## [8,] -0.0180783168
## [9,] 0.0031396548
## [10,] -0.0032857592
## [11,] -0.0019906252
## [12,] -0.0171428170
## [13,] -0.0001249223
##
## $logtsinver
## dltspib
## [1,] 0.000000000
## [2,] -0.008384933
## [3,] -0.005864085
## [4,] -0.004581675
## [5,] -0.006809240
## [6,] -0.005280147
## [7,] -0.002855727
## [8,] -0.004306556
## [9,] -0.005484615
## [10,] -0.004344302
## [11,] -0.002247495
## [12,] -0.003008251
## [13,] -0.004821137
##
## $dltstasatrim
## dltspib
## [1,] 0.000000000
## [2,] -0.007314664
## [3,] -0.006502190
## [4,] -0.009923220
## [5,] -0.006122769
## [6,] -0.006217463
## [7,] -0.004239504
## [8,] -0.006317390
## [9,] -0.005514109
## [10,] -0.005363973
## [11,] -0.001098867
## [12,] -0.003922228
## [13,] -0.004173028
##
## $logtsriesgotrim
## dltspib
## [1,] 0.0000000000
## [2,] -0.0097554383
## [3,] -0.0068066505
## [4,] -0.0050257021
## [5,] -0.0047724416
## [6,] -0.0089008602
## [7,] -0.0070246589
## [8,] -0.0032058623
## [9,] -0.0020900186
## [10,] -0.0065227140
## [11,] -0.0052706961
## [12,] -0.0031535406
## [13,] -0.0009668054
##
##
## Upper Band, CI= 0.95
## $dltspib
## dltspib
## [1,] 0.039027299
## [2,] 0.005101827
## [3,] 0.004230325
## [4,] -0.004632939
## [5,] 0.023071688
## [6,] 0.010800087
## [7,] 0.008911690
## [8,] -0.003308741
## [9,] 0.017731205
## [10,] 0.010205114
## [11,] 0.012854287
## [12,] -0.002894856
## [13,] 0.014363961
##
## $logtsinver
## dltspib
## [1,] 0.000000000
## [2,] 0.002731214
## [3,] 0.005557569
## [4,] 0.002970020
## [5,] 0.003822892
## [6,] 0.005050239
## [7,] 0.004734325
## [8,] 0.003291351
## [9,] 0.003176007
## [10,] 0.003078533
## [11,] 0.004312876
## [12,] 0.003336954
## [13,] 0.002741595
##
## $dltstasatrim
## dltspib
## [1,] 0.000000000
## [2,] 0.006039706
## [3,] 0.005912353
## [4,] 0.002459758
## [5,] 0.004988492
## [6,] 0.005529094
## [7,] 0.007025424
## [8,] 0.004277386
## [9,] 0.004826245
## [10,] 0.004801412
## [11,] 0.006311598
## [12,] 0.003396726
## [13,] 0.005770062
##
## $logtsriesgotrim
## dltspib
## [1,] 0.0000000000
## [2,] 0.0012859499
## [3,] 0.0053504312
## [4,] 0.0028050483
## [5,] 0.0035883591
## [6,] 0.0005720276
## [7,] 0.0041840521
## [8,] 0.0036827998
## [9,] 0.0045699342
## [10,] 0.0022729956
## [11,] 0.0042914331
## [12,] 0.0033166928
## [13,] 0.0049276756plot(IR_dltspib)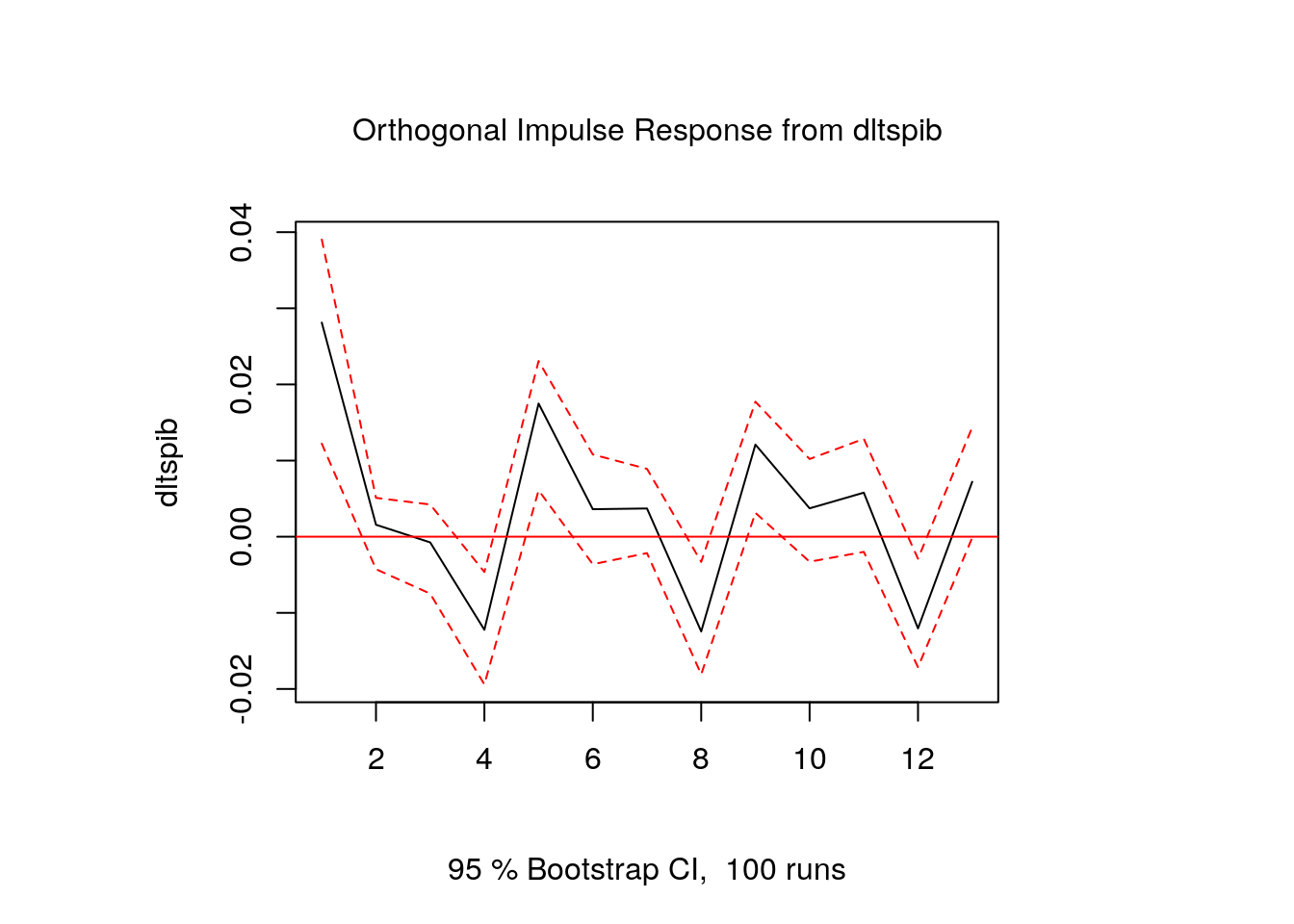
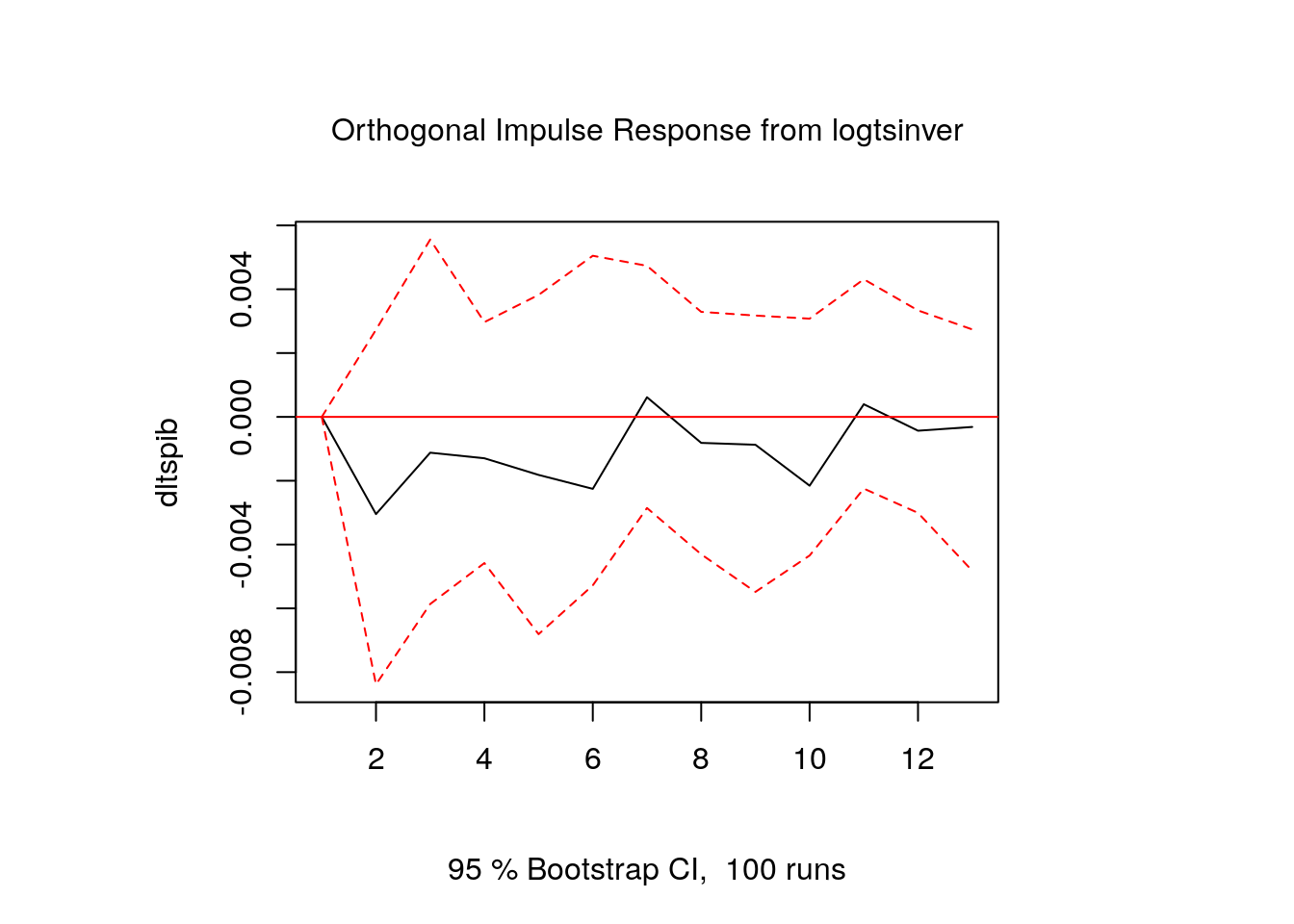
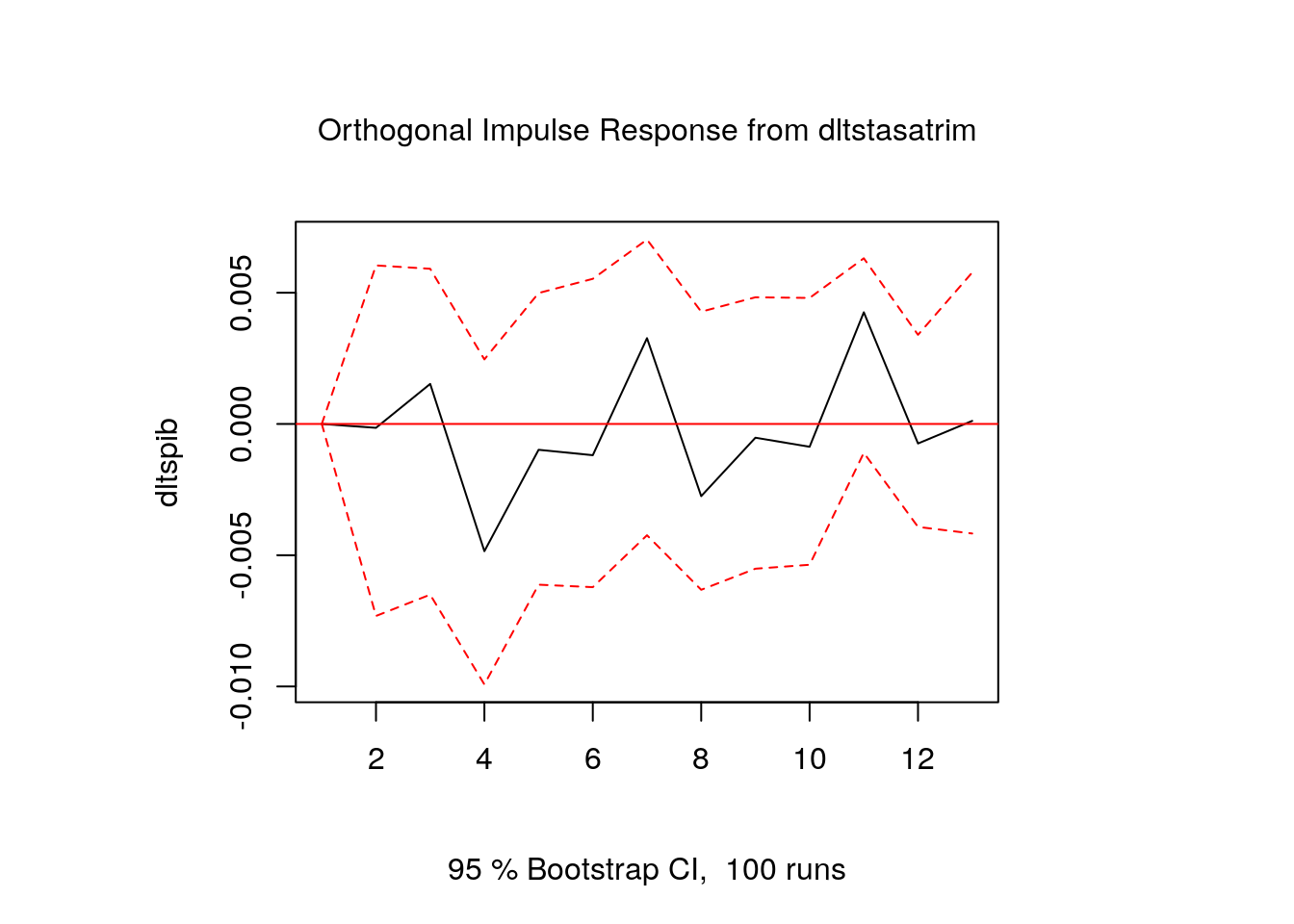
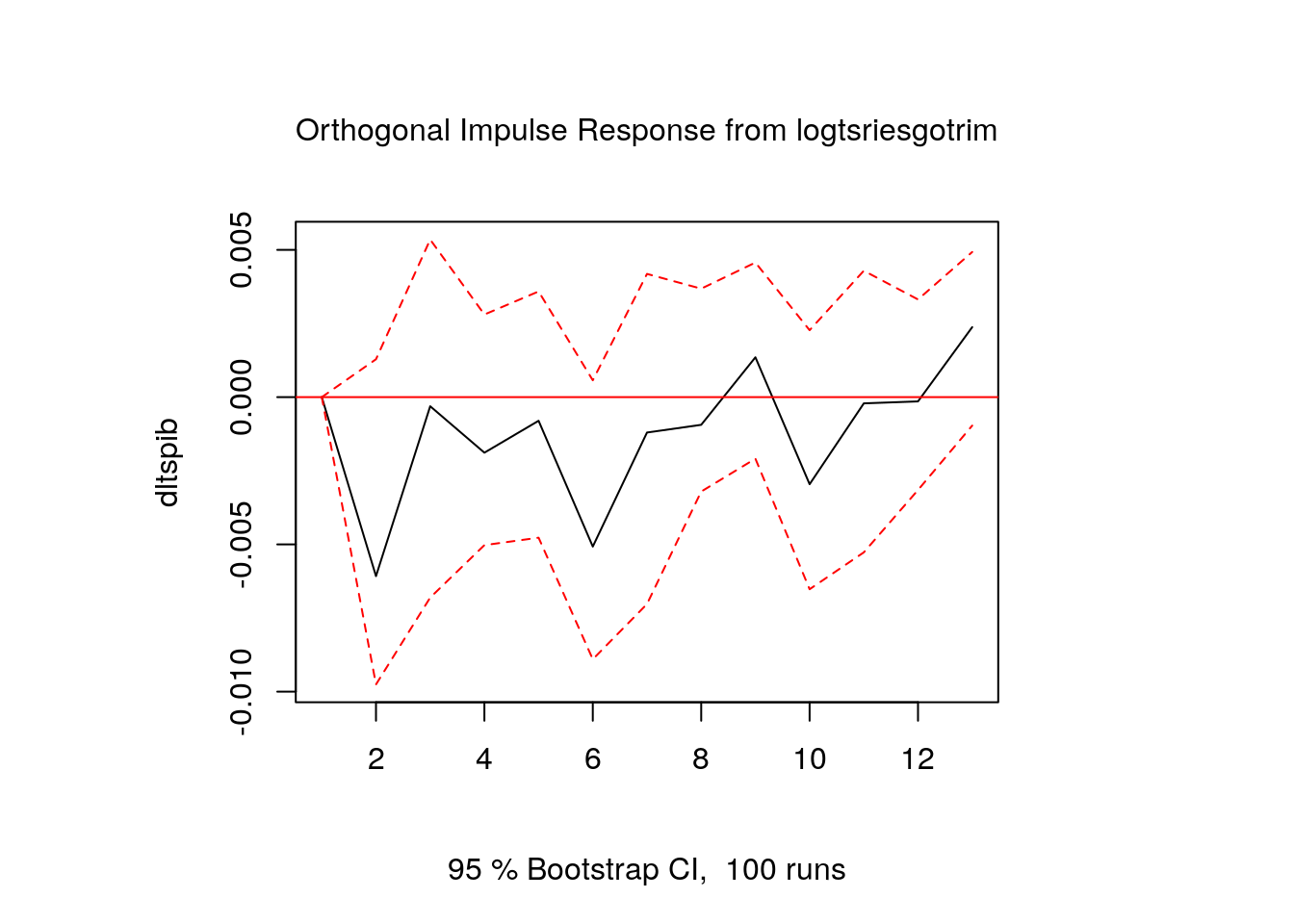
# Segunda ecuación
IR_logtsinver <- irf(VAR_p, n.ahead = 12, boot = TRUE,
ci = 0.95, response = "logtsinver")
IR_logtsinver##
## Impulse response coefficients
## $dltspib
## logtsinver
## [1,] 0.000371553
## [2,] 0.003905215
## [3,] 0.174053530
## [4,] 0.079358446
## [5,] -0.151310759
## [6,] -0.100469245
## [7,] 0.148353869
## [8,] 0.153468463
## [9,] -0.072619927
## [10,] -0.106099208
## [11,] 0.098733380
## [12,] 0.168968464
## [13,] -0.006610274
##
## $logtsinver
## logtsinver
## [1,] 0.3968286644
## [2,] 0.0085390571
## [3,] -0.0630504163
## [4,] 0.0323298077
## [5,] 0.0219402287
## [6,] -0.0075097566
## [7,] -0.0137190023
## [8,] -0.0018416605
## [9,] 0.0150051565
## [10,] 0.0036387162
## [11,] -0.0161945661
## [12,] -0.0179045024
## [13,] -0.0008903528
##
## $dltstasatrim
## logtsinver
## [1,] 0.0000000000
## [2,] 0.0384054004
## [3,] 0.0004127262
## [4,] 0.0163045020
## [5,] 0.0482312241
## [6,] -0.0258460051
## [7,] -0.0487948500
## [8,] -0.0016730882
## [9,] 0.0193084574
## [10,] -0.0234488956
## [11,] -0.0440532652
## [12,] 0.0032696763
## [13,] 0.0377412514
##
## $logtsriesgotrim
## logtsinver
## [1,] 0.000000000
## [2,] 0.046887831
## [3,] 0.098954693
## [4,] -0.075971855
## [5,] -0.060702627
## [6,] 0.028172933
## [7,] -0.022813760
## [8,] -0.076420727
## [9,] -0.043112651
## [10,] 0.003608355
## [11,] -0.011114673
## [12,] -0.047419355
## [13,] -0.035226824
##
##
## Lower Band, CI= 0.95
## $dltspib
## logtsinver
## [1,] -0.092093416
## [2,] -0.087473632
## [3,] 0.058076438
## [4,] -0.022106721
## [5,] -0.259747296
## [6,] -0.168061846
## [7,] 0.024443811
## [8,] 0.037877650
## [9,] -0.168287356
## [10,] -0.169844180
## [11,] 0.009014486
## [12,] 0.042435579
## [13,] -0.103629735
##
## $logtsinver
## logtsinver
## [1,] 0.26327663
## [2,] -0.09000495
## [3,] -0.12465380
## [4,] -0.04495567
## [5,] -0.06942559
## [6,] -0.06768717
## [7,] -0.05472155
## [8,] -0.06694799
## [9,] -0.05554013
## [10,] -0.06475270
## [11,] -0.07437627
## [12,] -0.05831589
## [13,] -0.06161913
##
## $dltstasatrim
## logtsinver
## [1,] 0.00000000
## [2,] -0.04165430
## [3,] -0.08794927
## [4,] -0.08115508
## [5,] -0.02535264
## [6,] -0.09595800
## [7,] -0.11901663
## [8,] -0.06123373
## [9,] -0.03862249
## [10,] -0.08086646
## [11,] -0.09703985
## [12,] -0.04987584
## [13,] -0.02297074
##
## $logtsriesgotrim
## logtsinver
## [1,] 0.00000000
## [2,] -0.03837320
## [3,] -0.00306613
## [4,] -0.14796444
## [5,] -0.11980950
## [6,] -0.04620345
## [7,] -0.09545330
## [8,] -0.12720737
## [9,] -0.09275824
## [10,] -0.05160177
## [11,] -0.07048079
## [12,] -0.09273060
## [13,] -0.09160637
##
##
## Upper Band, CI= 0.95
## $dltspib
## logtsinver
## [1,] 0.079217715
## [2,] 0.077027240
## [3,] 0.253939638
## [4,] 0.137828284
## [5,] -0.051638226
## [6,] -0.004009862
## [7,] 0.233374487
## [8,] 0.258702812
## [9,] 0.004065537
## [10,] -0.002308429
## [11,] 0.204825056
## [12,] 0.257303983
## [13,] 0.073305659
##
## $logtsinver
## logtsinver
## [1,] 0.41196663
## [2,] 0.06763041
## [3,] 0.01348908
## [4,] 0.08947298
## [5,] 0.10455063
## [6,] 0.05682323
## [7,] 0.07087566
## [8,] 0.05989654
## [9,] 0.07101142
## [10,] 0.06156927
## [11,] 0.04720624
## [12,] 0.03222381
## [13,] 0.04590514
##
## $dltstasatrim
## logtsinver
## [1,] 0.00000000
## [2,] 0.10165503
## [3,] 0.06720699
## [4,] 0.10598942
## [5,] 0.14447302
## [6,] 0.05122629
## [7,] 0.01566961
## [8,] 0.08033864
## [9,] 0.07811666
## [10,] 0.03596416
## [11,] 0.01520236
## [12,] 0.07457858
## [13,] 0.07759022
##
## $logtsriesgotrim
## logtsinver
## [1,] 0.0000000000
## [2,] 0.1131732217
## [3,] 0.1710909824
## [4,] -0.0002395182
## [5,] 0.0157793326
## [6,] 0.0870911203
## [7,] 0.0308461461
## [8,] -0.0046517881
## [9,] 0.0379648978
## [10,] 0.0550060708
## [11,] 0.0438304997
## [12,] 0.0209246659
## [13,] 0.0408045467plot(IR_logtsinver)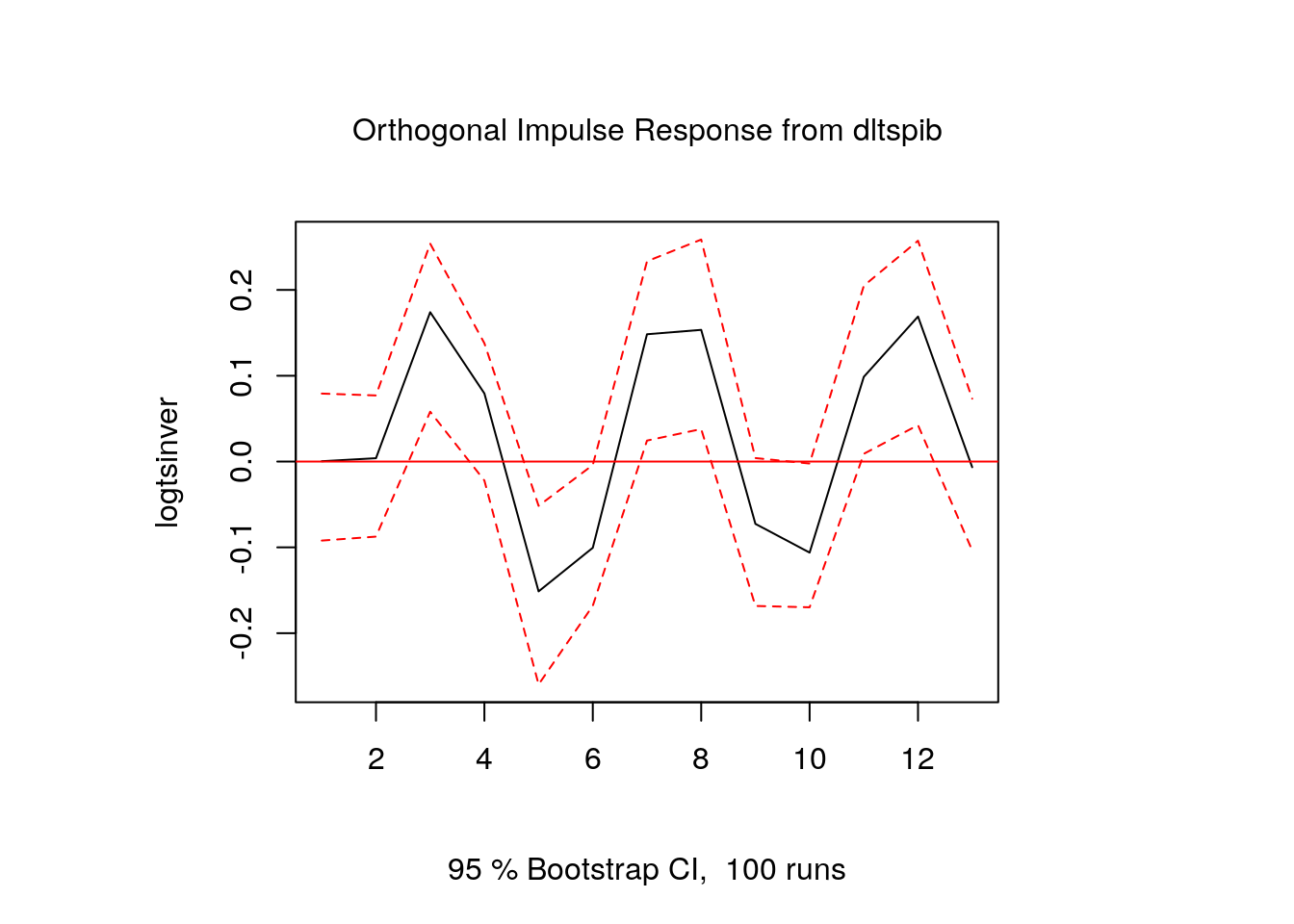
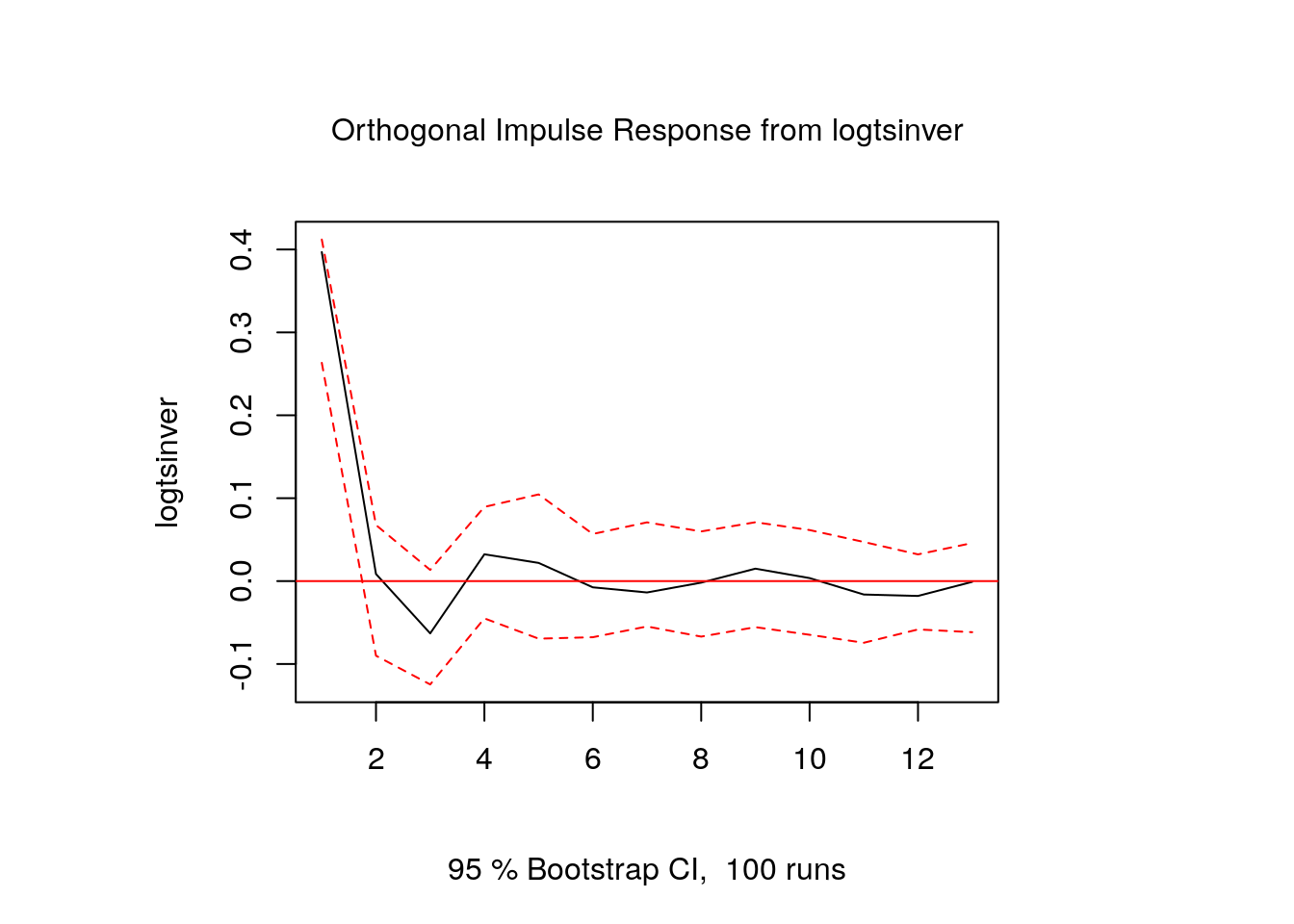
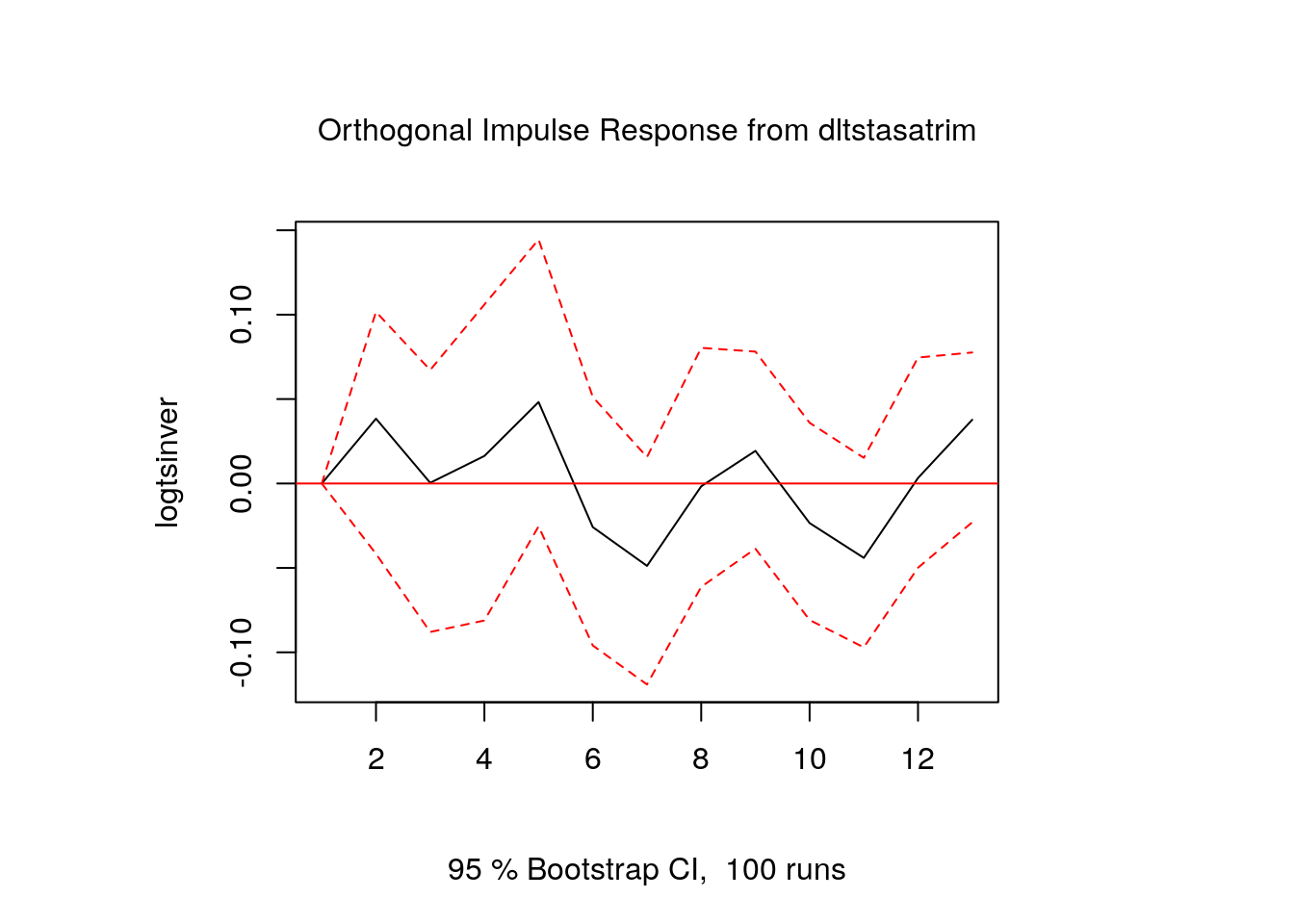
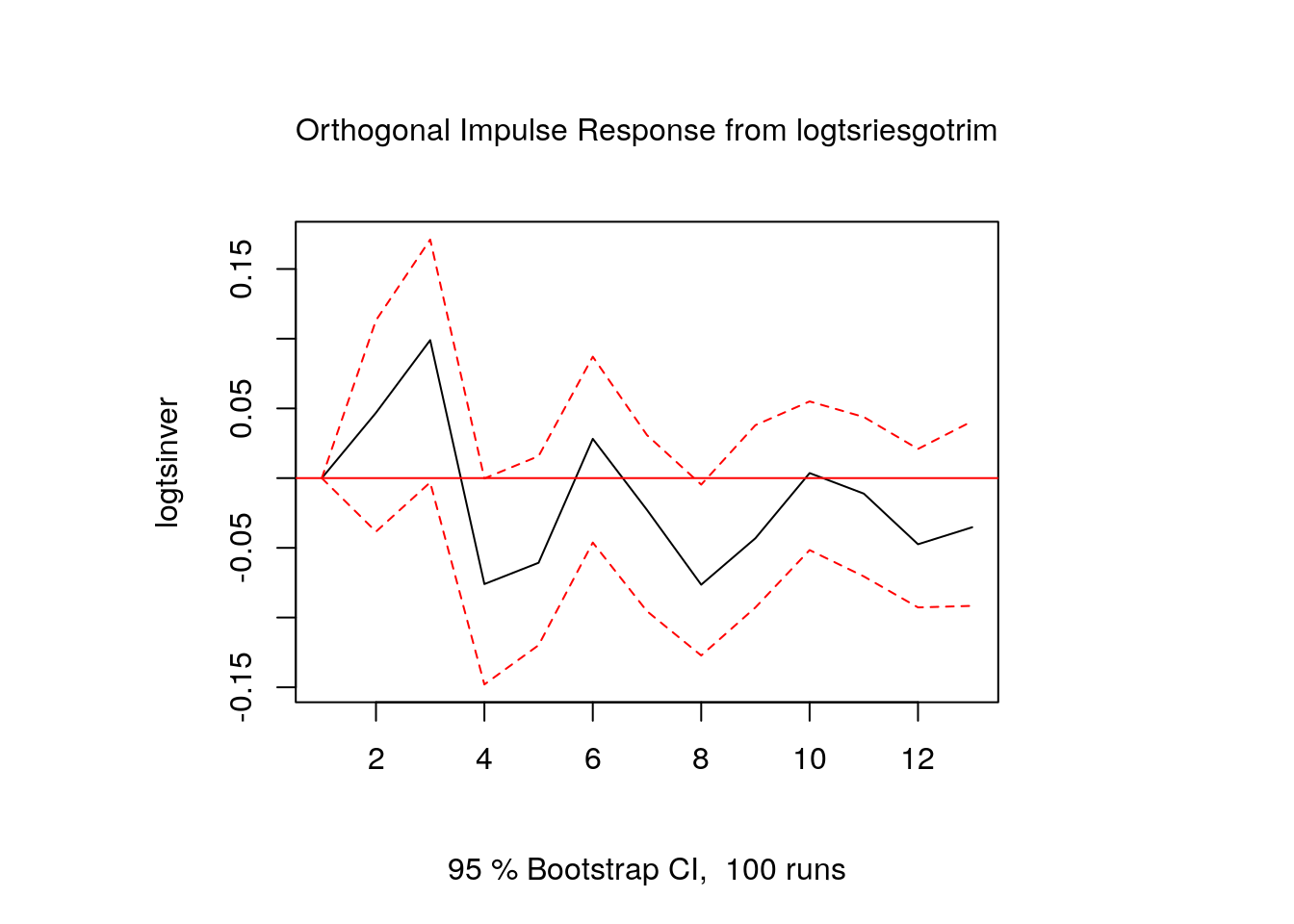
# Tercera ecuación
IR_dltstasatrim <- irf(VAR_p, n.ahead = 12, boot = TRUE,
ci = 0.95, response = "dltstasatrim")
IR_dltstasatrim##
## Impulse response coefficients
## $dltspib
## dltstasatrim
## [1,] 0.0227480177
## [2,] 0.0398205961
## [3,] 0.0527987138
## [4,] 0.0198720445
## [5,] -0.0159976134
## [6,] 0.0017526366
## [7,] 0.0384048732
## [8,] 0.0405147588
## [9,] 0.0008589858
## [10,] -0.0021537035
## [11,] 0.0272366335
## [12,] 0.0445486140
## [13,] 0.0129753555
##
## $logtsinver
## dltstasatrim
## [1,] -0.0075689453
## [2,] -0.0037782876
## [3,] 0.0140482557
## [4,] -0.0125923436
## [5,] -0.0006634151
## [6,] 0.0021824447
## [7,] -0.0032402826
## [8,] -0.0072648891
## [9,] -0.0037972445
## [10,] -0.0023536810
## [11,] -0.0065446551
## [12,] -0.0079549665
## [13,] -0.0047561880
##
## $dltstasatrim
## dltstasatrim
## [1,] 0.097321446
## [2,] 0.034095120
## [3,] -0.006273162
## [4,] -0.014049947
## [5,] -0.005372732
## [6,] -0.009429857
## [7,] -0.013517941
## [8,] -0.008066256
## [9,] -0.002425066
## [10,] -0.004497878
## [11,] -0.006238936
## [12,] 0.002636546
## [13,] 0.008543791
##
## $logtsriesgotrim
## dltstasatrim
## [1,] 0.0000000000
## [2,] -0.0001974035
## [3,] -0.0280472657
## [4,] -0.0216196256
## [5,] -0.0086264992
## [6,] -0.0150523339
## [7,] -0.0216240105
## [8,] -0.0229888189
## [9,] -0.0191343608
## [10,] -0.0106767744
## [11,] -0.0097146750
## [12,] -0.0119084439
## [13,] -0.0100420583
##
##
## Lower Band, CI= 0.95
## $dltspib
## dltstasatrim
## [1,] 0.008605900
## [2,] 0.012552868
## [3,] 0.014615858
## [4,] -0.009627304
## [5,] -0.052569483
## [6,] -0.030001675
## [7,] 0.004910610
## [8,] 0.006475955
## [9,] -0.027433717
## [10,] -0.029640037
## [11,] 0.002075688
## [12,] 0.012126447
## [13,] -0.009725261
##
## $logtsinver
## dltstasatrim
## [1,] -0.026754877
## [2,] -0.025658271
## [3,] -0.007730351
## [4,] -0.035049855
## [5,] -0.020019565
## [6,] -0.015747224
## [7,] -0.026238665
## [8,] -0.018904216
## [9,] -0.016436875
## [10,] -0.014421936
## [11,] -0.019436284
## [12,] -0.021849841
## [13,] -0.019397758
##
## $dltstasatrim
## dltstasatrim
## [1,] 0.060474217
## [2,] 0.009829571
## [3,] -0.027183369
## [4,] -0.046585708
## [5,] -0.035132689
## [6,] -0.034520459
## [7,] -0.036353853
## [8,] -0.028119260
## [9,] -0.029620287
## [10,] -0.021003527
## [11,] -0.018342436
## [12,] -0.013635349
## [13,] -0.016026771
##
## $logtsriesgotrim
## dltstasatrim
## [1,] 0.00000000
## [2,] -0.01720671
## [3,] -0.04287777
## [4,] -0.03537349
## [5,] -0.02581916
## [6,] -0.02531798
## [7,] -0.03462506
## [8,] -0.03444395
## [9,] -0.03526158
## [10,] -0.02174006
## [11,] -0.02167543
## [12,] -0.02461832
## [13,] -0.02201438
##
##
## Upper Band, CI= 0.95
## $dltspib
## dltstasatrim
## [1,] 0.035444379
## [2,] 0.058505662
## [3,] 0.074836456
## [4,] 0.042193176
## [5,] 0.007519905
## [6,] 0.018617409
## [7,] 0.069271058
## [8,] 0.065877580
## [9,] 0.018133826
## [10,] 0.014038671
## [11,] 0.050445403
## [12,] 0.079988569
## [13,] 0.036479523
##
## $logtsinver
## dltstasatrim
## [1,] 0.014594515
## [2,] 0.016276993
## [3,] 0.030871112
## [4,] 0.012392950
## [5,] 0.018501120
## [6,] 0.018111472
## [7,] 0.012796154
## [8,] 0.010807542
## [9,] 0.014332516
## [10,] 0.011696525
## [11,] 0.008566941
## [12,] 0.002516340
## [13,] 0.010923344
##
## $dltstasatrim
## dltstasatrim
## [1,] 0.110277729
## [2,] 0.046554303
## [3,] 0.010685603
## [4,] 0.006465391
## [5,] 0.011052992
## [6,] 0.010091441
## [7,] 0.004276486
## [8,] 0.011469592
## [9,] 0.019032460
## [10,] 0.012673614
## [11,] 0.010467468
## [12,] 0.015408367
## [13,] 0.021758115
##
## $logtsriesgotrim
## dltstasatrim
## [1,] 0.0000000000
## [2,] 0.0186170046
## [3,] -0.0032655932
## [4,] 0.0038773362
## [5,] 0.0130431893
## [6,] 0.0014720020
## [7,] -0.0005006913
## [8,] 0.0031236091
## [9,] 0.0006453530
## [10,] 0.0080356899
## [11,] 0.0061787971
## [12,] 0.0053971362
## [13,] 0.0064033898plot(IR_dltstasatrim)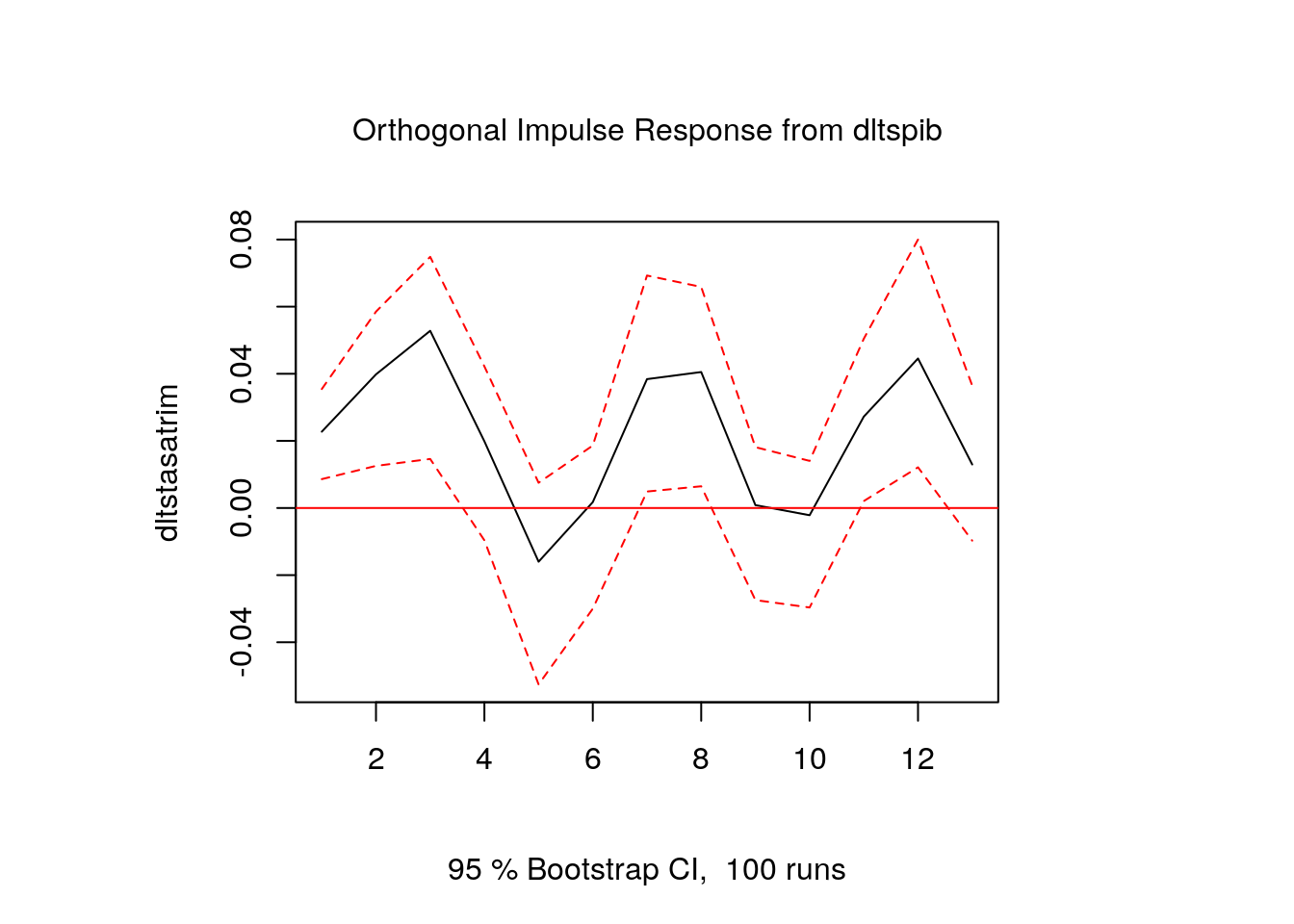
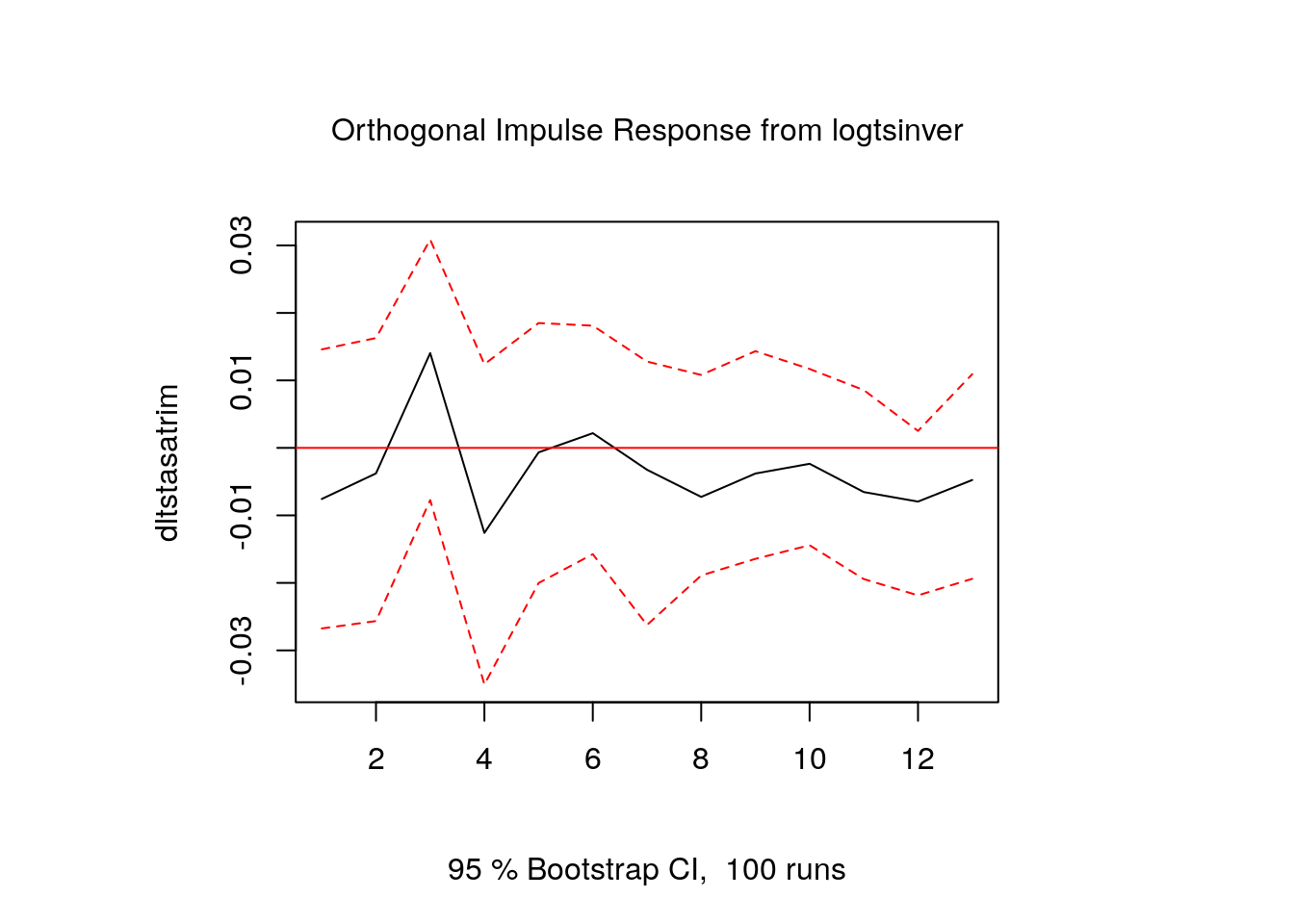
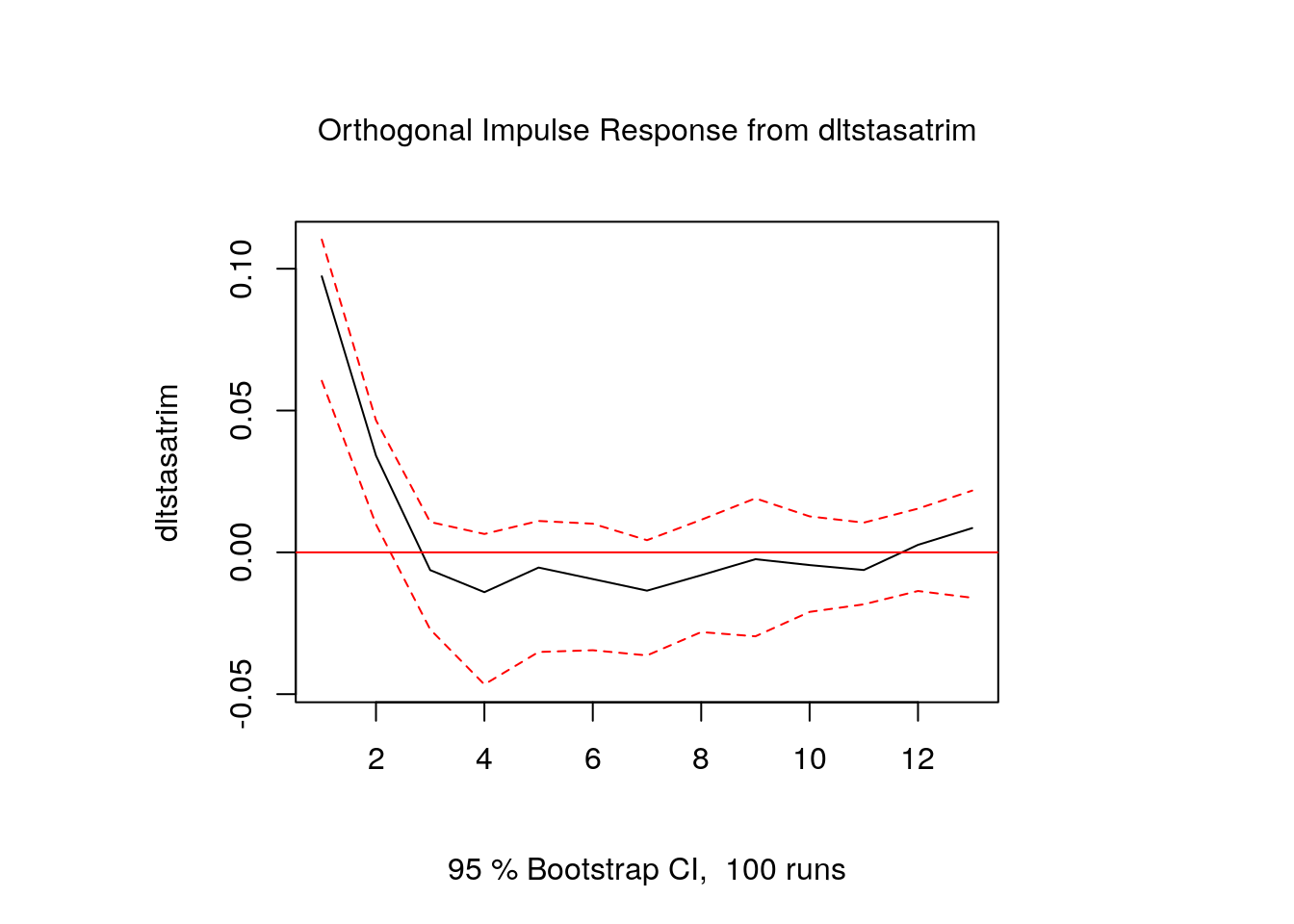
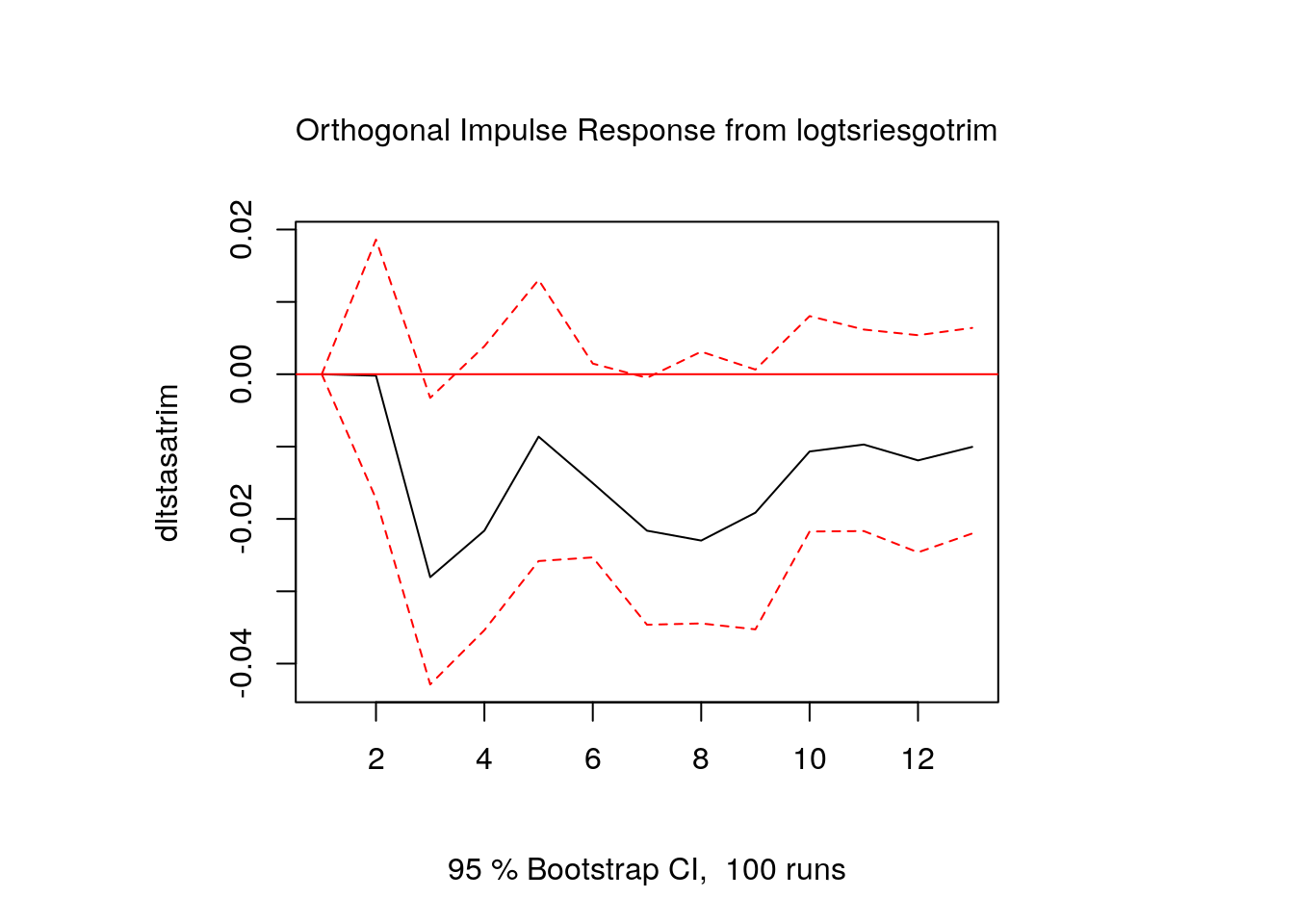
# Cuarta ecuación
IR_logtsriesgotrim <- irf(VAR_p, n.ahead = 12, boot = TRUE,
ci = 0.95, response = "logtsriesgotrim")
IR_logtsriesgotrim##
## Impulse response coefficients
## $dltspib
## logtsriesgotrim
## [1,] 0.005048879
## [2,] 0.011110860
## [3,] 0.034160520
## [4,] 0.010947810
## [5,] -0.056691595
## [6,] -0.100536856
## [7,] -0.085178471
## [8,] -0.061488495
## [9,] -0.080673564
## [10,] -0.105465359
## [11,] -0.085803143
## [12,] -0.040282173
## [13,] -0.028705981
##
## $logtsinver
## logtsriesgotrim
## [1,] -0.017371828
## [2,] -0.014189225
## [3,] 0.010365137
## [4,] -0.001668690
## [5,] -0.001072418
## [6,] 0.010151418
## [7,] 0.017647888
## [8,] 0.016854825
## [9,] 0.020314083
## [10,] 0.025852351
## [11,] 0.024779703
## [12,] 0.019723473
## [13,] 0.018248811
##
## $dltstasatrim
## logtsriesgotrim
## [1,] 0.11163883
## [2,] 0.14193359
## [3,] 0.11880439
## [4,] 0.08481447
## [5,] 0.06578104
## [6,] 0.04130571
## [7,] 0.01210918
## [8,] -0.00872892
## [9,] -0.01854025
## [10,] -0.02895034
## [11,] -0.03934945
## [12,] -0.03802708
## [13,] -0.02676202
##
## $logtsriesgotrim
## logtsriesgotrim
## [1,] 0.066057707
## [2,] 0.111513086
## [3,] 0.097535158
## [4,] 0.090233705
## [5,] 0.096966655
## [6,] 0.088358998
## [7,] 0.067810360
## [8,] 0.045169562
## [9,] 0.027221213
## [10,] 0.017582972
## [11,] 0.009720685
## [12,] -0.001719807
## [13,] -0.011572243
##
##
## Lower Band, CI= 0.95
## $dltspib
## logtsriesgotrim
## [1,] -0.01307511
## [2,] -0.02853731
## [3,] -0.02037553
## [4,] -0.04658872
## [5,] -0.10498046
## [6,] -0.15036303
## [7,] -0.13812606
## [8,] -0.12300739
## [9,] -0.14220593
## [10,] -0.15654981
## [11,] -0.13652198
## [12,] -0.08880609
## [13,] -0.07496545
##
## $logtsinver
## logtsriesgotrim
## [1,] -0.04483564
## [2,] -0.05261748
## [3,] -0.03640528
## [4,] -0.06221593
## [5,] -0.05888151
## [6,] -0.04601246
## [7,] -0.02983868
## [8,] -0.02838038
## [9,] -0.02357520
## [10,] -0.01700081
## [11,] -0.01751655
## [12,] -0.02040339
## [13,] -0.02140667
##
## $dltstasatrim
## logtsriesgotrim
## [1,] 0.067830311
## [2,] 0.077065520
## [3,] 0.046639750
## [4,] 0.012448334
## [5,] -0.000977941
## [6,] -0.021234037
## [7,] -0.043258590
## [8,] -0.056891775
## [9,] -0.067135765
## [10,] -0.074458850
## [11,] -0.073219911
## [12,] -0.075691333
## [13,] -0.064584194
##
## $logtsriesgotrim
## logtsriesgotrim
## [1,] 0.042770264
## [2,] 0.057326360
## [3,] 0.039756377
## [4,] 0.031805110
## [5,] 0.036933615
## [6,] 0.032136619
## [7,] 0.010111347
## [8,] -0.007742477
## [9,] -0.017959076
## [10,] -0.030611466
## [11,] -0.034709157
## [12,] -0.044943961
## [13,] -0.050150705
##
##
## Upper Band, CI= 0.95
## $dltspib
## logtsriesgotrim
## [1,] 0.042056359
## [2,] 0.070301882
## [3,] 0.088251424
## [4,] 0.062946115
## [5,] 0.021702580
## [6,] 0.006215233
## [7,] 0.007139219
## [8,] 0.008536740
## [9,] -0.008185494
## [10,] -0.018257191
## [11,] -0.008299864
## [12,] 0.027902930
## [13,] 0.034221349
##
## $logtsinver
## logtsriesgotrim
## [1,] 0.008068183
## [2,] 0.024182920
## [3,] 0.059970708
## [4,] 0.048488709
## [5,] 0.054613230
## [6,] 0.054866613
## [7,] 0.054009875
## [8,] 0.057918824
## [9,] 0.056532458
## [10,] 0.062479118
## [11,] 0.065996014
## [12,] 0.063504384
## [13,] 0.054361258
##
## $dltstasatrim
## logtsriesgotrim
## [1,] 0.13507513
## [2,] 0.17672465
## [3,] 0.15511301
## [4,] 0.13117591
## [5,] 0.11671049
## [6,] 0.09464936
## [7,] 0.06657016
## [8,] 0.04098353
## [9,] 0.02891311
## [10,] 0.02555720
## [11,] 0.02061561
## [12,] 0.01669947
## [13,] 0.01797741
##
## $logtsriesgotrim
## logtsriesgotrim
## [1,] 0.07242593
## [2,] 0.12654834
## [3,] 0.12148212
## [4,] 0.12120983
## [5,] 0.12905524
## [6,] 0.12358960
## [7,] 0.10427394
## [8,] 0.08437108
## [9,] 0.05968248
## [10,] 0.04789980
## [11,] 0.04309626
## [12,] 0.03653778
## [13,] 0.02607450plot(IR_logtsriesgotrim)