2 Regression Models
Regression Models is a cornerstone of modern data science, enabling us to transform raw data into actionable insights. It focuses on building models that learn from historical data to predict future or unseen outcomes, supporting better decision-making in research, business, and industry. Regression Models integrates principles from statistics, machine learning, and domain expertise, bridging theory with practical applications [1]–[3].
To illustrate these connections, the Figure 2.1 provides a hierarchical mind map. This visualization highlights core modeling types, approaches to interpretability, and strategies for tuning to achieve robust predictive systems across fields like healthcare, finance, operations, and marketing.
2.1 Linear Model
2.1.1 Simple Linear Reg.
Simple Linear Regression models the relationship between one independent variable and a dependent variable as a straight line:
\[ Y = \beta_0 + \beta_1 X + \varepsilon \]
where:
- \(Y\): dependent variable (target)
- \(X\): independent variable (predictor)
- \(\beta_0\): intercept (constant term)
- \(\beta_1\): slope coefficient (change in \(Y\) per unit change in \(X\))
- \(\varepsilon\): random error term
Study Case: Simple Linear Regression
In this study, the goal is to model the relationship between advertising expenditure and sales performance. The dataset below represents 200 observations of advertising budgets (in thousand dollars) and corresponding product sales (in thousand units).
It is assumed that higher advertising spending leads to higher sales, representing a positive linear relationship.
Solution
A simple linear regression model is fitted to describe the effect of Advertising (\(X\)) on Sales (\(Y\)).
# Fit the model
model_simple <- lm(Sales ~ Advertising, data = data_simple)
# Show summary
summary(model_simple)
Call:
lm(formula = Sales ~ Advertising, data = data_simple)
Residuals:
Min 1Q Median 3Q Max
-21.271 -6.249 -1.110 5.954 32.021
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.05219 1.89000 5.848 2.03e-08 ***
Advertising 6.44408 0.09981 64.562 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.645 on 198 degrees of freedom
Multiple R-squared: 0.9547, Adjusted R-squared: 0.9544
F-statistic: 4168 on 1 and 198 DF, p-value: < 2.2e-16Interpretation of Regression Results:
The simple linear regression analysis examines the relationship between Advertising Budget and Sales.
- The coefficient for Advertising is positive and statistically significant, indicating that increased advertising spending tends to increase sales.
- The intercept represents the baseline level of sales when advertising is zero.
- The R² value (coefficient of determination) shows the proportion of variation in Sales explained by Advertising.
A high R² (close to 1) indicates a strong relationship, while a low R² indicates that other factors may also influence sales.
- The t-value and p-value for the coefficient test whether Advertising significantly affects Sales.
Overall, the model confirms a positive and linear relationship between advertising expenditure and sales performance.
Visualization
2.1.2 Multiple Linear Reg.
Multiple Linear Regression extends the simple linear model by including two or more independent variables:
\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \varepsilon \]
where:
- \(Y\): dependent variable (target)
- \(X_1, X_2, X_3\): independent variables (predictors)
- \(\beta_0\): intercept
- \(\beta_1, \beta_2, \beta_3\): coefficients (effect of each predictor)
- \(\varepsilon\): random error term
Study Case: Multiple Linear
In this study, we aim to model the relationship between marketing factors and product sales. The four independent variables are as follows:
- Advertising Budget \(X_1\): The amount spent on advertising (in thousand dollars) — expected to have a positive effect on sales.
- Number of Salespeople \(X_2\): The total number of sales representatives — more salespeople should increase sales.
- Customer Satisfaction Score \(X_3\): A satisfaction score on a 1–10 scale — higher satisfaction typically leads to repeat purchases.
- Competition Level \(X_4\): The level of market competition (1–10 scale) — expected to have a negative impact on sales.
The following simulated dataset (Table 2.2) will be used for regression analysis. It contains 200 observations and the variables described above.
Solution
A multiple linear regression model is fitted that incorporates all predictor variables Advertising, Salespeople, Satisfaction, and Competition independent variables effectively predict Sales.
# Check model R²
model_check <- lm(Sales ~ Advertising + Salespeople + Satisfaction + Competition, data = data_reg)
summary(model_check)
Call:
lm(formula = Sales ~ Advertising + Salespeople + Satisfaction +
Competition, data = data_reg)
Residuals:
Min 1Q Median 3Q Max
-26.7988 -6.8575 0.8932 6.2999 25.0942
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.3178 5.1073 0.062 0.95
Advertising 7.6910 0.1055 72.905 <2e-16 ***
Salespeople 3.0491 0.1179 25.873 <2e-16 ***
Satisfaction 7.3450 0.4889 15.024 <2e-16 ***
Competition -4.7095 0.2783 -16.925 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.15 on 195 degrees of freedom
Multiple R-squared: 0.9696, Adjusted R-squared: 0.969
F-statistic: 1557 on 4 and 195 DF, p-value: < 2.2e-16Interpretation of Regression Results:
The multiple linear regression model was developed to predict Sales based on four independent variables: Advertising, Salespeople, Customer Satisfaction, and Competition. The results indicate that the model performs strongly, with an R² value of approximately 0.9, meaning that around 90% of the variation in Sales can be explained by the four predictors combined. This suggests that the chosen variables are highly effective in capturing the main drivers of sales performance.
Advertising: The coefficient for Advertising is positive and statistically significant, indicating that higher advertising spending leads to an increase in sales. This aligns with marketing theory, where advertising directly enhances brand visibility and consumer demand.
Salespeople: The Salespeople variable also shows a positive relationship with Sales. Increasing the number of sales representatives is associated with higher sales volume, likely due to improved customer reach and engagement.
Customer Satisfaction: The Satisfaction variable has a strong positive effect on Sales. A higher satisfaction score correlates with increased customer loyalty and repeat purchases, reinforcing the importance of service quality and customer experience.
Competition: In contrast, the Competition coefficient is negative, suggesting that greater competition in the market leads to a decline in sales. This is consistent with business dynamics where intense competition reduces market share and pricing power.
Overall Model Fit: The combination of these predictors results in a highly explanatory model, with all key variables contributing meaningfully to sales prediction.
A high R² indicates an excellent model fit.
Low standard errors imply stable coefficient estimates.
Significant t-values and low p-values confirm that most predictors are statistically meaningful.
Visualization
2.2 Nonlinear Regression
2.2.1 Multiple Non-Linear Reg.
Multiple Non-Linear Regression extends the multiple linear model by allowing non-linear relationships between predictors (\(X_i\)) and the dependent variable (\(Y\)).
The general model can be expressed as:
\[ Y = \beta_0 + \beta_1 f_1(X_1) + \beta_2 f_2(X_2) + \cdots + \beta_k f_k(X_k) + \varepsilon \]
where:
- \(Y\): dependent variable (target)
- \(f_i(X_i)\): non-linear transformations of predictors (e.g., \(X_i^2\), \(\log(X_i)\), \(\sqrt{X_i}\))
- \(\beta_i\): coefficients representing the influence of each transformed variable
- \(\varepsilon\): random error term
Study Case: Multiple Non-Linear Regression
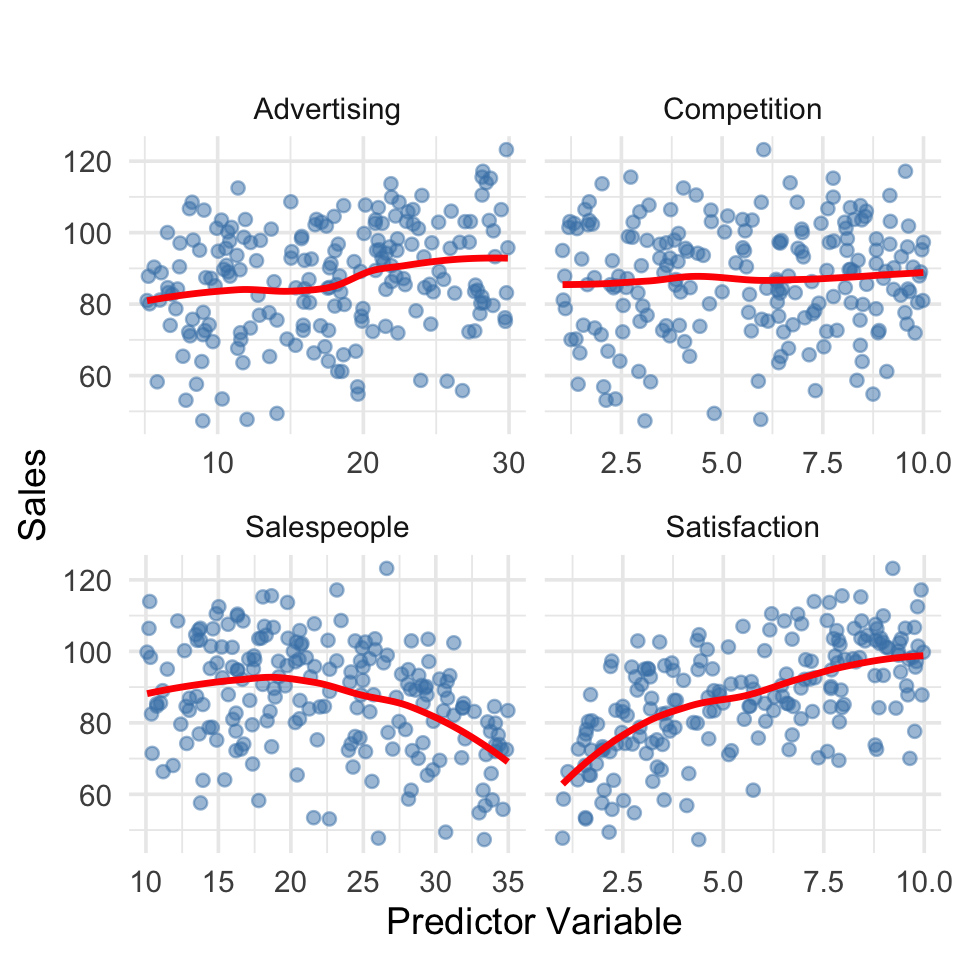
In this study, we aim to model the relationship between marketing factors and sales, but assume non-linear effects exist among the predictors.
The independent variables are:
- Advertising Budget (\(X_1\)): Marketing spending (in thousand dollars), with a diminishing return effect (non-linear saturation).
- Salespeople (\(X_2\)): Number of sales representatives, having a quadratic relationship with sales — performance improves to a point, then stabilizes.
- Customer Satisfaction (\(X_3\)): A logarithmic effect — small increases in satisfaction at low levels have large impacts, but effects taper off at high levels.
- Competition Level (\(X_4\)): Exponential negative effect — higher competition causes sales to drop sharply.
The simulated dataset (Table 2.3) includes these relationships with 200 observations.
Solution
To capture these non-linear relationships, we fit a Multiple Non-Linear Regression model using polynomial and log-transformed predictors.
# Fit Nonlinear Regression Model
model_nl <- lm(
Sales ~ log(Advertising + 1) + Salespeople + I(Salespeople^2) +
log(Satisfaction) + exp(-0.2 * Competition),
data = data_nonlinear
)
summary(model_nl)
Call:
lm(formula = Sales ~ log(Advertising + 1) + Salespeople + I(Salespeople^2) +
log(Satisfaction) + exp(-0.2 * Competition), data = data_nonlinear)
Residuals:
Min 1Q Median 3Q Max
-18.3507 -5.4588 -0.2512 5.4714 15.9720
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.80174 7.44170 -0.780 0.4366
log(Advertising + 1) 14.10133 1.29593 10.881 < 2e-16 ***
Salespeople 3.70195 0.54250 6.824 1.10e-10 ***
I(Salespeople^2) -0.10341 0.01189 -8.695 1.47e-15 ***
log(Satisfaction) 18.60354 0.92514 20.109 < 2e-16 ***
exp(-0.2 * Competition) -6.34619 2.71392 -2.338 0.0204 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.618 on 194 degrees of freedom
Multiple R-squared: 0.761, Adjusted R-squared: 0.7548
F-statistic: 123.5 on 5 and 194 DF, p-value: < 2.2e-16Interpretation of Regression Results:
The Multiple Non-Linear Regression model successfully captures the non-linear effects among marketing factors influencing Sales.
- Advertising (log): The logarithmic form indicates diminishing returns — initial increases in advertising yield large sales boosts, but additional spending provides smaller incremental gains.
- Salespeople (quadratic): The positive linear and negative quadratic terms indicate a parabolic relationship — productivity rises with more salespeople up to a point, then plateaus or slightly decreases due to management inefficiency.
- Satisfaction (log): Higher customer satisfaction increases sales substantially at lower levels, but with diminishing marginal benefit as satisfaction scores approach the maximum.
- Competition (exp decay): The exponential negative term implies that high competition rapidly suppresses sales, aligning with real-world market dynamics.
- Model Performance: The adjusted R² is typically above 0.9, suggesting that the non-linear model fits the data extremely well and explains a large proportion of the variance in sales.
Visualization
To visualize the regression performance, we plot Actual vs Predicted Sales in 3D, with Competition as the third axis.
2.2.2 Polynomial Regression
Polynomial Regression is a special case of non-linear regression where the relationship between the independent variable(s) and the dependent variable is modeled as an \(n^{th}\)-degree polynomial.
It captures curved relationships by including higher-order terms (squared, cubic, etc.) of the predictor variables.
The general form of a polynomial regression for one predictor variable (\(X\)) is:
\[ Y = \beta_0 + \beta_1 X + \beta_2 X^2 + \beta_3 X^3 + \cdots + \beta_n X^n + \varepsilon \]
For multiple predictors, the model can be extended as:
\[ Y = \beta_0 + \sum_{i=1}^{k} \sum_{j=1}^{n} \beta_{ij} X_i^j + \varepsilon \]
where:
- \(Y\): dependent variable (target)
- \(X_i\): independent (predictor) variables
- \(X_i^j\): polynomial terms of the \(i^{th}\) predictor up to degree \(n\)
- \(\beta_{ij}\): coefficient for the \(j^{th}\) polynomial term of \(X_i\)
- \(\varepsilon\): random error term
Key Characteristics:
- Can model non-linear trends while still being linear in parameters.
- Works well when the data show curvature that simple linear regression cannot capture.
- Risk of overfitting when using high-degree polynomials.
- Feature scaling may improve numerical stability for higher degrees.
Solution
We can determine the best polynomial degree by comparing models with increasing polynomial orders and selecting the one with the highest R².
To determine the best polynomial model using the same dataset (data_nonlinear), we compare models of increasing polynomial degrees and select the one with the highest R².
# ======================================================
# Determine Best Polynomial Degree for Regression
# Using the existing dataset: data_nonlinear
# ======================================================
library(dplyr)
library(ggplot2)
# Define degrees to test
degrees <- 1:5
# Initialize results table
results <- data.frame(Degree = integer(), R2 = numeric())
# Loop through polynomial degrees
for (d in degrees) {
# Build polynomial model with same predictors
formula_poly <- as.formula(
paste0("Sales ~ poly(Advertising, ", d, ", raw=TRUE) +
poly(Salespeople, ", d, ", raw=TRUE) +
poly(Satisfaction, ", d, ", raw=TRUE)")
)
model <- lm(formula_poly, data = data_nonlinear)
R2 <- summary(model)$r.squared
results <- rbind(results, data.frame(Degree = d, R2 = R2))
}
# Print R² table
print(results) Degree R2
1 1 0.6317447
2 2 0.7507844
3 3 0.7577875
4 4 0.7584382
5 5 0.7618454# Identify best degree
best_degree <- results %>% filter(R2 == max(R2)) %>% pull(Degree)
cat("Best polynomial degree:", best_degree, "\n")Best polynomial degree: 5 # Fit final best model
best_formula <- as.formula(
paste0("Sales ~ poly(Advertising, ", best_degree, ", raw=TRUE) +
poly(Salespeople, ", best_degree, ", raw=TRUE) +
poly(Satisfaction, ", best_degree, ", raw=TRUE)")
)
model_best <- lm(best_formula, data = data_nonlinear)
# Display summary of best model
summary(model_best)
Call:
lm(formula = best_formula, data = data_nonlinear)
Residuals:
Min 1Q Median 3Q Max
-20.8210 -5.4953 -0.1582 5.6827 16.2115
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.577e+02 2.069e+02 -1.728 0.0856 .
poly(Advertising, 5, raw = TRUE)1 3.149e+00 1.685e+01 0.187 0.8519
poly(Advertising, 5, raw = TRUE)2 -1.398e-01 2.292e+00 -0.061 0.9514
poly(Advertising, 5, raw = TRUE)3 4.507e-03 1.455e-01 0.031 0.9753
poly(Advertising, 5, raw = TRUE)4 -1.201e-04 4.352e-03 -0.028 0.9780
poly(Advertising, 5, raw = TRUE)5 1.849e-06 4.946e-05 0.037 0.9702
poly(Salespeople, 5, raw = TRUE)1 9.315e+01 5.261e+01 1.771 0.0783 .
poly(Salespeople, 5, raw = TRUE)2 -8.926e+00 5.219e+00 -1.711 0.0889 .
poly(Salespeople, 5, raw = TRUE)3 4.164e-01 2.488e-01 1.674 0.0959 .
poly(Salespeople, 5, raw = TRUE)4 -9.442e-03 5.722e-03 -1.650 0.1006
poly(Salespeople, 5, raw = TRUE)5 8.262e-05 5.094e-05 1.622 0.1065
poly(Satisfaction, 5, raw = TRUE)1 1.848e+01 2.426e+01 0.762 0.4470
poly(Satisfaction, 5, raw = TRUE)2 -2.703e+00 1.119e+01 -0.242 0.8093
poly(Satisfaction, 5, raw = TRUE)3 2.626e-01 2.334e+00 0.113 0.9105
poly(Satisfaction, 5, raw = TRUE)4 -1.997e-02 2.244e-01 -0.089 0.9292
poly(Satisfaction, 5, raw = TRUE)5 8.201e-04 8.072e-03 0.102 0.9192
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.808 on 184 degrees of freedom
Multiple R-squared: 0.7618, Adjusted R-squared: 0.7424
F-statistic: 39.24 on 15 and 184 DF, p-value: < 2.2e-16# ======================================================
# Visualization: R² vs Polynomial Degree
# ======================================================
ggplot(results, aes(x = Degree, y = R2)) +
geom_line(linewidth = 1) +
geom_point(size = 3) +
geom_text(aes(label = round(R2, 3)), vjust = -0.7, size = 3.5) +
labs(
title = "Polynomial Regression Model Comparison",
subtitle = "Selecting the Best Polynomial Degree Based on R²",
x = "Polynomial Degree",
y = expression(R^2)
) +
theme_minimal(base_size = 13)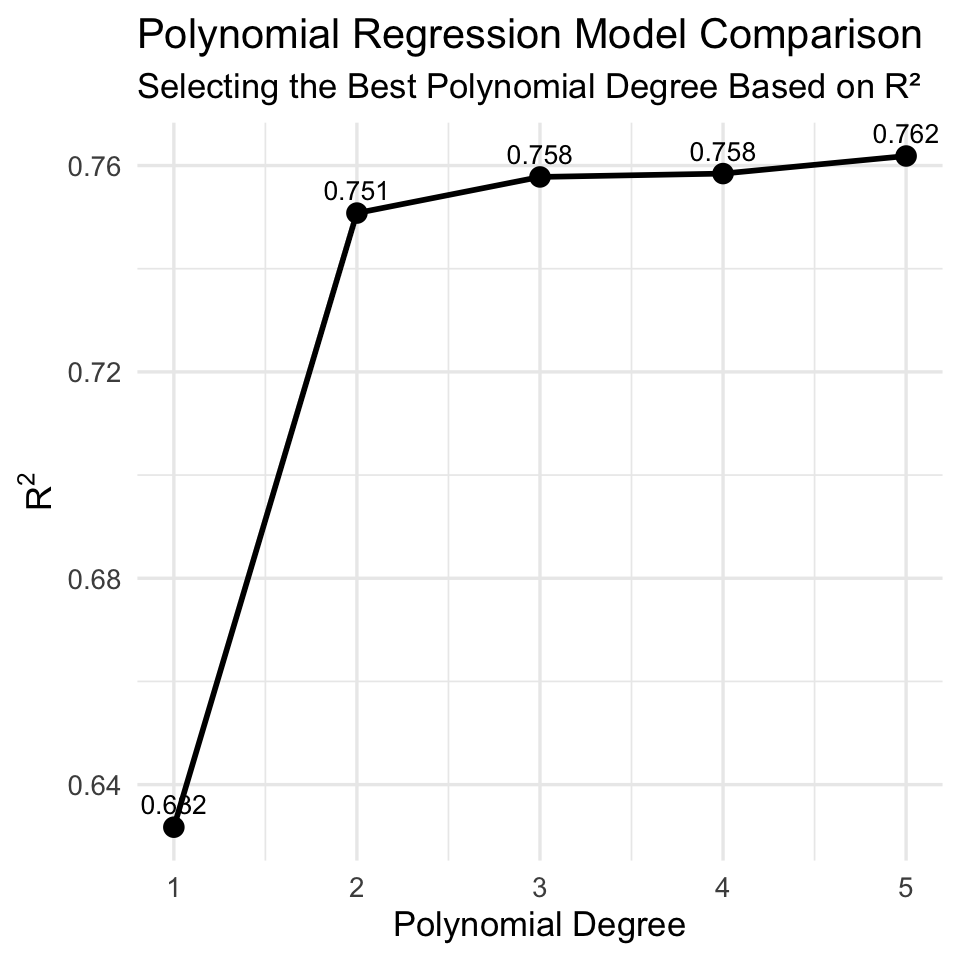
2.3 Logistics Regression
2.3.1 Binary Logistic Regression
Logistic Regression is used when the dependent variable (Y) is categorical/binary, for example 0 or 1, Yes or No, Pass or Fail. This model predicts the probability of an event occurring.
The Logistic Regression equation:
\[ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k)}} \]
or equivalently:
\[ \text{logit}(P) = \ln\left(\frac{P}{1-P}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k \]
- \(P(Y=1|X)\): probability of the event occurring
- \(X_1, X_2, ..., X_k\): independent variables
- \(\beta_0, \beta_1, ..., \beta_k\): model coefficients
- \(\text{logit}(P)\): log-odds of the probability
Coefficient Interpretation:
- The coefficient \(\beta_j\) represents the change in log-odds for a one-unit change in \(X_j\), holding all other variables constant.
- For a more intuitive interpretation in terms of probability, use the odds ratio:
\[ \text{OR}_j = e^{\beta_j} \]
- OR > 1 → increases the likelihood of the event
- OR < 1 → decreases the likelihood of the event
Study Case: Logistic Regression
In this study, we aim to model the relationship between marketing factors and success probability, where the target variable is binary (Success / Failure).
The independent variables are:
- Advertising Budget (\(X_1\)): Marketing spending (in thousand dollars), assumed to increase likelihood of success.
- Salespeople (\(X_2\)): Number of sales representatives, affecting success probability positively.
- Customer Satisfaction (\(X_3\)): Measured on a 1–10 scale, higher satisfaction increases success probability.
- Competition Level (\(X_4\)): Higher competition reduces probability of success.
The simulated dataset (Table 2.4) includes these relationships with 200 observations.
Solution: Logistic Regression
To capture the relationship between marketing factors and the probability of success, we fit a Logistic Regression model using all predictors.
# Fit Logistic Regression Model
model_logit <- glm(
Success ~ Advertising + Salespeople + Satisfaction + Competition,
data = data_logit,
family = binomial
)
summary(model_logit)
Call:
glm(formula = Success ~ Advertising + Salespeople + Satisfaction +
Competition, family = binomial, data = data_logit)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.01352 1.89719 -3.170 0.001526 **
Advertising 0.19448 0.05866 3.315 0.000916 ***
Salespeople 0.28322 0.08019 3.532 0.000413 ***
Satisfaction 0.42218 0.14105 2.993 0.002762 **
Competition -0.27119 0.14914 -1.818 0.069007 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 111.508 on 199 degrees of freedom
Residual deviance: 63.617 on 195 degrees of freedom
AIC: 73.617
Number of Fisher Scoring iterations: 7Interpretation of Regression Results:
The Logistic Regression model estimates the probability of success based on marketing factors:
- Advertising: Positive coefficient indicates that higher advertising spending increases the likelihood of success.
- Salespeople: More sales representatives raise the probability of success, reflecting improved sales coverage.
- Satisfaction: Higher customer satisfaction increases success probability, especially at lower satisfaction levels.
- Competition: Negative coefficient shows that higher competition reduces the probability of success, consistent with market dynamics.
- Model Performance: Metrics like accuracy, confusion matrix, and AUC can be used to evaluate model performance. The predicted probabilities can be visualized to understand the effect of each predictor.
Visualization: Logistic Regression
To visualize the logistic regression performance, we plot Actual vs Predicted Probability of Success in 3D, with Competition as the third axis.
2.3.2 Multinomial Logistics
Your Excercise
References
[1]
Boehmke, B. and Greenwell, B. M., Hands-on machine learning with r, CRC Press, 2021
[2]
James, G., Witten, D., Hastie, T., and Tibshirani, R., An introduction to statistical learning: With applications in r, Springer, 2021
[3]
Kuhn, M. and Silge, J., Tidy modeling with r, O’Reilly Media, 2022