4 Estimation vs. testing
The two major approaches to statistical inference are the testing and estimation approaches.
4.1 The testing approach to inference
The testing approach uses data to test a single hypothesis, or to choose between competing hypotheses. There are frequentist and Bayesian approaches to testing.
What we call “hypothesis testing” or sometimes “null hypothesis significance testing” (aka NHST) can be traced back to two different approaches, both introduced in the first half of the \(20^{th}\) century.
4.1.1 Fisher’s Significance Testing
“Significance testing” was originally put forth by Ronald Fisher as a method for assessing how much a set of data agree or disagree with a hypothesis, using a p-value.
The p-value is interpreted as quantifying how strongly the data disagree with the hypothesis being tested.
This hypothesis could be a “null” hypothesis, representing the absence of a theorized “true” effect. But, it doesn’t have to be this kind of hypothesis. One could set up a hypothesis that represents a prediction made by a theory, and test whether data disagree with this prediction.
This approach does not involve an “alternative” hypothesis. There is only the null, or what Fisher called the “test hypothesis”.
Fisher recommended the 5% level of signficance for testing, but was not strict about it. Some relevant quotes:
“If P is between .1 and .9 there is certainly no reason to suspect the hypothesis tested. If it is below .02 it is strongly indicated that the hypothesis fails to account for the whole of the facts. We shall not often be astray if we draw a conventional line at .05…”
“It is usual and convenient for experimenters to take 5 per cent as a standard level of significance, in the sense that they are prepared to ignore all results which fail to reach this standard, and, by this means, to eliminate from further discussion the greater part of the fluctuations which chance causes have introduced into their experimental results.”
“We thereby admit that no isolated experiment, however significant in itself, can suffix for the experimental demonstration of any natural phenomenon … In order to assert that a natural phenomenon is experimentally demonstrable we need, not an isolated record, but a reliable method of procedure. In relation to the test of significance, we may say that a phenomenon is experimentally demonstrable when we know how to conduct an experiment which will rarely fail to give us a statistically significant result”
4.1.2 Neyman and Pearson’s Hypothesis Testing
Neyman and Pearson introducted “hypothesis testing”, which differed from Fisher’s “significance testing” in some important ways:
An alternative hypothesis was introduced, usually denoted as \(H_A\) or \(H_1\). Convention today is to set up a null hypothesis representing “there is no true effect”, and then the alternative is “there is an effect”.
The two possible decisions were “reject \(H_0\)” and “accept \(H_0\)”. These days the language “accept \(H_0\)” is discouraged; under the original hypothesis testing framework this language was not so objectionable, for reasons we’ll see in a moment.w
Type I and Type II error rates must be declared. A Type I error is rejecting a true \(H_0\). A Type II error is accepting a false \(H_0\)
Neyman and Pearson considered hypothesis testing to be a decision making procedure, not a method that tells you what to believe. P-values could be used, but the primary purpose was to choose between \(H_0\) and \(H_A\); directly interpreting p-values was discouraged. In their words:
“We are inclined to think that as far as a particular hypothesis is concerned, no test based upon a theory of probability can by itself provide any valuable evidence of the truth or falsehood of a hypothesis”
The strength of the inference made from a hypothesis test was given by its error rates. The researcher states the Type I and Type II error rates, then states the decision. The decision is justified on the grounds of these error rates, e.g. “I am accepting \(H_0\) using a procedure that has a Type II error rate of 10%”.
Power analysis was introduced, as statistical power is defined as the probability of committing a Type II error, and the probability of a Type II error needs to be declared.
Neyman and Pearson’s approach for choosing a test statistic was to first state a Type I error rate, and then choose a test statistic that makes the Type II error rate as small as possible, subject to the Type I error rate. This means that the best test is the test that gives the most statistical power, given the Type I error rate selected.
A few notes on hypothesis testing:
The language “accept \(H_0\)” is discouraged today because it sounds like “the data suggest that \(H_0\) is true” or “we should believe that \(H_0\) is true. The original purpose of hypothesis testing was strictly decision making. One makes a decision, and states the error rate for the method used to make the decision. Choosing to act as though \(H_0\) is true is not to be confused with choosing to believe that \(H_0\) is true.
As with significance testing, there is no rule that the null hypothesis needs to represent “there is no effect.” Neyman and Pearson envisioned their method as being used to test against competing substantive scientific hypotheses, e.g. by identifying predictions made by the two scientific hypotheses, and using statistical hypothesis testing to choose between them.
Some popular parameters can show the “direction” of an effect via sign. For instance, \(\mu_1-\mu_2\) is negative is \(\mu_2>\mu_1\) and postive if \(\mu_1>\mu_2\); \(\beta_1\) is negative if \(Y\) is on average smaller when \(X_1\) is larger, and positive if \(Y\) is on average larger when \(X_1\) is larger. A “two-sided” alternative allows \(H_0\) to be rejected for both negative and positive effects. A “one-sided” alternative states a single direction, and \(H_0\) is only rejected when the parameter’s direction is in line with the alternative (e.g. \(\bar{x}_1>\bar{x}_2\) cannot reject \(H_0\) if \(H_A\) says \(\mu_1-\mu_2<0\))
4.1.3 Bayesian approaches
There are Bayesian hypothesis testing approaches, in which priors are incorporated and combined with data in order to choose between competing statistical hypotheses.
A popular method uses a “Bayes factor”, which compares the probability of data under two competing hypotheses. Prior probabilities of the two hypotheses are incorporated via Bayes’ Rule. If we call our hypotheses \(H_0\) and \(H_A\),
\[ \frac{P(data|H_A)}{P(data|H_0)}=\frac{\frac{P(H_A|data)P(data)}{P(H_A)}}{\frac{P(H_0|data)P(data)}{P(H_0)}}=\frac{P(H_A|data)P(H_0)}{P(H_0|data)P(H_A)} \]
Some notes:
The Bayes factor quantifies how much the data changes the posterior probability of each hypothesis relative to its prior probability, then gives the ratio of the two. It can be interpreted as how much the data changes the relative probability of \(H_A\) to \(H_0\).
- If the prior probabilities are equal, the Bayes factor tells you how much more likely the numerator hypothesis is than the denominator hypothesis, after incorporating the data.
- If the prior probabilities are not equal, the Bayes factor adjusts the above ratio by giving relatively more weight to the posterior probability of the hypothesis that started with a smaller prior probability.
Example: suppose the probabilities of \(H_0\) and \(H_A\) are both 0.4, but their probabilities were 0.75 and 0.25 respectively. Then we have a Bayes factor of \(\frac{0.4\cdot 0.75}{0.4\cdot 0.25}\) = 3, telling us that the ratio of \(P(H_A)\) to \(P(H_0)\) is 3 times greater after observing the data than it was before observing the data.
\(H_0\) and \(H_A\) can refer to single hypothesized parameter values (e.g. \(H_0:\mu=10\) vs \(H_A:\mu=15\)) or ranges of values (e.g. \(H_0:\mu<0\) vs \(H_A:\mu>0\)) or a combination of both. A single hypothesized value will have a prior probability; a range of values will have a prior distribution across these values.
4.1.4 Evidence vs. decisions
In frequentist testing, the p-value is a popular statistic that quantifies how much the data “disagree” with a null hypothesis. Smaller values are thought of as showing stronger evidence against the null.
In Bayesian testing, the Bayes factor is a popular statistic that quantifies how much the data change the probability of one hypothesis compared to another. This is thought of as showing how much evidence the data provide for one hypothesis compared to the other.
In either case, there is no requirement that a “decision” be made. One can report a p-value without saying “therefore I reject \(H_0\)” or “therefore I do not reject \(H_0\). One can report a Bayes factor without saying “therefore I chose hypothesis A over hypothesis B”.
We are using the phrase “statistical test” here to refer to methods that use data to quantify evidence for or against a hypothesis. This does not necessarily have to be followed by a formal decision. Some people have a strong preference for stating a decision; some have a strong aversion to it.
4.1.5 Statistical hypotheses vs. scientific hypotheses
Statistical hypotheses are usually set up so that they’ll reflect a “real world” scientific hypothesis. A statistical model is stated, followed by a null hypothesis under that model. Example:
We are testing the scientific hypothesis that text message reminders make it more likely that registered voters will choose to vote.
Let \(Y_{ij}\) be a Bernoulli distributed binary variable indicating whether a registered voter chose to vote in the last election. The Bernoulli distribution is a one-parameter probability distribution for modeling binary data. The one parameter is the probability that \(Y_{ij}=1\), and is denoted \(\pi\).
We run an experiment where known registered voters are randomly assigned to receive or not receive text message reminders, and then we look at updated voter rolls to see if each person voted. Here is the model and null hypothesis:
\(Y_{1j}\sim Bernoulli(\pi_1)\)
\(Y_{2j}\sim Bernoulli(\pi_2)\)
\(H_0:\pi_1 - \pi_2 = 0\)
This model seems to represent the scientific hypothesis well, but it is not the scientific hypothesis itself. Some differences:
We assume there is a single “population” probability of voting for those getting reminders, and another population probability for those who don’t.
4.1.6 Testing against scientific hypotheses vs. testing against statistical hypotheses
There is a popular approach to scientific hypothesis testing known as falsificationism. Under the falsificationist approach, hypotheses are tested through the use of experiments that would be capable of falsifying the hypothesis, were the hypothesis false (the idea that hypotheses can be strictly “true” or that they can be shown definitively false is controversial, in which case we might say that our experiment should be capable of showing the ways in which a hypothesis might be deficient or flawed).
This approach was popularized by the philosopher Karl Popper. Popper’s argument is that it is extremely difficult (maybe impossibe) to show definitively that a hypothesis is true, because it could always be false in a manner you are simply unaware of. But, it is simple to show a hypothesis to be false: you just need to show that a logical consequence of the hypothesis does not hold true.
The falsificationist approach has been integrated from philosophy into statistics most notably by philosopher Deborah Mayo, who advocates for a “serve testing” approach to statistical inference.
In brief, a scientific hypothesis is subjected to a critical or severe test, and if it fails the test, it is rejected. If it survives the test, we just say that it has survived our attempt to falsify it; we don’t claim to have shown it to be true.
This looks a lot like statistical null hypothesis significance testing (NHST). Under NHST, \(H_0\) is subjected to potential rejection using an approach that has some statistical power (hopefully high) to reject it, if is false. But if \(H_0\) is not rejected, we don’t claim to have shown it to be true.
There is however an very important difference between the scientific and statistical approachs to hypothesis testing described above. Under the statistical NHST approach, the null is set to up to represent the scientific hypothesis being false (e.g. “the difference in population mean outcomes for the experimental groups is zero”). And so, the scientific hypothesis is not what is being subjected to potential falsification. Rather, what is subjected to potential falsification is the scientific hypothesis being wrong in some particular manner.
Statistical NHST thus appears to be a confirmationist approach to hypothesis testing, rather than a falsificationist approach. The scientific test, according to the falsificationist approach, is capable of falsifying the hypothesis, but cannot show it to be true. Whereas the null hypothesis test is capable of falsifying a particular version of “not the hypothesis”, but cannot show “not the hypothesis” to be true.
This point is explored more deeply in one of the assigned articles for this class:
[meehl_1967_theorytesting]
Important: this is a criticism of NHST as popularly practiced, but NHST is only one version of statistical hypothesis testing. There is no requirement that statistical tests be directed against a “null” hypothesis set up to represent the absence of a real world effect. A statistical test can be directed against a consequence of a scientific hypothesis being true, rather than false. It can be set up to test two scientific hypotheses against each other, rather than one scientific hypothesis again “nothing”.
4.2 The estimation approach to inference
So far, we have looked at three testing approaches to inference:
Fisher’s significance testing, in which a p-value is used to quantify the extent to which data contradict a test hypothesis, and a “significant” deviation from the test hypothesis is declared if the p-value falls below some conventional threshold (usually 0.05)
Neyman and Pearson’s hypothesis testing, in which data are used to make a choice between two competing hypotheses (typically called “null” and “alternative”), and that choice is justified by appealing to the Type I and Type II error rates of the testing procedure.
Bayes factors, which quantify the extent to which data give support to one hypothesis over the other. This is achieved by comparing the ratio of prior probabilities for the two hypotheses to the ratio of posterior probabilities of the two hypotheses; the change from prior to posterior represents the effect of the data on the probability of that hypothesis being true.
The first and third of these produce statistics that are meant to be interpreted. The second is strictly a decision making procedure. What they all have in common is that they require hypotheses.
The estimation approach differs fundamentally from the testing approach in that it does not require hypotheses. Rather, it requires an unknown quantity of interest, and the goal is to use data to draw inference on this unknown quantity.
4.2.1 Point estimates and confidence intervals
Suppose there is some uknown quantity \(\theta\), which is taken to exist at the population level. \(\theta\) could represent all kinds of quantities. Examples:
- The effectiveness of a medical intervention, defined as average outcome for those receiving the intervention minus average outcome for those not receiving the intervention, at the population level.
- The population level correlation between money spent on advertisements aired on podcasts and subsequent change in revenue (for US based companies).
- The proprtion of all registered US voters who intend to vote in the next mid-tern election.
We collect data, and we calculate the kind of value that \(\theta\) represents. This is a point estimate for theta. Examples:
The proportion of registered voters in a survey who intend to vote in the next mid-term election is a “point estimate” for the proportion of all registered voters who intend to vote in the mid-term election.
The difference in mean outcomes between participants in a control group an those in an intervention group is a “point estimate” for the difference between:
- Mean outcome for all people in the population, were they to be assigned to the control group
- Mean outcome for all people in the population, were they to be assigned to the control group.
If an estimate is unbiased, then its “expected value” is the population level quantity being estimated. But, we don’t actually expect that the numeric value of a statistical estimate will be equal to the value of the population parameter that it estimates20.
confidence intervals A confidence interval is created using a method that, under some assumptions, would achieve the desired “success rate” over the long run, if we were to keep taking new samples and keep calculating new confidence intervals. A “success” is defined as the unknown population-level value being contained within a confidence interval.
Confidence intervals have some good selling points relative to hypothesis testing:
They give a range within which a quantity of interest may lie, rather than reducing inference down to a binary decision.
They convey uncertainty via their width.
They are in the units of the original outcome variable (e.g. dollars, velocity, age, etc).
They aren’t as volatile as p-values under repeated sampling (the sampling distribution of the p-value is right skewed, and extremely right skewed when power is low-to-moderate).
4.2.2 Confidence intervals as inverted hypothesis tests
Jerzy Neyman, who developed hypothesis testing, also developed confidence intervals. The basic connection between the two is this: find all the possible vales for the test (aka null) hypothesis that would not be rejected if tested against using the data at hand. The confidence interval contains all of these values,
This approach should make sense; we are “confident” that the true population parameter value is one that our data does not reject. We would be suspicious of proposed parameter values that our data would reject.
It turns out that intervals made in this matter also achieve their desired coverage rate. Make intervals that contain all values that your data would not reject at the $ level, and 95% of the time these intervals will contain the unknown parameter value.
4.2.3 Bayesian credible intervals
Bayesians create intervals to represent uncertainty, too. They call theirs “credible intervals. The interpretation of a credible interval is one that is not allowed for confidence intervals. If you have a 95% credible interval for \(\theta\), you can say that there is a 95% chance the unknown parameter is in that interval.
Example: we have a 95% credible interval for \(\beta_1\) of \((1.47,5.88)\), then there is a 95% chance that \(beta_1\) lies somewhere between 1.47 and 5.88.
4.2.4 Confidence intervals as conveying more information than p-values or statistical significance
There is a strong case to be made that confidence intervals are objectively more informative than p-values or statements regarding significance. The argument is that, given a confidence interval, one can calculate the corresponding p-value for a desired null hypothesis. But the converse isn’t true: given a p-value for some null hypothesis, there are an infinity of possible confidence intervals that would produce that p-value.
Visual example:
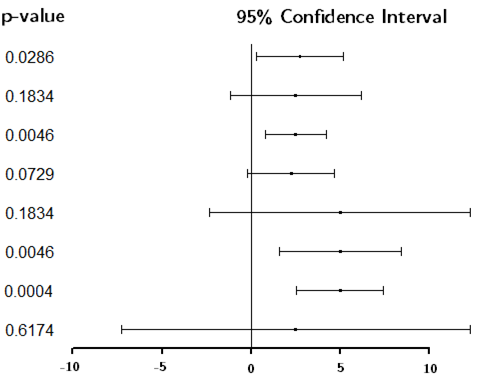
Notice:
As expected, the intervals containing zero produce \(p>0.05\), and those not containing zero produce \(p<0.05\).
There are some confidence intervals that are different, but have the same p-value. This is possible because the point estimate and width of the interval are both changing.
The p-values change in value a lot, even for seemingly small changes in the confidence interval.
A case for reporting confidence intervals rather than p-values is this: given that a confidence interval can be used to conduct a hypothesis test, it is not clear what is to be gained from reporting a p-value as well. But, if only a p-value had been reported, also reporting a confidence interval would give the reader an estimate for the quantity of interest, surrounded by bounds that represent uncertainty in that estimate. (Exception: some hypothesis tests do not have a corresponding interpretable statistic on which inference can be drawn by inverting the test)
4.3 First applied example: heart stent study
https://www.nytimes.com/2017/11/02/health/heart-disease-stents.html
This New York Times article describes a randomized controlled trial (RCT) to assess the effectiveness of heart stents on easing chest pain.
The article claims that the stents were shown not to work. Here is the original paper describing the study and the results:
We see here that the primary outcome of interest was amount of time (in seconds) patients were able to spend exercising on a treadmill. The 95% CI for the mean difference between treatment and placebo groups is \((-8.9,42)\), which contains zero.
In the paper, this is interpreted as, essentially, “the null is true”:
Remember, the 95% CI was %(-8.9, 42)%. Zero seconds is a “plausible” value for the difference; so is 33 seconds. So is any value in that confidence interval. (If the researchers had stated ahead of them that they would not be interested in any average improvement less than, say, 60 seconds, this 95% CI could be interpreted as showing that any effect of heart stents on chest pain is too small.)
4.4 Second applied example: knee surgery
Here is another study on the effectiveness of a surgical procedure. Link here
This one is about knee surgery. As with the previous example, this as a randomized controlled trial (RCT) in which roughly half the participants underwent a placebo surgery. And, it is another study in which no “significant” evidence was found to support the effectiveness of the real procedure relative to placebo.
We will look at a 2-year follow up study, performed by the same researchers:
The 95% CI for the difference in mean outcomes between “real” and “sham” surgery groups was \((-11.3,2.6)\), with negative values indicating improvement on an index score (“WOMET”) quantifying severity of symptoms and disability.
Here, we see that the researchers identified the minimum “clinically important improvement” in WOMET score to be 15.5.
4.5 Critiques of testing
We’ll briefly outline the major critiques of the testing approach, some of which have already come up. These are arguments that you may or may not find convincing, and that are sometimes topics of debate among statisticians and philosophers.
4.5.1 Implausible nulls
The Meehl and Tukey papers on Canvas both argue that a “point” null hypothesis of zero is usually implausible. This is a major challenge to standard null hypothesis significance testing (NHST): if the null was implausible before data were collected, what do we learn when we say that the data lead us to reject this null?
4.5.2 Unnecessary dichotomization
Suppose we have calculated a p-value of 0.018. We declare the result “statistically significant”, because \(p<0.05\).
What was the purpose of the second sentence above? The reader can see that the p-value is 0.018. What additional information is conveyed by pointing out that 0.018 is smaller than 0.05? Since it is obvious to anyone that 0.018 < 0.05, the only reason for pointing this out must be that there is something special about 0.05. Is there?
The story is the sample for p-values greater than 0.05. Suppose we get a p-value of 0.088. We would only expect to get a test statistic at least as large as ours 8.8% of the time, if the null were true. This, according to the “p < 0.05” standard, is not good enough. Does the act of declaring 0.088 “not good enough” convey more information than would have been conveyed by simply reporting 0.088?
The Neyman-Pearson hypothesis testing approach says that this a decision making procedure, and so a cutoff is required. The practical question, then, is: what is being decided? If the decision is simply between saying “reject \(H_0\)” and “no not reject \(H_0\)”, then the decision is trivial: we are using a decision making procedure because we want to decide between two phrases. What is the purpose of this? If the choice between “reject” and “do not reject” is meant to inform our belief regarding the truth of the null, then the problem of prior belief comes into play. It seems like the dichotomous decision procedure is only justified if there is an actionable decision to be made.
4.5.3 Tiny significant effects
An estimated effect can be very small and also “statistically significant”. Here is an example:
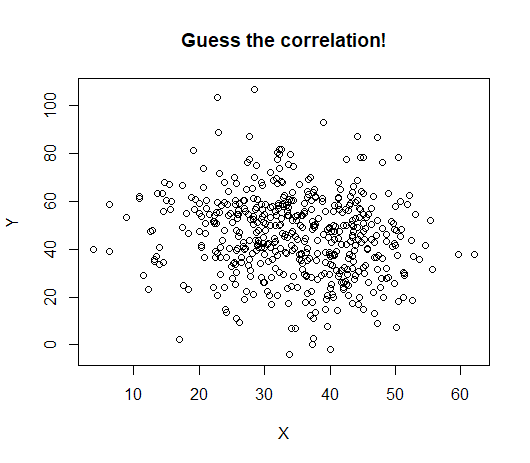The data displayed have a highly statistically significant correlation: \(p = 0.0008\)
The correlation itself is -0.15:
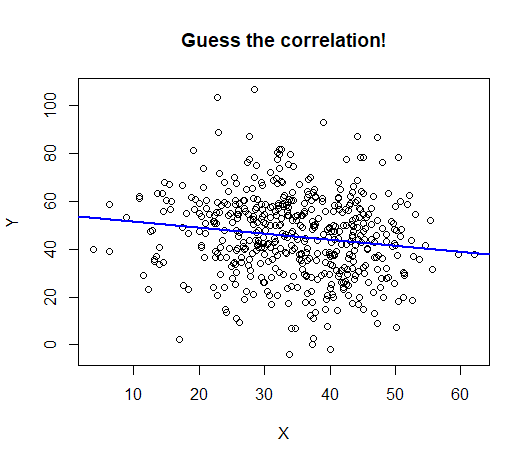This happens often when sample sizes are large. Here is a study that used ebay data and compared male and female buyers and sellers:
From the results:
This was a serious study that came to non-trivial conclusions. It is hard to imagine the authors would have bothered to report a difference in probability of 0.0002 (or 0.02 percentage points), had it not been accompanied by “p < 0.05”
4.5.4 “Not significant” \(\neq\) “not real”
This has been covered in previous notes many times, so we won’t belabor it here. Failure to reject a null hypothesis cannot be taken as evidence that the null hypothesis is true. If we are taking a Bayesian approach and assigning a prior probability to \(H_0\), then it is true that failing to reject \(H_0\) will make the posterior probaility of \(H_0\) increase by some amount relative to the prior. It is also true that, if a study is very highly powered to detect some specified effect, then a failure to reject \(H_0\) is suggestive that the effect is at least smaller than the one the study was powered to. But, it is a fallacy to presume that failing to reject \(H_0\) implies that the null is probably true.
4.6 In support of testing
4.6.1 Testing hypotheses is integral to science
A common retort to critiques of testing is that, for science to progress, we must test hypotheses. It is fine to report estimates, but for a science that cares about theory and explanation, claims must be made and testing against. Otherwise we have a pile of numbers and no way to decide between competing explanations or competing theories.
4.6.2 Sometimes the null hypothesis is plausible or of scientific interest.
The critique that “the null is implausible” only holds when the null is… implausible. If the null is plausible prior to seeing any data, then rejecting it coveys real information.
4.6.3 We don’t want to be fooled by randomness
The original motivation for significance testing was that it is very easy to see patterns in random or noisy data. Just as a cloud might look like a face, raw data might look like a trend. Significance testing is a tool for determining if we think it’s reasonably to conclude that there is a “signal” in noisy data.
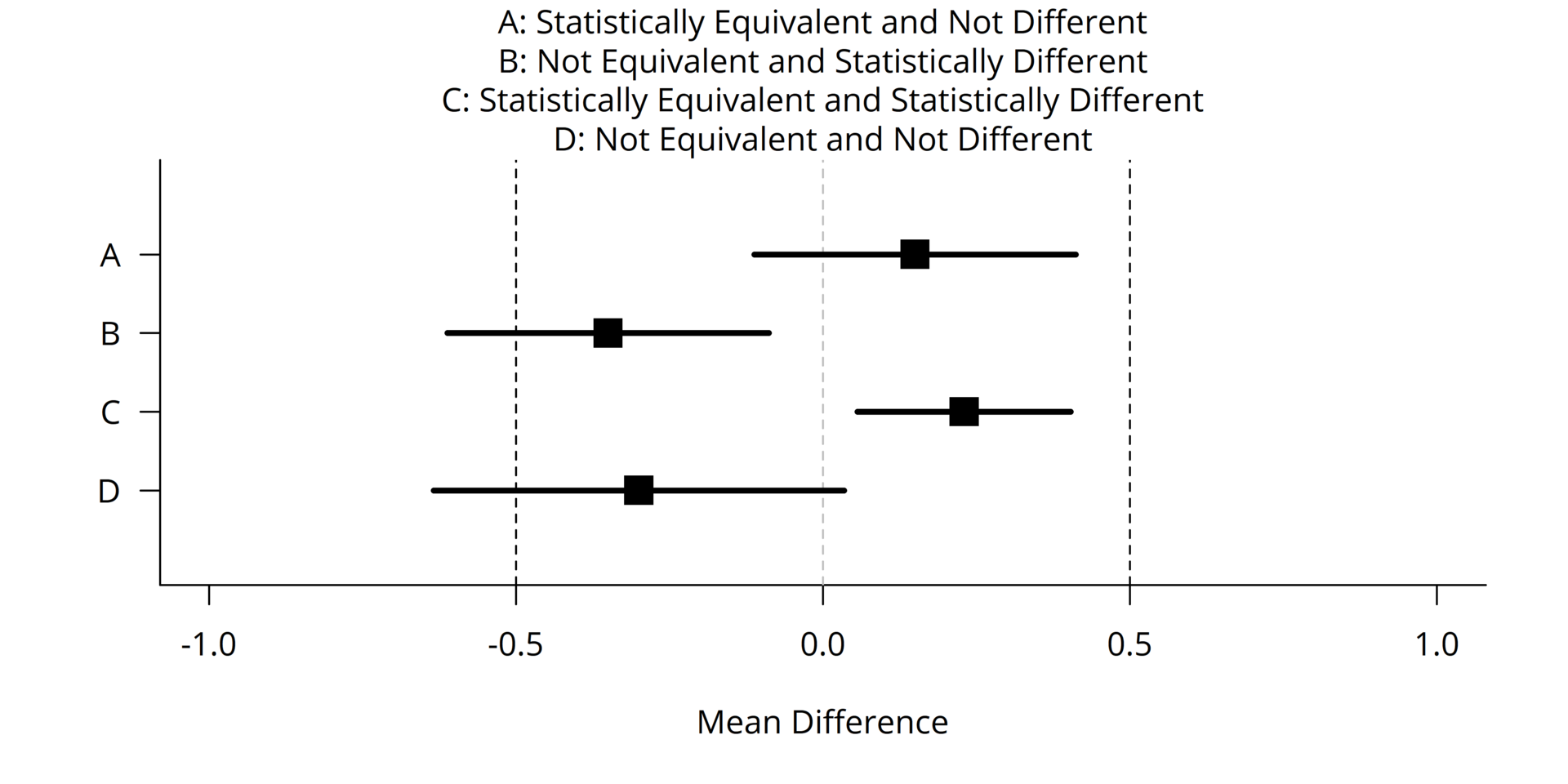
4.7 One compromise: testing interval nulls
We saw a sign of compromise in the knee surgery example: not only was the surgey “not significantly different” from placebo, but the largest value in its 95% confidence interval was smaller than the minimum level of improvement that would be considered valuable.
Stating a “smallest effect size of interest” (SESOI) allows for a null hypothesis that is neither a point value (e.g. \(H_0: \beta_1 = 0\)), nor an inequality that goes out to inifnity (e.g. \(H_0: \beta_1<0\)). Rather, the null is an interval.
- To reject such a null, a confidence interval must be entirely above the SESOI.
- Such a null can be “accepted” if a confidence interval lies entirely below the SESOI, as we saw in the knee surgery example.
- Formal method: “Equivalence testing”:
This is assuming you’re on board with parameters and populations being real in the first place↩︎