Kapitola 1 Úvod do R

R je prostredie pre štatistické výpočty a vizualizáciu údajov, vyvíjané pod slobodnou licenciou a pre rôzne platformy. Inštalačné súbory, návod na inštaláciu ako aj dokumentáciu je možné nájsť na domovskej stránke projektu www.r-project.org. Základom je interpretovaný⁴ počítačový jazyk R umožňujúci vetvenie, cyklenie a modulárne programovanie pomocou funkcií.

Z hladiska historického vývoja je R dialektom jazyka S. Ten neprišiel spomedzi tradičných programovacích jazykov. Cieľom jeho autorov bolo vymyslieť, ako uľahčiť analýzu údajov. Kľúčovým tu bol prechod od používateľa ku vývojárovi. R si zachovalo pôvodnú filozofiu jazyka S, teda poskytnúť jednak interaktivitu pri práci, jednak možnosti vývoja nových nástrojov. Technicky je bližšie skôr ku jazyku Scheme než ku S. Podrobnejšie sa vzniku a vlastnostiam R venuje časť (R. D. Peng 2016, kap. 2 History and Overview of R).

Distribúcia R obsahuje funkcionalitu pre veľký počet štatistických metód ako napr. lineárne a nelineárne regresné modely, analýzu časových radov a priestorových údajov, klasické parametrické a neparametrické testy, zhlukovú analýzu či klasifikáciu, ďalej množstvo funkcií je poskytovaných nástrojmi pre grafickú reprezentáciu údajov, no najväčšou výhodou systému R je nesmierne veľká databáza voľne dostupných rozširujúcich softvérových balíkov (angl. packages) tvorených komunitou používateľov a vývojárov z akademickej i komerčnej sféry.

Základné vývojové prostredie R (v operačnom systéme Windows a macOS) tvorí textový editor, pomocou ktorého používateľ píše zdrojový kód v jazyku R, a príkazový riadok (konzola), v ktorom je odoslaný kód interpretovaný. Grafické výstupy sú presmerované do samostatných okien. Pre pohodlnú prácu odporúčame použitie integrovaného vývojového prostredia RStudio, ktoré farebne zvýrazňuje syntax, poskytuje nápovedu, sprístupňuje zoznam definovaných objektov, uľahčuje tvorbu dokumentácie a veľa ďaľších užitočných nástrojov.

Zdrojový kód sa na interpretáciu do príkazového riadku posiela typicky buď po riadkoch alebo vyznačením časti kódu, a stlačením kombinácie kláves (Ctrl-R v základnom prostredí, a Ctrl-Enter v prostredí RStudio).

1.1 R ako lepšia kalkulačka

R sa dá použiť podobne ako kalkulačka na rôzne jednoduché výpočty a zobrazenie, pričom základný výstup z príkazového riadku je čisto textový, a tak tradičný matematický zápis matematických symbolov ako napr. $\sqrt{x^3}$ nepodporuje.

1.1.1 Základné matematické operátory a funkcie

Najčastejšou operáciou je sčítanie. Po prijatí textového vstupu v príkazovom riadku (začína sa znakom >) systém R vypíše výsledok, v nasledujúcom príklade je to číslo 5. Keďže však v R je všetko nejaká forma poľa, aj jediné číslo je uložené vo forme vektora, a to dĺžky 1. Výpis dlhších vektorov sa v konzole zalamuje do riadkov, pričom každý začína indexom prvého elementu v danom riadku. To vysvetľuje reťazec [1] pred výsledkom nášho príkladu.

> 2+3

[1] 5

V nasledujúcom texte prispôsobíme formátovanie textu tak, aby vstup a výstup nezaberal príliš veľa miesta v našej publikácii (zlúčime obe polia do jedného), zároveň aby sa vstup dal pohodlne kopírovať do svojho skúšobného scriptového súboru (odstránime >) a aby sa výstup líšil od vstupu (bude začínať znakmi ##). Krátke poznámky budú uvádzané za znakom pre komentár (#).

Pokračujme základnými matematickými operátormi a matematickými funkciami, ktoré sú dostupné na bežných kalkulačkách:

3/2
## [1] 1.5

2^3
## [1] 8

4 ^ 2 - 3 * 2 # pri vyhodnotení má násobenie prednosť pred odčítaním
## [1] 10

(56-14)/6 - 4*7*10/(5^2-5) # často je potrebné použiť zátvorky
## [1] -7

sqrt(2)  # pomenovaná funkcia pre odmocnenie 
## [1] 1.414214

abs(2-4)        # |2-4|
## [1] 2

cos(4*pi)       # ďaľšie sú sin(), tan(), atan(), atan2() ...
## [1] 1

log(0)      # funkcia pre tento argument nie je definovaná
## [1] -Inf
exp(1)    # Eulerovo číslo, e^1
## [1] 2.718282

factorial(6)   # 6!
## [1] 720

choose(52,5)   # kombinačné číslo (52 nad 5) = 52!/(47!5!)
## [1] 2598960

Vidíme, že funkcie sa zavolajú svojím menom a uvedením všetkých relevantných argumentov v okrúhlych zátvorkách a oddelených čiarkou. Argumenty je možné identifikovať ich jedinečným názvom pomocou operátora =:

log(1000, base = 10)    # dekadický logaritmus
## [1] 3

Podobne sa dajú zapísať aj základné matematické operácie, iba názov funkcie tvorí znak operátora v spätných úvodzovkách (môže sa to hodiť v zložitejších programoch).

`+`(2,3)
## [1] 5

Zoznam všetkých argumentov danej funkcie sa dá zistiť v nápovede (v RStudiu umiestnením kurzora na funkciu a stlačením [F1], alebo nastavením kurzora do zátvoriek za názvom funkcie a vyvolaním kontextovej pomoci klávesou [Tab]).

1.1.2 Priradenie hodnoty premennej

S hodnotami je často potrebné počítať viackrát. Vtedy sa hodí uložiť si ich do premennej. Možností vytvorenia premennej a pridelenia jej hodnoty (alebo prepísania hodnoty existujúcej premennej) je v R niekoľko. Najbežnejší je dvojicou znakov < a - tvoriacich šípku v smere priradenia:

n <- 5   # premennej n priraď hodnotu 5
n        # zobraz hodnotu premennej n
## [1] 5

V RStudiu na rýchlejšie vloženie operátora priradenia slúži klávesová skratka [Alt] + [-]. Priradenie je možné aj operátorom v opačnom smere, alebo funkciou assign,

15 -> n; n   # príkazy v jednom riadku sa oddelujú bodkočiarkou
## [1] 15

assign("n", 25)

rovnako je možné použiť aj tradičný operátor =, no ten je povolený iba v prostredí najvyššej úrovne. Vo všeobecnosti sa odporúča používať ho výhradne na identifikáciu argumentov funkcií.

n = 35; n
## [1] 35

Zobrazenie práve priradenej hodnoty sa dá urobiť aj pomocou zátvoriek:

(n <- 2*3)   # tri v jednom: vypočíta, priradí a vypíše hodnotu
## [1] 6

Priradenie sa dá reťaziť:

m <- n <- 45
c(m, n)
## [1] 45 45

1.1.3 Vektorizácia

Podobne ako s jednoprvkovým vektorom sa v R pracuje aj s ľubovoľne dlhým vektorom. Najprv vytvoríme dva rovnako dlhé vektory, a to skombinovaním hodnôt pomocou funkcie c (angl. combine):

x <- c(1,2,3,4)      
y <- c(2,4,7,11)

Väčšina operácií v R je vektorizovaná, to znamená, že sa aplikujú postupne na všetky prvky vektora, resp. zodpovedajúce si prvky viacerých vektorov:

x*y; y/x; y-x; y^x   # výsledky sú postupne v nasledujúcich 4 riadkoch
## [1]  2  8 21 44
## [1] 2.000000 2.000000 2.333333 2.750000
## [1] 1 2 4 7
## [1]     2    16   343 14641

cos(x*pi) + cos(y*pi)  # výsledný vektor má opäť 4 prvky
## [1]  0  2 -2  0

Operácia sa vykoná, aj keď vektory nie sú rovnakej dĺžky. Vtedy sa kratší zreplikuje na dĺžku toho dlhšieho (a ak dĺžky nie sú celočíselným násobkom jedna druhej, systém zobrazí varovanie).

c(1,2,3,4) * c(1,2)
## [1] 1 4 3 8

Niektoré funkcie pracujú s viacerými prvkami vektorov naraz:


length(x)       # dĺžka vektora
## [1] 4

sum(x)          # 1+2+3+4
## [1] 10

prod(x)         # 1*2*3*4
## [1] 24

cumsum(x)  # 1, 1+2, 1+2+3, 1+2+3+4
## [1]  1  3  6 10

diff(y)        # 2-1, 4-2, 7-4, 11-7
## [1] 2 3 4

diff(y, lag=2)  # 7-2, 11-4
## [1] 5 7

1.1.4 Operátory

Dosiaľ sme použili iba niektoré matematické a priraďovacie operátory. S ďalšími sa zoznámime v nasledujúcich kapitolách, no už tu uvedieme prehľadný zoznam všetkých operátorov definovaných v základných knižniciach jazyka R (rozširujúce balíky môžu pridávať ďašie). Sú zoradené podľa priority pri vyhodnocovaní príkazov:

:: ::: prístup ku objektom prostredia (napr. k funkciám v balíkoch)
$ @ prístup ku prvkom objektov
[ [[ prístup ku prvkom polí a zoznamov
^ umocnenie
- + unárne operátory (napr. -2)
: postupnosť
%operator% |> špeciálne operátory
* / násobenie a delenie
+ - súčet a rozdiel
< > <= >= == != porovnávanie
! negácia
& && logická spojka a
| || logická spojka alebo
~ oddelenie ľavej a pravej strany vo vzorcoch
-> ->> priradenie (z ľava do prava)
<- <<- priradenie (z prava do ľava)
= priradenie (z prava do ľava)
? nápoveda

Znalosť priority pomôže udržať kód bez zbytočných zátvoriek, ktoré ho môžu robiť menej prehľadným:

n <- -3 + 16/2^3  # namiesto n <- ((-3) + (16/(2^3)))

Zoznam operátorov zoradených podľa priority dokumentuje stránka v nápovede vyvolaná príkazom ?Syntax.

1.2 Dátove objekty

Vnútorná štruktúra dátových objektov v R je pomerne komplikovaná, na bežné používanie však stačí poznať tie základné: (atomic) vector, factor, ts, matrix, array, data frame a list.

Sú charakterizované menom, obsahom ale aj atribútmi, ktoré špecifikujú typ obsahu. Základnými atribútmi sú dĺžka (length) a typ (mode). Ďalšími sú napr. rozmer (dim) pri viacrozmerných pravidelných objektoch ako matrix, array a data.frame, ďalej trieda (class), názvy prvkov (names, dimnames, row.names) či komentár (comment).

Typy dátových objektov sú numeric, character, complex, logical, function, expression, a ďalšie.

Iba data frame a list sú heterogénne, teda môžu obsahovať prvky viac ako jedného typu.

1.2.1 Vektor

Vytvorenie

V nasledujúcich príkladoch vytvoríme nový vektor zadaním dĺžky, módu a konkrétneho prvku. Nezadané hodnoty sú doplnené prednastavenými, napr. dĺžka rovná nule alebo ostatné prvky rovné hodnote FALSE (ekvivalentom v numerickom móde je nula), prípadne nie sú definované vôbec (NA vo význame „not available”).

v <- vector(mode="logical", length = 0); v
## logical(0)
v <- vector(mode="logical", length = 2); v
## [1] FALSE FALSE

Nový vektor dĺžky 0 je predurčený obsahovať logické hodnoty „áno” (TRUE) alebo „nie” (FALSE), alternatívne sa vytvorí aj príkazom v <- logical().

v <- logical(); v[2] <- TRUE; v   # definovanie posledného prvku určí dĺžku vektora
## [1]   NA TRUE
v <- logical(3); v[2] <- TRUE; v
## [1] FALSE  TRUE FALSE

Samozrejme, nový vektor akéhokoľvek typu sa dá vytvoriť priamo:

odpoveď <- c(TRUE, TRUE, FALSE, TRUE, FALSE)
ovocie <- c("jablko", "hruška", "pomaranč")
( komplexny_vektor <- c(1, 2i, 1+2i) )
## [1] 1+0i 0+2i 1+2i

Sekvencia

Pomerne často je treba vytvoriť číselný rad (angl. sequence), napr. $a, a+1, \ldots, b$. Na to poslúži príkaz so syntaxou a:b:

-2:5         # sekvencia s krokom 1
## [1] -2 -1  0  1  2  3  4  5

Viac možností ponúka funkcia seq:

seq(-2, 5)  # -2:5
## [1] -2 -1  0  1  2  3  4  5

seq(-2, 5, by = .5)     # prírastok o 0.5
##  [1] -2.0 -1.5 -1.0 -0.5  0.0  0.5  1.0  1.5  2.0  2.5  3.0  3.5  4.0  4.5  5.0

seq(-2, 5, length.out = 4)  # dĺžka sekvencie bude 4
## [1] -2.0000000  0.3333333  2.6666667  5.0000000

Sekvencia opakovaním jedného alebo viacerých prvkov sa dosiahne funkciou rep:

rep(9, times = 5)   # opakuj číslo 9 päť-krát
## [1] 9 9 9 9 9

rep(1:4, 2)  # opakuj sekvenciu 2-krát
## [1] 1 2 3 4 1 2 3 4
rep(1:4, each = 2)   # opakuj každý prvok sekvencie 2-krát
## [1] 1 1 2 2 3 3 4 4
rep(1:4, each=2, times=3)  # opakuj každý prvok 2-krát a to celé 3-krát
##  [1] 1 1 2 2 3 3 4 4 1 1 2 2 3 3 4 4 1 1 2 2 3 3 4 4
rep(1:4, 1:4)  # prvý prvok jedenkrát, druhý prvok 2-krát, ...
##  [1] 1 2 2 3 3 3 4 4 4 4

Manipulácia s prvkami

Výber prvkov (angl. subsetting) vektora sa najčastejšie robí pomocou hranatých zátvoriek:

x <- 10:17

x[1]            # prvý prvok
## [1] 10
x[c(5,8)]       # piaty A ôsmy prvok
## [1] 14 17
x[5:8]          # piaty AŽ ôsmy prvok
## [1] 14 15 16 17

x[-(5:8)]       # všetky okrem prvkov zadaných zápornym indexom
## [1] 10 11 12 13

Zvolené prvky je možné prepísať novými hodnotami:

x[1] <- 10.1      # ôsmemu prvku je priradená iná hodnota
x[c(7,8)] <- c(16.1, 17.1)
x                 # zároveň prebehla konverzia z typu integer na numeric
## [1] 10.1 11.0 12.0 13.0 14.0 15.0 16.1 17.1

Výber sa dá urobiť nielen indexami, ale aj logickými hodnotami, ktoré vznikli napr. porovnaním:

x > 15           # výsledkom porovnania je vektor logických hodnôt
## [1] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE

x[x>15 & x<17]          # výber všetkých prvkov x spĺňajúcich podmienku 15<x<17
## [1] 16.1

Ak vektor logických hodnôt nie je rovnakej veľkosti ako manipulovaný vektor, zreplikuje sa na potrebnú dĺžku.

(1:20)[c(TRUE,FALSE)]  # všetky nepárne čísla menšie ako 20
##  [1]  1  3  5  7  9 11 13 15 17 19

Konverzia medzi typmi

Konverzie medzi typmi atomických vektorov väčšinou prebiehajú implicitne, na pozadí,

c(TRUE, FALSE) * 1
## [1] 1 0

no niekedy je dobré vedieť konvertovať vektor aj explicitne.

as.numeric(c(TRUE,FALSE))
## [1] 1 0
as.numeric("4")
## [1] 4

as.logical(c(-1,0,1,2))
## [1]  TRUE FALSE  TRUE  TRUE
as.logical(c("FALSE","F"))
## [1] FALSE FALSE

as.character(1)
## [1] "1"
as.character(TRUE)
## [1] "TRUE"

Niektoré konverzie, prirodzene, nie sú definované:

as.numeric(c("A","Z"))
## Warning: NAs introduced by coercion
## [1] NA NA
as.logical("A")
## [1] NA

Porovnávanie

Porovnanie dvoch vektorov sa dá vykonať po prvkoch alebo súhrnne:

x <- 1:3     # priradenie sa dá reťaziť 
y <- c(1,2,3)
x == y            # porovnanie po prvkoch
## [1] TRUE TRUE TRUE
all.equal(x, y)   # približné porovnanie objektov ako celku
## [1] TRUE
identical(x, y)   # exaktné porovnanie objektov
## [1] FALSE

Výsledok posledného súhrnného porovnania je na prvý pohľad prekvapivý, ale to len do chvíle, kým neporovnáme spôsob uloženia oboch vektorov v pamäti (mode). Ak hodnoty y zaradíme medzi prirodzené čísla explicitne pomocou špeciálneho znaku L, vektory budú totožné:

typeof(x); typeof(y)
## [1] "integer"
## [1] "double"

y <- c(1L,2L,3L)
identical(x, y)
## [1] TRUE

Porovnanie reálnych čísel môže byť pri zaokrúhľovaní na úrovni strojovej presnosti zradné

0.9 == 1.1 - 0.2            # porovnanie numerických hodnôt
## [1] FALSE
identical(0.9, 1.1 - 0.2)
## [1] FALSE
all.equal(0.9, 1.1 - 0.2)
## [1] TRUE
# po prekročení zadanej tolerancie  zobrazí strednú relatívnu chybu:
all.equal(0.9, 1.1 - 0.2, tolerance = 1e-18)  
## [1] "Mean relative difference: 1.233581e-16"

1.2.2 Faktor

Dátový typ factor je interne reprezentovaný ako vektor obsahujúci iba prirodzené čísla (poradové čísla, indexy) a atribút levels (úrovne), v ktorom sú uložené jedinečné hodnoty vo forme znakových reťazcov. Navonok sa zobrazuje ako vektor týchto reťazcov postupne vyberaných z levels svojim indexom.

v <- c(10,40,40,30,40,30)    # vstupné hodnoty, môžu byť aj číselné
fv <- factor(v); fv          # funkcia ich zoradí a prevedie na znakové reťazce
## [1] 10 40 40 30 40 30
## Levels: 10 30 40
str(fv)     # uskladnenie v pamäti je však úspornejšie, než pri type character
##  Factor w/ 3 levels "10","30","40": 1 3 3 2 3 2
fv*2        # aritmetická operácia zlyhá, factor nie je ani character ani integer
## Warning in Ops.factor(fv, 2): '*' not meaningful for factors
## [1] NA NA NA NA NA NA
as.numeric(fv)                # konverzia na numerický typ vráti iba indexy úrovní
## [1] 1 3 3 2 3 2
as.numeric(as.character(fv))  # až dvojitou konverziou dostaneme pôvodný vektor
## [1] 10 40 40 30 40 30

1.2.3 Matica a viacrozmerné pole

Vytvorenie

Dátový typ matica je (interne) len vektor s atribútom dim (dimensions, rozmery) obsahujúcim počet riadkov a počet stĺpcov matice, pričom hodnoty vektora sú do matice napĺňané po stĺpcoch:

A <- 1:10
dim(A) <- c(2,5)    
A
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    3    5    7    9
## [2,]    2    4    6    8   10

Bežnejší spôsob vytvorenia matice je jej zaplnenie jedným vektorom pomocou funkcie matrix,

matrix(1:10, nrow = 5, ncol = 2)
##      [,1] [,2]
## [1,]    1    6
## [2,]    2    7
## [3,]    3    8
## [4,]    4    9
## [5,]    5   10
matrix(1:10, nrow = 5, ncol = 2, byrow = TRUE)  # zapĺňanie matice po riadkoch
##      [,1] [,2]
## [1,]    1    2
## [2,]    3    4
## [3,]    5    6
## [4,]    7    8
## [5,]    9   10

alebo zlepením viacerých vektorov do stĺpcov resp. riadkov.

cbind(1:5, 6:10)
##      [,1] [,2]
## [1,]    1    6
## [2,]    2    7
## [3,]    3    8
## [4,]    4    9
## [5,]    5   10
rbind(1:5, 6:10)
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    2    3    4    5
## [2,]    6    7    8    9   10

Maticové operácie

Videli sme, že klasický aritmetický operátor * násobil vektory po prvkoch. To isté by urobil aj s maticou (interne je vektorom), preto maticové násobenie je definované špeciálnym operátorom:

B <- A %*% t(A)
B
##      [,1] [,2]
## [1,]  165  190
## [2,]  190  220

Aby v príklade boli matice rozmerovo kompatibilné, druhá vznikla transpozíciou prvej. Ďalšie typické operácie s maticami je výpočet determinantu a inverznej matice:

det(B)    # determinant
## [1] 200
solve(B)
##       [,1]   [,2]
## [1,]  1.10 -0.950
## [2,] -0.95  0.825

Funkcia solve sa primárne používa na riešenie sústavy lineárnych algebraických rovníc, tu sme využili fakt, že inverzná matica $B^{-1}$ je riešením $x$ rovnice $Bx=I$, kde $I$ je jednotková matica.
Mimochodom, jednotková matica sa dá vytvoriť pomocou funkcie diag:

diag(1, nrow = 4)
##      [,1] [,2] [,3] [,4]
## [1,]    1    0    0    0
## [2,]    0    1    0    0
## [3,]    0    0    1    0
## [4,]    0    0    0    1

Manipulácia s prvkami

Výber prvkov sa opäť realizuje jednoduchými hranatými zátvorkami:

A
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    3    5    7    9
## [2,]    2    4    6    8   10
A[1,2]          # prvok z 1.riadku a 2.stĺpca matice A
## [1] 3
A[,2]           # druhý stlpec, výstup je štandardne zjednodušený na vektor
## [1] 3 4
A[1,,drop=FALSE]  # prvý riadok, vo výstupe nedošlo k vypusteniu druhého rozmeru
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    3    5    7    9

Viacrozmerné pole

Matica je špeciálnym prípadom viacrozmerného poľa (array). Vytvorme trojrozmerné pole z vektora znakov latinskej abecedy:

C <- array(letters[1:(3*4*2)], dim = c(3,4,2))
C    # výpis vo forme dvojrozmerných rezov
## , , 1
## 
##      [,1] [,2] [,3] [,4]
## [1,] "a"  "d"  "g"  "j" 
## [2,] "b"  "e"  "h"  "k" 
## [3,] "c"  "f"  "i"  "l" 
## 
## , , 2
## 
##      [,1] [,2] [,3] [,4]
## [1,] "m"  "p"  "s"  "v" 
## [2,] "n"  "q"  "t"  "w" 
## [3,] "o"  "r"  "u"  "x"

Výber prvkov poľa je podobný ako pri maticiach:

C[2,,1]
## [1] "b" "e" "h" "k"

1.2.4 Dátový rámec

Objekt data frame sa na prvý pohľad tvári ako matica, ale na rozdiel od nej dátový rámec môže mať stĺpce odlišného typu. Interne je to skôr zoznam (list, pozri nižšie) obsahujúci iba vektory rovnakej dĺžky, takže sa dá zobraziť ako tabuľka. Každý stĺpec zvyčajne predstavuje jednu pozorovanú veličinu a každý riadok jedno pozorovanie (pre každú veličinu).

Vytvorenie

Ak napríklad na križovatke pozorujeme, koľko pasažierov sa nachádza v každom aute a či sú všetci pripútaní bezpečnostným pásom, výsledný súbor údajov vo forme tabuľky data frame môže vyzerať nasledovne:

pocet_pasazierov <- c(1,3,2,5,2,2,1,1,2,1)
priputani <- c(T,T,F,T,F,F,T,F,F,T)  # skrátený zápis logických hodnôt
auta <- data.frame(pocet_pasazierov, priputani)
auta
##    pocet_pasazierov priputani
## 1                 1      TRUE
## 2                 3      TRUE
## 3                 2     FALSE
## 4                 5      TRUE
## 5                 2     FALSE
## 6                 2     FALSE
## 7                 1      TRUE
## 8                 1     FALSE
## 9                 2     FALSE
## 10                1      TRUE

Interná štruktúra dátového objektu:

attributes(auta)
## $names
## [1] "pocet_pasazierov" "priputani"       
## 
## $class
## [1] "data.frame"
## 
## $row.names
##  [1]  1  2  3  4  5  6  7  8  9 10
str(auta)
## 'data.frame':    10 obs. of  2 variables:
##  $ pocet_pasazierov: num  1 3 2 5 2 2 1 1 2 1
##  $ priputani       : logi  TRUE TRUE FALSE TRUE FALSE FALSE ...

Pozorované údaje sa v praxi častejšie (než manuálnym zadávaním) zvyknú do R načítať z externých dátových súborov - štandardne vo formáte CSV (z angl. comma-separated values). Napr. naše pozorovanie z križovatky by bolo uložené v súbore auta.txt:

Prieskum zo dňa 2.2.2022
počet_pasažierov pripútaní
1 áno
3 áno
2 nie
...

Najprv je dobré nastaviť pracovný adresár (najmä, ak sa importuje/exportuje viacero súborov). Na import textových dátových súborov slúži funkcia read.table:

setwd("D:/cesta/ku/súboru")  # alebo interaktívne pomocou funkcie choose.dir()
auta <- read.table("auta.txt", header = TRUE, sep = "", dec=".", skip=1)

Prostredníctvom argumentov sme funkcii povedali, nech načítanie začne druhým riadkom (skip), ako prvé nájde hlavičku tabuľky (header), že jednotlivé hodnoty sú oddelené „bielymi’ znakmi, napr. medzerami (sep) a akým znakom sú oddelené desatinné miesta reálnych čísel (dec, v našom prípade neuplatnené). Prostredie RStudio ponúka import dátových súborov interaktívne cez ponuku [File > Import dataset].

Výber prvkov

Pre ilustračné a výukové účely prostredie R obsahuje veľké množstvo vlastných súborov dát, príkazom data() sa otvorí ich zoznam v samostatnom okne (na samostatnej záložke). Vyberieme z nich napríklad merania priemeru (stĺpec s mätúcim názvom Girth), výšky (Height) a objemu (Volume) na vzorke jedného druhu okrasných stromov.

data(trees)  # načítanie dátového súboru, ktorý je súčasťou R
trees
##    Girth Height Volume
## 1    8.3     70   10.3
## 2    8.6     65   10.3
## 3    8.8     63   10.2
## 4   10.5     72   16.4
## 5   10.7     81   18.8
## 6   10.8     83   19.7
## 7   11.0     66   15.6
## 8   11.0     75   18.2
## 9   11.1     80   22.6
## 10  11.2     75   19.9
## 11  11.3     79   24.2
## 12  11.4     76   21.0
## 13  11.4     76   21.4
## 14  11.7     69   21.3
## 15  12.0     75   19.1
## 16  12.9     74   22.2
## 17  12.9     85   33.8
## 18  13.3     86   27.4
## 19  13.7     71   25.7
## 20  13.8     64   24.9
## 21  14.0     78   34.5
## 22  14.2     80   31.7
## 23  14.5     74   36.3
## 24  16.0     72   38.3
## 25  16.3     77   42.6
## 26  17.3     81   55.4
## 27  17.5     82   55.7
## 28  17.9     80   58.3
## 29  18.0     80   51.5
## 30  18.0     80   51.0
## 31  20.6     87   77.0

Z tabuľky potom možno stĺpce vyberať rôznymi spôsobmi:

trees[c("Girth","Height")]  # konkrétne stĺpce ich názvom
##    Girth Height
## 1    8.3     70
## 2    8.6     65
## 3    8.8     63
## 4   10.5     72
## 5   10.7     81
## 6   10.8     83
## 7   11.0     66
## 8   11.0     75
## 9   11.1     80
## 10  11.2     75
## 11  11.3     79
## 12  11.4     76
## 13  11.4     76
## 14  11.7     69
## 15  12.0     75
## 16  12.9     74
## 17  12.9     85
## 18  13.3     86
## 19  13.7     71
## 20  13.8     64
## 21  14.0     78
## 22  14.2     80
## 23  14.5     74
## 24  16.0     72
## 25  16.3     77
## 26  17.3     81
## 27  17.5     82
## 28  17.9     80
## 29  18.0     80
## 30  18.0     80
## 31  20.6     87
trees[1]  # konkrétny stĺpec jeho poradím; alebo napr. trees[c(1,2)]
##    Girth
## 1    8.3
## 2    8.6
## 3    8.8
## 4   10.5
## 5   10.7
## 6   10.8
## 7   11.0
## 8   11.0
## 9   11.1
## 10  11.2
## 11  11.3
## 12  11.4
## 13  11.4
## 14  11.7
## 15  12.0
## 16  12.9
## 17  12.9
## 18  13.3
## 19  13.7
## 20  13.8
## 21  14.0
## 22  14.2
## 23  14.5
## 24  16.0
## 25  16.3
## 26  17.3
## 27  17.5
## 28  17.9
## 29  18.0
## 30  18.0
## 31  20.6
trees[[1]]  # výsledkom však už nie je data.frame ale vektor
##  [1]  8.3  8.6  8.8 10.5 10.7 10.8 11.0 11.0 11.1 11.2 11.3 11.4 11.4 11.7 12.0
## [16] 12.9 12.9 13.3 13.7 13.8 14.0 14.2 14.5 16.0 16.3 17.3 17.5 17.9 18.0 18.0
## [31] 20.6
trees$Girth  # opäť vektor
##  [1]  8.3  8.6  8.8 10.5 10.7 10.8 11.0 11.0 11.1 11.2 11.3 11.4 11.4 11.7 12.0
## [16] 12.9 12.9 13.3 13.7 13.8 14.0 14.2 14.5 16.0 16.3 17.3 17.5 17.9 18.0 18.0
## [31] 20.6

Premennú Girth by sme medzi objektami v globálnom prostredí márne hľadali, existuje iba ako prvok dátového rámca trees,

Girth
## Error in eval(expr, envir, enclos): object 'Girth' not found

ale ak ho do globálneho prostredia pripojíme príkazom attach, prvok Girth je prístupný ako každý iný dátový objekt typu vektor:

attach(trees)  # sprístupnenie obsahu dátového rámca  
Girth
##  [1]  8.3  8.6  8.8 10.5 10.7 10.8 11.0 11.0 11.1 11.2 11.3 11.4 11.4 11.7 12.0
## [16] 12.9 12.9 13.3 13.7 13.8 14.0 14.2 14.5 16.0 16.3 17.3 17.5 17.9 18.0 18.0
## [31] 20.6
detach(trees)  # odpojenie

Prístup k premenným môže byť aj lokálny pomocou funkcie with:

with(trees, head(Girth) )  # head štandardne zobrazí prvých 6 hodnôt
## [1]  8.3  8.6  8.8 10.5 10.7 10.8

Možný je výber stĺpcov (od výšky po priemer) a riadkov podľa zadaných podmienok (výška väčšia ako 80 stôp a priemer väčší ako 10 palcov) prostredníctvom hranatých zátvoriek, alebo ešte elegantnejšie funkciou subset:

trees[trees$Height>80 & trees$Girth>10.0, c("Height","Volume")]     # klasika
##    Height Volume
## 5      81   18.8
## 6      83   19.7
## 17     85   33.8
## 18     86   27.4
## 26     81   55.4
## 27     82   55.7
## 31     87   77.0
subset(trees, subset = Height>80 & Girth>10.0, select = Height:Volume)
##    Height Volume
## 5      81   18.8
## 6      83   19.7
## 17     85   33.8
## 18     86   27.4
## 26     81   55.4
## 27     82   55.7
## 31     87   77.0

Tu vidieť, že operátor : niekedy poslúži na indikovanie inej než numerickej sekvencie.

1.2.5 Zoznam

Zoznam (list) je najvšeobecnejšia dátová štruktúra, môže obsahovať rôzne ďalšie dátové objekty, nielen vektor.

zoznam <- list(položka1 = c(1,2,3), položka2=c("hruska","jablko"), položka3=FALSE)
zoznam  # nemusí mať rovnaký počet riadkov/stĺpcov (na rozdiel od predošlých objektov)
## $položka1
## [1] 1 2 3
## 
## $položka2
## [1] "hruska" "jablko"
## 
## $položka3
## [1] FALSE

Výber prvkov (subsetting) funguje podobne ako pri data frame, pochopiteľne okrem výberu riadkov.

1.2.6 Časový rad

Dátový typ ts (angl. time series) je iba vektor s atribútom tsp, ktorý obsahuje začiatočný čas (ku ktorému sa vzťahuje prvá hodnota vektora), koncový čas a vzorkovaciu frekvenciu (počet údajov za prirodzenú časovú jednotku, napr. rok alebo deň).

rad <- ts(c(6,3,2,5, 7,3,4,5, 8,4), start=c(2020,1), frequency = 4)
rad    # štvrťročný časový rad od roku 2020
##      Qtr1 Qtr2 Qtr3 Qtr4
## 2020    6    3    2    5
## 2021    7    3    4    5
## 2022    8    4
tsp(rad)
## [1] 2020.00 2022.25    4.00

Môže obsahovať aj viac časových radov, vtedy je prvým argumentom namiesto vektoru matica.

1.2.7 Výraz

Tento dátový typ (angl. expression) je užitočný napr. pri symbolických výpočtoch alebo zobrazení matematických vzorcov v grafoch.

x <- 3; y <- 2.5; z <- 1
výraz <- expression( x/(y+exp(z)) )  # vytvorenie symbolického výrazu
výraz
## expression(x/(y + exp(z)))
eval(výraz)    # vyhodnotenie (evaluácia), čiže dosadenie skutočných hodnôt
## [1] 0.5749019

D(výraz, "y")  # parciálna derivácia podľa premennej y
## -(x/(y + exp(z))^2)

Jazyk R nie je veľmi vhodný na symbolické výpočty, na to sú určené počítačové algebraické systémy (angl. computer algebra system, skr. CAS) ako napr. Wolfram Mathematica/Alpha, Maxima alebo Yacas. Pomocou rozširujúceho balíka Ryacas sa však dá využiť funkcionalita systému Yacas:

Ryacas::yac("Factor(x^2+x-6)")
## [1] "(x-2)*(x+3)"

1.3 Jednoduché grafy

Funkciou na zobrazenie grafickej informácie v jazyku R je funkcia plot zo štandardnej knižnice base. Podľa triedy objektu vstupujúceho ako argument potom funkcia zavolá špecializovanú zobrazovaciu funkciu (metódu) z konkrétneho balíka. To je princíp fungovania objektovo orientovaného systému⁵, v jazyku R je najpoužívanejším systém S3. Metódy sú indikované názvom generickej funkcie a príponou „.trieda”. Nechajme si teraz vypísať všetky dostupné metódy pre funkciu plot:

methods("plot")
##  [1] plot.acf*           plot.data.frame*    plot.decomposed.ts*
##  [4] plot.default        plot.dendrogram*    plot.density*      
##  [7] plot.ecdf           plot.factor*        plot.formula*      
## [10] plot.function       plot.hclust*        plot.histogram*    
## [13] plot.HoltWinters*   plot.isoreg*        plot.lm*           
## [16] plot.medpolish*     plot.mlm*           plot.ppr*          
## [19] plot.prcomp*        plot.princomp*      plot.profile.nls*  
## [22] plot.R6*            plot.raster*        plot.spec*         
## [25] plot.stepfun        plot.stl*           plot.table*        
## [28] plot.ts             plot.tskernel*      plot.TukeyHSD*     
## see '?methods' for accessing help and source code

Zoznam závisí od toho, aké balíky sú aktuálne nainštalované. Teraz zobrazíme napríklad graf funkcie sínus:

plot(sin, from = 0, to = 2*pi, xlab = "os x")  # použije plot.function

Metóda plot.function si interne diskretizovala hodnoty premennej $x\in[0,2\pi]$, vypočítala v nich funkčné hodnoty a zavolala inú metódu (pravdepodobne plot.default), ktorej podala oba vektory so súradnicami a popis osi $x$ (xlab). To môžme urobiť aj sami, a v jednom príklade si zároveň ukážeme, ako

umiestniť viac grafov vedľa seba (par + mfrow),
zmeniť typ grafu, t.j. geometrickú reprezentáciu diskrétnych bodov (type),
skladať viac grafov do jedného (plot + lines/points),
vložiť matematický výraz (pozri nápovedu ?plotmath),
pridať legendu:

par(mfrow=c(1,2))      # rozdelenie zobrazovanej oblasti do matice 1x2
x <- seq(0, 2*pi, length=16+1)           # diskrétne hodnoty premennej x
# prvý graf:
plot(x, y = sin(x), type="b", lty="dashed")  # graf dvojíc {x[i], sin(x[i])}
# druhý graf:
plot(x, sin(x),          # prvá zobrazovacia funkcia určuje rozsah zobrazenia
     ylab = "",          # popis osí (môže byť aj prázdny znak)
     main = expression(  # aj nadpis
       "McLaurinov rozvoj: sin(x)" %~~% x + frac(x^3, "3!") - frac(x^5, "5!")
       ),    # ak má text obsahovať matematické výrazy, musí byť typu expression
     type="p",   # typ geometrie: p=body, l=čiara, b=obe, s=schody, h=histogram
     pch="+",   # tvar bodovej značky (číselne alebo znakom)
     cex.main = 0.9    # koeficient zväčšenia nadpisu
     )    
lines(x, x - x^3/6 + x^5/factorial(5),  # funkcie ako lines a points pridajú vrstvy
      col = 4,      # color 1=čierna, 2=červená, 3=zelená, 4=modrá ...
      lty = "dashed"   # linetype: 0=blank, 1=solid, 2=dashed, 3=dotted, 4=dotdash ...
      )   
points(x = 0, y = 0, pch = 19, col = 2)
legend("bottomleft",      # umiestnenie legendy
       legend = c("funkcia", "polynóm", "bod aproximácie"),   # text
       lty = c("blank","dashed",NA),   # grafické parametre každej položky ...
       pch = c(3,NA,19), 
       col = c(1,4,2)
       )


par(mfrow=c(1,1))     # nastavenie mriežky grafického okna na pôvodné hodnoty

Iný príklad metódy je pre časový rad, keď hodnoty horizontálnej súradnice odvodí z časového atribútu vektoru rad (definovaný vyššie):

plot(rad)   # lepši výsledok externým balíkom pomocou plot(xts::as.xts(rad))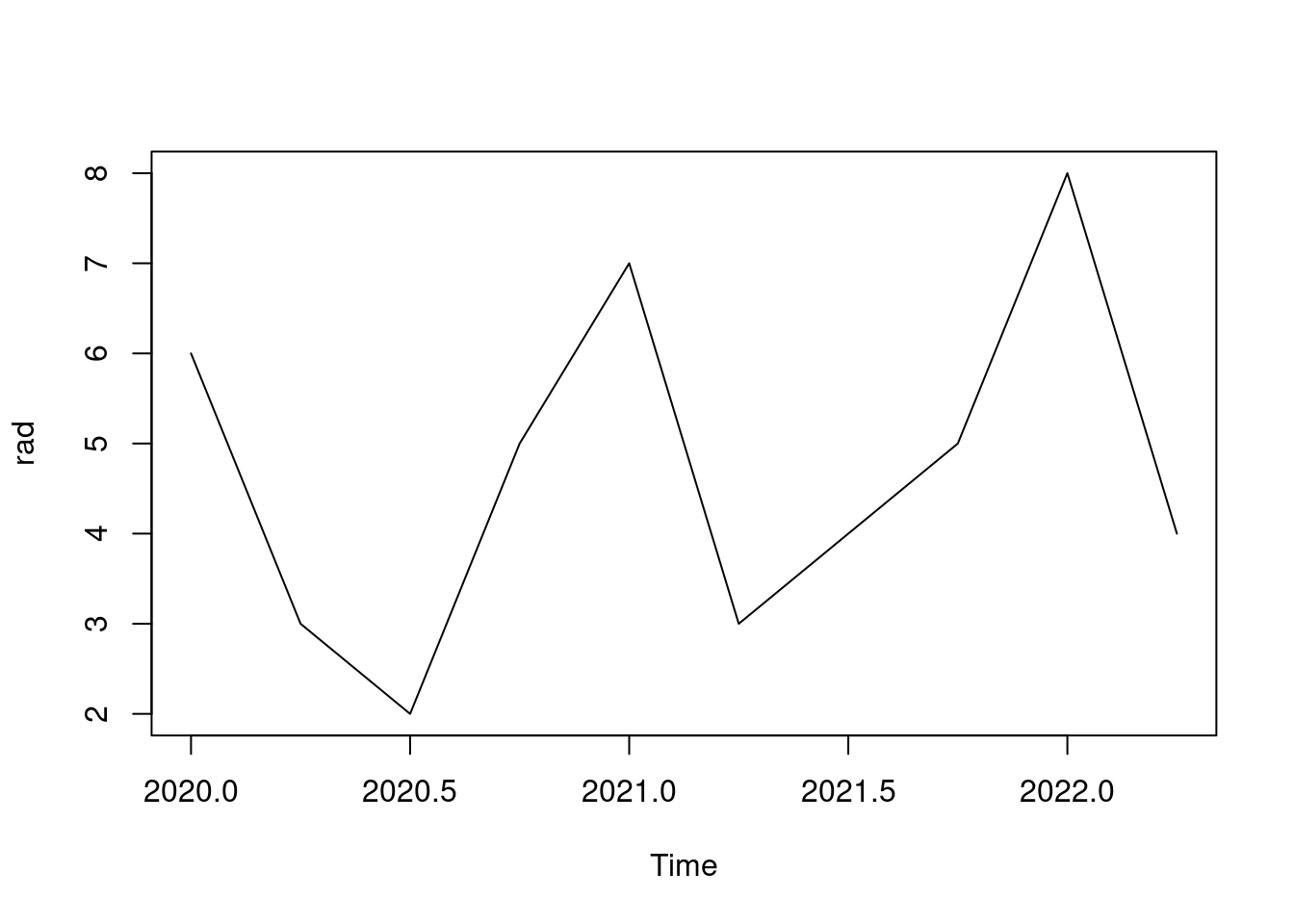

Export obrázku do súboru sa deje presmerovaním grafického výstupu do tzv. grafického zariadenia (device), napr. vo formáte PNG, BMP, JPEG, PDF a ďalších. Prvý príkaz dané zariadenie otvorí, posledný zavrie.

png(file="sinus.png", width=600, height=400, units="px")
plot(sin, from=0, to=2*pi) 
dev.off()

V prostredí RStudio sa dajú obrázky exportovať aj z kontextovej ponuky.

Demonštračné ukážky základnej grafiky, či už dvoj alebo trojrozmernej, si možno pozrieť pomocou generickej funkcie demo:

demo(graphics)
demo(persp)

Ukážkami pokročilejšej grafiky sa inšpirujeme napr. na stránkach:

http://www.r-graph-gallery.com/
http://rgraphgallery.blogspot.sk/
vyhladaním “r graphics” v skupine Images
galéria interaktívnej grafiky https://shiny.rstudio.com/gallery/

1.4 Programovanie

Hoci je prostredie R vďaka rozsiahlej zásobe preddefinovaných funkcií silným analytickým softvérom, predsa by jeho použiteľnosť silno utrpela, keby sa nedali vytvárať vlastné funkcie a tie jednoducho aplikovať po prvkoch dátových objektov, ako je zvykom v programovacích jazykoch. Prejdeme si tie základné.

1.4.1 Cykly a podmienky

Podmienky a cykly sa dajú zapísať pomocou rovnakých slov ako v známom jazyku C: if, else, for, while, repeat, break, next.

Majme údaje uložené v dátovom rámci

dat <- data.frame(
  a = 1:5,
  b = runif(5),   # náhodné čísla z rovnomerného rozdelenia v intervale [0,1]
  c = c(2,0.3,4,-1,0)
); dat
##   a         b    c
## 1 1 0.6206360  2.0
## 2 2 0.9257996  0.3
## 3 3 0.6881803  4.0
## 4 4 0.2752442 -1.0
## 5 5 0.4423349  0.0

pre ktorý chceme zistiť medián každého stĺpca. Z hľadiska elegancie riešenia môžeme na problém ísť buď so „sekerou”,

median(dat$a)
## [1] 3
median(dat$b)
## [1] 0.620636
median(dat$c)
## [1] 0.3

alebo „motorovou pílou”,

vysledok <- vector("double", ncol(dat))  # inicializácia kontajnera
for (i in 1:length(vysledok)) {     # i = 1,2,3  (pozor, i je globálna premenná)
  vysledok[i] <- median(dat[[i]])      
}
vysledok
## [1] 3.000000 0.620636 0.300000

no pokročilý používateľ R si vyberie „laserový meč” (ako v Hviezdnych vojnách).

sapply(dat, median)     
##        a        b        c 
## 3.000000 0.620636 0.300000

Funkcia sapply (z angl. apply and simplify) je len jednou zo skupiny funkcií, ktoré aplikujú funkciu na jednotlivé prvky dátového objektu, ďalšie sú napr. apply (aplikovanie na stĺpce alebo riadky matice), lapply (podobne ako sapply, len bez pokusu o zjednodušenie výstupu), mapply (cez prvky viacerých objektov).

apply(dat, MARGIN = 2, FUN = median)  # pre MARGIN=1 by FUN bola aplikovaná na riadky
##        a        b        c 
## 3.000000 0.620636 0.300000
lapply(dat, median)
## $a
## [1] 3
## 
## $b
## [1] 0.620636
## 
## $c
## [1] 0.3

mapply(FUN = '^', 1:5, 5:1)    # alternatívne (1:5)^(5:1)
## [1]  1 16 27 16  5

Hoci je for cyklus výpočtovo oveľa pomalší než vektorizované fukcie jazyka R, stále sa využíva. Jednak ide o klasiku, ktorej rozumejú aj ľudia so znalosťou iných pogramovacích jazykov, no najmä je ho výhodné použiť v iteračných cykloch (so známym počtom opakovaní), kedy každé opakovanie závisí od toho predošlého (cyklus sa nedá vykonať paralelne).

Konštrukcie while a repeat sa využívajú v iteračných cykoch s vopred neznámym počtom opakovaní. Nasledujú ilustračné príklady, kde je okrem ovládacích slov next (ukončí aktuálne pokračovanie, cyklus pokračuje ďalším) a break (ukončí opakovanie aj cyklus) použitá aj podmienková konštrukcia if-else (ak platí podmienka, vykoná sa jeden príkaz, inak sa vykoná druhý príkaz):

a <- 0
for (i in 1:20) {
  a <- i^2
  if(a <= 10 ) {
    cat('a = ', a, '(<= 10)'); cat('\n')   # okamžitý výpis, so zalomením riadku
    next
  } else {
    cat("Kritická hodnota prekročená, koniec cyklu!")
    break
  }
}
## a =  1 (<= 10)
## a =  4 (<= 10)
## a =  9 (<= 10)
## Kritická hodnota prekročená, koniec cyklu!
i     # hodnota iteračnej premennej nie je po skončení cyklu vymazaná
## [1] 4

Pre úplnosť, vektorizovanou náhradou za podmienkovú konštrukciu if(cond) expr1 else expr2 je funkcia ifelse(cond,expr1,expr2):

a <- c(-1,2,10); b <- c(2,2,2)
ifelse(a > b, a, b)           # v tomto prípade má rovnaký efekt aj pmax(a,b)
## [1]  2  2 10

V nasledujúcom príklade sa opakuje telo cyklu pokiaľ je na jeho začiatku splnená podmienka:

i <- a <- 1
while(a < 10) {
  cat(a, ", ")
  i <- i + 1
  a <- i^2
}
## 1 , 4 , 9 ,

V ďalšom príklade sa podmienka nachádza na konci opakovania. To tvorí náhodný výpis čísla z N(0,1) rozdelenia (zaokrúhleného pomocou round), kým čislo nepresiahne nastavenú hodnotu. Funkcia set.seed nastaví generátor pseudonáhodných čísel, aby bolo možné kedykoľvek zreprodukovať rovnaký výsledok:

set.seed(123)  
repeat {a <- round(rnorm(1), digit=2); if (a > 1.6) break; cat(a, " ")}
## -0.56  -0.23  1.56  0.07  0.13

1.4.2 Vlastné funkcie

Vytvoríme jednoduchú kvadratickú funkciu a zavoláme ju s argumentom $x = 3$:

f <- function(x) x^2       
f(3)
## [1] 9

Teraz definujeme všeobecnejšiu funkciu $f(x,y) = x^y$:

f1 <- function(zaklad=5, exponent) zaklad^exponent
# Príklad použitia:
f1()        # skončí chybou, ak chýba prednastavená hodnota
## Error in f1(): argument "exponent" is missing, with no default
f1(exponent = 2)
## [1] 25
f1(,2)      # ak je argument nepomenovaný, musí byť dodaný v stanovenom poradí
## [1] 25
f1(exponent = 2, zaklad = 4)  # pomenované argumenty v inom poradí
## [1] 16
f1(ex = 5:1, zak = 1:5)       # názvy argumentov možno skracovať, ak sú jedinečné
## [1]  1 16 27 16  5

Všimnime si z posledného príkladu, že naša funkcia f1 je vďaka operátoru ^ automaticky vektorizovaná.

Nasledujúca funkcia vráti maximum dvoch skalárnych čísel alebo reťazec znakov:

f2 <- function(a, b) {
  if(is.numeric(c(a,b))) {
    if(a < b) return(b)
    if(a > b) return(a)
    else return("Sú rovnaké.")
  }
  else return("Akceptujem iba čísla.")
}
# Príklad použitia:
f2(4,7)
## [1] 7
f2(0, exp(log(0)))
## [1] "Sú rovnaké."
f2("Adam","Eva")
## [1] "Akceptujem iba čísla."
f2(1:5, 5:1)
## Error in if (a < b) return(b): the condition has length > 1

Funkcia f2 nie je vektorizovaná, preto ak by sme ju chceli aplikovať postupne na všetky prvky s rovnakým poradím vo vstupných vektoroch, museli by sme použiť funkciu mapply:

mapply(f2, 1:5, 5:1)
## [1] "5"           "4"           "Sú rovnaké." "4"           "5"

Existuje aj iné riešenie, funkcia sa dá explicitne vektorizovať:

f2 <- Vectorize(f2)
f2(1:5, 5:1)
## [1] "5"           "4"           "Sú rovnaké." "4"           "5"

Výsledný vektor je skonvertovaný na znakový, pretože aspoň jeden prvok je reťazec znakov.

Funkcia môže byť aj bez názvu (tzv. anonymná funkcia):

( function(x) x^2 )(1:5)     # skrátený zápis funkcie: (\(x) x^2)(5)
## [1]  1  4  9 16 25

Užitočným nástrojom pri hľadaní chýb vo vlastnej funkcii (angl. debugging) je príkaz browser() umiestnený do tela funkcie. Po zavolaní funkcie s konkrétnymi argumentami nám sprístupní jej prostredie aj so všetkými lokálnymi premennými.

Po čase plodného používania R je pravdepodobné, že budeme mať vytvorené kolekcie funkcií (prípadne iných objektov) určených pre riešenie konkrétneho okruhu úloh. Ak uložíme definície funkcií (objektov) do súboru, povedzme mojeprogramy.r, môžme ich kedykoľvek použiť v inom skriptovom súbore pripojením na začiatku pomocou príkazu source("mojeprogramy.r").

1.4.3 Prostredie lokálnych premenných

Niekedy chceme urobiť výpočet s pomocnými premennými, ktoré nemajú byť globálne viditeľné, napríklad preto, aby neprepísali hodnotu nejakej existujúcej premennej s rovnakým menom:

a <- 0     # definícia hodnoty v globálnom prostredí
local({
  b <- a
  a <- 8   # hodnota premennej a v lokálnom prostredí
  a + b    # 8 + 0
})
## [1] 8
a          # globálna hodnota sa nezmenila
## [1] 0

Ako lokálne premenné sa dajú použiť aj prvky dátového objektu typu list alebo data.frame:

with(dat, a+c)
## [1] 3.0 2.3 7.0 3.0 5.0

1.5 Webstránky pre samoštúdium

Manuály v slovenčine/češtine:
* seriál na IT spravodajskom portáli Root.cz https://www.root.cz/serialy/programovaci-jazyk-r/ (Tišňovský 2020)
* od študentov http://rmanual.fri.uniza.sk/
* publikácia Jak pracovat s jazykem R https://www.math.muni.cz/~kolacek/vyuka/vypsyst/navod_R.pdf

Množstvo manuálov a tématicky zameranej literatúry vo svetovom jazyku:
* https://cran.r-project.org/other-docs.html
* https://bookdown.org/

Zábavná literatúra:
* YaRrr! The Pirate’s Guide to R https://bookdown.org/ndphillips/YaRrr/
* The R inferno https://www.burns-stat.com/pages/Tutor/R_inferno.pdf

Odporúčané:
* Advanced R http://adv-r.had.co.nz/ (Wickham 2019)
* R for data science http://r4ds.had.co.nz/ (Wickham a Grolemund 2016)
* R style guide https://style.tidyverse.org

Tématický prehľad populárnych balíkov:
* Oficiálny archív https://cran.r-project.org/web/views/
* Najpopulárnejšie https://support.rstudio.com/hc/en-us/articles/201057987-Quick-list-of-useful-R-packages
* Balíky, prostredia, zdroje informácií https://github.com/qinwf/awesome-R

1.6 Cvičenie

Načítajte súbor údajov mtcars z balíka datasets a uložte ho do premennej s názvom dat.
Zobrazte štruktúru objektu dat a prvých 5 riadkov. Zoznámte sa s významom jednotlivých stĺpcov.
Preveďte premennú mpg na jednotky km/l a uložte ako novú premennú kml do toho istého objektu.
Vytvorte logický vektor aut indikujúci, či ide o auto s automatickou prevodovkou a pomocou neho vypočítajte priemerný dojazd (v km na 1l paliva) automobilov zvlášť s automatickou a zvlášť s manuálnou prevodovkou.
Zobrazte tabuľku všetkých áut s piatimi rýchlostnými stupňami a hmotnosťou do 3000 libier, ktorá obsahuje iba údaje o počte valcov, zdvihovom objeme a výkone motora.
Vytvorte funkciu na prevod jednotiek, ktorá bude mať 3 argumenty (s názvom)[s hodnotami]: prevádzanú hodnotu (x), imperiálnu jednotku (impunit)[míľa, galón, palec, libra], smer prevodu do SI (toSI)[TRUE,FALSE], pričom zodpovedajúcimi jednotkami v metrickej sústave SI budú km, l, dm, kg. (Využite pri tom funkciu switch a automatickú konverziu módu vektora toSI z logického na numerický.)
Pomocou for cyklu skonvertujte hodnoty zdvihového objemu valcov z kubických palcov na litre. Pomocou funkcie sapply preveďte hmotnosť vozidiel na tony. Zachovajte pri tom pôvodné názvy premenných a použite funkciu na prevod jednotiek z predošlej úlohy.
Nastavte pracovný adresár a načítajte tabuľku údajov zo súboru mtcars.txt (uloženého v pracovnom adresári) do objektu typu data.frame. Dbajte pri tom na správne nastavenie parametrov importu ako počet riadkov neštrukturovaného popisu, prítomnosť názvu stĺpcov, oddelovací znak desatinných miest, znak oddelujúci stĺpce tabuľky a znak chýbajúcich hodnôt (NA). Porovnajte načítaný data frame s pôvodným dat.

Literatúra

Peng, Roger D. 2016. R programming for data science. Leanpub. https://bookdown.org/rdpeng/rprogdatascience.

Tišňovský, Pavel. 2020. “Seriál Programovací jazyk R”. https://www.root.cz/serialy/programovaci-jazyk-r/.

———. 2019. Advanced R. CRC press. https://adv-r.hadley.nz.

Wickham, Hadley, a Garrett Grolemund. 2016. R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. 1st vyd. O’Reilly Media, Inc. https://r4ds.had.co.nz/.

Programovacie jazyky sa podľa svojej prevládajúcej implementácie delia na interpretované a kompilované. Výhodou druhej skupiny je optimalizácia na oveľa rýchlejší beh programu, naopak nevýhodou je obmedzenie interakcie pri tvorbe programu. Príkladom kompilovaných jazykov sú C a Fortran, na ktorých stojí aj množstvo výpočtových knižníc samotného systému R.↩︎
Trieda definuje správanie objektov (jej členov) popísaním ich vlastností a vzťahu ku iným triedam. Metóda je zodpovedná za vykonanie operácie nad objektom z konkrétnej triedy.↩︎