Capítulo 5 Modelos en R
5.1 Paquetes necesarios para este capítulo
Para este capítulo necesitas tener instalado el paquete tidyverse, broom y MuMIn.
En este capítulo se explicará como generar modelos en R, el como obtener información y tablas a partir de los modelos con el paquete Broom (Robinson and Hayes 2018) y una leve introducción a la selección de modelos con el paquete MuMIn (Barton 2018)
Dado que este libro es un apoyo para el curso BIO4022, esta clase puede también ser seguida en este link. El video de la clase se encontrará disponible en este link.
5.2 Modelos estadísticos
Un modelo estadístico intenta explicar las causas de un suceso basado en un muestreo de la población total. El supuesto es que si la muestra que obtenemos de la población es representativa de esta, podremos inferir las causas de la variación de la población midiendo variables explicativas. En general tenemos una variable respuesta (fenómeno que queremos explicar), y una o varias variables explicativas que generarían deterministamente parte de la variabilidad en la variable respuesta.
5.2.1 Ejemplo
Tomemos el ejemplo de la base de datos CO2 presente en R (Potvin, Lechowicz, and Tardif 1990). Supongamos que nos interesa saber que factores afectan la captación de \(CO_2\) en las plantas.
| Plant | Type | Treatment | conc | uptake |
|---|---|---|---|---|
| Qn1 | Quebec | nonchilled | 95 | 16.0 |
| Qn1 | Quebec | nonchilled | 175 | 30.4 |
| Qn1 | Quebec | nonchilled | 250 | 34.8 |
| Qn1 | Quebec | nonchilled | 350 | 37.2 |
| Qn1 | Quebec | nonchilled | 500 | 35.3 |
| Qn1 | Quebec | nonchilled | 675 | 39.2 |
| Qn1 | Quebec | nonchilled | 1000 | 39.7 |
| Qn2 | Quebec | nonchilled | 95 | 13.6 |
| Qn2 | Quebec | nonchilled | 175 | 27.3 |
| Qn2 | Quebec | nonchilled | 250 | 37.1 |
| Qn2 | Quebec | nonchilled | 350 | 41.8 |
| Qn2 | Quebec | nonchilled | 500 | 40.6 |
| Qn2 | Quebec | nonchilled | 675 | 41.4 |
| Qn2 | Quebec | nonchilled | 1000 | 44.3 |
| Qn3 | Quebec | nonchilled | 95 | 16.2 |
| Qn3 | Quebec | nonchilled | 175 | 32.4 |
| Qn3 | Quebec | nonchilled | 250 | 40.3 |
| Qn3 | Quebec | nonchilled | 350 | 42.1 |
| Qn3 | Quebec | nonchilled | 500 | 42.9 |
| Qn3 | Quebec | nonchilled | 675 | 43.9 |
En la tabla 5.1 vemos las primeras 20 observaciones de esta base de datos. Vemos que dentro de los factores que tenemos para explicar la captación de \(CO_2\) estan:
- Type: Subespecie de la planta (Missisipi o Quebec)
- Treatment: Tratamiento de la plnata, enfriado (chilled) o no enfriado (nonchilled)
- conc: Concentración ambiental de \(CO_2\), en mL/L.
Una posible explicación que nos permitiría intentar explicar este fenómeno, es que las plantas de distintas subespecies, tendrán distinta captación de \(CO_2\), lo cual exlploramos en el gráfico 5.1:
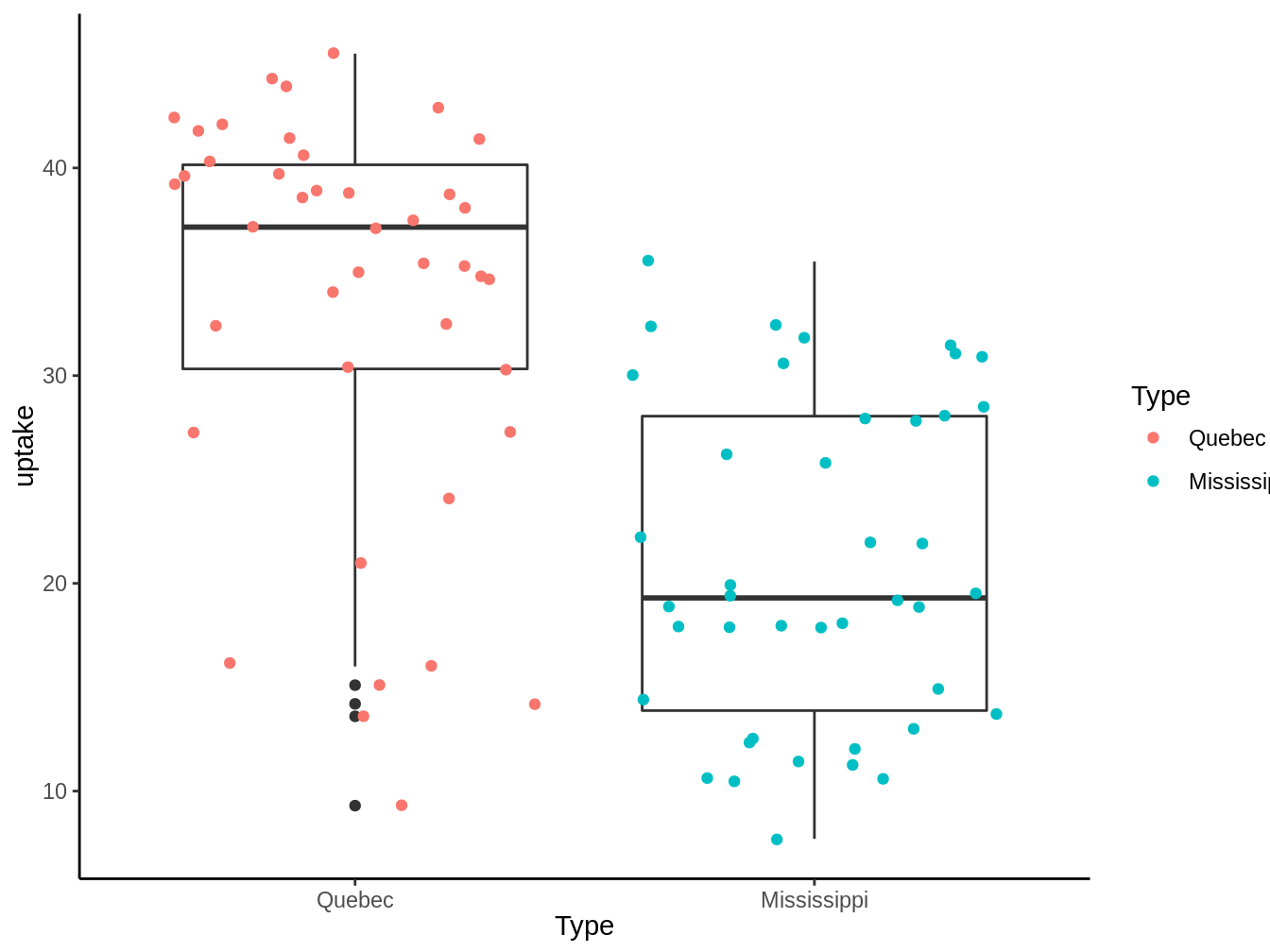
Figura 5.1: Captación de CO2 por plantas dependiente de su subespecie
Vemos que se observa una tendencia a que las plantas con origen en Quebec capten más \(CO_2\) que las que estan en el Mississippi, pero ¿Podemos decir efectivamente que ambas poblaciónes tienen medias distintas medias? Es ahí donde entran los modelos.
5.2.2 Representando un modelo en R
En R la mayoría de los modelos se representan con el siguiente codigo:
En este modelo, tenemos la variable respuesta Y, la cual puede estar explcada por una o multiples variables explicativas X, es por esto que el simbolo ~ se lee explicado por, donde lo que esta a su izquerada es la variable respuesta y a la derecha la variable explicativa. Los datos se encuentran en un data frame y finalmente usaremos alguna función, que identificará algún modelo. Algunas de estas funciones las encontramos en la tabla 5.2
| Modelos | Funcion |
|---|---|
| Prueba de t | t.test() |
| ANOVA | aov() |
| Modelo lineal simple | lm() |
| modelo lineal generalizado | glm() |
| Modelo aditivo | gam() |
| Modelo no lineal | nls() |
| modelos lineales mixtos | lmer() |
| Boosted regression trees | gbm() |
5.2.3 Volvamos al ejemplo de las plantas
Para este ejemplo usaremos un modelo lineal simple, para esto siguiendo la tabla 5.2 usaremos la función lm:
5.2.3.1 usando broom para sacarle más a tu modelo
El paquete broom (Robinson and Hayes 2018) es un paquete adyacente al tidyverse (por lo que debes cargarlo aparte del tidyverse), el cual nos permite tomar información de modelos generados en formato tidy. Hoy veremos 3 funciones de broom, estas son glance, tidy y augment.
5.2.3.1.1 glance
la función glance, nos entregará información general del modelo, como el valor de p, el \(R^2\), log-likelihood, grados de libertad, y/o otros parametros dependiendo del modelo a utilizar. Esta información nos es entregada en un formato de data frame, como vemos en el código siguiente y en la tabla 5.3
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.346713 | 0.3387461 | 8.794012 | 43.5191 | 0 | 2 | -300.8007 | 607.6014 | 614.8939 | 6341.441 | 82 |
5.2.3.1.2 tidy
la función tidy, nos entregará información sobre los parametros del modelo, esto es el intercepto, la pendiente y/o interacciones, como vemos en el código siguiente y en la tabla 5.4
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 33.54286 | 1.356945 | 24.719384 | 0 |
| TypeMississippi | -12.65952 | 1.919011 | -6.596901 | 0 |
5.2.3.1.3 augment
la función augment, nos entregará para cada observación de nuestro modelo, varios parametros importantes como el valor predicho, los residuales, el distancia de cook entre otros, esto nos sirve principalmente para estudiar los supuestos de nuestro modelo. A continuación vemos el uso de la función augment y 20 de sus observaciones en la tabla 5.5
| uptake | Type | .fitted | .se.fit | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|---|
| 25.8 | Mississippi | 20.88333 | 1.356945 | 4.916667 | 0.0238095 | 8.830837 | 0.0039050 | 0.5658697 |
| 39.2 | Quebec | 33.54286 | 1.356945 | 5.657143 | 0.0238095 | 8.825228 | 0.0051698 | 0.6510927 |
| 14.4 | Mississippi | 20.88333 | 1.356945 | -6.483333 | 0.0238095 | 8.818039 | 0.0067901 | -0.7461807 |
| 22.0 | Mississippi | 20.88333 | 1.356945 | 1.116667 | 0.0238095 | 8.847238 | 0.0002014 | 0.1285196 |
| 32.4 | Mississippi | 20.88333 | 1.356945 | 11.516667 | 0.0238095 | 8.752828 | 0.0214255 | 1.3254778 |
| 12.3 | Mississippi | 20.88333 | 1.356945 | -8.583333 | 0.0238095 | 8.795321 | 0.0119012 | -0.9878742 |
| 28.1 | Mississippi | 20.88333 | 1.356945 | 7.216667 | 0.0238095 | 8.810831 | 0.0084130 | 0.8305816 |
| 13.0 | Mississippi | 20.88333 | 1.356945 | -7.883333 | 0.0238095 | 8.803604 | 0.0100392 | -0.9073097 |
| 12.5 | Mississippi | 20.88333 | 1.356945 | -8.383333 | 0.0238095 | 8.797760 | 0.0113530 | -0.9648558 |
| 26.2 | Mississippi | 20.88333 | 1.356945 | 5.316667 | 0.0238095 | 8.827905 | 0.0045662 | 0.6119065 |
| 35.5 | Mississippi | 20.88333 | 1.356945 | 14.616667 | 0.0238095 | 8.694104 | 0.0345123 | 1.6822634 |
| 42.1 | Quebec | 33.54286 | 1.356945 | 8.557143 | 0.0238095 | 8.795643 | 0.0118286 | 0.9848599 |
| 31.1 | Mississippi | 20.88333 | 1.356945 | 10.216667 | 0.0238095 | 8.773216 | 0.0168615 | 1.1758580 |
| 30.3 | Quebec | 33.54286 | 1.356945 | -3.242857 | 0.0238095 | 8.840611 | 0.0016988 | -0.3732274 |
| 10.6 | Mississippi | 20.88333 | 1.356945 | -10.283333 | 0.0238095 | 8.772231 | 0.0170823 | -1.1835308 |
| 28.5 | Mississippi | 20.88333 | 1.356945 | 7.616667 | 0.0238095 | 8.806572 | 0.0093715 | 0.8766185 |
| 22.2 | Mississippi | 20.88333 | 1.356945 | 1.316667 | 0.0238095 | 8.846891 | 0.0002800 | 0.1515380 |
| 10.5 | Mississippi | 20.88333 | 1.356945 | -10.383333 | 0.0238095 | 8.770741 | 0.0174161 | -1.1950400 |
| 37.2 | Quebec | 33.54286 | 1.356945 | 3.657143 | 0.0238095 | 8.838566 | 0.0021605 | 0.4209084 |
| 27.9 | Mississippi | 20.88333 | 1.356945 | 7.016667 | 0.0238095 | 8.812874 | 0.0079531 | 0.8075632 |
5.2.3.2 Selección de modelos usando broom y el AIC
El AIC, o Criterio de informacion de Akaike (Aho, Derryberry, and Peterson 2014), es una medida de cuanta información nos entrega un modelo dada su complejidad. Esta última medida a partir del número de parámetros que tiene. Cuanto más bajo sea el AIC, mejor comparativamente es un modelo, y en general, un modelo que sea dos unidades de AIC menor que otro modelo, será considerado un modelo que es significativamente mejor que otro.
La formula del criterio de selección de Akaike es la que vemos en la ecuación (5.1).
\[\begin{equation} AIC = 2 K - 2 \ln{(\hat{L})} \tag{5.1} \end{equation}\]
Donde \(K\) es el número de parametros, lo cual podemos ver con tidy, si vemos la tabla 5.4, vemos que el modelo Fit1 tiene 2 parametros, esto es \(K\) es igual a 2.
El log-likelihood del modelo (\(\ln{(\hat{L})}\)) es el ajuste que este tiene a los datos. Cuanto más positivo es este valor mejor se ajusta el modelo a los datos, y cuanto mas negativo es, menos se ajusta a los datos, en nuestro modelo, usando glance, podemos ver que el valor del log-likelyhood del modelo es de -300.8 (ver tabla 5.4).
Por lo tanto remplazando la ecuación (5.1), obtenemos 605.6, que es un valor muy cercano a los 608, que aparecen en el glance del modelo (tabla 5.4).
5.2.3.2.1 Modelos candidatos
Veamos la figura 5.2. para pensar cuales podrían ser modelos interesantes a explorar.
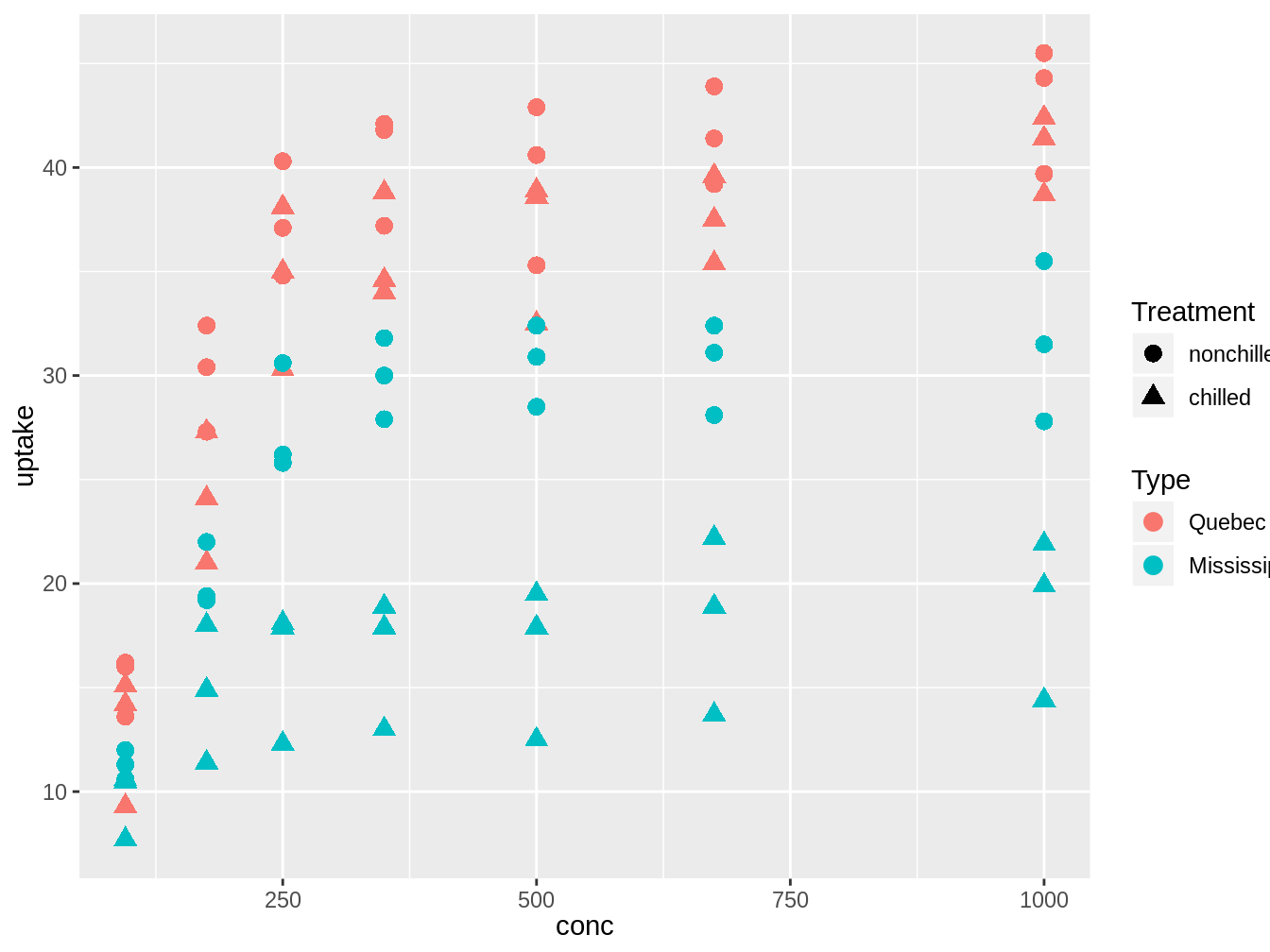
Figura 5.2: Gráfico exploratorio para generar modelos de la base de datos CO2
Referencias
Aho, Ken, DeWayne Derryberry, and Teri Peterson. 2014. “Model Selection for Ecologists: The Worldviews of Aic and Bic.” Ecology 95 (3). Wiley Online Library: 631–36.
Barton, Kamil. 2018. MuMIn: Multi-Model Inference. https://CRAN.R-project.org/package=MuMIn.
Potvin, Catherine, Martin J Lechowicz, and Serge Tardif. 1990. “The Statistical Analysis of Ecophysiological Response Curves Obtained from Experiments Involving Repeated Measures.” Ecology 71 (4). Wiley Online Library: 1389–1400.
Robinson, David, and Alex Hayes. 2018. Broom: Convert Statistical Analysis Objects into Tidy Tibbles. https://CRAN.R-project.org/package=broom.