6 Ensambladores: Random Forest - Parte II
6.1 Ejemplo introductorio
Tomado de https://datascienceplus.com/random-forests-in-r/
require(randomForest)## Loading required package: randomForest## randomForest 4.6-12## Type rfNews() to see new features/changes/bug fixes.##
## Attaching package: 'randomForest'## The following object is masked from 'package:dplyr':
##
## combine## The following object is masked from 'package:ggplot2':
##
## marginrequire(MASS)#Package which contains the Boston housing dataset## Loading required package: MASS##
## Attaching package: 'MASS'## The following object is masked from 'package:dplyr':
##
## selectattach(Boston)
set.seed(101)
dim(Boston)## [1] 506 14##training Sample with 300 observations
train=sample(1:nrow(Boston),300)
str(Boston) ## 'data.frame': 506 obs. of 14 variables:
## $ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
## $ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
## $ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
## $ chas : int 0 0 0 0 0 0 0 0 0 0 ...
## $ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
## $ rm : num 6.58 6.42 7.18 7 7.15 ...
## $ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
## $ dis : num 4.09 4.97 4.97 6.06 6.06 ...
## $ rad : int 1 2 2 3 3 3 5 5 5 5 ...
## $ tax : num 296 242 242 222 222 222 311 311 311 311 ...
## $ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
## $ black : num 397 397 393 395 397 ...
## $ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
## $ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...Usaremos la variable medv como la variable objetivo la cual es la mediana del costo de vivienda. Se usará 500 árboles.
Boston.rf=randomForest(medv ~ . , data = Boston , subset = train)
Boston.rf##
## Call:
## randomForest(formula = medv ~ ., data = Boston, subset = train)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 4
##
## Mean of squared residuals: 12.34243
## % Var explained: 85.09El error medio cuadrático y la varianza explicada son calculados usando la estimación OBB. Los 2/3 se usa para el entrenamiento y el restante 1/3 para la validación de los árboles. El número de variables seleccionadas aleatoriamente en cada ramificación es 4 por defecto.
#Plotting the Error vs Number of Trees Graph.
plot(Boston.rf)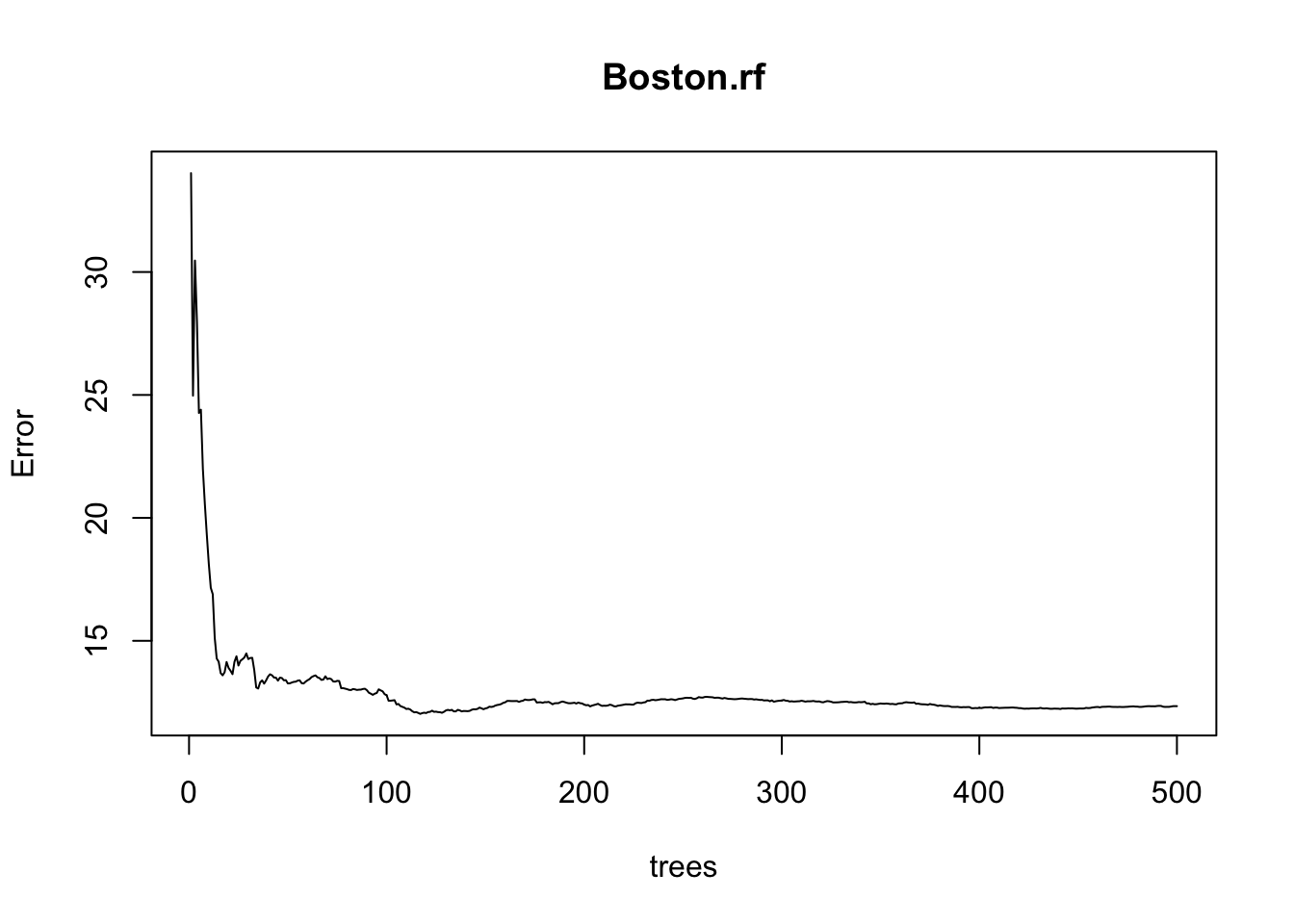
Este gráfico muestra el error vs. el número de árboles. Se puede ver como el error disminuye a medida que se incrementa el número de árboles. Para este ejemplo hemos dejado por fuera un conjunto adicional de test (a pesar de que indicamos que por la naturaleza del algoritmo esto no sería necesario). Inspeccionemos como efectivamente cambian o no los valores de error evaluados en los dos conjuntos diferentes: test y OOB sample.
Para esto vamos a probar como cambia el error de acuerdo al número de atributos aleatorios candidatos en cada ramificación de los árboles.
oob.err=double(13)
test.err=double(13)
##mtry is no of Variables randomly chosen at each split
for(mtry in 1:13)
{
rf=randomForest(medv ~ . , data = Boston , subset = train,mtry=mtry,ntree=400)
oob.err[mtry] = rf$mse[400]
pred<-predict(rf,Boston[-train,]) #Predictions on Test Set for each Tree
test.err[mtry]= with(Boston[-train,], mean( (medv - pred)^2)) #Mean Squared Test Error
cat(mtry," ") #printing the output to the console
}## 1 2 3 4 5 6 7 8 9 10 11 12 13test.err## [1] 26.07809 18.45827 15.91703 14.82310 14.42375 14.43336 14.45756
## [8] 14.62056 14.46458 14.79109 14.90324 15.13335 15.30873oob.err## [1] 20.04025 14.31230 13.19824 12.48773 12.93861 12.96235 12.86396
## [8] 13.69076 13.81878 14.36594 14.83846 14.85143 14.84741Un gráfico que ilustra los resultados previos.
matplot(1:mtry , cbind(oob.err,test.err), pch=19 , col=c("red","blue"),type="b",ylab="Mean Squared Error",xlab="Number of Predictors Considered at each Split")
legend("topright",legend=c("Out of Bag Error","Test Error"),pch=19, col=c("red","blue"))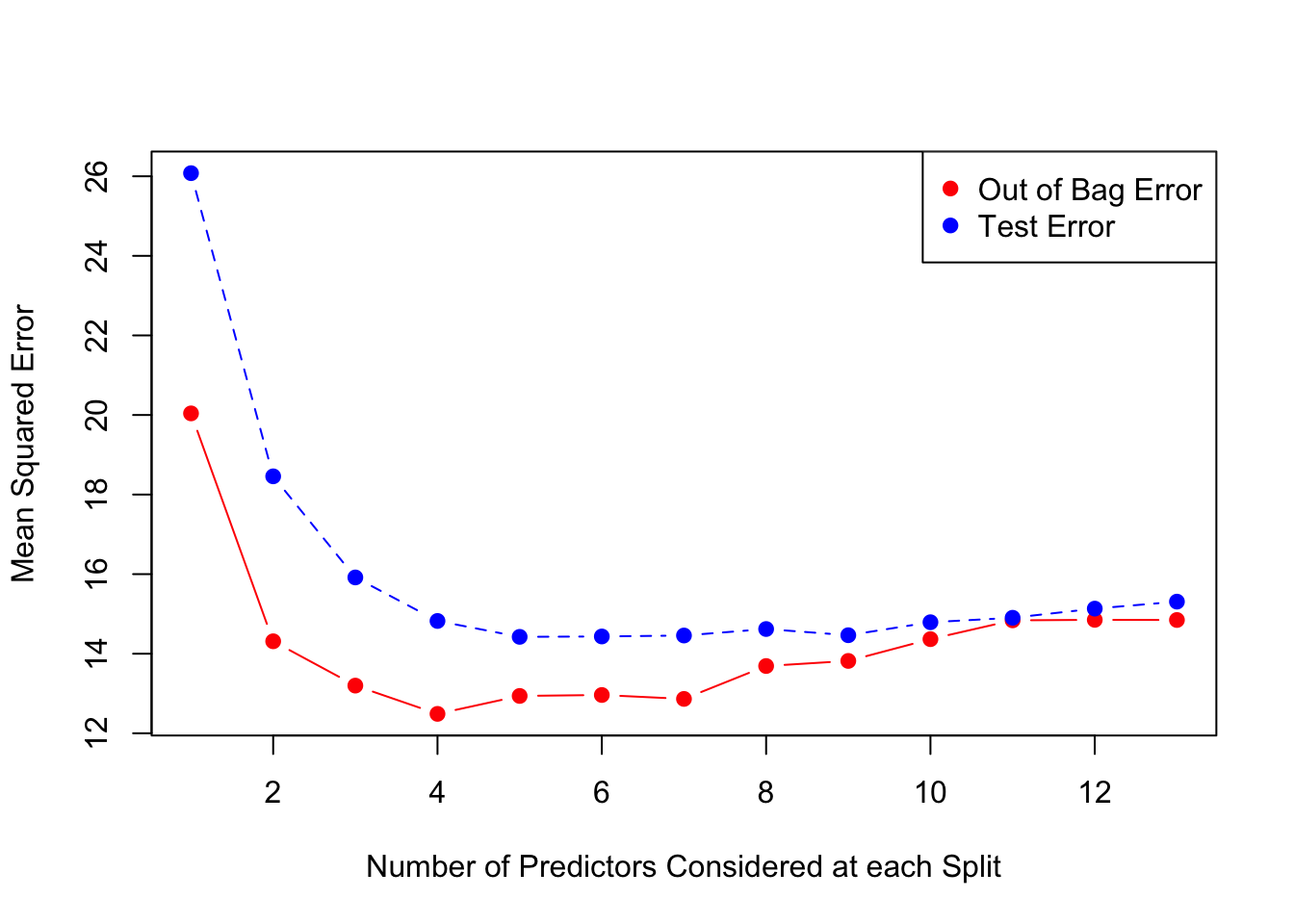
El caso extremo de la derecha con 13 variables aleatorias (todos los predictores posibles) se reduce al modelo de Bagging. Finalmente un primer acercamiento a la visualización de la importancia de atributos.
varImpPlot(rf)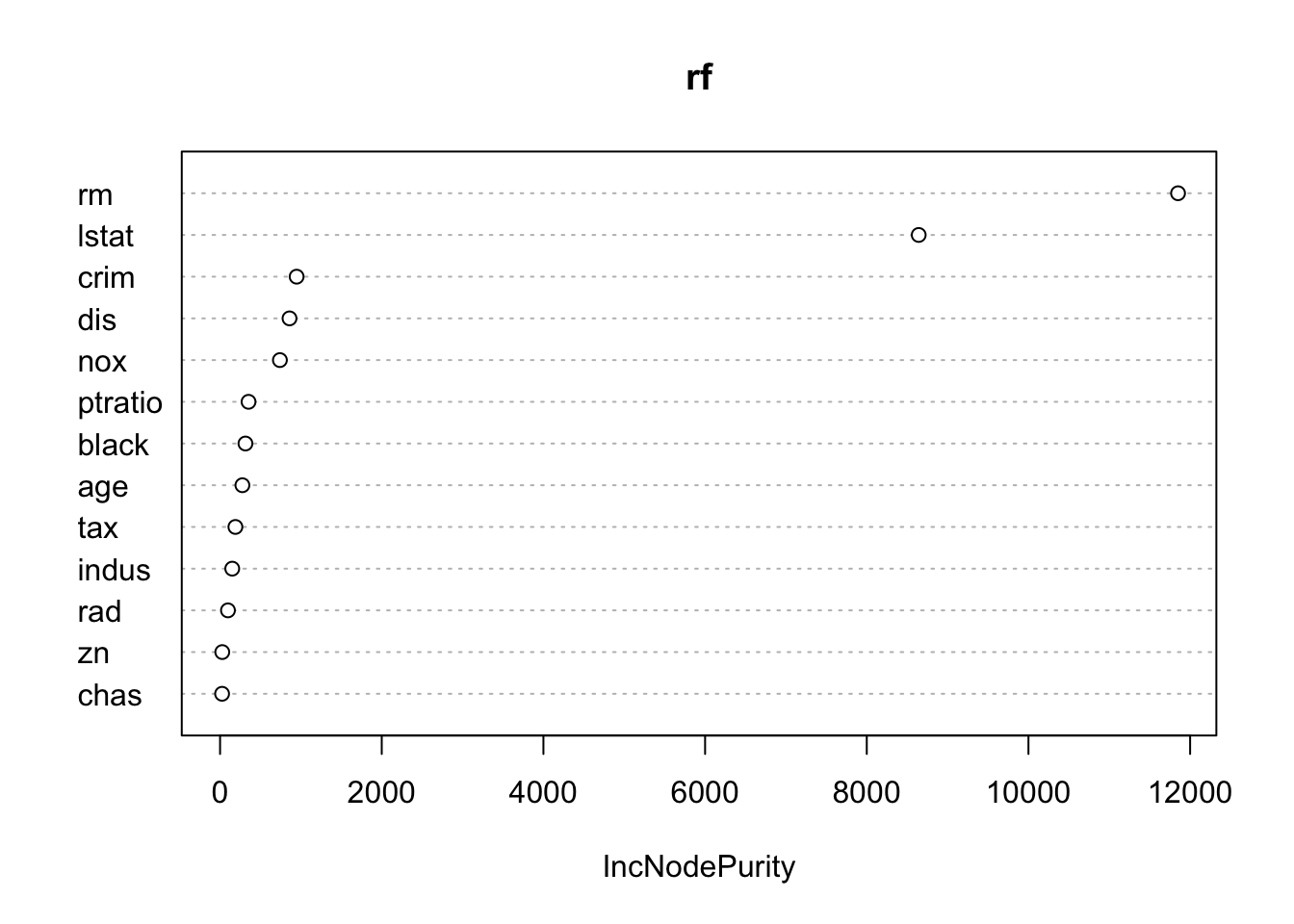
6.2 Ejemplo de regresión + tuning
library(AmesHousing)
library(rsample) # data splitting
library(dplyr) # data wrangling
library(ranger) # más rápida que randomforest##
## Attaching package: 'ranger'## The following object is masked from 'package:randomForest':
##
## importancelibrary(h2o) # computación distribuida##
## ----------------------------------------------------------------------
##
## Your next step is to start H2O:
## > h2o.init()
##
## For H2O package documentation, ask for help:
## > ??h2o
##
## After starting H2O, you can use the Web UI at http://localhost:54321
## For more information visit http://docs.h2o.ai
##
## ----------------------------------------------------------------------##
## Attaching package: 'h2o'## The following objects are masked from 'package:stats':
##
## cor, sd, var## The following objects are masked from 'package:base':
##
## %*%, %in%, &&, apply, as.factor, as.numeric, colnames,
## colnames<-, ifelse, is.character, is.factor, is.numeric, log,
## log10, log1p, log2, round, signif, trunc, ||library(ggplot2)Cargamos los datos y los separamos en entreanmiento y test.
# Entrenamiento (70%) y test (30%) a partir de AmesHousing::make_ames() data.
# Usar semilla para reproducibilidad: set.seed
set.seed(123)
ames_split <- initial_split(AmesHousing::make_ames(), prop = .7)
ames_train <- training(ames_split)
ames_test <- testing(ames_split)
str(ames_train)## Classes 'tbl_df', 'tbl' and 'data.frame': 2051 obs. of 81 variables:
## $ MS_SubClass : Factor w/ 16 levels "One_Story_1946_and_Newer_All_Styles",..: 1 1 6 6 12 12 6 6 1 6 ...
## $ MS_Zoning : Factor w/ 7 levels "Floating_Village_Residential",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ Lot_Frontage : num 141 93 74 78 41 43 60 75 0 63 ...
## $ Lot_Area : int 31770 11160 13830 9978 4920 5005 7500 10000 7980 8402 ...
## $ Street : Factor w/ 2 levels "Grvl","Pave": 2 2 2 2 2 2 2 2 2 2 ...
## $ Alley : Factor w/ 3 levels "Gravel","No_Alley_Access",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ Lot_Shape : Factor w/ 4 levels "Regular","Slightly_Irregular",..: 2 1 2 2 1 2 1 2 2 2 ...
## $ Land_Contour : Factor w/ 4 levels "Bnk","HLS","Low",..: 4 4 4 4 4 2 4 4 4 4 ...
## $ Utilities : Factor w/ 3 levels "AllPub","NoSeWa",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ Lot_Config : Factor w/ 5 levels "Corner","CulDSac",..: 1 1 5 5 5 5 5 1 5 5 ...
## $ Land_Slope : Factor w/ 3 levels "Gtl","Mod","Sev": 1 1 1 1 1 1 1 1 1 1 ...
## $ Neighborhood : Factor w/ 28 levels "North_Ames","College_Creek",..: 1 1 7 7 17 17 7 7 7 7 ...
## $ Condition_1 : Factor w/ 9 levels "Artery","Feedr",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ Condition_2 : Factor w/ 8 levels "Artery","Feedr",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ Bldg_Type : Factor w/ 5 levels "OneFam","TwoFmCon",..: 1 1 1 1 5 5 1 1 1 1 ...
## $ House_Style : Factor w/ 8 levels "One_Story","One_and_Half_Fin",..: 1 1 6 6 1 1 6 6 1 6 ...
## $ Overall_Qual : Factor w/ 10 levels "Very_Poor","Poor",..: 6 7 5 6 8 8 7 6 6 6 ...
## $ Overall_Cond : Factor w/ 10 levels "Very_Poor","Poor",..: 5 5 5 6 5 5 5 5 7 5 ...
## $ Year_Built : int 1960 1968 1997 1998 2001 1992 1999 1993 1992 1998 ...
## $ Year_Remod_Add : int 1960 1968 1998 1998 2001 1992 1999 1994 2007 1998 ...
## $ Roof_Style : Factor w/ 6 levels "Flat","Gable",..: 4 4 2 2 2 2 2 2 2 2 ...
## $ Roof_Matl : Factor w/ 8 levels "ClyTile","CompShg",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ Exterior_1st : Factor w/ 16 levels "AsbShng","AsphShn",..: 4 4 14 14 6 7 14 7 7 14 ...
## $ Exterior_2nd : Factor w/ 17 levels "AsbShng","AsphShn",..: 11 4 15 15 6 7 15 7 7 15 ...
## $ Mas_Vnr_Type : Factor w/ 5 levels "BrkCmn","BrkFace",..: 5 4 4 2 4 4 4 4 4 4 ...
## $ Mas_Vnr_Area : num 112 0 0 20 0 0 0 0 0 0 ...
## $ Exter_Qual : Factor w/ 4 levels "Excellent","Fair",..: 4 3 4 4 3 3 4 4 4 4 ...
## $ Exter_Cond : Factor w/ 5 levels "Excellent","Fair",..: 5 5 5 5 5 5 5 5 3 5 ...
## $ Foundation : Factor w/ 6 levels "BrkTil","CBlock",..: 2 2 3 3 3 3 3 3 3 3 ...
## $ Bsmt_Qual : Factor w/ 6 levels "Excellent","Fair",..: 6 6 3 6 3 3 6 3 3 3 ...
## $ Bsmt_Cond : Factor w/ 6 levels "Excellent","Fair",..: 3 6 6 6 6 6 6 6 6 6 ...
## $ Bsmt_Exposure : Factor w/ 5 levels "Av","Gd","Mn",..: 2 4 4 4 3 4 4 4 4 4 ...
## $ BsmtFin_Type_1 : Factor w/ 7 levels "ALQ","BLQ","GLQ",..: 2 1 3 3 3 1 7 7 1 7 ...
## $ BsmtFin_SF_1 : num 2 1 3 3 3 1 7 7 1 7 ...
## $ BsmtFin_Type_2 : Factor w/ 7 levels "ALQ","BLQ","GLQ",..: 7 7 7 7 7 7 7 7 7 7 ...
## $ BsmtFin_SF_2 : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bsmt_Unf_SF : num 441 1045 137 324 722 ...
## $ Total_Bsmt_SF : num 1080 2110 928 926 1338 ...
## $ Heating : Factor w/ 6 levels "Floor","GasA",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ Heating_QC : Factor w/ 5 levels "Excellent","Fair",..: 2 1 3 1 1 1 3 3 1 3 ...
## $ Central_Air : Factor w/ 2 levels "N","Y": 2 2 2 2 2 2 2 2 2 2 ...
## $ Electrical : Factor w/ 6 levels "FuseA","FuseF",..: 5 5 5 5 5 5 5 5 5 5 ...
## $ First_Flr_SF : int 1656 2110 928 926 1338 1280 1028 763 1187 789 ...
## $ Second_Flr_SF : int 0 0 701 678 0 0 776 892 0 676 ...
## $ Low_Qual_Fin_SF : int 0 0 0 0 0 0 0 0 0 0 ...
## $ Gr_Liv_Area : int 1656 2110 1629 1604 1338 1280 1804 1655 1187 1465 ...
## $ Bsmt_Full_Bath : num 1 1 0 0 1 0 0 0 1 0 ...
## $ Bsmt_Half_Bath : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Full_Bath : int 1 2 2 2 2 2 2 2 2 2 ...
## $ Half_Bath : int 0 1 1 1 0 0 1 1 0 1 ...
## $ Bedroom_AbvGr : int 3 3 3 3 2 2 3 3 3 3 ...
## $ Kitchen_AbvGr : int 1 1 1 1 1 1 1 1 1 1 ...
## $ Kitchen_Qual : Factor w/ 5 levels "Excellent","Fair",..: 5 1 5 3 3 3 3 5 5 5 ...
## $ TotRms_AbvGrd : int 7 8 6 7 6 5 7 7 6 7 ...
## $ Functional : Factor w/ 8 levels "Maj1","Maj2",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ Fireplaces : int 2 2 1 1 0 0 1 1 0 1 ...
## $ Fireplace_Qu : Factor w/ 6 levels "Excellent","Fair",..: 3 6 6 3 4 4 6 6 4 3 ...
## $ Garage_Type : Factor w/ 7 levels "Attchd","Basment",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ Garage_Finish : Factor w/ 4 levels "Fin","No_Garage",..: 1 1 1 1 1 3 1 1 1 1 ...
## $ Garage_Cars : num 2 2 2 2 2 2 2 2 2 2 ...
## $ Garage_Area : num 528 522 482 470 582 506 442 440 420 393 ...
## $ Garage_Qual : Factor w/ 6 levels "Excellent","Fair",..: 6 6 6 6 6 6 6 6 6 6 ...
## $ Garage_Cond : Factor w/ 6 levels "Excellent","Fair",..: 6 6 6 6 6 6 6 6 6 6 ...
## $ Paved_Drive : Factor w/ 3 levels "Dirt_Gravel",..: 2 3 3 3 3 3 3 3 3 3 ...
## $ Wood_Deck_SF : int 210 0 212 360 0 0 140 157 483 0 ...
## $ Open_Porch_SF : int 62 0 34 36 0 82 60 84 21 75 ...
## $ Enclosed_Porch : int 0 0 0 0 170 0 0 0 0 0 ...
## $ Three_season_porch: int 0 0 0 0 0 0 0 0 0 0 ...
## $ Screen_Porch : int 0 0 0 0 0 144 0 0 0 0 ...
## $ Pool_Area : int 0 0 0 0 0 0 0 0 0 0 ...
## $ Pool_QC : Factor w/ 5 levels "Excellent","Fair",..: 4 4 4 4 4 4 4 4 4 4 ...
## $ Fence : Factor w/ 5 levels "Good_Privacy",..: 5 5 3 5 5 5 5 5 1 5 ...
## $ Misc_Feature : Factor w/ 6 levels "Elev","Gar2",..: 3 3 3 3 3 3 3 3 5 3 ...
## $ Misc_Val : int 0 0 0 0 0 0 0 0 500 0 ...
## $ Mo_Sold : int 5 4 3 6 4 1 6 4 3 5 ...
## $ Year_Sold : int 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 ...
## $ Sale_Type : Factor w/ 10 levels "COD","CWD","Con",..: 10 10 10 10 10 10 10 10 10 10 ...
## $ Sale_Condition : Factor w/ 6 levels "Abnorml","AdjLand",..: 5 5 5 5 5 5 5 5 5 5 ...
## $ Sale_Price : int 215000 244000 189900 195500 213500 191500 189000 175900 185000 180400 ...
## $ Longitude : num -93.6 -93.6 -93.6 -93.6 -93.6 ...
## $ Latitude : num 42.1 42.1 42.1 42.1 42.1 ...set.seed(123)
# default RF model
m1 <- randomForest(
formula = Sale_Price ~ .,
data = ames_train
)
m1##
## Call:
## randomForest(formula = Sale_Price ~ ., data = ames_train)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 26
##
## Mean of squared residuals: 659550782
## % Var explained: 89.83# número de árboles con el menor MSE
which.min(m1$mse)## [1] 344# RMSE de este modelo óptimo RF
sqrt(m1$mse[which.min(m1$mse)])## [1] 25673.56.2.1 Tuning inicial
Si se desea ajustar inicialmente el parámetro mtry se puede usar el comando randomForest::tuneRF para una evaluación rápida y sencilla.
La función tuneRF necesita indicar de manera separada los datos predictores y la variable objetivo (respuesta).
# names of features
features <- setdiff(names(ames_train), "Sale_Price")
set.seed(123)
m2 <- tuneRF(
x = ames_train[features],
y = ames_train$Sale_Price,
ntreeTry = 350, # número de árboles
mtryStart = 5, # valor inicial
stepFactor = 1.5, # factor de paso para incremento de mtry
improve = 0.01, # OBB error para si ha tenido una mejora del 1%
trace = TRUE #
)## mtry = 5 OOB error = 762415867
## Searching left ...
## mtry = 4 OOB error = 802224340
## -0.0522136 0.01
## Searching right ...
## mtry = 7 OOB error = 726606619
## 0.04696813 0.01
## mtry = 10 OOB error = 692769021
## 0.04656935 0.01
## mtry = 15 OOB error = 671771621
## 0.03030938 0.01
## mtry = 22 OOB error = 664775551
## 0.01041436 0.01
## mtry = 33 OOB error = 669849982
## -0.007633299 0.01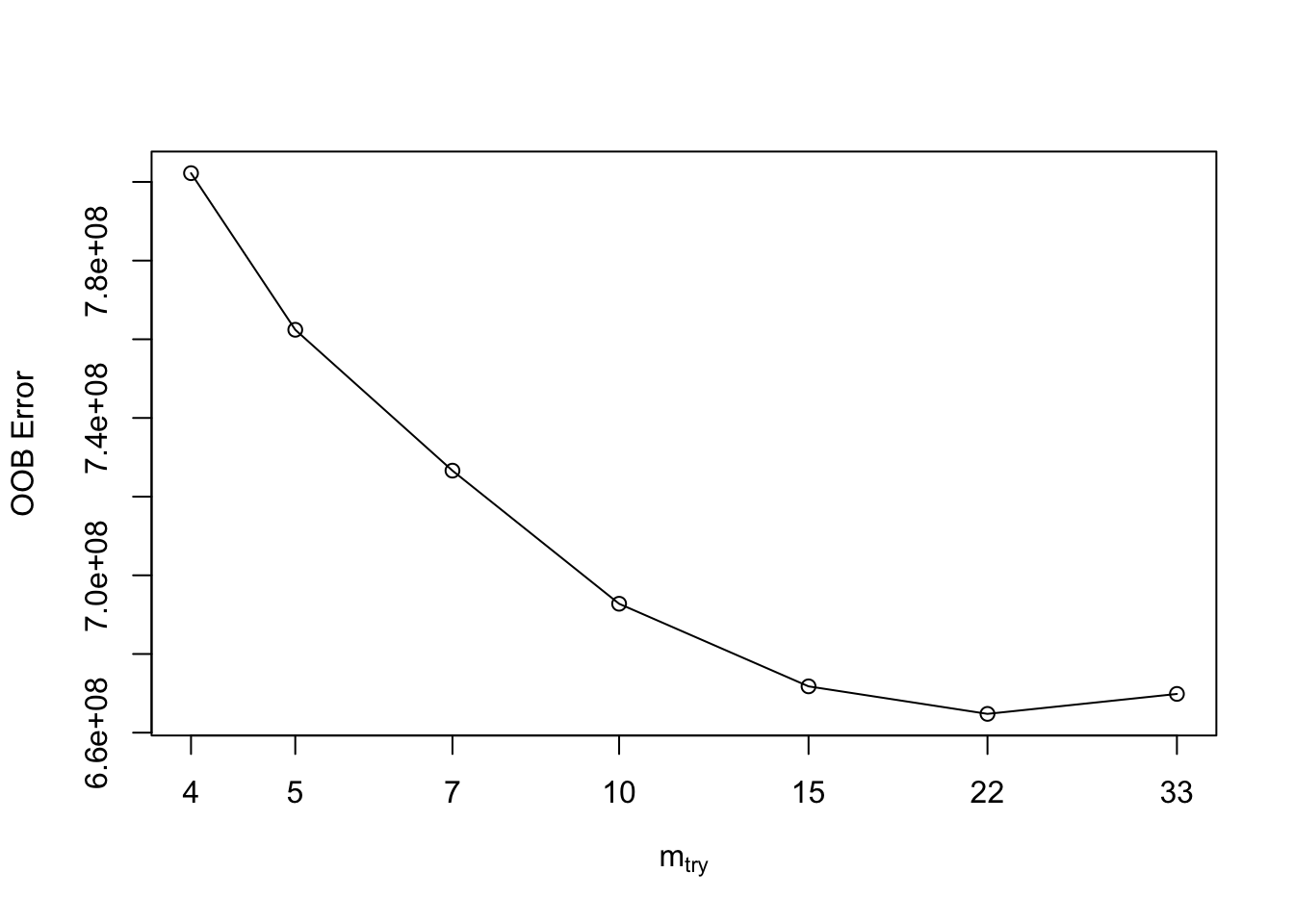
6.3 Utilizando la librería ranger
Esta librería puede ser 6 veces más rápida que randomforest.
# randomForest speed
system.time(
ames_randomForest <- randomForest(
formula = Sale_Price ~ .,
data = ames_train,
ntree = 350,
mtry = floor(length(features) / 3)
)
)## user system elapsed
## 24.128 0.063 24.227# ranger speed
system.time(
ames_ranger <- ranger(
formula = Sale_Price ~ .,
data = ames_train,
num.trees = 350,
mtry = floor(length(features) / 3)
)
)## user system elapsed
## 4.836 0.054 0.453Para generar un “grid search”, vamos a construir nuestra grilla de hyper-parámetros. Vamos a buscar a través de 96 modelos diferentes con variaciones en mtry, mínimo tamaño de muestras en el nodo, y tamaño de la muestra.
# hyperparameter grid search
hyper_grid <- expand.grid(
mtry = seq(20, 30, by = 2),
node_size = seq(3, 9, by = 2),
sampe_size = c(.55, .632, .70, .80),
OOB_RMSE = 0
)
# total number of combinations
nrow(hyper_grid)## [1] 96Ahora iteramos a través de las combinaciones y aplicamos 350 árboles (similar al valor que obtuvimos en pasos anteriores, 344) para simplificar el ejemplo y el tiempo de cómputo.
Resultados:
- El OOB RMSE tiene un rango entre ~26,000-27,000.
- Los 10 mejores modelos tienen valores RMSE justo alrededor de los 26,000
- Los modelos con muestras ligeramente más grandes (70-80%) y árboles más profundos (3-5 observationes en un nodo hoja) tienen un mejor rendimiento.
- Se obtienen diferentes valores de mtry values en los 10 mejores modelos lo que denota que no es en extremo influyente.
for(i in 1:nrow(hyper_grid)) {
# train model
model <- ranger(
formula = Sale_Price ~ .,
data = ames_train,
num.trees = 305,
mtry = hyper_grid$mtry[i],
min.node.size = hyper_grid$node_size[i],
sample.fraction = hyper_grid$sampe_size[i],
seed = 123 # Notese el seteo de la semilla
)
# add OOB error to grid
hyper_grid$OOB_RMSE[i] <- sqrt(model$prediction.error)
}
hyper_grid %>%
dplyr::arrange(OOB_RMSE) %>%
head(10)## mtry node_size sampe_size OOB_RMSE
## 1 20 5 0.8 26059.73
## 2 20 3 0.8 26074.55
## 3 28 3 0.8 26081.40
## 4 22 3 0.8 26128.50
## 5 28 5 0.8 26162.54
## 6 26 3 0.8 26162.87
## 7 26 5 0.7 26162.92
## 8 26 5 0.8 26180.37
## 9 22 5 0.8 26180.89
## 10 26 7 0.8 26200.37Ahora definimos nuestro mejor modelo de acuerdo a lo que hemos identificado anteriormente.
OOB_RMSE <- vector(mode = "numeric", length = 100)
for(i in seq_along(OOB_RMSE)) {
optimal_ranger <- ranger(
formula = Sale_Price ~ .,
data = ames_train,
num.trees = 350,
mtry = 22,
min.node.size = 5,
sample.fraction = .8,
importance = 'impurity' #para evaluar importancia de variables
)
OOB_RMSE[i] <- sqrt(optimal_ranger$prediction.error)
}
hist(OOB_RMSE, breaks = 20)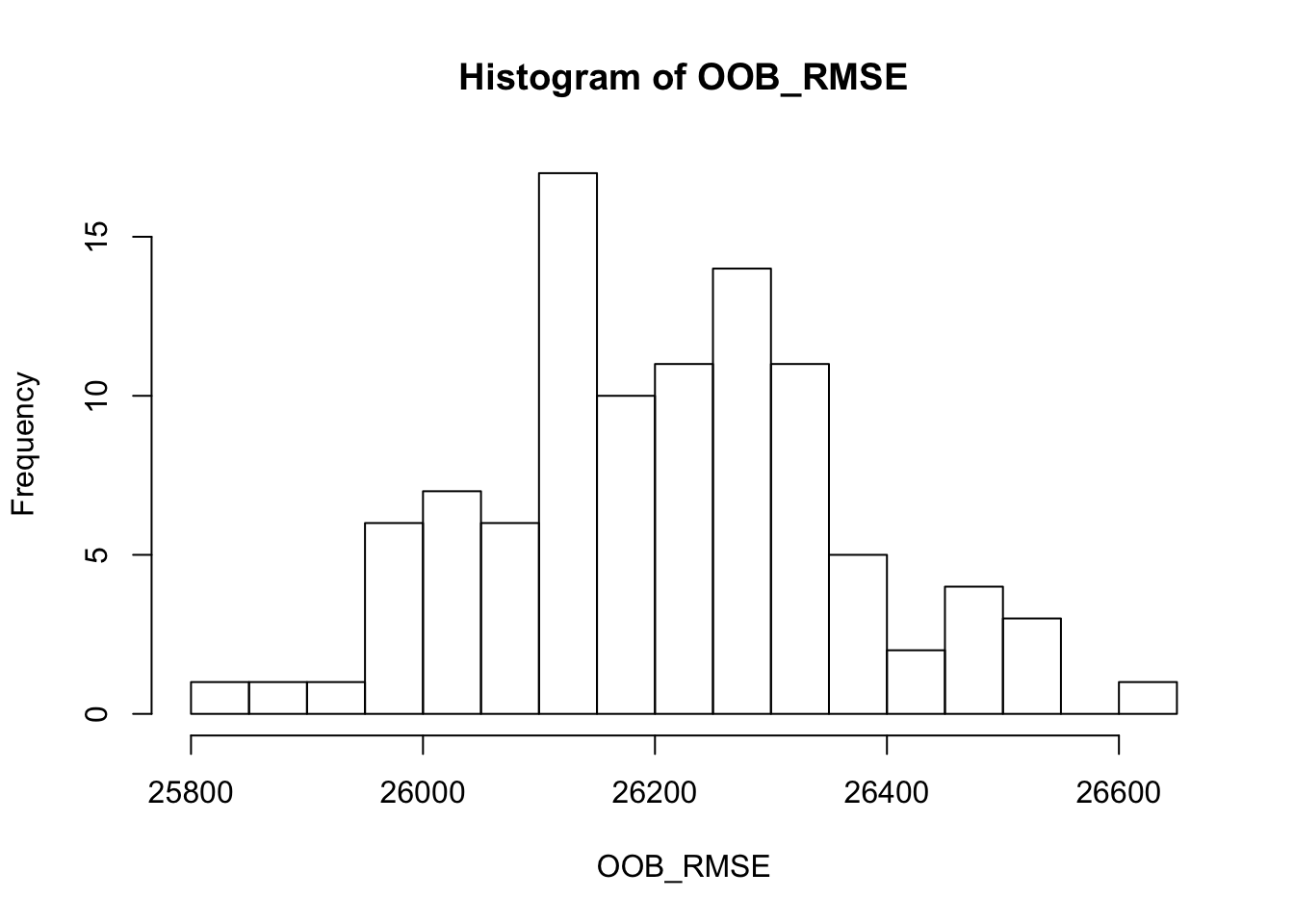
Inspecciones los resultados de importancia de atributos.
optimal_ranger$variable.importance## MS_SubClass MS_Zoning Lot_Frontage
## 2.383412e+10 2.598857e+10 5.649101e+10
## Lot_Area Street Alley
## 1.851665e+11 8.723654e+08 2.389873e+09
## Lot_Shape Land_Contour Utilities
## 9.719195e+09 2.143386e+10 5.107861e+07
## Lot_Config Land_Slope Neighborhood
## 7.601668e+09 9.803425e+09 5.107236e+10
## Condition_1 Condition_2 Bldg_Type
## 7.380356e+09 1.517712e+09 1.023225e+10
## House_Style Overall_Qual Overall_Cond
## 1.728124e+10 2.423575e+12 3.589149e+10
## Year_Built Year_Remod_Add Roof_Style
## 5.556295e+11 1.259489e+11 1.228007e+10
## Roof_Matl Exterior_1st Exterior_2nd
## 7.530494e+09 2.421003e+10 2.138768e+10
## Mas_Vnr_Type Mas_Vnr_Area Exter_Qual
## 8.980558e+09 1.292766e+11 6.003321e+11
## Exter_Cond Foundation Bsmt_Qual
## 6.127954e+09 3.195972e+10 8.198886e+11
## Bsmt_Cond Bsmt_Exposure BsmtFin_Type_1
## 4.483529e+09 1.743399e+10 3.016338e+10
## BsmtFin_SF_1 BsmtFin_Type_2 BsmtFin_SF_2
## 2.518336e+10 5.740365e+09 5.801121e+09
## Bsmt_Unf_SF Total_Bsmt_SF Heating
## 5.375453e+10 5.425982e+11 1.285165e+09
## Heating_QC Central_Air Electrical
## 1.202852e+10 1.769784e+10 2.673107e+09
## First_Flr_SF Second_Flr_SF Low_Qual_Fin_SF
## 4.480740e+11 1.689317e+11 8.780560e+08
## Gr_Liv_Area Bsmt_Full_Bath Bsmt_Half_Bath
## 1.018169e+12 2.226521e+10 3.829746e+09
## Full_Bath Half_Bath Bedroom_AbvGr
## 1.550351e+11 1.879208e+10 2.951400e+10
## Kitchen_AbvGr Kitchen_Qual TotRms_AbvGrd
## 3.435490e+09 2.368400e+11 7.200721e+10
## Functional Fireplaces Fireplace_Qu
## 3.923851e+09 1.056745e+11 2.764051e+10
## Garage_Type Garage_Finish Garage_Cars
## 6.851481e+10 2.185210e+10 1.110687e+12
## Garage_Area Garage_Qual Garage_Cond
## 5.452131e+11 1.049091e+10 1.185353e+10
## Paved_Drive Wood_Deck_SF Open_Porch_SF
## 1.778479e+10 4.306222e+10 5.307117e+10
## Enclosed_Porch Three_season_porch Screen_Porch
## 8.480061e+09 6.637285e+08 3.127910e+10
## Pool_Area Pool_QC Fence
## 7.913716e+08 1.549350e+09 4.394394e+09
## Misc_Feature Misc_Val Mo_Sold
## 1.396489e+09 1.863706e+09 4.869890e+10
## Year_Sold Sale_Type Sale_Condition
## 1.420325e+10 6.876117e+09 1.568422e+10
## Longitude Latitude
## 8.645152e+10 8.924475e+10list_features=data.frame("feature"= names(optimal_ranger$variable.importance),"value"=unname(optimal_ranger$variable.importance))
list_features %>%
dplyr::arrange(desc(value)) %>%
dplyr::top_n(25) %>%
ggplot(aes(reorder(feature, value), value)) +
geom_col() +
coord_flip() +
ggtitle("Top 25 important variables")## Selecting by value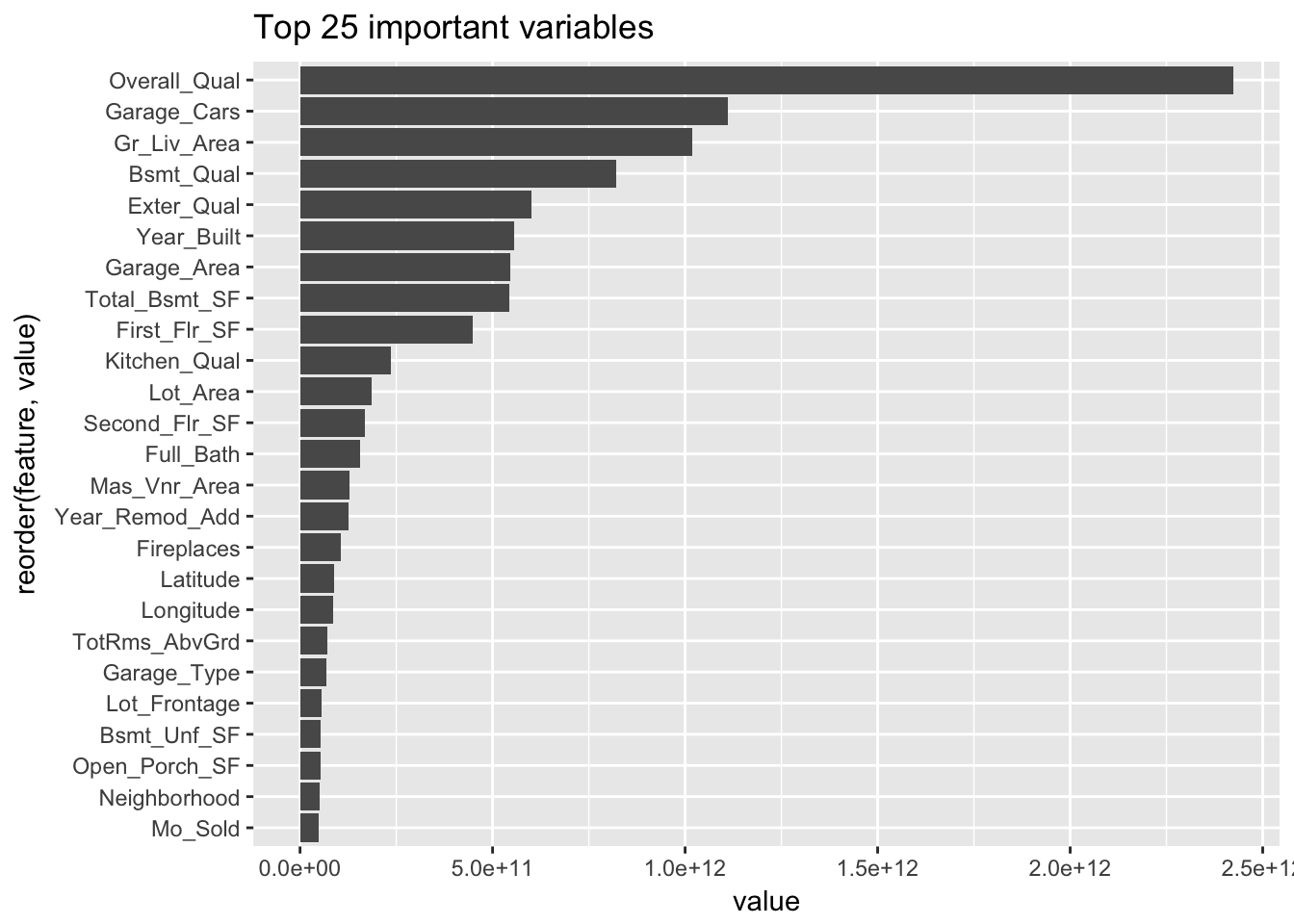
6.3.1 H2O una librería para cómputo distribuido.
Búsqueda exhaustiva con grid search usando H2O
El código anterior es muy demorado debido a la implementación de bucles for, los cuales son muy ineficientes en R. A pesar de que la librería ranger es computacionalmente eficiente, esto no basta.
H2O es una una poderosa y eficiente interfaz basada en java que provee algoritmos de paralelización distribuida. Un ejemplo de como usar esta librería.
Nota: Debido a las prestaciones de cada computador y al tiempo de cálculo solo inspeccionaremos el código y se deja al lector probar su implementación. Debe tener presente que la paralelización distribuida require una importante cantidad de memoria en el computador.
# start up h2o (I turn off progress bars when creating reports/tutorials)
h2o.no_progress()
h2o.init(max_mem_size = "5g")## Connection successful!
##
## R is connected to the H2O cluster:
## H2O cluster uptime: 2 hours 44 minutes
## H2O cluster timezone: America/Guayaquil
## H2O data parsing timezone: UTC
## H2O cluster version: 3.20.0.8
## H2O cluster version age: 1 month and 24 days
## H2O cluster name: H2O_started_from_R_johannaorellana_kmg728
## H2O cluster total nodes: 1
## H2O cluster total memory: 0.00 GB
## H2O cluster total cores: 12
## H2O cluster allowed cores: 12
## H2O cluster healthy: TRUE
## H2O Connection ip: localhost
## H2O Connection port: 54321
## H2O Connection proxy: NA
## H2O Internal Security: FALSE
## H2O API Extensions: XGBoost, Algos, AutoML, Core V3, Core V4
## R Version: R version 3.3.3 (2017-03-06)# create feature names
y <- "Sale_Price"
x <- setdiff(names(ames_train), y)
# turn training set into h2o object
train.h2o <- as.h2o(ames_train)
# hyperparameter grid
hyper_grid.h2o <- list(
ntrees = seq(200, 500, by = 100),
mtries = seq(20, 30, by = 2),
sample_rate = c(.55, .632, .70, .80)
)
# build grid search
grid <- h2o.grid(
algorithm = "randomForest",
grid_id = "rf_grid",
x = x,
y = y,
training_frame = train.h2o,
hyper_params = hyper_grid.h2o,
search_criteria = list(strategy = "Cartesian")
)
# collect the results and sort by our model performance metric of choice
grid_perf <- h2o.getGrid(
grid_id = "rf_grid",
sort_by = "mse",
decreasing = FALSE
)
print(grid_perf)Una (no muy corta) prueba con algunos resultados.
#H2O Grid Details
#================
# Grid ID: rf_grid
#Used hyper parameters:
# - mtries
#- ntrees
# - sample_rate
# Number of models: 96
# Number of failed models: 1
#
# Hyper-Parameter Search Summary: ordered by increasing mse
# mtries ntrees sample_rate model_ids mse
# 1 22 200 0.8 rf_grid_model_92 5.959833334434386E8
# 2 24 400 0.8 rf_grid_model_105 6.117881496530541E8
# 3 20 400 0.8 rf_grid_model_103 6.168158567573317E8
# 4 24 500 0.8 rf_grid_model_111 6.183128897636861E8
# 5 22 500 0.8 rf_grid_model_110 6.18855139151295E8
#
# ---
# mtries ntrees sample_rate model_ids mse
# 91 22 200 0.55 rf_grid_model_1 6.672565213436959E8
# 92 20 200 0.55 rf_grid_model_0 6.691233582975057E8
# 93 24 200 0.55 rf_grid_model_2 6.695830321897688E8
# 94 24 300 0.55 rf_grid_model_8 6.705963772893049E8
# 95 26 300 0.55 rf_grid_model_9 6.716723861811426E8
# 96 26 200 0.55 rf_grid_model_3 6.731654202001693E8
# Failed models
# -------------
# mtries ntrees sample_rate status_failed msgs_failed
# 22 500 0.55 FAIL "NA"Búsqueda Discreta Randómica
Aquí una versión optimizada de lo anterior, donde no se hace la búsqueda en un espacio cartesiano sino tomando combinaciones randómicas o definiendo criterios de parada de prueba de los modelos RF. Generalmente el resultado es muy parecido al óptimo.
# hyperparameter grid
hyper_grid.h2o <- list(
ntrees = seq(200, 500, by = 150),
mtries = seq(15, 35, by = 10),
max_depth = seq(20, 40, by = 5),
min_rows = seq(1, 5, by = 2),
nbins = seq(10, 30, by = 5),
sample_rate = c(.55, .632, .75)
)
# random grid search criteria
search_criteria <- list(
strategy = "RandomDiscrete",
stopping_metric = "mse",
stopping_tolerance = 0.005,
stopping_rounds = 10,
max_runtime_secs = 30*60
)
# build grid search
random_grid <- h2o.grid(
algorithm = "randomForest",
grid_id = "rf_grid2",
x = x,
y = y,
training_frame = train.h2o,
hyper_params = hyper_grid.h2o,
search_criteria = search_criteria
)
# collect the results and sort by our model performance metric of choice
grid_perf2 <- h2o.getGrid(
grid_id = "rf_grid2",
sort_by = "mse",
decreasing = FALSE
)
print(grid_perf2)
#Identificar el mejor modelo, que se encuentra al tope de la lista y aplicarlo con los datos de test
best_model_id <- grid_perf2@model_ids[[1]]
best_model <- h2o.getModel(best_model_id)
# Now let’s evaluate the model performance on a test set
ames_test.h2o <- as.h2o(ames_test)
best_model_perf <- h2o.performance(model = best_model, newdata = ames_test.h2o)
# RMSE of best model
h2o.mse(best_model_perf) %>% sqrt()6.3.2 Predicción
Independientemente si el el modelo ha sido generado (entrenado) usando la librería randomforest, ranger, h2o; se puede utilizar la función tradicional predict para obtener las predicciones.
No obstante, las predicciones podrían variar ligeramente entre ellas.
# randomForest
pred_randomForest <- predict(ames_randomForest, ames_test)
head(pred_randomForest)## 1 2 3 4 5 6
## 129741.9 153747.9 267093.1 382370.9 208447.3 209501.6# ranger
pred_ranger <- predict(ames_ranger, ames_test)
head(pred_ranger$predictions)## [1] 125340.1 153001.1 270957.3 393530.7 223134.0 216577.0