5 Ensambladores: Random Forest - Parte I

El término ensamblador significa grupo. Los métodos tipo ensamblador están formados de un grupo de modelos predictivos que permiten alcanzar una mejor precisión y estabilidad del modelo. Estos proveen una mejora significativa a los modelos de árboles de decisión.

¿Por qué surgen los ensambladores de árboles?

Así como todos los modelos, un árbol de decisión también sufre de los problemas de sesgo y varianza. Es decir, ‘cuánto en promedio son los valores predecidos diferentes de los valores reales’ (sesgo) y ‘cuan diferentes serán las predicciones de un modelo en un mismo punto si muestras diferentes se tomaran de la misma población’ (varianza).
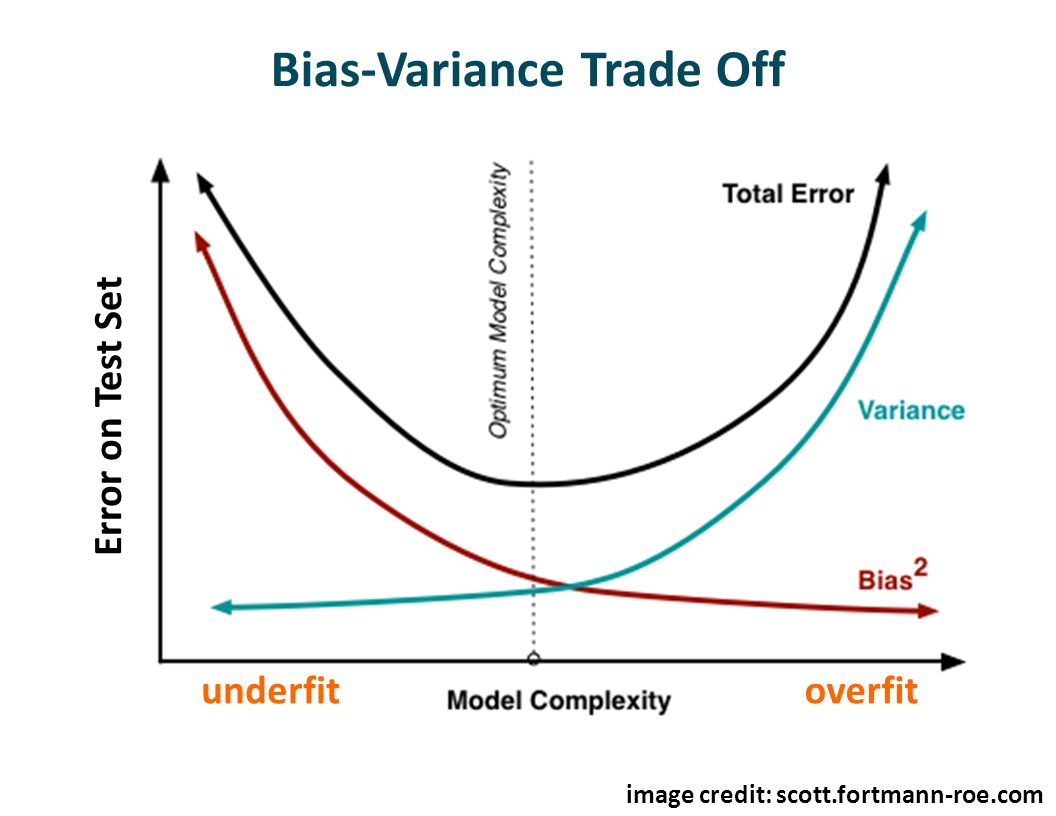
Al construir un árbol pequeño se obtendrá un modelo con baja varianza y alto sesgo. Normalmente, al incrementar la complejidad del modelo, se verá una reducción en el error de predicción debido a un sesgo más bajo en el modelo. En un punto el modelo será muy complejo y se producirá un sobre-ajuste del modelo el cual empezará a sufrir de varianza alta.
El modelo óptimo debería mantener un balance entre estos dos tipos de errores. A esto se le conoce como “trade-off” (equilibrio) entre errores de sesgo y varianza. El uso de ensambladores es una forma de aplicar este “trade-off”.

Ensambladores comunes: Bagging, Boosting and Stacking. Random Forest es del primer tipo.

¿Qué es el proceso de bagging y cómo funciona?

Bagging es una técnica usada para reducir la varianza de las predicciones a través de la combinación de los resultados de varios clasificadores, cada uno de ellos modelados con diferentes subconjuntos tomados de la misma población.

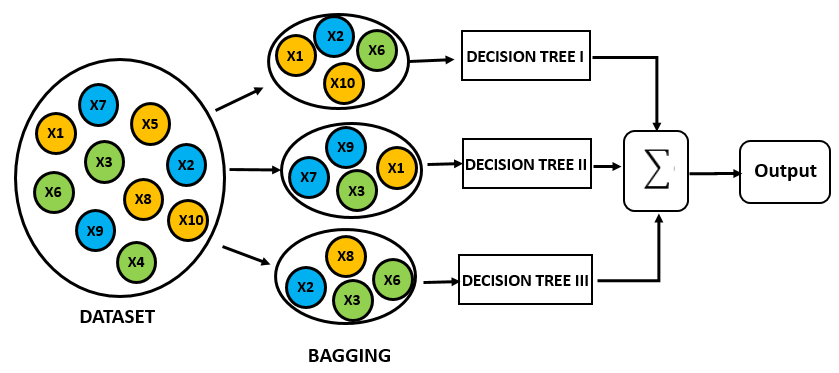
En resumen:

Crear múltiples subconjuntos de datos
Construir múltiples modelos
Combinar los modelos.

5.1 Random Forest

Random Forest se considera como la “panacea” en todos los problemas de ciencia de datos.
Util para regresión y clasificación.
Un grupo de modelos “débiles”, se combinan en un modelo robusto.
Sirve como una técnica para reducción de la dimensionalidad.
Se generan múltiples árboles (a diferencia de CART).
Cada árbol da una classificación (vota por una clase). Y el resultado es la clase con mayor número de votos en todo el bosque (forest).
Para regresión, se toma el promedio de las salidas (predicciones) de todos los árboles.

5.1.1 ¿Cómo se construye un modelo random forest?

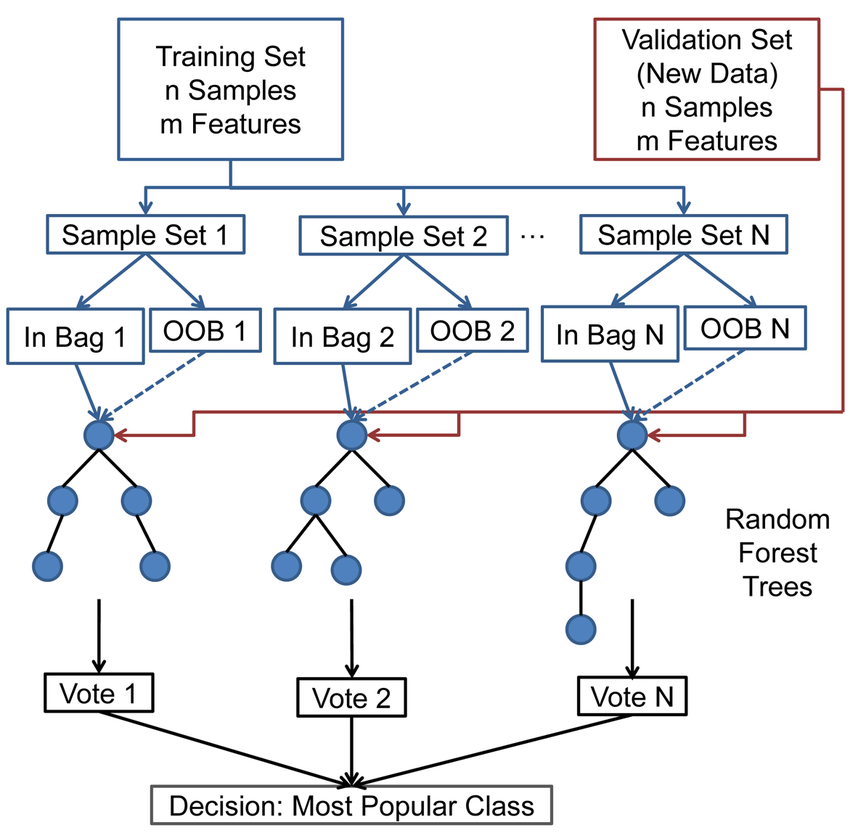
Cada árbol se construye así:

Dado que el número de casos en el conjunto de entrenamiento es N. Una muestra de esos N casos se toma aleatoriamente pero CON REEMPLAZO. Esta muestra será el conjunto de entrenamiento para construir el árbol i.
Si existen M varibles de entrada, un número m<M se especifica tal que para cada nodo, m variables se seleccionan aleatoriamente de M. La mejor división de estos m atributos es usado para ramificar el árbol. El valor m se mantiene constante durante la generación de todo el bosque.
Cada árbol crece hasta su máxima extensión posible y NO hay proceso de poda.
Nuevas instancias se predicen a partir de la agregación de las predicciones de los x árboles (i.e., mayoría de votos para clasificación, promedio para regresión)

5.1.1.1 Out of bag samples y out of bag error

El proceso de muestreo de los datos con reemplazo se denomina bootstrap.
Un tercio de los datos no se usan para el entrenamiento y pueden ser usados para test.
Este conjunto se denomina out of bag (OOB )samples.

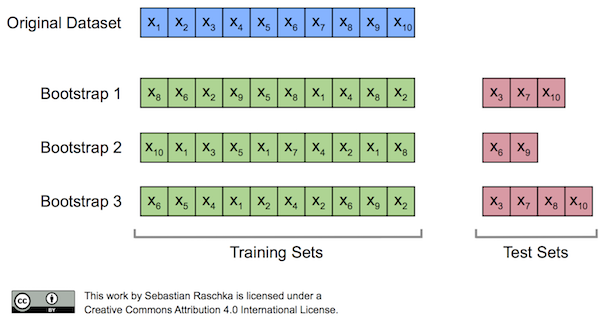
El error estimado en estos out of bag samples se conoce como out of bag error (OOB error)
Usar este conjunto de test (OOB) es tan preciso como si se usara un conjunto de test del mismo tamaño que el de entrenamiento.
Sería posible no usar un conjunto de test adicional.

5.2 Hyper-parámetros

El hyper-parámetro más importante para ajustar es el número de variables candidatas a seleccionar para evaluar cada ramificación. Sin embargo, existen algunos adicionales que deben considerarse. Independientemente de los nombres en las distintas librerías, al menos los siguientes deberían estar presentes.

ntree: número de árboles en el bosque. Se quiere estabilizar el error, pero usar demasiados árboles puede ser innecesariamente ineficiente.
mtry: número de variables aleatorias como candidatas en cada ramifiación.
sampsize: el número de muestras sobre las cuales entrenar. El valor por defecto es 63.25%. Valores más bajos podrían introducir sesgo y reducir el tiempo.Valores más altos podrían incrementar el rendimiento del modelo pero a riesgo de causar overfitting. Generalmente se mantiene en el rango 60-80%.
nodesize: mínimo número de muestras dentro de los nodos terminales.Equilibrio entre bias-varianza
maxnodes: máximo número de nodos terminales.

5.2.1 Ventajas de Random Forest

Existen muy pocas suposiciones y por lo tanto la preparación de los datos es mínima.
Puede manejar hasta miles de variables de entrada e identificar las más significativas. Método de reducción de dimensionalidad.
Una de las salidas del modelo es la importancia de variables.
Incorpora métodos efectivos para estimar valores faltantes.
Es posible usarlo como método no supervisado (clustering) y detección de outliers.

5.2.2 Desventajas de Random Forest

Pérdida de interpretación
Bueno para clasificación, no tanto para regresión. Las predicciones no son de naturaleza continua.
En regresión, no puede predecir más allá del rango de valores del conjunto de entrenamiento.
Poco control en lo que hace el modelo (modelo caja negra para modeladores estadísticos)

5.3 Importancia de atributos

5.3.1 ¿Cómo se calcula?

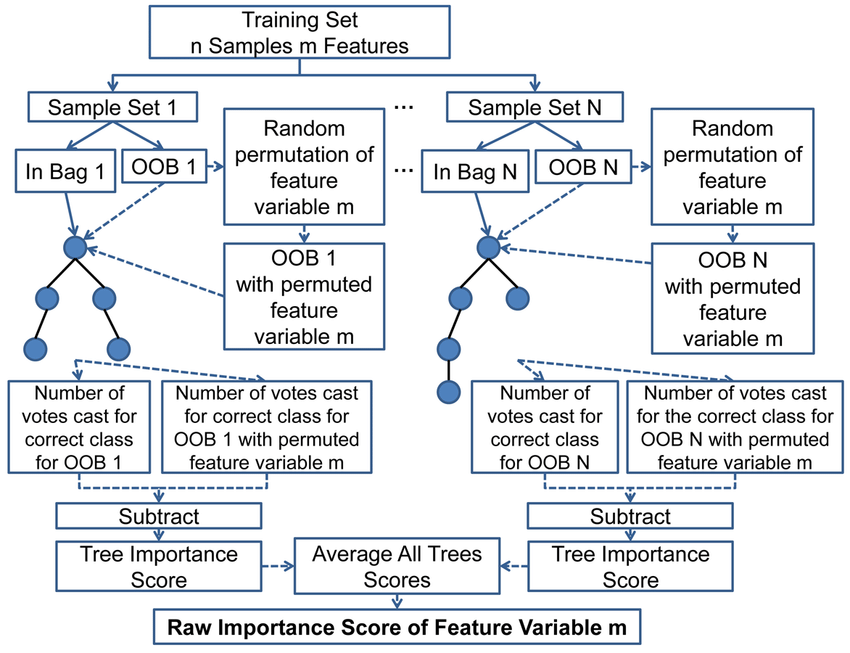
Para cada árbol en el bosque, calcule el número de votos por la clase correcta en la muestra (OOB)
Efectuar una permutación aleatoria de los valores de un predictor (e.g., variable-k) en la muestra (OOB) y verifique el número de votos por la clase correcta. Por permutuación aleatoria de una variable nos referimos a “barajar” (shuffling).
Sustraer el número de votos de la clase correcta in en los datos de variable-k permutada, del número de votos por la clase correcta en la muestra OOB original.
El promedio de este número sobre todos los árboles en el bosque es el “score” de importancia sin normalizar. Este score es normalizado a partir de la desviación estándar.
Las variables que tiene valores altos para este score son clasificadas (ranked) como las más importantes Variables having large values for this score are ranked as more important.
Esto significa que si el modelo fuera construido sin los valores originales de una variable específica, las predicciones serían peores. Por lo tanto, la variables es importante.

En conclusión: La importancia de un atributo es el incremento en el error del modelo de predicción luego de que el valor de dicho atraibuto ha sido permutado (se rompre la relación entre el atributo y la salida del modelo).

5.3.2 Ventajas

Fácil interpretación: Importancia de atributos es el incremento del error del modelo cuando la información del atributo se “destruye”.
Provee una visión resumida y global del comportamiento del modelo.
La medida de la importancia toma automáticamente en cuenta todas las interacciones con otros atributos. A través de la permutación del atributo también se destruyen los efectos de interacción con otros atributos. Es decir que tanto el efecto principal como relacional de atributos se ven afectados por la permutación del atributo.

Nota: Esta es también una desventaja pues la importancia de la interacción entre dos atributos se incluirá en la medida de importancia de ambos. Esto significa que las importancias de los atributos no afectan acumulativamente al rendimiento del modelo. Solamente cuando no existe interacción entre los atributos, como en el caso de un modelo lineal, las importancias podrían representar gruesamente un efecto acumulado respecto al rendimiento del modelo.

No se requiere re-entrenar el modelo. Otros métodos sugieren eliminar un atributo, re-entrenar el modelo y comparar el error del modelo. Esto último podría parecer intuitivo, no obstante un modelo reducido es inútil para identificar la importancia del atributo. Ejm: en un árbol de decisión se quiere analizar la importaacia del atributo escogido como primera ramificación. Se remueve el atributo y se re-entrena el modelo. Como un nuevo atributo será escogido como primera ramificación, la estructura del árbol podría ser muy diferente, lo cual podría derivar en la comparación de árboles completamente diferentes.

5.3.3 Desventajas

La medida de importancia de atributos está ligada al error del model. En algunos casos sería preferible saber cuánto varía la salida del modelo para un atributo ignorando como afecta en el rendimiento.

Ejemplo: Se quisiera identificar cuan robusta es la salida del modelo dado que que alguien manipula los atributos. En ese caso no nos interesaría saber cuanto disminuyó el rendimiento del modelo, sino más bien cuánta de la varianza es explicada por cada atributo.

Se necesita tener acceso a las observaciones de la variable objetivo.
El proceso de permutación añade aleatoriedad a la medida de importancia del atributo. Si el proceso de permutación se repite, los resultados podrían ser diferentes. Repetir la permutación y promediar las medida de importancia sobre varias repeticiones estabiliza la métrica pero incrementa el tiempo de cómputo.
Cuando los atributos están correlacionados, la medida de importancia de atributos puede estar sesgada por datos de instancias no realistas. La permutación de los atributos genera instancias poco probables cuando dos atributos están correlacionados. Ejemplo: cuando los atributos están correlacionados positiviamente (como la altura y el peso de una persona) y al permutar uno de los atributos se crean instancias poco probables o incluso físicamente imposibles (persona de 2m con peso de 30Kg.). No obstante estas nuevas instancias se usan para el cálculo de la importancia. Podría penalizar a mi modelo por observaciones generadas que nunca ocurrirán en la realidad.
Verificar si los atributos están fuertemente correlacionados y ser cuidadoso con la interpretación de la importancia de atributos.
Añadir un atributo correlacionado puede reducir la importancia del atributo asociado y “dividir” la importancia de ambos atributos. Ejemplo.

Se desea predecir la probabilidad de lluvia y se usa la temperatura a las 8:00 AM del día anterior junto a otros atributos no correlacionados.
Otro escenario donde adicionalmente incluimos la temperaturo a las 9:00 AM el cual es altamente correlacionado con la temperatura a las 8:00 AM.