3 Arboles de Decisión - Parte I
3.1 Conceptos Introductorios
3.1.1 ¿Qué es machine learning?
Quizás la idea general que muchas personas tienen…

Lo que es en realidad…
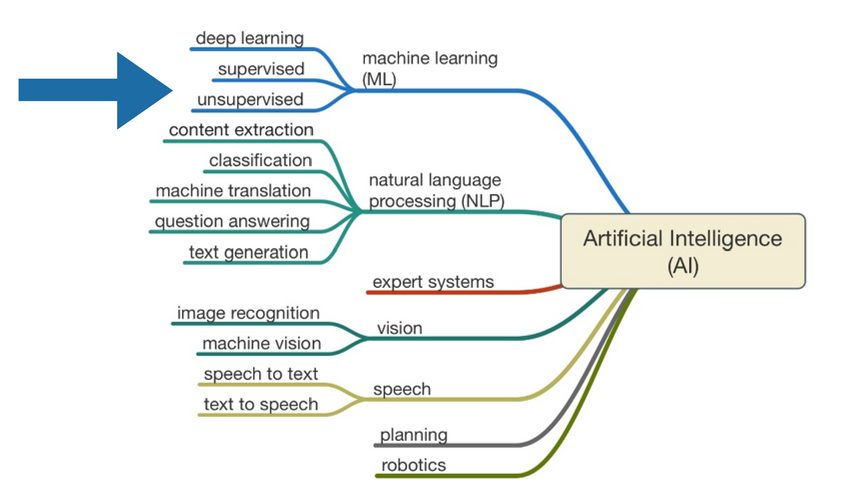
3.1.2 Tipos de técnicas y algoritmos
Existen varios métodos-técnicas de aprendizaje supervisado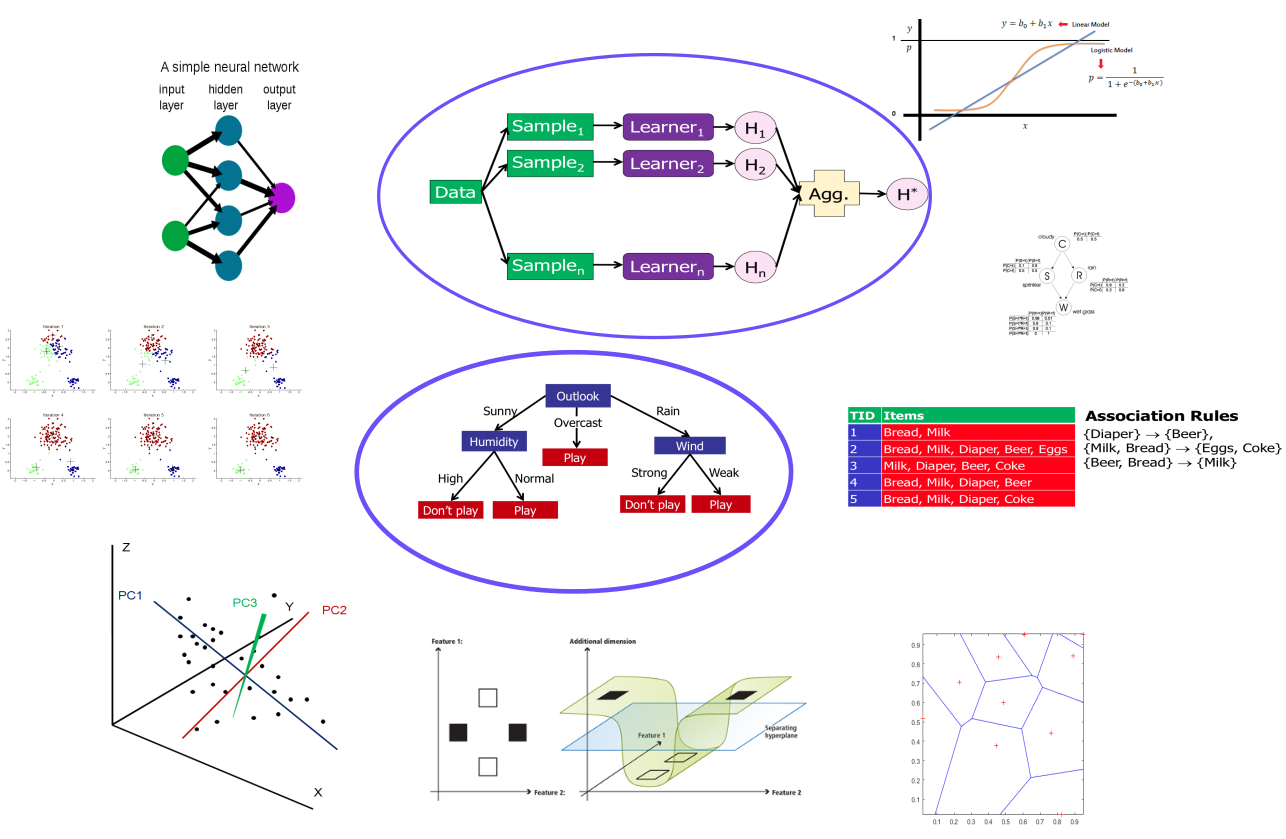
3.1.3 Conjunto de entrenamiento y conjunto de test
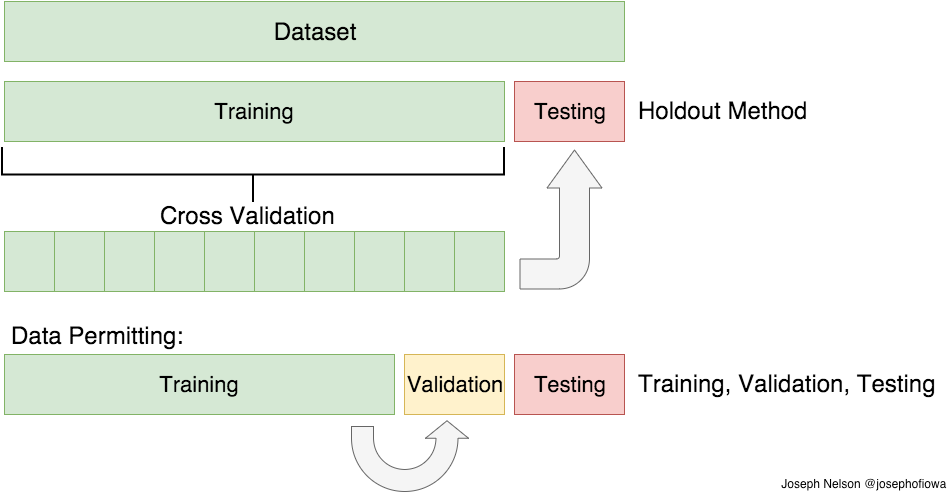
3.1.4 Sesgo (bias) y varianza
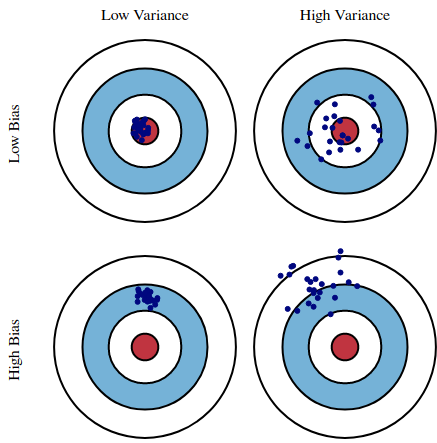
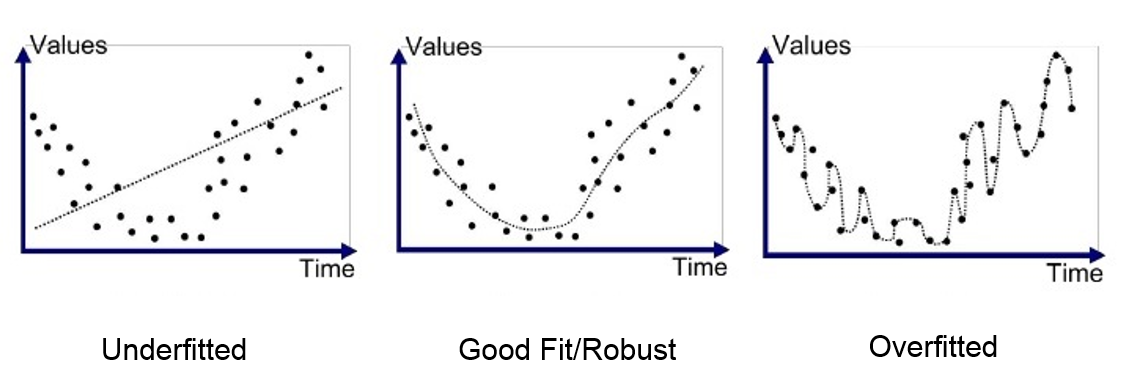
3.1.5 Sobreajuste u “overfitting”
Explicar el conjunto de datos de entrenamiento, en lugar de encontrar patrones que generalizan. El modelo se ajusta bien al conjunto de datos de entrenamiento pero falla en el conjunto de datos de test.
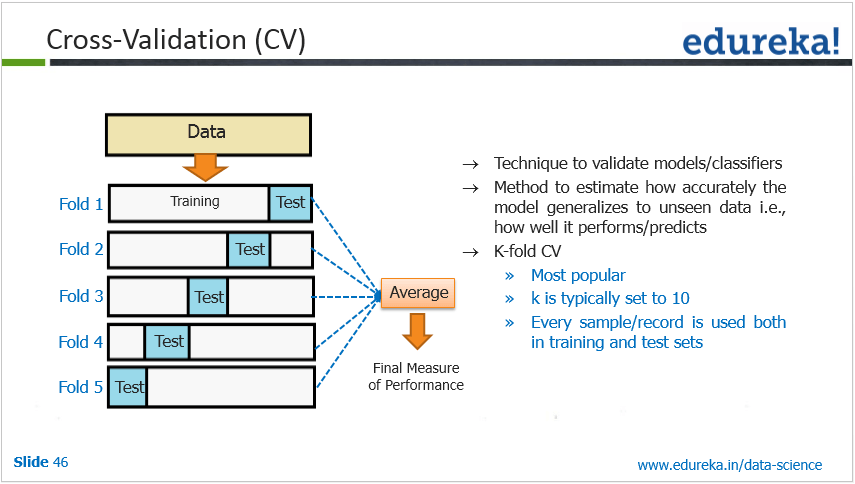
3.1.6 Validación cruzada
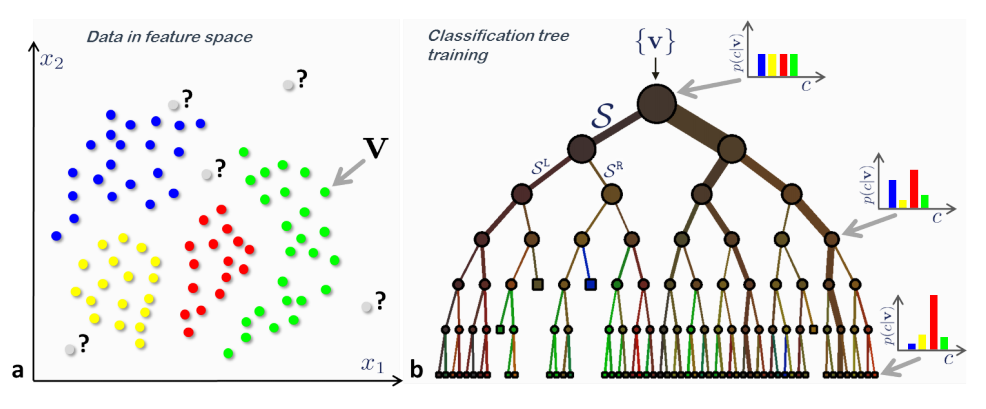
3.2 ¿Qué son los árboles de decisión?
- El enfoque classification and regression tree (CART) fue desarrollado por Breiman et al. (1984).
- Son un tipo de algoritmos de aprendizaje supervisado (i.e., existe una variable objetivo predefinida).
- Principalmente usados en problemas de clasificación.
- Las variables de entrada y salida pueden ser categóricas o continuas.
- Divide el espacio de predictores (variables independientes) en regiones distintas y no sobrepuestas.
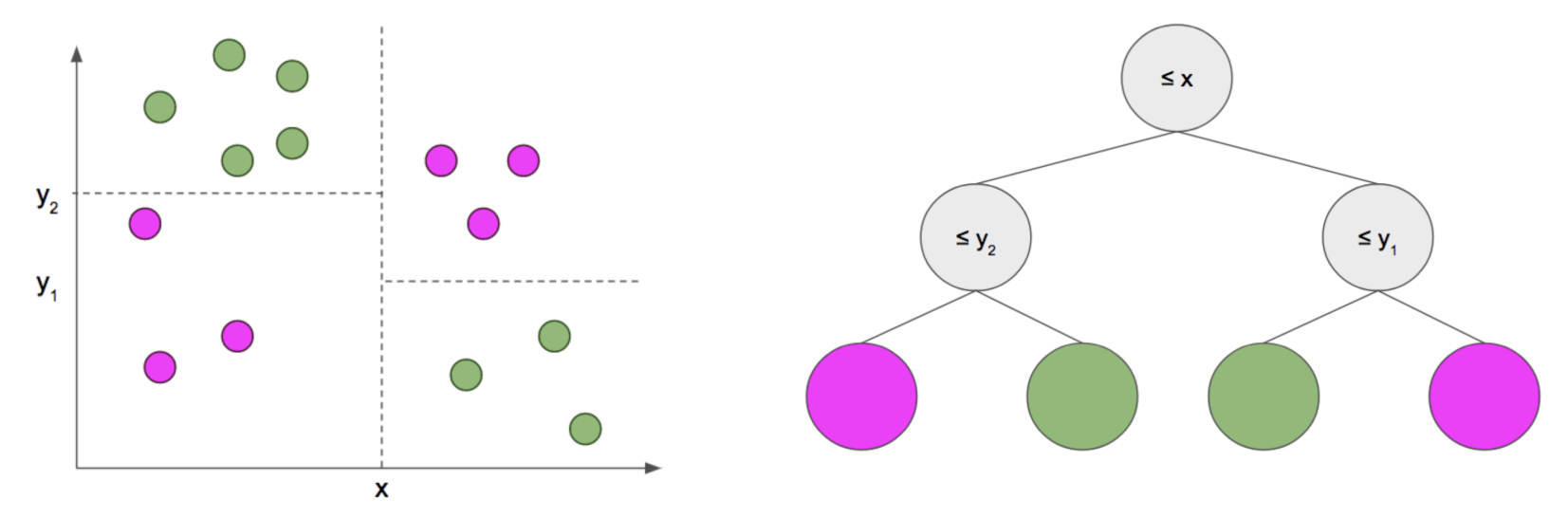
Generalizando…
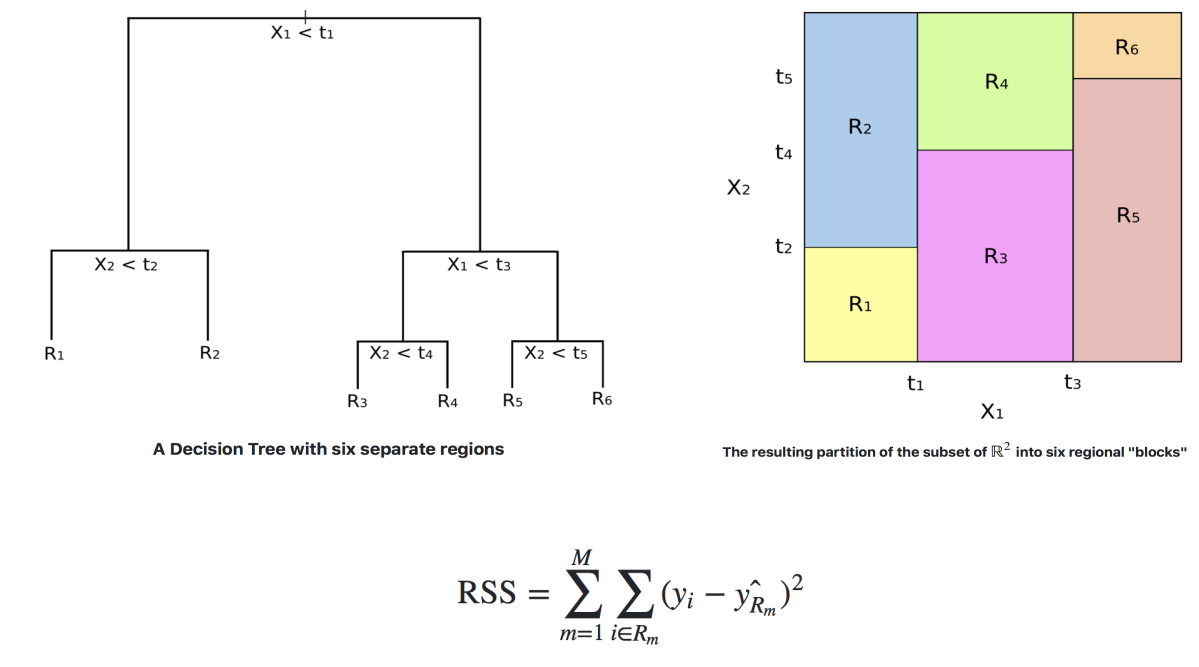
- Se divide la población o muestra en conjuntos homegéneos basados en la variable de entrada más significativa.
- La construcción del árbol sigue un enfoque de división binaria recursiva (top-down greddy approach). Greedy -> analiza la mejor variable para ramificación sólo en el proceso de división actual.
3.2.1 Ejemplo
- 30 estudiantes
- 3 variables: Género (hombre/mujer), Clase (IX/X) y Altura (5 a 6 pies).
- 15 estudiantes juegan cricket en su tiempo libre
- Crear un modelo para predecir quien jugará cricket
- Segregar estudiantes basados en todos los valores de las 3 variables e identificar aquella variable que crea los conjuntos más homogéneos de estudiantes y que a su vez son heterogéneos entre ellos.
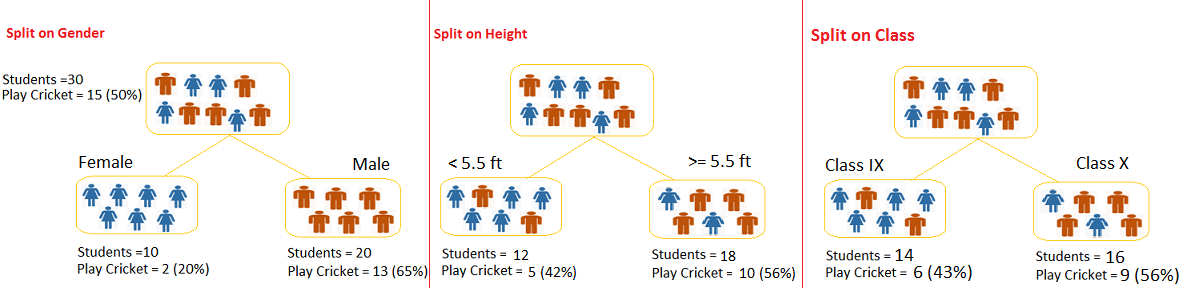
¿Qué variable es la más significativa para la mejor división de la población?
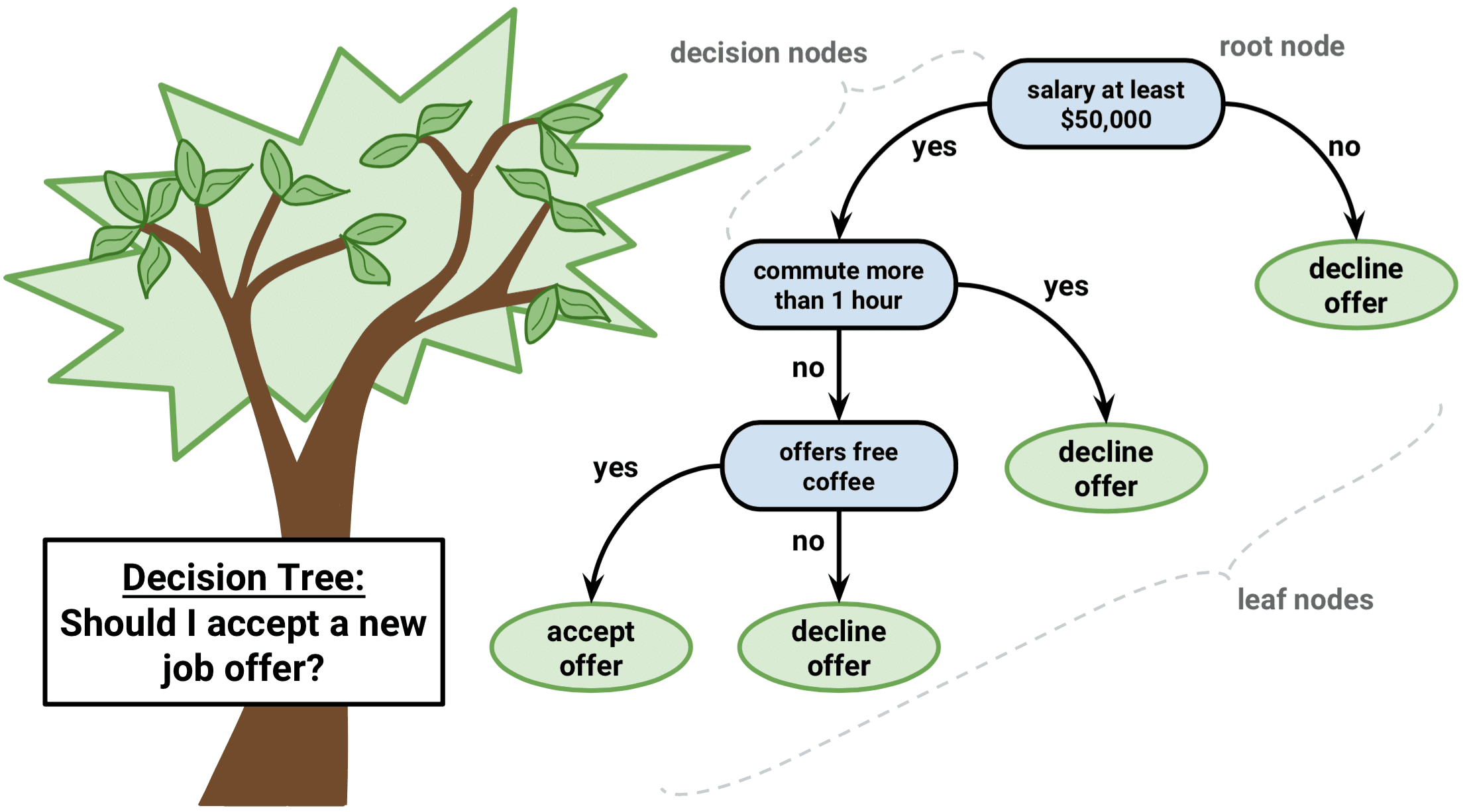
3.3 Terminología
- Nodo raíz: población completa o muestra
- Ramificación
- Nodo de decisión
- Nodo terminal y hoja
- Poda
- Rama/sub-árbol
- Nodos padre e hijo
3.4 Arboles de Regressión vs. árboles de clasificación
| Regresión | Clasificación |
|---|---|
| Variable dependiente es continua | Variable dependiente es categórica |
| Valores de los nodos terminales se reducen a la media de las observaciones en esa región. | El valor en el nodo terminal se reduce a la moda de las observaciones del conjunto de entrenamiento que han “caído” en esa región. |
3.5 Ventajas y desventajas
3.5.1 Ventajas
- Fácil de entender
- Util en exploración de datos:identificar importancia de variables a partir de cientos de variables.
- Menos limpieza de datos: outliers y valores faltantes no influencian el modelo (A un cierto grado)
- El tipo de datos no es una restricción
- Es un método no paramétrico (i.e., no hay suposición acerca del espacio de distribución y la estructura del clasificador)
3.5.2 Desventajas
- Sobreajuste
- Pérdida de información al categorizar variables continuas
- Precisión: métodos como SVM y clasificadores tipo ensamblador a menudo tienen tasas de error 30% más bajas que CART (Classification and Regression Trees)
- Inestabilidad: un pequeño cambio en los datos puede modificar ampliamente la estructura del árbol. Por lo tanto la interpretación no es tan directa como parece.
3.6 ¿Cómo decide un árbol donde ramificarse?
- La decisión de hacer divisiones estratégicas afecta altamente la precisión del árbol.
- Los criterios de decisión son diferentes para árboles de clasificación y regresión.
- Existen varios algortmos para decidir la ramificación.
- La creación de subnodos incrementa la homogeneidad de los subnodos resultantes. Es decir, la pureza del nodo se incrementa respecto a la variable objetivo.
- Se prueba la división con todas las variables y se escoge la que produce subnodos más homogéneos.
Algunos algoritmos más comunes para la selección: Indice Gini, Chi Cuadrado, Ganancia de la información y Reducción en la varianza
3.6.1 Indice Gini
“Si seleccionamos aletoriamente dos items de una población, entonces estos deben ser de la misma clase y la probabilidad de esto es 1 si la población es pura”.
- Variable objetivo categórica: “Success” o “Failure”
- Solo divisiones binarias
- A mayor valor de índice Gini, mayor la homogeneidad
- CART (Classification and Regression Tree) usa el método de Gini para la división binaria.
3.6.1.1 Cálculo de índice Gini
- Calcular Gini para los subnodos usando la fórmula de la suma de los cuadrados de probabilidad para success y failure (p^2 + q^2).
- Calcular Gini para la división usando score Gini ponderado para cada nodo de la división.
3.6.1.2 Ejemplo

| Género | Clase | ||
|---|---|---|---|
| Mujer | (0.2)^2 + (0.8)^2 = 0.68 | IX | (0.43)^2 +(0.57)^2 = 0.51 |
| Hombre | (0.65)^2 + (0.35)^2 = 0.55 | X | (0.56)^2 +(0.44)^2 = 0.51 |
| Pond. | (10/30)0.68 + (20/30)0.55 = 0.59 | Pond. | (14/30)0.51 + (16/30)0.51 = 0.51 |
- ¿Cuál es el resultado para la variable “Altura”?
- ¿Cuál es el variable que se debe escoger para la primera división?
3.6.2 Chi Cuadrado
Un algoritmo para encontrar la significancia estadística de las diferencias entre subnodos y un nodo padre. Se mide a partir de la suma de los cuadrados de las diferencia estandarizadas entre las frecuencias observadas y esperadas de la variable objetivo.
- Variable objetivo categórica “Success” o “Failure”.
- Dos o más divisiones
- A más alto valor de Chi-Cuadrado, màs alta la significancia estadística de las diferencias entre cada nodo y el nodo padre.
- Fórmula: ((Real – Esperado)^2 / Esperado)^1/2
3.6.2.1 Cálculo de Chi-Cuadrado
- Calcular Chi-Cuadrado para cada nodo individualmente a través de la desviación para ambos: Success y Failure
- Calcular Chi-Cuadrado de la división usando la suma de todos los Chi-Cuadrado de Success y Failure de cada nodo en la división.
3.6.2.2 Ejemplo
- Para el nodo “Mujer”. Los valores reales para “Play Cricket” y “Not Play Cricket” son 2 y 8 repectivamente.
- Para calcular el valor esperado, asignaremos la misma probabilidad que su nodo padre (50%). Por lo tanto para ambos casos el valor sería 5 considerando el total de elementos “Mujer” (10).
- Calcular las diferencias para usar en la fórmula, Real-Esperado. Para “Play Cricket” (2-5=-3) y para “No Play Cricket” (8-5=3)
- Calcular Chi-Cuadrado del nodo para “Play Cricket” y “No Play Cricket” usando la fórmula completa ((Real – Esperado)^2 / Esperado)^1/2.
- Seguir los pasos 1-4 para el caso del nodo “Hombre”.
- finalmente sumar todos los Chi-Cuadrado para caclular el Chi-Cuadrado para la división de la variable Género.

Lso resultados para la división de la variable “Class”.

- ¿Cuál es el resultado para la variable “Altura”?
- ¿Cuál es el variable que se debe escoger para la primera división?
3.6.3 Ganancia de información
- Un nodo menos impuro requiere menos infomación para ser descrito mientra sun nodo más impuro necesita más información.
- La teoría de la información es una medida para definir este grado de desorganización en un sistema denominado como Entropía.
- Muestra completamente homogénea = entropía 0.
- Muestra igualmente dividida (50% – 50%) = entropía 1.
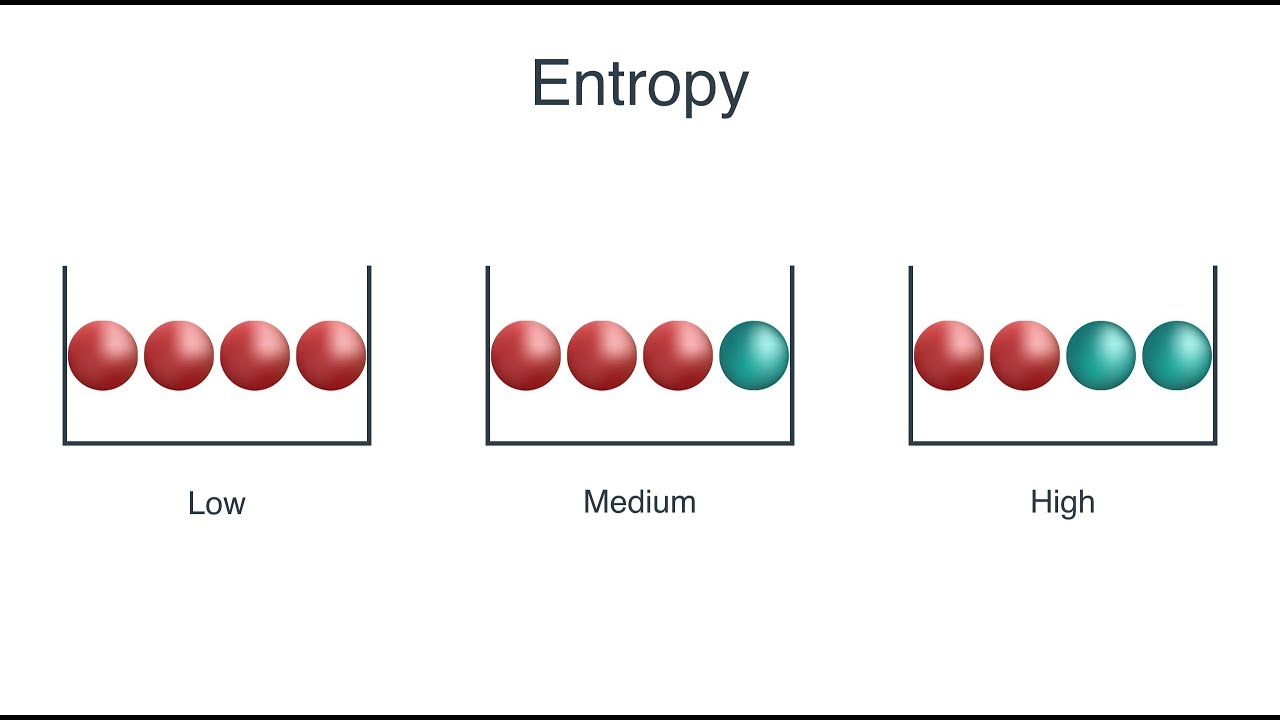
La entropía puede ser calculada así:
\[Entropía = -p.log_{2}(p) - q.log_{2}(q) \]
Aquí, p y q es la probabilidad de “success” y “failure” respectivamente en el nodo. La entropía es también usada con variable objetivo categórica. Se escoje la división con la entropía más baja comparada con el nodo padre y otras variables de división. Mientras menor la entropía, mejor.
3.6.3.1 Cálculo de la entropía
Calculate entropy of parent node Calculate entropy of each individual node of split and calculate weighted average of all sub-nodes available in split.
3.6.3.2 Ejemplo
| Criterio | Entropy |
|---|---|
| Nodo Padre | -(15/30) log2 (15/30) – (15/30) log2 (15/30) = 1 |
| Nodo Mujer | -(2/10) log2 (2/10) – (8/10) log2 (8/10) = 0.72 |
| Nodo Hombre | -(13/20) log2 (13/20) – (7/20) log2 (7/20) = 0.93 |
| Género ponderado | (10/30)0.72 + (20/30)0.93 = 0.86 |
| Nodo Clase IX | -(6/14) log2 (6/14) – (8/14) log2 (8/14) = 0.99 |
| Nodo Clase X | -(9/16) log2 (9/16) – (7/16) log2 (7/16) = 0.99. |
| Clase ponderado | (14/30)0.99 + (16/30)0.99 = 0.99 |
La entropía para la división por la variable “Género” es la más baja. Se puede derivar la ganancia de infomación a partir de la entropía así: 1-Entropía.
3.6.4 Reducción en la varianza (regresión)
Los algoritmos anteriores se aplicaban para problemas de clasificación con variables objetivo categóricas. La reducción en la varianza es un algoritmo usado para variables objetivo continuas (problemas de regresión). Este algoritmo usa la fórmula estándar de la varianza para escoger el criterio de división. La división con la varianza más baja se escoje para dividir la población:
\[Varianza = \frac{\sum_{}(X-\bar{X})^{2}}{n} \]
3.6.4.1 Cálculo de varianza
- Calcular la varianza para cada nodo.
- Calcular la varianza para cada división como un promedio ponderado de las varianzas de cada nodo.
3.6.4.2 Ejemplo
Asumiremos que vamos a convertir a valores numéricos de 1 para “play cricket” u valor de 0 para “No play cricket”.
| Criterio | Mean | Varianza |
|---|---|---|
| Nodo Padre | (15x1 + 15x0)/30 = 0.5 | (15x(1-0.5)^2 + 15x(0-0.5)^2) / 30 = 0.25 |
| Nodo Mujer | (2x1 + 8x0)/10=0.2 | (2x(1-0.2)^2 + 8x(0-0.2)^2) / 10 = 0.16 |
| Nodo Hombre | (13x1 + 7x0)/20=0.65 | (13x(1-0.65)^2 + 7*(0-0.65)^2) / 20 = 0.23 |
| Género ponderado | (10/30)x0.16 + (20/30) *0.23 = 0.21 | |
| Nodo Clase IX | (6x1 + 8x0)/14=0.43 | (6x(1-0.43)^2 + 8x(0-0.43)^2) / 14= 0.24 |
| Nodo Clase X | (9x1 + 7x0)/16=0.56 | (9x(1-0.56)^2 + 7x(0-0.56)^2) / 16 = 0.25 |
| Clase ponderado | (14/30)x0.24 + (16/30) x0.25 = 0.25 |
3.7 Parámetros del modelo y como evitar sobreajuste en árboles de decisión
El sobreajuste es uno de los desafíos más importantes en el proceso de modelación de árboles de decisión. Si no se definen límites, el árbol tendrá un 100% de precisión en el conjunto de datos de entrenamiento. En el peor caso tendrá una hoja por cada observación.
Dos formas de evitar el sobreajuste: (a) Definir restricciones sobre el tamaño del árbol y (b) Podar el árbol.
3.7.1 Definir restricciones sobre el tamaño del árbol (prepruning)
Uso de parámetros para definir un árbol. Los parámetros son independientes de la herramienta de programación (R & Python)
1. Mínimo de observaciones para dividir un nodo
- Mínimo número de muestras u observaciones que se requieren en un nodo para ser considerado para ramificación.
- Valores más altos previenen que el modelo aprenda relaciones muy específicas.
- Valores demasiado altos pueden causar un pobre ajuste del modelo. El parámetro debe ajustarse usando validación cruzada.
2. Mínimo número de observaciones para un nodo terminal
- Valores más bajos son necesarios para problemas de clases no balanceadas.
3. Máxima profundidad del árbol (vertical)
- Una mayor profundidad permite aprender relaciones más específicas.
- Debe ajustarse con validación cruzada.
4. Máximo número de nodos hoja
- Se puede definir en lugar de máxima profundidad. Profundidad n = máximo 2^n hojas
5. Máximo número de atributos a considerar para la ramificación
- Seleccionados aleatoriamente.
- Como regla general, la raíz cuadrada del número total de atributos funciona apropiadamente. Sin embargo, se debe probar hasta un 30%-40% del número total de atributos.
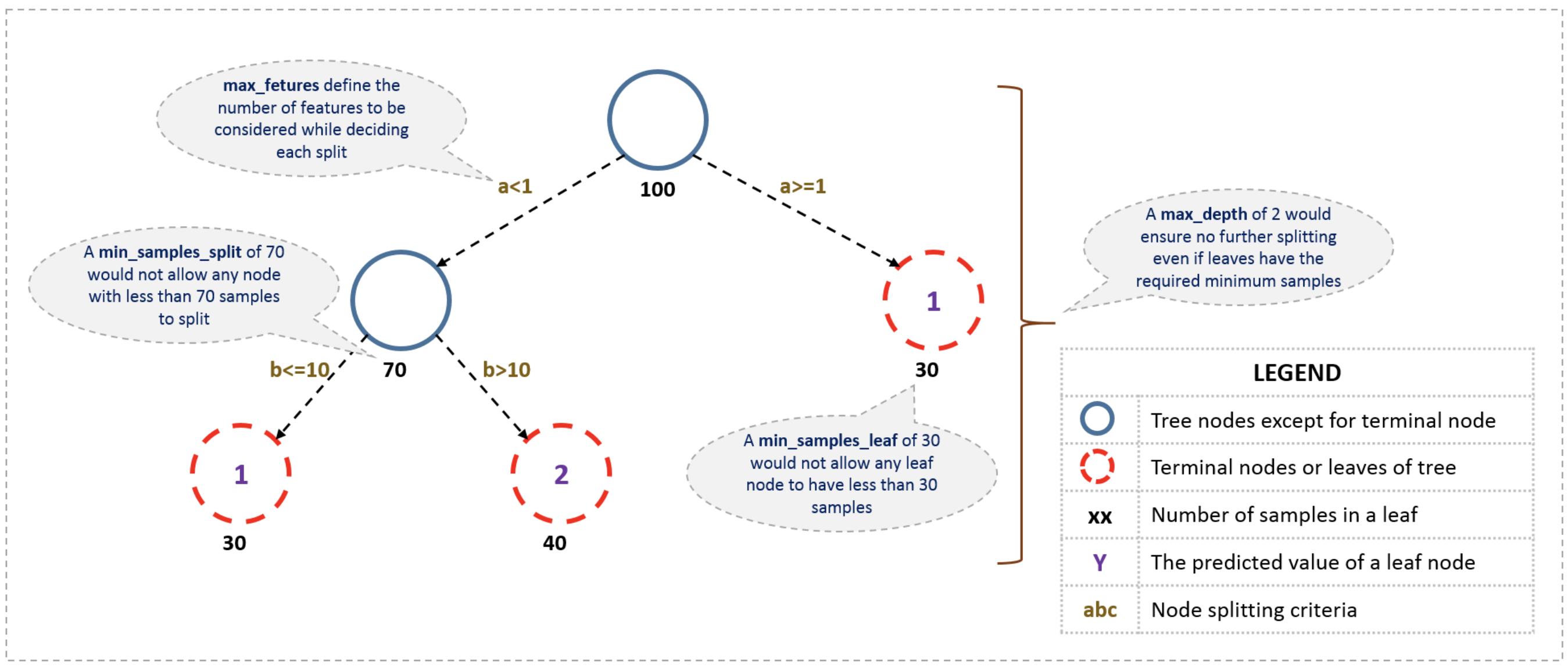
3.7.2 Poda del árbol (postpruning)
Un ejemplo para ilustrar la lógica del proceso de poda.
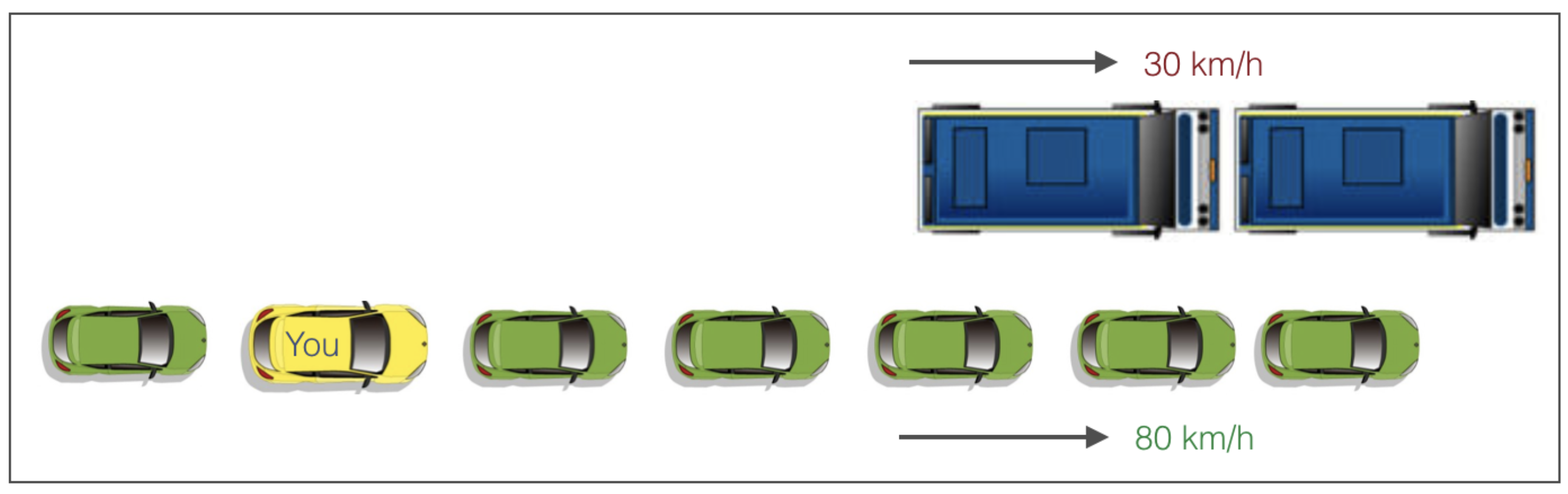
Un árbol de decisión con restricciones no verá el camión más adelante y adoptará un “greddy approach” al tomar la izquierda. Al contrario, si usamos el proceso de poda, en efecto se mirará algunos pasos adelante para tomar una decisión.
Por lo tanto sabemos que hacer la poda es mejor. Su implementación es sencilla.
- Construir el árbol a un profundidad extensa.
- Remover las hojas que den un valor negativo comparado desde la raíz. Existen varios criterios que pueden ser utilizados, algunos basados en heurísticas y otros en parámetros de regularización (penalización).
Ejemplo: Supongamos que un nodo de decisión da una ganacia de -10 (pérdida de 10) y la siguiente ramificación da una ganancia de 20. Un árbol de decisión simple pararía en el paso uno, sin embargo, el proceso de poda considerará la ganacia general de +10 y mantendrá ambas hojas.
Librerías: El clasificador de árbol de decisión en la libraría de python Scikit actualmente no soporta el proceso de poda. Paquetes avanzados como xgboost lo incoporan. Por otra parte, el paquete de R rpart provee una función de poda directamente.