Rozdział 2 Rozkład empiryczny cech
2.1 Szeregi statystyczne
Dane statystyczne przedstawione w formie tabelarycznej (lub w formie tekstu) nazywa się po polsku często szeregiem statystycznym.
2.1.1 Szereg szczegółowy
Kiedy przedstawiamy wszystkie zebrane informacje bez grupowania, np. w formie kolumny w tabeli lub listy oddzielonej przecinkami mówimy o szeregu szczegółowym. Inna nazwa tego szeregu to szereg wyliczający. Często też mówi się w tym kontekście o „danych surowych”.
Szereg szczegółowy może dotyczyć zarówno danych jakościowych, jak i ilościowych.
2.1.2 Szereg rozdzielczy punktowy
Szereg rozdzielczy to dane pogrupowane. Szereg rozdzielczy punktowy polega na przedstawieniu wszystkich możliwych wartości zmiennej wraz z liczebnością (tzn. informacją, ile razy dana wartość wystąpiła).
Szereg rozdzielczy punktowy może dotyczyć zarówno cech jakościowych, jak i ilościowych dyskretnych.
W przypadku szeregu rozdzielczego nie następuje utrata informacji, tzn. jesteśmy w stanie odtworzyć szereg szczegółowy.
Przykład:
| Obwód klatki piersiowej w calach | Liczba obserwacji |
|---|---|
| 33 | 3 |
| 34 | 18 |
| 35 | 81 |
| 36 | 185 |
| 37 | 420 |
| 38 | 749 |
| 39 | 1073 |
| 40 | 1079 |
| 41 | 934 |
| 42 | 658 |
| 43 | 370 |
| 44 | 92 |
| 45 | 50 |
| 46 | 21 |
| 47 | 4 |
| 48 | 1 |
2.1.3 Szereg rozdzielczy przedziałowy
Szereg rozdzielczy przedziałowy to przedstawienie przedziałów wartości wraz z podaną liczebnością.
W przypadku szeregu rozdzielczego przedziałowego następuje utrata informacji; nie jesteśmy w stanie odtworzyć szeregu szczegółowego z szeregu przedziałowego. Szereg rozdzielczy można sporządzać dla cech ilościowych.
Na podstawie szeregu rozdzielczego przedziałowego można stworzyć histogram.
Przykład:
| Przedział | Liczba spraw |
|---|---|
| do 15 dni | 161 328 |
| powyżej 15 dni do 1 mies. | 118 435 |
| powyżej 1 do 2 mies. | 265 533 |
| powyżej 2 do 3 mies. | 263 151 |
| powyżej 3 do 6 miesięcy | 309 985 |
| powyżej 6 do 12 miesięcy | 141 561 |
| powyżej 12 miesięcy do 2 lat | 68 070 |
| powyżej 2 do 3 lat | 23 978 |
| powyżej 3 do 5 lat | 11 973 |
| powyżej 5 do 8 lat | 3 911 |
| ponad 8 lat | 2 305 |
2.3 Histogram – wizualizacja rozkładu cechy ilościowej
Histogram to wykres, który pozwala poznać kształt rozkładu cechy ilościowej. Stworzenie histogramu wymaga wcześniejszego pogrupowania obserwacji w przedziały klasowe (czyli przygotowania szeregu rozdzielczego przedziałowego). Przedziały zaznacza się na osi X. Dla tak utworzonych przedziałów wyznacza się liczebność obserwacji w poszczególnych przedziałach.
Przedziały są zwykle równej szerokości, jednak jest możliwe przygotowanie przedziałów, których szerokości będą się różnić.
2.3.1 Co jest na osi Y?
W histogramie znaczenie mają pola prostokątów, z których się składa, a ich wysokość jest kwestią wtórną. Jeżeli szerokości przedziałów klasowych są równe, na osi Y mogą znaleźć się po prostu liczebności (w sytuacji równych szerokości przedziałów pola prostokątów są wprost proporcjonalne do ich wysokości) lub udziały w łącznej liczebności zbiorowości (wyrażone jako ułamek lub procent). Jeżeli szerokości przedziałów klasowych histogramu nie są równe, na osi Y nie mogą znaleźć się liczebności, w takiej sytuacji tzw. gęstość częstości (ang. frequency density).
2.3.2 Kształty histogramów
Typowe kształty histogramów:
- rozkład (w przybliżeniu) symetryczny, jednomodalny
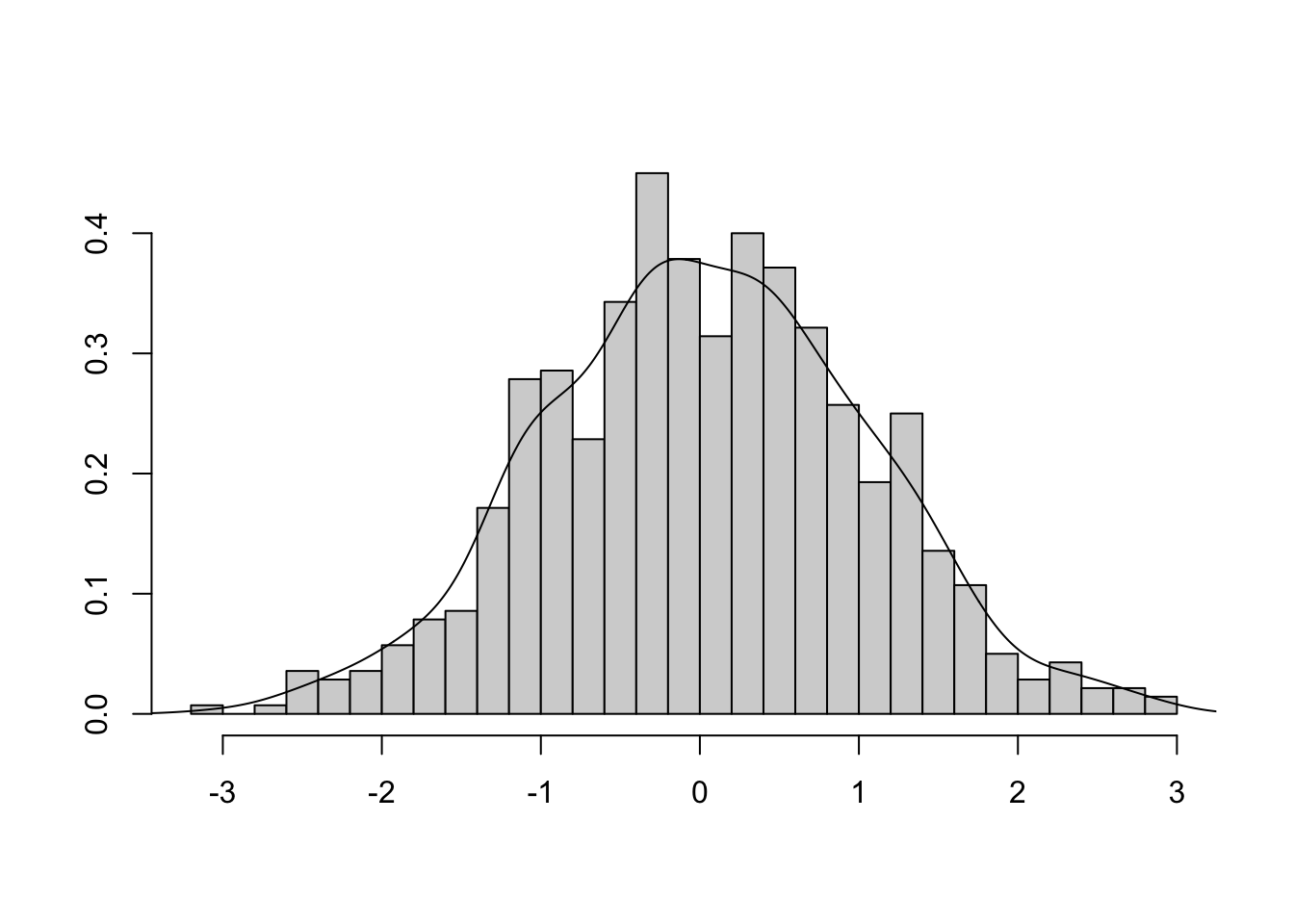
- rozkład prawostronnie skośny
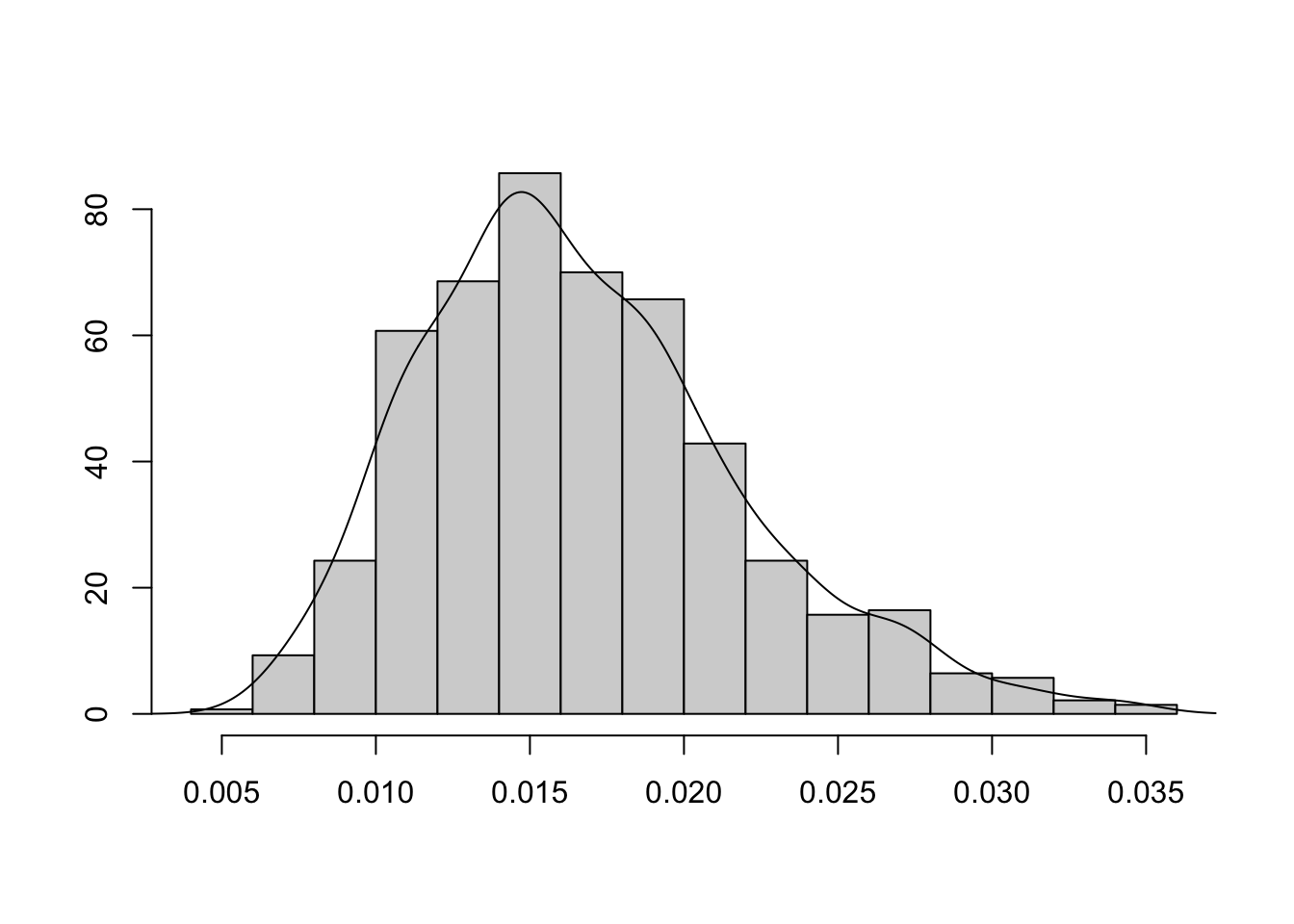
- rozkład skrajnie (prawostronnie) asymetryczny
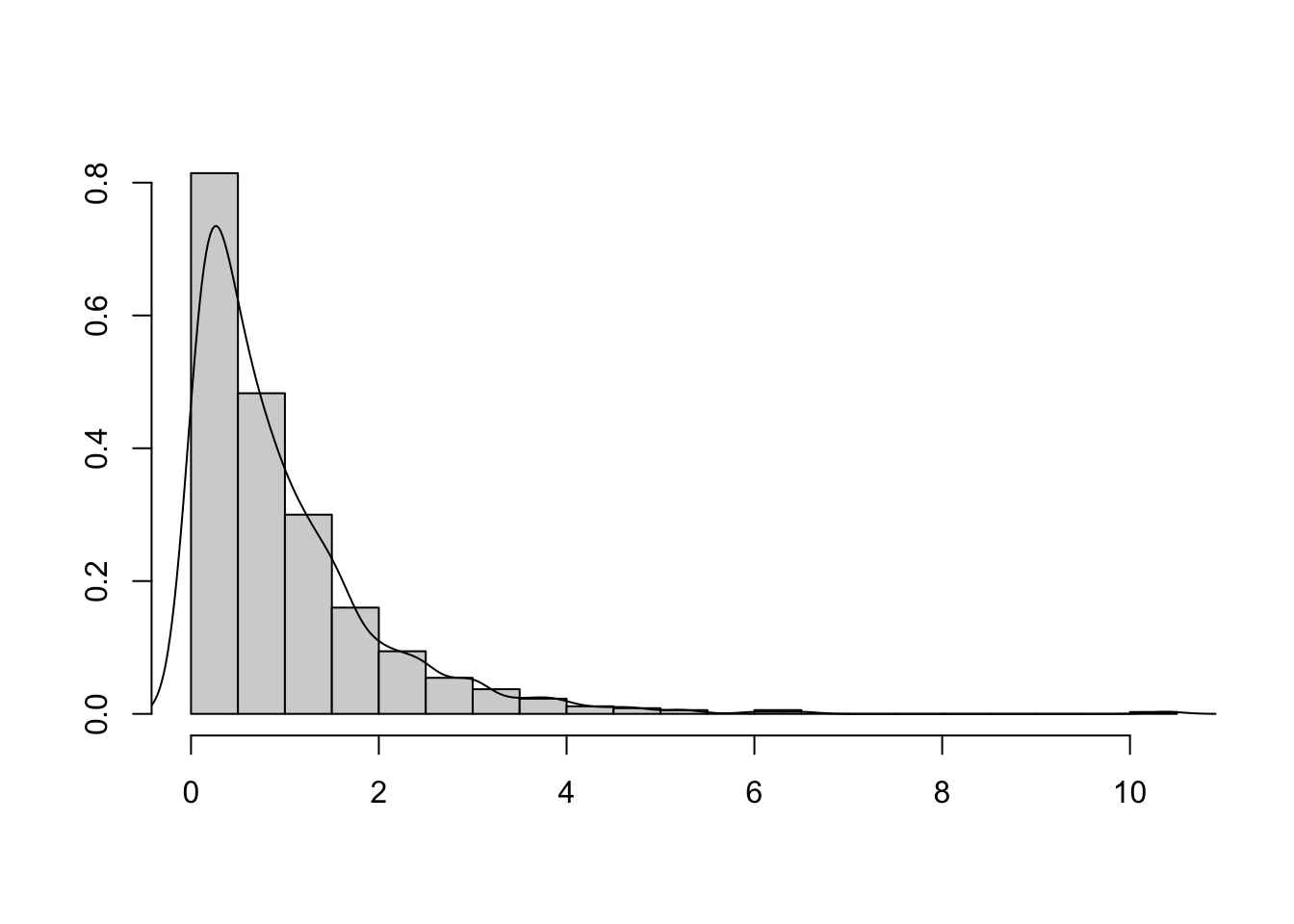
- rozkład lewostronnie skośny
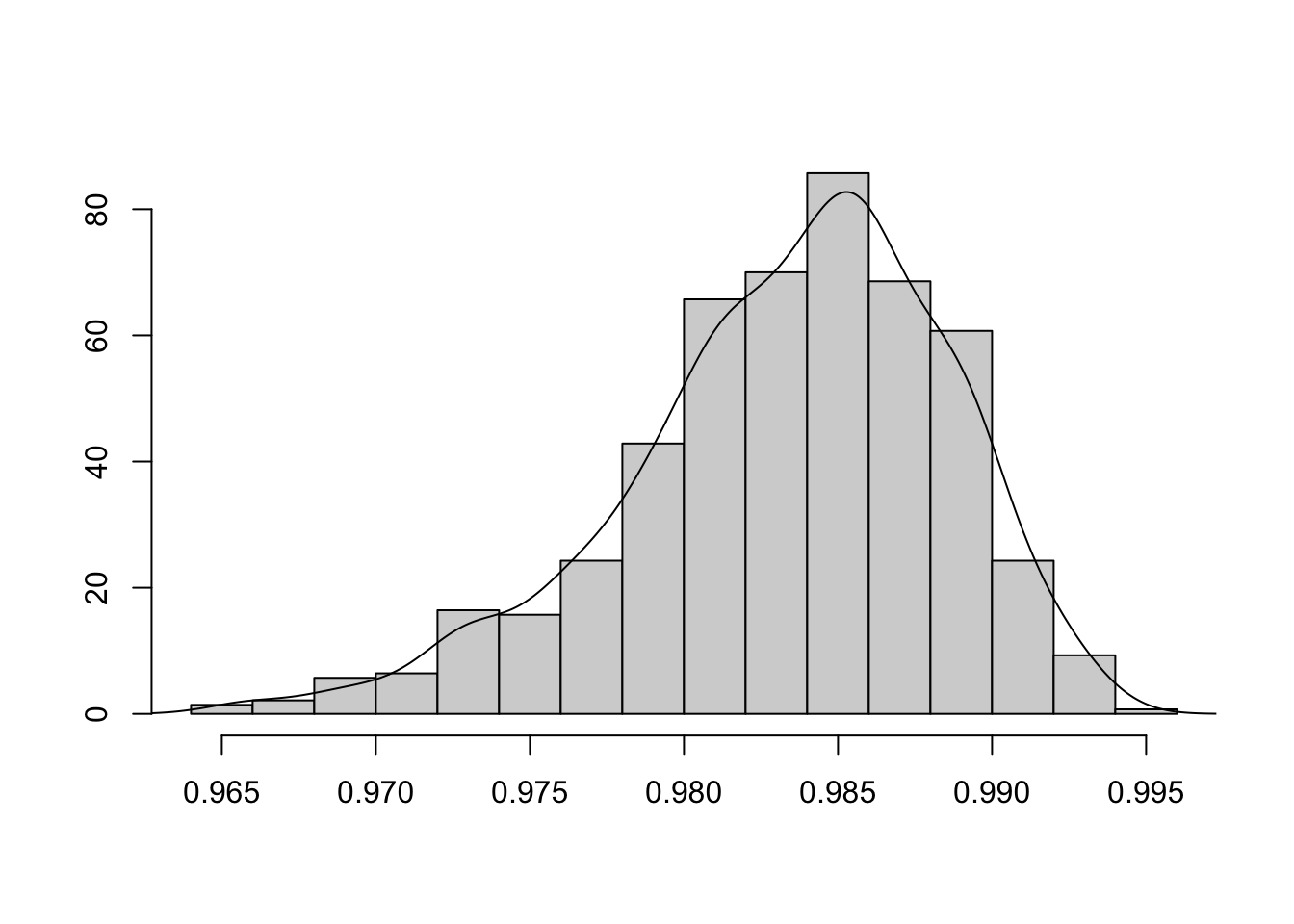
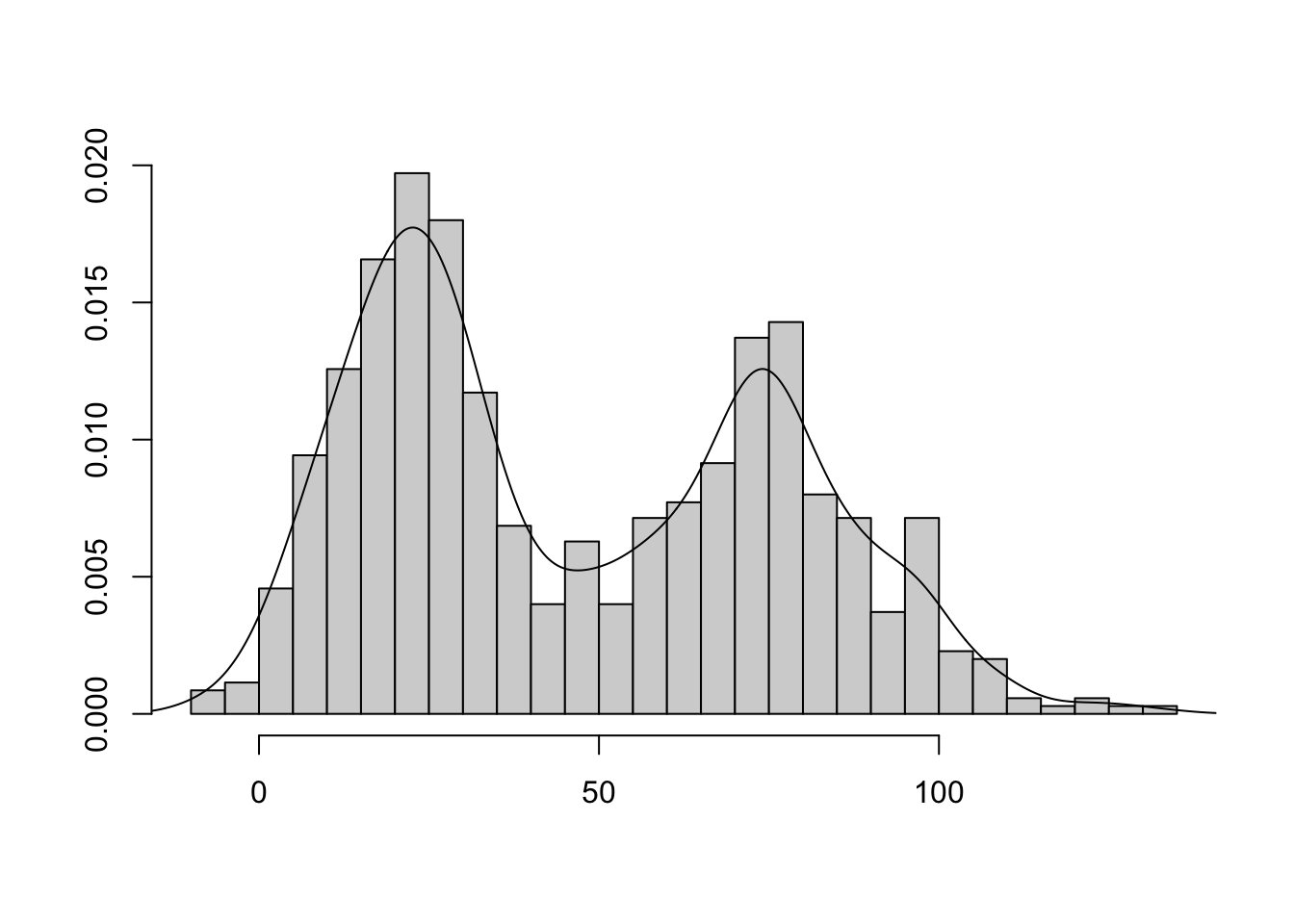
- rozkład dwumodalny
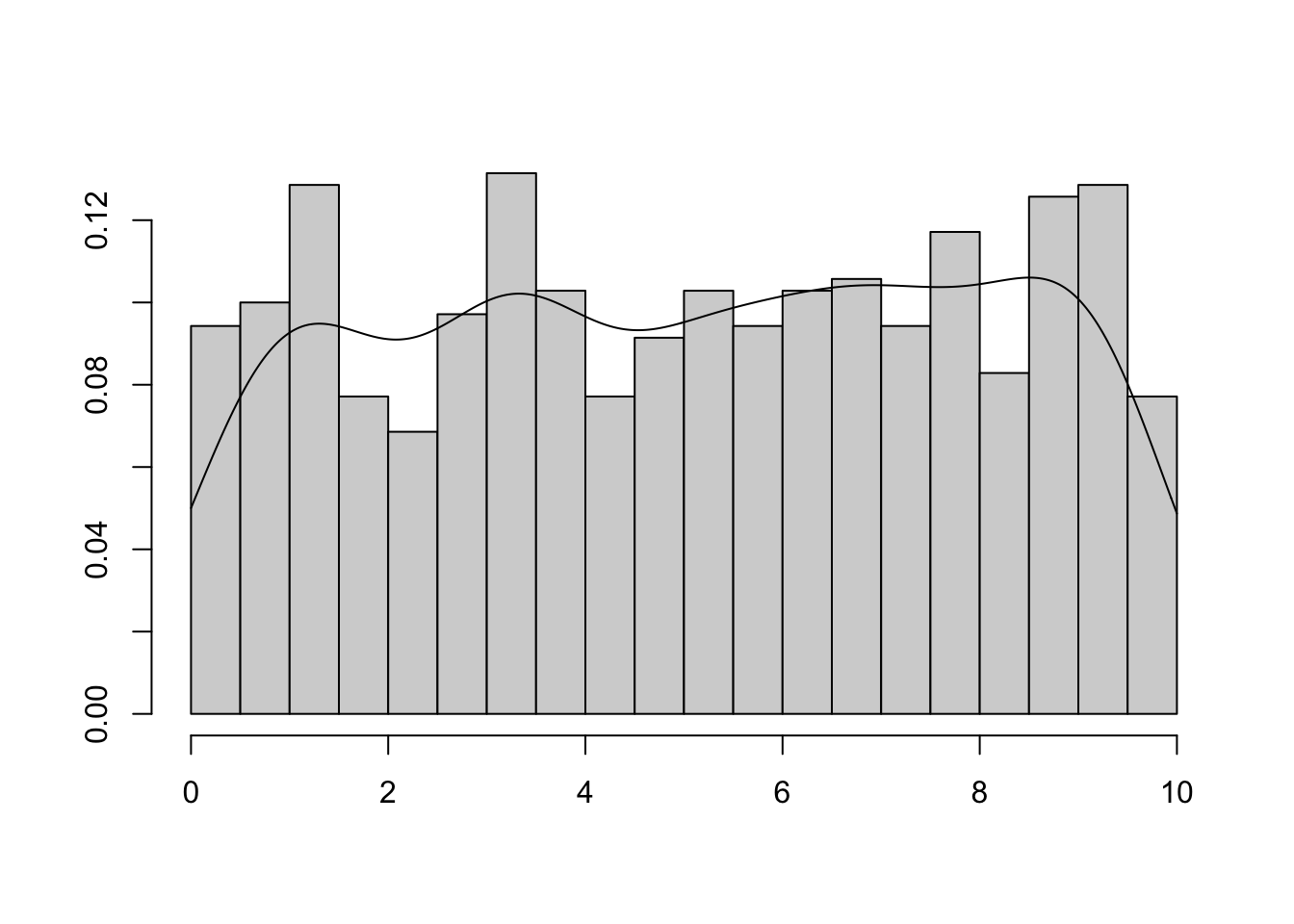
- rozkład równomierny (jednostajny)
2.3.3 Liczba przedziałów klasowych
Istnieją różne reguły dotyczące liczby przedziałów klasowych lub (co jest ściśle powiązane) ich szerokości.
Najważniejszą regułą jest jednak reguła "wzrokowa". Histogram musi dobrze wyglądać: przedziały nie mogą być ani za szerokie (będzie ich wtedy zbyt mało), ani za wąskie (zbyt liczne).
2.5 Zadania
Zadanie 2.1 Wykorzystując dane z pliku SpeedRadarData.csv sporządź histogram przedstawiający prędność jednośladów w okolicach radaru. Z czego może wynikać kształt histogramu? Jak się nazywa taki kształt rozkładu?
2.6 Linki
Wizualizacja frakcji (rozkład zmiennych nominalnych)
Histogram — jak liczba/szerokość przedziałów klasowych wpływa na histogram? Symulacja internetowa: https://college.cengage.com/nextbook/statistics/utts_13540/student/html/simulation2_1.html