Rozdział 8 Korelacja

8.1 Wykres rozrzutu

8.2 Współczynnik korelacji Pearsona

Współczynnik korelacji Pearsona¹ mierzy siłę asocjacji (statystycznego skojarzenia, współzależności, powiązania) pomiędzy dwiema cechami.

Wartości współczynnika korelacji mogą przyjmować wartości z przedziału od -1 do 1 (włącznie).

Jeżeli "chmura punktów" na wykresie wznosi się w kierunku wzrostu wartości na osi x (czyli w prawo), oznacza to, że w miarę wzrostu jednej zmiennej, rośnie — średnio rzecz biorąc — również druga. W takiej sytuacji korelacja jest dodatnia.

Ujemna korelacja występuje, kiedy chmura punktów na wykresie rozrzutu opada (w prawo). Dzieje się tak wtedy, gdy w miarę wzrostu jednej zmiennej tzn. gdy jedna zmienna rośnie, druga maleje.

Korelacja równa dokładnie 1 lub -1 oznacza zależność funkcyjną, liniową, między dwoma cechami. Znak (1 lub -1) zależy od znaku współczynnika nachylenia funkcji pozwalającej przekształcać jedną zmienną w drugą.

Im "luźniej" punkty są zgromadzone wokół linii prostej, tym bliższa zeru jest wartość współczynnika korelacji Pearsona. Punkty zgromadzone ciasno wokół linii prostej odpowiadają wartościom współczynnika bliskim 1 lub -1.

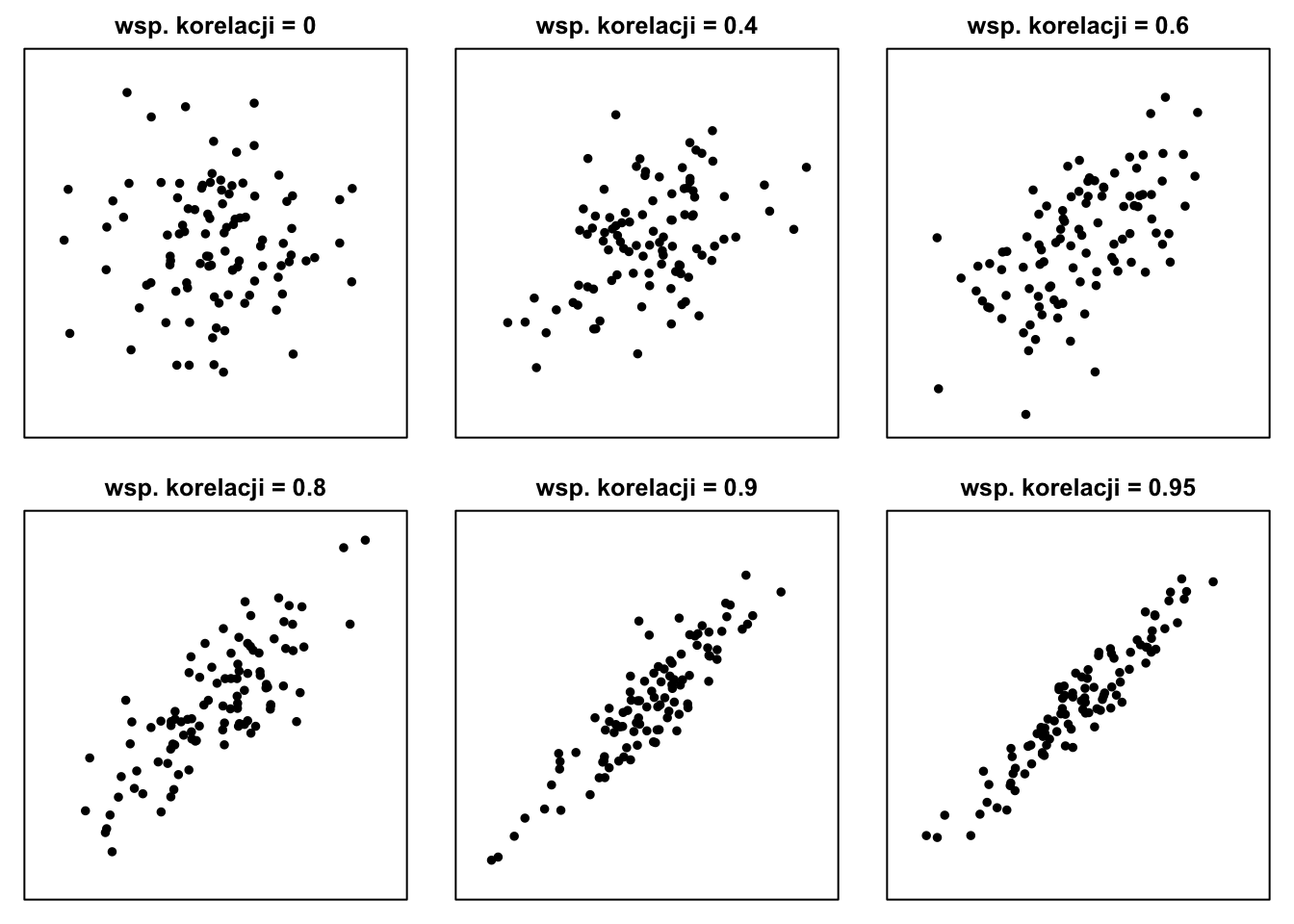
Rysunek 8.1: Przykładowe wykresy rozrzutu dla nieujemnych wartości współczynnika korelacji

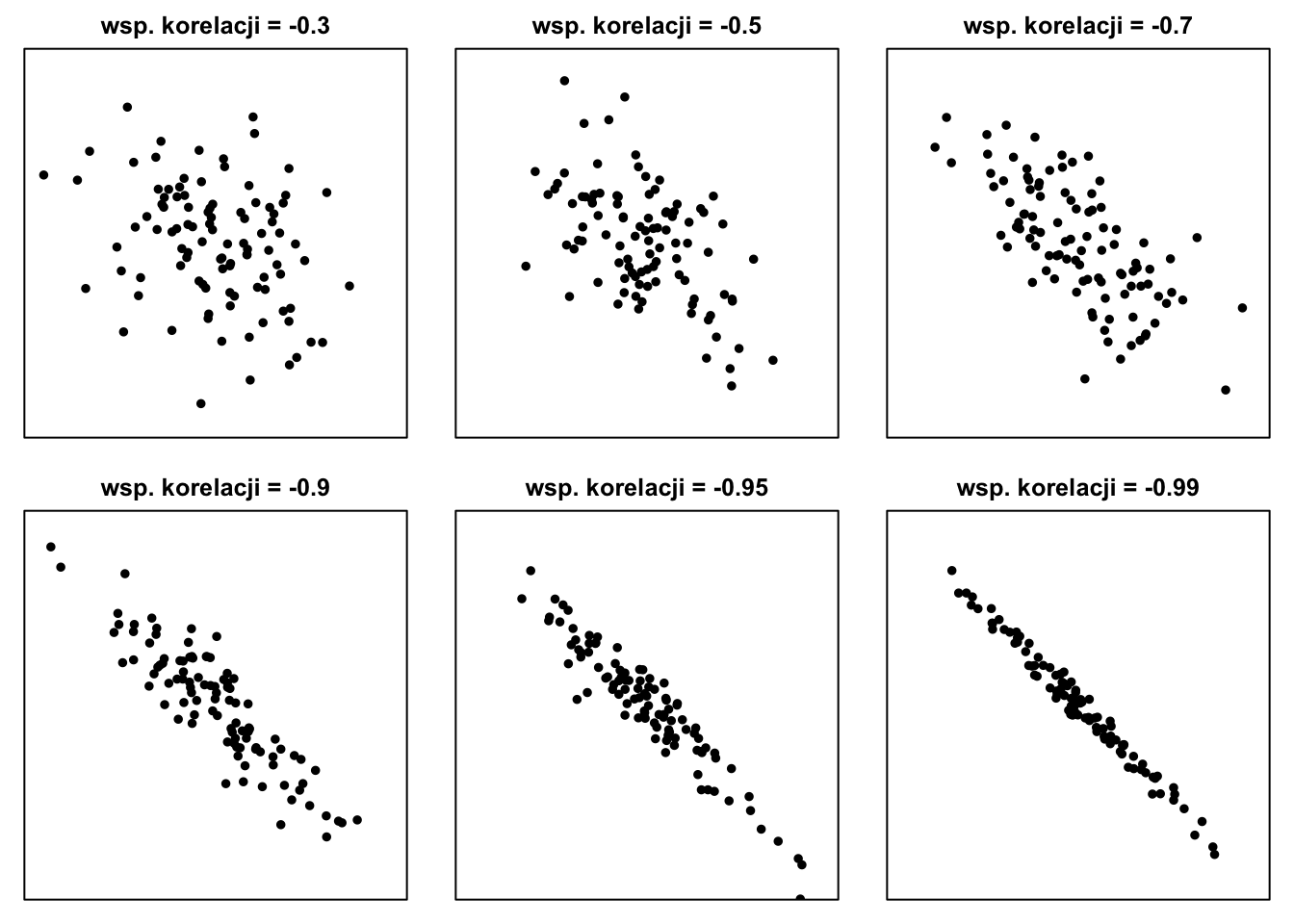
Rysunek 8.2: Przykładowe wykresy rozrzutu dla ujemnych wartości współczynnika korelacji

Jeżeli na wykresie rozrzutu punkty układają się tak, jak przedstawiono na wykresach 8.1 i 8.2 — tzn. grupują się wokół linii prostej, w przypadku niższej współzależności kształt przypomina pochyloną elipsę, — to do opisu łącznego rozkładu dwóch cech można użyć pięciu liczb:

• średniej zmiennej X,

• odchylenia standardowego zmiennej X,

• średniej zmiennej Y,

• odchylenia standardowego zmiennej Y

• oraz współczynnika korelacji pomiędzy zmienną X i zmiennej Y.

8.2.1 Współczynnik korelacji — wzór

Wzór na współczynnik korelacji możemy zapisać na wiele równoważnych sposobów.

Korzystając tylko z wartości cech X i Y oraz ich średnich, współczynnik korelacji Pearsona można obliczyć następująco:

$$r(X,Y) = r_{xy} = \frac{\sum_i{(x_i-\bar{x})(y_i-\bar{y})}}{\sqrt{\sum_i(x_i-\bar{x})^2\sum_i(y_i-\bar{y})^2}} \tag{8.1}$$

Alternatywny popularny zapis wzoru na współczynnik korelacji liniowej Pearsona jest następujący:

$$r_{xy} = \frac{s_{xy}}{s_x s_y} \tag{8.2}$$

W powyższym wzorze $s_{xy}$ to kowariancja (zob. niżej), a $s_x$ i $s_y$ to odchylenia standardowe zmiennych $X$ i $Y$.

Korelację z próby możemy więc interpretować jako standaryzowaną kowariancję.

Korelację dla próby oznaczamy często literą $r$, zaś korelację dla populacji możemy oznaczać literą $\rho$ ("ro"). Jeżeli z kontekstu to nie wynika, warto zaznaczyć, których zmiennych dotyczy korelacja (np. pisząc $r(X,Y)$ albo $r_{xy}$).

Wzór (8.1) możemy stosować zarówno dla próby, jak i populacji, zaś we wzorze (8.2) powinniśmy albo zarówno kowariancję, jak i odchylenia wyznaczać za pomocą wzorów dla próby, albo w obu przypadkach korzystać ze wzorów dla populacji. Wynik będzie ten sam.

8.2.2 Kowariancja

Kowariancja to miar pokazująca "współzmienność" dwóch cech.

Wzór na kowariancję "dla próby" to:

$$s_{xy} = \frac{\sum_{i=1}^n \left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{n-1} \tag{8.3}$$

Wzór na kowariancję "dla populacji" to:

$$\sigma_{XY} = \frac{\sum_{i=1}^N \left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{N} \tag{8.4}$$

8.2.3 Współczynnik korelacji i kowariancja w arkuszach kalkulacyjnych

W arkuszach kalkulacyjnych można obliczyć współczynnik korelacji liniowej Pearsona używając funkcji WSP.KORELACJI (ang. CORREL) — Arkusze Google, Excel lub funkcji PEARSON — Arkusze Google, Excel.

Aby wyznaczyć kowariancję "dla populacji", w arkuszach można zastosować funkcję KOWARIANCJA (COVAR) arkusze Google, Excel lub KOWARIANCJA.POPUL (COVARIANCE.P) — arkusze Google, Excel.

Aby wyznaczyć kowariancję dla próby, w arkuszach używamy funkcji KOWARIANCJA.PRÓBKI (COVARIANCE.S) — arkusze Google, Excel.

Rangi w arkuszach kalkulacyjnych wyznacza się za pomocą funkcuji POZYCJA.ŚR (RANK.AVG) — arkusze Google, Excel.

8.2.4 Test współczynnika korelacji

8.3 Współczynnik korelacji rang Spearmana

Współczynnik korelacji Spearmana to po prostu współczynnik korelacji Pearsona obliczony dla rang zmiennych X i Y.

$$\mathit{r_s}=r\left( Rank(X), Rank(Y)\right)$$

Oznacza to, że licząc współczynnik rang Spearmana, najpierw zamieniamy wartości $x_i$ oraz $y_i$ na rangi, a następnie obliczamy współczynnik Pearsona dla tak wyznaczonych rang.

8.3.1 Zamiana wartości cechy na rangi

Przyjęło się, że w zastosowaniach statystycznych rangi nadaje się rosnąco, tzn. najniższa wartość dostaje rangę 1, kolejna 2, itd.

Kiedy wartości cechy powtarzają się w szeregu szczegółówym stosuje się średnią z rang, które przysługiwałyby powtórzonym wartościom. Mówimy wtedy o wartościach/rangach "wiązanych".

Przykład:

wartości	rangi
5	1,5
5	1,5
9	3,0
11	4,0
14	6,0
14	6,0
14	6,0
20	8,0

8.3.2 Uproszczony wzór dla współczynnika korelacji rang Spearmana

Uproszczony wzór dla współczynnika Spearmana można stosować w sytuacji, gdy nie ma rang wiązanych (każda wartość $x_i$ jest inna oraz każda wartość $y_i$ jest inna).

$$r_s = 1 - \frac{6\sum_{i=1}^n d_i^2}{n(n^2-1)}$$

W powyższym wzorze $d_i$ to różnica między rangami dla obserwacji $i$:

$$d_i = Rank(x_i)-Rank(y_i)$$

8.4 Tau Kendalla

8.5 Korelacja cząstkowa

8.6 Inne miary oparte na współczynniku Pearsona

8.7 Linki

Wykres rozrzutu i przykłady korelacji — aplikacja webowa: https://istats.shinyapps.io/Association_Quantitative/

Wykres rozrzutu i korelacje — aplikacja webowa: https://rpsychologist.com/correlation/

Odgadnij korelację — aplikacja webowa: https://istats.shinyapps.io/guesscorr/

Korelacje regionalne w USA: https://college.cengage.com/nextbook/statistics/utts_13540/student/html/simulation3_2.html

---

1. Jeżeli ktoś używa terminu współczynnik korelacji,bez dodatkowych dopowiedzeń, należy zwykle zakładać, że odwołuje się współczynnika korelacji Pearsona.↩︎