8 探索性資料分析
本章為 Wickham and Grolemund (2016) 第 5 章內容。
資料一拿來就先跑跑看長什麼樣子!
8.1 事前準備
探索性資料分析(Exploratory Data Analysis, EDA)的目標就是要更了解資料,而步驟可以為:
構思關於這筆資料的問題。
透過視覺化、轉換和建模,試著尋找答案。
經由所得的結果,重整原先的問題,或者構思、增加新的問題。
8.2 問題
Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.
—John Tukey
你可以問這兩類的問題:
What type of variation occurs within my variables?
What type of covariation occurs between my variables?
8.3 Variation
Variation 即每次測量變數值所得的趨勢(tendency)。每個變數都有自己的 variation,而要看出 variation,最好的方法是視覺化變數值的分配。
8.3.1 視覺化分配
如果是類別變數,我們可以使用 bar chart 來視覺化,因為它只有一小組變數值,而存成 factors 或 characters 的向量,如:
ggplot(data = diamonds) +
geom_bar(mapping = aes(x = cut))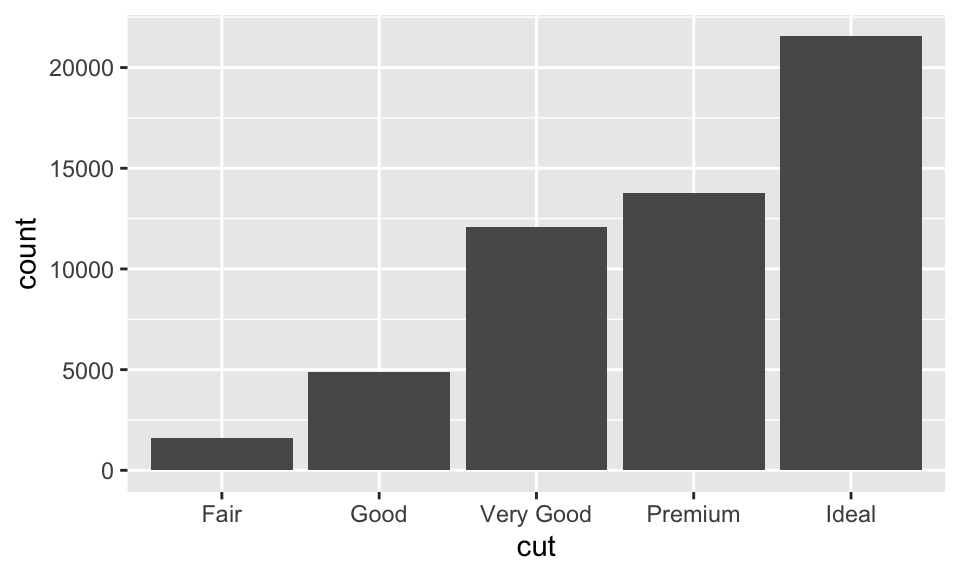
也可以使用 dplyr 的 count() 來計算究竟各種品質的鑽石有多少,如:
diamonds %>%
count(cut)## # A tibble: 5 × 2
## cut n
## <ord> <int>
## 1 Fair 1610
## 2 Good 4906
## 3 Very Good 12082
## 4 Premium 13791
## 5 Ideal 21551如果是連續變數,例如數字與日期時間,我們則要使用 histogram,如:
# binwidth 引數即直方圖的直方寬度
ggplot(data = diamonds) +
geom_histogram(mapping = aes(x = carat), binwidth = 0.5)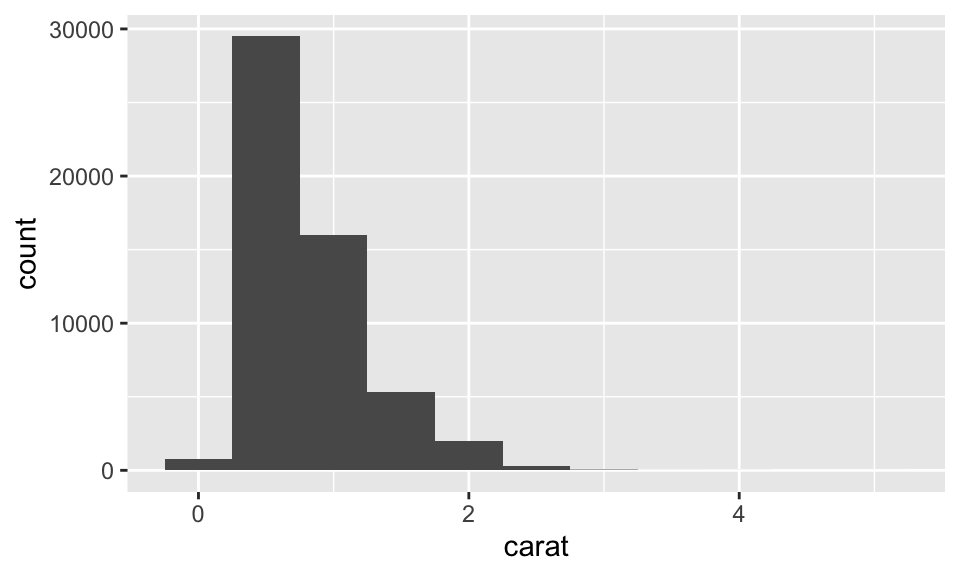
我們也可以用 count() 來計算,如:
diamonds %>%
count(cut_width(carat, 0.5))## # A tibble: 11 × 2
## `cut_width(carat, 0.5)` n
## <fct> <int>
## 1 [-0.25,0.25] 785
## 2 (0.25,0.75] 29498
## 3 (0.75,1.25] 15977
## 4 (1.25,1.75] 5313
## 5 (1.75,2.25] 2002
## 6 (2.25,2.75] 322
## 7 (2.75,3.25] 32
## 8 (3.25,3.75] 5
## 9 (3.75,4.25] 4
## 10 (4.25,4.75] 1
## 11 (4.75,5.25] 1如果想要重疊多個直方圖,使用 geom_frepoly() 而非 geom_histogram()。兩者的算法一樣,但前者以線來呈現,後者以直方來呈現,如:
ggplot(data = diamonds, mapping = aes(x = carat, color = cut)) +
geom_freqpoly(binwidth = 0.1)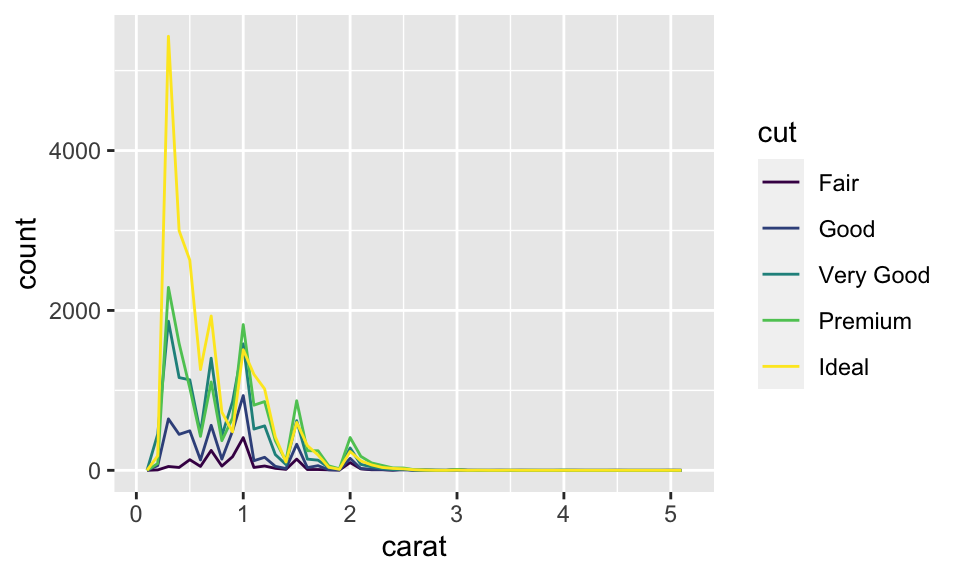
8.3.2 代表性的變數值
哪些是變數值經常出現?哪些變數值很少出現?其中有什麼規律?
ggplot(data = diamonds, mapping = aes(x = carat)) +
geom_histogram(binwidth = 0.01)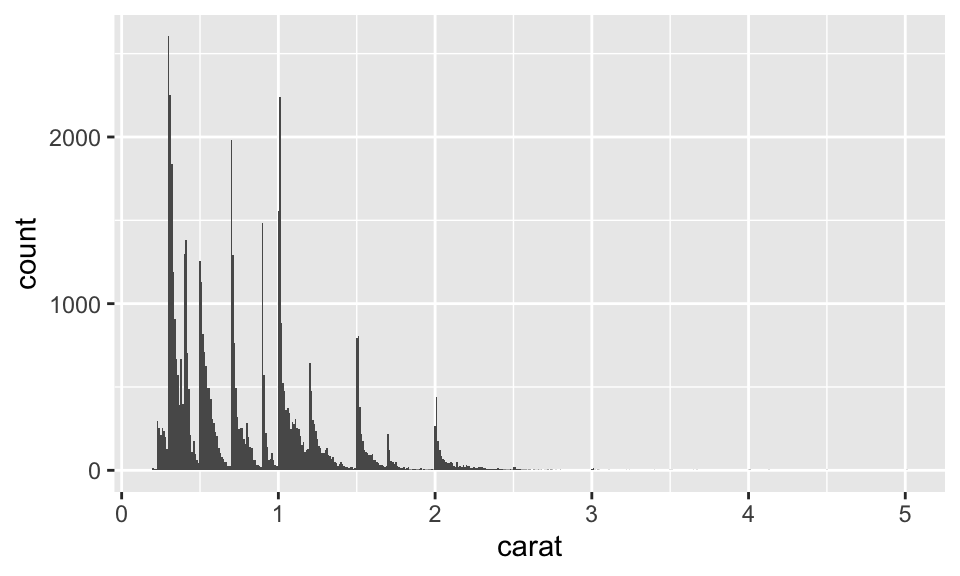
為何克拉數為整數與某些常見的有理數的觀察值特別多?為何每個高峰的右側都比左側更緩?為何超過 3 克拉的鑽石很稀有?
類似的值的群集(cluster)通常意味著資料中有子群(subgroup)。我們可以質問幾個問題:
每個 subgroup 中的觀察值與其他 subgroups 之間有何相異或相似?
如何描述或解釋群集?
為何群集的外觀可能產生誤導?
8.3.3 不尋常的變數值
Outliers 即不尋常的變數值,可能源自資料輸入錯誤,也可能是一些不一樣的東西。
要注意的是,當樣本很大時,使用直方圖很難看出 outliers;例如上一張圖中,事實上 3 克拉到 5 克拉之間都還有觀察值,可是從直方圖幾乎看不出來。我們可以透過 coord_cartesian(),來改變 y 軸的上下限,這樣就可以辨識稀有的觀察值了,如:
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5) +
coord_cartesian(ylim = c(0, 50))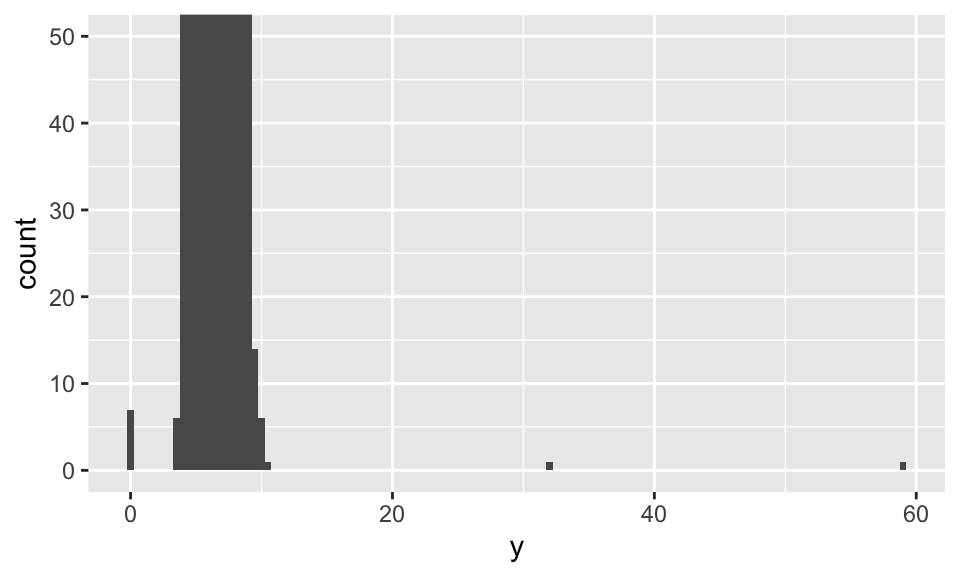
或者,我們也可以使用 dplyr,列出寬度小於 3 mm 或超過 20 mm 的觀察值:
unusual <- diamonds %>%
filter(y < 3 | y > 20) %>%
arrange(y)
unusual## # A tibble: 9 × 10
## carat cut color clarity depth table price x y z
## <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
## 1 1 Very Good H VS2 63.3 53 5139 0 0 0
## 2 1.14 Fair G VS1 57.5 67 6381 0 0 0
## 3 1.56 Ideal G VS2 62.2 54 12800 0 0 0
## 4 1.2 Premium D VVS1 62.1 59 15686 0 0 0
## 5 2.25 Premium H SI2 62.8 59 18034 0 0 0
## 6 0.71 Good F SI2 64.1 60 2130 0 0 0
## 7 0.71 Good F SI2 64.1 60 2130 0 0 0
## 8 0.51 Ideal E VS1 61.8 55 2075 5.15 31.8 5.12
## 9 2 Premium H SI2 58.9 57 12210 8.09 58.9 8.06我們可以發現,寬度等於 0 mm 的鑽石根本不可能存在,顯然是打錯了;而寬度為 31.8 mm 與 58.9 mm 那兩個觀察值的價格也不合理。此種錯誤(像是輸入錯誤)所出現的 outliers 就該丟掉。但也不是逢 outliers 就該丟掉,如果其有真實的意義,那還是必須保留。
8.4 Missing Value
8.4.1 替換掉 Outliers
遇到 outliers,有兩種做法:
- 丟棄有奇怪的變數值的觀察值。可是,其中一個變數輸入錯誤不代表其他變數就也輸入錯誤。而且如果資料品質不良,可能最後什麼都不剩。
# 丟棄有奇怪的變數值的觀察
diamonds2 <- diamonds %>%
filter(between(y, 3, 20))- (推薦)把 outliers 的變數值換成
NA。我們可以使用mutate()與ifelse(),如:
# 把 outliers 的變數值換成 NA
diamonds2 <- diamonds %>%
mutate(y = ifelse(y < 3 | y > 20, NA, y))# 這樣畫出來的散佈圖就不會是 y 的 outliers
ggplot(data = diamonds2, mapping = aes(x = x, y = y)) +
geom_point(na.rm = TRUE) # 注意:設定 na.rm = TRUE,忽略掉 NA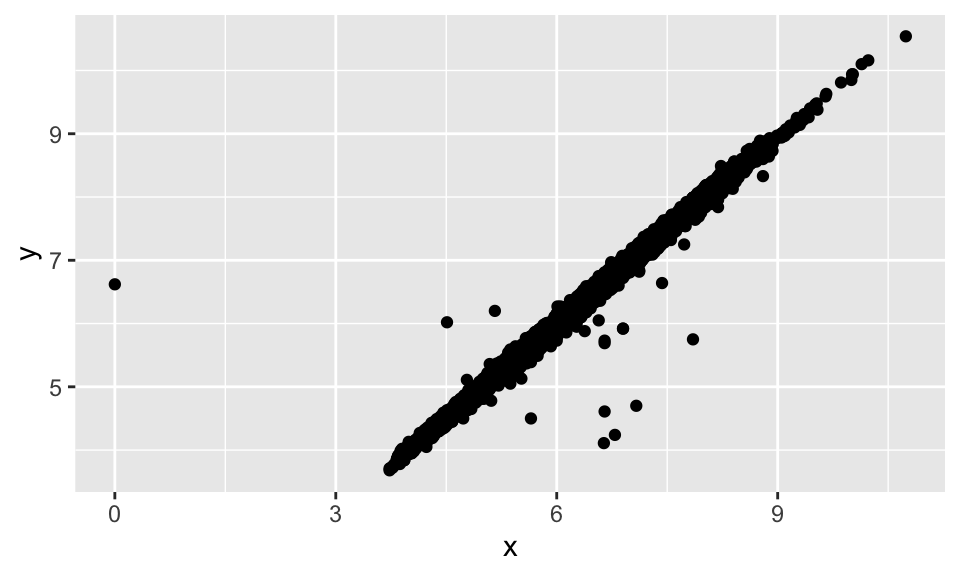
8.4.2 比較 NA 與否
有時候我們想了解具有 NA 的觀察值與有變數值的觀察值有何區別,那我們就可以使用 mutate() 與 is.na() 來記錄。在 nycflights13 的 flights 中,dep_time 如果是 NA,那表示航班取消。當我們想要比較取消航班與為取消航班之間的預計離開時間的差別,我們可以:
nycflights13::flights %>%
mutate(
cancelled = is.na(dep_time),
sched_hour = sched_dep_time %/% 100,
sched_min = sched_dep_time %% 100,
sched_dep_time = sched_hour + sched_min / 60) %>%
ggplot(mapping = aes(sched_dep_time)) +
geom_freqpoly(mapping = aes(color = cancelled), binwidth = 1/4)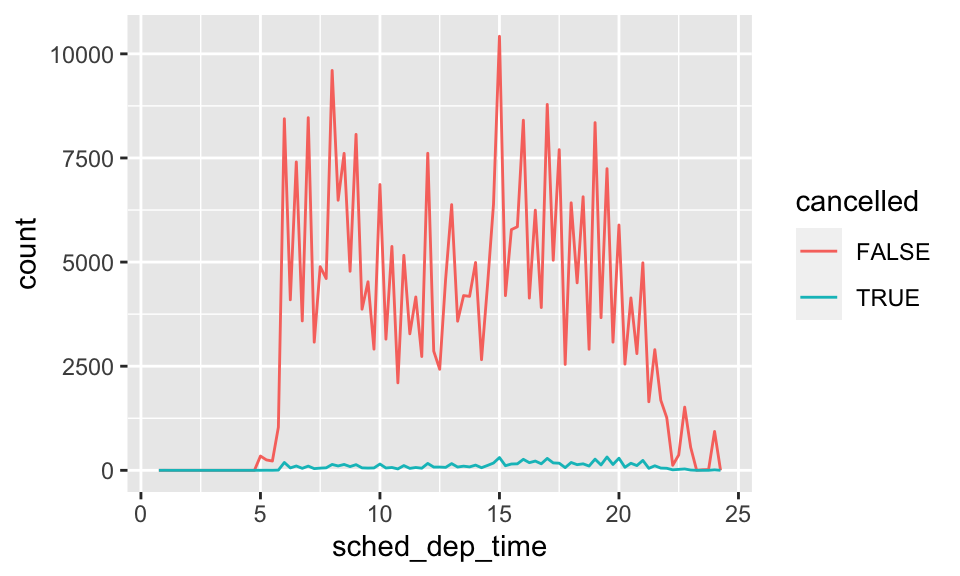
不過,因為未取消航班比取消的航班多太多了,因此下個章節我們要對此做些改進。
8.5 Covariation
Covariation 即兩個或多個變數變動的關係。想要發覺 covariation,最好的辦法就是視覺化它。但如何視覺化則牽涉到變數型態的問題。
8.5.1 類別與連續變數
為什麼我們剛剛所使用的
geom_freqpoly()不太適合拿來「比較」變數?
這是因為,geom_freqpoly() 的高度(縱軸)是出現次數,所以說如果有一組遠小於另一組,像剛剛的情況,那我們就很難看出其形狀的差異。以下還有另一個例子為比較不同品質的鑽石之間的價格差異:
ggplot(data = diamonds, mapping = aes(x = price)) +
geom_freqpoly(mapping = aes(color = cut), binwidth = 500)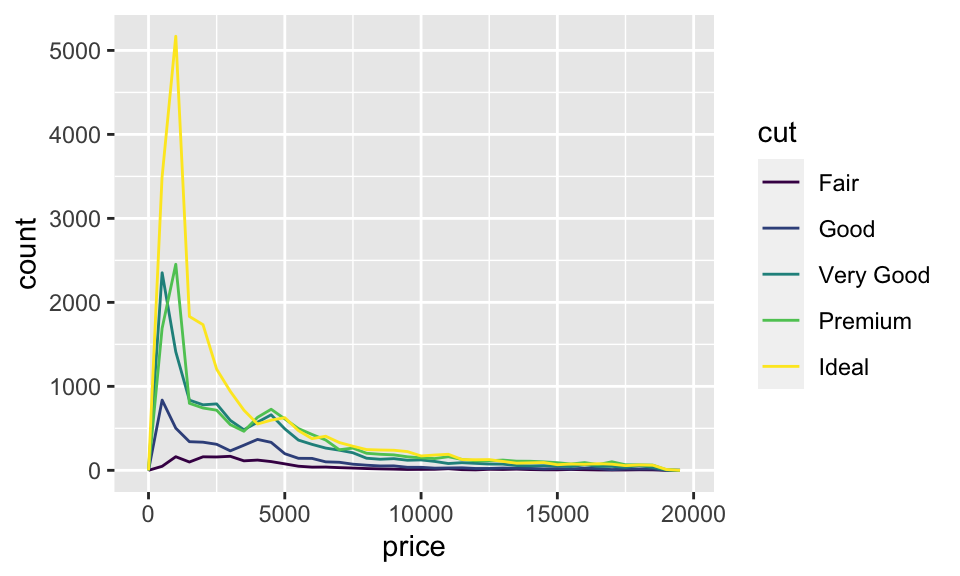
這種時候,我們可以把 \(y\) 軸從呈現 “count”,改成呈現 “density”,即經過標準化的 count,在每組的多邊形底下的面積都為 \(1\),如:
ggplot(data = diamonds, mapping = aes(x = price, y = ..density..)) +
geom_freqpoly(mapping = aes(color = cut), binwidth = 500)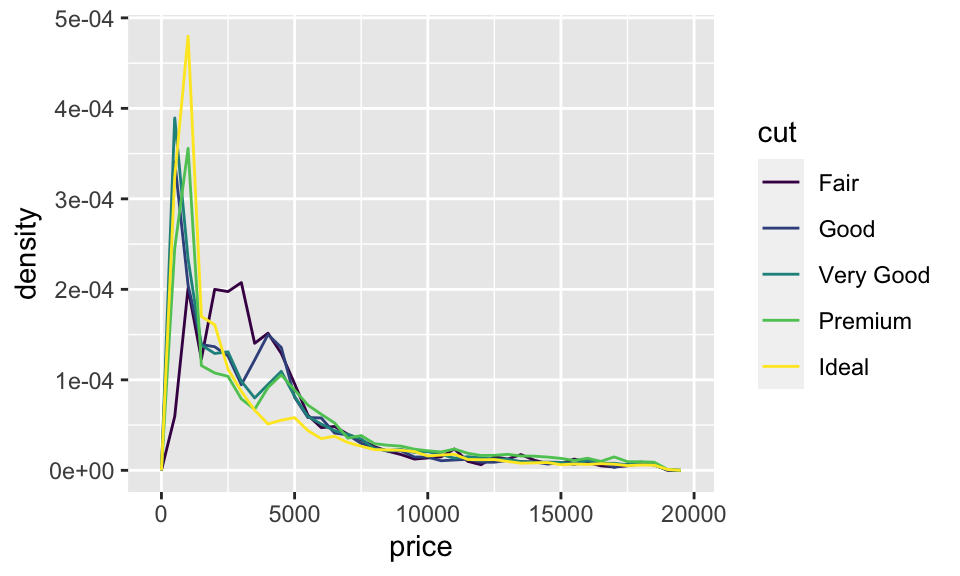
另一種把連續變數拆成類別變數然後呈現的方法是使用箱形圖(box plot),其可以把某些分佈的特徵給視覺化;即每個箱形圖中的箱子的底部都是 25 百分位,而頂部都是 75 百分位,箱子的中間則是中位數。我們可以大略看出分佈與偏態,而箱形圖中的點則是 outliers,線則是從箱子外延伸到非 outliers 的地方,如:
ggplot(data = diamonds, mapping = aes(x = cut, y = price)) +
geom_boxplot()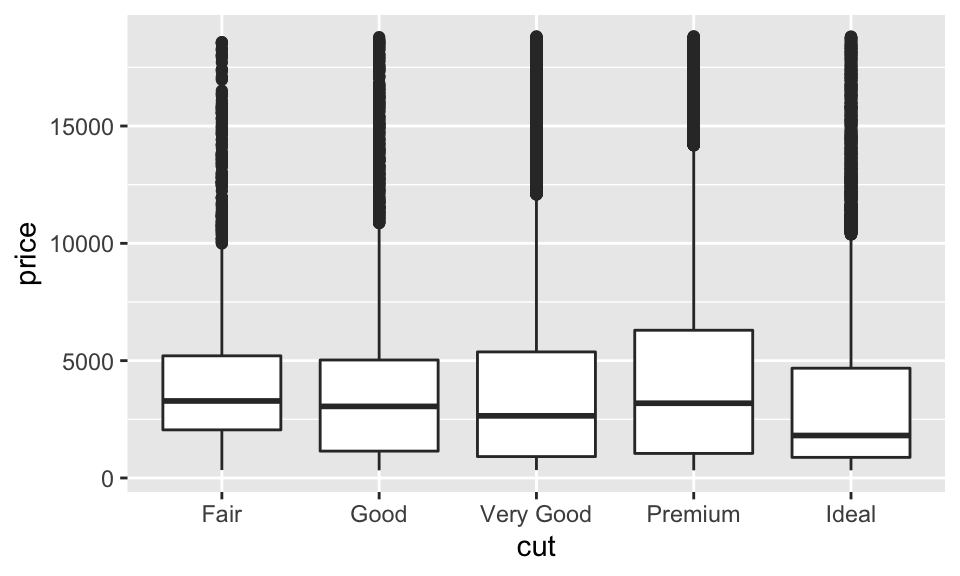
看起來似乎 fair 的比較貴!為什麼?實際上是因為 fair 的鑽石相對比較大顆,如:
ggplot(data = diamonds, mapping = aes(x = cut, y = carat)) +
geom_boxplot()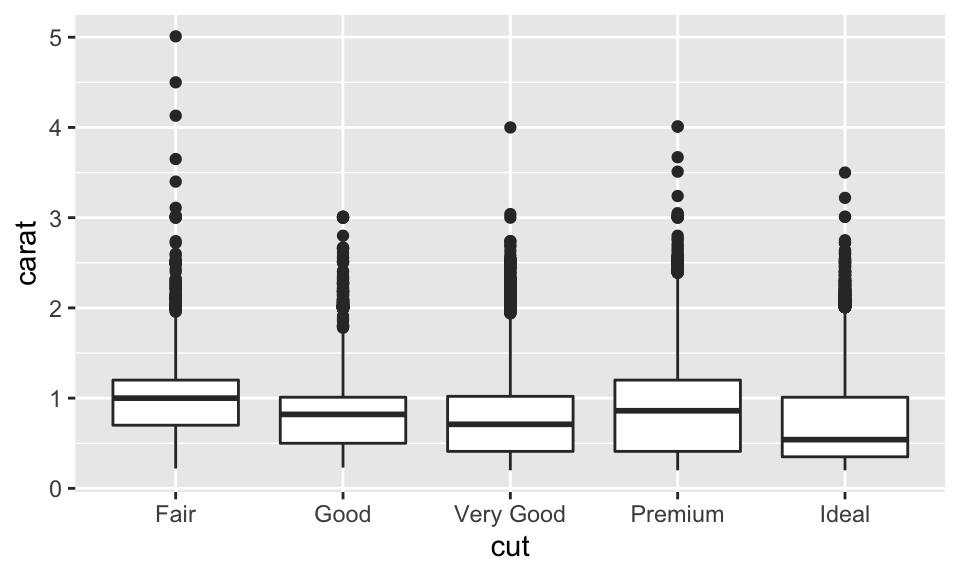
類別變數經常是有序的(例如 cut),但也有些並不然。如果類別變數無序,我們又希望它按照一定的方式來排序呢?可以使用 reorder()。例如,在 mpg 這個 dataset 中,class 其實是無序的,我們想知道各種 class 的 hwy 的話,以箱形圖描繪,就如:
ggplot(data = mpg, mapping = aes(x = class, y = hwy)) +
geom_boxplot()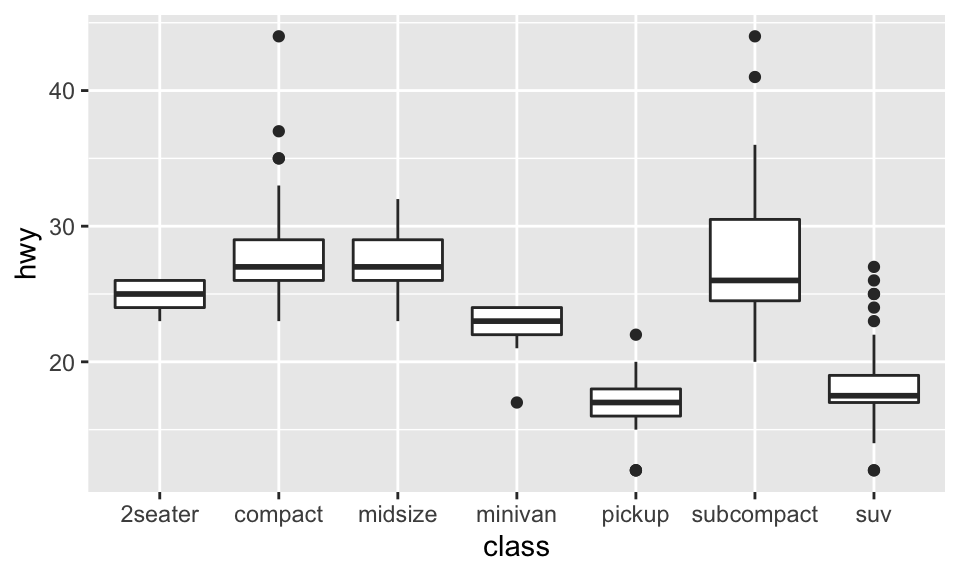
那如果我們想要依照中位數來排序 class 的變數值的話,根據說明文檔,reorder 的語法如:
reorder(x, X, FUN = mean, ...,
order = is.ordered(x))因此可以:
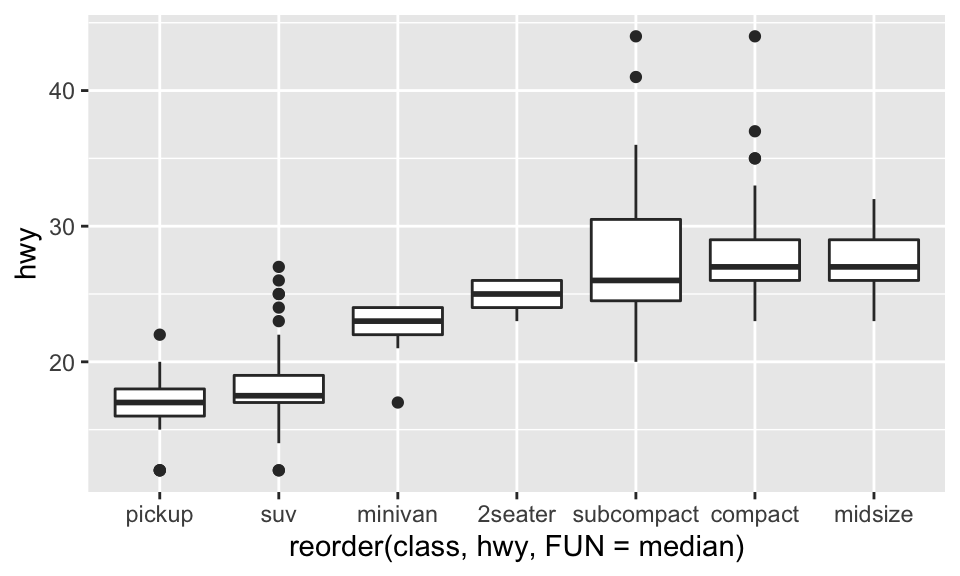
ggplot(data = mpg) +
geom_boxplot(mapping = aes(
x = reorder(class, hwy, FUN = median),
y = hwy
))
也可以仿效節 (coordinatedsystem) 的作法,加上 coord_flip(),將箱形圖旋轉 90 度,如:
ggplot(data = mpg) +
geom_boxplot(mapping = aes(
x = reorder(class, hwy, FUN = median),
y = hwy
)) + coord_flip()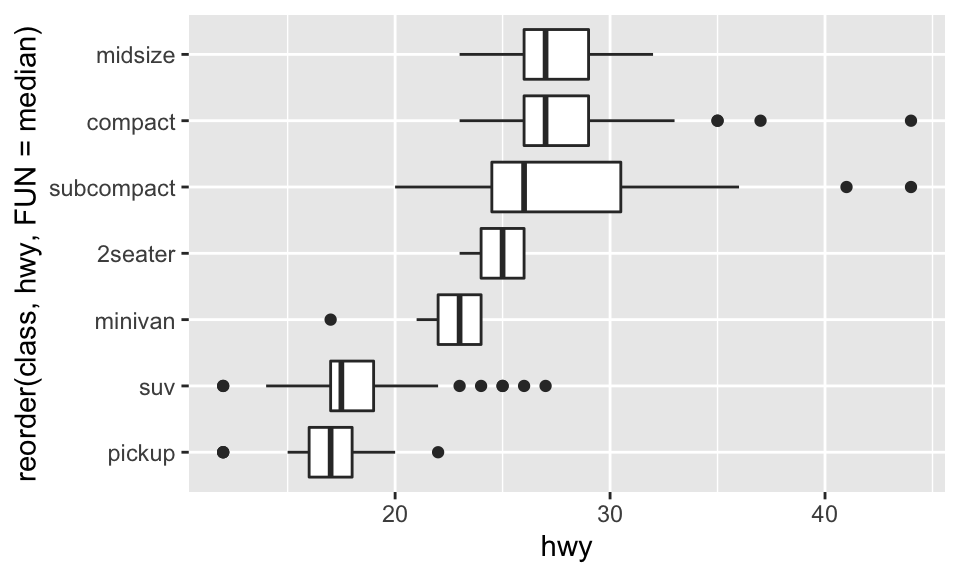
8.5.2 兩個類別變數
要視覺化兩個類別變數之間的 covariation,我們要計算各種組合有多少觀察值,如使用 geom_count():
ggplot(data = diamonds) +
geom_count(mapping = aes(x = cut, y = color))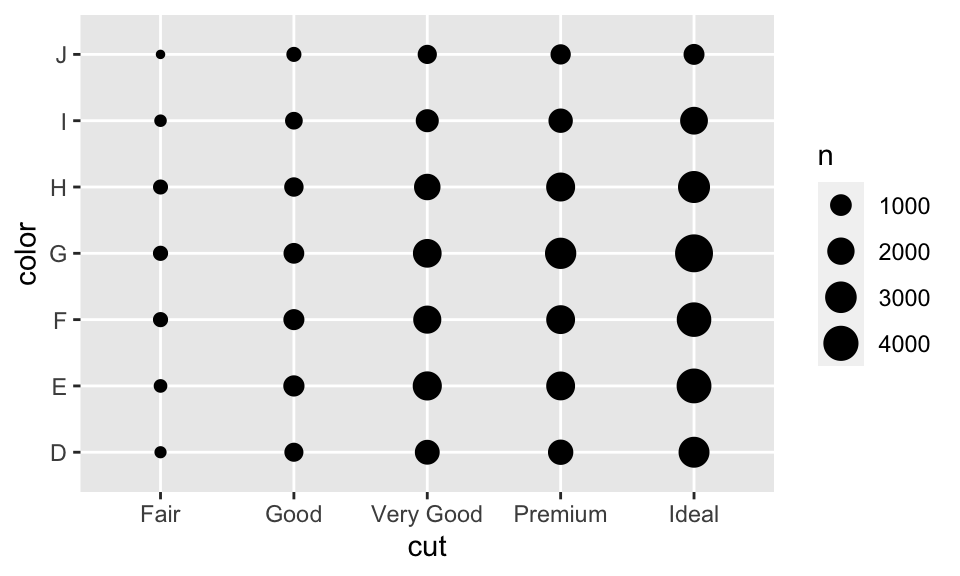
或者以 dplyr 來計算:
diamonds %>%
count(color, cut)## # A tibble: 35 × 3
## color cut n
## <ord> <ord> <int>
## 1 D Fair 163
## 2 D Good 662
## 3 D Very Good 1513
## 4 D Premium 1603
## 5 D Ideal 2834
## 6 E Fair 224
## 7 E Good 933
## 8 E Very Good 2400
## 9 E Premium 2337
## 10 E Ideal 3903
## # … with 25 more rows這也可以接著以 geom_title() 來視覺化,如:
diamonds %>%
count(color, cut) %>%
ggplot(mapping = aes(x = color, y = cut)) +
geom_tile(mapping = aes(fill = n))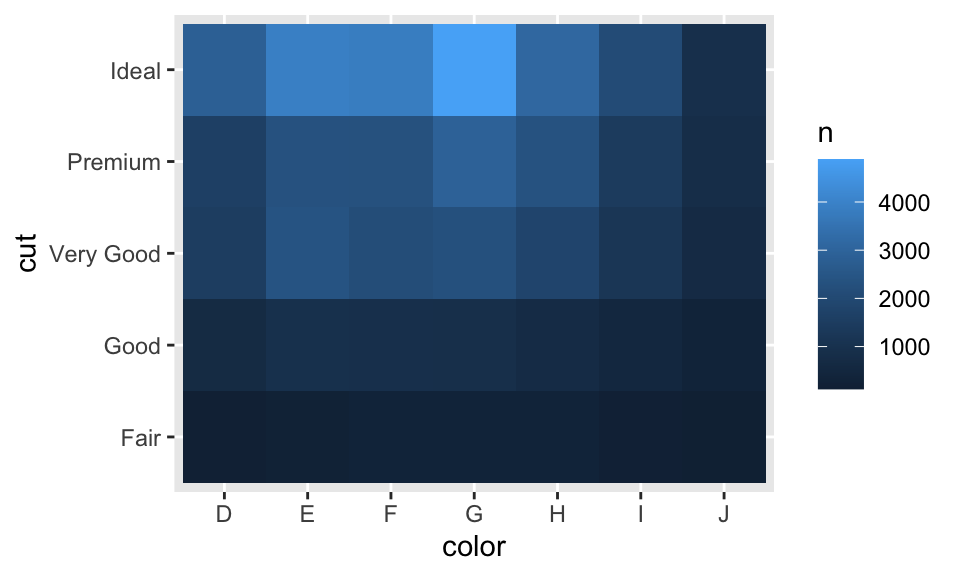
而如果類別變數是無序的,我們可能會需要使用 seration 套件來同時重新排序 rows 與 columns;如果想要畫更大的熱圖,可能會需要使用 d3heatmap 或 heatmaply 套件。
8.5.3 兩個連續變數
要視覺化兩個連續變數的可以 geom_point() 畫出散佈圖,如:
ggplot(data = diamonds) +
geom_point(mapping = aes(x = carat, y = price))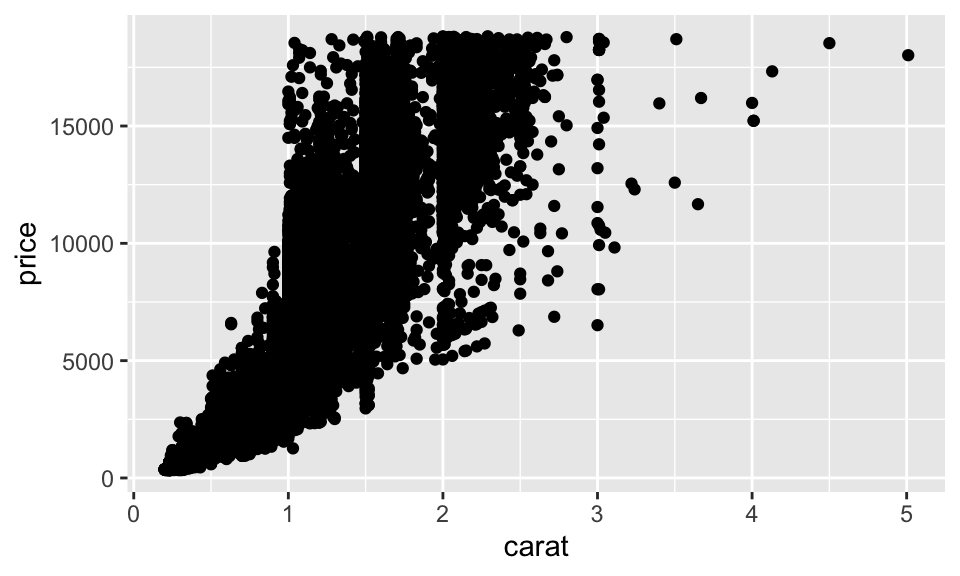
不過 overplot 的情況在小克拉的鑽石有點嚴重,因此我們可以更改透明度,如:
ggplot(data = diamonds) +
geom_point(mapping = aes(x = carat, y = price),
alpha = 1/100)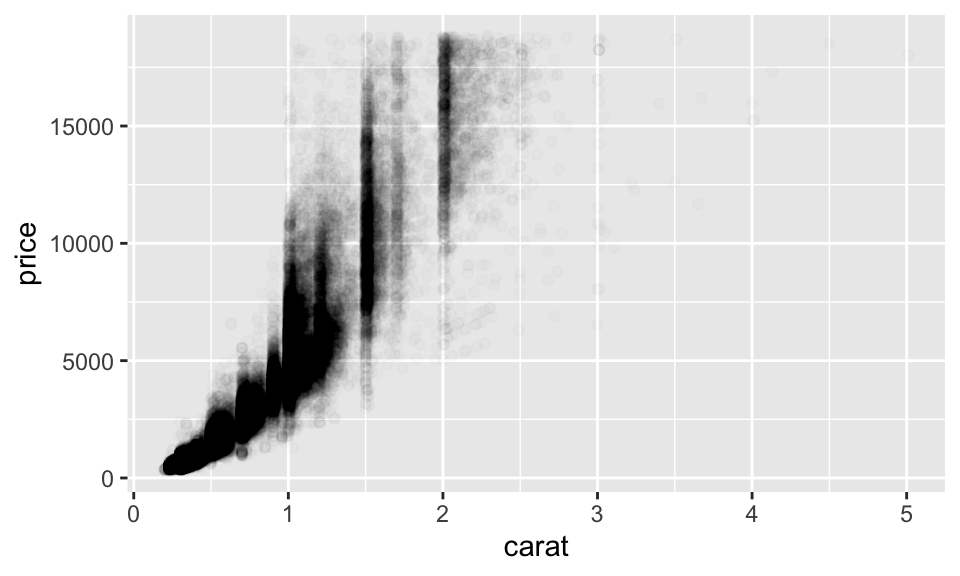
但其實在很大的 dataset 中,更改透明度也不見得是好辦法。
除了單純描繪散佈圖以外,另一個方法是使用 bin。以前的 geom_histogram() 與 geom_freqpoly() 為單向度的 bin,我們現在要使用 geom_bin2d() 與 geom_hex() 來描繪兩個向度的 bin。
geom_bin2d() 與 geom_hex() 所繪製出來的圖形樣式相似,都是有二維的 bins,而使用 fill 來表示數量,差別在 geom_bin2d() 繪製出來的是矩形,而 geom_hex() 繪製出來的是六邊形,如:
ggplot(data = diamonds) +
geom_bin2d(mapping = aes(x = carat, y = price))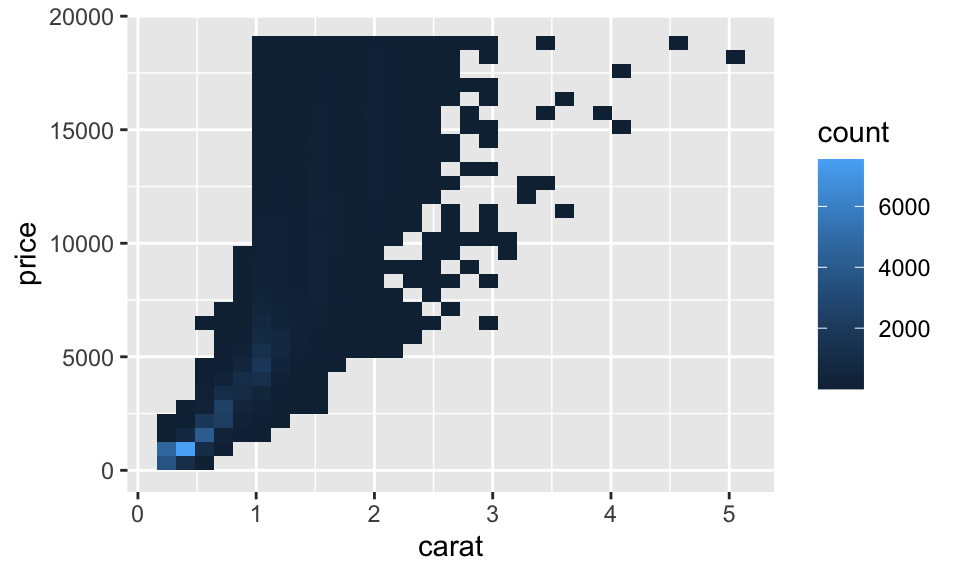
# install.packages("hexbin")
library(hexbin)
ggplot(data = diamonds) +
geom_hex(mapping = aes(x = carat, y = price))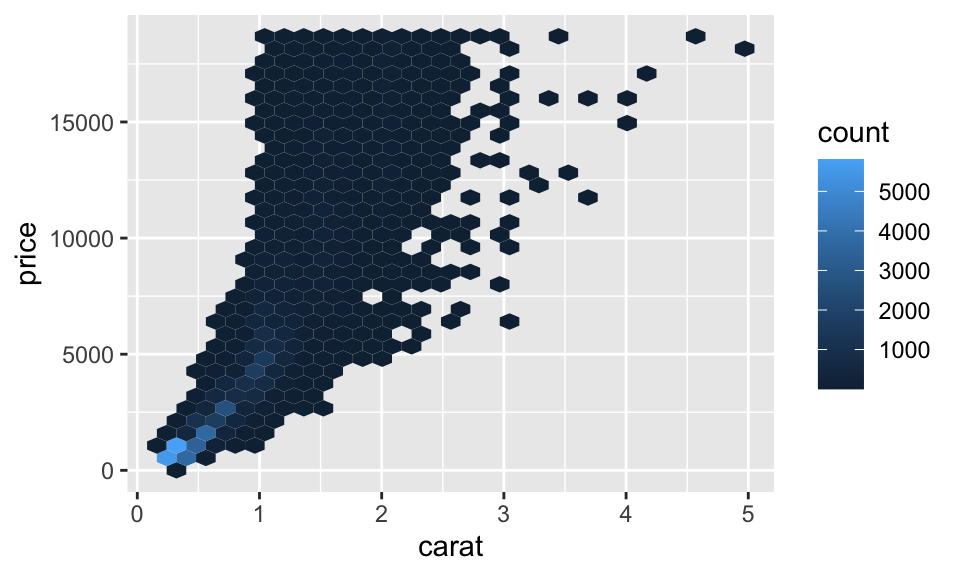
還有一種方式是把連續變數用 bin 拆成類別變數,然後繪製箱形圖,如下把克拉拆成類別變數:
ggplot(data = diamonds, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_width(carat, 0.3)))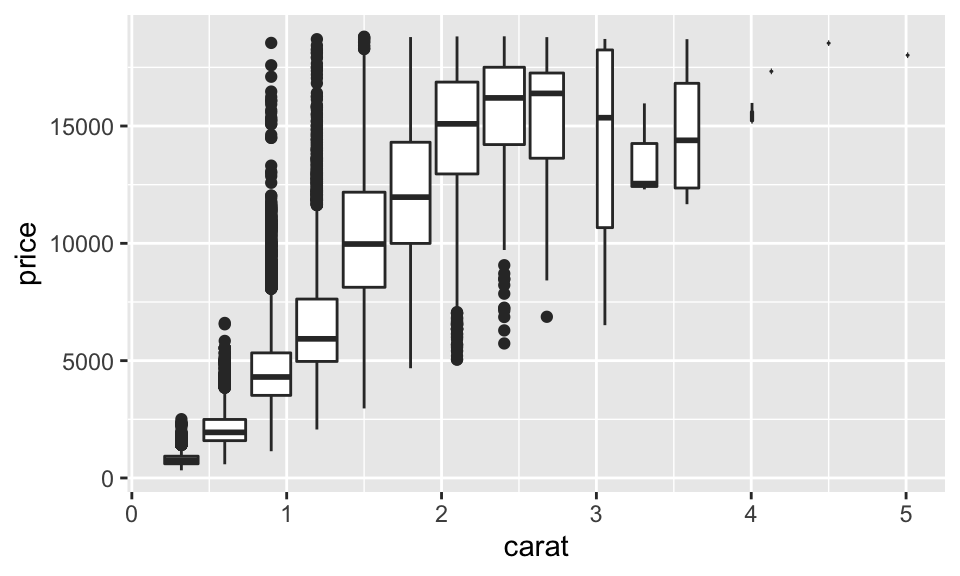
但我們如果使用箱形圖的話,要怎麼看出各個 bin 的觀察值數量呢?我們可以設置 varwidth = TRUE,這會讓箱子的寬度與觀察值的數量成比例,如:
ggplot(data = diamonds, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_width(carat, 0.3)), varwidth = TRUE)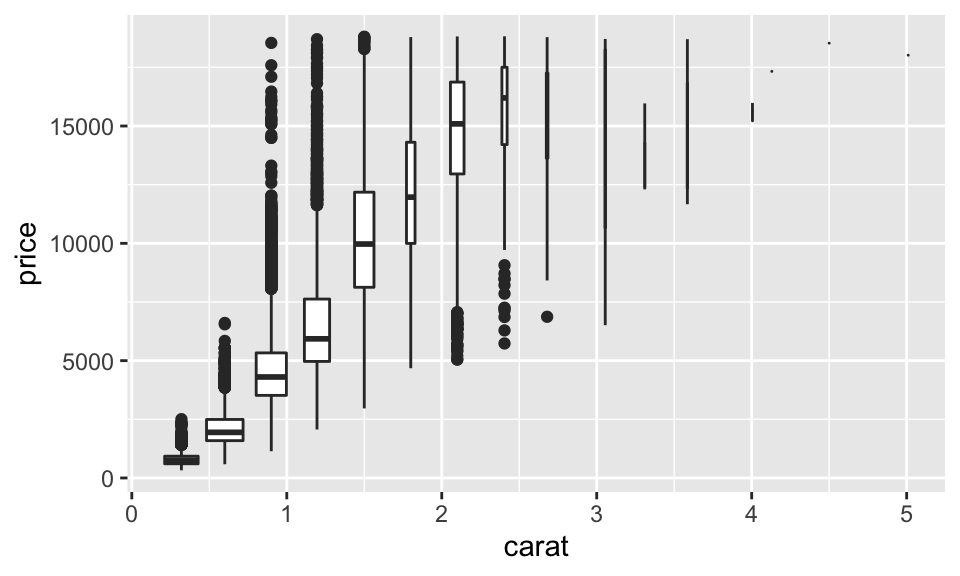
另一個看出觀察值數量的方法是使用 cut_number(),這會讓每個 bin 所包含的觀察值數量相當,以下圖而言,即克拉數大的鑽石很少:
ggplot(data = diamonds, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_number(carat, 20)))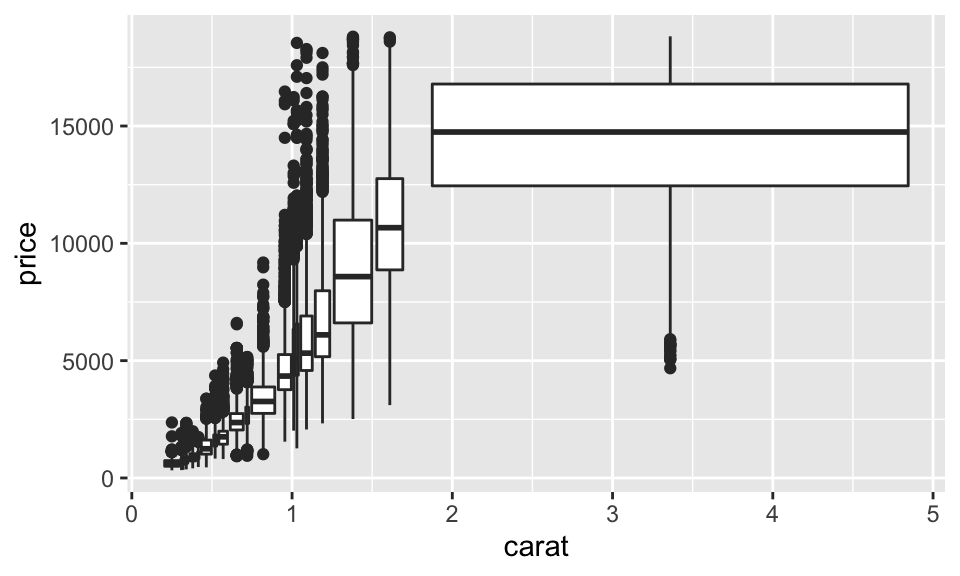
8.6 模式與模型
模式(patterns)為兩個變數之間系統性的關係,如:
ggplot(data = faithful) +
geom_point(mapping = aes(x = eruptions, y = waiting))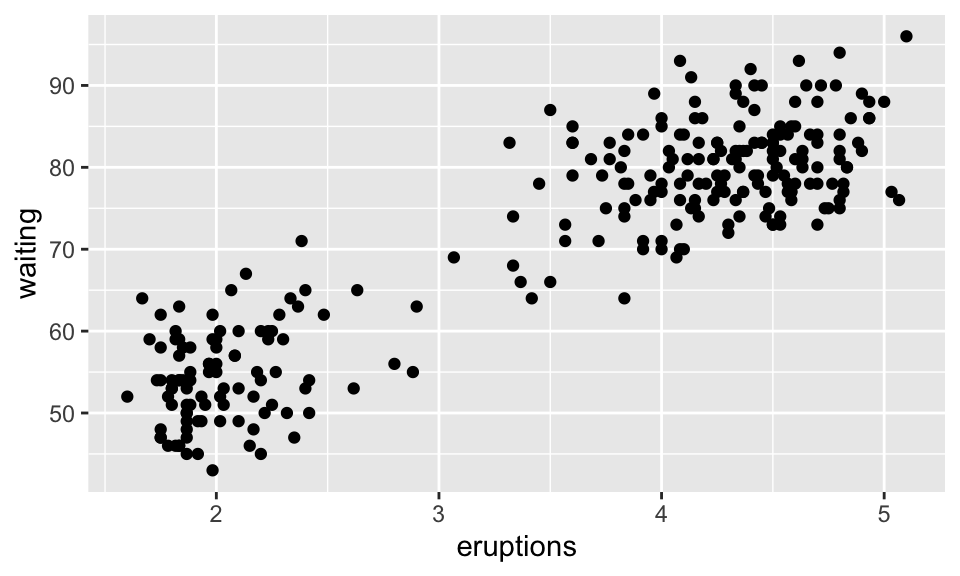
我們可以看出,等待時間越長伴隨著更長時間的爆發。
模型(models)則是從資料中萃取出 patterns 的工具。例如以 diamonds 資料集來說,我們很難弄清楚 cut 與 price 之間的關係,因為「cut 與 carat」及「carat 與 price」之間都密切相關。我們如果能使用模型移除掉 price 與 carat 之間的關係,那我們就能更清楚 cut 與 price 之間的關係。以下的程式碼就是先算出 carat 對 price 的效果,而其無法解釋的部份就在殘差項。我們能說,殘差項就撇除了 carat 對 price 的效果,那很有可能就是 cut 對 price 的效果,如:
library(modelr)
mod <- lm(log(price) ~ log(carat), data = diamonds)
diamonds2 <- diamonds %>%
add_residuals(mod) %>%
mutate(resid = exp(resid))
ggplot(data = diamonds2) +
geom_point(mapping = aes(x = carat, y = resid))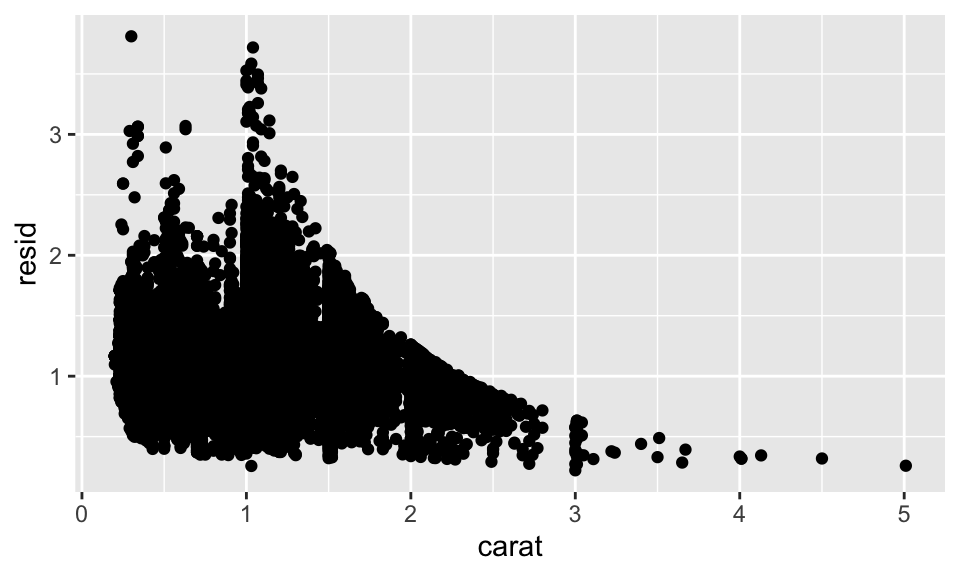
在我們移除了 carat 對 price 的效果後,很清楚地,可以看出 cut 與 price 之間的關係;即給定鑽石大小,品質越好的鑽石越貴!(非常符合直覺)
我們也能從箱形圖看「品質越好的鑽石越貴」這一現象:
ggplot(data = diamonds2) +
geom_boxplot(mapping = aes(x = cut, y = resid))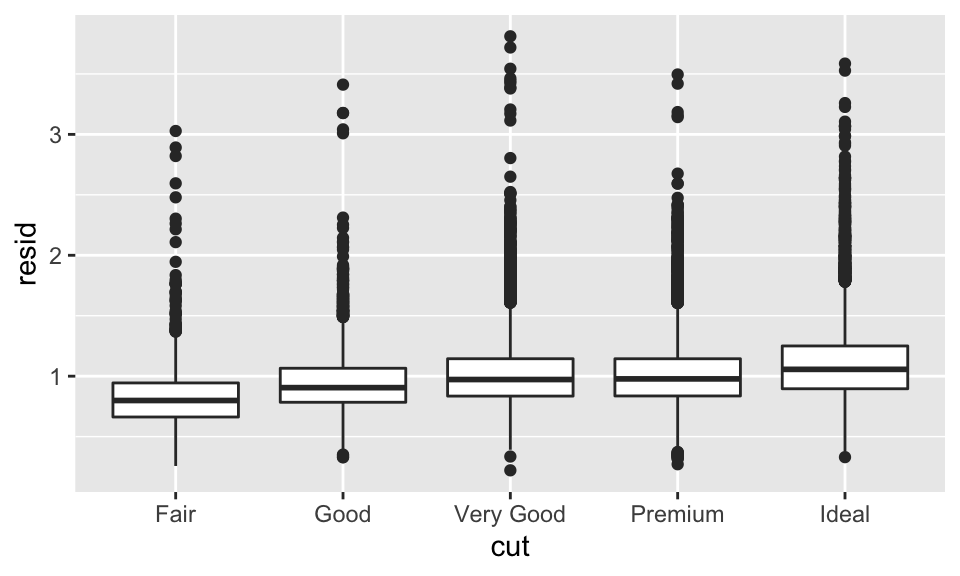
本書之後會更深入探討關於模型的問題。