Chapter 4 The First Law for Closed Systems

We have already encountered work and heat as two forms of energy. In order to complete the picture for closed systems, another type of energy, internal energy, must be taken into consideration. These three forms of energy will later be combined in the First Law of Thermodynamics.

4.1 Internal energy

Consider the heating of one kilogram of Helium in a rigid stationary container from $300K$ to $600K$. No work was performed as the volume stayed constant and the system remained stationary. Therefore the energy added to the system as heat, is absorbed by the molecules of the gas. It increased the kinetic energy of the individual Helium atoms. To name three:²⁶

Translational kinetic energy
Rotational kinetic energy
Vibrational kinetic energy

The sum of all these microscopic energies is called the internal energy of a substance. It can be shown that specific internal energy is a property. The symbol for specific internal energy is $u$ and its units are [$kJ/kg$]. The total internal energy of a system is $U [kJ]$ and is equal to $m\times u$. Because specific internal energy is a property, it is one of the variables that can be used to fix the state of a substance. For a single phase system it means if we know the value of the internal energy and either the value of temperature or pressure or specific volume, the state is fixed and the value of the other properties can be determined.

The change in internal energy is calculated using the following equation (Sonntag and Borgnakke 2012 Equation 14.30):

\[\begin{equation} du = C_vdT + \left[ T \left(\frac{\partial P} {\partial T}\right)_v - P\right] dv \tag{4.1} \end{equation}\]

Where $C_v$ is the constant volume specific heat. It is defined as the amount of heat necessary to raise the temperature of a substance (at constant volume) by one degree.

4.1.1 Ideal gases

For an ideal gas it is assumed that the atoms or molecules do not attract or repulse each other. Therefore there is no energy associated with inter-particle interactions. The distance between particles is therefore irrelevant from an energy point of view. This means that the internal energy of an ideal gas is only made up of the kinetic energies of individual particles and that internal energy is not influenced by changes in density or pressure. The same is clear from Equation (4.1). For an ideal gas $\frac{\partial P} {\partial T}$ is equal to $\frac{R}{v}$ and the term in the square brackets reduces to zero. The change in internal energy for an ideal gas is therefore only dependent on the change in temperature and can be calculated as follows:

\[\begin{equation} u_2 - u_1 = \int_{T_1}^{T_2} \! C_{v} \, \mathrm{d} T \tag{4.2} \end{equation}\]

Where $C_v$ is the constant volume specific heat of the gas which can be a complex function of temperature. To avoid having to integrate Equation (4.2) every time, the internal energy of ideal gases as function of temperature (relative to a reference temperature $T_{ref}$ where the value of $u_{ref}$ is set to a chosen value²⁷), is tabulated as function of temperature.²⁸ A table giving the internal energy of air under the assumption of ideal gas behaviour, is given in Borgnakke and Sonntag, Table A7.1 (Sonntag and Borgnakke 2012).

Example
Calculate the temperature and specific volume of air at $200kPa$ with a specific internal energy of $315.64\frac{kJ}{kg}$.

Solution
From the table of the ideal gas properties of air (Sonntag and Borgnakke 2012) it can be determined that the temperature corresponding to the given internal energy is $440K$. The Ideal Gas Law can now be used to calculate the specific volume: $0.6314\frac{m^3}{kg}$

Note that because of the assumption of ideal gas behaviour, internal energy and temperature are no longer independent and both cannot be specified to fix the state of the system. Therefore $u$ can only be used in combination with $P$ and $v$.

4.1.2 Perfect gases

$C_v$ for a few gases as function of temperature are shown in Figure 4.1.

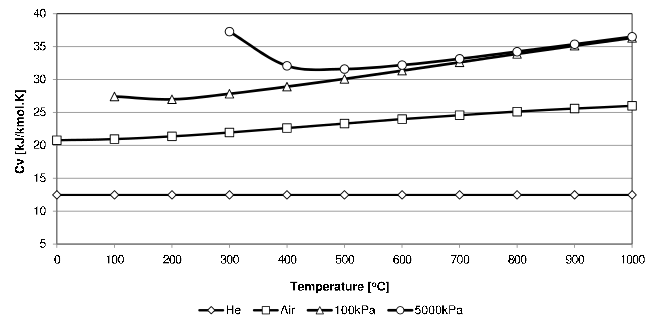
$\label{fig:Cpvalues}$C_v$ values for Helium, Air and Steam (at two pressures).$

Figure 4.1: $C_v$ values for Helium, Air and Steam (at two pressures).

From Figure 4.1 it is clear that the $C_v$ of Helium stays essentially constant.²⁹ In this text it will be assumed that the $C_v$ of the mono-atomic gases (Helium, Argon, Neon and Krypton), is independent of temperature and that they also obey the Ideal Gas Law. They are then collectively called Perfect Gases. For a $C_v$ independent of temperature, Equation (4.2) is easily integrated to give the change in internal energy for perfect gases:

\[\begin{equation} u_2 - u_1 = C_{v} (T_2-T_1) \tag{4.3} \end{equation}\]

Example
Helium at $400kPa$ and $300^\circ C$ is heated to $600^\circ C$ while the pressure changes to $500kPa$. Determine the change in volume and the change in specific internal energy.

Solution Using Equation (4.3) and obtaining the value of $C_v$ from an appropriate table containing properties of Ideal gases (Sonntag and Borgnakke 2012 Table A.5):

\[\begin{aligned} u_2-u_1 &= C_v(T_2-T_1)\\ &= 3.116\times(600-300)\\ &=934.8 \hspace{0.3em} \frac{kJ}{kg}\\ \end{aligned}\]

From the Ideal Gas Law:

\[\begin{aligned} v_2-v_1 &=\frac{R\times T_2}{P_2}-\frac{R\times T_1}{P_1}\\ &=\frac{2.0771\times873.15}{500}-\frac{2.0771\times573.15}{400}\\ % &=4.534-2.381\\ &=0.651 \hspace{0.3em} \frac{m^3}{kg} \\ \end{aligned}\]

It is important to note the following:

The value for $C_v$ found in tables is usually at a specific temperature but for a Perfect Gas can be used at any temperature because for Perfect Gases it is assumed to be independent of temperature.
Even though this is not a constant volume process, Equation (4.3) is still valid. It is valid for any perfect gas for any process: isobaric, isochoric, unspecified.… and can be used to calculate the change in internal energy as long as the change in temperature is known.
For a perfect gas, it is only possible to calculate the change in internal energy. This means that the internal energy of a perfect gas does not have a value that can be used to define the state. For perfect gases it is therefore necessary to use two of the other three intensive properties ($P, T, v$) we are familiar with at the moment to define the state.
A perfect gas is a special kind of ideal gas, therefore internal energy does not change with a change in pressure.
The temperature difference calculated in $^\circ C$ is the same as the temperature difference calculated in Kelvin.
In the Ideal Gas Law, the temperature must be in Kelvin.

4.1.3 Real gases

For real gases there are energy associated with inter-particle interactions (attraction or repulsion). Therefore density (and pressure) are important. From Table 4.1 below, the influence of pressure on the internal energy of steam at $400^\circ$C is clear.

Table 4.1: Influence of pressure on the specific internal energy of steam at 400 degrees Celsius.
Pressure ($kPa$)	Specific Internal Energy ($kJ/kg$)
10	2968.9
100	2967.9
1000	2957.3
10000	2832.4
25000	2430.1

Note that at low pressures, internal energy does not vary much with pressure. This is because at low pressures, the steam molecules are far apart and the energy associated with their interaction, small. As the pressure rises to higher values and especially close the critical point, internal energy is very sensitive to pressure. For a real gas it is necessary to know the value of two variables to fix the state. Any two of the variables we have encountered thus far (Temperature, Pressure, specific volume or specific internal energy) can be used.

4.1.4 Two phase systems

For two-phase systems, pressure and temperature are no longer independent. For a saturated liquid ($x=0$) and a saturated vapour, ($x=1$) the value for internal energy can be read directly from the table for saturated water at the appropriate temperature or pressure. Usually the reference point is the internal energy of the saturated liquid at $0.01^\circ C$ which is taken as zero. However, there is no reason why another reference point may not be chosen.

For a saturated two-phase mixture, a calculation must be done to determine the value of internal energy for the mixture. Quality ($x$) has already been defined as the mass of vapour in a $1kg$ two-phase mixture. Quality can now be used to calculate the specific internal energy of a two-phase mixture from the internal energy of the saturated liquid ($u_f$) and the saturated vapour ($u_g$) as follows: \[u = (1-x)u_f + xu_g\]

4.1.5 Compressed liquids

The internal energy for compressed (or sub-cooled) liquids as function of temperature and pressure can be found in the steam tables (Sonntag and Borgnakke 2012 Table B.1.4.) The effect of pressure on the internal energy of liquid water is very small as shown in Table 4.2 below.

Table 4.2: Influence of pressure on the internal energy of compressed liquid water at 100 degrees Celsius.
Pressure ($kPa$)	Specific Internal Energy ($kJ/kg$)	Density ($kg/m^3$)
101.325	419.0	958.4
1000.000	418.7	958.8
10000.000	416.1	963.0

For a hundred-fold increase in pressure, the internal energy changes by less that 1 percent. This is because the inter-particle distance changes very little as can be seen from the small variation in specific volume with the large change in pressure. For incompressible substances, pressure will not affect inter-particle distances at all and therefore also have no effect on the internal energy associated with inter-particle interactions and internal energy. As it is usually assumed that sub-cooled liquids and solids are incompressible, it is also assumed that their internal energies are not affected by pressure. In this text the internal energy for liquid water is therefore assumed to be only a function of temperature. This means that the internal energy for liquid water can be read from the tables for saturated liquid water. For example the internal energy of water at $10MPa$ and $100^\circ C$ is assumed to be equal to the internal energy of saturated liquid water at $100^\circ C$ even though the saturation pressure is only $101.325kPa$.

4.1.6 Solids

Usually constant specific heats are assumed for solids. Then the change in internal energy can be calculated using Equation (4.3). However, because of the small change in volume during heating, the values of $C_v$ and $C_p$ are essentially equal and often no distinction is made between the two or only $C_p$ is tabulated. This is discussed in more detail in Paragraph 5.4.1.

4.1.7 Determination of internal energy

Once the value of two independent properties are known the state is fixed and the value of the other properties can be determined³⁰. Let us consider a few examples involving internal energy.

Temperature and pressure.

The three phases of water as function of pressure and temperature are shown in Figure 2.2. The first step is to determine the phase as explained in Paragraph 2.4.1 by determining the position of the state relative to the phase boundaries.

Example
Determine the specific internal energy and specific volume of water at $100kPa$ and $50^\circ C$.

Solution
From the position on the phase diagram ($\Box$ in Figure 2.2), it is clear that it is a compressed liquid. Assuming that $u_{T,P}=u_{f_{sat@T}}$: $u=209.3\frac{kJ}{kg}$ and also for specific volume, $v=0.001012\frac{m^3}{kg}$. Quality is not defined for a compressed liquid.

Example
Determine the specific internal energy and specific volume of water at $100kPa$ and $150^\circ C$.

Solution
The state is indicated by the $\circ$ in Figure 2.2. From the position on the phase diagram, it is clear that it is a super-heated vapour. From the tables for super-heated water vapour, we can read the values for $u=2582.75\frac{kJ}{kg}$ and $v=1.93636\frac{m^3}{kg}$. Quality is not defined for a super-heated vapour.

Note that on a P-T diagram, the state can never lie on the line separating the phases. The line has zero thickness and therefore, for a specific temperature and pressure, the phase will be either a liquid or a vapour.

Temperature or pressure and internal energy

The phase is determined by comparing the internal energy of the system with the internal energy of the saturated vapour and saturated liquid at the specified pressure or temperature. If the specified value for internal energy falls inside the dome , it is a two phase mixture and the temperature is the saturation temperature. The quality can now be determined and from the quality, the specific volume.

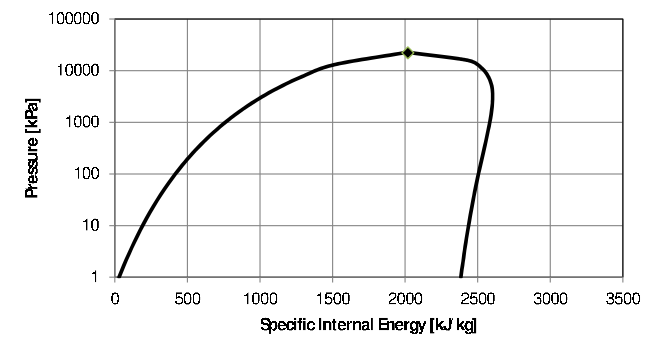
$\label{fig:DrukInEn}Phase diagram for water.$

Figure 4.2: Phase diagram for water.

Example
Determine the temperature, specific volume and quality of water at $200kPa$ with an internal energy of $2808.6kJ/kg$.

Solution
The specified internal energy is bigger than the internal energy of saturated vapour at $200kPa$, $2529\frac{kJ}{kg}$ and therefore it is a super-heated vapour. From the tables for super-heated water vapour at $200kPa$, the temperature that corresponds with the specified internal energy, is $300^\circ C$. The specific volume is $1.31616\frac{m^3}{kg}$. Quality is not defined for a super-heated vapour.

Example
Calculate the internal energy at $100kPa$ of a two-phase water mixture with a quality of $0.2$. ($835.1kJ/kg$)

Example
Determine the pressure of steam at $200^\circ C$ with an internal energy of 2656

Solution
The specified value for internal energy is bigger than than the internal energy of saturated vapour at $200^\circ C$, $2595\frac{kJ}{kg}$ and it is therefore a super-heated vapour. From the tables for super-heated steam, it is clear that the internal energy of steam at $200^\circ C$ and $100kPa$ is bigger; and the internal energy at $200^\circ C$ and $200kPa$ smaller than the specified value, 2656. The pressure of the system must therefore be between $100kPa$ and $200kPa$. Interpolation is therefore required. ($156kPa$).

4.2 The First Law for closed systems

The First Law simply states that energy cannot be destroyed or created — merely converted from one form to another. In a coal fired power station, heat is converted into work and electricity. The First Law gives the relation between the three forms of energy encountered so far - heat, work and internal energy. Consider the closed system in Figure 4.3 undergoing a process. Usually the substance contained in the piston-cylinder arrangement is taken as the system. Heat is added to the system, it expands and raises the piston, performing work.

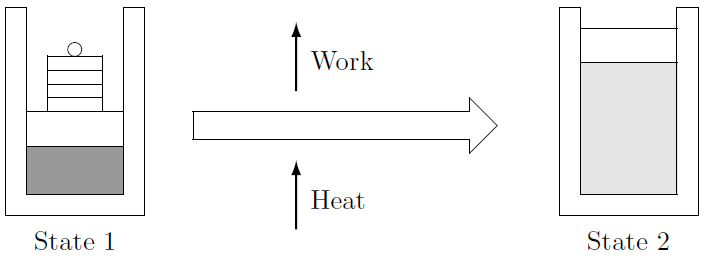
$\label{fig:ClosedSystem}Closed system undergoing a process.$

Figure 4.3: Closed system undergoing a process.

The First Law states that energy is conserved. This means that the amount of energy in the beginning, the total internal energy $U_1$, plus the amount of energy transferred to the system, the heat $Q_{in}$, must equal the the work done by the system, $W_{out}$, plus the amount of energy in the system at the end of the process, the total internal energy $U_2$. In mathematical terms: \[U_1 + Q_{in} = W_{out} + U_2\] or: \[m u_1 + Q_{in} = m u_2 + W_{out}\] It is important to note that the formulation of the First Law here deals with the amount (or quantity) of energy. The units are kilo-Joule or [$kJ$].³¹

Example
One kilogram of steam in a piston-cylinder arrangement is at $200^\circ C$ and $300kPa$. The steam is heated to $400^\circ C$ in a constant pressure process. Calculate the heat that must be added in order for the process to take place as described.

Solution
The First Law is rearranged: $Q_{in} = m(u_2 -u_1) + W_{out}$

The work performed in a constant pressure process: \[W_{out}=P(V_2-V_1)=300(1.03151-0.71629)=94.57kJ \Rightarrow Done\hspace{0.5em} by \hspace{0.5em}system\]

The First Law now becomes:\[Q_{in}=(2965.53-2650.65)+94.57=409.45kJ \Rightarrow Required\hspace{0.5em} by\hspace{0.5em} system\] Note that less than 25% of the energy added as heat is converted into work.

4.2.1 Kinetic and potential energy

Whereas internal energy is on a microscopic level, the system can also undergo changes in energy on a macroscopic level. If the center of gravity of the system changes height in a gravitational field or changes velocity because of interactions between the system and the environment, the energy associated with these changes must be taken into consideration and the First Law becomes: (Note that the kinetic energy ($\frac{1}{2}m\overline V^2$) and potential energy ($mgZ$) terms are divided by 1000 to ensure their units are in $kJ$). \[Q_{in} = U_2 - U_1 + \frac{m(\overline{V}_2^2 - \overline{V}_1^2)}{2000} + \frac{mg(Z_2-Z_1)}{1000} + {W_{out}}\] where $\overline{V}$ is the velocity of the center of gravity of the system (in $m/s$) and $Z$ is the height of the center of gravity of the system (in meters). Usually the changes in kinetic and potential energy are much smaller than the other terms and can safely be ignored. But there are instances where it must be taken in to consideration:

Example
In a paint ball gun, the ball (mass: $3 g$) is propelled by a fixed amount of high pressure air with an initial pressure of $5000 kPa$. Due to the pressure difference across the ball, it accelerates until it leaves the barrel. Let us calculate the velocity of the paintball as it leaves the barrel. The internal energy of the pressurized air provides the energy necessary to accelerate the paint ball and push away the atmospheric air. An energy balance becomes: \[m_a u_1=m_a u_2 + W_{atm} + \frac{m_{pb}\overline{V}^2}{2000}\] The pressure at the front end of the paint ball is equal to atmospheric. The work necessary to push away the atmosphere is: \[W_{atm}=P_{atm}(V_1-V_2)\] The initial volume of the pressurized air (assume a mass of $0.4 g$ of pressurized air): \[V_1=\frac{mRT_1}{P_1}=\frac{4\times 10^{-4}\times 0.287\times 298.15}{5000}=6.85\times 10^{-6}m^3\] Assume the pressurized air expands to 36 times its initial volume and that $P_{atm}=87kPa$. Then $W_{atm}=0.0209 kJ$. Furthermore, let us assume air is a perfect gas and that it expands adiabatically. For an initial air temperature of $25^\circ C$ the final temperature can be calculated (Paragraph 4.3): \[T_2=T_1\left(\frac{V^2}{V^1}\right)^{1-k}=71K\] This means: \[m_{a}(u_1-u_2)=m_{a}C_{v}(T_1-T_2)=0.0651kJ\] Therefore, the velocity of the paint ball when it leaves the barrel: \[\overline{V}=\left(2000 \times \frac{0.0651-0.0209}{0.003}\right)^{0.5}=171.7\frac{m}{s}\] Note that the (adiabatic) work done by the air on the paint ball will be more that the energy necessary to push away the atmosphere. The adiabatic work done by the air, minus the work necessary to push away the atmosphere, will be equal to the change in kinetic energy of the paint ball. It is left to the reader to calculate the adiabatic work performed by the expanding air and show that the numeric value of the adiabatic work is equal to the change in the internal energy of the air.

In our calculations, we ignored the kinetic energy of the pressurized air in the barrel as the paint ball leaves the barrel. A good assumption is to assume that as the ball leaves the barrel, that the centre of gravity of the air in the barrel will move at half the velocity of the paint ball: $\overline{V}_{air}= 0.5\overline {V}_{ball}$ and include the final kinetic energy of the air in the energy balance. This will reduce the calculated velocity of the paint ball to $166\frac{m}{s}$.

The calculations above we assumed a reversible (ideal) process which yielded the theoretical maximum velocity. The actual velocity of a paint ball is approximately $90\frac{m}{s}$ due to non-idealities such as friction.

Let us consider potential energy:

Example
A vertical piston/cylinder arrangement with a cross sectional area of $0.002m^2$ ($D=50.46 \hspace{0.1em} mm$) contains $1kg$ saturated liquid water at $100kPa$. The water is vaporised at constant pressure until saturated vapour results. Calculate the heat required.

Solution
The height of the column of the liquid water will be $0.521m$ and the height of the vapour column will be $846m$. The center of gravity in each case is $height/2$. The set-up is stationary so the kinetic energy does not change and the First Law becomes:

\[\begin{aligned} Q_{in} &= m\left((u_2-u_1) + g\frac{Z_2-Z_1}{1000}+P(v_2-v_1)\right)\\ &= (2506.06-417.3) + 9.81\frac{846-0.521}{2\times 1000}+100(1.693-0.001)\\ &= 2088.7 + 4.147 + 169.2 \\ &=2262kJ \end{aligned}\]

It is clear that even with this extreme change in elevation of the center of gravity, that the contribution of the change in potential energy is still small relative to the other terms.

4.2.2 Sign convention

Equation (3.1) gives the work done by a system undergoing a process from state 1 to state 2:

\[W_{out} = \int_{V_1}^{V_2} \! P \, \mathrm{d} V\]

Because the pressure in the equation above is the absolute pressure, it is always greater (or equal) to zero. If the volume increases, work is done BY the system and the value of $W_{out}$ will be $>0$. However, if work is done ON the system, the volume will decrease and the value of $W_{out}$ will be $<0$. In such cases, this text, in order to have a positive numerical value, the subscript “out” will be changed to “in” ensure that the numerical value is $>0$.

The heat necessary to heat an ideal gas in a constant volume process from $T_1$ to $T_2$, is given by:

\[Q_{in}=m \int^{T_2}_{T_1} C_v dT\]

If heat is added to the system, the temperature will rise and $T_2>T_1$ and the value of $Q_{in}$ will be $>0$. However, if heat is released by the system, $T_2<T_1$ and the value of $Q_{in}$ will be $<0$. This is true not only for constant volume processes, but for other processes also. In this text the appropriate subscript (${``in"}$ or ${``out"}$) will be used to ensure that the value of $Q$ is always $>0$.

4.3 Adiabatic processes

The first law can be used to derive Equation (3.3) for an adiabatic quasi-equilibrium process for a perfect gas. \[PV^k = c\] which is the same as: \[\frac{P_2}{P_1} = \left(\frac{V_1}{V_2}\right)^k\]

Now for the derivation. The first law in differential form: \[\delta{Q} = dU + \delta{W}\] For an adiabatic process $\delta{Q}=0$, for an ideal gas, $dU=mC_vdT$ and for a quasi-equilibrium process, $\delta{W}=PdV$. This gives: \[mC_vdT = -PdV\]

Dividing the left hand side of the equation by $mRT$ and the right hand side by $PV$, the following equation results for a Perfect Gas:

\[\frac{C_v}{R} \ln \frac{T_2}{T_1} = \ln \frac{V_1}{V_2}\]

Which can be written as:

\[\left(\frac{T_2}{T_1}\right)^{\frac{C_v}{R}} = \frac{V_1}{V_2}\]

From the Ideal Gas Law it follows that:

\[\frac{T_2}{T_1} = \frac{P_2}{P_1}\frac{V_2}{V_1}\]

The last two equations can be combined to give:

\[\frac{P_2}{P_1} ^ {\frac{C_v}{R}} = \frac{V_1}{V_2} ^{ \left( \frac{C_v}{R}+1 \right)}\]

Noting that that $C_p-C_v=R$ and after some manipulation, the following equation results: \[\frac{P_2}{P_1} = \left( \frac{V_1}{V_2} \right)^{\frac{C_p}{C_v}} = \left(\frac{V_1}{V_2}\right)^k\]

which is the equation we set out to derive. From the above it also follows that: \[\begin{equation} \frac{T_2}{T_1}=\left( \frac{P_2}{P_1} \right)^{\frac{k-1}{k}}=\left( \frac{V_2}{V_1} \right)^{1-k}=\left( \frac{v_2}{v_1} \right)^{1-k} \tag{4.4} \end{equation}\]

Optional textbook reading. A more elaborate discussion of molecular forms of energy is given in par 2.6 of Sonntag (Sonntag and Borgnakke 2012)↩︎
This reference value may be different for different tables with the result that the value of internal energy from one table may be different from the value of internal energy from another table. The change in internal energy with a change in temperature however, should be the same.↩︎
The internal energy is independent of pressure, therefore there is only one column - giving a single value of internal energy for each value of temperature. The reference to pressure that usually appears in the heading of such tables, is because the values of entropy, a property we have not encountered yet, is calculated at a certain pressure, usually $100kPa$.↩︎
In order to reduce the range of the y-axis, the units of $C_v$ in Figure 4.1 is in $\frac{kJ}{kmol \cdot K}$. Take care to use values with the right units in calculations.↩︎
The number of independent properties necessary to fix the state of a system is determined by the Gibbs phase rule. While it is not an intensive property, it is convenient to use quality as one of the variables to fix the state of a system. For example, when the values of the temperature and the quality are specified, it is possible to determine the (equilibrium) pressure and specific volume of the two-phase mixture. In the case of internal energy (and enthalpy) it can cause problems as the internal energy (and enthalpy) of the saturated vapour ($x=1$) is not a function as is clear from Figure 4.2. For example, for $x=1$ and $u=2500\frac{kJ}{m^3}$ two pressures are possible – approximately $100kPa$ and $1000kPa$. In a software programs such as EES this may result in incorrect answers.↩︎
It may help to understand the concept of amount by considering a substance such as water. The amount of water is measured in litres or kilograms. A domestic cup contains approximately $0.25kg$ of water. In open systems we will encounter flow rate. This is the amount of matter that cross the system boundary in a certain time. For instance, we can say that water from a tap flows at $0.25 kg /sec$. It will therefore take one second to fill a cup with water. The rate at which energy flows is measured in $kJ/sec$ or $[kW]$. An typical compact fluorescent light bulb requires electric energy at a rate of $11J/s$ or $11W$ while utility power stations can produce electric energy at a rate of thousands of $MW$.↩︎