Capítulo 7 Métodos paramétricos

7.1 Fundamentos

Una serie temporal es una secuencia de datos, observaciones o valores, medidos en determinados momentos y ordenados cronológicamente. Los datos pueden estar espaciados a intervalos iguales (como la temperatura en un observatorio meteorológico en días sucesivos a una determinada hora) o desiguales (como el peso de una persona en sucesivas mediciones a lo largo de su vida).

Para el análisis de series temporales se usan métodos que ayudan a interpretarlas y que permiten extraer información representativa sobre las relaciones subyacentes entre los datos de la serie. Estos métodos pueden extrapolar o interpolar los datos y así predecir el comportamiento de la serie en momentos no observados, ya sea en el futuro (extrapolación para pronóstico), en el pasado (extrapolación retrógrada) o en momentos intermedios (interpolación).

El análisis clásico de las series temporales se basa en que los valores que toma la variable de observación es la consecuencia de cuatro componentes, cuya actuación conjunta da como resultado los valores medidos.

Estas componentes son:

• Tendencia. Es la marcha general y persistente del fenómeno observado. Es una componente de la serie que refleja la evolución a largo plazo. Cuando se hace referencia a la “tendencia” en los datos de series de tiempo, significa que los datos tienen una trayectoria a largo plazo que puede ser una tendencia en la dirección positiva o negativa. Un ejemplo de tendencia sería un aumento a largo plazo de los datos de ventas de una empresa.

• Estacionalidad. Es el movimiento periódico de corto plazo. Se trata de una componente causal debida a la influencia de ciertos fenómenos que se repiten de manera periódica en un año (las estaciones), una semana (los fines de semana), un día (las horas punta) o cualquier otro periodo. Recoge las oscilaciones que se producen en esos períodos de repetición.

• Ciclo. Es la componente de la serie que recoge las oscilaciones periódicas de amplitud superior a un año. Movimientos normalmente irregulares alrededor de la tendencia, en las que a diferencia de las variaciones estacionales, tiene un período y amplitud variables, pudiendo clasificarse como cíclicos, cuasi cíclicos o recurrentes. Son períodos de repetición que no están relacionados con el calendario. Un ejemplo de esta componente son los ciclos económicos, como recesiones o expansiones económicas, pero que no están relacionados con el calendario en el sentido semanal, mensual o anual.

• Variación aleatoria o ruido, accidental, de carácter errático, también denominada residuo, no muestra ninguna regularidad (salvo las regularidades estadísticas). Es la componente irregular e impredecible de la serie, que describe las influencias aleatorias de la misma. Representa los residuos, es decir, lo que queda de la serie temporal después de que se hayan eliminado las otras componentes.

Algunos autores hablan además de otra componente:

• Variación accidental, de carácter errático debida a fenómenos aislados que son capaces de modificar el comportamiento de la serie (tendencia, estacionalidad, variaciones cíclicas y aleatoria).

Suele ser habitual que los algoritmos de pronóstico de series temporales fusionen las componentes de tendencia y ciclo en una sóla, de manera que las descomposiciones resultantes acaban estando compuestas de tendencia-ciclo, estacionalidad y ruido.

En el lenguaje de programación R las series temporales suelen trabajarse con el objeto ts. La frecuencia es el número de observaciones que se registran en un mismo patrón estacional. De este modo, cuando se define una serie temporal no sólo se indica la secuencia de números que la componen sino también la frecuencia que presenta esa secuencia.

Según el enfoque clásico, hay tres tipos de series temporales:

• Series aditivas, que se componen sumando tendencia, estacionalidad y ruido.

  \(X_{t} = T_{t} + E_{t} + R_{t}\)

• Series multiplicativas, que se componen multiplicando tendencia, estacionalidad y ruido:

  \(X_{t} = T_{t} \cdot E_{t} \cdot R_{t}\)

• Series mixtas, que se componen sumando y multiplicando (hay distintas variantes) tendencia, estacionalidad y ruido.

La notación más habitual para trabajar con series temporales suele ser:

\[X = \{X_{1},X_{2},\dots \} \text{ o } \{X_{k}\}_{k\geq 1}\]

También es frecuente expresarlas del modo:

\[Y = \{Y_{t}:t\in T\ \}\]

La descomposición es la de-construcción de los datos crudos de la serie en sus diversos componentes: tendencia, estacionalidad-ciclo y ruido (si existieran). Dependiendo de la serie, la descomposición será multiplicativa o aditiva.

El propósito de la descomposición es aislar los distintos componentes para que se puedan ver individualmente y realizar el análisis o pronósticos sin la influencia del ruido o la estacionalidad. Por ejemplo, si solo se desea ver la tendencia de una serie, hay que eliminar la estacionalidad que se encuentra en los datos, el ruido debido a la aleatoriedad y cualquier ciclo como la expansión económica.

Un ejemplo aplicado a nuestros datos tomados por los dispositivos de medida lo podemos ver en la Figura 7.1. En esta figura se define la serie con frecuencia diaria (4*24 registros por estación). Vemos que la tendencia tiene una variación que hace que se asemeje más bien a una estacionalidad semanal. Es decir, modelando la serie atendiendo únicamente a su componente estacional diaria vemos que el resultado no es satisfactorio. Dicho de otro modo, el ciclo repetitivo basado únicamente en la ventana de tiempo diaria no puede modelar los patrones cíclicos semanales, que vemos que acaban influyendo la componente de la tendencia.

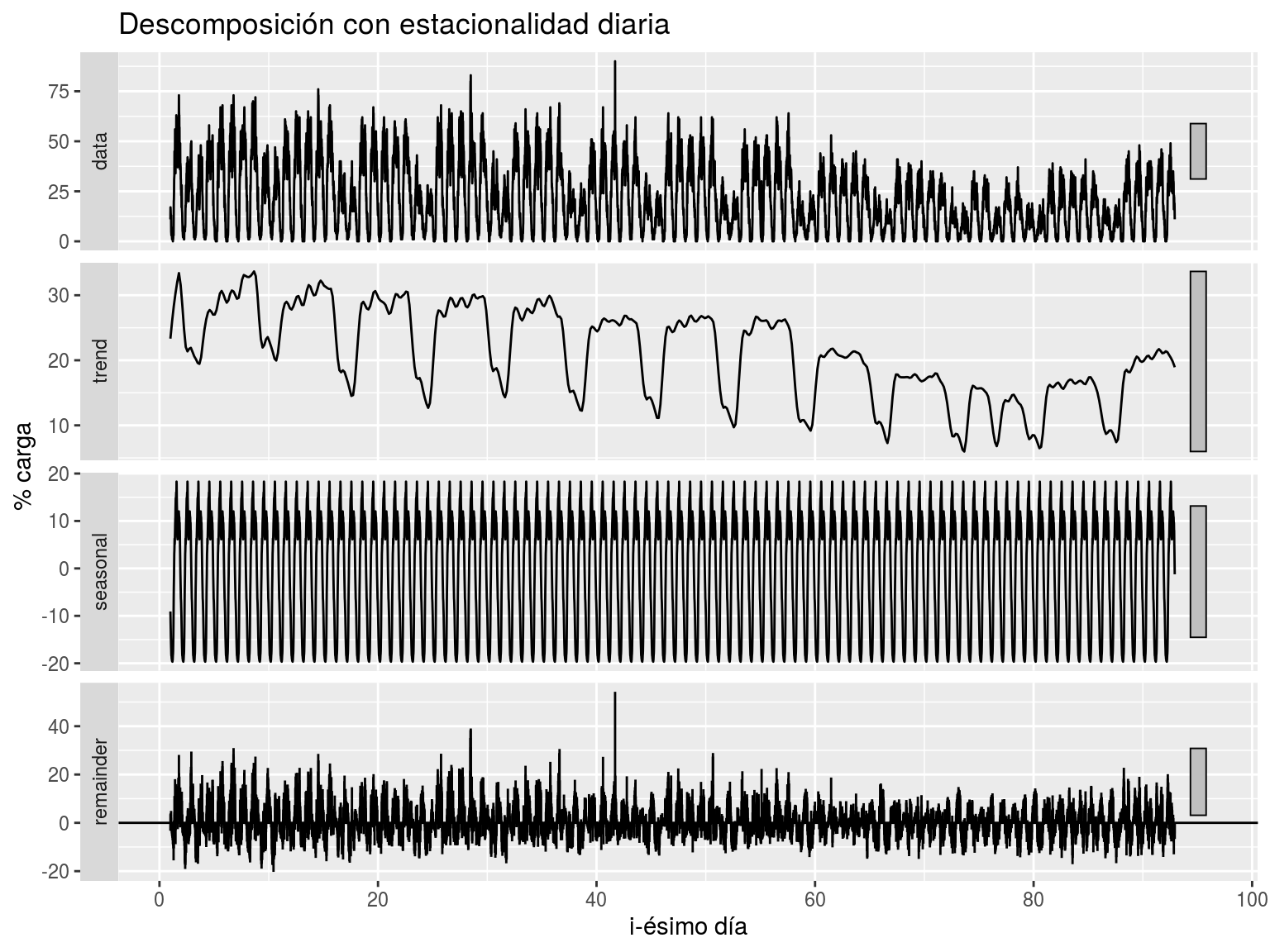
Figura 7.1: Descomposición aditiva con estacionalidad diaria para los datos reportados por el dispositivo 4.000 en el verano de 2018.

Veamos en la Figura 7.2 la descomposición considerando una frecuencia semanal (4*24*7 registros por estación). En este caso vemos que efectivamente la componente de estacionalidad realmente parece un patrón que se repite de forma estacional y vemos también como la tendencia es una línea que describe la evolución a más largo plazo que la estación.

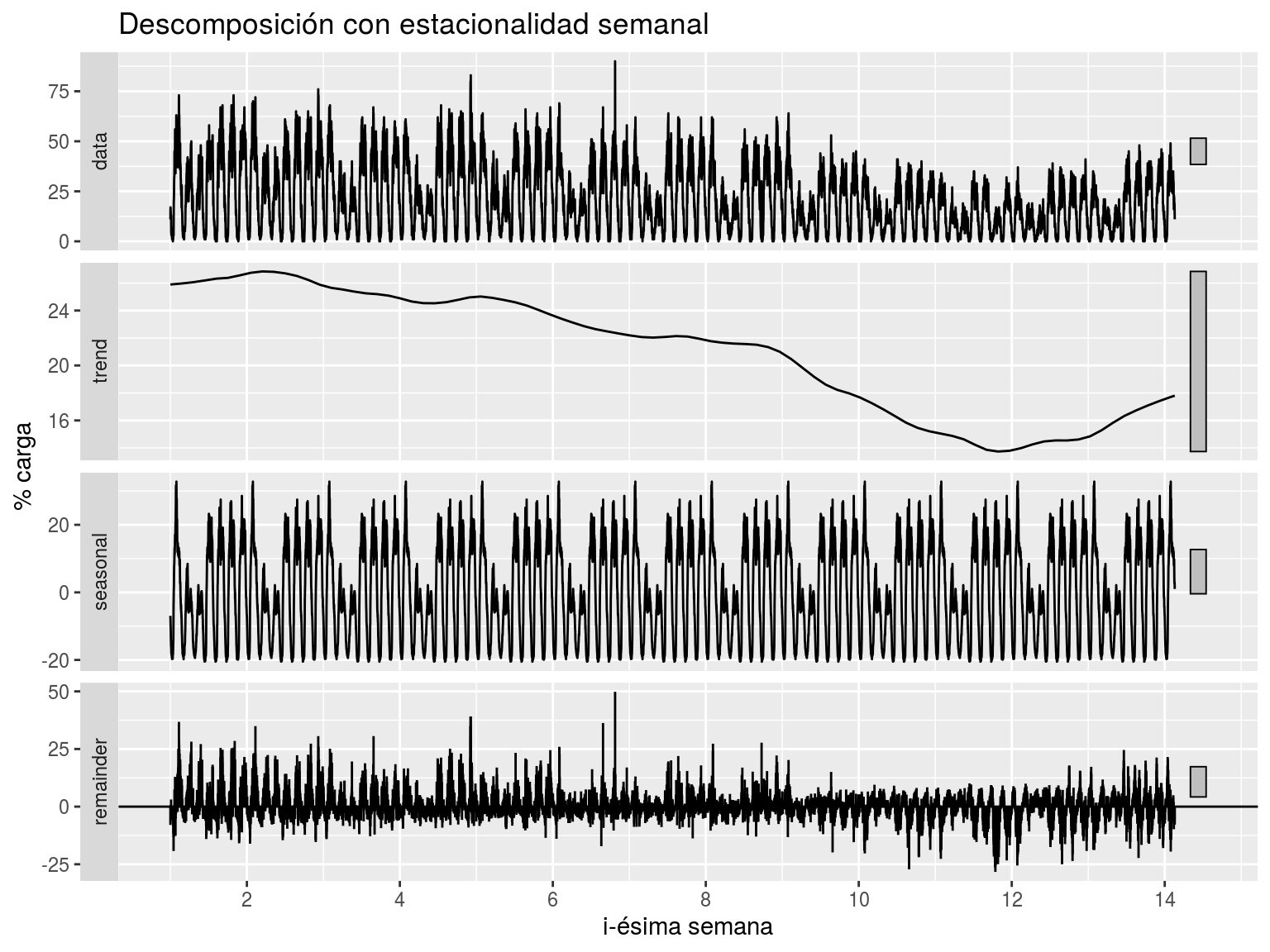
Figura 7.2: Descomposición aditiva con estacionalidad semanal para los datos reportados por el dispositivo 4.000 en el verano de 2018.

Por lo tanto, tal como ya vimos en el análisis de estacionalidad de la carga, es conveniente tener en consideración también las estacionalidades semanal y anual.

7.2 Método STL con estacionalidad única

STL es un método versátil y robusto para descomponer series temporales. STL es un acrónimo de “Descomposición estacional y de tendencias con Loess”, siendo Loess un método para estimar relaciones no lineales. El método STL fue desarrollado por Cleveland, McRae y Terpenning (Cleveland et al. 1990) .

En el lenguaje R podemos realizar una descomposición stl utilizando el paquete stats. Es importante notar que este método no permite series con estacionalidad múltiple. Más adelante veremos otros métodos que sí permiten series que presentan varios patrones de estacionalidad.

Los dos parámetros principales que se deben elegir cuando se usa STL son la ventana del ciclo-tendencia (t.window) y la ventana estacional (s.window). Estos parámetros controlan la rapidez con la que pueden cambiar las componentes de tendencia y estacionalidad. Valores pequeños permiten cambios más rápidos y valores grandes producen modelos con cambios más moderados en estas componentes. Ambos t.window y s.window deben ser números impares;

• t.window es el número de observaciones consecutivas que se utilizarán al estimar la tendencia-ciclo.
• s.window es el número de períodos consecutivos que se utilizarán para estimar cada valor en la componente estacional.

Si bien la descomposición es principalmente útil para estudiar datos de las series y para explorar cambios históricos a lo largo del tiempo, también se puede utilizar para pronosticar.

Para utilizar la descomposición STL para hacer pronósticos se procede del siguiente modo:

• la componente estacional se pronostica tomando la observación correspondiente del periodo inmediatamente anterior
• la componente compuesta por tendencia y ruido se suele pronosticar por cualquier algoritmo no estacional

Afortunadamente, el paquete forecast de R realiza todo este trabajo de forma transparente.

Hemos desarrollado una buena batería de funciones que permiten contrastar de forma rápida los pronósticos según distintos algoritmos y representar visualmente los resultados. Utilizando estas funciones y considerando los datos reportados en 2018 por el dispositivo 4.000, podemos poner a prueba la capacidad de pronóstico del algoritmo STL.

En la Figura 7.3 observamos pronósticos realizados considerando la serie con estacionalidad diaria, semanal, mensual y anual. Hemos hecho pruebas considerando todos los datos reportados por el dispositivo (133.302 valores) y también considerando únicamente los últimos datos recientes valores de la serie (20.000 valores).

Nótese como los pronósticos basados en estacionalidad diaria son bastante menos acertados para días de fin de semana; se entiende que el modelo tiende a acomodarse al comportamiento mayoritario día a día (5 días laborables a la semana son más del doble que 2 días no laborables). Esta tara vemos como queda bastante mejor corregida en el caso del modelo ajustado teniendo en cuenta estacionalidad semanal.

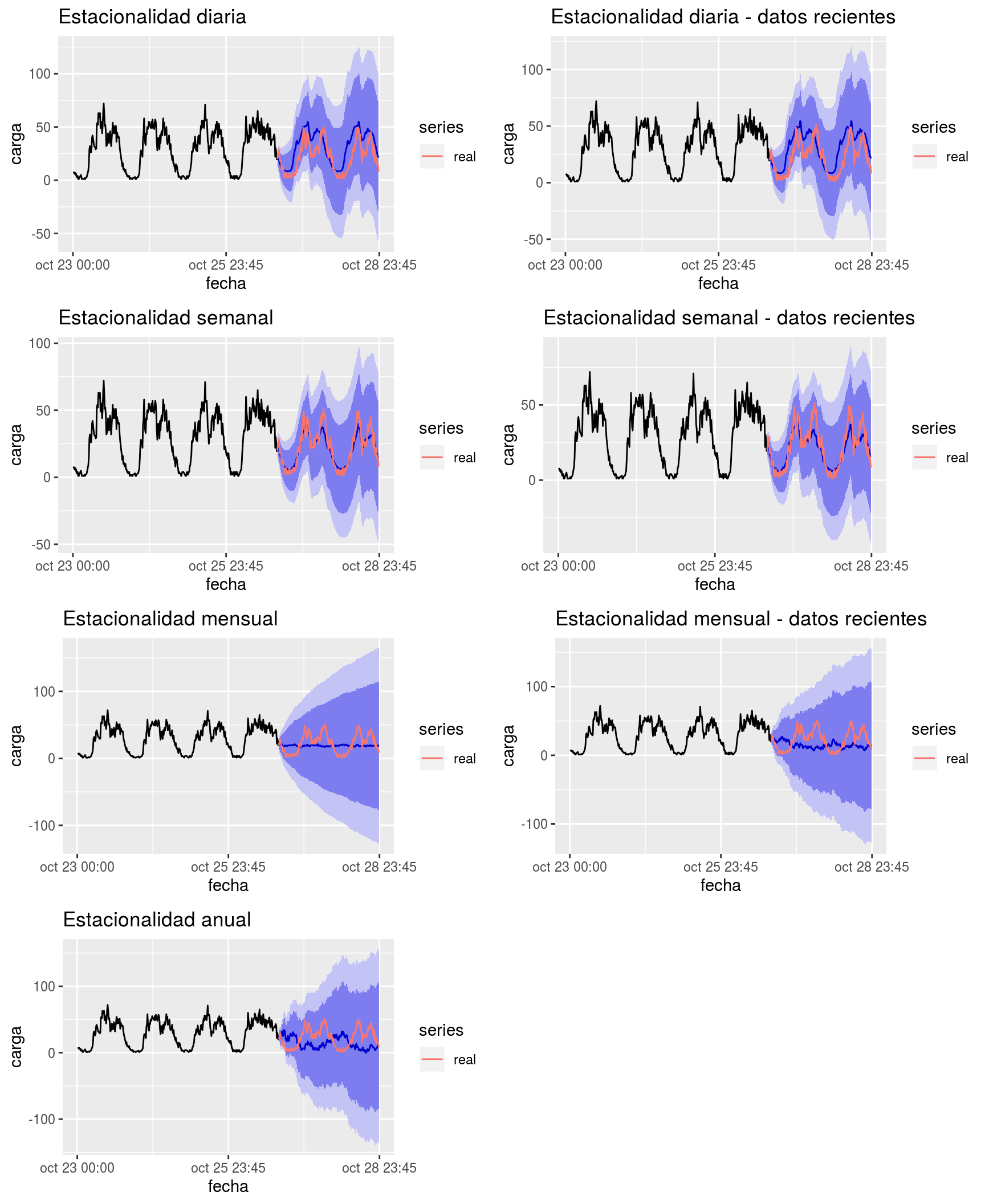
Figura 7.3: Ejemplo de pronósticos a 48 horas vista con el algoritmo STL para la serie reportada por el dispositivo 4.000 utilizando estacionalidad diaria, semanal, mensual o anual, considerando toda la serie o sólamente los 20.000 valores más recientes de la misma

Visualmente vemos que los resultados son mejorables aunque es difícil determinar qué tipo de estacionalidad, diaria o semanal, ofrece mejor rendimiento de pronóstico. Las estacionalidades mensual y anual claramente se delatan como no apropiadas (seguramente por no coincidir el patrón mensual o anual con el semanal, que es el más influyente en el caso del flujo de tráfico).

Más tarde, en el apartado de resultados, veremos la capacidad de pronóstico de este algoritmo comparada con el resto de métodos que ponemos a prueba en este trabajo.

7.3 Método MSTL - STL multiestacional

En series como las del flujo de tráfico es natural observar que las estacionalidades son varias:

• diaria, pues no a todas horas el flujo es igual.
• semanal, ya que según el día de la semana es normal que el tráfico fluya más o menos y en distintas regiones.
• anual, puesto que los periodos vacacionales, por ejemplo, claramente condicionan los flujos de tráfico.

Puede también considerarse una estacionalidad mensual, pero en el caso de los algoritmos STL y de nuestras series, no parece que ayude mucho, como hemos comentado en el punto anterior.

El paquete forecast de R ofrece una extensión del algoritmo STL con la que se puede aplicar pronósticos a series que presentan estacionalidad múltiple, cómo es el caso de nuestras series de estudio.

El algoritmo MSTL nuevamente descompone la serie en tendencia, estacionalidad y ruido. Sin embargo, en este caso en lugar de modelar una única estacionalidad, construye un modelo basado en tantas como indiquemos que tiene nuestra serie (series multi-estacionales). Las componentes estacionales se estiman de forma iterativa utilizando STL. La componente de tendencia se calcula en la última iteración de STL. En el caso de que las series fueran no estacionales, este método las descompone en tendencia y resto solamente. A diferencia de stl, en el paquete forecast mstl está completamente automatizado, lo cual significa que la estimación de los metaparámetros óptimos la realiza el propio algoritmo.

Podemos ver un ejemplo de descomposición multiestacional en la Figura 7.4.

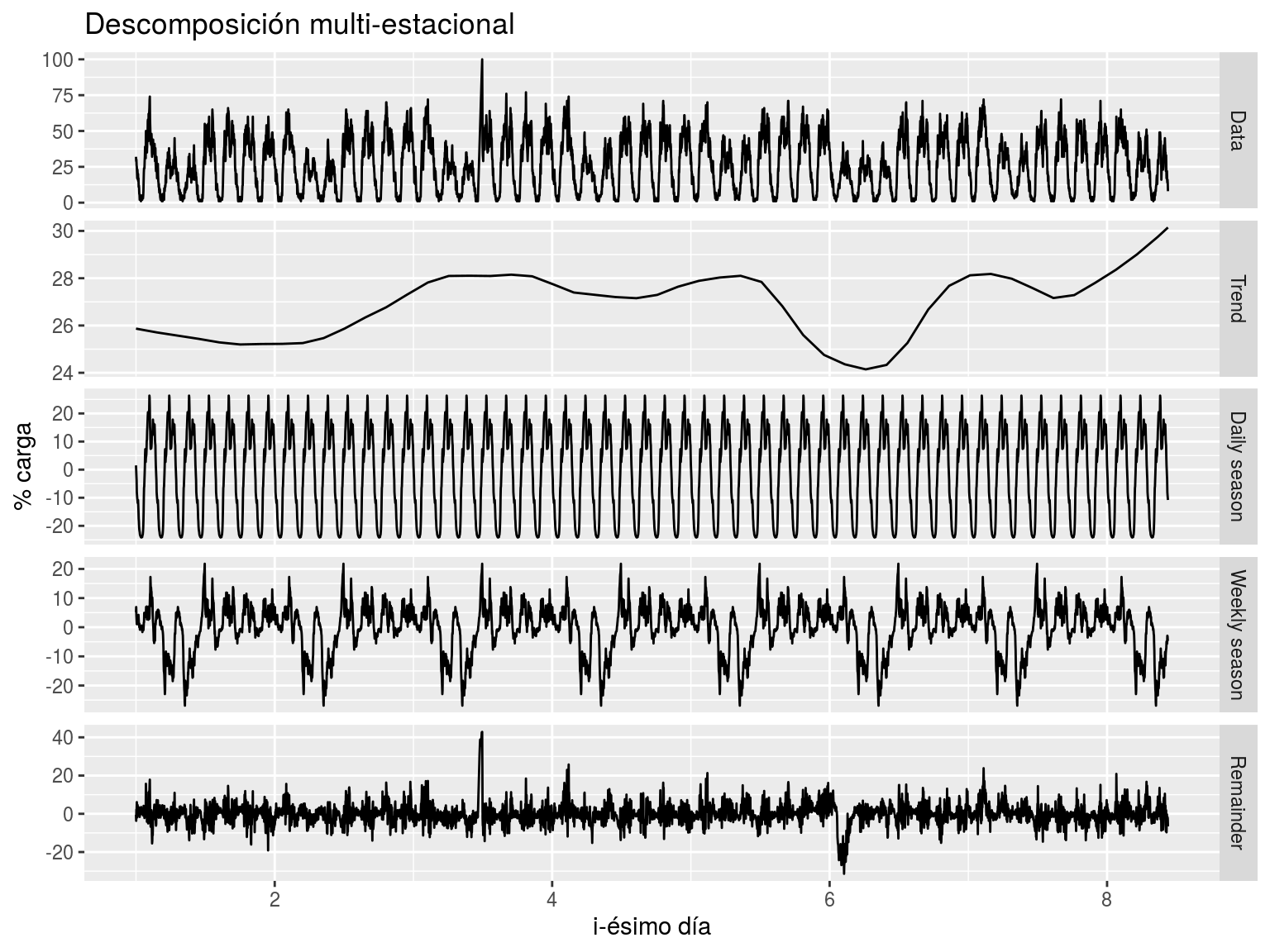
Figura 7.4: Ejemplo de descomposición multiestacional: dispositivo 4.000, últimos 5.000 valores reportados, estacionalidades diaria y semanal

Se han realizado el experimentos con estacionalidades diaria + semanal, diaria + semanal + mensual, diaria + semanal + anual y diaria + semanal + mensual + anual para todas las series de dispositivos de medida. Puede verse el resultado de uno de los experimentos para los datos reportados por el dispositivo 4.000 desde 2015 en la Figura 7.5.

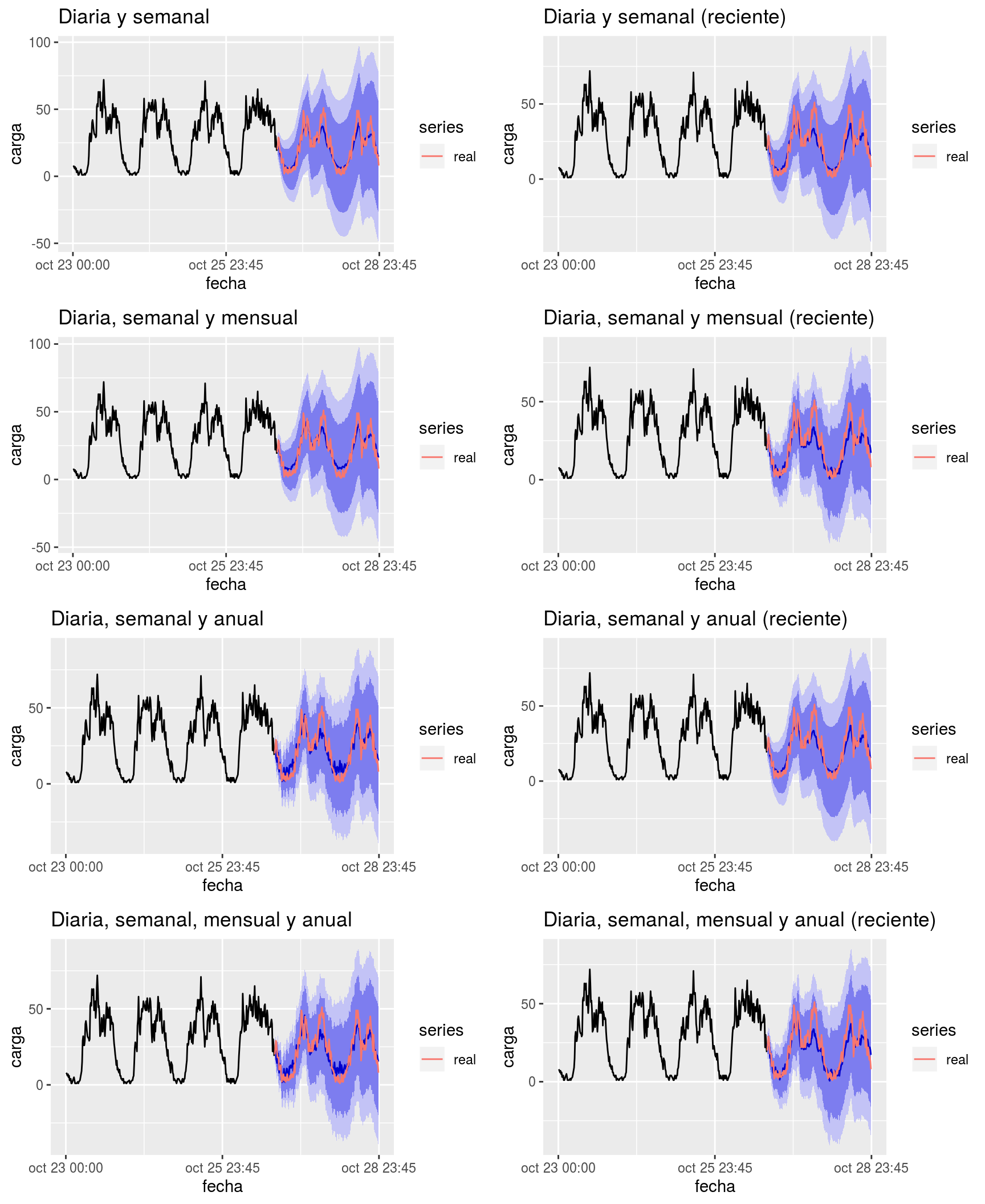
Figura 7.5: Ejemplo de pronósticos a 48 horas vista con el algoritmo MSTL para la serie reportada por el dispositivo 4.000 utilizando combinaciones de estacionalidad diaria, semanal, mensual o anual, considerando toda la serie o sólamente los 20.000 valores más recientes de la misma

Visualmente vemos que los resultados son muy prometedores. Pero no es fácil determinar qué combinación de estacionalidades puede ser la más productiva.

Más adelante, en el apartado de resultados de este capítulo, veremos cómo se comporta este método comparado con STL aplicado a todas las series que forman parte de este estudio.

7.4 Método ARIMA

Unos de los modelos clásicos más utilizados para el pronóstico de series temporales son los modelos ARIMA. Los modelos ARIMA intentan describir la auto correlación en los datos de la serie, por eso pueden incluir términos autorregresivos (AR) y/o términos de media móvil MA (traducido del término inglés “moving average”). Más adelante describiremos los modelos SARIMA (ARIMA estacional), que también los utilizamos en nuestra investigación.

Pero antes de entrar en detalle en de los modelos ARIMA conviene hablar de los conceptos de series estacionarias y diferenciación.

Una serie temporal estacionaria es aquella cuyas propiedades no dependen del momento en que se observa la serie. Por lo tanto, las series con tendencia, o con la estacionalidad, no son estacionarias: la tendencia y la estacionalidad afectan al valor de la serie en diferentes momentos.

Algunos casos pueden ser confusos: una serie temporal con comportamiento cíclico (pero sin tendencia o estacionalidad) es estacionaria. Esto se debe a que los ciclos no son de una longitud fija, por lo que antes de observar las series no podemos estar seguros de dónde estarán los picos y valles de los ciclos.

En general, una serie temporal estacionaria no tiene patrones predecibles a largo plazo. Su representación gráfica mostrará que la serie es aproximadamente horizontal (aunque es posible algún comportamiento cíclico), con una variación constante.

Más concretamente, una serie \(\{y_t\}\) es estacionaria si la distribución de \((y_t, ..., y_{t+s})\) no depende de \(t\) para todo \(s\).

Típicamente, cuando una serie no es estacionaria, una forma de transformarla en estacionaria es considerar los cambios de su valor en el tiempo en lugar de observar los datos en crudo, esto es, calcular las diferencias entre observaciones consecutivas. Esto se conoce como diferenciación. La diferenciación puede ayudar a estabilizar la media de una serie temporal y, por lo tanto, eliminar (o reducir) la tendencia y la estacionalidad. Por otro lado, para el caso de la varianza de la serie a lo largo del tiempo, a veces suelen aplicarse transformaciones logarítmicas.

La serie diferenciada se corresponde con la variación entre observaciones consecutivas en la serie original, y se puede escribir como: \[y^{\prime}_t=y_t-y_{t-1}\]

En ocasiones, los datos diferenciados siguen siendo no estacionarios y puede ser necesario diferenciar los datos una segunda vez para obtener una serie estacionaria. En la práctica, casi nunca es necesario ir más allá de las diferencias de segundo orden.

Una diferencia estacional es la diferencia entre una observación y la observación anterior de la misma temporada. Es decir, \[ y^{\prime}_t=y_t-y_{t-m}\] siendo \(m\) la longitud del periodo estacional.

Es importante interpretar correctamente las diferencias. Las primeras diferencias son el cambio entre una observación y la siguiente. Las diferencias estacionales son el cambio entre un mismo momento de una estación y el de la siguiente. Es poco probable que diferencias realizadas sobre otros retrasos (no inmediatamente anterior ni estacionales) tengan mucho sentido y deben evitarse.

Una forma de determinar de manera más objetiva si se requiere una diferenciación es utilizar un test de raíz unitaria. Son contrastes de hipótesis estadísticas que juzgan la estacionariedad de una serie para determinar si se requiere o no diferenciación. Por ejemplo, la función adf.test del paquete tseries o la función ur.kpss del paquete urca de R permiten realizar este tipo de contrastes.

Hemos dicho que los modelos ARIMA pueden tener una componente basada en autorregresión. En un modelo de autorregresión, se pronostica la variable de interés utilizando una combinación lineal de valores pasados de la variable. El término auto regresión indica que es una regresión de la variable contra sí misma. Esta parte del modelo puede expresarse con la fórmula:

\[y_{t} = c + \phi_{1}y_{t-1} + \phi_{2}y_{t-2} + \dots + \phi_{p}y_{t-p} + \varepsilon_{t}\] dónde \(\varepsilon_{t}\) es ruido blanco, \(\phi_{i}\) son parámetros y \(c\) es una constante. Este tipo de modelos suelen ser referidos como AR(p).

Normalmente los modelos autorregresivos requieren de series que sean estacionarias. De ahí las aclaraciones sobre estacionariedad que hemos realizado más arriba.

También hemos dicho más arriba que los modelos ARIMA pueden tener una componente basada en medias móviles. Un modelo de media móvil, en lugar de usar valores pasados de la variable de pronóstico en una regresión, utiliza errores de pronóstico pasados en un modelo similar a una regresión.

\[y_{t} = c + \varepsilon_t + \theta_{1}\varepsilon_{t-1} + \theta_{2}\varepsilon_{t-2} + \dots + \theta_{q}\varepsilon_{t-q},\] dónde \(\varepsilon_{t}\) es ruido blanco, \(\theta_{i}\) son parámetros y \(c\) es una constante. Este tipo de modelos suelen ser referidos como MA(q).

Si combinamos la diferenciación, la autorregresión y las medias móviles, obtenemos un modelo ARIMA no estacional. ARIMA es un acrónimo de Media Móvil Integrada Auto Regresiva (en este contexto, “integración” es lo contrario de la diferenciación). El modelo completo se puede escribir como:

\[ y'_{t} = c + \phi_{1}y'_{t-1} + \cdots + \phi_{p}y'_{t-p} + \theta_{1}\varepsilon_{t-1} + \cdots + \theta_{q}\varepsilon_{t-q} + \varepsilon_{t} \]

donde \(y'_{t}\) es la serie diferenciada (puede haber sido diferenciada más de una vez), \(p\) es el orden de la parte autorregresiva, \(d\) es el orden de la diferenciación y \(q\) es el orden de la parte de media móvil.

La parte más complicada en la construcción de los modelos ARIMA es la selección de los valores p, d, y q. A partir de una gráfica de la serie, no suele ser posible determinar los valores correctos para estos metaparámetros del modelo.

Sin embargo, para esta tarea suele ser muy útil valerse de las gráficas ACF y PACF de la serie y sus diferencias.

Las gráficas ACF muestran las autocorrelaciones que miden la relación entre \(y_t\) e \(y_{t-k}\) para diferentes valores de \(k\). Sin embargo, estas gráficas no son suficientes porque si cada valor está correlacionado con su predecesor, entonces también pueden existir correlaciones entre un un valor cualquiera y el que precede a su predecesor.

Para superar este problema, se utilizan las gráficas de autocorrelación parcial. Éstas miden la relación entre \(y_t\) e \(y_{t-k}\) después de eliminar los efectos de los retrasos \(1,2,...,k-1\).

Siguiendo las indicaciones de (Rob J Hyndman 2018), tenemos la heurística que se describe a continuación.

Los datos pueden seguir un modelo ARIMA(p,d,0) si los datos en crudo presentan las siguientes características:

• la curva ACF cae de forma exponencial o sinusoidal
• y hay un aumento significativo en el retraso p en la gráfica PACF, pero ninguno más allá del retraso p.

Los datos pueden seguir un modelo ARIMA(0,d,q) si los datos en crudo satisfacen:

• la gráfica PACF cae de forma exponencial o sinusoidal
• y hay un aumento significativo en el retraso q en el ACF, pero ninguno más allá del retraso q.

Por otro lado, según esta misma referencia, la heurística a seguir para determinar los parámetros de un modelo ARIMA es:

1. Representar los datos gráficamente.
2. Si es necesario, transformar los datos (utilizando una transformación de Box-Cox) para estabilizar la varianza.
3. Si los datos no son estacionarios, diferenciar hasta que los datos sean estacionarios.
4. Examinar las gráficas ACF/PACF: determinar si ARIMA(p,d,0) o ARIMA(0,d,q) son modelos apropiados según las indicaciones vistas más arriba.
5. Poner a prueba los modelos elegidos como prometedores.
6. Verificar los residuos del modelo elegido observando el ACF de los residuos. Si no se ven como ruido blanco, probar un modelo modificado.
7. Una vez que los residuos se vean como ruido blanco, el modelo es bueno.

En la Figura 7.6 podemos ver las gráficas ACF y PACF para nuestra serie de medidas tomadas por el dispositivo 4.000 a finales de Septiembre de 2018.

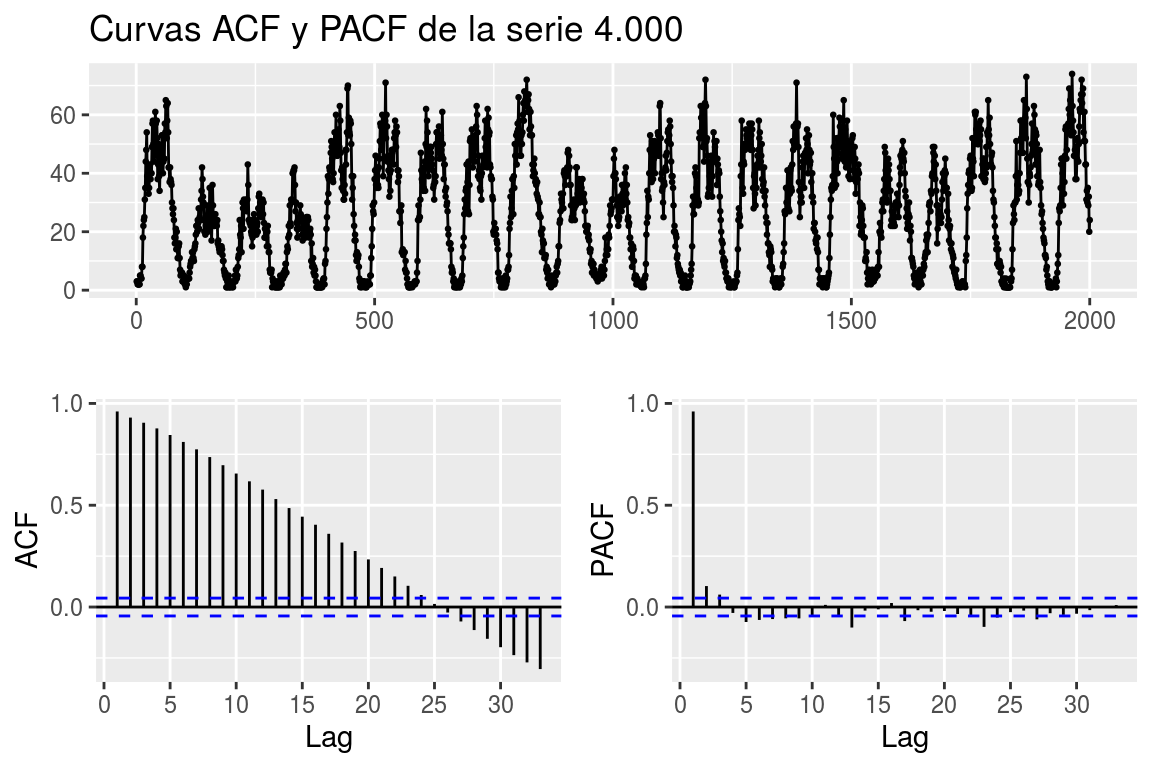
Figura 7.6: Original, ACF y PACF para los valores de carga del dispositivo 4.000 a finales de Septiembre de 2018

Según esta heurística, se han realizado distintas pruebas de ajuste de modelos ARIMA no estacionales. En ningún caso se ha llegado a resultados mínimamente satisfactorios.

Se ha utilizado incluso la función auto.arima del paquete forecast de R, que realiza una búsqueda de modelos mucho más exhaustiva sin haberse obtenido tampoco resultados que ofrezcan rendimiento aceptable. En la Figura 7.7, podemos ver un ejemplo de pronóstico realizado con este método.

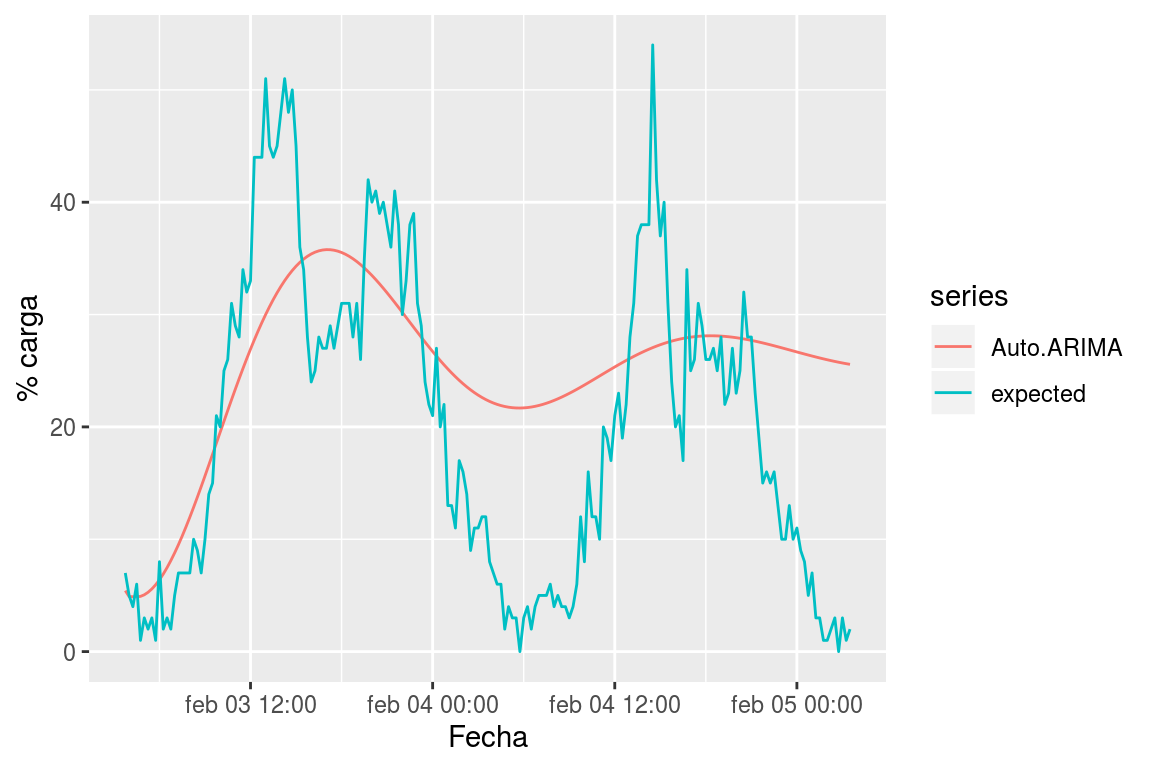
Figura 7.7: Pronóstico del flujo de carga para el terminal 4.000 con ARIMA

Los resultados arrojados por este método, como decíamos, han sido precarios. Sin embargo, no parece que sea una anomalía particular de este estudio sino que son numerosos las referencias en las que este comportamiento está documentado. Véase (Chatterjee 2019), (Rob J Hyndman 2018), etc. En general, parece que ARIMA (no estacional) tiene buena capacidad de pronóstico a muy corto plazo, pero en la medida en que incrementamos el horizonte de predicción su rendimiento se ve perjudicado. Efectivamente, esto mismo ha ocurrido en el caso de nuestros experimentos; para horizontes de entorno a los 15 minutos, las tasas de error son iguales o poco mayores que los mejores de los métodos de este estudio, pero en la medida en que el horizonte crece los resultados empeoran.

Nótese que en parte esto puede explicarse porque ARIMA (no estacional) calcula los valores futuros a partir de los pasados, pero sólo de los pasados recientes (no mucho más de los últimas 5 medidas reportadas, parámetros p y q). Además, para calcular los instantes futuros, más allá del primer instante, utiliza los valores pronosticados por el propio modelo; es decir, en nuestro caso, para pronosticar el instante futuro 192 lo que hace es pronosticar el instante futuro de manera recursiva 192 veces, retroalimentándose en cada iteración con los instantes ya calculados. Todo esto, de manera más intuitiva en este punto que otra cosa, invita a pensar que el propio modelo, en la medida en que va iterando el pronóstico va suavizándose o amortiguando su valor. Precisamente este es el comportamiento que podemos ver en la Figura 7.7.

Precisamente, según se observa en la literatura utilizada para este trabajo, el problema anterior parece que puede corregirse con modelos ARIMA estacionales, en dónde se incorpora la naturaleza estacional de las series (muy apropiado en el caso de nuestras series) al modelo y se saca ventaja de tal naturaleza. En el siguiente apartado hemos profundizado en el uso de modelos ARIMA con estacionalidad.

7.5 Método SARIMA - ARIMA estacional

En el apartado anterior nos hemos limitado a los datos no estacionales y los modelos ARIMA no estacionales. Y los resultados no han sido buenos. Sin embargo, los modelos ARIMA también son capaces de modelar una amplia gama de datos estacionales.

Un modelo ARIMA estacional se forma al incluir términos estacionales adicionales en los modelos ARIMA. La parte estacional del modelo consiste en términos que son similares a los componentes no estacionales del modelo, pero implican los cambios en el período estacional. Por ejemplo, un modelo \(ARIMA(1,1,1)(1,1,1)_4\) se refiere a un modelo que tiene en cuenta los datos estacionales con periodo 4 además de los datos recientes.

No es fácil determinar los parámetros p, d, q, P, D, Q y período en modelos SARIMA. Además, es complicado ajustar este tipo de modelo para períodos muy grandes. En el caso de nuestras series, por ejemplo, para considerar estacionalidad semanal tendríamos que considerar un período de \(4*24*7 = 672\) instantes. Sin embargo, sólo podemos aspirar a estudiar el comportamiento de modelos ARIMA estacionales con estacionalidad diaria (período 96) puesto que las librerías de R utilizadas no admiten estacionalidades tan grandes como 672.

En este caso, para la selección de metaparámetros se han seguido las indicaciones dadas en (“4.1 Seasonal Arima Models | Stat 510” 2019):

1. Representar gráficamente las series. Determinar características tales como tendencia y estacionalidad. Ver si existe un patrón estacional.

2. Hacer cualquier diferenciación necesaria. Las pautas generales son:

• Si no hay tendencia y sí estacionalidad, se toma una diferencia de retardo S. En nuestro caso 96, pues son las mediciones de un día.
  • Si hay una tendencia lineal y no hay una estacionalidad, entonces hacer la serie estacionaria.
  • Si hay tendencia y estacionalidad, aplicar una diferencia estacional a los datos y luego volver a evaluar la tendencia. Si la tendencia se mantiene, entonces diferenciar.
  • Si no hay tendencia obvia ni estacionalidad, no se diferencia.

3. Examinar las curvas ACF y el PACF de los datos diferenciados (si es necesaria la diferenciación):

• Términos no estacionales: los retrasos iniciales (1, 2, 3, …) determinan los términos no estacionales. Los picos en el ACF (en retrasos bajos) indican términos de MA no estacionales. Los picos en el PACF (en retrasos bajos) indicaron posibles términos de AR no estacionales.
  • Términos estacionales: examinar los patrones a través de los retrasos que son múltiplos de S. Interpretar las curvas ACF y PACF por los retrasos estacionales de la misma manera que se ha indicado antes.

4. Estimar los modelos que podrían ser razonables según las indicaciones del punto 3.

Hemos seguido los pasos anteriores para una muestra de series. En la Figura 7.8 se pueden ver el análisis tras realizar la diferenciación estacional de un dispositivo,

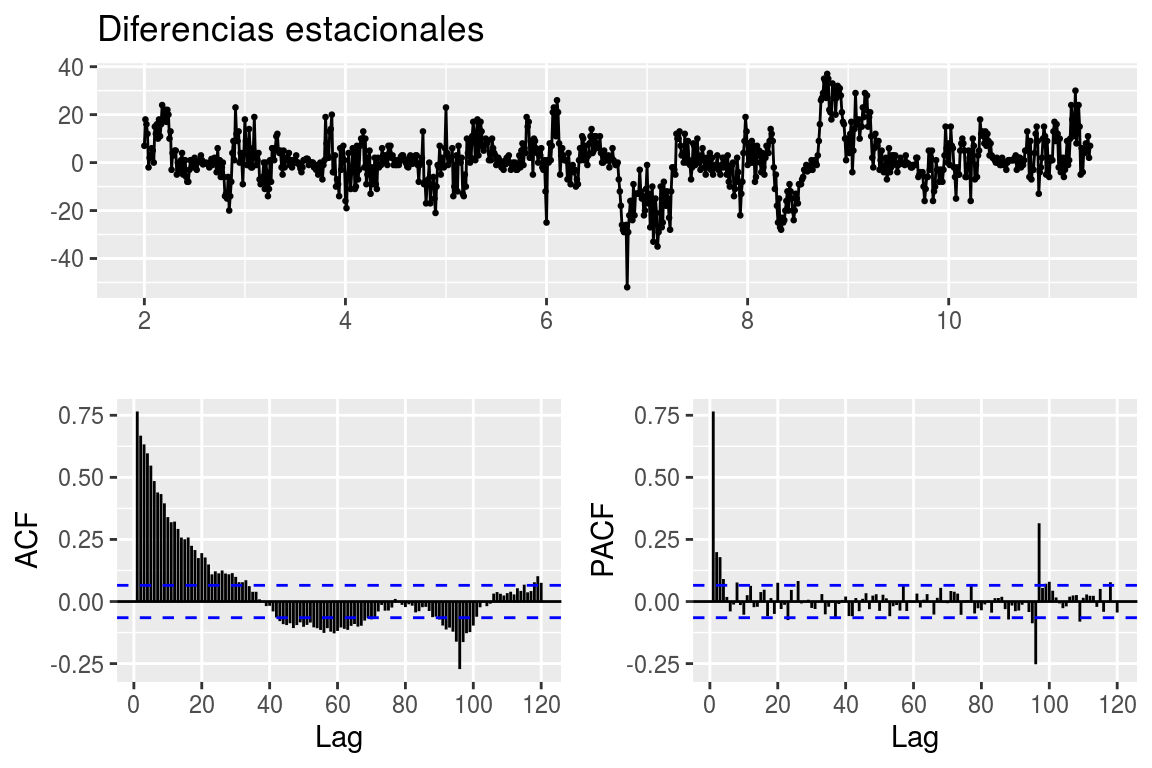
Figura 7.8: Curvas de las diferencias estacionales del dispositivo 4.000 a finales de Septiembre de 2018

Esta figura sugiere utilizar modelos con diferenciación estacional pero ninguna otra diferenciación. Igualmente, tanto en la parte estacional como en la no estacional del modelo, parecen relevantes tantos los parámetros de correlación como los de media móvil. Se han hecho pruebas manuales con distintas configuraciones y se ha observado que una buena opción podría ser un modelo \(ARIMA(1,0,1)(1,1,1)_{96}\).

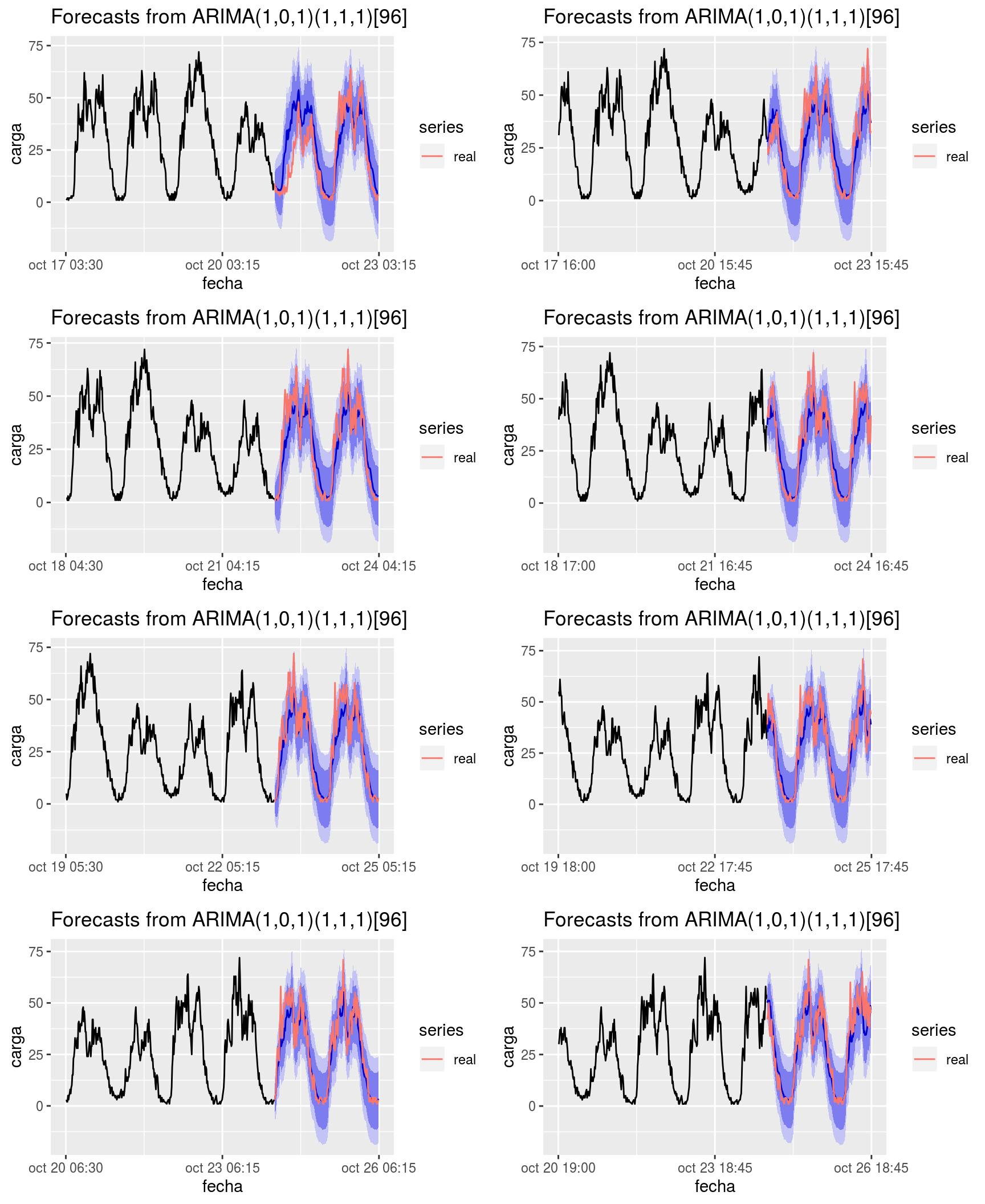
Figura 7.9: Ejemplo de pronósticos a 48 horas vista con el algoritmo SARIMA para la serie reportada por el dispositivo 4.000 en diferentes momentos

Procediendo de este modo, se han ajustado modelos de pronóstico basados en estos metaparámetros para todas nuestras series.

En la Figura 7.9 puede verse un ejemplo de pronósticos en diferentes instantes de una misma serie con ARIMA estacional.

Vemos que, al menos para esta serie, los resultados parecen bastante prometedores. El contraste de rendimiento de este modelo comparado con el resto de modelos de esta investigación podrá verse en el capítulo de resultados.

Bibliografía

“4.1 Seasonal Arima Models | Stat 510.” 2019. https://newonlinecourses.science.psu.edu/stat510/node/67/.

Chatterjee, Sharmistha. 2019. “ARIMA/Sarima Vs Lstm with Ensemble Learning Insights for Time Series Data.” https://towardsdatascience.com/arima-sarima-vs-lstm-with-ensemble-learning-insights-for-time-series-data-509a5d87f20a.

Cleveland, Robert B, William S Cleveland, Jean E McRae, and Irma Terpenning. 1990. “STL: A Seasonal-Trend Decomposition.” Journal of Official Statistics 6 (1): 3–73.

Rob J Hyndman, George Athanasopoulos. 2018. “Forecasting: Principles and Practice.” https://otexts.com/fpp2/. https://otexts.com/fpp2/.