Capítulo 4 Fundamentação Estatística
4.1 Introdução
A informação encontrada nas apresentações e na mídia de forma geral é passível de toda sorte de manipulação. Entretanto, com apenas algumas observações e o conhecimento de conceitos simples é mais fácil saber como questionar os dados apresentados, e compreender quais desses dados podem ser consumidos em nossas análises de negócio.
Alfabetização Quantitativa ou Alfabetização Estatística é a temática que envolve um conjunto completo de competências necessárias para compreensão das informações que são compartilhadas nos diversos contextos.
4.2 Competências Envolvidas
- Habilidade de ler e interpretar um gráfico
- Calcular Percentuais
- Compreender Modelos Matemáticos
- Avaliar os Dados consumidos em argumentações e contestar as decisões tomadas
- Saber quais tipos de informações podem ser usadas para diversos questionamentos
Com tais competências, é possível para qualquer analista observar um estudo, ou argumentação, e compreender as nuances conclusivas e quais argumentações são baseadas em evidências concretas e quais aquelas sem qualquer construção empírica.
Revisão de Conceitos Estatísticos
A seguir, apresentamos uma revisão dos conceitos estatísticos, úteis ao analista de negócio para melhor compreensão do tema e na construção de suas análises.
4.3 Variáveis
Trata-se da informação que está sendo observada durante o estudo ou contexto (é o “o quê?”). A avaliação de quantos homens ou mulheres participaram da Prova de Conceito Prova de Vida é uma busca pela variável gênero. Uma variável é algo que pode ser diferente para cada pessoa, no intervalo de tempo onde foi avaliada (exemplo: variável clima) ou para quê você precisa da informação (qual sua aplicação).
Variáveis são importantes pois:
- As publicações frequentemente apresentam resultados do tipo causa-efeito. Conseguir identificar exatamente quais variáveis estão sendo observadas ajuda a compreender a dimensão causal da análise.
- Pensar de forma mais abrangente sobre o que está sendo medido, por quem e com qual objetivo ajuda a formular questionamentos sobre a origem dos dados, sua qualidade e quais potenciais viéses foram incluídos na análise.
4.3.1 Exemplo
Uma escola que diz que 90% de seus estudantes que concluíram o ensino médio irão para universidades públicas é um número bastante expressivo. Entretanto, a informação de que apenas 40% efetivamente obteram vagas em tais universidades significa que a primeira análise apenas apresentou a intenção de participar do processo seletivo, enquanto a segunda apresentou efetivamente o resultado obtido.
A forma como algo é medido tambem afeta a maneira com que a informação é apresentada posteriormente. Perguntar qual a formação profissional das pessoas nem sempre permite usar essa informação na análise de salários, uma vez que não há uma forma simples de se diferenciar os que não iniciaram o ensino superior daqueles que não chegaram a concluí-lo.
Algo importante que deve ser perseguido durante o estudo da estatística é a compreensão de que, os números que vemos em todas as mídias, de fato representam variáveis, que foram medidas, manipuladas e apresentadas muitas vezes de forma a corroborar o discurso do autor. A análise crítica sobre a construção das variáveis é fundamental para o correto consumo da informação.
4.4 Percentuais, Taxas e Percentis
Sem contextualização, não é possível afirmar se os números apresentados estão corretos ou qual sua real representatividade. A padronização na apresentação dos números é um passo fundamental a correta compreensão da dimensão.
Por exemplo: Na nota de uma prova, o estudante tirou 40 pontos. Esse valor foi suficiente para ser aprovado? É necessário saber qual o valor máximo dos pontos obtidos. Considerando que a pontuação máxima era de 50 pontos, temos então:
# Nota do Aluno
nota <- 40
# Valor da Pontuação Maxima
pontuacao_maxima <- 50
# Para calcular o valor Percentual, vamos dividir a nota pela pontuação maxima e multiplicar por 100
(percentual_nota <- (nota/pontuacao_maxima) * 100)## [1] 80Observamos que o aluno obteve 80% da nota máxima da prova.
Em outro exemplo, a Escola ABC informou que 1010 alunos do sexo feminino foram aprovados em um exame admissional, de um universo de 2400 participantes enquanto a escola CDE informou que 76 alunas do sexo feminino foram aprovadas (de um universo de 130 estudantes). Qual escola é mais inclusiva?
Escola ABC: (1010/2400) * 100 = 42%
Escola CDE: (76/130) * 100 = 58%
De forma similar, taxas podem ser representadas pelo número de ocorrências observadas dividido pelo número de possibilidades. Normalmente se multiplica o resultado para efeito de comparação (muito comum se multiplicar por 1000). Por exemplo, o fenômeno da mortalidade infantil é representado pela taxa de mortes quando comparada ao número de nascimentos (Quantidade de mortes a cada 1000 nascidos vivos).
Como as porcentagens, as taxas permitem comparar as chances de algo acontecer.
Vamos supor, que em um intervalo de 1 ano, no município de João Pessoa (cenário hipotético):
Número de nascidos vivos: 5000
Número de mortes nos 5 primeiros meses: 17
Taxa de Mortalidade infantil nos 5 primeiros meses após o nascimento: 17/5000 = 0,0034 x 1000 = 3,4 crianças a cada 1000 nascidas vivas morrem nos 5 primeiros meses
Relacionadas aos percentuais, temos os percentis. Normalmente utilizados para comparar altura e peso de pessoas, o número apresentado como percentil é o percentual de ocorrências acima (ou abaixo) do valor comparado.
Uma pessoa cuja pontuação em um teste ficou no percentil de 90 pontuou mais do que 90% dos participantes.
# Vamos supor a existência de 50 notas para uma mesma prova (distribuição uniforme)
notas <- runif(50,1,10)
# Vamos identificar quais as notas de corte para que o aluno consiga ficar acima dos demais nos percentis 32, 57 e 98
quantile(notas, c(.32, .57, .98))## 32% 57% 98%
## 4.449349 5.892380 9.778691Apresentar valores numéricos sem um contexto é um erro bastante comum. Uma fato que ocorreu na cidade de Parma (Missouri - Estados Unidos) causou revolta na população: A manchete dizia que mais de 80% dos policiais haviam solicitado demissão após um prefeito negro ser eleito na cidade. O que parecia ser um episódio de preconceito racial, se mostrou algo mais simples: Na cidade haviam somente 6 policiais, e 5 haviam assinado demissão pois já haviam assumido outros compromissos.
Outro cenário comum está relacionado à divulgação do aumento da ocorrência de doenças infecto-contagiosas. Isso ocorre em decorrência de variações percentuais muito altas (ex.: aumento em 100% dos casos), o que é bastante comum quando o número de casos já é muito baixo.
4.5 Média e Tendência Central
Deve haver um cuidado grande quando se trabalha com valores médios para determinados cenários de estudo. Exemplo: se considerarmos somente a população de clientes do Starbucks para estimar o consumo médio de café por habitante, teremos um valor expressivamente maior que o da população real.
Há vários tipos de valores Médios em estatística. Segue alguns deles:
Moda: Número que ocorre com maior frequência dentro de um conjunto observado. A moda é a única média significativa que utilizamos quando estamos tentando compreender variáveis categóricas (como raça, gênero ou religião).
Mediana: É o valor que divide uma distribuição exatamente ao meio. A mediana deve ser usada em variáveis que resultam em respostas ordenadas (como questionários que classificam respostas em escala).
Média: Trata-se da média aritmética, como idade ou peso de um conjunto de pessoas. O valor de cada indivíduo é usado para calcular a média, o que significa que a presença de alguns poucos indivíduos com valores bastante distoantes pode influenciar no resultado da média.
# Vamos supor a existência de 50 notas para uma mesma prova (distribuição uniforme)
notas <- runif(50,1,10)
# Vamos calcular a média das Notas
mean(notas)## [1] 5.283446## [1] 5.12446# Implementando função para calculo da moda
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
# Vetor de Valores
v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)
# Calculando a Moda
(getmode(v))## [1] 2Saber qual média foi utilizada ou qual utilizar é fundamental para a análise. No exemplo apresentado acima, das notas, é possível observar a diferença entre os resultados. Caso uma escola possua alguns poucos alunos com notas baixas, a escola estará interessada em apresentar a mediana. Se alguns alunos conseguirem uma nota muito alta, será apresentada a média. De toda forma, é importante observar como as conclusões podem ser alteradas dependendo da medida de tendência central está sendo utilizada.
De toda forma, o ideal é apresentar, juntamente com a medida de tendência central, a informação da dispersão. Supondo em que a média e a mediana apresentassem o mesmo resultado em ambas as análises, saber qual a dispersão das notas nos dá uma noção melhor de como está o desempenho dos estudantes.
A dispersão pode ser medida em função da variância, que é uma medida que mostra o quão distante cada valor do conjunto representado está distante do valor central (médio). Uma outra medida de dispersão é o desvio padrão. O desvio padrão é capaz de identificar o “erro” em um conjunto de dados, caso quiséssemos substituir um dos valores coletados pela média aritmética. O desvio padrão aparece juntamente à média aritmética, informando o quão confiável é esse valor.
Para calcular o valor do desvio padrão em R temos a seguinte função:
## [1] 2.690467Observando a distribuição:
##
## Call:
## density.default(x = notas)
##
## Data: notas (50 obs.); Bandwidth 'bw' = 1.107
##
## x y
## Min. :-2.153 Min. :0.0001758
## 1st Qu.: 1.702 1st Qu.:0.0133759
## Median : 5.558 Median :0.0843594
## Mean : 5.558 Mean :0.0647686
## 3rd Qu.: 9.414 3rd Qu.:0.1040957
## Max. :13.269 Max. :0.1285396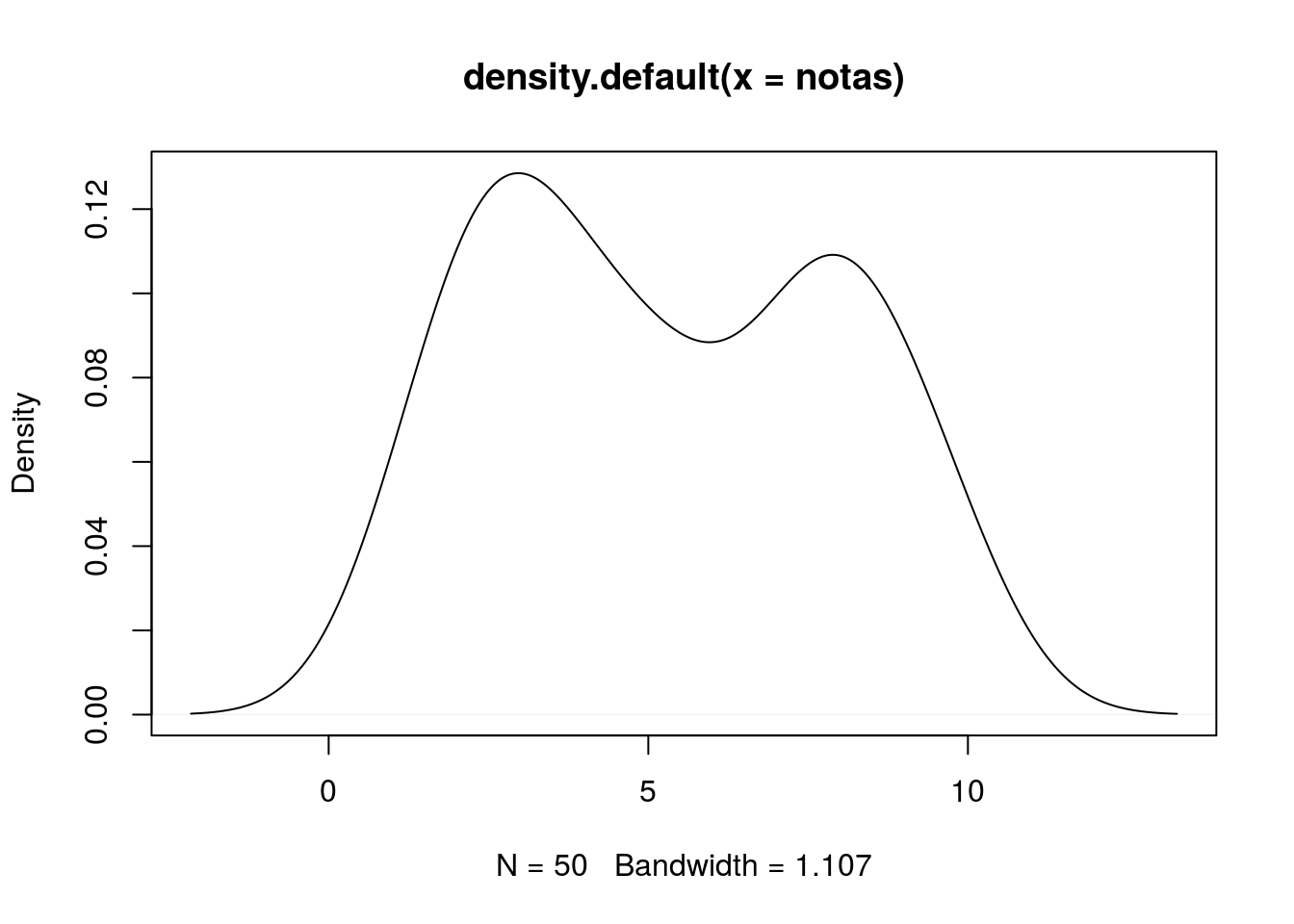
4.6 Amostragem
O Objetivo de se definir uma amostragem é, através da representação estatística de um grupo, obter informações relevantes e precisas sobre o todo. Para que uma amostra possa ser utilizada com esse objetivo, é determinante que ela seja escolhida de forma aleatória.
Uma amostra não-aleatória é formada quando o selecionador utiliza seu julgamento na definição de quem (ou o quê) irá participar da pesquisa, em detrimento de um grupo mais abrangente. Tal abordagem eventualmente pode ser utilizada quando o conjunto universo é muito complexo e há limitações financeiras para a construção da amostra aleatória. Entretanto, é importante reforçar para o público alvo as características daquele estudo, indicando que uma amostra não aleatória, sendo utilizada, pode incorrer em erros e vieses que somente serão capturados diante da análise do conjunto total.
Uma abordagem bastante comum para definição da amostra aleatória é a estratégia de abordagem aleatória de pessoas (em um modelo conhecido como random-digit dialing).
4.6.1 Como analisar uma amostragem em uma pesquisa?
As seguintes perguntas devem ser respondidas para uma análise estruturada:
- Quem foi o público-alvo?
- Quem foi efetivamente entrevistado?
- Quem (qual grupo) foi excluído?
- Para quem os resultados podem ser efetivamente generalizados?
Caso nenhuma informação sobre o processo de coleta da amostra seja fornecida, é importante ficar atento à pesquisa. Eventualmente, uma amostra enviesada pode trazer conclusões equivocadas.
4.6.2 Como calcular o tamanho da Amostra?
Alguns sites fornecem calculadoras específicas com esse objetivo. Por exemplo, o site Survey Monkey possui uma calculadora de tamanho da amostra:
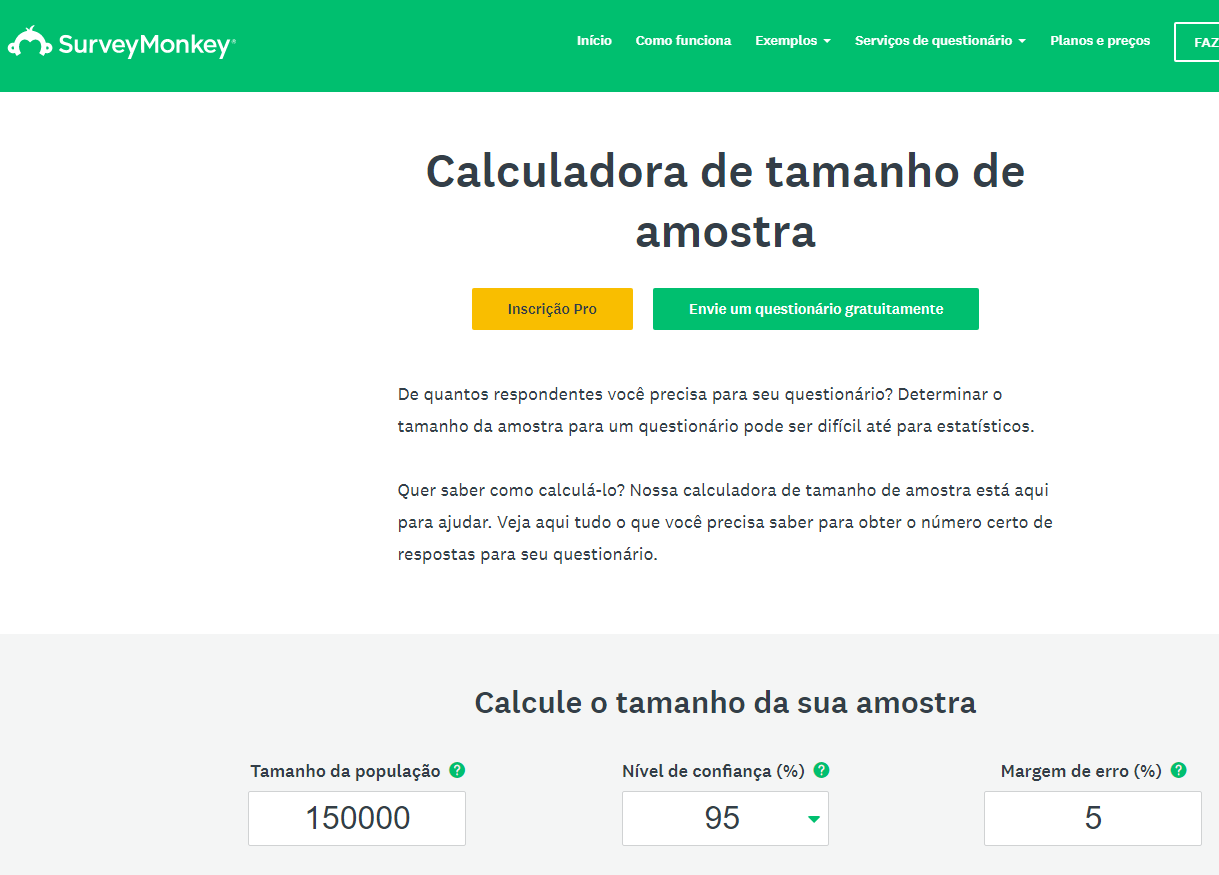
Figura 4.1: Calculadora Amostral do site Survey Monkey
4.6.3 Como recuperar amostras em R?
# Definindo "semente" para alcançar resultados reproduzíveis. O mesmo valor deve ser adotado em outras avaliações
set.seed(524)
# definindo uma população de 10000 valores na faixa de 1 a 100000
populacao <- runif(10000,1,100000)
# Utilizando a Calculadora Amostral, para uma população de 10000 elementos, nível de confiança 99% e margem de erro 5% temos uma amostra de 625 (ver próximo tópico)
tamanhoAmostra <- 625
# Escolhendo aleatoriamente 370 posições do vetor população
index <- sample(1:length(populacao), tamanhoAmostra)
# Separando a amostra
amostra <- populacao[index]Qual o valor da Média da População Original?
## [1] 49829.06Qual o valor da Média da Amostra?
## [1] 48945.79Qual o valor do Desvio Padrão da População Original?
## [1] 28629.13Qual o valor do Desvio Padrão da Amostra?
## [1] 28861.034.7 Margem de Erro / Intervalo de Confiança
Conforme apresentado anteriormente, o uso de amostras pode significar economia de tempo e recursos para chegar a conclusões sobre a população. Entretanto, a forma de coleta da população é importante para garantir a aleatoriedade da amostra.
Para entender o que é margem de erro, é necessário compreender que, durante a construção da amostra, são tomadas decisões que “limitam” o universo de observações. Escolher aleatoriamente um subconjunto implica em tomar a decisão de observar um subconjunto para compreender o todo. Como na maior parte das vezes é economicamente inviável colher todas as informações da população, é necessário, além do resultado da pesquisa, indicar qual o intervalo de erro que teremos que tolerar.
4.7.1 Mas como interpretar a margem de erro?
No caso apresentado anteriormente, escolhemos uma amostra com margem de erro de 5%, i.e., os resultados obtidos provavelmente terão uma variação de +- 5% em relação ao real. Tomando a média como exemplo, podemos fazer o comparativo:
## [1] 49829.06# Valor Mínimo da Amostra considerando Margem de erro de 5%
mediaAmostra <- mean(amostra)
(mediaAmostra - 0.05*mediaAmostra)## [1] 46498.5# Valor Máximo da Média da Amostra considerando Margem de erro de 5%
(mediaAmostra + 0.05*mediaAmostra)## [1] 51393.08O Intervalo de Confiança, por sua vez, está diretamente ligado à margem de erro. Ele representa a probabilidade de uma pesquisa ter os mesmos resultados se for aplicada com um outro grupo de pessoas, dentro do mesmo perfil de amostra e com a mesma margem de erro.No exemplo acima, temos um intervalo de confiança de 99%, i.e., a cada 100 pesquisas realizadas, provavelmente 99 irão retornar resultados semelhantes.
No seguinte link apresenta uma abordagem utilizando o pacote Rmisc para cálculo da margem de erro e intervalo de confiança.
4.8 Correlação
A correlação descreve matematicamente a conexão “implícita” que existe entre duas variáveis. Através da correlação é possível compreender a “força” e a “direção” do relacionamento entre duas variáveis.
Correlações podem ser positivas ou negativas. Uma correlação positiva indica que maiores (ou menores) valores de observação de uma variável implica em maiores(ou menores) valores para a outra variável. Correlações negativas implicam em um comportamento inverso: o aumento do valor de uma variável implica em uma diminuição do valor da outra variável.
Há duas considerações importantes sobre a correlação:
A correlação entre duas variáveis não significa obrigatoriamente que eles possuem uma relação causal (causa-efeito). Para que a causalidade seja configurada, é necessário ainda um nexo temporal entre os fenômenos (a mudança da primeira variável aconteceu antes da mudança da segunda?).
A correlação somente pode ser observada quando a associação ocorre de forma linear. Outros tipos de relação, como o nível de satisfação com a compra de um automóvel ou número de bugs em um software, ambas com curvas em formato em U, não apresentam correlação.
Exemplo de Uso de Correlação:
# Observação da Matriz exemplo (mtcars) completa utilizando metodo kendall
cor(mtcars, use="complete.obs", method="kendall")## mpg cyl disp hp drat wt
## mpg 1.0000000 -0.7953134 -0.7681311 -0.7428125 0.46454879 -0.7278321
## cyl -0.7953134 1.0000000 0.8144263 0.7851865 -0.55131785 0.7282611
## disp -0.7681311 0.8144263 1.0000000 0.6659987 -0.49898277 0.7433824
## hp -0.7428125 0.7851865 0.6659987 1.0000000 -0.38262689 0.6113081
## drat 0.4645488 -0.5513178 -0.4989828 -0.3826269 1.00000000 -0.5471495
## wt -0.7278321 0.7282611 0.7433824 0.6113081 -0.54714953 1.0000000
## qsec 0.3153652 -0.4489698 -0.3008155 -0.4729061 0.03272155 -0.1419881
## vs 0.5896790 -0.7710007 -0.6033059 -0.6305926 0.37510111 -0.4884787
## am 0.4690128 -0.4946212 -0.5202739 -0.3039956 0.57554849 -0.6138790
## gear 0.4331509 -0.5125435 -0.4759795 -0.2794458 0.58392476 -0.5435956
## carb -0.5043945 0.4654299 0.4137360 0.5959842 -0.09535193 0.3713741
## qsec vs am gear carb
## mpg 0.31536522 0.5896790 0.46901280 0.43315089 -0.50439455
## cyl -0.44896982 -0.7710007 -0.49462115 -0.51254349 0.46542994
## disp -0.30081549 -0.6033059 -0.52027392 -0.47597955 0.41373600
## hp -0.47290613 -0.6305926 -0.30399557 -0.27944584 0.59598416
## drat 0.03272155 0.3751011 0.57554849 0.58392476 -0.09535193
## wt -0.14198812 -0.4884787 -0.61387896 -0.54359562 0.37137413
## qsec 1.00000000 0.6575431 -0.16890405 -0.09126069 -0.50643945
## vs 0.65754312 1.0000000 0.16834512 0.26974788 -0.57692729
## am -0.16890405 0.1683451 1.00000000 0.77078758 -0.05859929
## gear -0.09126069 0.2697479 0.77078758 1.00000000 0.09801487
## carb -0.50643945 -0.5769273 -0.05859929 0.09801487 1.00000000Como curiosidade, deixo url Clique aqui com correlações espúrias (claramente sem nexo causal.)
Como exemplo, um gráfico com 99.79% de correlação indicando uma relação (positiva) muito forte entre os gastos do governo americano com determinados assuntos e o número de suicídios por enforcamento, estrangulação e sufocamento.
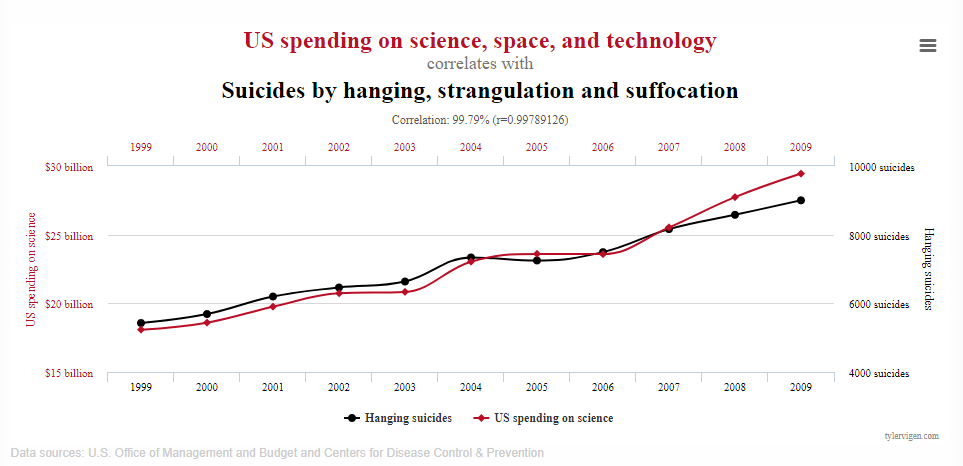
Figura 4.2: Exemplo de Correlação Espúria