Seção 2 Hietograma da Chuva de Projeto
Mudanças no uso e ocupação do solo, supressão da vegetação e impermeabilização das superfícies constituem ações típicas do processo de urbanização que interferem no ciclo hidrológico de uma bacia hidrográfica reduzindo a evapotranspiração, a infiltração e, consequentemente, aumentando o escoamento superficial.
Grande parte das cidades brasileiras encontra-se em um quadro de urbanização crescente que resulta na inexorável obsolescência das redes de drenagem. Em outras palavras, sarjetas, bocas de lobo, canais e galerias dimensionados décadas atrás para um determinado Tempo de Retorno (TR) e um dado cenário de impermeabilização e de uso e ocupação do solo, já não são mais suficientes para escoar as vazões geradas nas condições de urbanização atual.
Dentro desse contexto, a Prefeitura Municipal de Belo Horizonte solicitou a você um estudo de verificação do funcionamento de um canal na bacia hidrográfica do córrego Engenho Nogueira.
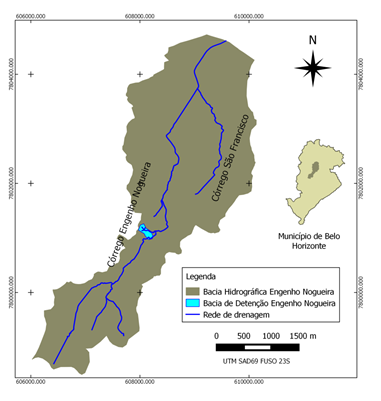
Tal estudo demandará análises hidrológicas e hidráulicas. Nesse primeiro exercício avaliativo vamos obter o hietograma de projeto e o hietograma de precipitação efetiva.
2.1 Questão 1
Obtenha a intensidade da chuva de projeto (em mm/h) a ser utilizada no presente estudo sabendo que o canal em questão foi dimensionado para o Tempo de Retorno de 20 anos e que a duração crítica para a chuva de projeto pode ser admitida igual ao tempo de concentração da bacia que é de 1 hora. Utilize a equação IDF para a Região Metropolitana de Belo Horizonte desenvolvida por Pinheiro e Naghettini (1998) e o valor de 1400 mm como precipitação média anual.
Usando a equação proposta por Pinheiro e Naghettini (1998): \(\check{I}_{T,d,j} = 0,76542 d^{-0,7059}P_{j}^{0,5360}\mu _{T,d}\)
Dados de entrada:
#Dados de entrada:
TR <- 20 #anos
TC <- 1 #horas
PmediaAnual <- 1400 #mmQuantis adimensionais \(\mu _{T,d}\):
| Duracoes(h) | TR_1.05 | TR_1.25 | TR_2 | TR_10 | TR_20 | TR_50 | TR_100 | TR_200 |
|---|---|---|---|---|---|---|---|---|
| 0.167 | 0.691 | 0.828 | 1.013 | 1.428 | 1.586 | 1.791 | 1.945 | 2.098 |
| 0.250 | 0.695 | 0.830 | 1.013 | 1.422 | 1.578 | 1.780 | 1.932 | 2.083 |
| 0.500 | 0.707 | 0.836 | 1.013 | 1.406 | 1.557 | 1.751 | 1.897 | 2.043 |
| 0.750 | 0.690 | 0.827 | 1.013 | 1.430 | 1.589 | 1.795 | 1.949 | 2.103 |
| 1.000 | 0.679 | 0.821 | 1.014 | 1.445 | 1.610 | 1.823 | 1.983 | 2.143 |
| 2.000 | 0.683 | 0.823 | 1.014 | 1.439 | 1.602 | 1.813 | 1.970 | 2.128 |
| 3.000 | 0.679 | 0.821 | 1.014 | 1.445 | 1.610 | 1.823 | 1.983 | 2.143 |
| 4.000 | 0.688 | 0.826 | 1.013 | 1.432 | 1.591 | 1.798 | 1.953 | 2.108 |
| 8.000 | 0.674 | 0.818 | 1.014 | 1.451 | 1.618 | 1.834 | 1.996 | 2.157 |
| 14.000 | 0.636 | 0.797 | 1.016 | 1.503 | 1.690 | 1.931 | 2.112 | 2.292 |
| 24.000 | 0.603 | 0.779 | 1.017 | 1.550 | 1.754 | 2.017 | 2.215 | 2.412 |
Construindo uma função para calcular a intensidade:
Intensidade <- function(TR, Duracao, PmediaAnual){
Quantil = Quantis_Adimensionais[
Quantis_Adimensionais[,1] == Duracao,
paste("TR_", TR, sep = "")
]
Intensidade = 0.76542 * Duracao ^ -0.7059 * PmediaAnual ^ 0.5360 * Quantil
return(Intensidade)
}
Intensidade(TR, TC, PmediaAnual)| TR_20 | |
|---|---|
| 1 Hora | 59.85 |
2.2 Questão 2
A partir da chuva de projeto calculada no exercício anterior, obtenha o hietograma de projeto utilizando um intervalo de discretização temporal de 15 minutos e os gráficos de distribuição temporal de precipitações na Região Metropolitana de Belo Horizonte propostos por Pinheiro e Naghettini (1998). Faça o upload da planilha de cálculo utilizada para obter o hietograma de projeto.
Para solucionar a questão, primeiro vamos importar a discretização de Huff para 1 hora:
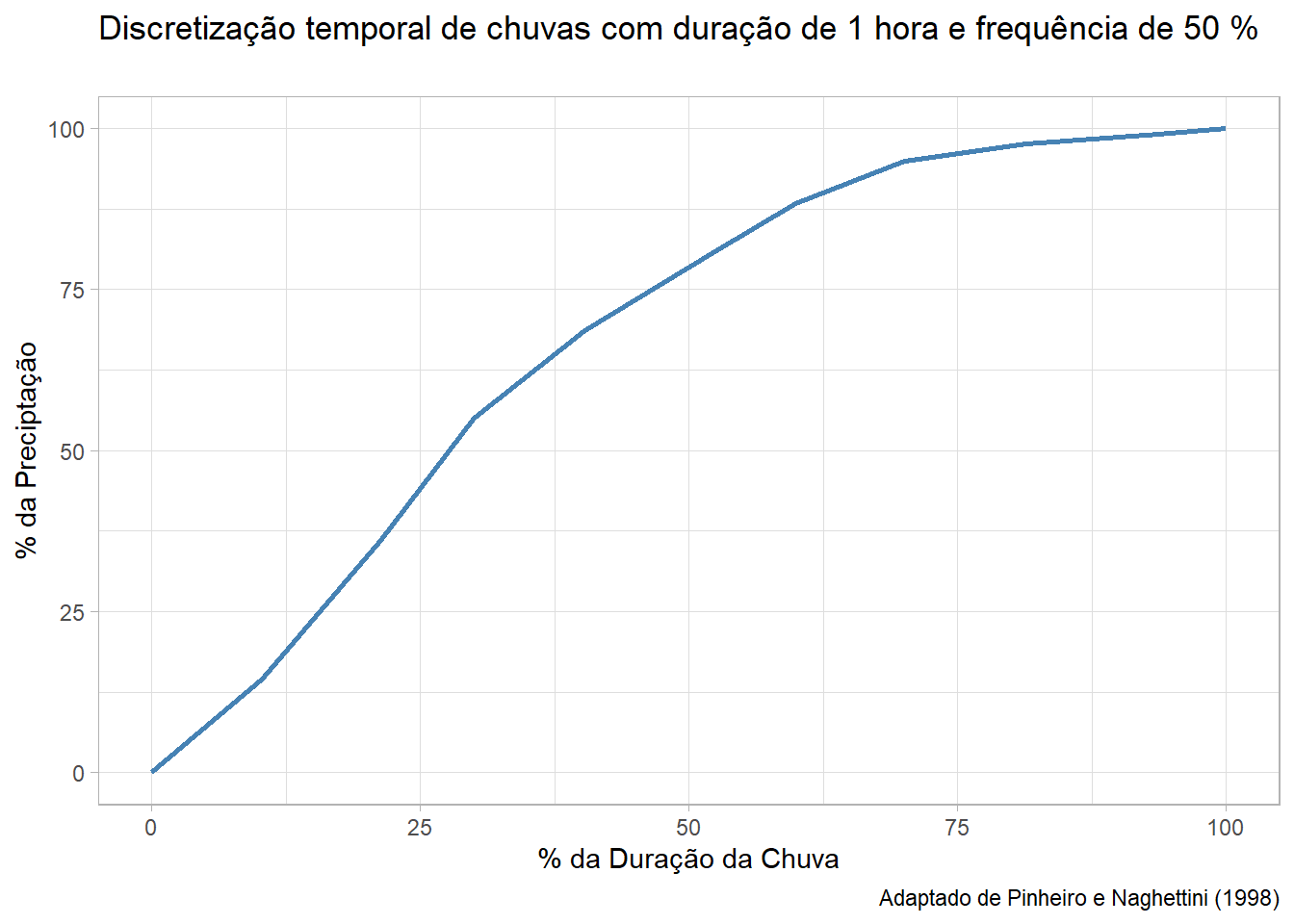
Figura 2.1: Discretização Temporal usada para a altura de chuva total de projeto
Transformando o gráfico obtido anteriormente em uma função, obtemos os valores da discretização para intervalos de 15 min usando a intensidade calculada anteriormente
Funcao_Huff <- approxfun(Huff_1hora)
Hietograma <- data.frame(Tempo_min = seq(0,60,15))
PrecipitacaoTotal = Intensidade(TR, TC, PmediaAnual) * TC
Hietograma$Precipitacao_porcent = sapply(Hietograma$Tempo_min / 60 * 100, FUN = Funcao_Huff)
Hietograma$PrecipitacaoTotalAcumulada_mm = Hietograma$Precipitacao_porcent * 59.8 / 100| Tempo_min | Precipitacao_porcent | PrecipitacaoTotalAcumulada_mm | PrecipitacaoIncremental_mm |
|---|---|---|---|
| 0 | 0.00000 | 0.00000 | 0.000000 |
| 15 | 44.13793 | 26.39448 | 26.394483 |
| 30 | 78.48017 | 46.93114 | 20.536656 |
| 45 | 96.17080 | 57.51014 | 10.578997 |
| 60 | 100.00000 | 59.80000 | 2.289864 |
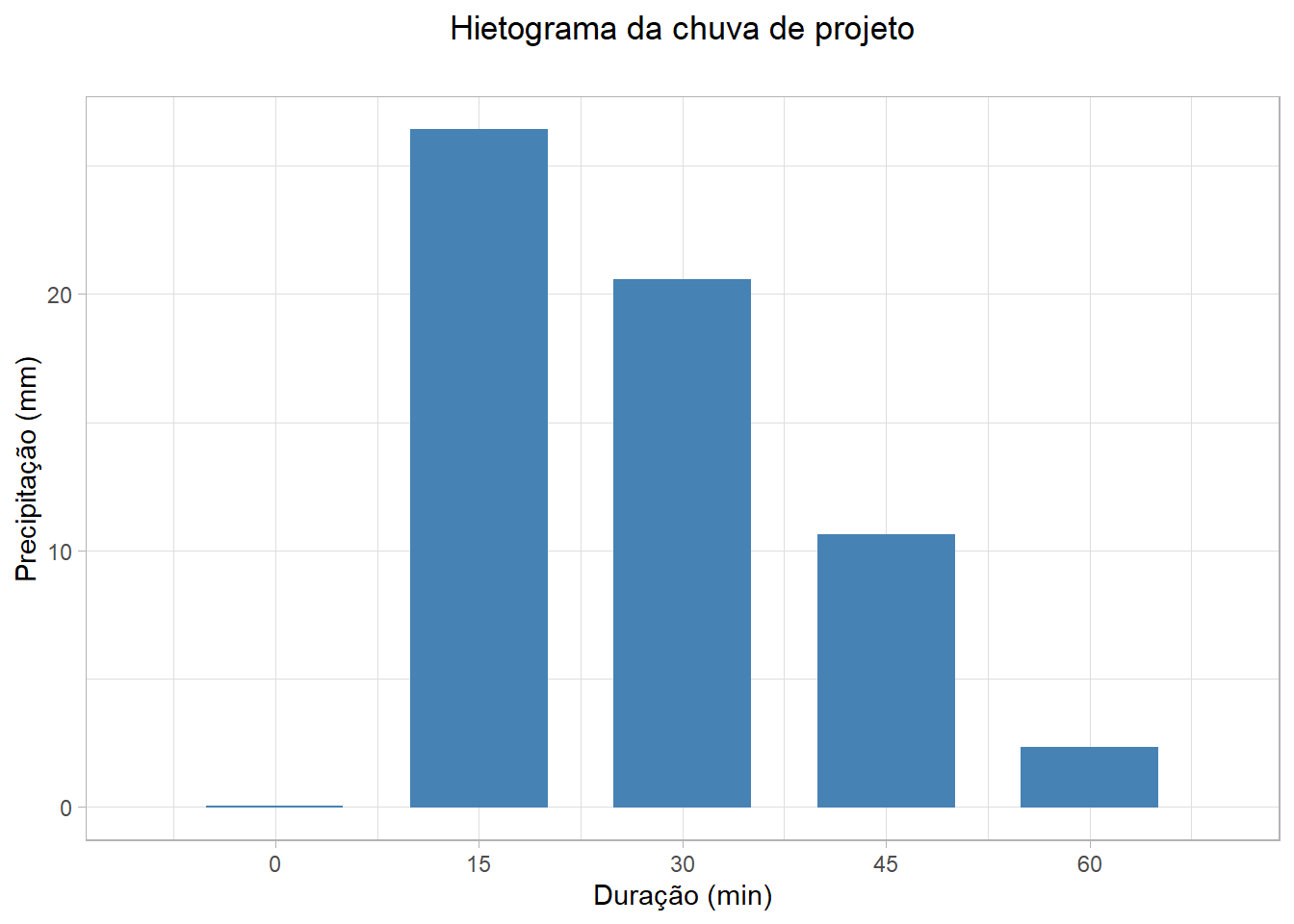
Figura 2.2: Hietograma da Chuva Total de Projeto
2.3 Questão 3
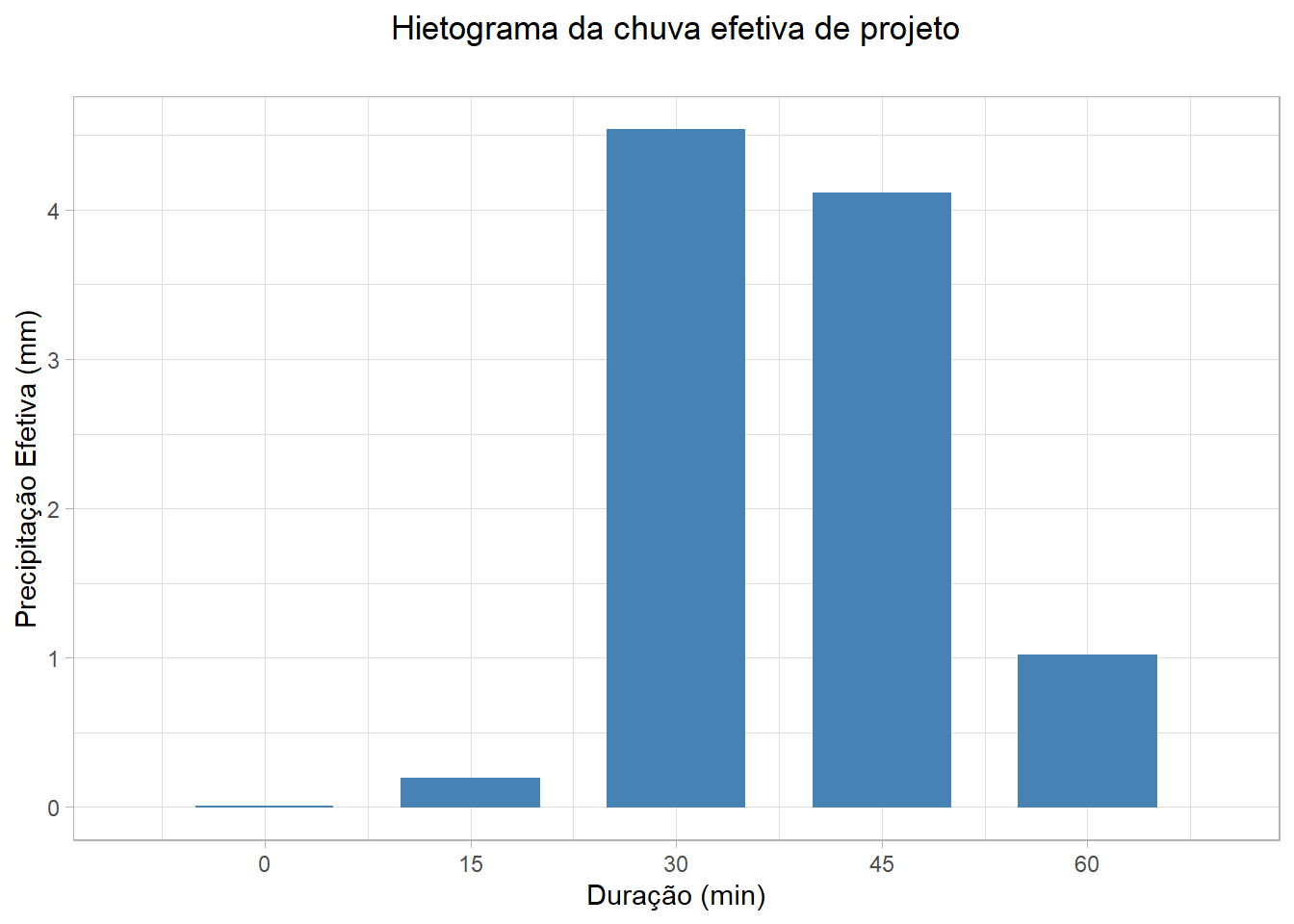
A partir do hietograma da chuva de projeto calculado no exercício anterior, obtenha o hietograma da precipitação efetiva de projeto sabendo que para essa bacia o valor do parâmetro CN é 70.
Para cumprir a demanda, vamos criar uma função que utilizará as funções do método do SCS representadas a seguir:
\[\begin{equation} S = \frac{25400}{CN} - 254 \tag{2.1} \end{equation}\]
\[\begin{equation} Pe = \frac{(P - 0.2S)^2}{(P+0.8S)} \tag{2.2} \end{equation}\]
\[\begin{equation} Pe = \frac{(P - Ia)^2}{(P-Ia + S)} \tag{2.3} \end{equation}\]
CN = 70
PrecipitacaoEfetiva_SCS <- function(P, CN) {
S = 25400/CN - 254 #(1)
Ia = 0.2 * S #(2)
Pe = (P - Ia)^2 / (P - Ia + S) #(3)
if (P > Ia) {
return(Pe)
} else {
return(0)
}
}
Precipitacao_Efetiva_SCS = map2(.x = Hietograma$PrecipitacaoTotalAcumulada_mm,
.y = CN,
.f = PrecipitacaoEfetiva_SCS)
Hietograma$Precipitacao_Efetiva_Acumulada_mm = unlist(Precipitacao_Efetiva_SCS)
Hietograma| Tempo_min | Precipitacao_porcent | PrecipitacaoTotalAcumulada_mm | PrecipitacaoIncremental_mm | Precipitacao_Efetiva_Acumulada_mm | PrecipitacaoEfetivaIncremental_mm |
|---|---|---|---|---|---|
| 0 | 0.00000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 |
| 15 | 44.13793 | 26.39448 | 26.394483 | 0.188338 | 0.188338 |
| 30 | 78.48017 | 46.93114 | 20.536656 | 4.723369 | 4.535031 |
| 45 | 96.17080 | 57.51014 | 10.578997 | 8.833277 | 4.109908 |
| 60 | 100.00000 | 59.80000 | 2.289864 | 9.845561 | 1.012284 |