Seção 3 Hidrograma Unitario
3.1 Questão 1
Considerando os hietogramas de projeto para precipitação total e precipitação efetiva obtidos no Exercício Avaliativo 1, calcule o coeficiente de escoamento superficial nessa sub-bacia.
Usando a relação a seguir, calculamos o C:
\[\begin{equation} C = \frac{Pe}{P} \tag{3.1} \end{equation}\]
ChuvaTotal = max(Hietograma$PrecipitacaoTotalAcumulada_mm)
ChuvaEfetiva = max(Hietograma$Precipitacao_Efetiva_Acumulada_mm)
C = ChuvaEfetiva / ChuvaTotal
round(C, 2) 3.2 Questão 2
Sabendo que a área de drenagem da sub-bacia que contribui para seção do canal em estudo é de 5 km2, calcule a vazão de projeto a ser utilizada na verificação do dimensionamento do canal por meio do Método Racional.
Em posse do coeficiente C, da área (km²) e da intensidade de chuva (mm/h), podemos calcular a vazão de projeto com a relação do método racional a seguir:
\[\begin{equation} Qproj = 0.278 C I A \tag{3.2} \end{equation}\]
A = 5 #km²
Qproj = C * Intensidade(TR, TC, PmediaAnual) * A * 0.278 #Realiza o calculo anterior
round(as.double(Qproj), 2) #Transforma o valor em numerico e arredonda3.3 Questão 3 - REVISADO
Sabendo que a área de drenagem que contribui para a seção do canal em estudo é de 5 km2, obtenha o hidrograma unitário sintético para essa sub-bacia por meio do método do Hidrograma Unitário Triangular do SCS. Dados adicionais: o comprimento do talvegue do córrego principal dentro da sub-bacia é de 3,5 km e suas cotas de início e fim são, respectivamente, 899,0 m e 823,5 m. Utilizar a fórmula de Kirpich para estimativa do tempo de concentração e empregar a mesma discretização temporal do hietograma de projeto (15 minutos).
talvegue = 3.5 #km
cotainicial = 899 #m
cotafinal = 823.5 #m
discretizacao = 15 #min
DuracaoChuva = 1 #hora
DeltaCota = cotainicial - cotafinal
DuracaoChuva = 1 #hora
Area = 5 #km²
HU_SCS <- function(talvegue, DeltaCota, Duracao, A, plot = FALSE){
tc_kirpich = 0.946 * talvegue ^ 1.155 / (DeltaCota) ^ 0.385 #Resultado em horas
tp = 0.61 * tc_kirpich
Tp = tp + (discretizacao/60) / 2 #REVISADO
tb = Tp + 1.67 * Tp
Qpico = 0.208 * A / Tp
DadosHU = data.frame(Tempo = c(0, Tp, tb, tb + 60),
Q = c(0, Qpico, 0, 0 ))
fun_HU <- approxfun(DadosHU)
HU_SCS_Proj = data.frame(Tempo = c(seq(0, tb * 60 + 60, 15), Tp*60, tb*60))
HU_SCS_Proj$Qm3smm = sapply(HU_SCS_Proj$Tempo/60, FUN = fun_HU)
HU_SCS_Proj = HU_SCS_Proj[order(HU_SCS_Proj$Tempo),]
row.names(HU_SCS_Proj) <- 1:nrow(HU_SCS_Proj)
if(plot == FALSE){
return(HU_SCS_Proj)
}
if(plot == TRUE) {
plot <- ggplot(HU_SCS_Proj, aes(x = Tempo, y = Qm3smm)) +
geom_line(color = "steelblue", size = 1) +
labs(
title = "Hietograma sintético triangular do SCS\n",
y = "Vazão (m³/s.mm)",
x = "Duração (min)"
) +
scale_x_continuous(limits = c(0, 160), breaks = seq(0, 160, by = 15)) +
theme_light() +
theme(plot.title = element_text(hjust = 0.5))
return(plot)
}
}
HU_SCS(3.5, 75.5, 1, 5, F)
HU_SCS(3.5, 75.5, 1, 5, T)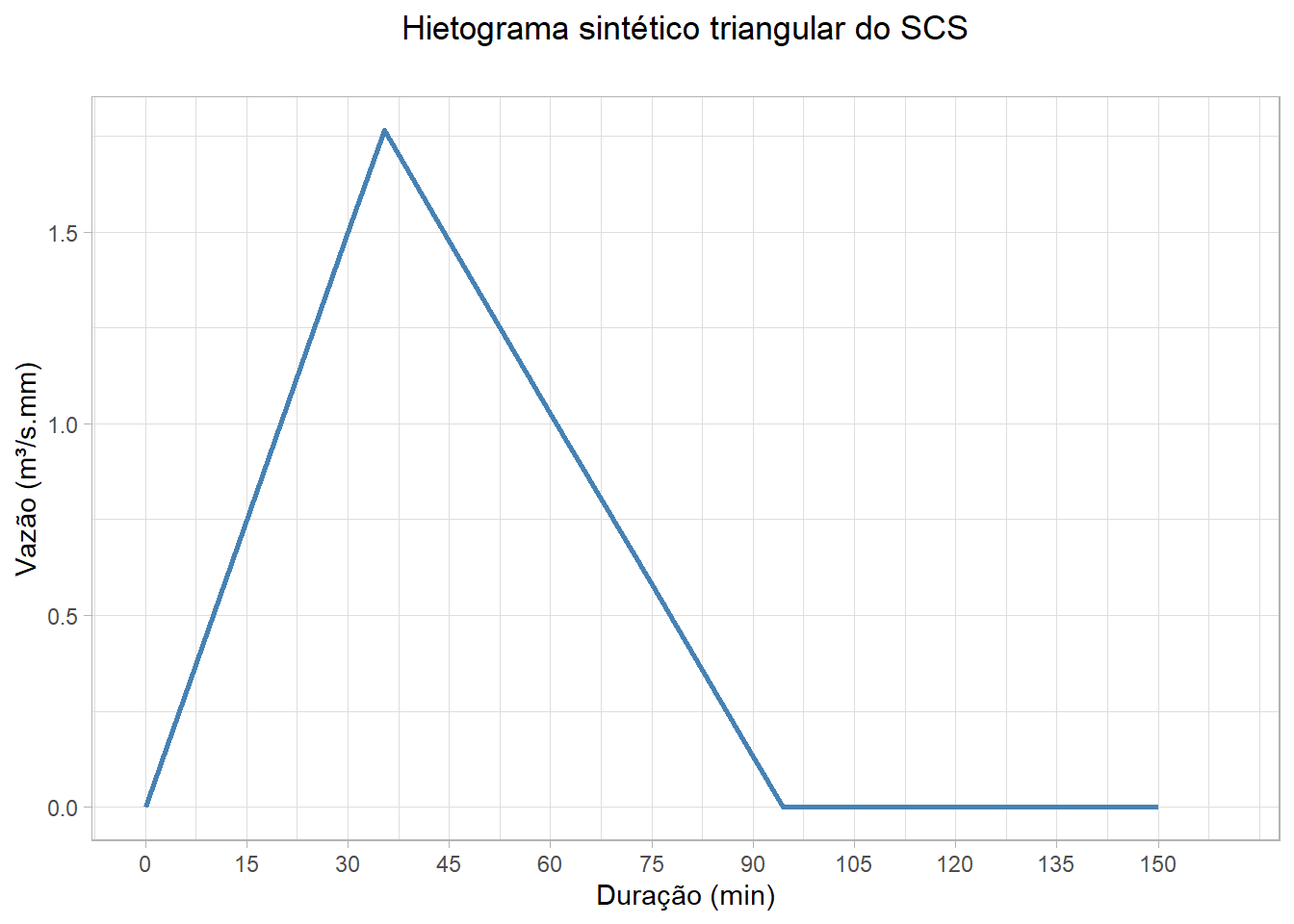
3.4 Questão 4 - REVISADO
Com base no hidrograma unitário sintético obtido para a sub-bacia na questão anterior, calcule a vazão de projeto a ser utilizada na verificação do dimensionamento do canal. Considere que o escoamento de base na sub-bacia é constante e equivale a 0,5 m3.s-1.
Para solucionar a questão, vamos usar a Precipitação Efetiva e as coordenadas do HU para obter o escoamento total.
Convolucao_HU_SCS <- HU_SCS(3.5, 75.5, 1, 5)
Pe <- Hietograma$PrecipitacaoEfetivaIncremental_mm
Convolucao_HU_SCS[3:(length(Pe))] <- 0
l = 1
for (i in 1:(length(Pe))) { #colunas
for(j in 1:(nrow(Convolucao_HU_SCS))) { #linhas
if (j < i) {
Convolucao_HU_SCS[j , i + 2] <- 0 #Adiciona o delay temporal
} else {
Convolucao_HU_SCS[j, i + 2] = Pe[i] * Convolucao_HU_SCS[l, 2]
colnames(Convolucao_HU_SCS)[i + 2] <- paste("HUxPe_", round(Pe[i],2), sep = "")
l = l + 1
}
}
l = 1
}
ConvolucaoTotal_HU_SCS <- Convolucao_HU_SCS
ConvolucaoTotal_HU_SCS[,2:7] <- data.table::shift(Convolucao_HU_SCS[,2:7],
n = 1,
fill = NA,
type="lead") #REVISADO
ConvolucaoTotal_HU_SCS <- ConvolucaoTotal_HU_SCS %>%
mutate(Qtotal = select(., HUxPe_0:HUxPe_1.01) %>% rowSums(na.rm = TRUE))| Tempo | Qm3smm | HUxPe_0 | HUxPe_0.19 | HUxPe_4.54 | HUxPe_4.11 | HUxPe_1.01 | Qtotal |
|---|---|---|---|---|---|---|---|
| 0.00000 | 0.7492000 | 0 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| 15.00000 | 1.4984001 | 0 | 0.1411028 | 0.0000000 | 0.0000000 | 0.0000000 | 0.1411028 |
| 30.00000 | 1.7654099 | 0 | 0.2822056 | 3.3976453 | 0.0000000 | 0.0000000 | 3.6798509 |
| 35.34590 | 1.4766733 | 0 | 0.3324937 | 6.7952906 | 3.0791436 | 0.0000000 | 10.2069279 |
| 45.00000 | 1.0280505 | 0 | 0.2781136 | 8.0061884 | 6.1582871 | 0.7584030 | 15.2009922 |
| 60.00000 | 0.5794277 | 0 | 0.1936209 | 6.6967588 | 7.2556731 | 1.5168060 | 15.6628588 |
| 75.00000 | 0.1308049 | 0 | 0.1091282 | 4.6622406 | 6.0689919 | 1.7870957 | 12.6274564 |
| 90.00000 | 0.0000000 | 0 | 0.0246355 | 2.6277225 | 4.2251933 | 1.4948123 | 8.3723636 |
| 94.37355 | 0.0000000 | 0 | 0.0000000 | 0.5932043 | 2.3813948 | 1.0406788 | 4.0152779 |
| 105.00000 | 0.0000000 | 0 | 0.0000000 | 0.0000000 | 0.5375962 | 0.5865452 | 1.1241415 |
| 120.00000 | 0.0000000 | 0 | 0.0000000 | 0.0000000 | 0.0000000 | 0.1324117 | 0.1324117 |
| 135.00000 | 0.0000000 | 0 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| 150.00000 | NA | NA | NA | NA | NA | NA | 0.0000000 |
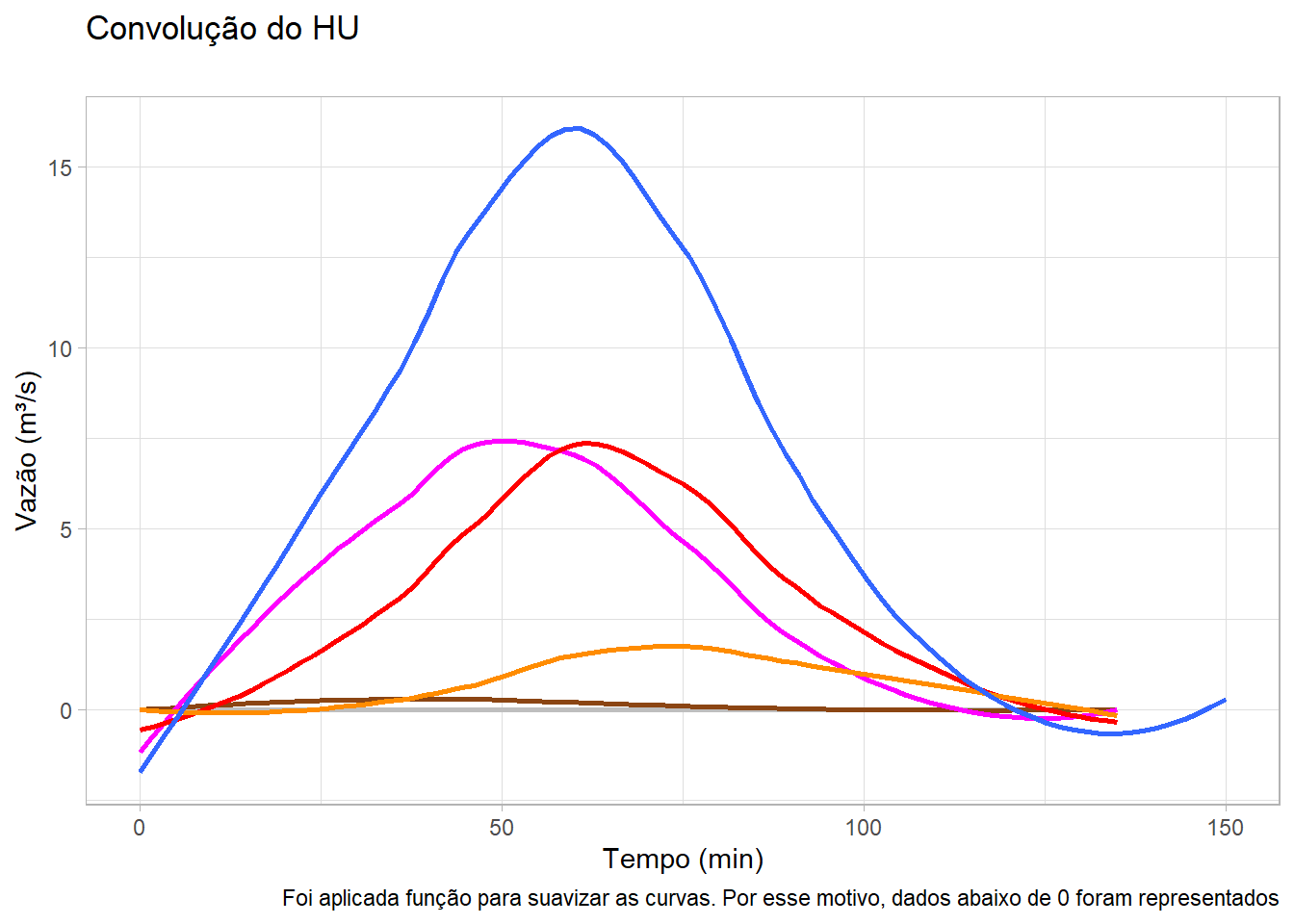
3.5 Questão 5 - REVISADO
Nas questões anteriores você calculou a vazão de projeto a ser utilizada nesse estudo por meio de dois métodos: método racional e método do hidrograma sintético triangular do SCS. Para verificar o funcionamento hidráulico do canal é necessário escolher entre as vazões de projeto calculadas. Qual delas você acredita ser mais apropriada para esse estudo? Justifique sua escolha.
O método racional é amplamente difundido e de fácil aplicação, porém apresenta limitações para médias e grandes bacias hidrográficas. O método do SCS envolve estudos mais aprofundados do uso do solo da bacia hidrográfica e condições de umidade antecedentes. Por tanto, para macrodrenagem (como no caso estudado) é preferencialmente usado o método do SCS e para microdrenagem o método racional.
3.6 Questão 6
Sabendo que o canal em questão possui as características descritas na tabela abaixo, verifique se o mesmo é capaz de escoar a vazão de projeto determinada na questão anterior.
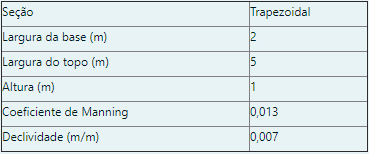
Usando a equação de manning abaixo, vamos verificar qual a vazão máxima suportada pelo canal
\[\begin{equation} Q = \frac{1}{n} A Rh^{2/3}I^{1/2} \tag{3.3} \end{equation}\]
VazaoProjeto = max(ConvolucaoTotal_HU_SCS$Qtotal)
b = 2 #m
B = 5 #m
n = 0.013
I = 0.007 #m/m
h = 1 #m
A = (B + b) / 2
Rh = A / ( b + 2 * h * (sqrt(((B-b)/2)^2 + 1)))
Q = 1 / n * A * I ^ 0.5 * Rh ^ (2/3)
round(Q, 2)## [1] 16.463.7 Questão 7
Caso a capacidade de escoamento do canal não fosse suficiente, quais alternativas poderiam ser utilizadas para ampliá-la?
- Ampliar a seção do canal
- Alterar o uso do solo à montante, visando diminuir o escoamento superficial
- Aumentar a declividade do canal
- A depender dos riscos envolvidos, pode-se justificar a criação de uma bacia de contenção