Seção 4 Hidrologia Estatistica
4.1 Questão 1
A construção da ponte levará 3,5 anos para ser concluída e fixou-se um risco de 7% de que o canteiro de obras seja inundando pelo menos uma vez nesse período. Considerando-se o risco fixado, para qual período de retorno deve ser calculada a vazão de projeto para dimensionamento das ensecadeiras (estruturas que manterão seco o canteiro de obras para a construção dos pilares da ponte)? Arredonde o valor calculado para o múltiplo de 10 superior mais próximo.
Para concluir a resolução desse problema, é necessário construir a relação abaixo (4.1) no R, mas solucionar para o valor de TR
\[\begin{equation} RP = 1 - (1 - \frac{1}{TR})^n \tag{4.1} \end{equation}\]
RP <- function(TR, n) {
rp <- 1 - (1 - 1/TR) ^ n #funcao RP(TR, n)
}
TR <- uniroot(function(TR, n) RP(TR, n) - 0.07, #método de encontrar a raíz
interval = c(1, 10000), #intervalo de TR analisado
n = 3.5) #tempo exposto no problema
round(TR, 10)## [1] 504.2 Questão 2
Com base no período de retorno obtido na questão anterior, calcule qual será a vazão de projeto para o dimensionamento das ensecadeiras.
Nessa e nas próximas questões, sempre que pertinente, considere que a distribuição de probabillidade de Gumbel é a que melhor se ajusta às vazões médias diárias máximas anuais medidas nesse posto fluviométrico.
Primeiramente, vamos importar os dados de vazões médias diárias máximas anuais do posto fluviométrico
Dados_EA_3 <- read_excel("Dados_EA_3.xlsx")
View(Dados_EA_3)| Ano | Q (m3/s) |
|---|---|
| 40 | 576 |
| 41 | 414 |
| 42 | 472 |
| 43 | 458 |
| 44 | 684 |
| 45 | 408 |
| 46 | 371 |
| 47 | 333 |
| 48 | 570 |
| 49 | 502 |
| 50 | 810 |
| 51 | 366 |
| 52 | 690 |
| 53 | 570 |
| 54 | 288 |
| 55 | 295 |
| 56 | 498 |
| 57 | 470 |
| 58 | 774 |
| 59 | 388 |
| 60 | 408 |
| 61 | 448 |
| 62 | 822 |
| 63 | 414 |
| 64 | 515 |
| 65 | 748 |
| 66 | 570 |
| 67 | 726 |
| 68 | 580 |
| 69 | 450 |
| 70 | 478 |
| 71 | 340 |
| 72 | 246 |
| 73 | 568 |
| 74 | 520 |
| 75 | 449 |
| 76 | 357 |
| 77 | 276 |
| 78 | 736 |
| 79 | 822 |
| 80 | 550 |
| 81 | 698 |
| 82 | 585 |
| 83 | 1017 |
| 84 | 437 |
| 85 | 549 |
| 86 | 601 |
| 87 | 288 |
| 88 | 481 |
| 89 | 927 |
| 90 | 827 |
| 91 | 424 |
| 92 | 603 |
| 93 | 633 |
| 94 | 695 |
| 95 | 296 |
| 96 | 427 |
O próximo passo é calcular os parâmetros da distribuição de probabilidade de Gumbel:
\[\begin{equation} \alpha = 0,7797 S \tag{4.2} \end{equation}\]
\[\begin{equation} \beta = \bar{x} - 0,45 S \tag{4.3} \end{equation}\]
media <- mean(Dados_EA_3$`Q (m3/s)`) #Media
S <- sd(Dados_EA_3$`Q (m3/s)`) #Desvio Padrao
alfa <- 0.7797 * S
beta = media - 0.45 * S
gumbel <- function(alfa, beta, TR) {
gumbel <- beta + alfa * (- log(- log(1 - 1 / TR)))
return(round(gumbel,2))
}
gumbel(alfa , beta, 50)## [1] 990.46Encontrando o valor de \[990,46 m^{3}/s\]
4.3 Questão 3
O tabuleiro da ponte deve ter cota mínima suficiente para permitir a passagem da cheia bicentenária. Qual o valor da vazão de projeto para dimensionamento da ponte?
gumbel(alfa , beta, 200)## [1] 1181.76A vazão para a ponte deve ser de \[1181,76 m^{3}/s\]
4.4 Questão 4
Sabendo que a equação da curva chave desse posto fluviométrico é Q=10+40.h+15.h2, onde Q representa a vazão em m3/s e h é a leitura da régua linimétrica em metros. Determine a cota altimétrica mínima do tabuleiro da ponte, sabendo que o zero da régua está na cota 731,350 m.
curva_chave <- function(h){
Q = 10 + 40 * h + 15 * h ^ 2
}
TR <- uniroot(
function(h) curva_chave(h) - 1181.76,
interval = c(0, 50)
)
cota_minima_ponte = TR$root + 731.350A cota mínima para a ponte estudada é de \[738.96 m\]
4.5 Questão 5
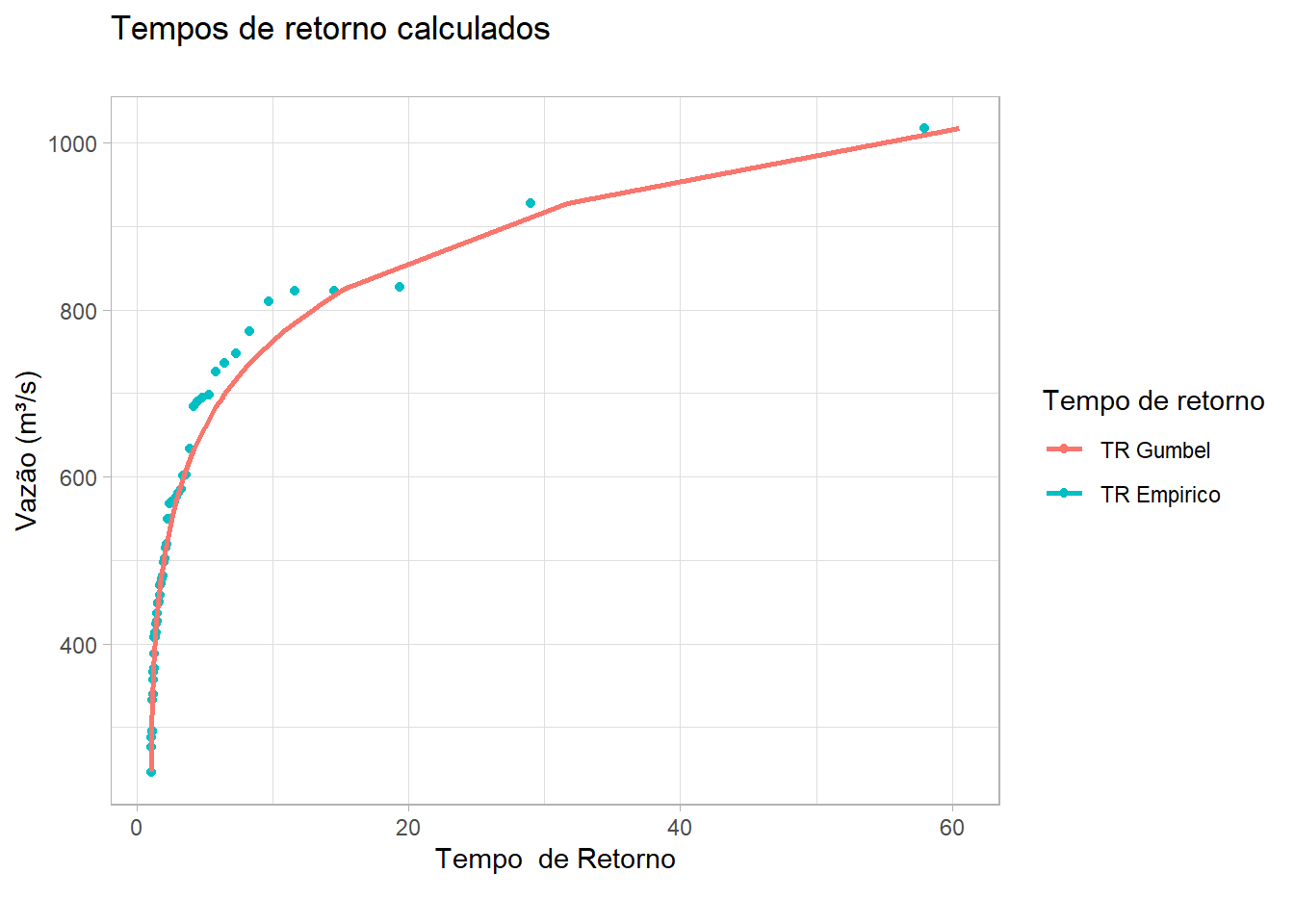
Em um gráfico, plote as vazões observadas e respectivos tempos de retorno empíricos (calculados via posição de plotagem) e a curva da distribuição de probabilidades teórica utilizada. Anexe a planilha com esse gráfico, assim como a memória de cálculos das demais questões.
Plotagem <- Dados_EA_3 %>%
arrange(desc(`Q (m3/s)`)) %>%
rowid_to_column("Numero_da_linha") %>%
mutate(Posicao_plotagem_Empirica = Numero_da_linha/(nrow(Dados_EA_3) + 1),
TR_Empirico = 1/Posicao_plotagem_Empirica) %>%
mutate(y = (`Q (m3/s)` - beta)/alfa,
TR_Gumbel = 1/(1-exp(-exp(-(y)))),
n_gumbel = seq(nrow(Dados_EA_3), 1, - 1))%>%
select( -y)
ggplot(Plotagem, mapping = aes(y = `Q (m3/s)`)) +
geom_point(aes(x = TR_Empirico, color = "red")) +
geom_line(aes(x = TR_Gumbel, colour = "green"), size = 1) +
scale_color_discrete(name = "Tempo de retorno", labels = c("TR Gumbel", "TR Empirico")) +
labs(
title = "Tempos de retorno calculados \n",
y = "Vazão (m³/s)",
x = "Tempo de Retorno",
caption = ""
) +
theme_light()