Seção 5 Analise Hidraulica
Para fins de organização, as funções a serem utilizadas ao longo das resoluções serão demonstradas abaixo:
energia <- function(y, Q, B, g = 9.81){
energia <- y + (Q / B) ^ 2 /(2 * g * y ^ 2)
}
yc <- function(Q, B, g = 9.81){
yc <- ((Q / B) ^ 2 / g) ^ ( 1 / 3)
}
manning <- function(n, B, y, i){
A = B * y
P = B + 2 * y
Rh = A / P
Q = (1 / n)* A * Rh ^ (2/3) * i ^ 0.5
return (Q)
}
yn <- function(n, B, i, Q){
uniroot(function(n, B, y, i) manning(n, B, y, i) - Q,
interval = c(0,5000),
n = n,
B = B,
i = i)$root
}
y_DadoAEnergia <- function(energia, Q, B, inter1, inter2) {
uniroot(function(y, Q, B, g = 9.81) energia(y, Q, B, g = 9.81) - energia,
interval = c(inter1*0.99, inter2),
Q = Q, B = B)$root
}Para todas as questões a seguir considere a ponte que será construída na seção fluvial do Exercício Avaliativo 3, assim como a vazão de dimensionamento que foi calculada nesse exercício. Despreze as perdas de carga localizadas e considere também a aceleração da gravidade g = 9,81 m/s2. A planilha com a memória de cálculo deverá ser anexada na última questão.
5.1 Questão 1
A seção fluvial onde será construída a ponte tem forma aproximadamente retangular com largura de 50 m. O revestimento é em concreto (n = 0,018) e a declividade I = 0,001 m/m. Após o término da obra, a largura do rio na seção da ponte será reduzida em 10 m (ou seja, passará para 40 m) devido à construção das bases de dois pilares de sustentação da ponte nas margens do rio. Sob essas condições, qual será a profundidade do escoamento na seção da ponte?
Dicas para resolução:
· A alteração na largura da seção fluvial faz com que esse problema não possa ser analisado considerando-se apenas a ocorrência do escoamento permanente uniforme.
· Calcule a profundidade normal nesse canal para a vazão de dimensionamento do exercício avaliativo 3. Calcule as profundidades críticas correspondentes às seções de diferentes larguras e as energias específicas associadas à profundidade normal e às profundidades críticas.
· Verifique: qual é o regime de escoamento (subcrítico, crítico ou supercrítico)?
· Esboce o gráfico da energia específica com as duas curvas (B = 50 m e B = 40 m) e represente as profundidades calculadas e as respectivas energias específicas. Analise o gráfico e avalie qual será o efeito do estreitamento causado pelos pilares da ponte. Responda à questão.
#Dados de entrada
g = 9.81 #m/s²
Q = 1181.76 #m³/s
n = 0.018
i = 0.001 #m/m
Bi = 50 #m
Bf = 40 #m
#Parametros Hidraulicos
#Seco 1 - 50m
yc1 <- yc(Q, Bi)
yn1 <- yn(n, Bi, i, Q)
energia_yc1 <- energia(yc1, Q, Bi)
energia_yn1 <- energia(yn1, Q, Bi)
#Parametros Hidraulicos
#Secao 2 - 40m
yc2 <- yc(Q, Bf)
energia_yc2 <- energia(yc2, Q, Bf)
#Grafico da energia especifica
Dados_y = data.frame(y = seq(2,
7,
by = 0.001))
Dados_energia <- Dados_y %>%
mutate(energia_y1 = energia(y, Q, Bi),
energia_y2 = energia(y, Q, Bf))
ggplot(Dados_energia, aes(y = y)) +
geom_path(aes(x = energia_y1), color = "red") +
geom_path(aes(x = energia_y2), color = "blue") +
geom_vline(xintercept = c(energia_yn1, energia_yc2), linetype="dotted") +
stat_function(fun = function(x) y_DadoAEnergia(energia_yc2, Q, Bi, yc1, 200), linetype="dotted") +
stat_function(fun = function(x) yn1, linetype="dotted") +
labs(
title = "Curvas de Energia \n",
y = "Profundidade (m)",
x = "Energia (m)",
caption = ""
) +
theme_light() +
annotate("segment", x = energia_yc2, xend = energia_yc2, y = y_DadoAEnergia(energia_yc2, Q, Bi, yc1, 200), yend = yc2, colour = "grey", size=2, alpha=0.7, arrow=arrow()) +
annotate("text", x = 9, y = 6.1, label = "Profundidade adquirida pela seção 1") +
annotate("text", x = 9, y = 5.4, label = "Profundidade normal da seção 1") +
annotate("text", x = 6, y = 3.5, label = "Energia inicial da seção 1", angle = 90) + annotate("text", x = 6.5, y = 3.5, label = "Energia Final da seção 1", angle = 90) 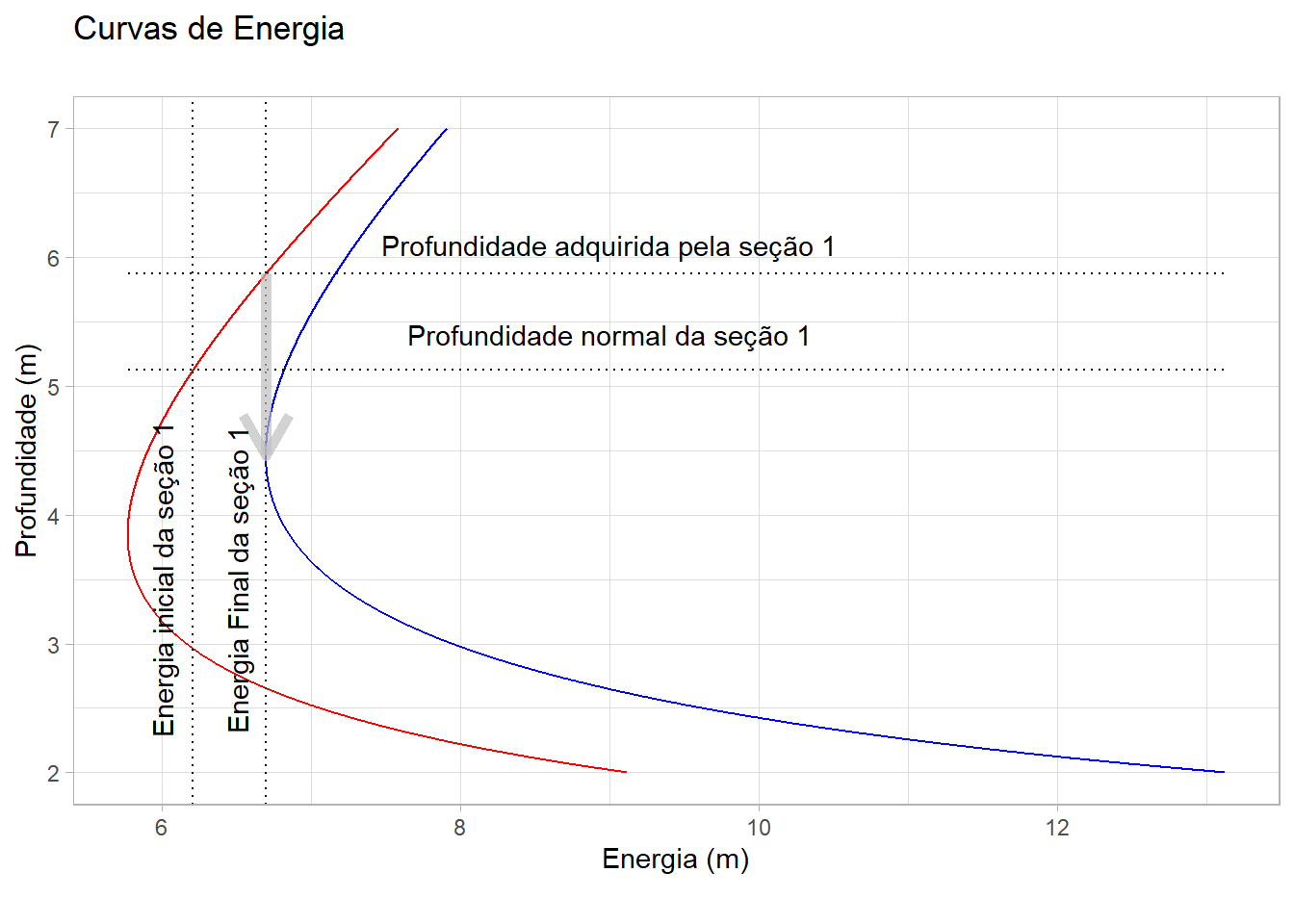
Como podemos analisar pelo gráfico, haverá uma elevação da altura de água na seção 1 para que a energia se iguale à mínima energia da curva da seção 2.
Por isso, a altura d’agua na seção 2 será a crítica que é igual a 4.46 m
5.2 Questão 2
Qual será a profundidade do escoamento a montante da ponte?
· Dica: analisando o gráfico da energia específica, identifique qual será o valor da energia específica a montante da seção da ponte. Utilize a equação da energia específica para obter a profundidade do escoamento correspondente a esse valor de energia específica.
y_montante_ponte = y_DadoAEnergia(energia_yc2, Q, Bi, yc1, 10)
y_montante_ponteA profundidade à montante da ponte será de 5.87 m
5.3 Questão 3
Qual será a profundidade do escoamento a jusante da ponte?
· Dica: analisando o gráfico da energia específica, identifique qual será o valor da energia específica a jusante da seção da ponte. Utilize a equação da energia específica para obter a profundidade do escoamento correspondente a esse valor de energia específica.
y_DadoAEnergia(energia_yc2, Q, Bi, 0, yc1)## [1] 2.653854A profundidade à jusante da ponte será de 2.65 m
5.4 Questão 4
Explique porque o ocorrerá um ressalto hidráulico em algum ponto a jusante da seção onde será construída a ponte.
O ressalto hidráulico é a única forma de passagem do regime supercritico para o subcritico. E como a declividade do canal se mantém (abaixo da crítica), esse regime tenderá a se formar.
5.5 Questão 5
Qual o valor da profundidade conjugada de jusante do ressalto?
yn2 <- yn(n, Bi, i, Q)Considerando que a profundidade conjugada de jusante é igual ao yn do canal após o alargamento, o valor desta é de 5.13 m
5.6 Questão 6
Qual o valor da profundidade conjugada de montante do ressalto?
U2 = Q /(Bi * yn2)
Fr2 = U2/(g * yn2) ^ 0.5
y1 = ((1 / 2) * (sqrt(1 + 8 * Fr2 ^ 2) -1)) * yn2
y1## [1] 2.802986Obtemos o valor de 2.8 m para a altura conjugada de montante do ressalto
5.7 Questão 7
Qual o valor do comprimento do ressalto?
Lr = 6.9 * (yn2 - y1)
Lr## [1] 16.02199O comprimento do ressalto é de 16.02 m
5.8 Questão 8
Elabore um esboço qualitativo do perfil da linha d’água desde o trecho a montante onde ocorre escoamento permanente uniforme (efeito do estreitamento causado pela ponte já não ocorre) até o trecho a jusante onde o escoamento permanente uniforme é reestabelecido. Indique os tipos de curva de remanso existentes no trecho, o ressalto, as profundidades características calculadas nas questões anteriores e os controles hidráulicos.
Caso elabore o perfil a mão, tire uma foto e anexe a essa questão.
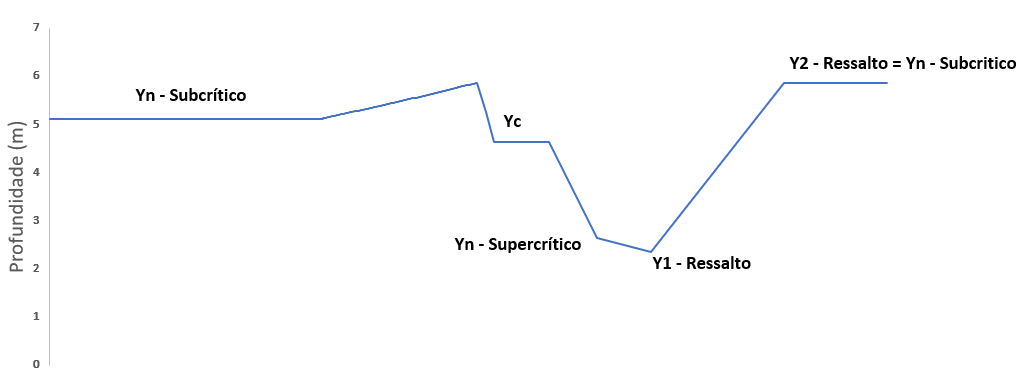
Y1 foi retratado abaixo do calculado
5.9 Questão 9
Utilizando o Step Method, calcule do comprimento da curva de remanso a montante da seção onde será construída a ponte em metros. Utilize como intervalo de discretização Δy = 0,01 m.
x = -0.01
y_montante_ponte = y_DadoAEnergia(energia_yc2, Q, Bi, yc2, 20
)
df <- data.frame(y = y_montante_ponte, Energia = energia(y_montante_ponte, Q, Bi))
variaveis <- c("Umedio", "RhMedio", "Sf", "DeltaX")
df[,variaveis] <- 0
yteste1 = 1
i = 2
while(abs(yteste1 - yn1) > 0.01){
df[i,"y"] = df[i-1,"y"] + x
df[i,"Umedio"] = (Q/(df[i,"y"]*Bi) + Q/(df[i-1,"y"]*Bi))/2
df[i, "Energia"] = energia(df[i,"y"], Q, Bi)
df[i, "RhMedio"] = (df[i,"y"] * Bi/ (Bi + 2 * df[i,"y"]) + df[i-1,"y"] * Bi/(Bi + 2 * df[i-1,"y"]))/2
df[i, "Sf"] = (n ^ 2 * df[i,"Umedio"] ^ 2)/(df[i, "RhMedio"] ^ (4/3))
df[i, "DeltaX"] = (df[i, "Energia"] - df[i-1, "Energia"]) / (0.001 - df[i, "Sf"])
yteste1 = df[i,"y"]
i = i + 1
}
knitr::kable(df, caption = "Step Method")
sum(df$DeltaX, na.rm = T)| y | Energia | Umedio | RhMedio | Sf | DeltaX |
|---|---|---|---|---|---|
| 5.870262 | 6.696499 | 0.000000 | 0.000000 | 0.0000000 | 0.00000 |
| 5.860262 | 6.689321 | 4.029695 | 4.750698 | 0.0006588 | -21.03624 |
| 5.850262 | 6.682157 | 4.036577 | 4.744135 | 0.0006623 | -21.20959 |
| 5.840262 | 6.675009 | 4.043483 | 4.737568 | 0.0006658 | -21.38782 |
| 5.830262 | 6.667875 | 4.050413 | 4.730997 | 0.0006693 | -21.57114 |
| 5.820262 | 6.660755 | 4.057366 | 4.724421 | 0.0006728 | -21.75977 |
| 5.810262 | 6.653651 | 4.064343 | 4.717842 | 0.0006764 | -21.95393 |
| 5.800262 | 6.646562 | 4.071344 | 4.711258 | 0.0006800 | -22.15388 |
| 5.790262 | 6.639487 | 4.078369 | 4.704669 | 0.0006836 | -22.35988 |
| 5.780262 | 6.632428 | 4.085419 | 4.698077 | 0.0006873 | -22.57218 |
| 5.770262 | 6.625385 | 4.092493 | 4.691480 | 0.0006909 | -22.79110 |
| 5.760262 | 6.618356 | 4.099592 | 4.684879 | 0.0006946 | -23.01694 |
| 5.750262 | 6.611343 | 4.106715 | 4.678273 | 0.0006984 | -23.25002 |
| 5.740262 | 6.604346 | 4.113863 | 4.671664 | 0.0007021 | -23.49070 |
| 5.730262 | 6.597365 | 4.121036 | 4.665050 | 0.0007059 | -23.73936 |
| 5.720262 | 6.590399 | 4.128234 | 4.658431 | 0.0007097 | -23.99638 |
| 5.710262 | 6.583449 | 4.135457 | 4.651809 | 0.0007136 | -24.26221 |
| 5.700262 | 6.576516 | 4.142705 | 4.645182 | 0.0007174 | -24.53728 |
| 5.690262 | 6.569598 | 4.149979 | 4.638551 | 0.0007213 | -24.82210 |
| 5.680262 | 6.562697 | 4.157279 | 4.631915 | 0.0007252 | -25.11718 |
| 5.670262 | 6.555812 | 4.164604 | 4.625275 | 0.0007292 | -25.42308 |
| 5.660262 | 6.548944 | 4.171955 | 4.618631 | 0.0007332 | -25.74040 |
| 5.650262 | 6.542092 | 4.179333 | 4.611982 | 0.0007372 | -26.06980 |
| 5.640262 | 6.535258 | 4.186736 | 4.605329 | 0.0007412 | -26.41195 |
| 5.630262 | 6.528440 | 4.194165 | 4.598672 | 0.0007453 | -26.76763 |
| 5.620262 | 6.521639 | 4.201621 | 4.592010 | 0.0007494 | -27.13763 |
| 5.610262 | 6.514855 | 4.209104 | 4.585345 | 0.0007535 | -27.52284 |
| 5.600262 | 6.508088 | 4.216613 | 4.578674 | 0.0007577 | -27.92420 |
| 5.590262 | 6.501339 | 4.224149 | 4.572000 | 0.0007619 | -28.34275 |
| 5.580262 | 6.494607 | 4.231712 | 4.565321 | 0.0007661 | -28.77961 |
| 5.570262 | 6.487893 | 4.239302 | 4.558637 | 0.0007703 | -29.23600 |
| 5.560262 | 6.481197 | 4.246920 | 4.551949 | 0.0007746 | -29.71324 |
| 5.550262 | 6.474518 | 4.254565 | 4.545257 | 0.0007790 | -30.21279 |
| 5.540262 | 6.467858 | 4.262237 | 4.538561 | 0.0007833 | -30.73626 |
| 5.530262 | 6.461216 | 4.269937 | 4.531860 | 0.0007877 | -31.28537 |
| 5.520262 | 6.454592 | 4.277665 | 4.525154 | 0.0007921 | -31.86207 |
| 5.510262 | 6.447986 | 4.285421 | 4.518445 | 0.0007966 | -32.46847 |
| 5.500262 | 6.441399 | 4.293206 | 4.511731 | 0.0008010 | -33.10691 |
| 5.490262 | 6.434830 | 4.301018 | 4.505012 | 0.0008056 | -33.77998 |
| 5.480262 | 6.428280 | 4.308859 | 4.498289 | 0.0008101 | -34.49059 |
| 5.470262 | 6.421750 | 4.316729 | 4.491562 | 0.0008147 | -35.24193 |
| 5.460262 | 6.415238 | 4.324627 | 4.484830 | 0.0008193 | -36.03761 |
| 5.450262 | 6.408746 | 4.332555 | 4.478094 | 0.0008240 | -36.88164 |
| 5.440262 | 6.402272 | 4.340511 | 4.471353 | 0.0008287 | -37.77857 |
| 5.430262 | 6.395819 | 4.348497 | 4.464608 | 0.0008334 | -38.73351 |
| 5.420262 | 6.389385 | 4.356513 | 4.457859 | 0.0008381 | -39.75224 |
| 5.410262 | 6.382971 | 4.364557 | 4.451105 | 0.0008429 | -40.84138 |
| 5.400262 | 6.376577 | 4.372632 | 4.444347 | 0.0008478 | -42.00844 |
| 5.390262 | 6.370203 | 4.380737 | 4.437584 | 0.0008527 | -43.26210 |
| 5.380262 | 6.363849 | 4.388871 | 4.430817 | 0.0008576 | -44.61232 |
| 5.370262 | 6.357515 | 4.397036 | 4.424045 | 0.0008625 | -46.07068 |
| 5.360262 | 6.351202 | 4.405232 | 4.417269 | 0.0008675 | -47.65070 |
| 5.350262 | 6.344910 | 4.413458 | 4.410488 | 0.0008725 | -49.36821 |
| 5.340262 | 6.338638 | 4.421715 | 4.403703 | 0.0008776 | -51.24196 |
| 5.330262 | 6.332388 | 4.430002 | 4.396914 | 0.0008827 | -53.29422 |
| 5.320262 | 6.326159 | 4.438321 | 4.390119 | 0.0008879 | -55.55176 |
| 5.310262 | 6.319951 | 4.446671 | 4.383321 | 0.0008931 | -58.04692 |
| 5.300262 | 6.313764 | 4.455053 | 4.376518 | 0.0008983 | -60.81927 |
| 5.290262 | 6.307600 | 4.463466 | 4.369711 | 0.0009036 | -63.91765 |
| 5.280262 | 6.301457 | 4.471911 | 4.362899 | 0.0009089 | -67.40308 |
| 5.270262 | 6.295336 | 4.480389 | 4.356082 | 0.0009142 | -71.35286 |
| 5.260262 | 6.289237 | 4.488898 | 4.349261 | 0.0009196 | -75.86629 |
| 5.250262 | 6.283160 | 4.497440 | 4.342435 | 0.0009250 | -81.07321 |
| 5.240262 | 6.277106 | 4.506014 | 4.335605 | 0.0009305 | -87.14661 |
| 5.230262 | 6.271075 | 4.514621 | 4.328771 | 0.0009361 | -94.32225 |
| 5.220262 | 6.265066 | 4.523261 | 4.321932 | 0.0009416 | -102.92995 |
| 5.210262 | 6.259080 | 4.531934 | 4.315088 | 0.0009472 | -113.44572 |
| 5.200262 | 6.253118 | 4.540641 | 4.308240 | 0.0009529 | -126.58278 |
| 5.190262 | 6.247179 | 4.549380 | 4.301388 | 0.0009586 | -143.46042 |
| 5.180262 | 6.241263 | 4.558154 | 4.294530 | 0.0009644 | -165.94093 |
| 5.170262 | 6.235372 | 4.566962 | 4.287669 | 0.0009701 | -197.36879 |
| 5.160262 | 6.229504 | 4.575804 | 4.280802 | 0.0009760 | -244.41152 |
| 5.150262 | 6.223660 | 4.584680 | 4.273931 | 0.0009819 | -322.55094 |
| 5.140262 | 6.217841 | 4.593590 | 4.267056 | 0.0009878 | -477.83829 |
| 5.130262 | 6.212046 | 4.602535 | 4.260176 | 0.0009938 | -935.89885 |
| 5.125013 | 6.209014 | 4.609375 | 4.254928 | 0.0009984 | -1899.11513 |
## [1] -7109.858