Chapter 1 Introduction

Welcome to “Mathematics of Financial Derivatives” a 15 credit module that is part of the MSc Quantitative Risk Management with Machine Learning programme and is also open as an option to students from MSc Mathematical Finance and MSc Mathematics/Statistics with Financial Modeling. The pre-requisites for this module are kept to a minimum. I will assume that you have some familiarity with standard calculus; you will know that if you are supplied with a function $f(x)$ then its derivative, often denoted as $f^{\prime}(x),$ is interpreted as the slope of its graph and that the integral of a function is the area under the graph of the function. You will have used calculus before to find the maximum or minimum of a function; the famous recipe of finding the solutions $x^{*}$ of $f^{\prime}(x)=0$ (the so-called stationary points) and then testing their nature by finding the sign of $f^{\prime \prime}(x^{*})$ (positive indicating a local minimum and negative indicating a local maximum). You will be equipped with some tools and rule that allow you to differentiate functions (eg. the chain, product, quotient rules) and to integrate them (by substitution, by parts, by parial fractions). Hopefully you will have encountered derivatives in their role of providing the so called Taylor-approximations of a function; this application will be used in this course and it will be reviewed again when needed. Put simply, if we are interested in the behaviour of a function $f(x)$ in a region very close to an anchor point $'a'$ say, then we can approximate this using the tangent line $\ell(x)$ and we write

\[ f(x)\approx \ell(x)=f(a)+f^{\prime}(a)(x-a),\quad {\rm{for}}\,\, x\,\,{\rm{close}}\,\,{\rm{to}}\,\,a. \]

The straight line $\ell(x)$ is often referred to as the first order Taylor approximation of $f(x)$ at the location $'a'.$ If we want an improved approximation we can add a quadratic correction to the above to produce $q(x)$ the so-called second order Taylor approximation of $f(x)$ at the location $'a'$ as:

\[ \begin{aligned} f(x)\approx q(x)&= \ell(x)+\frac{1}{2}f^{\prime\prime}(a)(x-a)^{2}\\ &=f(a)+f^{\prime}(a)(x-a)+\frac{1}{2}f^{\prime\prime}(a)(x-a)^{2},\quad {\rm{for}}\,\, x\,\,{\rm{close}}\,\,{\rm{to}}\,\,a. \end{aligned} \]

It is possible to continue, i.e., we could add a cubic and/or quartic etc… corrections to provide third, fourth etc… Taylor approximations but, given we are only interested in the behaviour very close to the anchor point $'a'$ these terms hardly add any value because the sizes of $(x-a)^{3},(x-a)^{4},\ldots$ will be very, very small. I expect that you have seen the above before but it is worth my while mentioning it very early on because, as I’ve alluded to, it will be useful in this course. You may also be familiar with calculus in higher dimensions, if not don’t worry, it will be reviewed as and when it is needed. That said I can easily convey the main concept that you will need by considering a function of two variables $z=f(x,y),$ visually this is a surface over the $(x,y)$ plane. In this case, we can compute so-called partial derivatives. If we imagine ourselves standing on the surface corresponding to some anchor point $(a,b)$ say, then we know that the slope can be different in different directions. The evaluation at $(a,b)$ of the partial derivative with respect to $x,$ which we write as $f_{x}(a,b)=\frac{\partial f}{\partial x}(a,b)$ tells us the slope of the surface in the $x-$direction. This is nicely illustrated in the image below - the green curve is the graph of $f(x,b)$ (the remains when we slice the surface by the plane $y=b,$) and the partial derivative is the slope of the tangent line of this green curve at $x=a.$

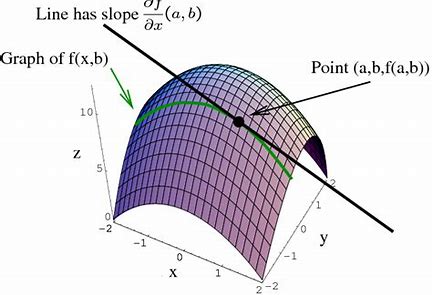
If you feel the need to refresh your knowledge on partial derivatives here is a nice video for you to refer to.

Youtube clip with more examples

$\,$
The key conept that we will need is the extension of the first order Taylor approximation ( a line for a function of $x$) to two variables. Once again, we fix an anchor point $P=(a,b)$ say then provided we do not move too far away from this anchor point we can approximate the surface nearby with the flat tangent plane. This is nicely illustrated in the picture below

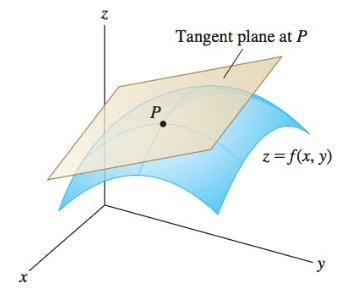
Introducing the mathematical equation of the tangent plane (first order Taylor approximation) we can write

\[ f(x,y)\approx \ell(x,y)=f(a,b)+f_{x}(a,b)(x-a)+f_{y}(a,b)(y-b),\quad {\rm{for}}\,\, (x,y)\,\,{\rm{close}}\,\,{\rm{to}}\,\,(a,b). \]

Hopefully this ‘light’ review of calculus exactly matches what you already know; if so then you are well equipped to take this course on.

Of course the financial products that we will be grappling with are, by their nature, ‘risky’! By ‘risky’ I mean that we cannot be certain how they will evolve in the future. Mathematically, this means they are examples of what we call random variables. If you have a background in probability theory you will understand what might be involved here; even if not I’m sure you will be aware that when dealing with a random quantity (e.g. the outcome of a repeated experiment) then we speak of its expected value (mean), its standard deviation and its associated distribution (how likelihood of the random outcomes are distributed). Also, when there are random quantities have some interdependence we speak of their correlation and thier joint distribution. We will spend time developing all of this background probability as we and when we need it, so there is no need for any alarm if these notions are a little vague now.

Now is the right time to make a start. Here’s the plan for this first lecture:

$\diamond$ Introduce the derivative products that we are going to be investigating.

$\diamond$ The idea of arbitrage which will play a key role in how we are able to assign a value to the derivative products. This is captured in the so-called “Absence of Arbitrage” result which will be presented and proved.

$\diamond$ The notion of the risk free bank. This is the fall back investment for those who do not wish to open themselves to any financial risk, they can place it in the risk free account, safe in the knowledge that it will grow at a rate that we can be certain of (usually a pretty low rate).

$\diamond$ A non-mathematical exploration of the properties of various financial derivatives. Here we use appeal to the absence of arbitrage result alone to derive some features that our financial derivatives must possess.

1.1 Financial Derivatives

Suppose that we have invested in an asset $S$ (for example this could be a number of shares in Apple stock, a certain amount of Japanese Yen, a number of barrels of oil ). We will use $t=0$ to denote todays date and, equipped with this asset, we look ahead into the future, lets say the future date $T$ is particularly important for us; e.g. this could be 1 year ahead, 6 months ahead (1/2 year), 3months ahead (1/4 year), 201 days ahead (201/365 year). Observe here that, in order to be consistent in measuring our future investment horizon we will always quote it in years.

Back to our financial future… Supoose that $T$ is important to us because we have calculated that if, on that future date $T,$ the value of our asset drops below a certain level $K$ say, then we will be in financial difficulty. The problem for us is that even if today’s (at $t=0$) value of the asset $S_{0}$ is currently trading above $K$ we simply have no way of being certain that the future value, whose unknown value we will denote by $S_{T},$ will stay above $K$ too. Given that there are potential ‘financial difficulties’ lying ahead we should not just bury our head in the sand and hope for the best… We should look to the financial markets for some insurance against this outcome.

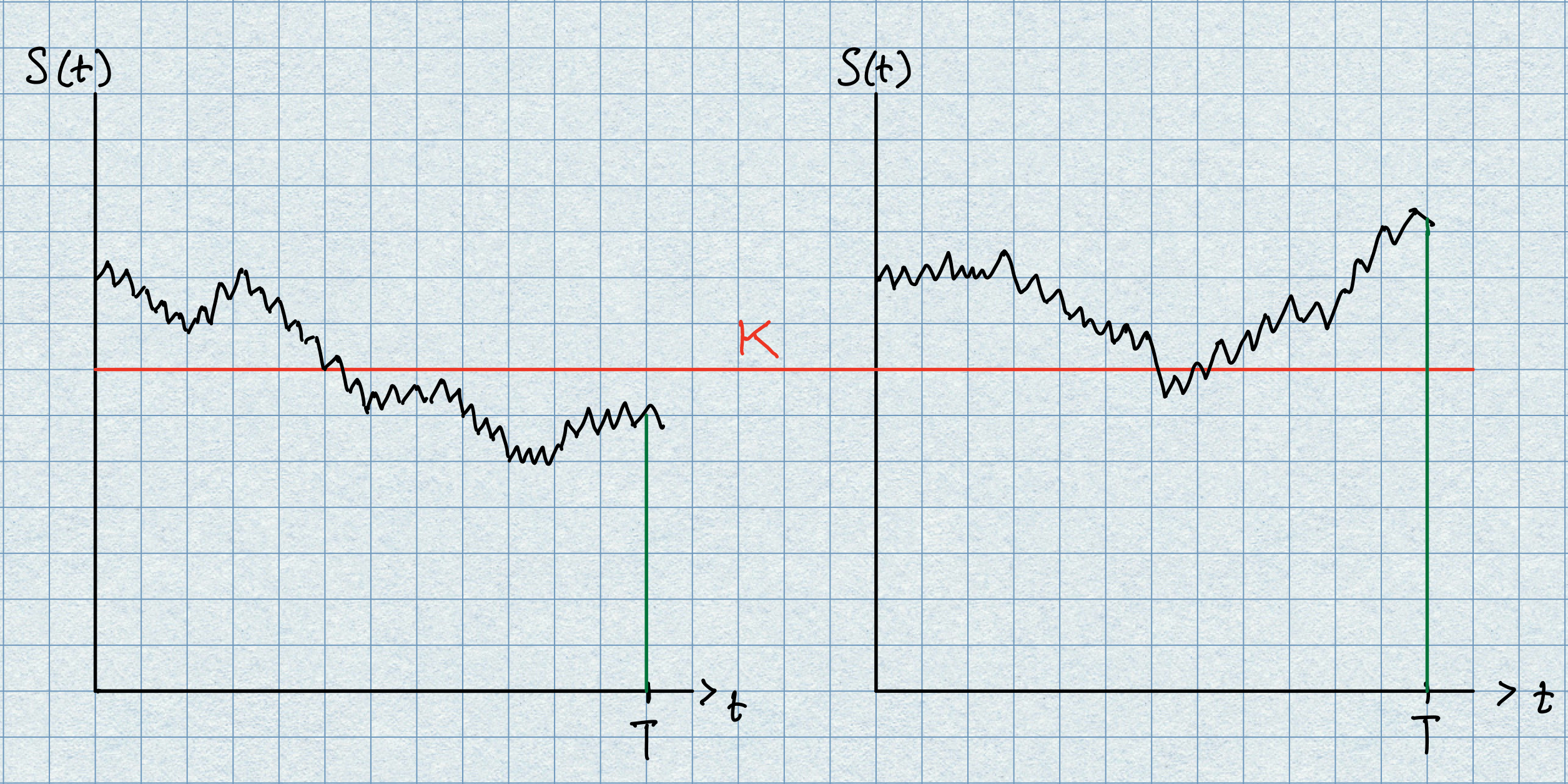
The picture above shows us two possible path scenarios for our asset. The scenario on the right is just as we would like it to be, at the crucial time $T$ the price of the asset has stayed above the critical level $K.$ The scenario on the left is the disaster situation - the asset price has fell below $K$ and we’re in ‘financial trouble.’

One way to gain some financial security would be to explore the financial markents for a product that is designed to shield us from the disastrous situation. This product would allow us the option to sell the asset at $T$ if its price (sadly) dropped below $K.$ Note, the ${\rm{if}}$ is crucual here, because in the ideal scenario where the asset price remains above $K$ then we simply keep hold of it (celebrating that it didn’t drop). Such a product exists and is known as a European Put Option. Here is its formal definition

Definition 1.1 (European Put Option) A European put option is a contract with the conditions: The holder MAY:

$\diamond$ at a prescribed future date $T$ (the maturity/expiry date of the option)

$\diamond$ SELL a prescribed asset $S$ (the underlying of the option)

$\diamond$ for a prescribed amount $K$ (the strike price of the option)

Let’s suppose we bought this product at $t=0$ and consult the picture above again with the two possible scenarios. On the right hand picture all is well at time $T$ and we certainly would not choose to exercise our right to sell the asset for $K$ when its actual value is worth so much more. The scanario on the left hand side is now longer such a problem now - yes, the asset has dropped below the danger level $K$ BUT armed with our put option, this time we do exercise our right to sell the asset for $K$ even though it is worth much less. The put option has given us protection against the fall in the asset value. The big question is…

Question: How much should we pay for the European put option?

Answering questions like this, for the put option and other financial derivatives, will be the focus of much of our time in this course.

The put option allows us the opportunity to BUY the asset for a certain fixed strike price at time $T$. The product that allows us to SELL the asset for a certain fixed strike price at time $T$ is called a European Call Option. For completeness we give its definition here.

Definition 1.2 (European Call Option) A European call option is a contract with the conditions: The holder MAY:

$\diamond$ at a prescribed future date $T$ (the maturity/expiry date of the option)

$\diamond$ BUY a prescribed asset $S$ (the underlying of the option)

$\diamond$ for a prescribed amount $K$ (the strike price of the option)

In terms of assigning a value to either the put or call option the only thing we can do with any certainty is to consider what they mean to us (as the holder of these prodicts) at expiry $T.$

$\diamond$ The put option: Let $P(S_{T},T)$ denote the value of the put option at $T.$ The intrinsic value of this product at this future moment all depends upon where $S_{T}$ lies relative to the strike price $K.$ Let’s consider the two cases:

\[ \begin{aligned} &S_{T}\ge K: \,\,\,\,\, {\rm{NO}}\,\, {\rm{do}}\,\, {\rm{NOT}}\,\, {\rm{sell}}\,\, {\rm{the}}\,\, {\rm{asset}}\,\, {\rm{for}}\,\, K\,\, {\rm{when}}\,\, {\rm{it}}\,\, {\rm{is}}\,\, {\rm{trading}}\,\, {\rm{at}}\,\, {\rm{a}}\,\,{\rm{higher}}\,\,{\rm{value!}}\\ &S_{T}< K:\,\,\, \,\, {\rm{YES}}\,\, {\rm{sell}}\,\, {\rm{the}}\,\, {\rm{asset}}\,\, {\rm{for}}\,\,K ,\,\, {\rm{then}}\,\, {\rm{buy}}\,\, {\rm{it}}\,\, {\rm{back}}\,\,{\rm{at}}\,\, {\rm{its}}\,\, {\rm{cheaper}}\,\, {\rm{trading}}\,\,{\rm{price}}\,\,S_{T}! \end{aligned} \]

In the two scenarios above the put option has no intrinsic value when $S_{T}\ge K$ however, when $S_{T}<K$ we are able to employ the suggested strategy, sell for $K$ and buy back for $S_{T}$ to lock in a profit, this profit of $K-S_{T}$ is the intrinsic value of the put in this scenario.

Mathematically we express this as

\[ P(S_{T},T)= \begin{cases} 0 \quad &{\rm{if}}\,\,\, S_{T}\ge K;\\ K-S_{T}\quad &{\rm{if}}\,\,\, S_{T}< K. \end{cases} \]

$\diamond$ The call option: Let $C(S_{T},T)$ denote the value of the call option at $T.$ Again, the intrinsic value of this product at this future moment all depends upon where $S_{T}$ lies relative to the strike price $K.$ Let’s consider the two cases:

\[ \begin{aligned} &S_{T}> K: \,\,\,\,\, {\rm{YES}}\,\, {\rm{buy}}\,\, {\rm{the}}\,\, {\rm{asset}}\,\, {\rm{for}}\,\, {\rm{the}}\,\, {\rm{cheap}}\,\, {\rm{price}}\,\, K\,\, {\rm{then}}\,\, {\rm{sell}}\,\, {\rm{it}}\,\, {\rm{at}}\,\, {\rm{its}}\,\,{\rm{higher}}\,\,{\rm{value}}\,\,S_{T}\\ &S_{T}\le K:\,\,\, \,\, {\rm{NO}}\,\, {\rm{do}}\,\, {\rm{not}}\,\, {\rm{buy}}\,\, {\rm{the}}\,\, {\rm{asset}} \,\, {\rm{for}}\,\, K\,\,{\rm{when}}\,\, {\rm{its}}\,\, {\rm{market}}\,\,{\rm{price}}\,\, {\rm{is}}\,\, {\rm{cheaper!}} \end{aligned} \]

In the two scenarios above the call option has no intrinsic value when $S_{T}\le K$ however, when $S_{T}>K$ we are able to employ the suggested strategy, buy for $K$ and then sell on for $S_{T}$ to lock in a profit, this profit of $S_{T}-K$ is the intrinsic value of the put in this scenario.

Mathematically we express this as

\[ C(S_{T},T)= \begin{cases} 0 \quad &{\rm{if}}\,\,\, S_{T}\le K;\\ S_{T}-K\quad &{\rm{if}}\,\,\, S_{T}> K. \end{cases} \] Illustration of the payoff profiles

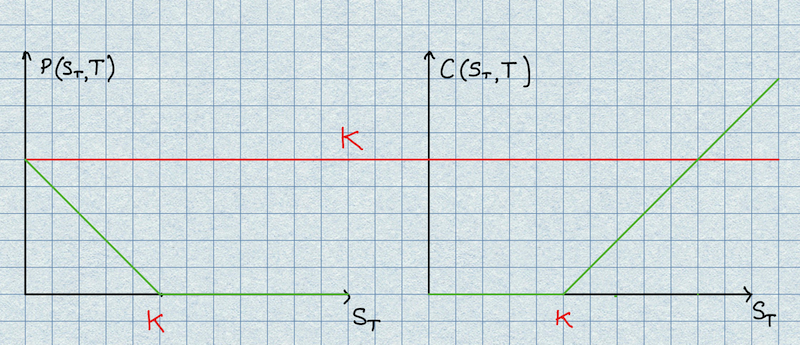
The picture above show the payoff profiles of the two most commonly use options, the put on the left hand side and the call on the right. Notice that the payoff of a put option is limited to the strike price of option (in the unlikely event that the asset would drop to zero) whereas the profit associated with the call option is (theoretically unlimited). Both profiles have the familiar hockey stick shape,

So, up to now, we have established a formula for the payoff of these two options at expiry. Our aim is to determine these option prices, which for ease of expression we will denote as $P_{t}$ and $C_{t},$ at earlier dates $t<T$ with the time $t=0$ (today’s date) being of particular interest.

Without giving too much of the game away we will be albe to achieve this with $2$ key ingredients and 2 important concepts. The key ingredients are:

A statistical model for $S_{t}$ for $0\le t\le T.$ (We will develop this in due course)

A risk-free savings account. (We all need a bit of certainty, we’ll develop this shortly)

The two important concepts are:

Absence of arbitrage. (Loosely speaking: no such thing as a free lunch)

The ability to hedge. (Reducing our risk exposure using a combination of other products)

1.2 Arbitrage

Roughly speaking an arbitrage opportunity is a chance to make a positive gain from an initial cost-free investment without running any risks. We’ll illustrate by way of an example.

Example 1.1 (Arbitrage Opportunity) Suppose there are two banks $A$ and $B.$

$\diamond$ Bank $A$ will lend money at a rate $r_{A}.$

$\diamond$ Bank $B$ has a savings account paying a rate $r_{B}.$

If $r_{A}<r_{B}$ then we can execute the following strategy:

$\diamond$ Take a loan out for $\$X$ from bank $A.$

$\diamond$ Place the $\$X$ into the savings account of bank $B.$

Keeping our interest rate calculations very simple, the interest we earn from bank $B$ amonuts to $\$Xr_{B}$ and the amount of interest we have to pay back on our loan is $\$Xr_{A}.$ Now, since $r_{B}>r_{A}$ the interest earned from the saver is enough to cover the interest we need to pay back on the loan. This means the loan can be paid back and there we are able to keep the difference of $\$X(r_{B}-r_{A})!$

What is remarkable about this example is that it was completely cost free (bank $A$ loaned us $\$X$) we spotted a mismatch in the saving v interest rates and exploited it, without taking on any risk, to make a profit.

We will assume that arbirtrage opportunities such as the one described above do not exist. We say there is an Absence of Arbitrage AoA in the financial markets. We will now strengthen this concept up and provde a more rigorous account of what we need. This will be the first moment in the course where general financial product are treated mathematically. To begin we suppose that we have two ‘investments’ these could be financial asset or portfolios of assets (its that general), we will let $X$ denote one and $Y$ denote the other. Given the risky nature of these investment we cannot know their value at some future time $T.$ However, even though we don’t know the realised values we are going to assume that, at time T, the value of $X$ will dominate the value of $Y.$ What we mean by this is that, no matter what the state of the market, it will be the case that, at time $T,$ the value of investment $X$ will be greater than (or equal to) the value of investment $Y.$ If we think of this in terms of probability theory it means that

$\diamond$ The likelihood of the event $\{X_{T}\ge Y_{T}\}$ occurring is one, (i.e., the event will occur at the given time $T.$)

$\diamond$ $\mathbb{P}(X_{T}\ge Y_{T})=1$.

It is important to view the above in the probabilistic framework, you may think that I’m making too much of a big deal of it but the event $\{X_{T}\ge Y_{T}\}$ involves two random variables - it is not an inequality betwen two fixed numbers (as we don’t know what the outcomes will be). Hopefully this makes sense, so we can now state the famous Absence of Arbitrage result:

Theorem 1.1 (Absence of Arbirtrage (AoA) Result) Let $X$ and $Y$ denote two financial investments for which, at some future time $T,$ the value of $X$ will dominate the value of $Y,$ i.e. $X_{T}\ge Y_{T}.$ If we assume there are No Arbitrage Opportunities then the value of $X$ will dominate the value of $Y$ at all times prior to $T,$ i.e., $X_{t}\ge Y_{t}$ for all $0\le t \le T.$ In particular, this means under the Absence of Arbirtrage

\[ X_{T}\ge Y_{T}\implies X_{0}\ge Y_{0}. \]

Before we launch into the proof of this result we pause to consider how in practice an investor decides on their strategy when considering taking on a financial asset. The most straight forward approach occurs when the investor believes that the asset will grow in value over time - here the investor will simply ‘buy now’ and hope that their ‘gut instinct’ is correct, so they make a profit. But what if the belief is that the asset price will fall in value over time. Well, here they can take part in what is known as a short-selling strategy:

$\diamond$ Right now, at $t=0$ they borrow the asset from another trader, it is acknowledged that the asset will be returned to the trader at the future date $T.$

$\diamond$ As soon as the investor has the asset they sell it on the market and so they receive its market value $S_{0}$ dollars. You may think this is dubious, selling something that you have borrowed from someone else, well, in some sense it is - it is a risky strategy (as well see in the next step) and there are rules in place to make sure this is done sensibly.

$\diamond$ Time $T$ comes around. The investor must buy back the asset for $S_{T}$ dollars in order to return it back to the trader. Now if the price has dropped below $S_{0}$ then the investor can use the $S_{0}$ dollars they received from cheekily selling it to easily buy it back with a profit of $S_{T}-S_{0}$ locked in as profit. Of course, it the investor has mis-read the assets price trajectory and it ends up trading much higher thant $S_{0}$ then they will need to make up the extra $S_{T}-S_{0}$ somehow and this is posted as a loss.

We are now well equipped to prove the AoA result.

Proof: The proof proceeds using a classic trick on mathematics, we make the assumption that the stated result is actually false and we try to argue the case for it before, inevitably, we end up cornered with some nonsense statement - we reach what is know as a contradiction and that is the name given to this style of proof. So, by contradiction we assume that $X_{0}<Y_{0}$ (of course we could replace $0$ with a general $t<T$ but I want to prove the result for $t=0$ as this is the time that we’ve chosen to signify ‘today’). OK, given that we’re assuming $X_{0}<Y_{0}$ and, no matter what, we know $X_{T}\ge Y_{T}.$ We can act on this information in the following way:

$\diamond$ At $t=0$ we can short sell $Y$ for $Y_{0}$ dollars and, since $X_{0}<Y_{0},$ we can use the proceeds to but $X$ for $X_{0}$ dollars. Note: so far the investment has not cost us anything and we immediately gain the investment $X$ together with $Y_{0}-X_{0}$ dollars in cash.

$\diamond$ At $t=T$ we can sell investment $X$ for $X_{T}$dollars we don’t know how much this will be but we do know that $X_{T}\ge Y_{T}$ and so we can use the proceeds of this to buy back $Y$ and return it (as part of the short selling deal).

If we think about the above strategy. It is completely cost free, there is no risk of making a loss and in fact we make a guaranteed profit from the $Y_{0}-X_{0}$ dollars in cash we lock into at the beginning (this could be placed in a savings account for instance). This strategy is precisely an arbitrage opportunity BUT the contradicts the absence of arbtitrage assumption stated in the theorem, thus $X_{0}<Y_{0}$ cannot be true and we do, indeed, have that $X_{0}\ge Y_{0}.$ $\square$

An important instance of the AoA result (and one which we will commonly use) is the equality case, stated as follows:

Corollary 1.1 (Absence of Arbirtrage (AoA) Result) Let $X$ and $Y$ denote two financial investments for which, at some future time $T,$ the value of $X$ will match the value of $Y,$ i.e. $X_{T}:= Y_{T}.$ If we assume there are No Arbitrage Opportunities then the value of $X$ will match the value of $Y$ at all times prior to $T,$ i.e., $X_{t}:= Y_{t}$ for all $0\le t \le T.$ In particular, this means under the Absence of Arbirtrage

\[ X_{T}:=Y_{T}\implies X_{0}:= Y_{0}. \]

We end the discussion on arbitrage by pointing out that from an investment perspective there is no reason to be interested in constructing different portfolios such that one dominates or matches another. It is interesting from a theoretical angle that it can be done and it is this theoretical angle that we will use to play with some artificially constructed portfolios with the required properties because, as we shall see, these will open the way to unlocking the price of some of our derivative products (whose payoffs at time $T$ can be matched by simpler, but very different, investments). An important component of these artificial portfolios is investing cash in a risk free bank and, given its importance, we’ll devote attention to it in the next subsection.

1.3 Risk Free Bank Account

Suppose we have $\$1$ today. We can place it in a risk-free bank account where the annual risk free rates (which we assume to be constant) is denoted by $r\%$. Then, as the years go by we will see our investment grow as follows

\[</center> \$1\,\,{\rm{(today)}}\,\,\Rightarrow \,\,\$1(1+r)\,\,{\rm{(after}}\,\,{\rm{one}}\,\,{\rm{year)}} \,\,\Rightarrow \,\,\$1(1+r)(1+r)\,\,{\rm{(after}}\,\,{\rm{two}}\,\,{\rm{years)}}... \]

and in general

\[ \$1\,\,{\rm{(today)}}\,\,\Rightarrow \,\,\$1(1+r)^{n}\,\,{\rm{(after}}\,\,n\,\,{\rm{years)}} \]

Suppose now that, instead of waiting until the end of the year to receive the interest, we have it spread out over the year across $m$ regular payment dates. In this case, we do not receive the full rate $r\%$ on each occasion but rather the fraction $\frac{1}{m}\cdot r\%$ (i.e., the full $r\%$ is spread out equally). In this case, as the year unfolds, our dollar investment grows as follows:

\[ \begin{aligned} \$1\,\,{\rm{(today)}}\,\,&\Rightarrow \,\,\$1\left(1+\frac{r}{m}\right)\,\,{\rm{(pay}}\,\,{\rm{date}}\,\,1)\\ &\Rightarrow \,\,\$1\left(1+\frac{r}{m}\right)^{2}\,\,{\rm{(pay}}\,\,{\rm{date}}\,\,2)\\ &\,\,\,\,\vdots \\ &\Rightarrow \,\,\$1\left(1+\frac{r}{m}\right)^{m}\,\,{\rm{(pay}}\,\,{\rm{date}}\,\,m\,\,=\,\,1\,\,{\rm{year}})\ \end{aligned} \]

How about receiving the interest continuously? This means we allow $m \to \infty$ and then we have

\[ \$1\,\,{\rm{(today)}}\,\,\Rightarrow \,\,\$ \lim_{m \to \infty}\left(1+\frac{r}{m}\right)^{m}\,\,{\rm{(after}}\,\,1\,\,{\rm{year).}} \]

We can now turn dig deep in our memory bank to recall that in mathematics there are several ways of characterizing the famous exponential function $\exp(x)$ and no investigation of the exponential function is complete without also speaking about its inverse, the natural logarithm. So, here we take a short diversion to review this famous pair.

The Exponential Function:
The exponential function is can be defined in several different ways. Perhaps the most satisfying is by its power series, given by

\[ \exp(x):=\sum_{n=0}^{\infty}\frac{x^{n}}{n!}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}\cdots, \quad x \in \mathbb{R}. \]

This definition reveals one of the exponential function’s most important properties; it is the derivative of itself, that is,

\[ \frac{d}{dx}\exp(x) = \exp(x). \]

We recall some of the imprtant properties of the exponential function

\[\begin{eqnarray*} (i)& \,\,\,\,\,\exp(x+y) &=& \exp(x)\exp(y);\\ (ii)& \,\,\,\,\,\exp(0) &=&1;\\ (iii)& \,\,\,\,\,\exp(x-y) &=& \frac{\exp(x)}{\exp(y)};\\ (iv) & \,\,\,\,\,\exp(x)&<&\exp(y)\,\,\,{\rm{when}}\,\,x<y\,\,\implies,\,\exp(-y)<\exp(-x)\,\,\,{\rm{when}}\,\,x<y;\\ (v) &\,\,\,\,\,\,\left(1+\frac{x}{m}\right)^{m} &\to& \exp(x)\quad {\rm{as}} \,\,\,\, m\to \infty. \end{eqnarray*}\]

The Log Function:

The exponential function maps the real number line to the half line of positive numbers; mathematically we write

\[ \exp: \mathbb{R}\to (0,\infty). \]

The inverse of the exponential function is called the natural logarithm, we denote this by

\[ \ln:(0,\infty) \to \mathbb{R} \]

and mathematically define it by

\[ \ln\left(\exp(x)\right)= x \,\,\,\,\,\, {\rm{(for}} \,\, x \in \mathbb{R})\,\,\, \,\,\,\,\,\,{\rm{and}}\,\,\,\,\,\,\,\,\, \exp\left(\ln(x)\right)=x\,\,\,\,\,\,{\rm{(for}} \,\, x \in (0,\infty)). \]

We recall some of the important properties of the log function:

\[\begin{eqnarray*} (i)& \,\,\,\,\,\frac{d}{dx}\ln(x) &=& \frac{1}{x};\\ (ii)& \,\,\,\,\,\ln(xy)&=&\ln(x)+\log(y);\\ (iii)& \,\,\,\,\,\ln(1) &=& 0;\\ (iv)& \,\,\,\,\,\ln\left(\frac{x}{y}\right) &=& \ln(x)-\ln(y); \\ (v)& \,\,\,\,\, \ln(x^{y}) &=&y\ln(x). \end{eqnarray*}\]

Using the definition and property $(v)$ above, we can also deduce that

\[ a^{x}=\exp\left(\log(a^{x})\right) = \exp\left(x\log(a)\right)\,\,\,\,\,\,\, {\rm{provided}}\,\,\,a>0\,\,\,{\rm{and}}\,\,\, x \in \mathbb{R}. \tag{1.1} \]

We let $e$ denote the value of the exponential function when $x=1,$ i.e., $e=\exp(1) = 2.71828...$ This number is commonly called base of the log function since $\ln(e) = \ln(\exp(1)) = 1.$ We can use this relationship together with (1.1) to deduce that

\[ e^{x}=\exp\left(x\log (e)\right) = \exp(x), \quad {\rm{for}} \,\,\,{\rm{any}} \,\,\, x \in \mathbb{R}. \]

This provides us with a much easier way of calculating the exponential function.

You will notice property $(v)$ of the exponenital function review is the definition that links to what we are doing now. Before we move on, let us try and convince ourselves of this limit. Note, the following development doesn’t constitute a proof (in dealing with the logarithmic and exponential functions we are ‘anticipating’ the result, so what we have here is a verification). In order to fully appreciate matters you should also recall the first-principles definition of a derivative, i.e., the derivative of a function $f$ at some ‘anchor’ point ‘a’ is defined by

\[ f^{\prime}(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}. \tag{1.2} \]

OK, lets take a look at

\[ \left(1+\frac{x}{m}\right)^{m}. \]

Let’s set $h=\frac{x}{m}$ and write the above as

\[ \left(1+h\right)^{\frac{x}{h}}=\left((1+h)^{\frac{1}{h}}\right)^{x} \tag{1.3} \]

Now using (1.1) we can develop the expression above (that is raised to the power $x$) as follows

\[ (1+h)^{\frac{1}{h}}=\exp\left(\frac{1}{h}\ln(1+h)\right)=\exp\left(\frac{\ln(1+h)-\ln(1)}{h}\right) \]

We note that the final equality is true since $\ln(1)=0.$ The reason for expressing it this way is to help in the next step. Recall, we want to examine the limit of $=(1+\frac{x}{m})^{m}$ as $m\to \infty,$ and given the substitution of $h=\frac{x}{m}$ this is the same as examining the limit of @(eq:trans) as $h\to 0$ and when we do this we see from @(eq:firstprinc) that this involves evaluating the derivative of the natural logarithm function at $1$, i.e., we get

\[ \lim_{h\to 0}(1+h)^{\frac{1}{h}}=\exp\left(\lim_{h\to 0}\frac{\ln(1+h)-\ln(1)}{h}\right) =exp\left(\frac{d}{dx}\ln(x)\bigg|_{x=1}\right)=\exp(1)=e. \]

Piecing all of this together we do indeed have that

\[ \lim_{m\to\infty}\left(1+\frac{x}{m}\right)^{m}=\lim_{h\to 0}\left((1+h)^{\frac{1}{h}}\right)^{x} =\left(\lim_{h\to 0}(1+h)^{\frac{1}{h}}\right)^{x} =e^{x}. \]

Thus, in view of what we have above we see that, when the interest rate is delivered continuously we have

\[ \$1\,\,{\rm{(today)}}\,\,\Rightarrow \,\,\$ e^{r}\,\,{\rm{(after}}\,\,1\,\,{\rm{year).}} \]

or, more generally, that

\[ \$1\,\,{\rm{(today)}}\,\,\Rightarrow \,\,\$ e^{rt}\,\,{\rm{(after}}\,\,t\,\,{\rm{year).}} \]

or, even more generally, that

\[ \$x\,\,{\rm{(today)}}\,\,\Rightarrow \,\,\$x\cdot e^{rt}\,\,{\rm{(after}}\,\,t\,\,{\rm{year).}} \]

In practice different rates will be quoted depending upon the way the bank offers to deliver the interest over the year. This method is called the compunding frequency and they are usually offers as annually (delivered once each year), semi-annually (delivered every $6$ months), quarterly (delivered every $3$ months) and continuously (as above)

Important: In this course we will always assume, unless stated otherwise, that the risk free rate of interest is quoted as a continuously compounded rate.

Before we leave this behind and go off to explore what we can about different styles of option contracts we really should address a simple, but important, financial calculation: discounting. With the continuously compounded interest rate $r$ we know that our dollar today ($t=0$) will grow to $\$e^{rt}$ at time $t>0.$ Thinking about this a different way we can also ask the question:

$\diamond$ How much do I need to deposit today in order to ensure that I have $\$1$ at time $t>0?$

The answer to this is straight forward, it is the value of $x$ that solves

\[ x\cdot e^{rt}=1 \implies x = e^{-rt}. \]

The term $e^{-rt}$ is commonly referred to a the discount factor; when it is applied to a future cash flow $\$C$ say (to be delivered at time $t$), the result $\$C\cdot e^{-rt}$ tells us the present $(t=0)$ value of that cash-flow. Discounting future cash-flows to the present is a routine financial calculation and one that we will be performing frequently in this course.

With that wrapped uo we can move onto the promised exploration of the properties of the most popular financial derivatives.

1.4 Characteristics of Financial Deriviatives

In this section we will derive a range of characteristics on the prices of options using only the assumption of no arbitrage, i.e., we will appeal only to the AoA result. To fix our notation:

$\diamond$ we will let $C$ denote a European call option (right to buy) on an underlying asset $S$ with strike price $K$ and time to maturity $T.$

$\diamond$ we will let $P$ denote a European put option (right to sell) on an underlying asset $S$ with strike price $K$ and time to maturity $T.$

$\diamond$ we will let $r$ denote the prevailing risk-free interest rate.

You may be puzzled as to why the products are said to be European. I believe it is due to the historical development of the products. In Europe, privilege contracts (with some optionality built in) began trading in the late $18^{th}$ century and the practice involved monthly settlement periods. In America things developed differently, the American privilege contracts allowed for each day to be a so-called settling day. This leads us to define the American version of the put and call option contracts.

Definition 1.3 (American Option) An American call (put) option is a contract with the conditions: The holder MAY:

$\diamond$ at any time befere a prescribed future date $T$ (the maturity/expiry date of the option)

$\diamond$ buy (sell) a prescribed asset $S$ (the underlying of the option)

$\diamond$ for a prescribed amount $K$ (the strike price of the option)

To distinguish an American option from its European version (when the context is not clear) we will use the notation $C^{A}$ and $P^{A}$ to signify the American call and put respectively. The first thing to notice is that as the American versions offer many more privileges this will be reflected in their prices. Thus, we can assume without any controversy that

\[ C\le C^{A}\quad {\rm{and}}\quad P\le P^{A}. \]

Let us now focus on developing some of the promised properties of options. We begin with a lower bound for the call price.

Proposition 1.1 (Lower bound) In the absence of arbitrage we have:

\[ C_{0}\ge S_{0}-Ke^{-rT} \]

Proof: $\,$ At time $t=0$ we set up TWO portfolios, the first one is very simple:

\[ X:\,{\rm{the}}\,\,{\rm{underlying}}\,\,{\rm{asset}}\,\, S. \]

The second portfolio is:

\[ Y:= \,{\rm{a}}\,\,{\rm{call}}\,\,{\rm{option}}\,\, +\,\, {\rm{cash}}\,\, {\rm{amount}}\,\, (=\$Ke^{-rT}), \]

here, we assume that the cash amount resides in the risk free bank account.

Consider the value of these investments at time $T.$ Well, obviously the first one is simply the value of the asset at $T,$ i.e., $X_{T}=S_{T}.$ For the second portfolio the cash component has grown from $Ke^{-rT}$ to $Ke^{-rT}e^{rT}=K$ and so we have

\[ Y_{T}=C_{T}+K=\max(S_{T}-K,0)+K=\max(S_{T},K) \ge S_{T} = X_{T} \]

Thus, we see that at $T$ portfolio $Y$ dominates portfolio $X.$ We now appeal to the AoA result to conclude that we must also have that

\[ Y_{0}\le X_{0}\implies C_{0}+Ke^{-rT}\ge S_{0}\implies C_{0}\ge S_{0}-Ke^{-rT}. \]

$\square$

Next we will embark on a scenario analysis where we explore how the option prices will change by changing some of the underlying parameters.

Scenario I: Different expiry dates.

Here we will consider a pair of American options (call or put). The options in the pair are almost identical, the only difference is that one has expiry $T_{1}$ and the other has expiry $T_{2}$ where, $T_{1}>T_{2}.$ Fixing the notation, we have

\[ {\rm{for}}\,\,{\rm{American}}\,\,{\rm{calls}}:\,\, C^{A}(S,T_{1},K)\,\,{\rm{and}}\,\,C^{A}(S,T_{2},K) \]

and

\[ {\rm{for}}\,\,{\rm{American}}\,\,{\rm{puts}}:\,\, P^{A}(S,T_{1},K) \,\, {\rm{and}}\,\,P^{A}(S,T_{2},K). \]

Clearly it is not controversial to suggest that the longer lived option will be worth at least as much the shorter lived one and so we have

\[ C^{A}(S,T_{1},K)\ge C^{A}(S,T_{2},K)\quad {\rm{and}}\quad P^{A}(S,T_{1},K)\ge P^{A}(S,T_{2},K)\,\,\,{\rm{when}}\,\,T_{1}>T_{2}. \]

Mathematically, if we consider the option as a function of all of its parameters we can say that American option price is an increasing function of expiry time.

Scenario I: Different strike prices.

In this investigation we will consider two almost identical call options (European or American). The only difference is that one has a strike price $K_{1}$ say and the other has a strike price $K_{2},$ where $K_{1}<K_{2}.$ Fixing the notation, we have

\[ {\rm{American}}:\,\, C^{A}(S,T,K_{1})\,\,{\rm{and}}\,\,C^{A}(S,T,K_{2}) \]

and

\[ {\rm{European}}:\,\, C(S,T,K_{1})\,\,{\rm{and}}\,\,C(S,T,K_{2}). \]

The picture below shows the payoff profiles for the two call options. Clearly the opportunity to exercise (whether early or at expiry) is more remote for the larger strike price. The price of the option should take this into account and so, it is not controversial to expect the option with the higher strike will be cheaper than one with a lower strike.

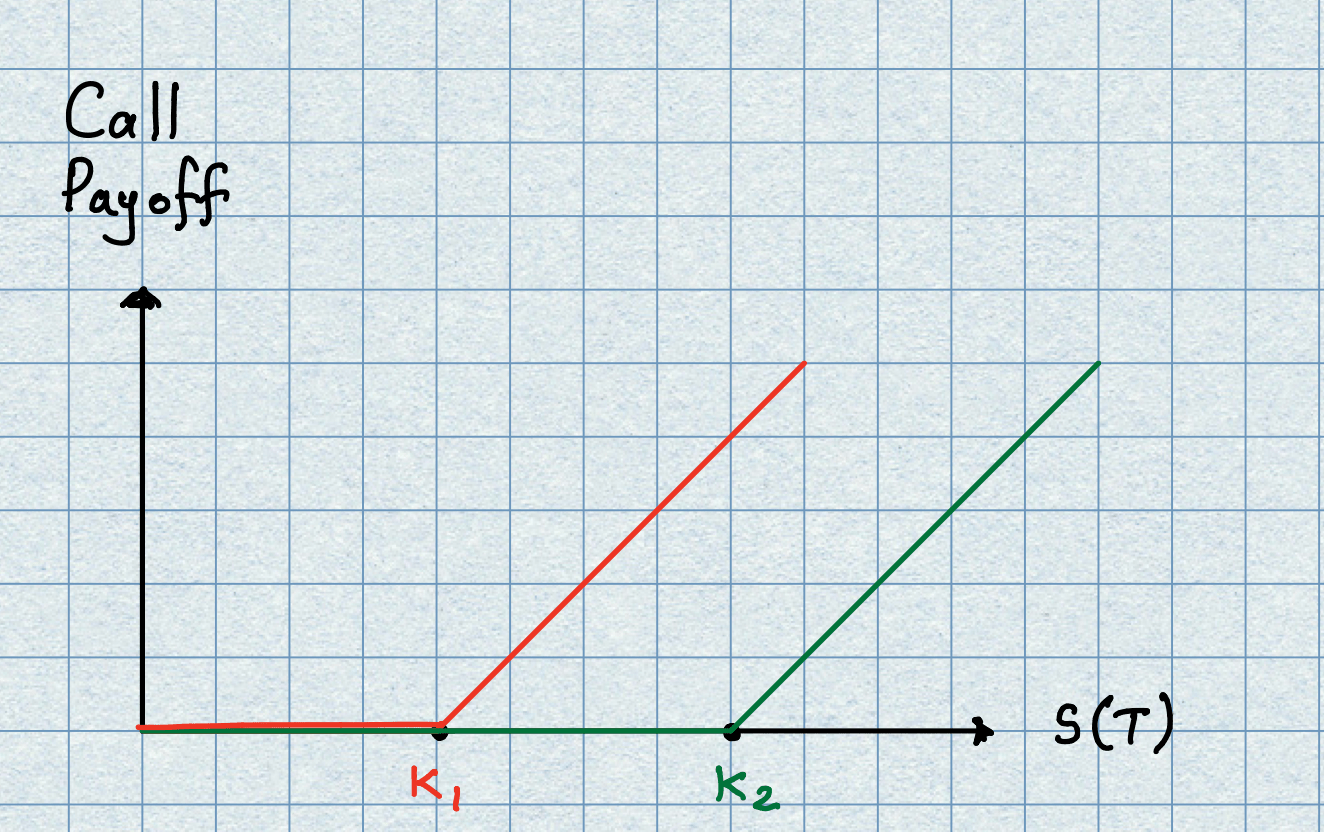
Thus we have that

\[ C^{A}(S,T,K_{1})\ge C^{A}(S,T,K_{2})\quad {\rm{and}}\quad C(S,T,K_{1})\ge C(S,T,K_{2})\,\,\,{\rm{when}}\,\,K_{1}\le K_{2}. \]

Mathematically, we say that when the call option is viewed as a function of its underlying parameters then $C$ and $C^{A}$ are decreasing functions of strike price. This means the mathematical derivative of the functions are negative (they slope downward along the strike axis) and we have:

\[ \frac{\partial C}{\partial K}< 0. \]

We have a lower bound on the price of a European call. What about an upper bound? To do this we consider a strange sounding version of the financial derivative.

Definition 1.4 (Perpetual Option) A perpetual call option is one whose expiry is infinitely far away, i.e., $T=\infty.$

Let us ponder the following odd-sounding product: a perpetual American call option with $strike price* $=0!$ Let’s untangle this:

$\diamond$ it is the option to buy the asset for free at any time!

$\diamond$ this is exactly the same as owning the asset!

Thus, even though it looks a bit of a strange way of saying it, we have that

\[ S=C^{A}(S,\infty,0). \]

Now, using scenario $I$ we know the option gets cheaper when the expiry date drops, so we can state

\[ S=C^{A}(S,\infty,0)\ge C^{A}(S,T,0) \]

Now, using sceanrio $II$ we know the call option gets cheaper when the strike price increases. In the above inequality the strike is zero and so we can state

\[ S=C^{A}(S,\infty,0)\ge C^{A}(S,T,0)\ge C^{A}(S,T,K) \]

Finally, we know the American call will NOT be cheaper that its Euorpean counterpart and so we have

\[ S=C^{A}(S,\infty,0)\ge C^{A}(S,T,0)\ge C^{A}(S,T,K)\ge C(S,T,K). \]

This means the price of a call (European or American) will be no greater than the value of the underlying asset price. Taking the lower bound we discovered earlier we conclude that

\[ S-Ke^{-rT}\le C(S,T,K)\le S. \]

The call optin is also never negative and so we can strengthen this to give

\[ \max(S-Ke^{-rT},0) \le C(S,T,K)\le S. \]

The picture below show the bounds on the European call option (the purple corridor being the region of feasible prices).

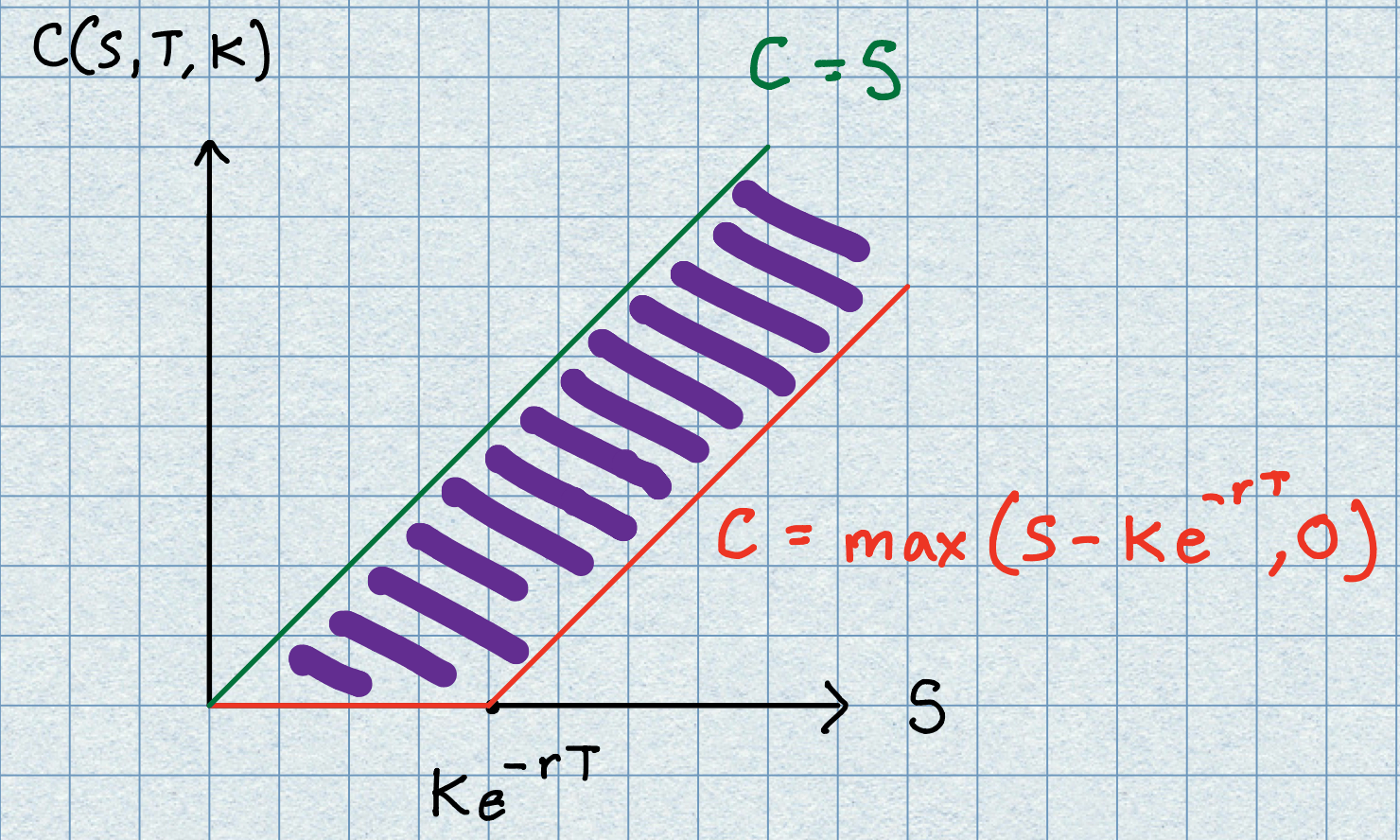
We now return to the American version of the call. Now, our expectation would be that the American contract ought to be more valuable than the American call (given the seemingly attractive additional early exercise feature). Well, we are in for a surprise - it turns out they have the same value!

Proposition 1.2 (American call = European call) Let $C_{t}^{A}=C^{A}(S,K,T-t)$ denote the price of an American call at time $0\le t\le T.$ Let $C_{t}=C(S,K,T-t)$ denote the price of the corresponding European call.Then,

\[ C_{t}=C_{t}^{A}. \]

Proof: $\,\,$ Firstly, we know that $C_{t}\le C_{t}^{A},$ the American version is worth at least as much as the European version. Now using the lower bound on the European call option we have

\[ C_{t}^{A} \ge C_{t} \le S_{t}-Ke^{-r(T-t)}\ge S_{t}-K,\tag{1.4} \]

the final inequality being true since $0<e^{-r(T-t)}\le 1,$ for $0\le t \le T.$ Now, if we were ever to exercise the American call early we would do so when $S_{t}>K$ and, as such, we would receive $S_{t}-K$ but shows that

\[ {\rm{intrinsic}}\,\, {\rm{value}}\,\,{\rm{of}}\,\, {\rm{the}}\,\,{\rm{American}}\,\, {\rm{call}}\,\, \ge \,\,{\rm{its}}\,\, {\rm{exercise}}\,\,{\rm{value}} \]

This means there is never an incentive to exercise before expiry and so payoff is postponed until $T,$ in which case it is the same as the European call. $\square$

We close oure investigation with a very useful result which connects the prices of a European call with its corresponding Eurpoean put.

Proposition 1.3 (Put-Call Parity) Let $P$ and $C$ denote the European put and call on the same underlying asset $S,$ sharing the same strike $K$ and expiry $T.$ Then,

\[ C_{t}-P_{t}=S_{t}-Ke^{-r(T-t)}. \]

Proof:$\,\,$ At time $t < T$ we set up two portfolios. The first one is

\[ X:= \,{\rm{the}}\,\,{\rm{European}}\,\,{\rm{call}}\,\,{\rm{option}}\,\,C\,\, +\,\, {\rm{cash}}\,\, {\rm{amount}}\,\, (=\$Ke^{-rT}), \]

as before, we assume that the cash component resides in the risk free bank. The second portfolio is

\[ Y:= \,{\rm{the}}\,\,{\rm{European}}\,\,{\rm{pall}}\,\,{\rm{option}}\,\,P\,\, +\,\, {\rm{the}}\,\, {\rm{underlying}}\,\,{\rm{asset}}\,\, S. \]

Consider the values at $T.$ As before, the cash component of portfolio $X$ will have grown from $Ke^{-rT}$ to $Ke^{-rT}e^{rT}=K$ and so

\[ X_{T}= C_{T}+K=\max(S_{T}-K,0)+K=\max(S_{T},K). \]

For portfolio $Y$ we have

\[ Y_{T}= P_{T}+S=\max(K-S_{T},0)+S_{T}=\max(K,S_{T}). \] Hence $X_{T}=Y_{T}$ and so by the Absence of Arbirtrage result these portfolios must match at all times $t<T.$ Note, by time $t$ the cash component of portfolio $X$ will have grown from $Ke^{-rT}$ to $Ke^{-rT}e^{rt}=Ke^{-t(T-t)},$ thus, matching up we have \[ C_{t}+Ke^{-r(T-t)}=X_{t}=Y_{t}=P_{t}+S_{t}\implies C_{t}-P_{t}=S_{t}-Ke^{-r(T-t)}. \]

$\square$

1.5 Practice Questions

Now that you have completed this chapter try the following practice questions. These are all direct applications of either the put-call parity formula and/or the bounds derived in the chapter.

We have obtained upper and lower bounds on the price of a European call. Use the put-call parity formula to demonstrate that the corresponding upper and lower bounds on the European put are as follows

\[ \max(Ke^{-r(T-t)}-S_{t},0)\le P_{t}\le Ke^{-r(T-t)} \]

By taking the horizontal axis to the the asset price $S$ and the vertical axis to be the put price $P$ draw a sketch to illustrate the region where the fair value $P_{E}$ of the European put must lie.
If a share in an asset is currently selling for $\$31,$ a three-month European call option is $\$3$ with a strike price of $\$31$ and the risk free interest rate is $10\%.$ What is the arbitrage free European option price for the security?
If a share in an asset is currently selling for $\$31,$ a three-month European call option is $\$3$, a three-month European put option is $\$2.25$, and the risk free interest rate is $10\%.$ What is the arbitrage free strike price for the security?
The put-call parity formula holds in the absence of arbitrage, a violation of the formula indicates an arbitrage opportunity exists. Decide whether or not an arbitrage opportunity exists in the following cases:

$\bullet$ A share in a security is currently selling for $\$31,$ a six month European call option is $\$3.23,$ a six month European put is $\$1.09$, the strike for both options is $\$30$ and the risk free rate is $3\%.$

$\bullet$ A share in a security is currently selling for $\$24,$ a six month European call option is $\$2.12,$ a six month European put is $\$2.75$, the strike for both options is $\$25$ and the risk free rate is $3\%.$

In a case of a violation set out a strategy that could be employed to take advantage of the arbitrage opportunity.