Chapter 2 Probability Theory

The future of most financial investments is uncertain. We are unable to make statements such as

\[ ..in \,\, T\,\, days\,\, time\,\, our \,\, invesmtent\,\, WILL \,\, be \,\, worth... \]

Instead, the uncertain world is full of open questions such as

\[ \begin{aligned} ..what\,\, is\,\,&the\,\, LIKELIHOOD \,\, that, \,\, in\,\, T \,\, days\,\,time,\\ &our \,\, investment \,\, will \,\,be \,\, worth...? \end{aligned} \]

Probability theory is the branch of mathematics that studies the likelihood of random events and so provides us with the scientific approach we need to describe and analyze the nature of financial investments. In this chapter we set up a toolbox of precisely the right mixture of probabilistic concepts that we will need to make a start; as the story evolves then so too will this toolbox.

2.1 Random Variable

In the certain world we talk of a function $f$ as a kind of machine that requires the input of a set $A$ of real variables, this set is called the domain of the function and it usually represents an interval or the whole real line. The function itself specifies a rule which governs how each $x \in A$ transforms into a (potentially) new value $f(x).$ We write

\[ f: A \to \mathbb{R} \quad {\rm{by}} \quad f:x \mapsto f(x). \]

In the uncertain world there are no such rules that fix the outcome of a variable, we deal with random quantities that can take on any one of a range of possible values; some of these outcomes will be more likely to occur than others.

We begin by considering a simple case of a random quantity $X$ that can take on any one of a finite number of specific values $x_{1},x_{2},\ldots,x_{n}$ say. We assume further that associated with each outcome $x_{i}$ there is a probability $p_{i}$ that represents the relative chance of $X$ taking on the value $x_{i}.$ The probabilities are non-negative and sum up to $1.$ Each $p_{i}$ can be thought of as the relative frequency with which $x_{i}$ would occur if the experiment could be repeated infinitely often.

The classic example of such an experiment is that of rolling an ordinary six sided die, if $X$ denotes the number obtained then the range of $X$ is $\{1,2,3,4,5,6\}$ and each has probability $1/6.$

Let us consider a random variable $X$ which takes values on the real line (e.g. $X$ could be a model for value of an asset at a future date $T.$). Now, because $X$ can theoretically take on any value on a continuum of real numbers (which cannot be counted) it is impossible to assign a specific propbability (likelihood) value to a particular outcome. Instead we replace the probabilities with a probability function $p(x)$, commonly referred to as the density function associated with the random variable. Just as the discrete probabilities are non-negative and sum to one, the probability density function is also non-negative and its integral (across $\mathbb{R}$) must equal one. In this setting the probability of events such as $\{ X \in [a,b] \}$ or $\{X \in (-\infty, b]\}$ are quantified by integrating $p(x)$ across the appropriate range. All of this is summarized in the following definition:

Definition 2.1 (Random variables) Suppose $X$ is a random quantity.

If $X$ can take on any one of the values $x_{1},x_{2},\ldots,x_{n}$ and there are numbers $p_{1},p_{2},\ldots,p_{n}$ such that

\[ \mathbb{P}(X=x_{i})=p_{i} \ge 0, \quad i=1,2, \ldots, n,\quad {\rm{and}}\quad \sum_{i=1}^{n}p_{i}=1 \]

then we say $X$ is a discrete random variable.

If $X$ can take on any value in $\mathbb{R}=(-\infty,\infty)$ and there is a nonnegative function $p(x)$ such that

\[ \mathbb{P}(X \in [a,b])=\int_{a}^{b}p(x)dx\quad {\rm{and}}\quad \int_{-\infty}^{\infty}p(x)dx=1, \]

then we say $X$ is a continuous random variable.

2.2 Expectation

Although we cannot say what the realised value of a random variable will be we are able to use the its probabilistic information to provide the value which, on average, it is most likely to be. A nice way to view this is to consider the so-called expectation operator which we shall denote by $\mathbb{E}.$ This operator ‘acts on’ random variables and in so doing, it produces, as mentioned above, the ‘expected’ value (or the ‘mean’) of $X$ which we denote by $\mu_{X}.$ We visualise this as

\[ \mathbb{E}:{\rm{random}}\,\,{\rm{variable}}\to {\rm{the}}\,\,{\rm{value}}\,\,{\rm{which,}}\,\,{\rm{on}}\,\,{\rm{average}} \,\,{\rm{is}}\,\,{\rm{most}}\,\,{\rm{likely}}\quad {\rm{i.e.,}}\,\,\,\,\,\mathbb{E}[X]= \mu_{X}. \]

If $X$ is a discrete random variable with range $\{x_{1}, \ldots, x_{n}\}$ then its expected value is just the probability weighted average

\[ \mathbb{E}(X)=\sum_{i=1}^{n}p_{i}x_{i}= \mu_{X}. \]

If $X$ is a continuous random variable then its expectation is the probability weighted integral

\[ \mathbb{E}(X)=\int_{-\infty}^{\infty}p(x)xdx = \mu_{X}. \]

If the integral does not exist, neither does the expectation. In practice, this is rarely the case.

The mathematical expectation or 8mean* $\mathbb{E}(X)$ of a random variable is just the average over all values weighted by their probabilities. \

If $X$ is a discrete random variable with range $\{x_{1}, \ldots, x_{n}\}$ then the mean is just the probability weighted average

\[ \mathbb{E}(X)=\sum_{i=1}^{n}p_{i}x_{i}= \mu_{X}. \]

If $X$ is a continuous random variable then its expectation is

\[ \mathbb{E}(X)=\int_{-\infty}^{\infty}p(x)xdx = \mu_{X}. \]

If the integral does not exist, neither does the expectation. In practice, this is rarely the case.

The expected value operation is that we shall use a lot in our calculations, so it is useful to note some of its basic (and somewhat obvious) properties:

Certain value: If X is a known value (not random) then $\mathbb{E}(X)=X.$ Hence, as we would expect, the expected value of a non-random quantity is the quantity itself.
Linearity: If $X$ and $Y$ are random variables then

\[ \mathbb{E}(\alpha X + \beta Y)= \alpha \mathbb{E}(X) + \beta \mathbb{E}(Y), \]

for any $\alpha, \beta \in \mathbb{R}.$

Non-negativity. If $X$ is a random variable and $X \ge 0$ then $\mathbb{E}(X) \ge 0.$ Hence, the expectation operator is sign-preserving.

The next result on the face of it looks pretty straight forward. Don’t let it pass you by, later in this course we will be so happy that we can rely on this it, it will prove to be the key to moving many of our developments on to new places!

Theorem 2.1 (The Law of The Unconscious Statistician) Let $p(x)$ denote the density function associated to a continuous random variable $X.$ If we apply a function $f$ to $X$ to create a new random variable $f(X),$ then its expecation is given by

\[ \mathbb{E}[f(X)]=\int_{-\infty}^{\infty}f(x)p(x)dx. \tag{2.1} \]

Note this important result has a rather illustrative title; the law of the law of the unconscious statistician. The reason for this is that it allows the statistician to compute an expectation of a random variable $f(X)$ without needing to find its density function; the density function that is being used here is that of $X$ and hopefully the statistician already knows this (perhaps it is a normal random variable for example) and the integral is not so difficult to evaluate. The alternative would be to take on the unenviable job of finding the density of $f(X),$ and if $f$ is non-linear this can be almost impossible!

2.3 Variance

The expected value of a random variable provides a useful summary of the probabilistic nature of the variable. However, we would also want, in addition, to have a measure of the degree of possible deviation from it. One such measure is the variance.

For a given random variable $X$ we want to have some measure of how much we can expect its value to deviate from its expected value $\mu_{X}.$ As a first attempt we could consider the quantity the quantity $X-\mu_{X},$ this itself is random but, because its expected value zero, it provides no insight. On the other hand, the quantity $(X-\mu_{X})^{2}$ is also a random variable and is always non-negative. In particular, its value is large when $X$ deviates greatly from $\mu_{X},$ it is much smaller when $X$ is close to $\mu_{X}.$ The expected value of this random variable is thus a useful measure of how much $X$ tends to vary from its expected value.\

In general, for any random variable $X$ with mean $\mu_{X}$ we define its variance as

\[ var(X)=\mathbb{E}( X - \mu_{X})^{2}=\mathbb{E}( X - \mathbb{E}[X])^{2}. \]

Expanding the squareand using the linearity and certainty properties, we can deduce

\[ var(X) =\mathbb{E}( X^{2} - 2\mathbb{E}[X]\cdot X + \mathbb{E}[X]^{2})=\mathbb{E}[X^{2}]-2\mathbb{E}[X]\cdot\mathbb{E}[X] +\mathbb{E}[X]^{2}=\mathbb{E}[X^{2}] -\mathbb{E}[X]^{2} \]

this formula is useful in computations.

If we scale a random variable bt a factor $\alpha$ say then, by the linearity of the expectation operator we have that

\[ \mathbb{E}[\alpha X]=\alpha\mathbb{E}[X]. \]

Applying the formula above we can investigating the variance of the scaled random variable

\[ \begin{aligned} var(\alpha X) =\mathbb{E}[ (\alpha X)^{2}] -\mathbb{E}[\alpha X]^{2}&=\alpha^{2}\mathbb{E}[X^{2}]-\alpha^{2}\mathbb{E}[X]^{2}\\ &=\alpha^{2}\left(\mathbb{E}[X^{2}]-\mathbb{E}[X]^{2}\right)=\alpha^{2}var(X). \end{aligned} \]

Observe, if we scale the random variable by the square root of a postive scalar then we get

\[ var(\sqrt{\alpha}X)=\alpha var(X) \]

We frequently use the non-negative square root of the variance. We write

\[\sigma_{X}=\sqrt{var(X)}=\sqrt{\mathbb{E}( X - \mu_{X})^{2}} \]

This quantity, the standard deviation of $X,$ has the same units as $X$ and is another measure of how much the random variable is likely to deviate from $\mathbb{E}[X].$ In the financial setting, when we are speaking about the random returns on an asset say, then the more expressive term volatility is used instead of standard deviation.

2.4 Independence

Suppose that we have a pair of random variables $X$ and $Y.$ Intuitively, we consider the pair to be (statistically) independent if it can be said that the value taken by $X$ does not depend on the value taken by $Y$ and vice versa. It takes quite a bit of mathematical theory to pin down the precise definition of independence, we’d need an excursion into distribution theory and you will meet this elsewhere in the programme. For our purposes we will say that the pair are independent if the following condition holds

\[ \mathbb{E}[f_{1}(X)f_{2}(Y)]=\mathbb{E}[f_{1}(X)]\mathbb{E}[f_{2}(Y)] \]

for all functions $f_{1},f_{2}:\mathbb{R}\to\mathbb{R}$ such that the expectations on the right hand side are finite. Obviously, this is not a straight-forward condition to check but it will prove useful. For instance, of both $f_{1}$ and $f_{2}$ are taken to be the indentity function then we can see that, when $X$ and $Y$ are independent then we have

\[ \mathbb{E}[X\cdot Y]=\mathbb{E}[X]\cdot\mathbb{E}[Y] \tag{2.2} \]

We will, on many occasions in this course (and others), encounter sequences of random variables $X_{1},X_{2},X_{3},\ldots$ that are described as independent and equally distributed written as i.i.d for short. You will probably hear the phase ‘a sequence of i.i.d random variables’ so often that it is worthwhile to pin down exactly what is meant by this. Saying $X_{1},X_{2},X_{3},\ldots$ is i.i.d means

If we know the values of any subset of the sequence then, sadly, this tells us nothing about the outcomes of the remaining random variables.
Each random variable shares the same probability density function (in the continuous case) or the same assigned proababilties for their shared outcomes (in the discrete case).

Note, point 1. takes care of the first $i$ (for independence) and point 2. takes care of the $i.d$ (that the random variable are identically distributed).

2.5 Covariance

A more mathematically accessible way of assessing the degree to which a pair of random variables interact with each other is to consider their covariance. If $X_{1}$ and $X_{2}$ are two random variables with expected values $\mu_{1}$ and $\mu_{2}$ respectively, then the covariance between them is defined to be

\[ \sigma_{12}=cov(X_{1},X_{2}) = \mathbb{E}\left[ (X_{1} - \mu_{1})( X_{2} - \mu_{2}) \right] \]

We note that by symmetry that $\sigma_{12}=\sigma_{21},$ also the covariance between a random variable $X$ and itself is its variance, that is $cov(X,X)=\sigma_{X}^{2},$ this follows from the defintion of variance.\

Exercise 2.1 (Covariance Identity) Use the properties of the expectation operator to show that

\[ \sigma_{12} =cov(X_{1},X_{2})=\mathbb{E}[ X_{1}X_{2}] - \mathbb{E}[ X_{1}]\mathbb{E}[ X_{2}]. \tag{2.3} \]

We recall that if two random variables $X_{1}$ and $X_{2}$ are independent then we have, from (2.2), that

\[ \mathbb{E}[ X_{1}X_{2}] =\mathbb{E}[ X_{1}]\mathbb{E}[ X_{2}], \]

and so, in view of (2.3), we see that two independent random variables have zero covariance (this is reassuring). Unfortunately, the converse is not true and we will see a little later that it is possible to have two random variables whose covariance is zero and yet they obviously are highly dependent on each other.

2.6 The Probability Distribution

In this short section we will turn attention to random variables. Of course we’ve encountered these earlier where they were described with reference to either a set of associated probabilities $\{p_{1},\ldots,p_{n}\}$ (in the discrete setting) or the connected probability density function $p(x)$ (in the continuous setting). We are revisiting matters here because by focusing on the $\{p_{1},\ldots,p_{n}\}$ and$p(x)$ we have by-passed an extremely important function - the so-called cumulative distribution function. For a given random variable (discrete or continuous) its cummulative distribution function is defined as

\[ F(x)=\mathbb{P}[X\le x],\quad x \in \mathbb{R}. \]

A function $F:\mathbb{R}\to [0,1]$ is a candidate to be a distribution function for some random variable, whether it be discrete or continuous, provide that is possesses three defining properties, these are summarized in the following definition.

Definition 2.2 (Distribution Function) A function $F:\mathbb{R}\to [0,1]$ is the cumulative distribution function of some random variable if and only if it has the following properties:

$F$ is ${\rm{nondecreasing}}$ (i.e., $F(x) \le F(y)$ whenever $x <y.)$
$F$ is ${\rm{right}}$ ${\rm{continuous,}}$ i.e.,

\[ \lim_{\epsilon \searrow 0}F(x+\epsilon) = F(x). \]

Note here $\searrow 0$ means the limit is taken from above.

$F$ is ${\rm{normalized}},$ i.e.,

\[ \lim_{x \to -\infty}F(x)=0 \quad {\rm{and}} \quad \lim_{x \to \infty}F(x)=1. \]

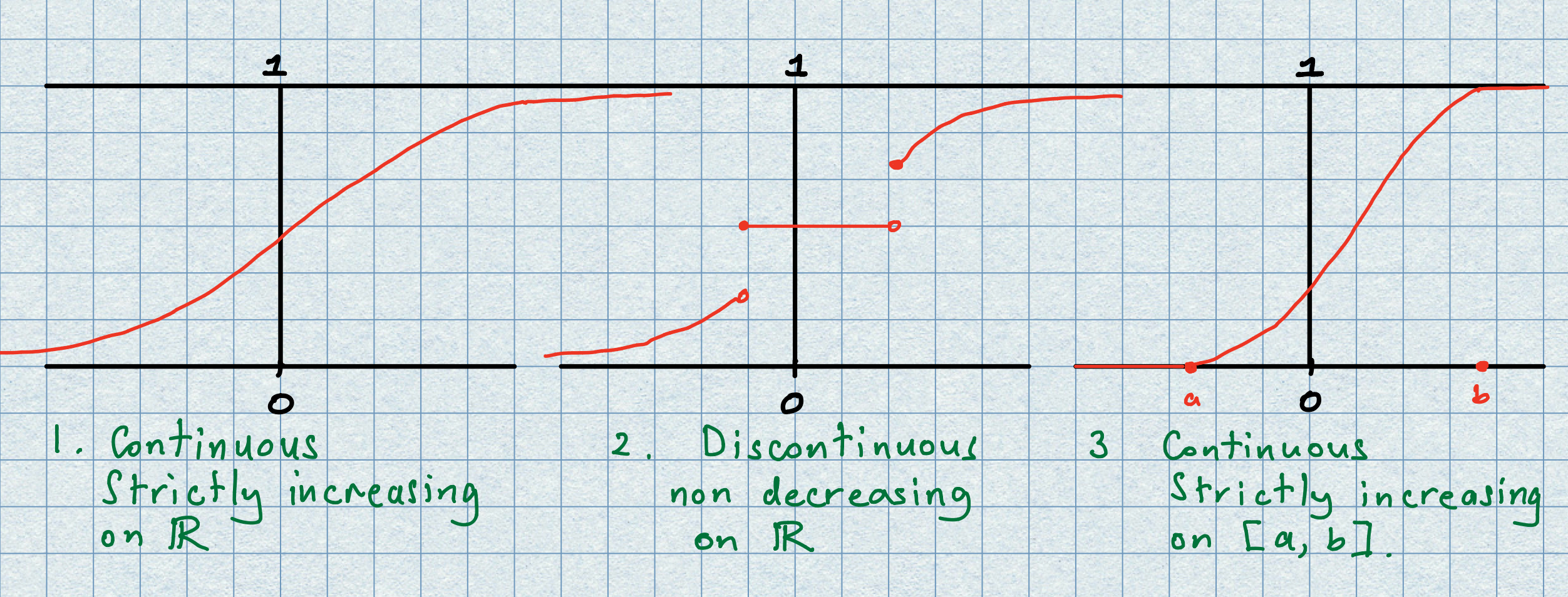
The definition above allows for a range of possible shapes for the cdf of a random variable;

it may continuously increase as $x$ varies from $-\infty$ to $\infty;$
it may not be defined on the whole of $\mathbb{R}$ but rather on some interval $[a,b],$ thus the probability begins accumulating at $x=a$ and is completely captured by $x=b;$

it may exhibit periods where the probability remains constant;

there may be points where the function suddenly jumps in value. \end{itemize}

Examples of these possible shapes are displayed in the picture below.

An extremely important use of a cdf is that it can be used to recover the probabilities of many useful events. For example, if $a < b$ we can write

\[\begin{aligned} F(b) = \mathbb{P}(X \le b)&= \mathbb{P}(X\le a)+\mathbb{P}(X \in (a,b])&\\ \, & \\ & = F(a) + \mathbb{P}\left[X \in (a,b]\right], \end{aligned} \]

thus

\[ \mathbb{P}\left[X \in (a,b]\right] = F(b)-F(a). \]

The distribution of a continuous random variable can often be described in terms of another function called the probability density function (pdf). We provide the following definition.

Definition 2.3 (Distribution and Density) Let $X$ be a continuous random variable whose distribution $F$ is a continuous function. If there exists a function $p:\mathbb{R}\to \mathbb{R}$ that satisfies

\[ p(x)\ge 0\,\,\,\, {\rm{and}} \,\,\,\,F(x)=\int_{-\infty}^{x}p(u)du \,\,\,\,{\rm{for}}\,\,{\rm{all}}\,\, x \in \mathbb{R}, \] we say that $p$ is the probability density function of $X.$

2.7 The Normal Distribution

In order to make progress in probability theory it is useful to become acquainted with some of the more popular families of distributions. These families are fixed by specifying a closed form representation for either the probability mass function, in the discrete case, or the probability density function in the continuous case. There are many different families (we will encounter some of these) thowever perhaps the most important is the so-called normal distribution of a continuous random variable. In this section we will define the normal distribution in the univariate settings. We have already encountered the properties of the exponential and the logarithm function in the previous chapter so we are well equipped to get to grips with the normal distribution.

The Normal Distribution:

A random variable $X$ with mean $\mu$ and variance $\sigma^{2}$ is said to be normally distributed if its probability density function is given by

\[ p(x) = \frac{1}{\sqrt{2\pi \sigma^{2}}}\exp\left(\frac{-(x-\mu)^{2}}{2\sigma^{2}}\right), \tag{2.4} \]

and, to signify this fact, we write $X \sim N(\mu,\sigma^{2}).$ We note that the distribution of $X$ is completely defined by its mean and its variance and its distribution is given by

\[ F(x) = \mathbb{P}(X \le x) = \frac{1}{\sqrt{2\pi \sigma^{2}}}\int_{-\infty}^{x}\exp\left(\frac{-(u-\mu)^{2}}{\sigma^{2}}\right)du. \]

Unfortunately the above integral has no closed form solution; numerical methods are required for its evaluation. In order to avoid this we can make a simple change of variable and set

\[ Z = \frac{X-\mu}{\sigma}, \]

thus the new random variable has zero mean and unit variance; we say that it has the standard normal distribution and we write $Z \sim N(0,1).$ In this standardized case we reserve a special notation; the standard normal density function is given by

\[ \varphi(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{z^{2}}{2}}, \]

and the standard normal distribution is given by

\[ \Phi(z) = \mathbb{P}[Z\le z] = \int_{-\infty}^{z}\varphi(u)du. \]

Fortunately, there exist statistical tables and computer packages which enable the user to

evaluate the function $\Phi(z) \in [0,1]$ for a given $z;$
find the value of $z$ for which $\Phi(z) = \alpha$ holds for a given $\alpha \in [0,1],$ i.e., we are able to evaluate the inverse function $\Phi^{-1}(\alpha)$ for $\alpha \in [0,1].$

The standard normal distribution and its tabulated values can be used to compute the distribution of any normally distributed random variable, this follows since

\[ \begin{aligned} F(x) = \mathbb{P}[X \le x] &= \mathbb{P}\left[Z\sigma +\mu \le x\right]\quad {\rm{(where}}\,\, Z = \frac{X-\mu}{\sigma}\sim N(0,1))\\ \, & \\ & = \mathbb{P}\left[Z\le \frac{x-\mu}{\sigma}\right] = \Phi\left(\frac{x-\mu}{\sigma}\right). \end{aligned} \]

2.8 The Moments of a Distribution

Soi far we know that the distribution function of a random variable $X$ is said to be continuous can be written as

\[ F(x)=\mathbb{P}[X \le x] = \int_{-\infty}^{x}p(u)du, \]

where $p:\mathbb{R} \to [0,\infty)$ is an integrable function called the probability density function of $X.$

We remark that these integrals can be bounded if we replace the power of $x$ by the power of its absolute value $|x|$ i.e., we can write

\[ \mu_{k}\le \int_{-\infty}^{\infty}|x|^{k}p(x)dx \]

The upper bounds on the moments are simply integrals of $p(x)$ multiplied by successively heavier weight functions $|x|,$ $|x|^{2},\ldots$ The value of any one of these bounding integrals will only be finite if the growth of the weight function $|x|^{k}$ say, is sufficiently smothered by the fast decay of density function $p(x).$ In view of this we say that

\[ {\rm{the}}\,\,{\rm{moment}}\,\,\mu_{k}\,\,{\rm{exists}}\,\,{\rm{only}}\,\,{\rm{if}}\,\, \int_{-\infty}^{\infty}|x|^{k}p(x)dx <\infty. \]

We note that the first moment of $X$ is precisely the expectation of $X,$ which we denote simply as $\mu.$ This quantity, as we know, serves as a measure of the central location of the distribution of $X.$ In fact, using $\mu$ as a centrality parameter we define the $k^{th}$ central moment of $X$ to be the integral

\[ m_{k}= \mathbb{E}[(X-\mu)^{k}]=\int_{-\infty}^{\infty}(x-\mu)^{k}p(x)dx,\,\,\,\,\,\,k=1,2,\ldots. \]

As before, we say that

\[ {\rm{the}}\,\,{\rm{central}}\,\,{\rm{moment}}\,\,m_{k}\,\,{\rm{exists}}\,\,{\rm{only}}\,\,{\rm{if}}\,\, \int_{-\infty}^{\infty}|x-\mu|^{k}p(x)dx <\infty. \]

The central moments of a distribution play an important role in characterizing the random variable $X.$ We make the following observations.

The first central moment is zero; this follows from the linearity of the expectation operator as

\[ m_{1}=\mathbb{E}[X-\mu]=\mathbb{E}[X]-\mu =0. \]
The second central moment is precisely the variance of $X,$ which we denote as $\sigma^{2}.$
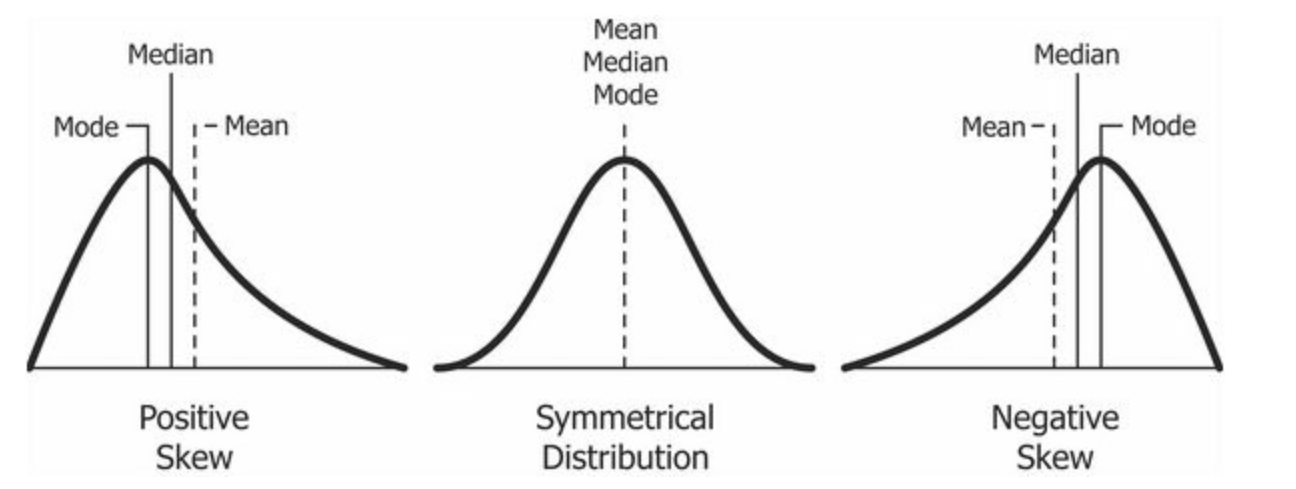
The third central moment is needed to compute the so-called skewness coefficient of a random variable which is defined by

\[ S(X)=\mathbb{E}\Bigl[\left(\frac{X-\mu}{\sigma}\right)^{3}\Bigr]. \]

If $S(X)=0$ then the probability weight is divided equally to the left and the right of the mean, in this case we say that $X$ has a symmetric distribution. If $S(X)>0$ then we say that the distribution is skewed. If we imagine the probability density function of $X$ as a hill and we are at its peak then the downward slope out into the direction of $+\infty$ will be much gentler than the steep drop in the direction of $-\infty;$ this indicates that there is more probability weight in the positive tail and we say that the distribution is skewed to the left. Similarly, if $S(X)<0$ then, using the same analogy as above, we say that the distribution is skewed to the right. An illustration is given in the picture below.

The fourth central moment is needed to compute the so-called kurtosis coefficient of a random variable defined by

\[ \mathcal{K}(X)=\mathbb{E}\Bigl[\left(\frac{X-\mu}{\sigma}\right)^{4}\Bigr]=\frac{\mathbb{E}[(X-\mu)^{4}]}{\sigma^{4}}. \]

This coefficient is commonly used to measure the thickness of the tails of a distribution. The reason for choosing this stems from the following result.

Proposition 2.1 (Benchmark normal kurtosis) If $X\sim N(\mu,\sigma^{2})$ then $\mathcal{K}(X)=3$.

Proof (Exercise - hint: use integration by parts) $\square$

The kurtosis coefficients for other random variable can be benchmarked against the value of $3$ the kurtosis coefficient of a normal random variable. Put simply if $\mathcal{K}(X)>3$ this is an indication that the distribution of $X$ exhibits fat tails, i.e., extreme values both positive and negative are likely to occur more frequently than would be the case for a normally distributed random variable. Analogously, $\mathcal{K}(X)< 3$ indicates a thin tailed distribution where extreme values are occur less frequently than for a normally distributed random variable.

2.9 The Characteristic Function

The characteristic function of a random variable is a highly useful tool in probability theory. In order to define it we need to access a few facts from functional analysis; the branch of mathematics that deals with spaces of functions and how they behave under certain operations. The function space that we are most interested in the space of integrable functions:

\[f:\mathbb{R}\to\mathbb{R} \,\,{\rm{is}}\,\,{\rm{integrable}}\,\, {\rm{if}}\,\,\,\int_{-\infty}^{\infty}|f(\textbf{x})|d\textbf{x} < \infty.\]

To signify that a function is integrable, we write $f \in L_{1}(\mathbb{R}).$

The operator that we are most interested in is the Fourier transform and this is defined for all integrable functions by the formula

\[ (\mathcal{F}f)(z) = \widehat{f}(z)=\int_{-\infty}^{\infty}\exp(-ixz)f(x)dx \,\,\,\,\,\,{\rm{for}}\,\,\,z \in \mathbb{R}. \]

We recall that for any real number $\theta$ the quantity $\exp(i\theta)$ represents the complex number $z=\cos\theta + i\sin\theta$ and $\exp(-i\theta)$ represents the complex number $z=\cos\theta -i\sin\theta$

It is well-known that we can recover $f \in L_{1}(\mathbb{R})$ from its Fourier transform via the inversion formula

\[ f(x)=(\mathcal{F}^{-1}\widehat{f})(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp(izx)\widehat{f}(z)dz. \]

Another nice property of Fourier theory establishes that the Fourier transform of a derivative can be seen as multiplication of the Fourier transform itself:

Proposition 2.2 (Fourier transform of a derivative) If a function $f$ and its derivative $f^{\prime}$ are both integrable functions then the following identities hold

\[ \widehat{ \frac{df}{dx}}(z)=iz\widehat{f}(z)\quad {\rm{and}}\quad \frac{d}{dz}\widehat{f}(z)=-i\widehat{(xf)}(z). \]

Proof: Given that $f$ and $f^{\prime}$ are both integrable they both decay to zero as $x \to \pm \infty.$ Using this fact, the first identity can be established using integration by parts:

\[\begin{aligned} \widehat{ \frac{df}{dx}}(z)&=\int_{-\infty}^{\infty}f^{\prime}(x)\exp(-ixz)dx= -\int_{-\infty}^{\infty}f(x)(-iz\exp(-ixz))dx\\ &=iz\int_{-\infty}^{\infty}f(x)\exp(-ixz)dx=iz\widehat{f}(z). \end{aligned} \]

The second identity is established by differentiating under the integral sign

\[ \begin{aligned}\frac{d}{dz}\widehat{f}(z)&=\frac{d}{dz}\int_{-\infty}^{\infty}f(x)\exp(-ixz)dx =\int_{-\infty}^{\infty}f(x)\frac{d}{dz}\exp(-ixz)dx\\&=\int_{-\infty}^{\infty}-ixf(x)\exp(-ixz)dx= -i\widehat{(xf)}(z). \end{aligned} \]

$\square$

A probability density function is a typical example of an integrable function and it turns out that its Fourier transform is a highly useful tool for discovering further probabilistic properties. To fix notation for the future investigations we provide the following definition.

Definition 2.4 (Characteristic Function) The characteristic function of a continuous random variable $X$ with density function $p(x)$ is defined to be

\[ \phi_{X}(u)=\mathbb{E}[\exp(iu X)]=\int_{-\infty}^{\infty}p(x)\exp(ix u)dx=\widehat{p}(-u). \]

We remark in passing that the characteristic function is equal to one when $u=0$ since

\[ \phi_{X}(0)=\int_{-\infty}^{\infty}p(x)\exp(0)dx=\int_{-\infty}^{\infty}p(x)dx =1. \tag{2.5} \]

Now, using the Fourier inversion result we can recover the density function uniquely from the characteristic function since

\[ p(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\phi_{X}(u)\exp(-ix u)du. \]

We observe that the integral expression () represents the Fourier transform of the probability density function. Thus we can deduce from the inversion formula (), that the characteristic function uniquely determines the distribution function of $X$ since

\[ p(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\phi_{X}(u)\exp(-iu x)du,\,\,\,\,\,{\rm{for}}\,\,\,x \in \mathbb{R}. \]

The following intriguing result shows a link between the smmothness of the charcteristic function of a random variable $X$ and the number (and size) of its moments.

(#prp:charmom ) (Characteristic Function and Moments) Let $X$ denote a continuous random variable for which only the first $n$ moments are finite. Then the corresponding characteristic function $\phi_{X}$ is $n-$times differentiable and

\[ \frac{d^{k}\phi_{X}}{du^{k}}(0)=i^{k}\mu_{k}, \quad {\rm{for}}\,\, k=1,2,\ldots,n. \]

There is a little trick to the proof of this result that may not immediately spring to mind. When dealing with the derivative here we consider its definition from first principles. You may cast you mind back to your high school calculus and recall that the derivative of a function $f$ at an anchor point ‘a’ is given by

\[ f^{\prime}(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}, \]

provided ths limit exists. Now that this fact has been refreshed we can give a quick sketch of the proof of the result.

Proof: $\,\,$ We begin by computing the first derivative, which is formally given as

\[ \begin{aligned} \frac{d\phi_{X}}{du}&=\lim_{h \to 0}\frac{\phi_{X}(u+h)-\phi_{X}(u)}{h}= \mathbb{E}\Bigl[\lim_{h \to 0}\frac{\exp(i(u+h)X)-\exp(iuX)}{h} \Bigr]\\&= \mathbb{E}\Bigl[\frac{d}{du}\exp(iuX)\Bigr]=i\mathbb{E}\Bigl[X\exp(iuX)\Bigr]. \end{aligned} \]

We note that we’ve glossed over the justification for taking the limit inside the expectation operator, it is perfectly legal but rather technical so we leave it aside. We can now set $u=0$ to reveal that

\[ \frac{d\phi_{X}}{du}(0)=i\mathbb{E}\Bigl[X\Bigr]=i\mu_{1}. \]

The other derivatives can be computed in a similar fashion:

\[ \frac{d^{2}\phi_{X}}{du^{2}}=\frac{d}{du}\mathbb{E}\Bigl[iX\exp(iuX)\Bigr]=\mathbb{E}\Bigl[i^{2}X^{2}\exp(iuX)\Bigr], \]

and so

\[ \frac{d^{2}\phi_{X}}{du^{2}}(0)=\frac{d}{du}\mathbb{E}\Bigl[iX\exp(iuX)\Bigr]=i^{2}\mathbb{E}\Bigl[X^{2}\Bigr]=i^{2}\mu_{2}, \]

and so on.$\square.$

We are now in a position to demonstrate the effectiveness of the characteristic function with the following examples.

Example 2.1 (Sum of Two Random Variables) Let us assume that we have two continuous, independent random variables, $X$ and $Y$ say, whose probability density functions are given by $p_{X}$ and $p_{Y}.$ The sum of these two variables $Z=X+Y$ say, is itself a random variable in its own right. The characteristic function of $Z$ has a particularly nice representation as the following development reveals

\[ \begin{aligned} \phi_{Z}(u)&=\mathbb{E}[\exp(iu(X+Y)]\\ & =\mathbb{E}[\exp(iuX)\cdot \exp(iuY)]\\ & = \mathbb{E}[\exp(iuX)]\cdot \mathbb{E}[\exp(iuY)]\,\,\,\,\,({\rm{due}}\,\,{\rm{to}}\,\,{\rm{independence}})\\ &=\phi_{X}(u)\cdots \phi_{Y}(u) \end{aligned} \]

Of course, this result is not restricted to the sum of two random variables and we have the following generalization.

Theorem 2.2 (Sum of Several Random Variables) Let $X_{1},\ldots,X_{n}$ denote $n$ independent continuous random variables whose characteristic functions are denoted by $\phi_{1},\ldots,\phi_{n}$ respectively. The characteristic function of the random variable $Z=X_{1}+\cdots +X_{n},$ is given by

\[ \phi_{Z}(u)=\phi_{1}(u)\cdots \phi_{n}(u). \]

Example 2.2 (Scaling a Random Variable) In the previous example we took a collection of independent, continuous random variables and considered their sum as a new random variable. We encountered expressions for the characteristic functions for this sum. In this example we take only one continuous random variable $X$ and we generate a new variable by applying a scale factor, i.e., we consider $\alpha X$ for some $\alpha>0.$ In this situation we can demonstrate the following links.

If $p_{X}$ and $p_{\alpha X}$ denote the density functions of $X$ and $\alpha X$ respectively then

\[ p_{\alpha X}(u)=\frac{1}{\alpha}p_{X}\left(\frac{u}{\alpha}\right). \tag{2.6} \]

This follows since

\[ \begin{aligned} \int_{a}^{b}p_{\alpha X}(u)du=\mathbb{P}[a \le \alpha X \le b] &= \mathbb{P}\left[\frac{a}{\alpha} \le X \le \frac{b}{\alpha}\right]\\ \, & \\ & = \int_{a/\alpha}^{b/\alpha}p_{X}(x)dx\,\,\,\,\,\,\,({\rm{now}}\,\,{\rm{set}}\,\,u = \alpha x)\\ \, & \\ & =\int_{a}^{b}\frac{1}{\alpha}p_{X}\left(\frac{u}{\alpha}\right)du. \end{aligned} \]

If $\phi_{X}$ and $\phi_{\alpha X+\beta}$ denote the characteristic functions of $X$ and $\alpha X+\beta$ respectively then we have

\[ \phi_{\alpha X+\beta}(u)=\mathbb{E}[\exp(i u(\alpha X+\beta)]=\exp(iu\beta)\mathbb{E}[\exp(iu \alpha\cdot X)]=\exp(iu\beta)\phi_{X}(\alpha u). \tag{2.7} \]

Example 2.3 (Normally Distributed Random Variables) Characteristic functions, as we’ve alluded to, are extremly useful objects and as such it is useful to be equipped with some examples. For our purposes the most commonly used case is that of the standard normal variable $Z\sim N(0,1).$ As a first step we let $, $ and, using (2.1), compute the following more general expectation

\[ \begin{aligned} \mathbb{E}[\exp(\alpha Z+\beta)]&=\int_{-\infty}^{\infty}\exp(\alpha z+\beta)\underbrace{\frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^{2}}{2}\right)}_{{\rm{density}}\,{\rm{of}}\,N(0,1)}dz\\ &=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}(z^{2}-2\alpha z - 2\beta)\right)dz \end{aligned} \]

The key to developing this expression is to take the quadratic in the exponential and ‘complete the square’ i.e. to write it, equivalently, as

\[ z^{2}-2\alpha z - 2\beta = (z-\alpha)^{2}-(\alpha^{2}+2\beta) \]

and then, using this, we have

\[ \begin{aligned} \mathbb{E}[\exp(\alpha Z+\beta)]&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}\left( (z-\alpha)^{2}-(\alpha^{2}+2\beta)\right)\right)dz\\ &=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}\left( (z-\alpha)^{2}-(\alpha^{2}+2\beta)\right)\right)dz\\ &=\exp\left(\frac{1}{2}(\alpha^{2}+2\beta)\right)\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}\left( z-\alpha\right)^{2}\right)dz\\ &= \exp\left(\frac{\alpha^{2}}{2}+\beta\right)\left(\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(z-\alpha)^{2}}{2}\right)dz\right) \end{aligned} \]

Note, if we make the change of variable $u=z-\alpha$ in the integral above then it transforms to the integral of standard normal density function $\varphi$ which must, of course equal one, to confirm this we have

\[ \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(z-\alpha)^{2}}{2}\right)dz =\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{u^{2}}{2}\right)du=\int_{-\infty}^{\infty}\varphi(u)du =1. \]

Thus, we reach our goal, we have established that

\[ \mathbb{E}[\exp(\alpha Z+\beta)]=\exp\left(\frac{\alpha^{2}}{2}+\beta\right) \tag{2.8} \]

At present the above calculation is much more than we really need BUT, mark my words we will need this later on in the course and when we do it will prove absolutely crucial. It can be shown that this identity holds true if we allow $\alpha$ to be a complex number as well. This is perfect for us because we can now set $\alpha = iu$ (where $u \in \mathbb{R}$) and $\beta=0$ to deliver the charcteristic function we need, i.e.,

\[ \phi_{Z}(u)=\mathbb{E}[\exp(iuZ)]=\exp\left(\frac{i^{2}u^{2}}{2}\right)=\exp\left(-\frac{u^{2}}{2}\right) \]

We can also appeal to @(eq:scale) to deduce that the characteristic function for a more general normal random variable $X\sim N(\mu,\sigma^{2}),$ which can be written as $X=\mu+\sigma Z$ ($Z\sim N(0,1)$), as

\[ \phi_{X}(u)=\phi_{Z}(\mu+\sigma Z)=\exp(i\mu u)=\phi_{Z}(\sigma u)=\exp(i\mu u-\frac{\sigma^{2}u^{2}}{2}). \tag{2.9} \]

We close this section on the properties of the characteristic function by delivering one final discovery. Suppose we have a batch of $n$ normally distributed random variables $\{X_{1},\ldots,X_{n}\},$ we’ll assume that they are independent but they don’t have to share the same distribution, i.e., we have that $X_{k}\sim N(\mu_{k},\sigma_{k}^{2})$ for $k=1,\ldots,n.$ The following result show that when we take the sum of them all, the resulting random variable,

\[ S_{n}= X_{1}+\cdots X_{n} \]

is also normally distributed. This is reassuring, but take note, it is the fact that these random variables are independent that makes this true. In general, it may not be the case and this is best illustrated by taking $X\sim N(\mu,\sigma^{2})$ and then defining $Y=-X\sim N(-\mu,\sigma^{2}),$ the dependence here could not be clearer and since $X+Y=0$ it is also clear that the result of the sum is not normally distributed.

Proposition 2.3 (Sum of Independent Normals is also Normal) Let $\{X_{k}:k=1,\ldots,n\}$ be a set of independent normal random variables, i.e., $X_{k}\sim N(\mu_{k},\sigma_{k}^{2})$ for $k=1,\ldots,n.$ The the sum $S_{n}= X_{1}+\cdots X_{n}$ is also a random variable and, in fact, we have

\[ S_{n}=X_{1}+\cdots X_{n}\sim N\left(\mu_{1}+\cdots+\mu_{n},\sigma_{1}^{2}+\cdots +\sigma_{n}^{2}\right). \]

The proof relies on the fact that there is a unique correspondence between the characteristic function of a random variable and its probability density function. This is really helpful in certain situations where working solely with the density function may be too complicated. For instance, the result of the above proposition would be settled if we were able to show that the probability density function of $S_{n}$ is

\[ p_{S_{n}}(x)=\frac{1}{\sqrt{2\pi(\sigma_{1}^{2}+\cdots +\sigma_{n}^{2})}}\exp\left(-\frac{1}{2}\frac{\left(x-(\mu_{1}+\cdots+\mu_{n})\right)^{2}}{\sigma_{1}^{2}+\cdots +\sigma_{n}^{2}}\right), \]

this looks a duanting challenge! However, we could by-pass this by focussing upon the characteristic function instead. The alternative approach would then be to establish that the characteristc function of $S_{n}$ is

\[ \phi_{S_{n}}(u)=\exp\left(iu(\mu_{1}+\cdots+\mu_{n})-\frac{(\sigma_{1}^{2}+\cdots +\sigma_{n}^{2})u^{2}}{2}\right). \]

Now, a glance back at Theorem 2.2 indicates that this is well within our grasp.

Proof: $\,\,$ The characteristic function of $X_{k}$ is given by

\[ \phi_{k}(u)=\exp\left(iu\mu_{k}-\frac{\sigma_{k}^{2}u^{2}}{2}\right), \quad k=1,\ldots,n. \]

Since the random variables are independent we can evoke Theorem 2.2 to deduce that

\[ \phi_{S_{n}}(u)=\exp\left(iu(\mu_{1}+\cdots+\mu_{n})-\frac{(\sigma_{1}^{2}+\cdots +\sigma_{n}^{2})u^{2}}{2}\right). \]

Thus, we conclude that $S_{n} \sim N(\mu_{1}+\cdots+\mu_{n},\sigma_{1}^{2}+\cdots +\sigma_{n}^{2}),$ as required. $\square.$

2.10 The Central Limit Theorem

In order to demonstrate the power of working with characteristic functions we embark here on an intriguing investigation which will lead us to one of the most famous of all probability theory results; the central limit theorem. To briefly sum up the central limit theorem in a line would be to say

the central limit theorem confirms that the sum of a large number of $i.i.d.$ random variables is approximately normally distributed

As you can imagine in order to prove this result will require some understanding of what we mean by ‘approximately’ in the above statement. Well, it turns out that the theorem itself is much stronger that an ‘approximation’ it actually says that if the ‘large number’ ($n$ say) is allowed to increase without bound (i.e., $n\to \infty$) then the distributions of the large sums actually converges to a normal distribution.\

The natural question from the above paragraph is to query the final statement and ask, which normal distribution? Well, firstly let’s put some notation down, we’ll let $(X_{k})_{k=1}^{\infty}$ denote our infinite sequence of $i.i.d$ random variables. Given that they are identically distributed, let’s say then that $\mu$ is their shared expected value and $\sigma^{2}$ is their shared variance, also, given we are dealing with sums, we will set

\[ S_{n}=X_{1}+\cdots +X_{n}. \]

Now, we already know from 2.3 that if the random variables $X_{k}$ were known to normally distributed then $S_{n}\sim N(n\mu,n\sigma^{2}).$ HOWEVER in what we are considering we do not know how the random variables are distributed. It is remarkable then that the central limit theorem says that

\[ {\rm{provided}}\,\, {\rm{that}}\,\,n\,\,{\rm{is}}\,\, {\rm{large}}\,\,{\rm{then}}\,\, S_{n} \,\,{\rm{is}}\,\, {\rm{approximately}}\,\,{\rm{a}}\,\, N(n\mu,n\sigma^{2})\,\,{\rm{random}}\,\,{\rm{variable!}} \]

There is still that word ‘approximately’ again. To tighten all of this up, what we are really going to reveal if we consider the sequence of normalised sums

\[ A_{n}=\frac{S_{n}-n\mu}{\sigma\sqrt{n}}=\frac{X_{1}-\mu}{\sigma\sqrt{n}}+\cdots \frac{X_{n}-\mu}{\sigma\sqrt{n}}, \quad n=1,2,\dots \]

then, this converges to a standard normal random variable as $n\to \infty,$ i.e.

\[ \lim_{n\to\infty}A_{n}\sim N(0,1). \]

I think you will agree this is quite a stunning result. This is why the normal distribution is at the forefront of large scale investigations of random phenomena. An experiment that takes place in the natural world is open to a huge number of random influences, of course, the experimenter cannot expect to capture all of these. However, armed with the central limit theorem, the experimenter circumvent this overwheling though by taking the view that if all of these fluctuations can approximated by a sequence of i.i.d random variables (a perfectly reasonable assumption). Once this is established then, the central limit theorem, tells the experimenter that overall cumulative impact of these contribution can be modelled by a random variable with an appropriate mean and variance.

Given the magnitude of this result I’d like to convey a little of how we come to discover it. As you can imagine, it is not a trivial result that can be established in a few lines. However, the following theorem gives us some insight as it links convergence of distributions function (precisely the heart of the central limit theorem) to the convergence of characteristic functions (something that we have some familiarity with!) Here it is:

Theorem 2.3 (Convergence of Distribution Functions) For every $n=1,2,\ldots,$ let $X_{n}$ be a random variable with distribution function $F_{n}$ and characteristic function $\phi_{n}.$ Let $X$ denote a random variable with distribution function $F$ and characteristic function $\phi.$ If $\phi_{n}(u)\to\phi(u)$ for all $u$ (as $n \to \infty$) and $\phi$ is continuously differentiable at $u=0,$ then we have that then we have that

\[ F_{n}(x)\to F(x),\,{\rm{as}}\,\,n \to \infty, \] for every value of $x$ at which $F$ is continuous. We say that $X_{n}$ converges to $X$ in distribution.

The proof of this result is rather technical and we do not present it here although the interested reader can consult Section III of (Berger 1992). We observe that result itself suggests that, by examining the behavior of a sequence of moment characteristic function we might be able to explain the limiting behaviour of the corresponding sequence of random variables. With this result at our disposal we can now present and prove the famous central limit theorem:

Theorem 2.4 (The Central Limit Theorem) Let $(X_{k})_{k=1}^{\infty}$ be a sequence of i.i.d random variable with expected value $\mu$, variance $\sigma^{2}$ and whose $3^{rd}$ moment $\mu_{3}$ is also finite. Let

\[ A_{n}=\frac{X_{1}-\mu}{\sigma\sqrt{n}}+\cdots \frac{X_{n}-\mu}{\sigma\sqrt{n}}, \quad n=1,2,\dots \]

then

\[ \lim_{n\to\infty}A_{n}\sim N(0,1). \]

Proof: $\,\,$ We shall assume, without loss, that each of random variable has zero mean and unit variance; otherwise we could just work with the standardized sequence $Y_{k}=(X_{k}-\mu)/\sigma$ and so we investigate

\[ A_{n}=\frac{X_{1}+\cdots +X_{n}}{\sqrt{n}}, \quad n=1,2,\dots \]

As all the random variables have the same distribution they also share the same characteristic function which we shall denote as $\phi.$ Furthermore, we know the random variables are independent so we can immediately appeal to Proposition @ref{prp:sumnrv} to deduce that

\[ \phi_{A_{n}}(u)=\phi^{n}\left(\frac{u}{\sqrt{n}}\right). \]

We know from @(eq:chone) that $\phi(0)=1$ and also, given that the random variables share a zero mean and unit variance we can, by Proposition @ref{prp:charmom), deduce that

\[ \phi^{\prime}(0)=i\mu = 0\quad {\rm{and}}\quad \phi^{\prime\prime}(0)=i^{2}\mu_{2}=-1. \]

Furthermore, since we’ve assumed that the each random variable has a finite third moment $\mu_{3}$ Proposition @ref{prp:charmom) also assures us that the third derivative of $\phi$ at $u=0$ is bounded. This allows us to use Taylors theorem to write

\[ \phi(u)=\phi(0)+\phi^{\prime}(0)u+\phi^{\prime\prime}(0)\frac{u^{2}}{2}+\mathcal{O}(u^{3})=1-\frac{u^{2}}{2}+\mathcal{O}(u^{3}) \]

where $\mathcal{O}(u^{3})$ signifies the contribution of the expression that can be bounded by a multiple of $u^{3}.$ In particular

\[ \phi_{A_{n}}(u)=\Biggl[1-\frac{u^{2}}{2n}+\mathcal{O}\left(\left(\frac{u}{\sqrt{n}}\right)^{3}\right)\Biggr]^{n} \]

Now a standard result from mathematical analysis of sequences tells us that if $(a_{n})_{n\ge 1}$ is a convergent sequence of real numbers such that $a_{n}\to a$ and $n\to \infty,$ then

\[ \left(1+\frac{a_{n}}{n}\right)^{n}\to \exp(a)\quad {\rm{as}}\,\,\, n\to \infty. \]

In our case we can define

\[ a_{n}=-\frac{u^{2}}{2}+\mathcal{O}\left(\frac{u^{3}}{\sqrt{n}}\right)\quad {\rm{for}}\,\,{\rm{which}}\,\,{\rm{we}}\,\,{\rm{have}}\,\, a_{n}\to -\frac{u^{2}}{2}, \]

and so, this allows us to conclude

\[ \lim_{n\to \infty}\phi_{A_{n}}(u)=\lim_{n\to \infty}\left(1+\frac{a_{n}}{n}\right)^{n}=\exp\left(-\frac{u^{2}}{2}\right). \]

We recognise this to be the characteristic function of the standard normal random variable and this observation, combined with Theorem 2.3 completes the proof. $\square.$

2.11 A Promise Kept

Earlier in this chapter I mention that it is possible to have two random variables where there is clear dependency yet this is not reflected in the covariance measure; which is zero! Here is an example to illustrate this. Let $X\sim N(0,1)$ be a standard normal random variable and let $Y=X^{2}.$ Of course, the outcome of $Y$ is absolutely $100\%$ dependent on the outcome of $X.$ Now famously, the standard normal distribution is symmetric about zero, this means that its third moment (used in the measure of skewness) is zero, so this means the random variable $X$ satisfies $\mathbb{E}[X]=\mathbb{E}[X^{3}]=0.$ OK, let us test the covariance measure between $X$ and $Y$:

\[ {\rm{cov}}(X,Y)=\mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y]=\mathbb{E}[X^{3}]-\mathbb{E}[X]\mathbb{E}[X^{2}]=0! \]

So, be warned, a zero covariance measure is not necessarily a signal of independence (even though independence certainly is a signal of zeron covariance).

References

Berger, M. A. 1992. An Introduction to Probability and Stochastic Processes. 2nd ed. Springer Texts in Statistics,Springer.