Chapter 4 Arbirtrage Free Derivative Pricing
Let us recall the model that we have proposed for the evolution of our asset. We wrote that over a time interval \([t,t+\delta t]\) the asset price moves according to:
or, equivalently, we have
The numerator of the right hand side is just the corresponding change in the asset price over the time interval \(\delta t,\) we can denote this as \(\delta S\) and write
We note that our incremental model (4.1) explicitly features an increment of Brownian motion and we write it as
In the differential limit as \(\delta t \to 0\) we get the continuous version of incremental model which we write as
This looks like a Brownian motion but it is not because of the \(S_{t}\) term. In fact, it is worth mentioning that a Brownian motion model is not a serious contender for the asset price because it can produce negative prices; which we never see in real financial markets.
What we have is what is known as a Geometric Brownian motion. To unlock this we turn again to It\(\hat{{\rm{o}}}\)’s Lemma, so what know is the plain Brownian motion
with drift rate \(\alpha\) and diffusion coefficient \(\sigma\) trivially satisfies the SDE/random walk
In It\(\hat{{\rm{o}}}\)’s Lemma terms, we are creating a new process by using the exponential function
the key derivatives are thus
Substituting into It\(\hat{{\rm{o}}}\)’s Lemma gives
What we have here has the form of the SDE/random walk model that we have proposed for the evolution of out asset. To capture it exactly we set
and so we see that the asset price process that satisfies our proposed model is
and this matches exactly with (??), the equation we arrived at in the previous Chapter.
4.1 The Black Scholes Partial Differential Equation
We recall that the a financial derivative is a contract that is written on an underlying asset \(S_{t},\) thus its value (which is precisely what we are interested in) at any given time \(t\) depends upon the price of its underlying asset \(S_{t}.\) Mathematically, we can quickly write that the price of a financial derivative is a function of \(S_{t}\) and time \(t.\) Let us pick the call option as the prototype example of a financial derivative and express its value as \(C(S_{t},t)\) We are now in familiar territory:
$$ We have a function of an underlying random process \(S_{t}.\)
\(\diamond\) We know the random walk/SDE of the underyling process, it is given by
\(\diamond\) We can apply It\(\hat{{\rm{o}}}\)’s Lemma to find the random walk/SDE that must be satisfied by \(C(S_{t},t)!\)
\(\diamond\) Under the assumption that \(C(x,t)\) is differentiable with respect to time and has (at least) two continuous second derivatives in \(x\) the random walk/SDE for the call price is
\(\diamond\) Note: there is nothing special about the call option here; any derivative on the underlying asset, whose value can be expressed as \(f(S_{t},t)\) will satisfy
We are now in a position to derive a partial differential equation (PDE) that must be satisfied by the call price (or the more general \(f\)). We arrive at this by showing how we can use (4.3) and (4.4) to combine the asset \(S_{t}\) and the call option \(C(S_{t})\) in such a way that it is free of any risk. Here’s the step:
We build a mini-portfolio \(\Pi\) consisting of a long position in the call option and a short position in the the underlying asset. Specifically, it is equaivalent to holding the call and short selling a quantity \(\Delta_{t}\) units of \(S_{t}.\) This means that at any time \(t\) the value of the portfolio is:
Using (4.3) and (4.4) we can work out the SDE/Random Walk for out portfolio
We note that, with a continuous rebalancing, where we always ensure the the number of units \(\Delta_{t}\) involved in the short side always matches the partial derivative \(\frac{\partial C}{\partial S},\) i.e., we always ensure that
then the two components that are underlined in the above SDE vanish. This has two very interesting consequences:
The term involving \(\mu,\) the drift rate in the asset price model (4.3) is eliminated.
The random component of the SDE is eliminated, meaning that a portfolio contstructed in this way is risk free!
Rebalancing the portfolio as suggested means that the random walk collapses to:
So, we have created a risk free investment! Now, given that we have agreed that there should be no arbitrage opportunities, this risk-free investment must be no different to the (easier) setting where we just place the amount \(C_{t}-\Delta_{t}S_{t}\) is a risk free bank and let is grow at the risk free rate \(r.\) Mathematically, this means:
Matching (4.6) with (??) we have
and, reaaraning, we arrive at the famous Black-Scholes partial differential equation of option pricing:
In what follows, to aid the presentation, I will drop the sub-script \(t\) on the asset (it should be clear that the asset price is a function of time). That said, the quantity \(\Delta\) being a mathematical derivative can be viewed as the sensitivity of the call option to small changes in the underlying asset; going back to high-school calculus \(\frac{\partial C}{\partial S}\) is the slope of surface of the plot of \(C(S,t)\) in the asset-space - if the slope is big it suggests that a small change in \(S\) can have a big impact on the price of the call. Continuing with the calculus motivation we can also think of the second derivative \(\frac{\partial^{2} C}{\partial S^{2}}\) and the time derivative as measure of sensitivity too. In the financial litereature these derivatives are assigned their own greek letter, collecting them together here we have
These are the so-called ‘greeks’ of option pricing. We will return to them later in the course because they play an important role in developing trading strategies. To set the scene the greeks are usually more informative when we have a portfolio \(\Pi\) of options on the same underlying, then we have:
\(\bullet\) the delta/gamma/theta of the portfolio is the appropriate weighted sum of the individual deltas/gammas/thetas of the options making up the portfolio.
If we employ a second order Taylor approximation for the change in portfolio value we have that
From the geometry of the situation we can see that if the portfolio is balanced so that \(\Delta =0\) then this reassures us that our portfolio is almost immune to small changes in the underlying asset price; in such a case the portfolio is said to be delta-neutral.
The gamma measure tells us how sensitive the portfolio is to its \(\Delta,\) remember, a rebalancing of the portfolio is needed to change its overall delta. Thus, if the gamma is high this suggests that the portfolio is very sensitive to the delta and, unfortunately for the portfolio manager, indicates that it needs to be rebalanced more often. Ideally, the portfolio manager who is concerned about risk, should try to ensure that the portfolio is both delta-neutral (\(\Delta =0\)) \(\underline{AND}\) gamma-neutral \((\Gamma =0)\); in normal applications the gamma should be kept small.
This just leaves the sensitivity to time. We have already shown, in the first chapter, that as time marches on and we approach the expiry date \(T\) of the option, it loses value (it is a decreasing function of time) and the \(\Theta\) will be negative.
I have introduced these concepts here so that I can present an alternative expression for the Black-Scholes PDE (4.7) using the ‘greeks’, i.e.,
Of course there are many functions that adhere to the Black-Scholes PDE, the PDE itself knows nothing about what kind of option we are evaluating. This is only pinned down with the final condition, so in our case for the European call we need also to add
For a put we could swap the \(C\) notation to a \(P\) and impose
The final condition tells us how the solution in the asset space direction at crucial moment of time. In addition, and in order to pin down a unique solution, we need to consider how the solution should behave when the asset price is at its two extremes; in mathematical terms this means when \(S=0\) and when \(S\to \infty.\) The solution must behave in the same way at all times when these conditions are imposed, they are called the boundary conditions of the PDE. These boundary conditions need to be condidered on a case by case basis, for the European call we argue as follows:
\(\bullet\) If \(S=0:\) In this case \(dS=0\) and so the asset price will never move, there is then no chance of the holder ever getting profit from a call option in this case. It will never be exercised and so its value is zero. So \(C(0,t)=0.\)
\(\bullet\) If \(S\sim \infty:\) This case is obviously not realistic but we can consider the situation when the asset price is already much, much bigger than the strike. In this case it is unlikely that you would find anyone willing to provide you with such a product as because it is guaranteed to deliver the payoff \(S-K,\) now when \(S\) is astronomically large then subtracting \(K\) is like removing a drop from the ocean and so the value of such an option would be the asset price itself \(S,\) so we say \(C(S,t)=S\) when \(S\to \infty.\)
So for completeness the price of the European call will emerge when we solve the Black-Sholes PDE subect to the terminal condition AND the two boundary conditions we have set out:
In developing the partial differential equation that all financial derivatives (who have \(S\) as an underlying) we have come a long way. The next step, of course, is to solve it. Well, if you were to present this particular PDE to someone with some skill in this area you may hear them groan; the reason for this is that they would notice that some of coefficients that multiply the various ‘driving’ terms (the parial derivatives) are not constant, they are functions of \(S.\) To highlight this I’ve underlined them here:
So what we have is a PDE with variable coefficient and, on most occasions, these are much harder to solve. However, in our case we fall lucky, with a clever change of variable (from \(S\) to \(x\) say) and a bit of elementary calculus we can transform the above PDE in \(S\) to a constant coefficient PDE in the new variable \(x.\) The change of variable that does the trick is to set
Using the chain rule we for a general change of variable we have that
In our case
and so we have
For the second derivative we have:
On the part that is underlined we apply the product rule so that we finally arrive at
We note from (4.9) that the red term is just \(\frac{\partial}{\partial x}\) and so, after rearraning the terms above, we can conclude that:
Now, give the change of variable, we emphasize this in the PDE too by setting
Then, using this and also (4.9) and (4.10), the plain Black-Scholes PDE transforms from
to
i.e., we have a constant coefficient version
Further simplifications can be made by considering the following further substitution:
As an exercise you can work through how the (4.11) would transform into an equation in \(v,\) you should be able to identify suitable choices for \(\alpha\) and \(\beta\) than allow you to discover that what you have collapses to
i.e., we are able to eliminate the first derivative term in \(x\) AND the reaction term \(ru.\) One final comment on this PDE… Usually PDEs are designed to model some natural phenomena like a chemical reaction or the dissipation of heat through some conducting material. In these cases we typically know the system at the very beginning (the initial condition) and the PDE governs the behaviour of the system through time. Our situation doesn’t fit into this way of thinking because, for a financial derivative, the information that we know is what happens at the end - we have a final condition. We can easily make our problem fit the standard structure by reversing time, that is insead of measuring time \(t\) as it ticks closer and closer to the expery date \(T,\) we can, instead, measure the time to go, the time to expiry, how long is left. If we give denote this by \(\tau\) then obviously we have
working with \(\tau\) instead of \(t\) has the relatively minor effect that
and so the transformed equation, above, can be written (finally) as
The reason I have laboured so much over this development is because (4.12) is the famous heat equation, one of those classic pdes that is well understood. In its simplest form it is given by
and it models how the temperature distribution across an infinitely long bar of a certain conductor, \(h(x,t)\) is the temperature at time \(t\) measured at the spatial position \(x\) along the bar. The equation comes from a heat balance, the temperature gradient is given by the first partial deriviative \(\frac{\partial h}{\partial x}.\) The second derivative \(\frac{\partial^{2} h}{\partial x^{2}}\) describes the change in this gradient over a small section of the material, we think of this as a measure of retained heat. This retained heat causes the temperature to change over time (measured by \(\frac{\partial h}{\partial t}\)) and so we say the two quantities, retained heat and rate of temperature change, must be proportional to each other - the heat equation above expresses with statement mathematically and the constant \(\kappa\) depends upon the conducting material being used. Suffice it to say this equation is well understood and we can use what has gone before us to work out the solution to our problem. I am now going to quote what you get for a call option, this expression is by no means obvious but later in the course I will return to show exactly how we get to it. The fair price of a European call in the Black-Scholes framework is given by
where \(\Phi(\cdot)\) is the standard normal distribution i.e.,
and where the parameters \(d_{1}\) and \(d_{2}\) are given by
You will notice that having spent all of that time strengthening up our probability theory knowledge, we haven’t really used it yet. Fear not, I will now leave the PDE approach to pricing behind and focus attention on an alternative view of pricing which does use probability theory arguments. We will start off with a very simple toy example and gradually build this up!
4.2 One Period Pricing
We begin with an appetizer; a simple example that contains most of the insights we will need. We will consider a simple single period world of now \(t=0\) and a future expiry date \(T.\) Across this period we will explore three things
Placing cash in the risk-free bank. This is straightforward, if the continuously compounded interest rate is \(r\) then one unit of our currency, lets follow the crowd and call it a dollar, will grow and be worth \(\$1\cdot e^{rT}\) at time \(T.\)
Buying an asset \(S\) (at \(t=0\)) and keeping in until \(T.\) This is obviously more risking than cash in the bank, we do not know the value of the asset at \(T\) but we will assume a very simple model, with only two states of the world (and up-state and a down-state) for its future price. We will say that if the asset is the an up-state its value is \(u\cdot S\) and if it is in the down-state its value is \(d\cdot S,\) here we assume that \(u>d>0\). In addition, we assign probabilities to these states and write
We will also assume that
I’ll return to this condition later but I think, because of the risky nature of the asset, it is not too controversial to expect it to be true. By taking on the risk you expect the reward (in the upstate) to be better than if we simply put \(\$S_{0}\) (the amount we would pay for the asset) in the risk free bank. But the risky nature of the investment means we also have to accept that we may find ourselves in a position (the downstate) where cash in the bank would have been the better idea.
- A call option on the underlying \(S\) with a strike price \(K\) with \(T\) as its maturity date. Here we can apply the payoff at time \(T,\) i.e., we can say something concrete at the future time but what we don’t know is what its fair value is, what price should we pay for it at \(t=0?\) What we know is summarize as follows
The plan of attack is to try an replicate the value option payoff values \(C_{u}\) and \(C_{d}\) by investing in a simple portfolio \(\Pi\) involving a combination of the asset and a safe cash deposit. Specifically, we will enact the following
\(\bullet\) At \(t=0\) we buy \(\alpha\) shares of \(S\) and place \(\beta\) dollars in the risk free bank.
The upshot of this stratagy at time \(T\) is illustrated by
Matching the outcome of this mini-portfolio against the outcome of owning a call option we get
Subtracting the second equation from the first leads to
From the first equation we have that
then substituting for (4.14) we get the following development
Now, taking a view on this… we’ve created a mini-investment \(\Pi\) whose value at time \(T\) is guaranteed to match the value of the payoff from the call option. This is often termed a replication strategy. Then, under the assumption of no arbitrage, these two seemingly different products \(\Pi\) and the call option \(C\) must also have the same value at time zero and hence we conclude
Plugging in the expressions for \({\color{red}{\alpha}}\) and \({\color{blue}{\beta}}\) we find that
Now if we let
then due to (4.13) we know that \(0<q<1\) and furthermore we have that
and so, in view of (4.15), we can view \(q\) as a probability and express the call price as
Thus, we have a probabilistic view of the value of the call option. It is found by discounting (applying \(e^{-rT}\)) the expected future pay-off using \(q\) and \(1-q\) as probabilities. Many students find this surprising… it appears that the true probabilities \(p\) and \(1-p\) (of the assets’ up and down states) play no part in the pricing of the option. Let us look at a couple of examples.
Example 4.1 (Replication In Action 1) If the prevailling risk-free interest rate is \(12\%\) find the price of a \(3\)month call option struck at \(\$21\) on an asset \(S\) whose current value is \(\$20\) and whose value at expiry is given by
Collecting the key information in the standard notation we have
The picture below brings together what we know of the asset, the risk free bank and the call option.
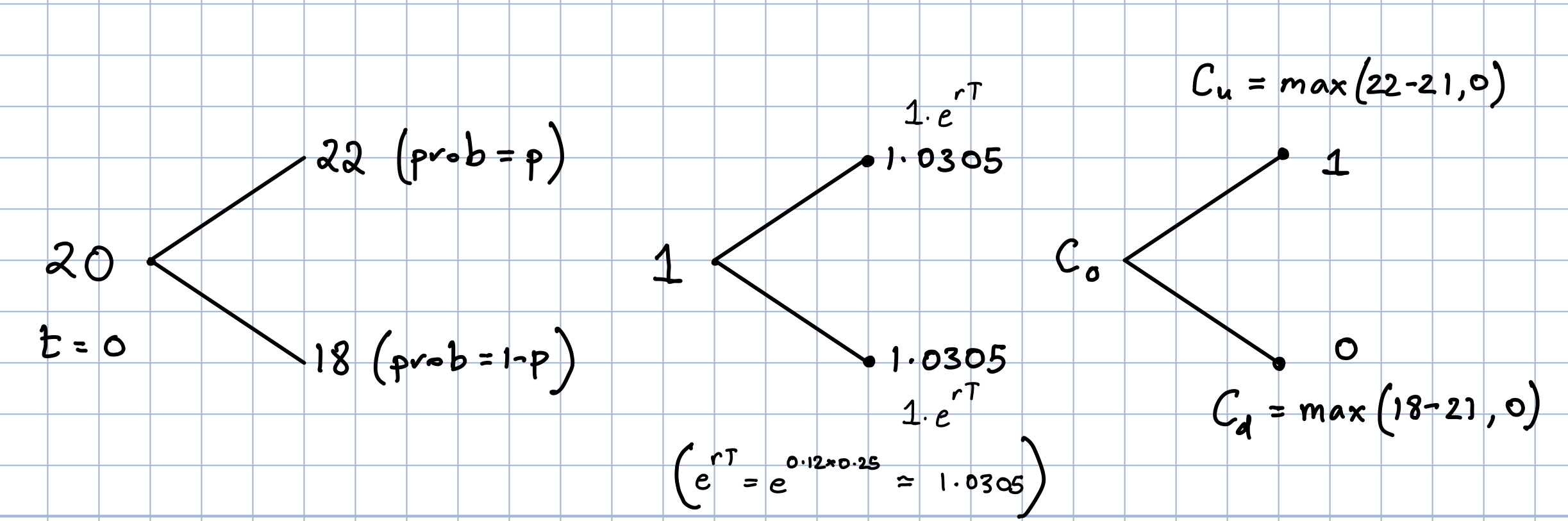
Applying the replication strategy we take \(\alpha\) shares of \(S\) and place \(\beta\) cash in the risk free bank. In three months we hit the maturity date \(T\) and the value of the investment is represented as
Meanwhile the payoff of the call option at this point is given by
Matching these up provides two equations:
Subtracting the second from the first gives
\[ 4\alpha =1 \implies \alpha = \frac{1}{4}. <center>\]
Substituting this value into the second equation gives
The negative sign indicates that we borrow from the risk free bank rather than deposit. Thus, the strategy we should employ to replicate the call price is
\(\bullet\) buy \(\frac{1}{4}\) of a share of the asset;
\(\bullet\) borrow \(\$4.37\) from the risk free bank.
Given that the strategy replicates the call at \(T\) then the value of the call (in the absence of arbitrage) must match the value of the strategy at \(t=0\) and so we conclude that
We remark that the approach outlined above in instructive however we could access the same result more quickly (but perhaps without the insight) if we simply employ (4.16). Specifically, we note that
and so
then we apply
Example 4.2 (Replication In Action 2) If the risk free growth of a deposit over a period \([0,T]\) is \(1.25,\) find the \(t=0\) price of a call option struck at \(\$5\) on an asset \(S\) whose current value is \(\$4\) and whose value at expiry is given by
The picture below brings together what we know of the asset, the risk free bank and the call option.
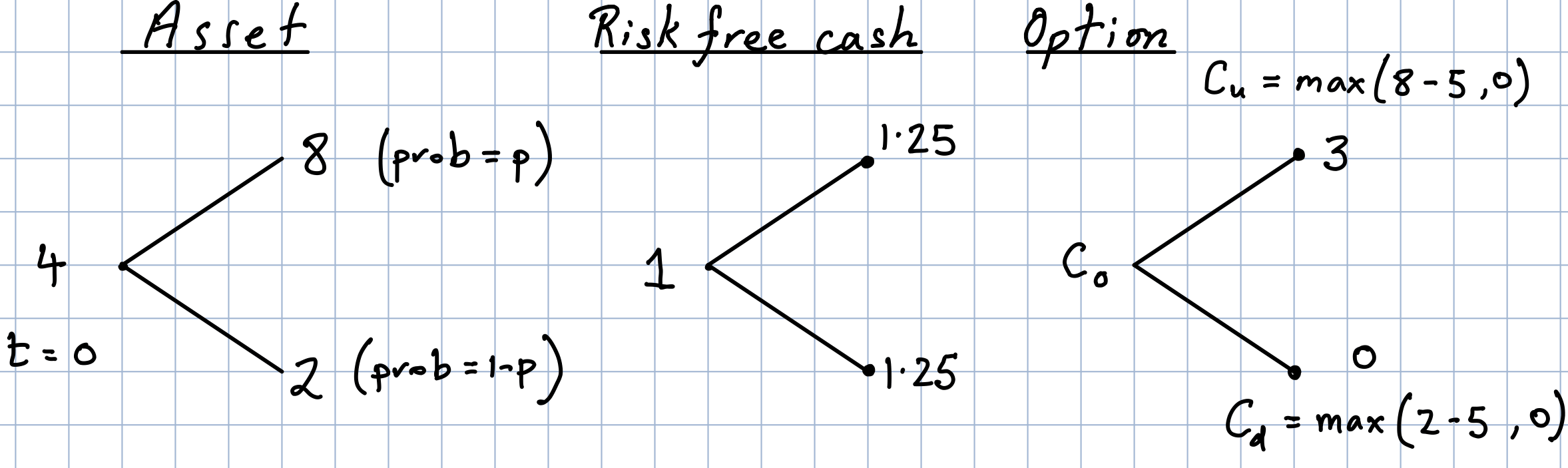
Applying the replication strategy we take \(\alpha\) shares of \(S\) and place \(\beta\) cash in the risk free bank. In three months we hit the maturity date \(T\) and the value of the investment is represented as
Meanwhile the payoff of the call option at this point is given by
Matching these up provides two equations:
Subtracting the second from the first gives
Substituting this value into the second equation gives
The negative sign indicates that we borrow from the risk free bank rather than deposit. Thus, the strategy we should employ to replicate the call price is
\(\bullet\) buy \(\frac{1}{2}\) of a share of the asset;
\(\bullet\) borrow \(\$0.80\) from the risk free bank.
Given that the strategy replicates the call at \(T\) then the value of the call (in the absence of arbitrage) must match the value of the strategy at \(t=0\) and so we conclude that
Equavalently if we simply employ (4.16) we note that
and so
then we apply
The pricing formula in the one-period world is worth repeating:
where the probabilities \(q\) and \(1-q\) are synthetic, meaning they are entirely independent of the real world probabilities \(p\) and \(1-p\) that are associated with likelihood that asset is in an upstate or a downstate. The suggestion is quite plausible, it says that we use the \((q,1-q)\) probabilities to compute the expected value of the option pay off and then apply the appropriate discount factor to arrive at its value today. This is captured in the picture below (across a more general time interval $[T-t,T]). The question is:
\(\bullet\) Just what is it about the \(q\) and \(1-q\) that make the formula work?
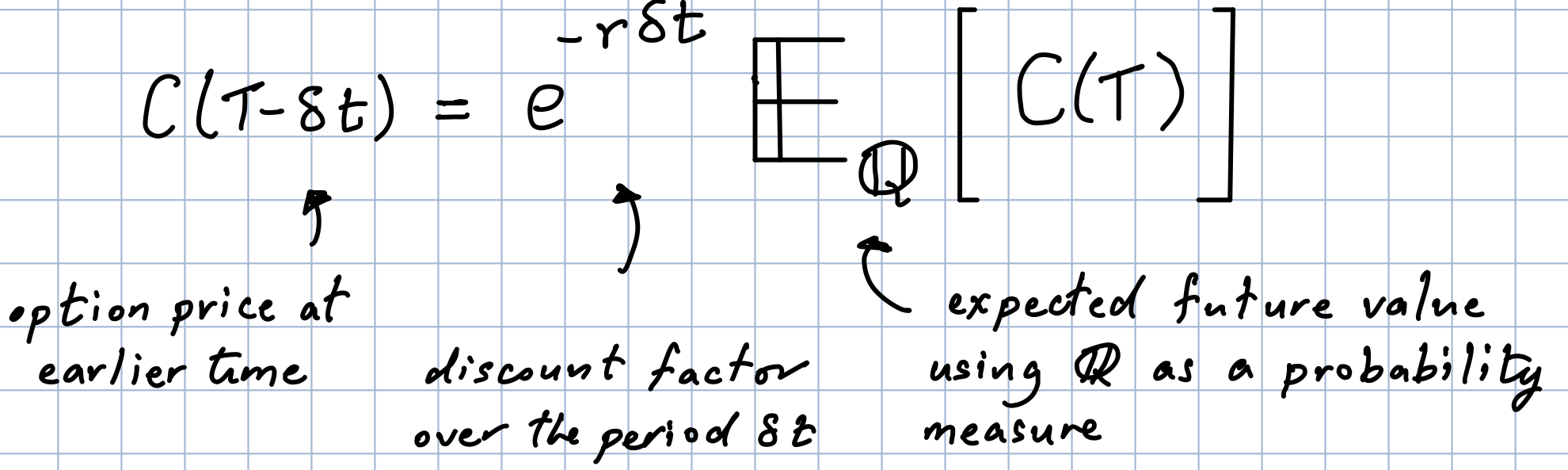
As an experiment let us see what happens if we average the asset price using the \(q\) probability. In the first example we had
We found that \(q= 0.6523\) and so switching to \(q\) we would have
Then, taking the expectation we find
now lets find the present value of this expectation
So we find that the discounted Expected value of the asset coincides with the current proce of the asset. This is no fluke, you can check the same conclusion from the data in the second example. The next result confirms this property beyond any shadow of doubt.
Proposition 4.1 (Martingale Property of q) Suppose that prevailing risk free interest rate is \(r\) and, over the period \([0,T],\) an asset evolves according to the simple two-state model
where \(0<d<e^{rT}<u.\) If we replace the realworld probability \(p\) with the synthetic probability \(q\) given by
then we have that
Before we embark on proving this result let us consider what it is really saying. From a probability theory perspective we can write define \(X_{t} = e^{-rt}S_{t}\) this is stochastic process that describes the discounted asset price. In the above result there are only two time points to consider: now, (at \(t=0\)) and the future (at \(t=T\)). The result states that the expected value (forecast) of \(X_{T},\) using the \(q\) probability, is the current value \(X_{0}=e^{0}S_{0}=S_{0}.\) We’ve encountered this before. We can say, using the more advanced language of probability theory, that the process \(X_{t}\) is a martingale when the expectation is taken with the \(q\) probability. Another (equivalent) way of saying the same thing is that expected value of the asset (using the \(q\) probability) precisely matches the amount we would have received if, instead, we place the amount spent on the asset into the risk-free bank, i.e., we have
For this reason, we say that \(q\) is the risk neutral probability. Let’s now complete the proof.
Proof \(\,\,\) This is just an exercise in verification:
\(\square\)
4.3 Pricing via Probability Theory
The development of the one period model in the previous section hints at a route for pricing a derivative in general. We have the following clues:
\(\bullet\) In the one period case we have a simple model for the asset price:
In the continuous world we have derived the more sophisticated model
\(\bullet\) In the one period model we found that ‘the process’ \(X_{t}=e^{-rt}S_{t}\) is a Martingale when the expectation is take with the risk-neutral probability \(q\) (as opposed the the real world probability \(p\)). Given that the risk free rate \(r\) is a constant (not random) this discovery can be expressed as:
In the discrete case \(q\) is known, we have a formula for it. In the continuous case the analogue of the discrete \(q\) is the probability denisty function \(q(x)\) such that we have
The task of identifying this \(q(x)\) looks like a tall order but it is manageable. Here is the recipe we will follow:
\(\diamond\) First we’ll compute the true probability density function \(p(x)\) for \(S_{t}.\)
\(\diamond\) Second we will compute the expectation of \(S_{t}\) (Note: This is really easy because we’ve actually done it before - back in Chapter 2 example 2.3). Given that we have gone to the effort of finding the density we will also verify this expectation directly, thus - same result with two different approaches! We will also compute the variance while we are at it as it is an easy by-product of the calculation.
\(\diamond\) As soon as we see the expectation calculation above it will become immediately apparent that a simple change is needed in order to make the expectation of \(S_{t}\) match exactly with \(S_{0}e^{rt}.\) When this change is implemented in the real probability density function \(p(x)\) we arrive at \(q(x)\) and this will be our proposed risk-neutral measure of probability in the continuous setting.
So lets make a start. First we’ll compute the distribution of \(S_{t}\) and we will get the density by differentiating it so…
- What is the distribution \(F(x)\) say, of the random variable \(S_{t}?\)
Using the trick that \(S_{0}=\exp(\ln(S_{0}))\) we have that
where
looks rather complicated but please stay with it, all will become much clearer in a short amount of time. Since \(\Theta_{t}\) is normally distributed (with mean \(\ln(S_{0})+\left(\mu-\frac{\sigma^{2}}{2}\right)t)\) and variance \(\sigma^{2}t\)) we can write its distribution as
By definition, the distribution of \(S_{t}\) is given by
Taking logs we arrive at
It mat look difficult, but we’ve got there - \(G(x)\) above is the distribution of \(S_{t}.\)
- What is the probability density function \(p(x)\) of \(S_{t}?\)
By definition the density is the derivative of the distribution and so we have
We have made it, note that \(p(x)\) is only defined for \(x\ge 0.\)
Moving on to the second item of out recipe. We want to compute the expected value of \(S_{t}.\) Well, given that we now have the density function for \(S_{t}\) this is, of course, just a matter of computing
note the \(x\) in the integrand cancels with the \(x\) in the denominator of the first factor of \(p(x).\) In can let you into a secret here, as I’ve already alluded to… we have computed this expectation before. Looking back at example 2.3 back in Chapter 2 we showed that, if \(Z\sim N(0,1)\) then
So, in our set up we have that:
It is very convenient to use this previous result to deliver the final answer, but seeing as though we’ve gone to the trouble of computing the actual probability density let’s verify it that way too. Well it will come as no surprise that we attempt this integral using a substiution, specifically we set
Accordingly the differential mapping is
and the limits pass over to
so the transformed integral becomes
This doesn’t look the most appealing of integrals to comute, but it can be done. In fact, in order to see the wood from the trees I will present the next result which, as you will easily notice, provides us with what we need (and more). It has to be done I’m afraid, we are going to have to expand the square on the numerator term within the exponential function and then tidy it up. To help see the wood from the trees the next result reveals where this development will eventually take us (and then we will show it!).
Proof \(\,\,\) We start off by writing slowly developing the integral into a form that we can manipulate. Here goes:
I’m afraid it has to be done! We are going to expand the quadratic in the numerator of the exponential function’s argument. This is done carefully over he following few lines:
The last step here comes from completing the square. If we pick up the two end terms of the above development we notice that we have a difference of two squares and this can easily be factorized as
This means that we can write the numerator part that we’ve been working on, in the following way:
This does seem like a fair amount of tedious algebra but it is all about to pay off, lets substitute in what we’ve got and get to where we need to go. We now have
\(\square\)
The next result is a simple corollary to the lemma, it is not necessarily vital to us right now, but it will come in handy later on when we are pricing options.
where
In particular, if the limits are the extreme ends of the real line we have:
and
Proof: The result easily follows by taking the following change of variable
and so, the integral we are interested in (on the right hand side)
becomes
with the \(\ell\) and \(u\) exactly as quoted, i.e., the integral on the right hand side. We note that the final pair of identities follow since
the final equation is true because of the symmetry of the standard normal distribution.
\(\square.\)
Armed with Lemma 4.1 we can now compute and verify the expectation because it allows us to write
The integral in red is unity because the integrand is precisely a probability density function, specifically, for a \(N\left(\mu+\frac{\sigma^{2}}{2},\sigma^{2}t\right)\) random variable. Thus, we have verified that the expected future value of the asset, under the real world measure of probability (density \(p(x)\)) matches \(S_{0}e^{\mu t}\) where \(\mu\) is the drift rate in the asset price model.
We can now see what needs to be done. We want the analogue of the discrete \(q\) probability from the (easy) one period approach. The crucial property that this discrete \(q\) probability has is:
We’ve discovered that above that, in the continuous setting, if we compute the future value of the asset with the true probability density function \(p(x)\) we get
This suggests that by setting \(\mu = r\) the corresponding risk neutral probability density is
and if we take the expectation with respect to \(q(x)\) we get the desired analagous result:
Now, armed with \(q(x)\) (the risk neutral probability measure) we now have a probabilistic way of computing option prices. For any financial derivative written on an asset \(S\) whose value we know at expiry time \(T\) to be
then the fair price of the option at any time \(0<t<T\) is given by
where \(q,\) as we’ve discovered, is the risk neutral probability density which, in the setting above, is given by
Before we launch in and show this formula in action we can tie up some loose ends by computing the variance of the future price of the asset. The caclulation relies on the identity
If, we have \(X= e^{\alpha Z +\beta}\) where \(Z\sim N(0,1)\) then we can return to the formula
to easily deduce that
We have seen how the first result, when applied to the continuous model for \(S_{t}\) leads to
Applying the second result we have
Thus, using the variance formula, we can deduce that
OK, not that we have pinned down the risk neutral probability measure that we should use for pricing, let’s price an option!
Theorem 4.1 (Fair Price of European Call) Let \(r\) denote the prevailing risk free rate of return. The fair value of a European call option on an underlying asset \(S\) with strike price \(K\) and expiry date \(T\) is given, at time \(0<t<T\) by
where \(\Phi(\cdot)\) and where the parameters \(d_{1}\) and \(d_{2}\) are given by
Proof \(\,\,\) We know the final condition for the call option
Thus, we can immediately appeal to (??) to yield that
We are in familiar territory here, when we evaluated (4.17) we made the change of variable to replace the \(\ln\) term with a new variable of integration. We do the same here, we set
Taking care of the limits of integration we find that
Now the max function only kicks in when \(S_{t}e^{y}-K>0,\) i.e., when
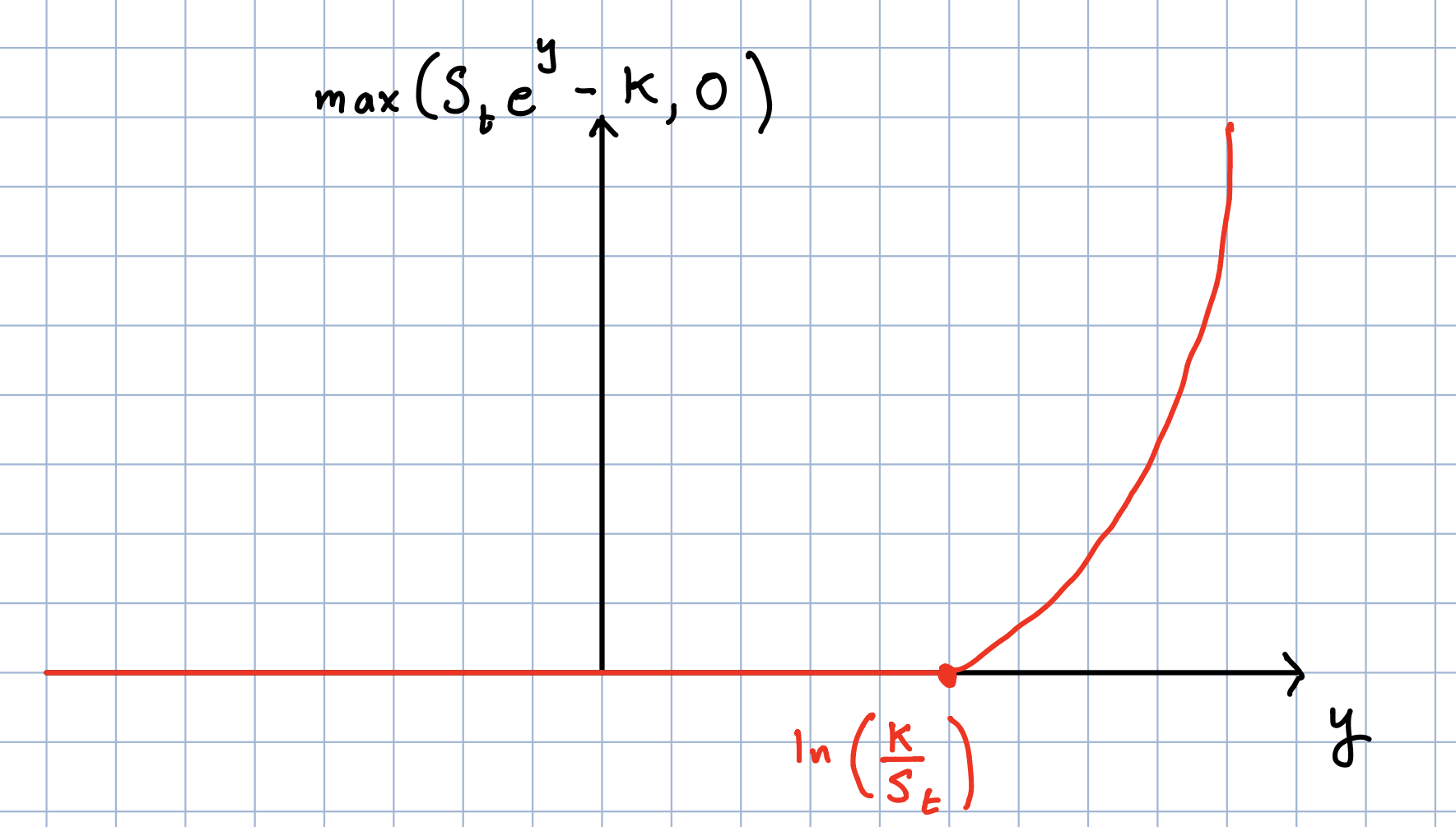
This means we can rewrite the intergal more accurately as
Using Lemma 4.1 on the first integral (with \(t\) replaced by \(T-t\) and \(\mu\) replaced by \(r\)) we we see that this can be written as
Now it is only a matter of appealling to the final quoted result of Corollary 4.1 (again with \(t\) replaced by \(T-t\) and \(\mu\) replaced by \(r\)) to deduce that
where
and
as required. \(\square\).
Let us take stock of what we have achieved.
Introduced the concept of no arbritrage in finacial markets.
Refreshed our understanding of probability threory.
Heuristically developed a model for the evolution of an asset price, building in a term \(\mu\) to describe the drift rate of the asset and a term \(\sigma\) to describe the volatility of the asset.
Strengthened our understanding of financial modelling by learning a splash of stochastic calculus: Brownian motion, Random walks, Ito’s Lemma and Stochastic Differential Equations.
Using the stochastic calculus together with an application of the principle of no arbitrage we derived the famous Black-Scholes partial differential equation (PDE) and showed how this can, with an appropriate change of variables, collapse to the even more famous heat equation.
We make the important observation that the drift rate \(\mu\) that appeared in our asset price model, does not feature in this PDE!
Without delving into the details of solving PDEs we simply quoted the solution for the case of a European call.
Leaving the PDE approach behind we presented an alternative route for pricing very simple classroom option pricing problems; one period pricing. Here there are only two time points to consider (today \(t=0\) and option maturity \(T\)). Using a simple two-state model for the underlying asset, we replicate the payoff of the option using a combination of buying or short selling the asset and borrowing or depositing cash in a risk free bank. The principle of no arbitrage is used to derive a fair price.
We notice once more that the real world dynamics of the asset do not feature. The fair price is express in the form of a discounted expectation but the expecation is done with respect to a probability \(q\) (not the real world probability \(p\)).
We investigate how the intruiging one step model can be generalised to the continuous setting. We note that a property of the \(q\) probability is that when used to find the expected value of the future asset price it delivers the same result as it we’d placed the asset in a risk free bank, i.e., we observe:
in technical terms this suggests that the discounted price process \(X_{t}=e^{-rT}S_{t}\) is a martingale.
The above observation gives us our hint for a route toward option pricing using a discounted expectation - where the expectation needs to be taken with respect to the correct probability density \(q(x)\) ( the analogue of the discrete \(q\) in the one period case).
We put together a plan to discover \(q(x).\) This plan involved first capturing the real-world probability density function \(p(x)\) of our underlying asset, here we used our probability theory knowledge.
Equipped with \(p(x)\) we then went on to use it to calculate the expected future of our asset using and we discovered that it was \(S_{0}e^{\mu T}.\)
In view of the above discovery, and the one period result that we want to emulate, it becomes apparent that we arrive at the desired \(q(x)\) by replacing the drift rate \(\mu\) with the risk free rate \(r.\)
With the \(q(x)\) pinned down we demonstrate its power by emulating the simple call option pricing formuala from the one period setting, i.e.,
to derive the price of a call option; we find that ths precisely matches (of course it does!) the one I quoted from the derivation of the Black-Scholes PDE.
We have come a long way. I would like to zip up the bag on this strand of our analysis BUT there is one thing that is bugging me; perhaps it is bugging you too? Reading through all of this the one (perhaps surprising) thing… form a pricing point of view the drift term \(\mu\) term never ever crops up. Of course, we are now blessed with this hindsight but it does make me wonder if things might be even easier if, armed with this hindsight, we just go back to the start and simply replace \(\mu\) with \(r,\) this means our model for the evolution of the asset return is not the real world one but the model in a risk neutral world, in which we’d write
Let’s say we are pricing a European call option just like the one we have already tackled.
The payoff function as we well know is given by
Now, what we could do here is to consider the above as a function of the standard normal random variable \(Z\) and compute the expected future payoff using the law of the unconscious statistician that we were exposed to in the Expectation section of Chapter 2. Here we don’t worry about having the right probability density function, we are armed with the hindsight that using the risk free rate innstead of any drift rate should (will) yield the right result. So we have
As before, the complicated looking integrand here is zero for much of the time and only kicks in with a non-zero value when
Looking back at the develoment that has gone before we recognise this lower limit to be \(-d_{2}\) in the Black-Scholes formula jargon. Thus we can set off with the next stage of our development
Hopefully the development from one equation to the next is easy to follow, the final line is just a shift of variable in the integration which is reflected in the change of the lower limit. Now we notice, once again from the notation that we have already established in the Black-Scholes framework that
and so, in the end we have
This is the expected future payoff of the call option. To get today’s fair price of this contract we apply the discount factor \(e^{-rT}\) and, surprise-surprise!, we have
the Black-Scholes price of the European call (derived with hindsight!).
4.4 The Black Scholes Formula
In this section we will shed some light on two terms that appear in the Black-Scholes option pricing formula, namely \(\Phi(d_{1})\) and \(\Phi(d_{2});\) our aim is to give these terms an economic interpretation.