笔记 7 统计推断

7.1 导论

定义用需要考虑不确定度的含噪音的统计学数据推断事实
工具随机化随机采样采样模型假设检验置信区间概率模型实验设计 bootstraping 排列交换随机
类型
频率派使用概率的频率解释来控制错误率
贝叶斯派给定概率与数据概率哪个靠谱

7.2 概率

术语
样本空间 Ω
事件样本空间子集 E
单独事件 ω
空事件 ∅
$ω∈E$ ω发生E发生
$ω∉E$ ω发生E不发生
$E⊂F$ E发生则F发生
$E∩F$ EF一起发生
$E∪F$ EF中至少一个发生
$E∩F=∅$ EF互斥
$E^c$ 或 $\bar E$ E不发生
概率

对事件 $E\subset \Omega$, $0 \leq P(E) \leq 1$
$P(\Omega) = 1$
如果 $E_1$ 与 $E_2$ 互斥有$P(E_1 \cup E_2) = P(E_1) + P(E_2)$.
概率无限可加性 $P(\cup_{i=1}^n A_i) = \sum_{i=1}^n P(A_i)$
$P(\emptyset) = 0$
$P(E) = 1 - P(E^c)$
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
如果 $A \subset B$ 则 $P(A) \leq P(B)$
$P\left(A \cup B\right) = 1 - P(A^c \cap B^c)$
$P(A \cap B^c) = P(A) - P(A \cap B)$
$P(\cup_{i=1}^n E_i) \leq \sum_{i=1}^n P(E_i)$
$P(\cup_{i=1}^n E_i) \geq \max_i P(E_i)$

随机变量
实验的数值输出
离散随机变量取可数的概率 $P(X = k)$
连续随机变量取连续区间子集概率 $P(X \in A)$
概率质量函数（PMF）<- 离散随机变量

对于所有 $x$ $p(x) \geq 0$
$\sum_{x} p(x) = 1$

概率密度函数（PDF）<- 连续随机变量

对于所有 $x$ $f(x) \geq 0$
$f(x)$ 下面积为1

累计概率函数（CDF）
定义 $F(x) = P(X \leq x)$
生存函数 $S(x) = P(X > x)$ $S(x) = 1 - F(x)$
对于连续函数 CDF是PDF的积分
分位数 $\alpha^{th}$
$F(x_\alpha) = \alpha$
$50^{th}$ 分位数是中位数

7.3 期望

离散随机变量均值 $E[X] = \sum_x xp(x)$
$E[X]$ 代表质量与位置的中心 $\{x, p(x)\}$
连续随机变量均值 $E[X] = \mbox{the area under the function}~~~ t f(t)$
期望值是线性可加的
如果 $a$ 与 $b$ 不随机 $X$ 与 $Y$ 是随机变量
$E[aX + b] = a E[X] + b$
$E[X + Y] = E[X] + E[Y]$
样本均值是总体均值$\mu$的无偏估计的证明 \[ \begin{eqnarray*} E\left[ \frac{1}{n}\sum_{i=1}^n X_i\right] & = & \frac{1}{n} E\left[\sum_{i=1}^n X_i\right] \\ & = & \frac{1}{n} \sum_{i=1}^n E\left[X_i\right] \\ & = & \frac{1}{n} \sum_{i=1}^n \mu = \mu. \end{eqnarray*} \]

7.4 方差

描述随机变量的离散情况
如果 $X$ 是均值 $\mu$ 的随机变量其方差为$Var(X) = E[(X - \mu)^2]$
离开均值距离期望的平方
计算公式 $Var(X) = E[X^2] - E[X]^2$
如果 $a$ 是常数有 $Var(aX) = a^2 Var(X)$
方差的开方是标准差单位与 $X$ 一致
车比雪夫不等式（Chebyshev’s inequality）边界极为保守 \[ P(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2} \]

7.5 独立性

独立事件
两事件 $A$ 与 $B$ 在 $P(A \cap B) = P(A)P(B)$ 下独立
在 $P([X \in A] \cap [Y \in B]) = P(X\in A)P(Y\in B)$ 下两随机变量 $X$ 与 $Y$ 独立
对于一组随机独立变量$X_1, X_2, \ldots, X_n$有 $f(x_1,\ldots, x_n) = \prod_{i=1}^n f_i(x_i)$
iid随机变量（independent and identically distributed）来自同一分布相互独立的随机变量
协方差（covariance）
$Cov(X, Y) = E[(X - \mu_x)(Y - \mu_y)] = E[X Y] - E[X]E[Y]$
$Cov(X, Y) = Cov(Y, X)$
$Cov(X, Y)$ 可以有正负
$|Cov(X, Y)| \leq \sqrt{Var(X) Var(y)}$
相关性（correlation）
$X$ 与 $Y$ 的相关性 $Cor(X, Y) = Cov(X, Y) / \sqrt{Var(X) Var(y)}$
$-1 \leq Cor(X, Y) \leq 1$
只有对常数 $a$ 与 $b$满足 $X = a + bY$ 时$Cor(X, Y) = \pm 1$
$Cor(X, Y)$ 无单位
$Cor(X, Y) = 0$ 时 $X$ 与 $Y$ 不相关
$Cor(X,Y)$ 越接近1 $X$ 与 $Y$ 越正相关反之接近-1 负相关
$\{X_i\}_{i=1}^n$ 是一组随机变量当 $\{X_i\}$ 不相关时 $Var\left(\sum_{i=1}^n a_i X_i + b\right) = \sum_{i=1}^n a_i^2 Var(X_i)$
如果一组随机变量$\{X_i\}$不相关方差的和等于和的方差非标准差
样本均值方差的推导 \[ \begin{eqnarray*} Var(\bar X) & = & Var \left( \frac{1}{n}\sum_{i=1}^n X_i \right)\\ \\ & = & \frac{1}{n^2} Var\left(\sum_{i=1}^n X_i \right)\\ \\ & = & \frac{1}{n^2} \sum_{i=1}^n Var(X_i) \\ \\ & = & \frac{1}{n^2} \times n\sigma^2 \\ \\ & = & \frac{\sigma^2}{n} \end{eqnarray*} \]
当 $X_i$ 独立且方差为 $Var(\bar X) = \frac{\sigma^2}{n}$
$\sigma/\sqrt{n}$ 为样本均值的标准误
样本均值的标准误就是样本均值分布的标准差
$\sigma$ 是一次观察分布的标准差
样本均值要比一次观察变化小因此除以$\sqrt{n}$
样本方差
$S^2 = \frac{\sum_{i=1}^n (X_i - \bar X)^2}{n-1}$
总体方差 $\sigma^2$的估计
计算 $\sum_{i=1}^n (X_i - \bar X)^2 = \sum_{i=1}^n X_i^2 - n \bar X^2$
均值偏差平方的均值
样本方差是总体方差的无偏估计 \[ \begin{eqnarray*} E\left[\sum_{i=1}^n (X_i - \bar X)^2\right] & = & \sum_{i=1}^n E\left[X_i^2\right] - n E\left[\bar X^2\right] \\ \\ & = & \sum_{i=1}^n \left\{Var(X_i) + \mu^2\right\} - n \left\{Var(\bar X) + \mu^2\right\} \\ \\ & = & \sum_{i=1}^n \left\{\sigma^2 + \mu^2\right\} - n \left\{\sigma^2 / n + \mu^2\right\} \\ \\ & = & n \sigma^2 + n \mu ^ 2 - \sigma^2 - n \mu^2 \\ \\ & = & (n - 1) \sigma^2 \end{eqnarray*} \]
澄清
假定 $X_i$ 是 iid 均值 $\mu$ 方差 $\sigma^2$
$S^2$ 估计 $\sigma^2$
$S^2$ 的计算涉及除 $n-1$
$S / \sqrt{n}$ 估计 $\sigma / \sqrt{n}$ 是均值的标准误

7.6 条件概率

$B$ 为一个事件有 $P(B) > 0$
$B$ 出现条件下 $A$ 的条件概率为 $P(A ~|~ B) = \frac{P(A \cap B)}{P(B)}$
如果 $A$ 与 $B$ 独立有 $P(A ~|~ B) = \frac{P(A) P(B)}{P(B)} = P(A)$

7.7 贝叶斯定理

\[ P(B ~|~ A) = \frac{P(A ~|~ B) P(B)}{P(A ~|~ B) P(B) + P(A ~|~ B^c)P(B^c)}. \]

2*2 列联表 - 诊断测试

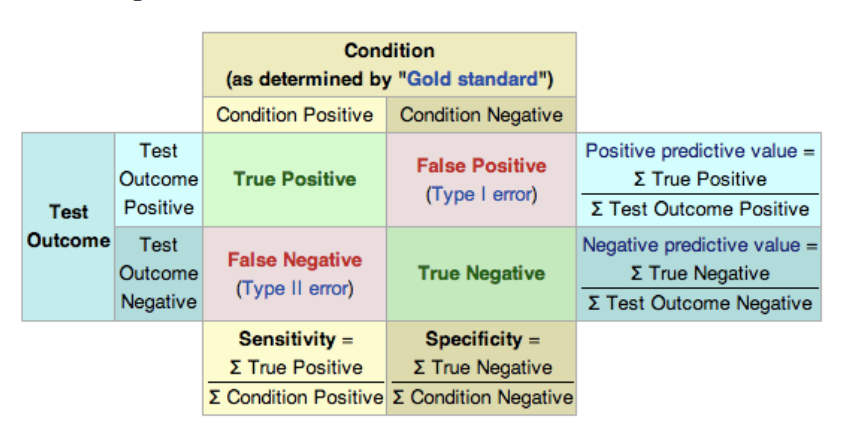
7.8 常见分布

贝努力分布
二元输出变量
数值为0或1 概率$p$ 与 $1-p$
$X$的PMF是$P(X = x) = p^x (1 - p)^{1 - x}$
均值 $p$ 方差 $p(1 - p)$
如果有iid的贝努力观察$x_1,\ldots, x_n$ 似然函数 $\prod_{i=1}^n p^{x_i} (1 - p)^{1 - x_i} = p^{\sum x_i} (1 - p)^{n - \sum x_i}$
似然函数依赖$x_i$的和 $\sum_i x_i / n$ 包含了所有 $p$ 的可能性
最大化似然函数可以得到 $p$ 的估计
二项分布
PMF \[ P(X = x) = \left( \begin{array}{c} n \\ x \end{array} \right) p^x(1 - p)^{n-x} \] 对于 $x=0,\ldots,n$
正态分布
PDF $(2\pi \sigma^2)^{-1/2}e^{-(x - \mu)^2/2\sigma^2}$
$X$ 为均值 $E[X] = \mu$ 方差 $Var(X) = \sigma^2$ 的iid随机变量
写作$X\sim \mbox{N}(\mu, \sigma^2)$
均值 $\mu = 0$ 方差 $\sigma = 1$ 是标准正态分布
标准正态函数写作 $\phi$
标准正态随机变量用 $Z$ 表示
如果 $X \sim \mbox{N}(\mu,\sigma^2)$ 并且 $Z = \frac{X -\mu}{\sigma}$ 是标准正态函数
如果 $Z$ 是标准正态函数 $X = \mu + \sigma Z \sim \mbox{N}(\mu, \sigma^2)$
非标准正态密度函数 $\phi\{(x - \mu) / \sigma\}/\sigma$
正态似然函数对方差的估计是有偏的
正态的和是正态样本均值正态
正态的平方是卡方
泊松分布
PMF $P(X = x; \lambda) = \frac{\lambda^x e^{-\lambda}}{x!}$
均值方差均为 $\lambda$
可看做很短时间间隔中发生事件的概率模拟速率其中$\lambda * h$小于1 则各时间段独立
$X \sim Poisson(\lambda t)$ $\lambda = E[X / t]$是速率 $t$ 是总时间
$n$ 大 $p$ 小是对二项分布的模拟
$X \sim \mbox{Binomial}(n, p)$, $\lambda = n p$

7.9 渐进

样本接近无穷大时统计量的行为
频率派的基石
大数理论（LLN）样本数量越多均值接近期望
中心极限理论 (CLT) iid 变量均值的分布标准化后随样本数增加接近标准正态分布 \[ \frac{\bar X_n - \mu}{\sigma / \sqrt{n}} = \frac{\mbox{Estimate} - \mbox{Mean of estimate}}{\mbox{Std. Err. of estimate}} \]
可根据变量分布来知道均值方差计算出样本均值标准误就可以根据CLT计算逼近的统计量
置信区间
根据CLT随机区间$\bar X_n \pm z_{1-\alpha/2}\sigma / \sqrt{n}$ 包括 $\mu$ 的概率逼近于 100$(1-\alpha)$% $z_{1-\alpha/2}$为标准正态分布$1-\alpha/2$的分位数 $100(1 - \alpha)$% 为置信区间 $\sigma$ 可用样本估计 $s$ 来近似
估计是基于分布假设的如果分布有解析解则置信区间可以更准确的得到估计
先生成不依赖参数的统计量
根据统计量的概率分布计算参数的边界

7.10 T 置信区间

卡方分布
假定 $S^2$ 是来自$n$个 iid $N(\mu,\sigma^2)$ 数据样本的方差有$\frac{(n - 1) S^2}{\sigma^2} \sim \chi^2_{n-1}$ 符合自由度$n-1$的卡方分布
不对称分布
均值是自由度方差是两倍的自由度
方差的置信区间 \[ \begin{eqnarray*} 1 - \alpha & = & P \left( \chi^2_{n-1, \alpha/2} \leq \frac{(n - 1) S^2}{\sigma^2} \leq \chi^2_{n-1,1 - \alpha/2} \right) \\ \\ & = & P\left(\frac{(n-1)S^2}{\chi^2_{n-1,1-\alpha/2}} \leq \sigma^2 \leq \frac{(n-1)S^2}{\chi^2_{n-1,\alpha/2}} \right) \\ \end{eqnarray*} \]
$\left[\frac{(n-1)S^2}{\chi^2_{n-1,1-\alpha/2}}, \frac{(n-1)S^2}{\chi^2_{n-1,\alpha/2}}\right]$ 是 $\sigma^2$ 的 $100(1-\alpha)\%$ 置信区间
依赖正态性假设开方后得到 $\sigma$ 的置信区间
Gosset的 t 分布
比正态分布尾厚
考虑自由度自由度大时接近正态分布
$\frac{Z}{\sqrt{\frac{\chi^2}{df}}}$
假定 $(X_1,\ldots,X_n)$ 是 iid $N(\mu,\sigma^2)$ 有 $\frac{\bar X - \mu}{\sigma / \sqrt{n}}$ 是标准正态分布 $\sqrt{\frac{(n - 1) S^2}{\sigma^2 (n - 1)}} = S / \sigma$ 是卡方除以自由度的开方
有 \[ \frac{\frac{\bar X - \mu}{\sigma /\sqrt{n}}}{S/\sigma} = \frac{\bar X - \mu}{S/\sqrt{n}} \] 服从自由度$n-1$的$t$分布
均值的置信区间 \[ \begin{eqnarray*} & & 1 - \alpha \\ & = & P\left(-t_{n-1,1-\alpha/2} \leq \frac{\bar X - \mu}{S/\sqrt{n}} \leq t_{n-1,1-\alpha/2}\right) \\ \\ & = & P\left(\bar X - t_{n-1,1-\alpha/2} S / \sqrt{n} \leq \mu \leq \bar X + t_{n-1,1-\alpha/2}S /\sqrt{n}\right) \end{eqnarray*} \] $t_{df,\alpha}$ 是t分布的 $\alpha^{th}$ 分位数自由度 $df$
t检验不适合有偏分布置信区间中心也不在均值上

7.11 似然函数

一组数据的似然函数是数据固定下参数的联合概率密度函数
似然函数可用来估计参数是参数的函数
似然函数比估计两个可能参数值的可能性
给定模型与数据似然函数包含所有参数可能性
样本独立时参数的似然函数是各独立样本似然函数的乘积
参数使似然函数概率取最大值时真实的可能性更大更支持这组数据这个估计是最大似然估计（MLE）

7.12 贝叶斯推断

$\mbox{Posterior} \propto \mbox{Likelihood} \times \mbox{Prior}$
先验beta分布
01之间
依赖 $\alpha$ $\beta$ 的概率密度函数 \[ \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} p ^ {\alpha - 1} (1 - p) ^ {\beta - 1} ~~~~\mbox{for} ~~ 0 \leq p \leq 1 \]
均值 $\alpha / (\alpha + \beta)$
方差 $\frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}$
$\alpha = \beta = 1$ 为均匀分布
后验beta分布
参数$\tilde \alpha = x + \alpha$ $\tilde \beta = n - x + \beta$ 的beta分布 \[ \begin{align} \mbox{Posterior} &\propto p^x(1 - p)^{n-x} \times p^{\alpha -1} (1 - p)^{\beta - 1} \\ & = p^{x + \alpha - 1} (1 - p)^{n - x + \beta - 1} \end{align} \]
后验均值 \[ \begin{align} E[p ~|~ X] & = \frac{\tilde \alpha}{\tilde \alpha + \tilde \beta}\\ \\ & = \frac{x + \alpha}{x + \alpha + n - x + \beta}\\ \\ & = \frac{x + \alpha}{n + \alpha + \beta} \\ \\ & = \frac{x}{n} \times \frac{n}{n + \alpha + \beta} + \frac{\alpha}{\alpha + \beta} \times \frac{\alpha + \beta}{n + \alpha + \beta} \\ \\ & = \mbox{MLE} \times \pi + \mbox{Prior Mean} \times (1 - \pi) \end{align} \]
后验均值是先验均值与最大似然估计的混合
当 $n$ 变大 $\pi$ 接近 $1$ 先验作用小
当 $n$ 很小先验作用大
当数据量够大时先验概率作用就很小了
当先验概率足够稳定数据就作用不大了
信任区间
$95\%$ 信任区间 $[a, b]$ 会满足$P(p \in [a, b] ~|~ x) = .95$
最高后验密度 (HPD) 区间

7.13 两独立样本t检验

$X_1,\ldots,X_{n_x}$ 为 iid $N(\mu_x,\sigma^2)$
$Y_1,\ldots,Y_{n_y}$ 为 iid $N(\mu_y, \sigma^2)$
$\bar X$, $\bar Y$, $S_x$, $S_y$ 为均值与标准差
根据均值与方差的线性组合有 $\bar Y - \bar X$ 也是正态均值 $\mu_y - \mu_x$ 方差 $\sigma^2 (\frac{1}{n_x} + \frac{1}{n_y})$
混合方差为 $S_p^2 = \{(n_x - 1) S_x^2 + (n_y - 1) S_y^2\}/(n_x + n_y - 2)$ 为$\sigma^2$的良好估计
该估计为无偏估计 \[ \begin{eqnarray*} E[S_p^2] & = & \frac{(n_x - 1) E[S_x^2] + (n_y - 1) E[S_y^2]}{n_x + n_y - 2}\\ & = & \frac{(n_x - 1)\sigma^2 + (n_y - 1)\sigma^2}{n_x + n_y - 2} \end{eqnarray*} \]
该估计独立于 $\bar Y - \bar X$ 因为方差独立于均值
两个独立的卡方变量之和是自由度之和的卡方值 \[ \begin{eqnarray*} (n_x + n_y - 2) S_p^2 / \sigma^2 & = & (n_x - 1)S_x^2 /\sigma^2 + (n_y - 1)S_y^2/\sigma^2 \\ \\ & = & \chi^2_{n_x - 1} + \chi^2_{n_y-1} \\ \\ & = & \chi^2_{n_x + n_y - 2} \end{eqnarray*} \]
构建统计量 \[ \frac{\frac{\bar Y - \bar X - (\mu_y - \mu_x)}{\sigma \left(\frac{1}{n_x} + \frac{1}{n_y}\right)^{1/2}}}{\sqrt{\frac{(n_x + n_y - 2) S_p^2}{(n_x + n_y - 2)\sigma^2}}} = \frac{\bar Y - \bar X - (\mu_y - \mu_x)}{S_p \left(\frac{1}{n_x} + \frac{1}{n_y}\right)^{1/2}} \]
该统计量为符合自由度 $n_x + n_y - 2$ 的 $t$ 分布
置信区间 \[ \bar Y - \bar X \pm t_{n_x + n_y - 2, 1 - \alpha/2}S_p\left(\frac{1}{n_x} + \frac{1}{n_y}\right)^{1/2} \]
方差不等 \[ \bar Y - \bar X \sim N\left(\mu_y - \mu_x, \frac{s_x^2}{n_x} + \frac{s_y^2}{n_y}\right) \]
统计量 \[ \frac{\bar Y - \bar X - (\mu_y - \mu_x)}{\left(\frac{s_x^2}{n_x} + \frac{s_y^2}{n_y}\right)^{1/2}} \] 近似于自由度 \[ \frac{\left(S_x^2 / n_x + S_y^2/n_y\right)^2} {\left(\frac{S_x^2}{n_x}\right)^2 / (n_x - 1) + \left(\frac{S_y^2}{n_y}\right)^2 / (n_y - 1)} \] 的$t$分布

7.14 假设检验

使用数据做决定
空假设 $H_0$ 无变化
备择假设 $H_a$ 或大或小或不等
真值表

Truth	Decide	Result
$H_0$	$H_0$	Correctly accept null
$H_0$	$H_a$	Type I error
$H_a$	$H_a$	Correctly reject null
$H_a$	$H_0$	Type II error

Z检验
Z检验 $H_0:\mu = \mu_0$ 与
- $H_1: \mu < \mu_0$
- $H_2: \mu \neq \mu_0$
- $H_3: \mu > \mu_0$
检验统计量 $TS = \frac{\bar{X} - \mu_0}{S / \sqrt{n}}$
拒绝空假设条件
- $TS \leq -Z_{1 - \alpha}$
- $|TS| \geq Z_{1 - \alpha / 2}$
- $TS \geq Z_{1 - \alpha}$
样本数要足够否则选 $t$ 检验
通过 $\alpha$ 控制了 Type I error 但没控制 $\beta$ Type II error 所以结论为没有拒绝 $H_0$ 而不是接受 $H_0$
拒绝 $H_0$ 的值域为拒绝域
二项分布不易做正态假设可精确计算拒绝域

7.15 P 值

假定没有事发生出现状况的可能性
先定义分布然后计算相关统计量对比常见阈值看数值是否够极端
阈值为达到显著性水平与p值有区别
p值可设定任意显著性水平小于就可以拒绝
两尾检验单尾概率翻倍
独立于假设检验但常常一起使用

7.16 功效

错误拒绝空假设的概率为功效（power）
Power $= 1 - \beta$ 对 Type II error 的控制
正态分布假设下的推导 \[ \begin{align} 1 -\beta & = P\left(\frac{\bar X - 30}{\sigma /\sqrt{n}} > z_{1-\alpha} ~|~ \mu = \mu_a \right)\\ & = P\left(\frac{\bar X - \mu_a + \mu_a - 30}{\sigma /\sqrt{n}} > z_{1-\alpha} ~|~ \mu = \mu_a \right)\\ \\ & = P\left(\frac{\bar X - \mu_a}{\sigma /\sqrt{n}} > z_{1-\alpha} - \frac{\mu_a - 30}{\sigma /\sqrt{n}} ~|~ \mu = \mu_a \right)\\ \\ & = P\left(Z > z_{1-\alpha} - \frac{\mu_a - 30}{\sigma /\sqrt{n}} ~|~ \mu = \mu_a \right)\\ \\ \end{align} \]

sigma <- 10; mu_0 = 0; mu_a = 2; n <- 100; alpha = .05
plot(c(-3, 6),c(0, dnorm(0)), type = "n", frame = F, xlab = "Z value", ylab = "")
xvals <- seq(-3, 6, length = 1000)
lines(xvals, dnorm(xvals), type = "l", lwd = 3)
lines(xvals, dnorm(xvals, mean = sqrt(n) * (mu_a - mu_0) / sigma), lwd =3)
abline(v = qnorm(1 - alpha))

- 计算步骤 - 考虑 $H_0 : \mu = \mu_0$ 与 $H_a : \mu > \mu_0$ 且在$H_a$下 $\mu = \mu_a$ - 在 $H_0$ 下统计量 $Z = \frac{\sqrt{n}(\bar X - \mu_0)}{\sigma}$ 符合 $N(0, 1)$ - 在$H_a$下 $Z$ 是 $N\left( \frac{\sqrt{n}(\mu_a - \mu_0)}{\sigma}, 1\right)$ - 如果 $Z > Z_{1-\alpha}$ 拒绝空假设也就是给定条件下功效不够 - 当检验 $H_a : \mu > \mu_0$, 如果功效为 $1 - \beta$ 那么 $1 - \beta = P\left(Z > z_{1-\alpha} - \frac{\mu_a - \mu_0}{\sigma /\sqrt{n}} ~|~ \mu = \mu_a \right) = P(Z > z_{\beta})$ 也就是 $z_{1-\alpha} - \frac{\sqrt{n}(\mu_a - \mu_0)}{\sigma} = z_{\beta}$ - $\mu_a$, $\sigma$, $n$, $\beta$, $\mu_0$, $\alpha$ 给定五个可解出剩余的 - 两尾检验考虑 $\alpha / 2$ - 功效在 $\alpha$ 提高单尾检验功效高于两尾 $\mu_1$ 距离 $\mu_0$ 远功效大样本数提高功效高 - 计算功效不需要特定样本只需要指定 $\frac{\mu_a - \mu_0}{\sigma}$ 也就是有效样本大小无单位 - R 中使用 power.t.test 来计算 $t$ 检验功效相关参数指定多数求一个

7.17 多重比较

多次进行比较会导致错误率与校正出现问题
False positive rate 错误结果是显著的比率 $\alpha$ 样本数增大错误增加
Family wise error rate (FWER) 所有比较中至少一个假阳性比率
Bonferroni correction
假设你进行m次测试控制 $\alpha$ 在某水平计算所有测试的 $p$ 值将 $\alpha$ 设为 $ /m$ 所有测试都在这个置信度下进行
容易计算过于保守
False discovery rate (FDR) 声称显著是错误的概率
$m$ 次测试水平 $\alpha$ 计算 $p$ 值排序 $P_{(i)} \leq \alpha \times \frac{i}{m}$ 为显著
相对容易计算不保守允许一定的假阳性
调节p值
$P_i^{fwer} = \max{m \times P_i,1}$ 类似FWER处理 $\alpha$ 的方式处理 $p$ 按照正常 $\alpha$ 检测
一般情况对 $p$ 值用 bonferroni/BH矫正就够了
对比间依赖强烈考虑 method=“BY”
多重比较从原理到应用从实用角度分类适合常见科研实验结果处理

7.18 重采样推断

jackknife
用来无偏估计偏差与标准误
每次估计删掉一个数据 $\bar \theta = \frac{1}{n}\sum_{i=1}^n \hat \theta_{i}$
偏差 $(n - 1) \left(\bar \theta - \hat \theta\right)$
标准误 $\left[\frac{n-1}{n}\sum_{i=1}^n (\hat \theta_i - \bar\theta )^2\right]^{1/2}$
可用来估计分位数是bootstrap的线性逼近但性质不好
假观察量角度理解jackknife $\mbox{Pseudo Obs} = n \hat \theta - (n - 1) \hat \theta_{i}$ 生成原数据集
bootstrap
构建置信区间与求标准误
假定采样分布是总体分布重采样估计统计量
有放回的重采样 $B$ 次 $N$ 个样本得到估计统计量的一个分布直接计算置信区间
非参方法偏差小进阶指南
置换检验
分组对比时取消原分组随机分组
重复进行记录分组差异
对比原参数与置换后参数差异进行推断

Truth	Decide	Result
\(H_0\)	\(H_0\)	Correctly accept null
\(H_0\)	\(H_a\)	Type I error
\(H_a\)	\(H_a\)	Correctly reject null
\(H_a\)	\(H_0\)	Type II error