Chapter 11 偏微分方程
最后更新日期:2020-04-29
本课程于第六学期修读,需要首先掌握高等代数、数学分析、常微分方程等相关知识,点击这里查看常微分方程笔记。
本篇讲讲数学物理方程(偏微分方程)课程开课两个月以来的课程小结. 参考教材: 朱长江, 阮立志. 偏微分方程简明教程.
偏微分方程课程主要讲了什么?
主要内容为对于双曲型、抛物型和椭圆型方程的求解, 这也是教材第四、五、六章的主要内容. 从物理学的角度来看, 它们是波动方程、热传导方程与位势方程.
在讲述实际的求解方法之前, 前三章先从偏微分方程基本概念与偏微分方程的物理与力学来源开始谈起, 介绍偏微分方程的特征理论与变量分离法进行特定形式的求解.
11.1 偏微分方程的若干基本概念
这里我们假定大家已经熟悉常微分方程和数学分析的知识.
11.1.1 偏微分方程的阶数
与常微分方程类似, 偏微分方程的阶数规定为: 方程中所含未知函数的偏导数中的最高阶数. 如方程 \[u_{t}+u u_{x}=u_{x x}\tag{1.1}\] 是二阶方程, 而方程 \[u_{t}+u u_{x}=(u_{x})^3\tag{1.2}\] 是一阶方程. 很多初学者会将式\((1.2)\)误认为是3阶方程, 混淆了阶数与次数的概念, 这是不正确的.
11.1.2 线性与非线性偏微分方程
线性微分方程的定义是: 微分方程中关于未知函数及其各阶偏导数都是线性的. 这一看其实对初学者是有点抽象的, 事实上, 这是要求未知函数及其各阶偏导数都要有系数,且系数仅能直接由各自变量构成, 我们给出下面的例子加以说明: \[u_t-u_{xx}+te^xu=0\tag{1.3}\] 是线性方程, 因为\(u_t\)与\(u_{xx}\)的系数为1, 而\(u\)的系数为\(te^x\), 是直接由自变量\(x\)与\(t\)构成的函数, 因而方程\((1.3)\)是齐次的. 而方程 \[u_t-(u_x)^2=0\tag{1.4}\] 不是线性方程, 问题出在\((u_x)^2\)项上, 该项显然不是线性的.
11.1.3 齐次与非齐次偏微分方程
如果微分方程中的自由项为\(0\), 换句话说, 不含有未知函数\(u\)及其偏导数的项为\(0\), 我们称其为齐次方程, 否则为非齐次方程. 这与常微分方程中的齐次定义一致, 此处不再阐述.
11.1.4 偏微分方程中的常用记号
下列记号是我们经常会遇到的.
Laplace算子\(\Delta\) \[\Delta=\frac{\partial^{2}}{\partial x_{1}^{2}}+\frac{\partial^{2}}{\partial x_{2}^{2}}+\cdots+\frac{\partial^{2}}{\partial x_{n}^{2}}.\] 我们将其称为\(n\)维空间的Laplace算子, 亦可记为\(\Delta_n\).
梯度算子\(\nabla\) \[\nabla=\frac{\partial}{\partial x_1} \bar{i_1}+\frac{\partial}{\partial x_2} \bar{i_2}+\cdots+\frac{\partial}{\partial x_n} \bar{i_n}.\] 梯度在数学分析中也有提到, 在后面几章中我们会用到这些记号.
\(\square\)算子 \[\square u=\frac{\partial^{2} u}{\partial t^{2}}-a^{2} \Delta u.\]
11.1.5 边界条件
边界条件主要分为三类:
第一边界条件(Dirichlet boundary): 给出未知函数在边界上的值, 即形如 \[\left.u\right|_{\Gamma}=\varphi(x, y, z, t)\tag{1.5}\] 第二边界条件(Neumann boundary): 给出未知函数在边界外法线的方向导数, 即形如 \[\left.\frac{\partial u}{\partial \nu}\right|_{\Gamma}=\varphi(x, y, z, t)\tag{1.6}\] 第三边界条件(Robin boundary): 给出未知函数在边界上的函数值和外法线的方向导数的线性组合, 即形如 \[\left.\left(\frac{\partial u}{\partial \nu}+\sigma u\right)\right|_{\Gamma}=\varphi(x, y, z, t)\tag{1.7}\]
关于其他类型的偏微分方程如: 拟线性、半线性、完全非线性偏微分方程, 可以参考教材, 此处亦不再阐述.
11.2 二阶方程的特征方程与方程的分类
本节我们将讨论范围限制在二阶偏微分方程上. 我们先从特征方程与特征曲面说起.
11.2.1 特征方程与特征曲面
对于\(n\)个自变量的二阶线性方程 \[\sum_{i, j=1}^{n} a_{i j} \frac{\partial^{2} u}{\partial x_{i} \partial x_{j}}+\sum_{i=1}^{n} b_{i} \frac{\partial u}{\partial x_{i}}+c u=f\tag{2.1}\] 其中\(a_{ij}=a_{ji}\), \(a,b,c,f\)都为\(x_1,\cdots,x_n\)的已知函数, 我们定义其特征方程为 \[\sum_{i, j=1}^{n} a_{i j} \alpha_{i} \alpha_{j}=0.\tag{2.2}\] 其中\(\alpha_{i}\)为方向余弦, 满足\(\sum_i\alpha_i^2=1\).
定义特征曲面为 \[\sum_{i, j=1}^{n} a_{i j} \frac{\partial G}{\partial x_{i}} \frac{\partial G}{\partial x_{j}}=0.\tag{2.3}\] 特别地, 对于两个自变量\(x,y\)的情形, 有方程 \[au_{xx}+2bu_{xy}+cu_{yy}=F\] 对应特征方程为 \[a\mathrm{d}y^2-2b\mathrm{d}x\mathrm{d}y+c\mathrm{d}x^2=0\tag{2.4}\] 可能看到这里会有一点懵, 不知道做这些是为了什么, 我们下面给出通过特征方程的首次积分诱导出变量替换, 进而把二阶方程化为标准形式的方法.
11.2.2 二阶方程的分类
我们直接给出如下结论:对于如下形式的方程 \[a u_{x x}+2 b u_{x y}+c u_{y y}+d u_{x}+e u_{y}+g u=f\tag{2.5}\] 其中\(a,b,c,d,e,g,f\)都是自变量\(x,y\)的已知函数, 且二阶偏导数连续, \(a,b,c\)不同时为\(0\), 则有判别式 \[\Delta=b^2-ac\tag{2.6}\] 是可逆自变量参数变换下的不变量. (这与微分几何中的第一、第二基本形式类似, 在可容许的参数变换下具有不变性), 并且应当注意与一元二次方程不同, 判别式是\(b^2-ac\)而不是\((2b)^2-ac\).
有了判别式之后, 我们给出二阶方程在二元情况下的分类. 设\(\Omega\subset\mathbb{R}^2\), \((x_0,y_0)\in\Omega\), 则有
若\(\Delta(x_0,y_0)>0\), 则方程\((2.5)\)在\((x_0,y_0)\)处为双曲型偏微分方程. 若在\(\Omega\)内每一点均为双曲型方程, 则称方程\((2.5)\)为双曲型偏微分方程.
若\(\Delta(x_0,y_0)=0\), 则方程\((2.5)\)在\((x_0,y_0)\)处为抛物型偏微分方程. 若在\(\Omega\)内每一点均为抛物型方程, 则称方程\((2.5)\)为抛物型偏微分方程.
若\(\Delta(x_0,y_0)<0\), 则方程\((2.5)\)在\((x_0,y_0)\)处为椭圆型偏微分方程. 若在\(\Omega\)内每一点均为椭圆型方程, 则称方程\((2.5)\)为椭圆型偏微分方程.
若方程\((2.5)\)在\(\Omega\)内某点为椭圆型方程, 在另一点为双曲型方程, 则称方程\((2.5)\)为混合型偏微分方程.
若方程\((2.5)\)在\(\Omega\)内某点为椭圆型方程, 在其余点为抛物型方程, 则称方程\((2.5)\)为退化椭圆型偏微分方程.
若方程\((2.5)\)在\(\Omega\)内某点为双曲型方程, 在其余点为抛物型方程, 则称方程\((2.5)\)为退化双曲型偏微分方程.
多元的情况我们放在下一小节进行分析.
11.2.3 二阶方程的标准型
下面我们通过上一解给出的结论进行二元二阶偏微分方程的标准化. 不妨假设式子\((2.5)\)中的数\(a,b,c,d,e,f\)均为常数.
若\(\Delta>0\), 则令\(\lambda_1=\frac{b+\sqrt[]{\Delta}}{a}\), \(\lambda_2=\frac{b-\sqrt[]{\Delta}}{a}\), 有首次积分后得到的两族特征线 \[\left\{\begin{array}{l} \varphi(x, y)=y-\lambda_{1} x=c_{1} \\ \psi(x, y)=y-\lambda_{2} x=c_{2} \end{array}\right.\tag{2.7}\] 其诱导了一可逆自变量变换 \[\left\{\begin{array}{l} \xi=\varphi(x, y)=y-\lambda_{1} x \\ \eta=\psi(x, y)=y-\lambda_{2} x \end{array}\right.\tag{2.8}\] 此时方程化为形如 这时方程变成 \[ u_{\xi \eta}=D u_{\xi}+E u_{\eta}+G u+F(\xi, \eta)\tag{2.9} \] 其中\(D,E,G\)都是常数. 我们称这一形式为双曲型方程的第一标准型. 若再引入新的自变量变换 \[\bar{x}=\xi+\eta, \quad \bar{y}=\xi-\eta\tag{2.10}\] 则方程又可化成 \[ u_{\bar{x} \bar{x}}-u_{\bar{y} \bar{y}}=D_{1} u_{\bar{x}}+E_{1} u_{\bar{y}}+G_{1} u+F_{1}(\bar{x}, \bar{y})\tag{2.11} \] 称为第二标准型.
若\(\Delta=0\), 此时仅有一族实特征线\(\varphi(x,y)=y-\frac bax\). 作可逆的自变量变换 \(\xi=\varphi(x, y)=y-\frac{b}{a} x, \eta=\psi(x, y)=y\), 化为 \[ u_{\eta \eta}=D_{2} u_{\xi}+E_{2} u_{\eta}+G_{2} u+F_{2}(\xi, \eta)\tag{2.12} \] 称为抛物型方程的标准型.
若\(\Delta<0\), 此时没有实的特征线, 为此我们令\[ \left\{\begin{array}{l} \bar{\xi}=y-\frac{b}{a} x \\ \bar{\eta}=-\frac{\sqrt{a c-b^{2}}}{a} x \end{array}\right.\tag{2.13} \] 可化为\[ u_{\bar{\xi} \bar{\xi}}+u_{\bar{\eta} \bar{\eta}}=D_{3} u_{\bar{\xi}}+E_{3} u_{\bar{\eta}}+G_{3} u+F_{3}(\bar{\xi}, \bar{\eta})\tag{2.14} \] 该式称为椭圆型方程的标准型.
对于二元情况下, 系数不为常数的二阶偏微分方程, 仍然可以通过对特征线进行如此的变换得到标准型.
下面我们考虑多元的情形, 对于下列形式的方程 \[\sum_{i, j=1}^{n} a_{i j} \frac{\partial^{2} u}{\partial x_{i} \partial x_{j}}+\sum_{i=1}^{n} b_{i}\left(x_{1}, \cdots, x_{n}\right) \frac{\partial u}{\partial x_{i}}+c\left(x_{1}, \cdots, x_{n}\right) u=f\left(x_{1}, \cdots, x_{n}\right)\tag{2.15}\] 通过第一节的分析, 在系数为常数的情况下, 其特征方程为 \[\sum_{i, j=1}^{n} a_{i j} \alpha_{i} \alpha_{j}=0\] 因此我们记 \[\mathcal{D}=\sum_{i, j=1}^{n} a_{i j} \alpha_{i} \alpha_{j}\tag{2.16}\] 为方程\((2.15)\)的特征二次型. 我们有如下结论:
将此二次型进行标准化, 如果标准化后的\(n\)个系数 \(\lambda_{i}(i=1, \cdots, n)\) 全为\(1\)或全是 \(-1,\) 则称方程\((2.15)\)为椭圆型偏微分方程.
如果 \(\lambda_{i}\) 中有一个为 1, \(\quad n-1\) 个为 \(-1,\) 或者一个为 \(-1, \quad n-1\) 个为\(1,\) 则称方程\((2.15)\)为双曲型偏微分方程.
如果\(\lambda_{i}\) 全不为0, 但取1或-1的个数都超过1, 这时我们称方程\((2.15)\)为 超双曲型偏微分方程.
如果\(\lambda_{i}\)中有一个为0, 其余全为1 或全为-1, 则称方程\((2.15)\)为抛物型偏微分方程.
11.3 分离变量法
此处我们直接阐述变量分离法的基本思想与求解方法, 以波动方程为例. 考虑方程 \[\left\{\begin{array}{ll} u_{tt}-a^{2} u_{x x}=0, & 0<x<l, t>0 \\ \left.u\right|_{t=0}=\varphi(x),\left.u_t\right|_{t=0}=\psi(x), & 0 \le x \le l \\ \left.u_{x}\right|_{x=0}=0,\left.\quad u_{x}\right|_{x=l}=0, & t\ge0 \end{array}\right.\tag{3.1}\] 若假设方程具有变量分离形式\(u(x,t)=X(x)T(t)\)形式的特解, 则应当满足 \[\frac{X^{\prime \prime}(x)}{X(x)}=\frac{1}{a^{2}} \frac{T^{\prime \prime}(t)}{T(t)}=-\lambda\tag{3.2}\] 其中\(\lambda\)为常数. 对于非零解有\(T(t)\neq0\), 则得到子问题 \[\left\{\begin{array}{l} X^{\prime \prime}(x)+\lambda X(x)=0 \\ X(0)=X(l)=0 \end{array}\right.\tag{3.3}\] 进一步分析可得到, 若要得到非平凡解, 则仅当\(\lambda>0\)时才可取得. 此时我们将问题\((3.3)\)解得的特征根\(\{\lambda_k\}\)构造满足\(\lambda=\lambda_k\)时式子\((3.2)\)确定的函数\(X\)和\(T\), 进而解出一个解\(u_k(x,t)=X_k(x)T_k(t)\). 再考虑当解取 \[u(x,t)=\sum_{k=1}^\infty u_k(x,t)\]时确定各\(u_k(x,t)\)中的待定参数, 便可以得到形式上的解, 再通过验证一致收敛性表明此时得到的解即为原问题的解, 因而成功进行求解.
我们通过一道习题进行说明.


11.4 Duhamel原理
对于一般的方程, 其相比于\((3.3)\)还增加了自由项和初值条件, 下面我们来分析这时候的处理办法. 为了简单起见,我们考虑一维波动方程的混合问题 \[\left\{\begin{array}{ll}u_{t t}-a^{2} u_{x x}=f(x, t), \quad 0<x<l,\ t>0 \\ u(x, 0)=\varphi(x),\quad u_{t}(x, 0)=\psi(x), \quad 0 \leqslant x \leqslant l \\ u(0, t)=\mu_{1}(t), \quad u(l, t)=\mu_{2}(t), \quad t \geqslant 0\end{array}\right.\tag{4.1}\] 首先将边界条件齐次化. 为此构造辅助函数 \[U(x, t)=\mu_{1}(t)+\frac{x}{l}\left(\mu_{2}(t)-\mu_{1}(t)\right)\] 然后作变换 \[v(x, t)=u(x, t)-U(x, t)\] 则函数\(v(x, t)\)满足如下定解问题 \[\left\{\begin{array}{ll}v_{t t}-a^{2} v_{x x}=f_{1}(x, t), & 0<x<l, \quad t>0 \\ \left.v\right|_{t=0}=\varphi_{1}(x),\left.\quad v_{t}\right|_{t=0}=\psi_{1}(x), & 0 \leqslant x \leqslant l \\ \left.v\right|_{x=0}=0,\left.\quad v\right|_{x=l}=0, & t \geqslant 0\end{array}\right.\tag{4.2}\] 下面通过叠加原理, 我们将问题\((4.2)\)其拆分为两个子问题进行求解 \[\left\{\begin{array}{l} v_{t t}-a^{2} v_{x x}=0, \quad 0<x<l, \quad t>0 \\ v(x, 0)=\varphi_{1}(x), \quad v_{t}(x, 0)=\psi_{1}(x), \quad 0 \leqslant x \leqslant l \\ v(0, t)=0, \quad v(l, t)=0, \quad t \geqslant 0 \end{array}\right.\tag{4.3}\] \[\left\{\begin{array}{l} v_{t t}-a^{2} v_{x x}=f_{1}(x, t), \quad 0<x<l, \quad t>0 \\ v(x, 0)=0, \quad v_{t}(x, 0)=0, \quad 0 \leqslant x \leqslant l \\ v(0, t)=0, \quad v(l, t)=0, \quad t \geqslant 0 \end{array}\right.\tag{4.4}\] 而通过Duhamel原理, 若函数\(w(x, t, \tau)\)是混合问题 \[\left\{\begin{array}{ll}w_{t t}-a^{2} w_{x x}=0, \quad 0<x<l, \ t>\tau \\ \left.w\right|_{t=\tau}=0,\left.\quad w_{t}\right|_{t=\tau}=f_{1}(x, \tau),\quad 0 \leqslant x \leqslant l \\ \left.w\right|_{x=0}=0, \left.w\right|_{x=l}=0, \quad t \geqslant \tau\end{array}\right.\] 的解, 则函数 \[v_{2}(x, t)=\int_{0}^{t} w(x, t, \tau) \mathrm{d} \tau\tag{4.5}\] 就是问题\((4.4)\)的解. 因此问题\((4.1)\)总可以化为问题\((4.4)\)的解, 而问题\((4.4)\)可以通过第三章的变量分离法进行求解, 从而这一类问题便得以解决.
11.5 双曲型方程的求解(波动方程)
11.5.1 D’Alembert公式
我们直接给出适用于求解齐次波动方程的D’Alembert公式. 对于如下的定解问题 \[\left\{\begin{array}{ll}u_{t t}-a^{2} u_{x x}=0, \quad -\infty<x<\infty,\ t>0 \\ u(x, 0)=\varphi(x),\quad u_{t}(x, 0)=\psi(x), \quad -\infty<x<\infty \end{array}\right.\tag{5.1}\] 当\(\varphi\in C^2(-\infty,\infty), \psi\in C^1(-\infty,\infty)\)时, 有解 \[u(x, t)=\frac{1}{2}[\varphi(x-a t)+\varphi(x+a t)]+\frac{1}{2 a} \int_{x-a t}^{x+a t} \psi(\tau) \mathrm{d} \tau.\tag{5.2}\] 对于半直线上的情况, \[\left\{\begin{array}{ll} u_{t t}-a^{2} u_{x x}=0, & 0<x<\infty, \quad t>0 \\ \left.u\right|_{t=0}=\varphi(x),\left.\quad u_{t}\right|_{t=0}=\psi(x), & 0 \leqslant x<\infty \\ \left.u\right|_{x=0}=0, \quad t \geqslant 0 \end{array}\right.\tag{5.3}\] 有解 \[\left\{\begin{array}{ll} \frac{1}{2}[\varphi(x-a t)+\varphi(x+a t)]+\frac{1}{2 a} \int_{x-a t}^{x+a t} \psi(\tau) \mathrm{d} \tau, & x\geqslant at \\ \frac{1}{2}[\varphi(x+a t)-\varphi(a t-x)]+\frac{1}{2 a} \int_{a t-x}^{x+a t} \psi(\tau) \mathrm{d} \tau, & 0 \leqslant x<at \end{array}\right.\tag{5.4}\] 对于不是齐次方程的情况, 可以使用Duhamel原理类似地转化为已知的问题, 进而进行求解.
对于三维齐次波动方程的Cauchy问题 \[ \left\{\begin{array}{l} u_{t t}-a^{2}\left(u_{x x}+u_{y y}+u_{z z}\right)=0, \quad-\infty<x, y, z<\infty, \quad t>0 \\ \left.u\right|_{t=0}=\varphi(x, y, z),\left.\quad u_{t}\right|_{t=0}=\psi(x, y, z), \quad-\infty<x, y, z<\infty \end{array}\right.\tag{5.5} \] 通过球面平均法思想, 可得其解为 \[u(x,y,z,t)=\frac{\partial}{\partial t}\left( \frac{1}{4 \pi a^{2} t} \iint_{S_{a t}(M)} \varphi \mathrm{d} S\right)+\frac{1}{4 \pi a^{2} t} \iint_{S_{a t}(M)} \varphi \mathrm{d} S\] 高维非齐次的情况依然可以使用Duhamel原理转化为已知的问题.
11.5.2 一维情形下的依赖区域、决定区域与影响区域
依赖区域: 从D’Alembert公式看出, \(u\)在点\((x, t)\)的值依赖于\(x\)轴上的区间\([x-a t, x+a t]\)上的初始条件,而与其它点上的初始条件无关. 我们称这个区间为点 \((x, t)\)的依赖区域.
决定区域: 在区间\([x_1,x_2]\)上给定初始数据, 其能完全决定区域\(D:\{(x,t)|x_1+at\leqslant x\leqslant x_2-at\ t>0\}\)上解的值, 因此称其为区间\([x_1,x_2]\)的决定区域.
影响区域: 在区间\([x_1,x_2]\)上给定数据, 其能影响到区域\(D:\{(x,t)|x_1-at\leqslant x\leqslant x_2+at,\ t>0\}\)上解的值, 因此称其为区间\([x_1,x_2]\)的影响区域.
对于多维的情况, 可以类似推导.
11.6 抛物型方程的求解(热传导方程)
抛物型方程的求解可以用后文提到的Fourier变换法进行求解, 此处我们使用相似变换法.
对于一维热传导方程的Cauchy问题 \[ \left\{\begin{array}{l} u_{t}-a^{2}u_{x x}=0, \quad-\infty<x<\infty, \quad t>0 \\ \left.u\right|_{t=0}=\varphi(x),\quad -\infty<x<\infty \end{array}\right.\tag{6.1}\] 其有解 \[u(x, t)=\frac{1}{2 a \sqrt{\pi t}} \int_{-\infty}^{\infty} \mathrm{e}^{-\frac{(x-y)^{2}}{4 a^{2} t}} \varphi(y) \mathrm{d} y=\int_{-\infty}^{\infty} G(x-y, t) \varphi(y) \mathrm{d} y\tag{6.2}\]
该公式称为Poisson公式, 其中函数\(G(x,t)\)称为热核函数. 对于非齐次的情形, 我们可以通过Duhamel原理进行求解. 下面我们给出一道习题加深理解. 在这一题中, 巧妙地使用了一个变换, 消去了原始方程中等式右侧的变量\(g(t)u\), 转化为可以使用Duhamel原理进行求解的形式, 虽然方法不唯一, 但是在这一方法中, 该变换是十分重要的.

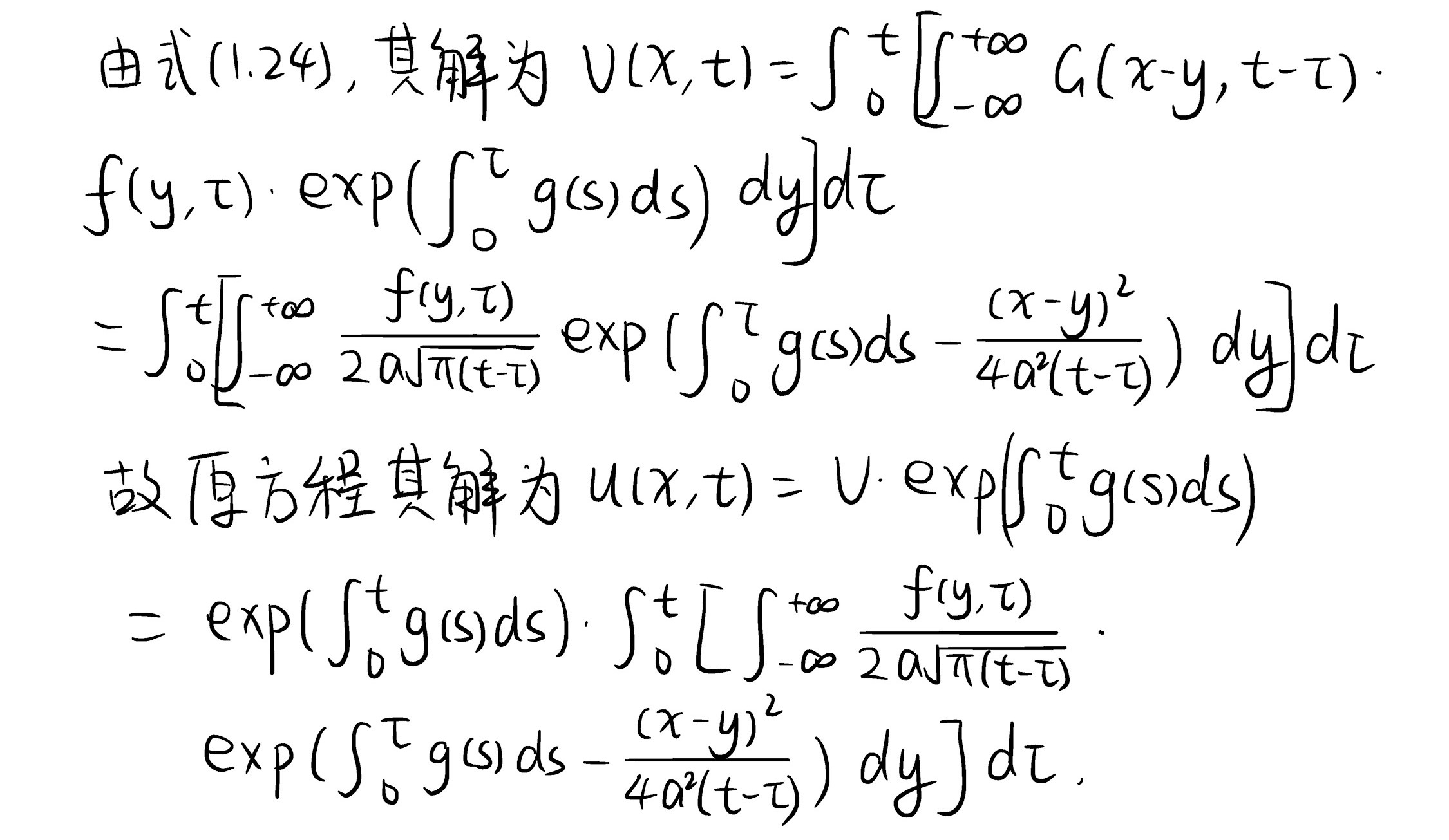
事实上, Poisson公式给出的关于热核函数的卷积积分有时候并不好求, 在实际求解过程中, 也可以考虑进行形如\(\frac{y-x}{2 a \sqrt{t}}=\alpha\)的变换, 得到\(\frac{d y}{2 a \sqrt{t}}=d \alpha\), 再考虑数学分析的方法进行求解, 可能会有较大的计算量.
11.7 椭圆型方程的求解(位势方程)
11.8 Fourier方法
TBA.