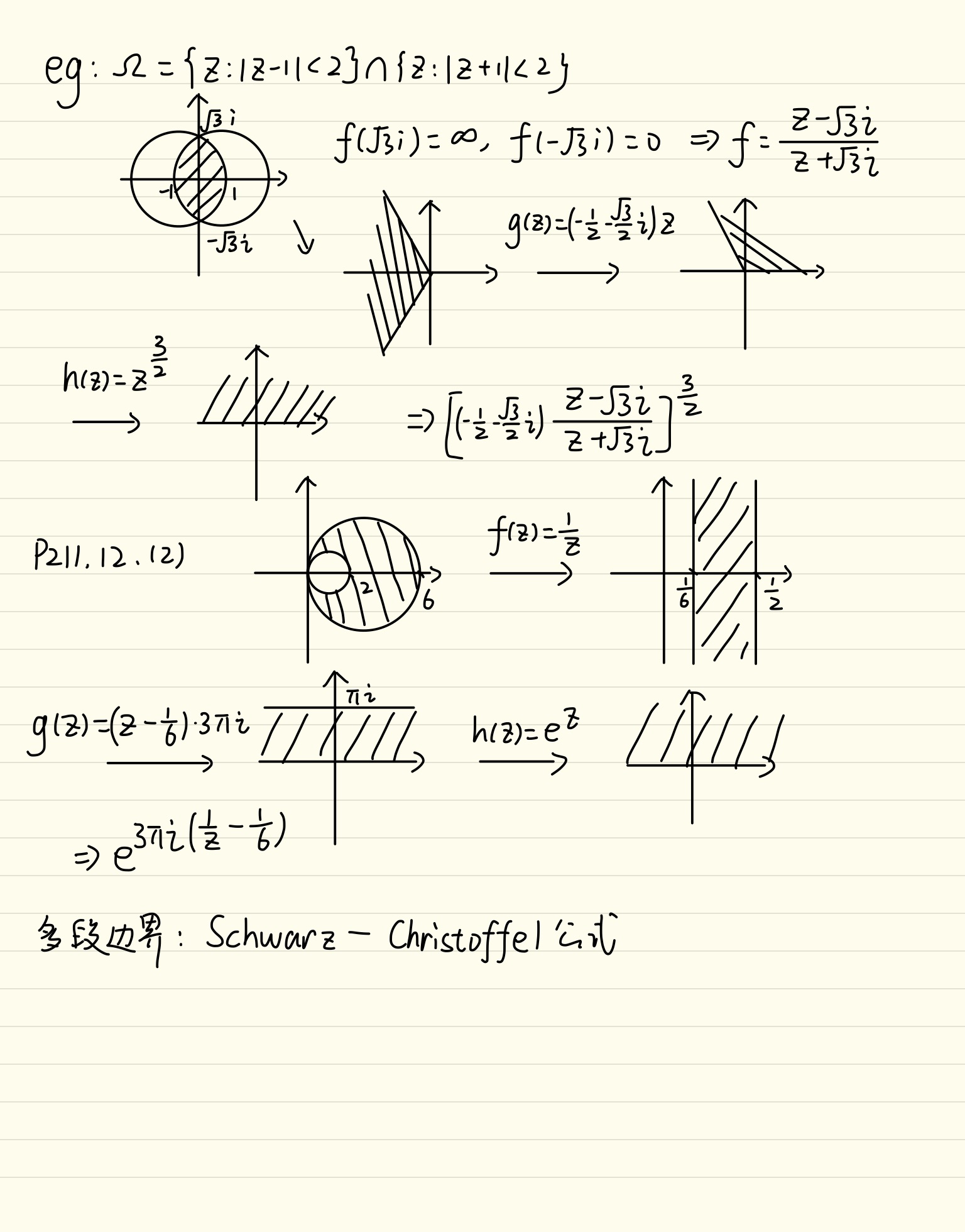
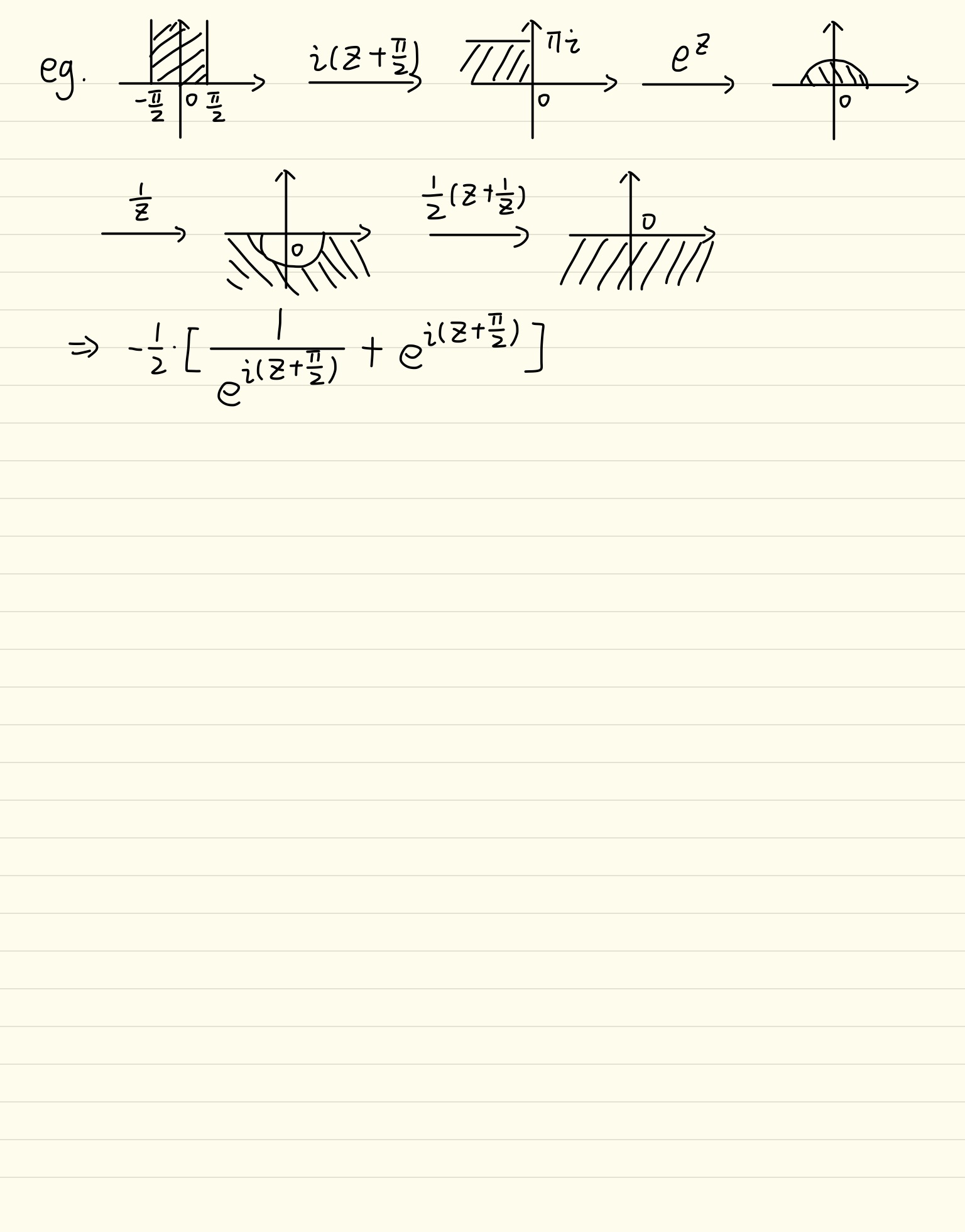Chapter 5 复变函数笔记
最后更新日期:2020-01-05
本课程于第四学期修读,需要首先掌握数学分析相关知识。
复变函数笔记主要内容包括复函数、全纯函数、Cauchy定理、Laurent级数、留数、共性映射等相关知识。


5.1 复函数与复平面的拓扑







5.2 解析函数



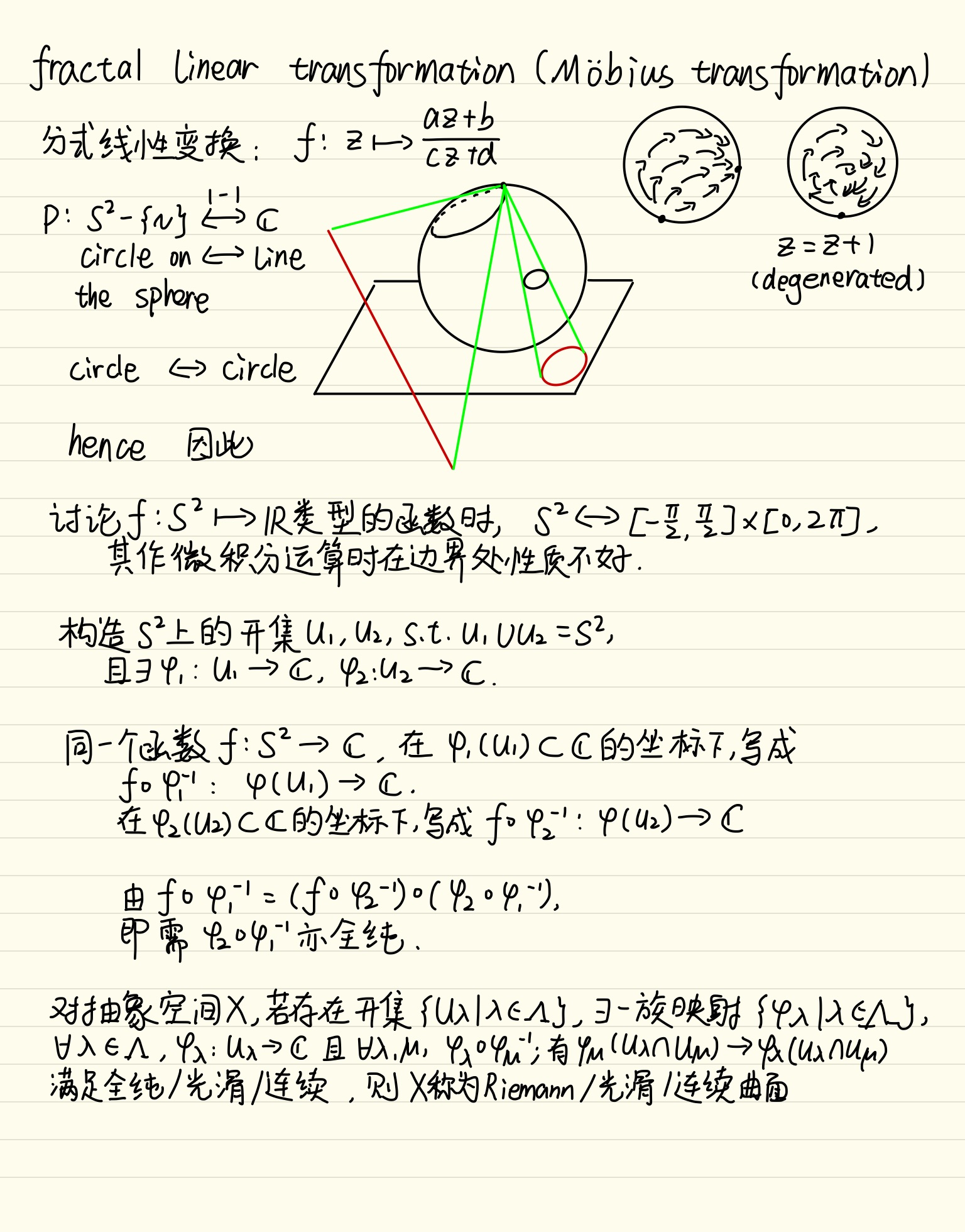








5.3 Cauchy定理












5.4 Laurent级数






5.5 留数


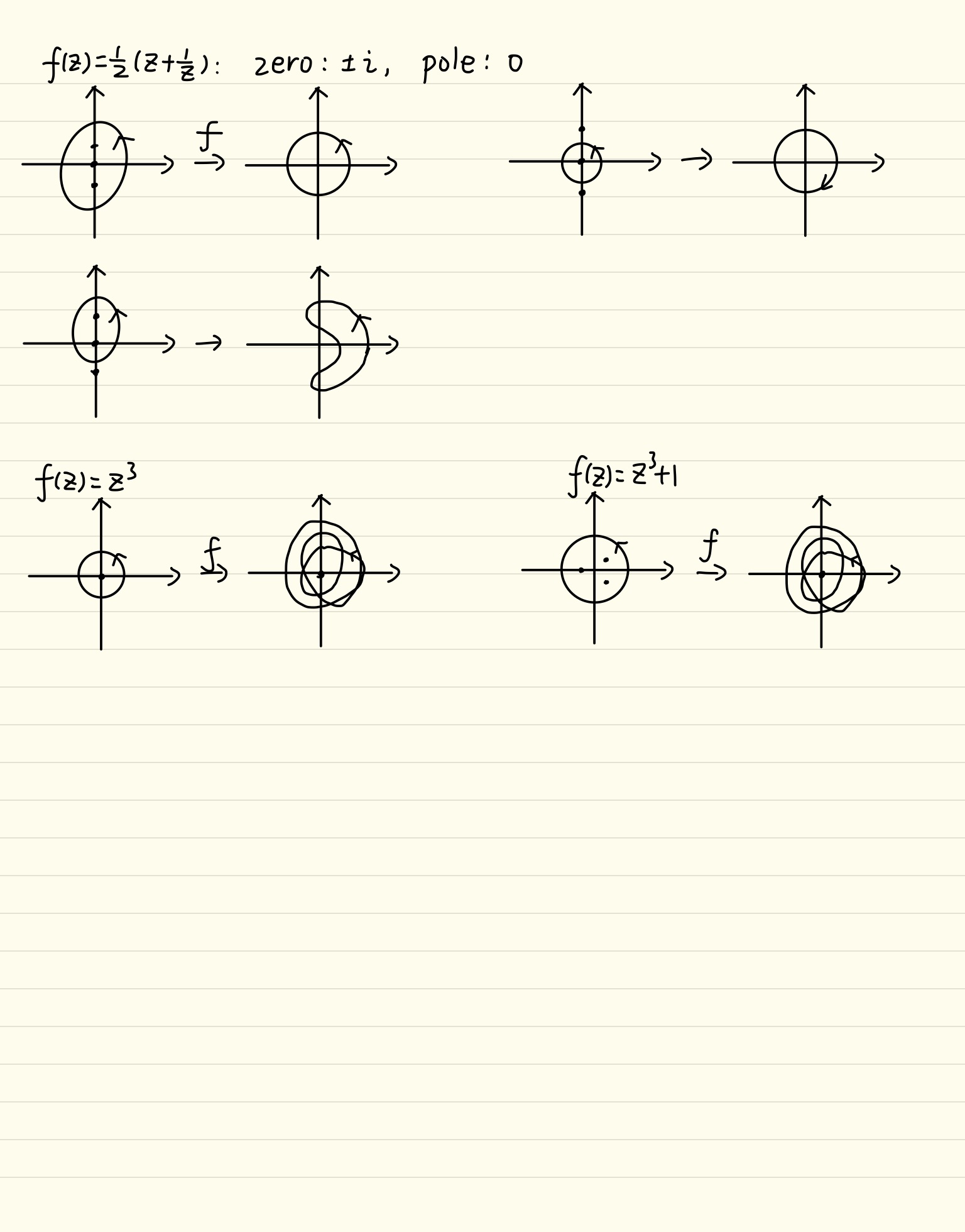

5.6 共形映射